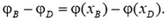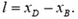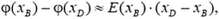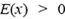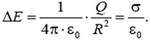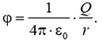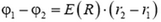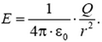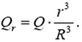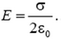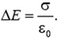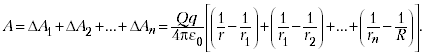Потенциальной диаграммой замкнутого контура называется графическая интерпретация распределения электронного потенциала вдоль замкнутого контура в зависимости от входящих в него сопротивлений.
Потребитель энергии отображается на электрической схеме как резистор с заданным сопротивлением R. Если такое элемент присутствует в участке цепи, то изменение потенциалов на концах участка будет соответствовать падению напряжения на этом резисторе.
Если на участке цепи присутствует источник напряжения, то на концах такого участка также будет наблюдаться разность потенциалов, численно равная ЭДС источника.
Построение потенциальной диаграммы
Бесплатная онлайн программа для построения потенциальной диаграммы.
Для построения потенциальной диаграммы, замкнутый контур разбивается на участки таким образом, чтобы каждый из них содержал только одного потребителя или один источник электроэнергии.
Потенциальная диаграмма строится в декартовой системе координат, где по оси абсцисс откладывается, с соблюдением масштаба, сопротивление участков цепи, а по оси ординат – потенциалы точек. Точки замкнутого контура и сопротивления элементов откладываются (отмечаются на диаграмме) в той последовательности, в которой они встречаются при обходе контура.
В начало координат диаграммы помещается точка, потенциал которой условно выбран нулевым.
Демонстрацию алгоритма и правил построения потенциальной диаграммы выполним на примере замкнутого контура abcdef (точки a и f совпадают), представленного на рисунке 1. Положительное направление обхода контура – по часовой стрелке. Для расчетов примем:
- Е1 = 2 В, Е2 = 3 В;
- R1 = 1 Ом, R2 = 1 Ом, R3 = 2 Ом;
- I1 = 1 А, I2 = 2 А, I3 = 1 А.
Замкнутый контур разбит на участки, каждый из которых содержит либо источник ЭДС, либо резистор.
Примем нулевым потенциал точки а
Следующая точка согласно выбранному направлению движения – b. На участке ab находится источник ЭДС E1. Так как движение на данном участке происходит от отрицательного полюса источника к положительному (направление обхода контура совпадает со стрелкой источника ЭДС), то значение потенциалы на участке повысится на величину E1:
Следующий рассматриваемый участок – bc. На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.
Аналогичные процессы происходят на участках cd и de. Следовательно,
На участке ef находится еще один источник ЭДС E2. Движение по данному участку реализуется от отрицательного полюса к положительному, следовательно потенциал повысится на величину E2
Если направление обхода контура не совпадает с направлением ЭДС, тогда ЭДС записывают со знаком минус
Значения потенциалов в точках а и f совпадают , что подтверждает правильность расчетов.
На основании полученных данных можно построить потенциальную диаграмму (рисунок 2).
По потенциальной диаграмме легко можно найти разность потенциалов между любыми точками электрической цепи.
Бесплатная онлайн программа для построения потенциальной диаграммы.
Как правильно строить потенциальные диаграммы
Содержание
- 1 Что такое потенциал
- 2 Как построить потенциальную диаграмму
- 3 Построение ПД онлайн
- 4 Заключение
- 5 Видео по теме
Потенциальной диаграммой (ПД) называют график, демонстрирующий распределение электропотенциала вдоль некоторого участка электроцепи. ПД строится в декартовых координатах. По оси абсцисс в необходимом масштабе обозначаются электросопротивления, присутствующие в контуре. Ось ординат служит для откладывания электропотенциалов выбранных точек. ПД даёт возможность получить информацию о разности электропотенциалов, то есть электронапряжении между произвольными точками электрической схемы.
Что такое потенциал
Заряженные частицы в электрическом поле приобретают дополнительную, потенциальную энергию W. В результате многочисленных экспериментов было доказано, что эта энергия прямо пропорциональна величине заряда q. Величина, равная частному от деления W на q, называется потенциалом. На рисунке ниже представлены основные формулы, показывающие связь потенциальной энергии W, работы A, совершённой электрическим полем, и зарядом q.
Поскольку электрическое поле является потенциальным, то работа, совершаемая им, не зависит от формы траектории (пути). Поэтому для практического применения важнее понятие разности потенциалов, которое называют напряжением U.
Как построить потенциальную диаграмму
На рисунке ниже показан пример ПД для внешнего контура из нескольких резисторов.
Чтобы построить потенциальную диаграмму, необходимо использовать следующий алгоритм:
- Выбирается замкнутый контур.
- В контуре выделяются участки, где находится либо нагрузка, либо источник тока.
- Потребитель энергии (нагрузка) обозначается на схеме в виде резистора, имеющего конкретное значение сопротивления Rн.
- При наличии в цепи источника напряжения (или источника постоянного тока) разность потенциалов на его концах будет равна электродвижущей силе (ЭДС).
- Точки раздела между участками маркируют либо с помощью цифр, либо букв.
- Одна из точек (любая) «заземляется», то есть ей присваивается электропотенциал равный нулю. Это начальная точка отсчёта всей диаграммы.
- От начальной точки следует перемещаться по контуру по ходу стрелки часов.
- Электропотенциал точки равен сумме электропотенциала предыдущей точки и изменения электропотенциала между данными ближайшими точками.
- На участках, потребляющих электроэнергию, разность электропотенциалов равна падению электронапряжения на Rн. С каким знаком (плюс или минус) будет эта разность, зависит от направления, протекающего на данном участке электротока. Если направление обхода совпадает с направленностью тока, то разность потенциалов берётся с плюсом. Если же направления противоположны, то с минусом.
- После определения электропотенциалов всего набора точек в декартовой системе координат строят ПД. Ось абсцисс служит для нанесения в определенном масштабе значений электросопротивлений (Ом, кОм). Последовательность нанесения должна соответствовать очерёдности, в которой они обозначались при обходе контуров. Ось ординат служит для выбора значений электропотенциалов (вольты).
- ПД «стартует» от нулевого электропотенциала и после полного обхода контура приходит в ту же точку.
На рисунке ниже представлена потенциальная диаграмма замкнутой электрической цепи.
Построение ПД онлайн
В интернете есть сайты, ориентированные на специалистов по электротехнике. На данных ресурсах предлагается (зачастую бесплатно) воспользоваться услугами программного обеспечения, с помощью которого может быть рассчитана потенциальная диаграмма онлайн. Ядром таких программ является графический редактор с библиотекой элементов (резисторов, конденсаторов, индуктивностей, источников электротока).
Чтобы попрактиковаться можно перейти по ссылке: https://clck.ru/ue7zB, там можно начертить свою схему и автоматически её рассчитать.
Чтобы воспользоваться таким приложением, достаточно выполнить следующие шаги:
- «Нарисовать» свою электросхему с помощью библиотеки, встроенной в графический редактор.
- Ввести величины электросопротивлений, ЭДС (или данные источников постоянного электротока).
- Обозначить выбранные контуры.
- Выбрать в меню программы режим, предусматривающий построение потенциальной диаграммы.
- Кликнуть кнопку «Выполнить расчёт».
- Получить на экране монитора или распечатать бумажную версию ПД.
Заключение
Потенциальная электрическая диаграмма позволяет получать полезную информацию о любой точке цепи, находить точки с одинаковым потенциалом (эквипотенциальные), определять напряжение между выбранными точками в схеме. Построение ПД может быть очень полезно при проектировании электрического оборудования, имеющего элементы между которыми присутствует значительная разница потенциалов. Для предотвращения электрического пробоя такие элементы необходимо размещать подальше друг от друга.
Видео по теме
Измерение потенциалов точек электрической цепи и построение потенциальной диаграммы
Электротехника
Электротехника
Страницы работы
7
страниц
(Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
любой ветви схемы можно найти по закону Ома для
участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома,
необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в
котором за неизвестные принимают потенциалы узлов схемы, называют методом
узловых потенциалов.
Допустим, что в схеме n узлов.
Так как любая (одна) точка схемы может быть заземлена без изменения
токораспределения в схеме, то один из узлов схемы можно мысленно заземлить, т.
е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1.
Число неизвестных в методе узловых потенциалов равно
числу уравнений, которые необходимо составить для схемы по первому закону
Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, — один из
основных расчетных приемов. В том случае, когда число узлов без единицы меньше
числа независимых контуров в схеме, данный метод является более экономичным,
чем метод контурных токов.
Вывод основных расчетных уравнений проведем применительно
к схеме рис. 2, в которой три узла. Если узел 3 мысленно заземлить, т. е.
принять =0, то необходимо определить потенциалы
только двух узлов:,.
Запишем уравнения по первому закону Кирхгофа для
независимых узлов, причем токи, направленные к узлу берем со знаком минус, а от
узла – со знаком плюс.
Для первого узла ,
Для второго узла .
Рис. 2. Схема для
расчета по методу узловых потенциалов
Запишем токи по закону Ома:
, , , ,
, .
Подставим токи в уравнения по первому закону Кирхгофа:
,
.
Перепишем уравнения:
,
;
,
;
,
, где ,
, , ,
,
,
G11— сумма проводимостей
ветвей, сходящихся в первом узле,
G12— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G21— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G11— сумма проводимостей
ветвей, сходящихся во втором узле,
I11— узловой ток первого
узла,
I22 — узловой ток второго
узла.
Запишем уравнения в матричной форме:
,
, , .
Решим эти уравнения относительно искомых потенциалов и
выразим токи ветвей, используя закон Ома.
После нахождения токов ветвей любым методом всегда
делается проверка по первому закону Кирхгофа.
Потенциальная диаграмма.
Под потенциальной диаграммой понимают график
распределения потенциала вдоль какого-либо участка цепи или замкнутого контура.
По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо
произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или
замкнутого контура соответствует своя точка на потенциальной диаграмме.
Построим потенциальную диаграмму для контура на рис.3. Пусть R1=10 Ом, R2=5 Ом, R3=15
Ом, E1=20 В, E2=10 В, I=1A.
Рис.3. Контур для
построения потенциальной диаграммы
,
,
,
,
,
.
Построим график.
Рис. 4. Потенциальная
диаграмма для контура на рис.3.
Таблица 1. Исходные
данные
|
Схема |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
E1 |
E2 |
|
|
Рис. |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
В |
В |
|
|
Вариант 1 |
5 |
15 |
10 |
25 |
20 |
10 |
30 |
100 |
60 |
|
Вариант 2 |
6 |
4 |
6 |
3 |
2 |
5 |
6 |
35 |
25 |
|
Вариант 3 |
7 |
5 |
1 |
6 |
4 |
2 |
6 |
10 |
30 |
|
Вариант 4 |
8 |
3 |
6 |
9 |
10 |
6 |
8 |
55 |
40 |
|
Вариант 5 |
5 |
6 |
6 |
8 |
8 |
10 |
12 |
70 |
45 |
|
Вариант 6 |
6 |
4 |
2 |
4 |
5 |
6 |
3 |
15 |
35 |
|
Вариант 7 |
7 |
1 |
2 |
5 |
1 |
3 |
3 |
10 |
15 |
|
Вариант 8 |
8 |
25 |
50 |
15 |
25 |
20 |
30 |
150 |
75 |
Порядок выполнения работы:
1.
схему. Записать данные.
2. Найти токи
ветвей методом контурных токов.
3. Сделать
проверку по первому закону Кирхгофа.
4. Найти токи
ветвей методом узловых потенциалов.
5. Рассчитанные
токи занести в таблицу 2.
Таблица
2
|
I1,A |
I2,A |
I3,A |
I4,A |
I5,A |
I6,A |
|
|
расчет |
||||||
|
эксперимент |
6.
7. Потенциалы точек отмеченных на схеме занести в таблицу
3.
Таблица 3
|
A, B |
B, B |
C, B |
D, B |
F, B |
|
|
расчет |
|||||
|
эксперимент |
8.
схему в программе Electronics Workbench.
9. Измерить
токи во всех ветвях. Для чего в каждую ветвь включить амперметр. Результаты
измерений занести в таблицу 2.
10. Заземлить узел, который
заземляли при расчете по методу узловых потенциалов.
11. Измерить потенциалы точек,
отмеченных на схеме. Результаты занести в таблицу 3.
12. Построить потенциальную
диаграмму заданного контура.
13. Сравнить измеренные данные с
расчетными.
14. Сделать вывод.
Содержание отчета:
1. Тема,
цель, приборы и оборудование.
2. Схема
заданной цепи. Исходные данные.
3. Расчет по
методу контурных токов и методу узловых потенциалов.
4. Заполненная
таблица 2.
5. Проверка
по первому закону Кирхгофа.
6. Баланс
мощностей.
7. Заполненная
таблица 3.
8. Токи
ветвей и потенциалы узлов цепи, измеренные в программе Electronics Workbench .
9. Потенциальная
диаграмма.
10. Вывод.
Вопросы на защиту:
1.
метода контурных токов.
2. Суть
метода узловых потенциалов.
3. Какой
используется закон Кирхгофа для составления уравнений по методу контурных
токов? Сформулировать его.
4. Какой
используется закон Кирхгофа для составления уравнений по методу узловых
потенциалов? Сформулировать его.
5. Как
называется сопротивление R11? Как оно
находится?
6. Как
называется сопротивление R12? Как оно
находится?
7. Что такое
Е11 в матричной записи уравнений по методу контурных токов?
8. Как
находится собственная проводимость узла по методу узловых потенциалов?
9. Матричная
форма записи уравнений по методу узловых потенциалов.
10. Как строится потенциальная
диаграмма контура сложной цепи
Похожие материалы
Информация о работе
Скачать файл
РАСЧЕТ ПОТЕНЦИАЛОВ ТОЧЕК ЦЕПИ — Мегаобучалка
Чтобы найти ток в цепи с несколькими источниками надо:
1) Сложить все Е, направленные в одну сторону;
2) Вычесть все Е, направленные в другую сторону
3) Разделить на сумму всех сопротивлений цепи
Ток течет в сторону большей суммы Е.
Пусть Е1 > Е2, тогда
Если ток и ЭДС совпадают по направлению, то источник работает в режиме генератора, если нет, то в режиме потребителя.
Е1 — генератор; Е2— потребитель
Потенциалом точки цепи называется напряжение между данной точкой и заземлённой.
φ0 = 0
При переходе через источник в режиме генератора потенциал повышается на величину ЭДС минус падение напряжения внутри источника.
φА = φ0 + Е1 — I∙Ri1
При переходе через резистор потенциал понижается на величину падения напряжений в нём:
φВ = φА — I∙R
При переходе через источник в режиме потребителя потенциал понижается на величину ЭДС и на величину падения напряжения внутри источника.
φ0 = φB — E2 — I∙Ri2
Потенциальная диаграмма — это график зависимости потенциалов точек цепи от величины сопротивления цепи.
Рассмотрим построение потенциальной диаграммы на конкретном примере. Одну точку цепи заземляем. Расставляем точки вдоль направления тока. При расчете снова должен получиться равным нулю
Пример решения задачи:
Дано:
Е1 = 25 B
Е2 = 35 В
Е3 = 18 В
Ri1 = 2 Ом
Ri2 = 1 Ом
Ri3 =2 Ом
R1 = 12 Ом
R2 = 5 Ом
R3 = 14 Ом
R4 = 6 Ом
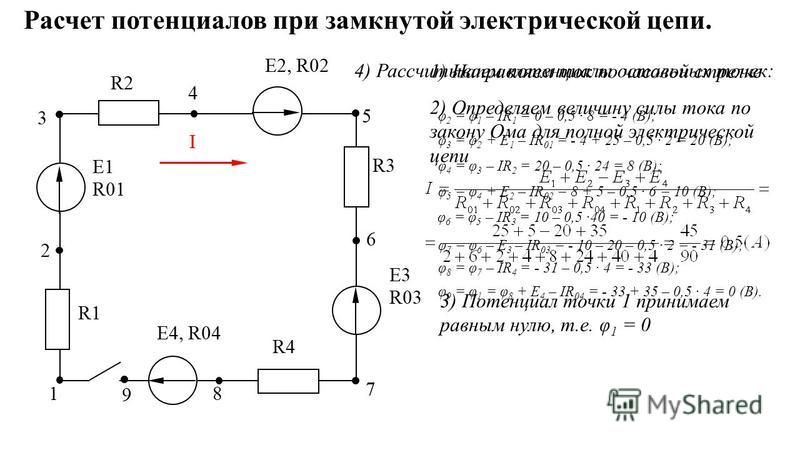
1) Рассчитаем ток в цепи и определяем его направление:
A
2) Рассчитаем потенциалы точек:
φ0 = 0
φ1 = φ0 — I∙R1 = 0 — 12 = -12 B
φ2 = φ1 + Е1 — I∙Ri1 = -12 + 25 — 2 = 11 B
φ3 = φ2 — I∙R2 = 11 — 5 = 6 B
φ4 = φ3 + E2 — I∙Ri2 = 6 + 35 — 1 = 40 B
φ5 = φ4 — E3 — I∙Ri3 = 40 — 18 — 2 = 20 B
φ6 = φ5 — I∙R3 = 20 — 14 = 6 B
φ0 = φ6 — I∙R4 = 6 — 6 = 0
Вывод: При переходе через резистор потенциал понижается плавно, через источник в режиме генератора резко увеличивается, а в режиме потребителя резко уменьшается.
Тестовые задания:
| Задание | Варианты ответов |
| 1.Являются ли напряжение между данной точкой цепи и заземленной потенциалом точки этой цепи? | Да; Нет. |
| 2. Источник работает в режиме генератора если… | а) ЭДС и ток направлены в разные стороны; б) ЭДС и ток направлены в одну сторону. |
РАБОТА ИСТОЧНИКА НА НАГРУЗКУ С ПЕРЕМЕННЫМ СОПРОТИВЛЕНИЕМ.
Построение зависимостей I, U, η = F(R).
Пусть сопротивление нагрузки изменяется от Rкз=0 до Rxx= . Рассмотрим величину тока в трех режимах короткое замыкание, холостой ход и согласованный режим.
1) Iкз = =
2) Iхх =
3)
Вывод 1: с ростом величины сопротивления ток в цепи уменьшается;
Вывод 2: ток максимальный в режиме короткого замыкания;
Рассмотрим величину напряжения в трех режимах
1) Uкз=
2)
3)
Вывод 1: с ростом величины сопротивления напряжение на зажимах источника растет;
Вывод 2: напряжение максимально в режиме Х.
Рассмотрим величину К.П.Д. в трех режимах
Вывод: η стремиться к 1 в режиме Х.Х., но использовать на практике этот режим невозможно, так как цепь разомкнута.
Построение зависимостей Pu, Pн = F(R)
Рассмотрим величину мощности источника в трех режимах
Pu = E∙I = E∙
Вывод: мощность источника максимальна в режиме короткого замыкания.
Рассмотрим величину мощности нагрузки в трех режимах
Исследуя функцию Pн = f(R) на экстремум доказано, что максимальная мощность выделяется в нагрузке при согласованном режиме. Поэтому линии связи и другие устройства работают в этом режиме. И хотя η = 50%, но в слаботочных цепях это не имеет значения.
Тестовые задания:
| Задание | Режим работы | Варианты ответов |
4. Укажите при каких режимах работы перечисленные в ответах величины максимальны. Укажите при каких режимах работы перечисленные в ответах величины максимальны.
|
1) режим холостого хода; 2) режим короткого замыкания; 3) согласованный режим. |
а) мощность источника; б) ток цепи; в) мощность нагрузки напряжение на зажимах источника. |
Калькулятор электрического потенциала
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
Содержание:
- Разность электрических потенциалов
- Что такое электрический потенциал? – Определение электрического потенциала
- Формула электрического потенциала
- Как рассчитать электрический потенциал?
- Как пользоваться калькулятором электрического потенциала
- Единицы измерения электрического потенциала
- Размерная формула электрического потенциала
- Часто задаваемые вопросы
Используйте калькулятор электрического потенциала, чтобы определить электрический потенциал в точке либо за счет одиночного точечного заряда, либо за счет системы точечных зарядов.
Если вы хотите рассчитать электрическое поле, создаваемое точечным зарядом, воспользуйтесь калькулятором электрического поля.
Продолжайте читать эту статью, чтобы узнать:
- Что такое электрический потенциал?
- Какая связь между электрическим потенциалом и электрической потенциальной энергией?
- Как рассчитать электрический потенциал?
- Что такое единица электрического потенциала?
Разность электрических потенциалов
Чтобы понять идею разности электрических потенциалов, рассмотрим некоторое распределение заряда. Это распределение заряда создаст электрическое поле. Теперь, если мы хотим переместить небольшой заряд qqq между любыми двумя точками в этом поле, необходимо совершить некоторую работу против кулоновской силы (вы можете использовать наш калькулятор закона Кулона, чтобы определить эту силу).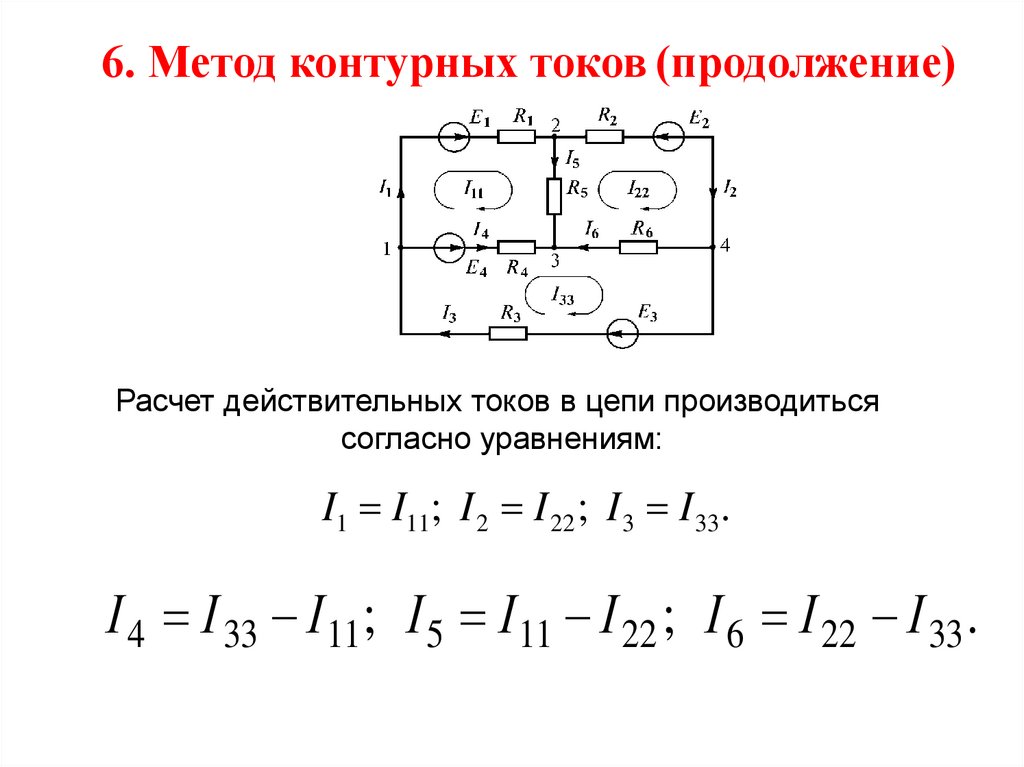
Если мы рассмотрим две произвольные точки, скажем A и B, то выполненная работа (WABW_{AB}WAB) и изменение потенциальной энергии (ΔUDelta UΔU) при перемещении заряда (qqq) из A в B можно записать как:
- WAB=ΔU=(VA−VB)qW_{AB} = Delta U = (V_A — V_B)qWAB=ΔU=(VA−VB)q …… (1)
, где VAV_AVA и VBV_BVB — электрические потенциалы в точках A и B соответственно (мы объясним, что это значит, в следующем разделе).
Если величина qqq равна единице (мы называем положительный заряд единичной величины пробным зарядом), уравнение меняется на:
- ΔV=(VA−VB)=WABq Delta V = (V_A — V_B) = frac{W_{AB}}{q}ΔV=(VA−VB)=qWAB …. .. (2)
Используя приведенное выше уравнение, мы можем определить разность электрических потенциалов (ΔVDelta VΔV) между двумя точками (B и A) как работу, выполненную для перемещения пробного заряда из A в B против электростатической силы .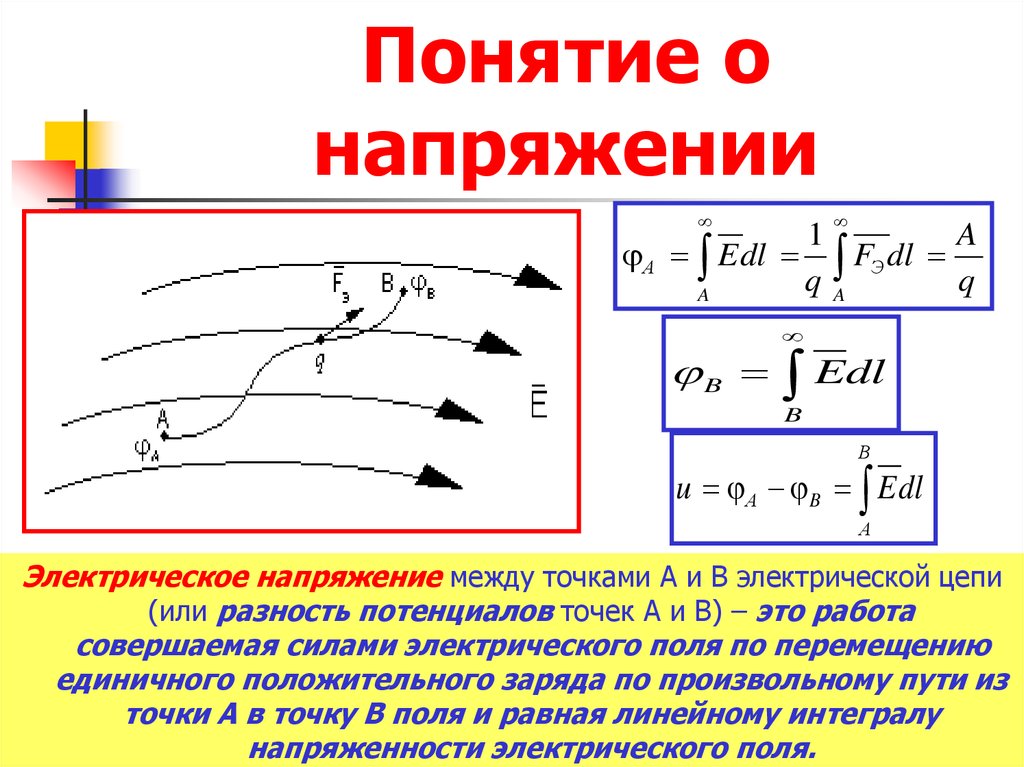
Помните, что потенциальную электрическую энергию нельзя рассчитать по стандартной формуле потенциальной энергии E=mghE=mghE=mgh.
Что такое электрический потенциал? – Определение электрического потенциала
Если мы возьмем одну из точек в предыдущем разделе, скажем, точку A, находящуюся в бесконечности, и выберем потенциал на бесконечности равным нулю, мы можем изменить формулу разности электрических потенциалов (уравнение 2) следующим образом:
- VB=W ∞Бк V_B = frac{W_{infty B}}{q}VB=qW∞B
Следовательно, мы можем определить электрический потенциал в любой точке как количество работы, выполненной при перемещении пробного заряда из бесконечности в эту точку .
Мы также можем определить электрический потенциал как электрическую потенциальную энергию на единицу заряда, т.е.:
- V=ΔUq V = frac{Delta U}{q}V=qΔU
Итак, вы видите, что электрический потенциал и электрическая потенциальная энергия — это не одно и то же.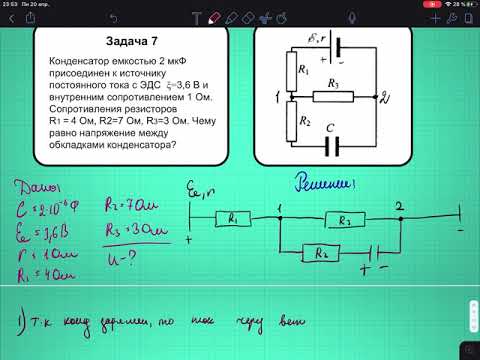
Формула электрического потенциала
Для расчета электрического потенциала в любой точке A от одного точечного заряда (см. рис. 1) воспользуемся формулой:
В=кквscriptsize
V = k frac{q}{r}V=krq
где:
- qqq — электростатический заряд;
- rrr — расстояние между точкой А и точечным зарядом; и
- k=14πϵ0k = frac{1}{4 pi epsilon_0}k=4πϵ01 — постоянная Кулона.
Рис. 1: Электрический потенциал точечного заряда.
Заметим, что когда заряд qqq положителен, электрический потенциал положителен. Когда заряд qqq отрицателен, электрический потенциал отрицателен.
Теперь рассмотрим случай, когда имеются четыре точечных заряда: q1q_1q1, q2q_2q2, q3q_3q3 и q4q_4q4 (см. рис. 2). Потенциал в точке A от заряда q1q_1q1 равен:
V1=kq1r1scriptsize
V_1 = k frac{q_1}{r_1}V1=kr1q1
Рис. 2: Электрический потенциал, обусловленный системой точечных зарядов.
Мы можем написать аналогичные выражения для потенциала в точке A от других зарядов:
V2=kq2r2V3=kq3r3V4=kq4r4scriptsize
начать{выравнивать*}
V_2 &= k frac{q_2}{r_2} \ \
V_3 &= k frac{q_3}{r_3} \ \
V_4 &= k frac{q_4}{r_4}
end{align*}V2V3V4=kr2q2=kr3q3=kr4q4
Чтобы получить результирующий потенциал в точке A, воспользуемся принципом суперпозиции, т.
V=V1+V2+V3+V4V=k(q1r1+q2r2+q3r3+q4r4)размер сценария
начать{выравнивать*}
V &= V_1 + V_2 + V_3 + V_4 \ \
V &= k left (frac{q_1}{r_1} + frac{q_2}{r_2} + frac{q_3}{r_3} + frac{q_4}{r_4}right ) \
end{align*}VV=V1+V2+V3+V4=k(r1q1+r2q2+r3q3+r4q4)
Для системы nnn точечных зарядов результирующий потенциал можно записать в виде: кирискриптсайз
начать{выравнивать*}
V &= V_1 + V_2 + V_3 + …. +V_n \ \
V &= k left (frac{q_1}{r_1} + frac{q_2}{r_2} + frac{q_3}{r_3} + …. +frac{q_n}{r_n}right ) \\
V & = k sum frac{q_i}{r_i}
end{align*}VVV=V1+V2+V3+….+Vn=k(r1q1+r2q2+r3q3+…. +rnqn)=k∑riqi 94 rm В3,6×104 В.
Как пользоваться калькулятором электрического потенциала
Теперь посмотрим, как можно решить ту же задачу с помощью нашего калькулятора электрического потенциала:
-
В раскрывающемся меню выберите электрический потенциал за счет точечного заряда .
-
Введите значение электрического заряда , т. е. 4e−074e-074e−07 и расстояние между точечным зарядом и точкой наблюдения (10 см10 rm см10 см). 94 rm В3,595×104 В.
Единицы электрического потенциала
Единицей электрического потенциала СИ является вольт (В) . Мы можем сказать, что электрический потенциал в точке равен 1 В , если 1 Дж работы совершается при переносе положительного заряда 1 Кл из бесконечности в эту точку против электростатической силы.
Единицей измерения разности потенциалов также является вольт. Возможно, вы более знакомы с напряжением, а не с термином «разность потенциалов». Например, когда мы говорим о 3 В , мы просто имеем в виду, что разность потенциалов между двумя его клеммами составляет 3 В .
💡 Наш калькулятор емкости аккумулятора — это удобный инструмент, который поможет вам узнать, сколько энергии хранится в вашем аккумуляторе.
Размерная формула электрического потенциала
Чтобы написать размерную формулу электрического потенциала (или разности электрических потенциалов), мы сначала напишем уравнение для электрического потенциала:
- V=Wq V = frac{W}{q} V=qW 9{-1}]V=[AT][M1L2T−2]=[M1L2T−3A−1]
Часто задаваемые вопросы
Как рассчитать электрический потенциал точечного заряда?
Для расчета электрического потенциала точечного заряда (q) на расстоянии (r) следуйте приведенным инструкциям:
-
Умножить заряд q на постоянную Кулона .
-
Разделить значение из шаг 1 на расстояние р.
-
Поздравляю! Вы вычислили электрический потенциал точечного заряда.
Может ли электрический потенциал быть отрицательным?
Да , электрический потенциал может быть отрицательным.
Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен.
Что такое разность электрических потенциалов?
Разность электрических потенциалов между двумя точками A и B определяется как работа, совершаемая для перемещения единичного положительного заряда из A в B . Единицей разности потенциалов в системе СИ является вольт (В).
Является ли электрический потенциал скалярной или векторной величиной?
Электрический потенциал является скалярной величиной , поскольку он не имеет направления.
Какова единица измерения электрического потенциала?
Электрический потенциал – электрическая потенциальная энергия на единицу заряда. Единицей электрической потенциальной энергии в системе СИ является джоуль (Дж), а единицы заряда — кулон (Кл). Следовательно, единицей электрического потенциала СИ является Дж/Кл, т. е. вольт (В) .
Чему равен электрический потенциал заряда в точке, удаленной на бесконечность?
Ноль . Электрический потенциал в точке
P, обусловленный зарядомq, обратно пропорционален расстоянию между ними. Следовательно, когда расстояние бесконечно, электрический потенциал равен нулю.Пурнима Сингх, доктор философии
Я хочу вычислить…..
Электрический потенциал
Заряд (q)
Расстояние (r)
Электрический потенциал (В)
Ознакомьтесь с 40 похожими калькуляторами электромагнетизма 🧲
Ускорение частицы в электрическом полеВатт переменного токаЕмкость… еще 37
3.3 Расчеты электрического потенциала – введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Расчет потенциала точечного заряда
- Расчет потенциала системы множественных точечных зарядов
- Описать электрический диполь
- Определить дипольный момент
- Расчет потенциала непрерывного распределения заряда
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи.
Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.
Мы можем использовать исчисление, чтобы найти работу, необходимую для перемещения пробного заряда с большого расстояния на расстояние от точечного заряда. Отмечая связь между работой и потенциалом, как и в предыдущем разделе, мы можем получить следующий результат.
ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
В ТОЧЕЧНЫЙ ЗАРЯД
Электрический потенциал точечного заряда определяется как
(3.3.1)
где постоянная, равная .
Потенциал на бесконечности выбран равным нулю. Таким образом, для точечного заряда уменьшается с расстоянием, тогда как для точечного заряда уменьшается с квадратом расстояния:
Напомним, что электрический потенциал — скаляр и не имеет направления, тогда как электрическое поле — вектор.
Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.
ПРИМЕР 3.3.1
Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов () до микрокулонов (). Каково напряжение вдали от центра твердого металлического шара диаметром, имеющего статический заряд?
Стратегия
Как мы обсуждали в разделе «Электрические заряды и поля», заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение.
Решение
Подставляя известные значения в выражение для потенциала точечного заряда, получаем
Значение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (более отрицательный), чем на больших расстояниях.
И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
ПРИМЕР 3.3.2
Что такое избыточный заряд генератора Ван де Граафа?
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром, которая создает напряжение вблизи ее поверхности (рис. 3.3.1). Какой избыточный заряд находится на шаре? (Предположим, что каждое числовое значение здесь показано с тремя значащими цифрами.)
(рис. 3.3.1)
Рисунок 3.3.1 Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.
Стратегия
Потенциал на поверхности такой же, как и у точечного заряда в центре сферы вдали. (Радиус сферы равен .) Таким образом, мы можем определить избыточный заряд, используя уравнение
Решение
Решение для и ввод известных значений дает
Значение
Это относительно небольшая зарядка, но выдает довольно большое напряжение.
У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.8
Каков потенциал внутри металлической сферы в Примере 3.3.1?
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось ранее, это аналогично уровню моря при рассмотрении потенциальной энергии гравитации.
Системы многоточечных зарядов
Как электрическое поле подчиняется принципу суперпозиции, так и электрический потенциал. Рассмотрим систему, состоящую из зарядов . Каков чистый электрический потенциал в точке пространства от этих зарядов? Каждый из этих зарядов является исходным зарядом, который создает свой собственный электрический потенциал в точке , независимо от того, какие другие изменения могут происходить.
Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку:
Обратите внимание, что электрический потенциал следует тому же принципу суперпозиции, что и электрическое поле и электрическая потенциальная энергия. Чтобы показать это более явно, обратите внимание, что тестовый заряд в точке пространства находится на расстоянии от зарядов, зафиксированных в пространстве выше, как показано на рисунке 3.3.2. Используя нашу формулу потенциала точечного заряда для каждого из этих (предполагаемых точечными) зарядов, находим, что
(3.3.2)
Следовательно, электрическая потенциальная энергия пробного заряда равна
, который аналогичен работе по вводу пробного заряда в систему, описанной в первом разделе главы.
(рис. 3.3.2)
Рисунок 3.3.2 Обозначение прямых расстояний от зарядов до точки пространства.
Электрический диполь
Электрический диполь – это система двух равных, но противоположных зарядов, находящихся на фиксированном расстоянии друг от друга. Эта система используется для моделирования многих систем реального мира, включая атомные и молекулярные взаимодействия. Одной из таких систем является молекула воды при определенных обстоятельствах. Эти обстоятельства встречаются внутри микроволновой печи, где электрические поля переменного направления заставляют молекулы воды менять ориентацию. Эта вибрация аналогична теплу на молекулярном уровне.
ПРИМЕР 3.3.3
Электрический потенциал диполя
Рассмотрим диполь на Рисунке 3.3.3 с величиной заряда и расстоянием разделения . Каков потенциал в следующих местах в космосе? (а) ; (б) ; (с) .
(рис. 3.3.3)
Рисунок 3.
3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
Стратегия
Применить к каждой из этих трех точек.
Решение
а.
б.
в.
Значение
Обратите внимание, что оценка потенциала значительно проще, чем электрического поля, поскольку потенциал является скаляром, а не вектором.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.9
Какой потенциал на -оси? -ось?
Теперь рассмотрим частный случай, когда расстояние точки от диполя много больше, чем расстояние между зарядами в диполе, ; например, когда нас интересует электрический потенциал поляризованной молекулы, такой как молекула воды. Это не так далеко (бесконечность), чтобы мы могли просто считать потенциал равным нулю, но расстояние достаточно велико, чтобы мы могли упростить наши вычисления по сравнению с предыдущим примером.
Начнем с того, что на рис. 3.3.4 потенциал представлен как
.
где
(рис. 3.3.4)
Рисунок 3.3.4 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
Это по-прежнему точная формула. Чтобы воспользоваться тем, что , мы перепишем радиусы в терминах полярных координат, с и . Это дает нам
Мы можем упростить это выражение, вытащив из корня,
, а затем умножить скобки на
.
Последний член в корне достаточно мал, чтобы им можно было пренебречь (помните, что и, следовательно, чрезвычайно мал, фактически равен нулю до уровня, который мы, вероятно, будем измерять), оставляя нам
Использование биномиального приближения (стандартный результат математики рядов, когда небольшое)
и подставив это в нашу формулу для , мы получим
Это может быть записано более удобно, если мы определим новую величину, электрический дипольный момент ,
(3.
3.3)
, где эти векторы указывают от отрицательного заряда к положительному. Обратите внимание, что это имеет величину . Эта величина позволяет нам записать потенциал в точке из-за диполя в начале координат как
.
(3.3.4)
Схема применения этой формулы показана на Рисунке 3.3.5.
(рис. 3.3.5)
Рисунок 3.3.5 Геометрия приложения потенциала диполя.
Существуют также моменты более высокого порядка для квадруполей, октуполей и т. д. Вы увидите их на следующих уроках.
Возможность непрерывного распределения заряда
Мы много работали с точечными зарядами, но как насчет непрерывного распределения заряда? Напомним из уравнения 3.3.2, что
Мы можем рассматривать непрерывное распределение заряда как набор бесконечно малых отдельных точек. Это дает интеграл
(3.3.5)
для потенциала в точке . Обратите внимание, что это расстояние от каждой отдельной точки распределения заряда до точки .
Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны
, где – линейная плотность заряда, – заряд на единицу площади и – заряд на единицу объема.
ПРИМЕР 3.3.4
Потенциал линии заряда
Найдите электрический потенциал однородно заряженного непроводящего провода с линейной плотностью (кулон/метр) и длиной в точке, лежащей на линии, которая делит провод на две равные части.
Стратегия
Для постановки задачи мы выбираем декартовы координаты таким образом, чтобы максимально использовать симметрию в задаче. Поместим начало координат в центр провода и ориентируем -ось вдоль провода так, чтобы концы провода находились в точках . Точка поля находится в -плоскости, и поскольку выбор осей зависит от нас, мы выбираем -ось для прохождения через точку поля, как показано на рисунке 3.3.6.
(рис. 3.3.6)
Рисунок 3.3.6 Мы хотим рассчитать электрический потенциал линии заряда.
Решение
Рассмотрим небольшой элемент распределения заряда между и . Заряд в этой ячейке равен , а расстояние от ячейки до точки поля равно . Таким образом, потенциал становится равным
.
Значение
Обратите внимание, что это было проще, чем эквивалентная задача для электрического поля, из-за использования скалярных величин. Напомним, что мы ожидаем, что нулевой уровень потенциала будет на бесконечности, когда у нас конечный заряд. Чтобы исследовать это, мы берем предел вышеуказанного потенциала по мере приближения к бесконечности; в этом случае члены внутри натурального логарифма стремятся к единице, и, следовательно, потенциал приближается к нулю в этом пределе. Обратите внимание, что мы могли бы решить эту задачу эквивалентно в цилиндрических координатах; единственный эффект будет состоять в том, чтобы заменить на и на .
ПРИМЕР 3.3.5
Потенциал из-за кольца заряда
Кольцо имеет однородную плотность заряда с единицами кулонов на единицу дугового метра.
Найти электрический потенциал в точке на оси, проходящей через центр кольца.
Стратегия
Используем ту же процедуру, что и для заряженного провода. Отличие здесь в том, что заряд распределяется по окружности. Мы делим окружность на бесконечно малые элементы в виде дуг на окружности и используем цилиндрические координаты, показанные на рис. 3.3.7.
(рис. 3.3.7)
Рисунок 3.3.7 Мы хотим рассчитать электрический потенциал из-за кольца заряда.
Решение
Общий элемент дуги между и имеет длину и поэтому содержит заряд, равный . Элемент находится на расстоянии от , и поэтому потенциал равен
Значение
Этот результат ожидаем, поскольку все элементы кольца находятся на одинаковом расстоянии от точки . Чистый потенциал при является потенциалом полного заряда, расположенного на общем расстоянии, .
ПРИМЕР 3.3.6
Потенциал за счет однородного диска заряда
Диск радиусом имеет однородную плотность заряда в единицах кулон-метр в квадрате.
Найти электрический потенциал в любой точке оси, проходящей через центр диска.
Стратегия
Мы делим диск на кольцеобразные ячейки и используем результат для кольца, полученный в предыдущем примере, затем интегрируем по в дополнение к . Это показано на Рисунке 3.3.8.
(рис. 3.3.8)
Рисунок 3.3.8 Мы хотим рассчитать электрический потенциал заряженного диска.
Решение
Ячейка бесконечно малой ширины между цилиндрическими координатами и изображенная на рис. 3.3.8 будет представлять собой кольцо зарядов, электрический потенциал которого в точке поля имеет следующее выражение
где
Суперпозиция потенциалов всех бесконечно малых колец, составляющих диск, дает суммарный потенциал в точке. Это достигается путем интеграции from to :
Значение
Основная процедура для диска состоит в том, чтобы сначала интегрировать , а затем . Это было продемонстрировано для однородной (постоянной) плотности заряда.
Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.
ПРИМЕР 3.3.7
Потенциал из-за бесконечного заряженного провода
Найдите электрический потенциал бесконечно длинного однородно заряженного провода.
Стратегия
Поскольку мы уже рассчитали потенциал провода конечной длины в примере 3.2.4, мы можем задаться вопросом, сработает ли наш предыдущий результат:
Однако этот предел не существует, потому что аргумент логарифма принимает вид , поэтому этот способ нахождения бесконечной проволоки не работает. Причину этой проблемы можно проследить в том, что заряды не локализованы в каком-то пространстве, а продолжаются на бесконечность в направлении провода. Следовательно, наше (негласное) предположение о том, что нулевой потенциал должен находиться на бесконечном расстоянии от провода, больше не имеет силы.
Чтобы избежать этой трудности при вычислении пределов, давайте воспользуемся определением потенциала путем интегрирования по электрическому полю из предыдущего раздела и значением электрического поля из этой конфигурации заряда из предыдущей главы.
Решение
Используем интеграл
, где — конечное расстояние от линии заряда, как показано на рис. 3.3.9.
(рис. 3.3.9)
Рисунок 3.3.9 Точки интереса для расчета потенциала бесконечной линии заряда.
В этой настройке мы используем и для получения
Теперь, если мы определим опорный потенциал при , это упрощается до
Обратите внимание, что эта форма потенциала вполне пригодна для использования; оно находится в бесконечности и не определено в бесконечности, поэтому мы не можем использовать последнее в качестве ссылки.
Значение
Хотя прямой расчет потенциала может быть весьма удобным, мы только что обнаружили систему, для которой эта стратегия не работает. В таких случаях возвращение к определению потенциала с точки зрения электрического поля может предложить путь вперед.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.10
Чему равен потенциал на оси неоднородного кольца заряда, где плотность заряда ?
Цитаты Кандела
Контент под лицензией CC, конкретное указание авторства
- Загрузите бесплатно по адресу http://cnx.
-
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Каждая точка электрического поля характеризуется векторной величиной – напряженностью поля. Напряженность поля в данной точке равна силе, действующей на положительный пробный заряд, помещенный в эту точку, и отнесенной к единице заряда. Это – силовая характеристика электрического поля.
При перемещении электрического заряда в поле совершается работа. Электростатическое поле обладает очень важным свойством потенциальностью: работа по перемещению заряда из одной точки поля в другую не зависит от формы траектории. Это позволяет ввести понятие напряжения (или разности потенциалов). Напряжение U между двумя точками поля (*Под словами «пояс», «электрическое поле» здесь и в дальнейшем мы будем понимать электростатическое поле, то есть поле, созданное неподвижными зарядами.) равно работе, совершаемой электрическим полем по перемещению единицы положительного заряда из одной точки в другую.
В отличие от напряженности, определенной в отдельно взятой точке, напряжение характеризует две точки ноля. Если зафиксировать одну точку, выбрав ее за начало отсчета, то любая точка поля будет иметь определенное напряжение по отношению к выбранной точке. Это напряжение называют потенциалом φ. Очевидно, что началу отсчета соответствует нулевой потенциал. Чаще всего нулевой потенциал приписывается точке, бесконечно удаленной от заряда, создающего поле. В этом случае потенциал φ некоторой точки поля равен работе, совершаемой электрическим полем по перемещению единицы положительного заряда из этой точки в бесконечность. Это – энергетическая характеристика электрического поля.
Иногда задавать в каждой точке скалярную величину – потенциал φ – удобнее, чем векторную величину напряженность . Естественно, что эти две величины должны быть связаны друг с другом.
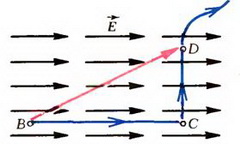
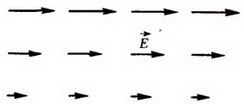
Рассмотрим вначале однородное электрическое поле. Его напряженность одинакова во всех точках; силовые линии такого поля – параллельные прямые (рис. 1).
Рис. 1
Найдем разность потенциалов между точками B и D. Потенциал φB точки B равен работе по перемещению единицы заряда из этой точки в бесконечность. Форма траектории при подсчете работы не имеет значения, поэтому будем перемещать заряд сначала по отрезку BC потом по отрезку CD а затем из точки D в бесконечность. Сила, действующая на единицу заряда со стороны электрического поля, равна напряженности. На отрезке ВС работа этой силы равна E·l, где E – проекция вектора напряженности на силовую линию, a l – длина отрезка ВС. На отрезке CD сила работы не совершает, так как она перпендикулярна перемещению. Наконец, работа по перемещению единицы заряда из точки D в бесконечность равна потенциалу φD. Поэтому: 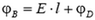
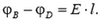
Для того чтобы формула (1) давала правильный знак разности потенциалов, величине l надо приписывать определенный знак в зависимости от расположения точек B и C на силовой линии. Будем считать, что l – это проекция вектора BD на направление силовой линии. Тогда знак положителен, если точка C лежит «ниже» по силовой линии, чем точка B и отрицателен в противоположном случае. Для случая, изображенного на рисунке 1, l > 0, и разность потенциалов 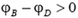
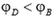
Итак, в однородном электрическом иоле между напряженностью и разностью потенциалов имеется простая связь, даваемая формулой (1).
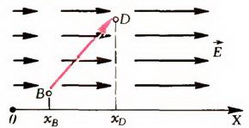
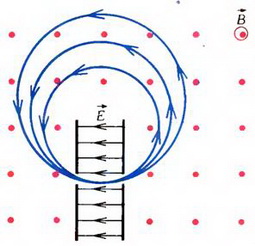
Какова связь между потенциалом и напряженностью в случае неоднородного электрического поля? В таком поле напряженность меняется от точки к точке. Пусть, для простоты рассуждений, изменение напряженности происходит только в одном направлении, которое примем за ось ОХ (рис. 2).
Рис. 2
Тогда напряженность поля зависит только от координаты x:
. Ясно, что в небольших участках пространства напряженность меняется мало, и электрическое поле там можно приближенно считать однородным. Возьмем близкие точки B и D и найдем разность потенциалов между ними. Воспользуемся формулой (1). Потенциал так же, как и напряженность, зависит только от координаты x (*Плоскость x = const эквипотенциальна, так как при перемещении единицы заряда в этой плоскости электрическое поле работы не совершает.):
Проекция вектора на ось ОХ равна разности координат точек D и B:
Таким образом, для близких точек B и D получаем:
или
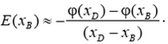
Чтобы формула (2) стала точной, надо устремить точку B к точке D и найти предел, к которому стремится правая часть при неограниченном сближении точек:
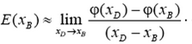
Легко увидеть, что правая часть формулы (3) – это производная потенциала, взятая с обратным знаком. Таким образом, в неоднородном электрическом поле связь между потенциалом и напряженностью в каждой точке следующая:
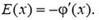
Знак минус в формуле (4) означает, что потенциал убывает вдоль силовой линии: поскольку проекция напряженности на силовую линию 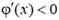
Если нарисовать график зависимости φ от x, то тангенс угла наклона α касательной к графику в каждой его точке равен производной 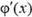
Рис. 3
Рассмотрим теперь несколько конкретных задач.
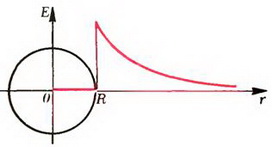
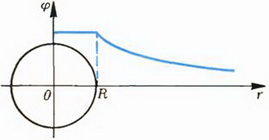
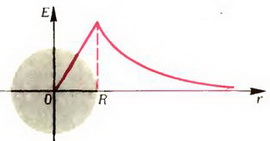
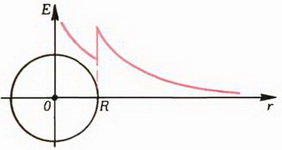
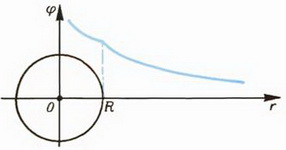
Задача 1. Сфера радиуса R имеет заряд Q. Найти зависимость напряженности и потенциала от расстояния r от центра сферы. Нарисовать графики.
Найдем вначале напряженность поля. Внутри сферы электрического поля нет: при r < RE = 0. Вне сферы напряженность поля такая же, как у точечного заряда Q помешенного в центр сферы: при r> R проекция напряженности на выбранное направление от центра 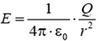
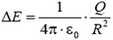
а
б
Рис. 4
Величину скачка ΔE можно выразить через поверхностную плотность заряда 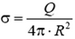
Заметим, что это общее свойство электростатического поля: на заряженной поверхности его проекция на направление нормали всегда испытывает скачок 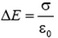
Выясним теперь, как меняется потенциал φ в зависимости от r. Мы уже знаем, что в любой точке тангенс угла наклона касательной к графику потенциала должен совпадать со значением проекции напряженности (взятой с противоположным знаком). При 0 < r < RE = 0, и, следовательно, во всех этих точках касательная к графику потенциала должна быть горизонтальной. Это означает, что на участке 0 < r < R потенциал не меняется: φ = const.
Вне сферы, при r > R производная 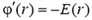
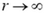
Может ли потенциал испытать скачок на поверхности сферы, то есть при r = R? Очевидно, что нет. Скачок потенциала означал бы, что при перемещении единичного заряда между двумя очень близкими точками 1 и 2 электрическое поле совершало бы конечную работу:
должно оставаться конечным при 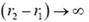
График зависимости φ от r изображен на рисунке 4, б.
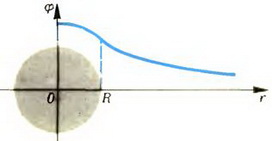
Задача 2. Шар радиуса R равномерно заряжен по всему объему. Полный заряд тара Q. Нарисуйте графики зависимости напряженности и потенциала от расстояния r от центра шара.
Такой шар можно представить себе состоящим из большого числа тонких заряженных сфер, вложенных одна в другую. Каждая сфера внутри себя поля не создает, а вне создает поле такое же, как точечный заряд, помещенный в ее центр. Поэтому вне шара, при r > R напряженность такая же, как напряженность поля точечного заряда Q помещенного в центр шара:
Внутри шара, на расстоянии R поле создают только сферы с радиусами от 0 до r (для сфер большего радиуса рассматриваемая точка находится внутри них). Следовательно, напряженность на расстоянии s от центра шара такая же, как напряженность поля точечного заряда Qr. помещенного в центр шара, где Qr – суммарный заряд всех сфер с радиусами от 0 до r, то есть заряд шара радиуса r. Если на шар радиуса R приходится заряд Q, то на шар радиуса r будет приходиться заряд
Таким образом, внутри шара напряженность поля 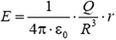
На поверхности шара, в точке r = R напряженность скачка не испытывает. Это находится в соответствии с общим правилом, так как поверхностная плотность заряда в данном случае равна нулю: шар заряжен однородно, и на бесконечно тонкий поверхностный слой приходится бесконечно малый заряд.
График зависимости E от r показан на рисунке 5, a.
а
б
Рис. 5
Нарисуем теперь график потенциала. Производная от потенциала
всегда отрицательна (E ≥ 0). Поэтому с увеличением r потенциал должен монотонно убывать. В точке r = 0 производная потенциала равна нулю. Следовательно, касательная к графику в. этой точке горизонтальна: в точке r = 0 потенциал имеет максимум. В точке r = R ни потенциал, ни его производная скачков не испытывают. Первое следует из общего правила для потенциала, о втором мы уже говорили выше. Поэтому кривые, изображающие зависимость потенциала от расстояния при r < R и r > R в точке r = R должны сопрягаться – гладко без излома переходить одна в другую. При 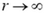
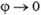
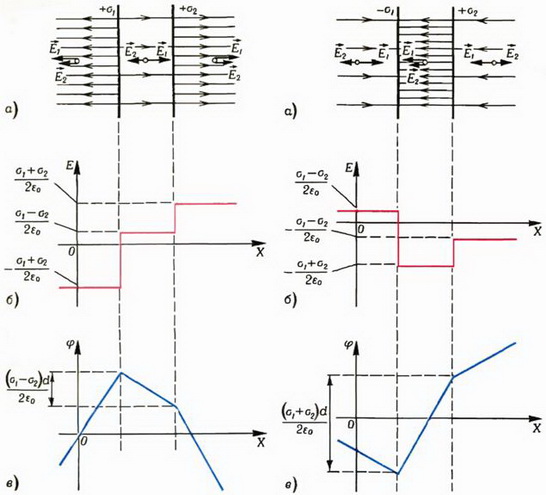
Задача 3. Две плоскости расположены параллельно друг другу на расстоянии d и заряжены с поверхностной плотностью заряда σ1 и σ2 соответственно. Нарисовать графики зависимости напряженности поля и потенциала от координаты x (ось ОХ перпендикулярна пластинам). Рассмотреть случаи одноименных (рис. 6, а) и разноименных (рис. 7, а) зарядов на пластинах.
Рис. 6 Рис. 7
Каждая плоскость создает по обе стороны от себя однородное электрическое поле, напряженность которого
Воспользовавшись принципом суперпозиции, для случая одноименных зарядов приходим к графику, показанному на рисунке 6, б, а для разноименных – к графику на рисунке 7, б. Скачки напряженности опять соответствуют общему правилу:
Соответствующие графики для потенциалов показаны на рисунках 6, в и 7, в. На отдельных участках зависимость потенциала от координаты – линейная, так как напряженность поля постоянна. Изломы происходят в тех местах, где напряженность поля испытывает скачок.
Заметим, что в данной задаче потенциал не стремится к нулю при 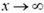
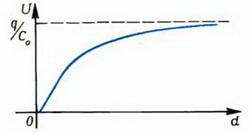
Задача 4. Две одинаковые параллельные пластины имеют заряды +q и –q. Как меняется разность потенциалов U между пластинами при увеличении расстояния d между ними? Нарисуйте график зависимости U от d.
Пока расстояние между пластинами значительно меньше их размеров, такую систему можно считать плоским конденсатором. Тогда 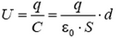
Рис. 8
Это соответствует тому, что напряженность поля 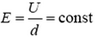
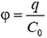
Краевые эффекты часто оказываются существенными при решении электростатических задач, связанных с законом сохранения энергии, рассмотрим, например, такой вариант ускорителя электронов.
Задача 5. В пластинах плоского конденсатора, заряженного до разности потенциалов U сделано сквозное отверстие. Конденсатор помещен в постоянное магнитное поле, направленное перпендикулярно электрическому полю в конденсаторе (рис. 9). Электрон влетает в пространство между пластинами конденсатора, ускоряется, приобретая энергию e·U вылетает через отверстие и. двигаясь в магнитном поле по окружности, возвращается в конденсатор. Затем он снова ускоряется, движется по окружности большего радиуса, опять входит в конденсатор и т.д. На первый взгляд кажется, что таким образом можно разогнать электрон до больших энергий, то есть создать ускоритель. Так ли это?
Рис. 9
Оказывается, такой ускоритель работать не будет – не учтен краевой эффект. Вне конденсатора всегда существует слабое электрическое поле, которое тормозит электрон при егодвижении по окружности. Отрицательная работа поля при этом в точности равна положительной работе при разгоне электрона в конденсаторе: работа в электростатическом поле не зависит от формы траектории. Магнитное поле работы не совершает (сила Лоренца перпендикулярна скорости движения электрона). Поэтому полная работа всех сил, действующих на электрон, при его возвращении в начальную точку будет равна нулю, и кинетическая энергия электрона не изменится. Ускоритель работать не будет.
Упражнения
1. Может ли существовать электростатическое поле, у которого силовые линии – параллельные прямые, а абсолютная величина напряженности меняется только в направлении, перпендикулярном силовым линиям (рис. 10)?
Рис. 10
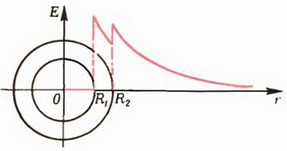
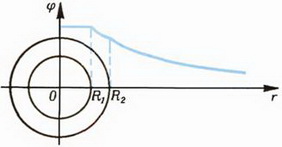
2. Две концентрические металлические сферы радиусов R1 и R2 имеют заряды Q1 и Q2 соответственно. Найдите напряженность и потенциал электрического поля на произвольном расстоянии r от центра сфер. Нарисуйте графики зависимости E от r и φ от r. Рассмотрите случаи одноименных и разноименных зарядов. Как выглядят графики для случая Q1 = –Q2 (сферический конденсатор)?
3. Точечный заряд q окружен металлической сферой радиуса R с зарядом Q. Найдите напряженность поля и потенциал на произвольном расстоянии r от заряда q если он находится в центре сферы; нарисуйте графики зависимости E от r и φ от r. Как изменятся графики, если заряд сместить из центра сферы? Решите ту же задачу для случая, когда металлическая сфера заземлена.
4. Электрон влетает в пространство между пластинами плоского конденсатора так, что его скорость составляет острый угол с направлением силовых линий. Тогда при движении в конденсаторе он будет тормозиться и вылетит с меньшей скоростью; его кинетическая энергии уменьшится. Увеличится ли при этом энергия конденсатора?
5. Два одинаковых конденсатора емкостью C каждый, один из которых заряжен до напряжения U а второй – не заряжен, соединяют параллельно. Найти энергию системы до и после соединения конденсаторов. Почему эти энергии не равны?
6. Точечный заряд q находится вне незаряженной металлической сферы радиуса R на расстоянии d от ее центра. Найти потенциал сферы.
Ответы.
1. Не может, иначе работа по перемещению заряда по замкнутому контуру была бы отлична от нуля.
2. При R1 > r > 0 напряженность E = 0 и 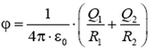
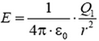
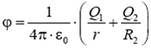
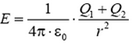
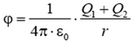
а
б
Рис. 11
3. При R > r > 0 напряженность 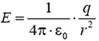
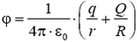
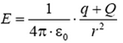
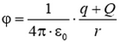
а
б
Рис. 12
4. Энергия конденсатора не изменяется; изменяется энергия взаимодействия электрона и конденсатора (работа по перемещению электрона в бесконечность из начальной и конечной точек не одна и та же).
5. 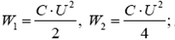
6. 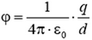
Электростатика: демонстрационный
эксперимент
Продолжение. См. № 17,
18, 19, 20,
21/07
В.В.МАЙЕР,
ГОУ ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: демонстрационный
эксперимент
Потенциал относится к самым сложным
понятиям электростатики. Учащиеся выучивают
определение потенциала электростатического
поля, решают многочисленные задачи, но у них нет
ощущения потенциала, они с трудом соотносят
теорию с реальностью. Поэтому роль учебного
эксперимента в формировании понятия потенциала
весьма высока. Нужны такие опыты, которые, с одной
стороны, иллюстрировали бы абстрактные
теоретические представления о потенциале, а с
другой, показывали полную обоснованность
экспериментом введения понятия потенциала.
Стремиться к особой точности количественных
результатов в этих опытах скорее вредно, чем
полезно.
6.1. Потенциальность
электростатического поля
На изолирующей подставке укрепим
проводящее тело и зарядим его. На длинной
изолированной нити подвесим лёгкий проводящий
шарик и сообщим ему пробный заряд, одноимённый с
зарядом тела. Шарик оттолкнётся от тела и из
положения 1 перейдёт в положение 2. Так
как высота шарика в поле тяготения увеличилась
на h, потенциальная энергия его
взаимодействия с Землёй возросла на mgh.
Значит, электрическое поле заряженного тела
совершило над пробным зарядом некоторую работу.
Повторим опыт, но в начальный момент не
просто отпустим пробный шарик, а толкнём его в
произвольном направлении, сообщив ему некоторую
кинетическую энергию. При этом обнаружим, что
двигаясь из положения 1 по сложной
траектории, шарик в конечном итоге остановится в
положении 2. Сообщённая шарику в начальный
момент кинетическая энергия, очевидно,
израсходовалась на преодоление сил трения при
движении шарика, а электрическое поле совершило
над шариком ту же работу, что и в первом случае. В
самом деле, если уберём заряженное тело, то тот же
самый толчок пробного шарика приводит к тому, что
из положения 2 он возвращается в положение 1.
Таким образом, опыт наводит на мысль,
что работа электрического поля над зарядом не
зависит от траектории движения заряда, а
определяется лишь положениями её начальной и
конечной точек. Иными словами, на замкнутой
траектории работа электростатического поля
всегда равна нулю. Поля, обладающие таким
свойством, называются потенциальными.
6.2. Потенциальность центрального
поля
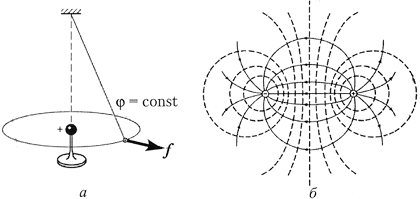
Опыт показывает, что в
электростатическом поле, создаваемом заряженным
проводящим шаром, действующая на пробный заряд
сила всегда направлена от центра заряженного
шара, она монотонно уменьшается с увеличением
расстояния и на равных расстояниях от него имеет
одинаковые значения. Такое поле называется центральным.
Пользуясь рисунком, нетрудно убедиться, что
центральное поле потенциально.
6.3. Потенциальная энергия заряда в
электростатическом поле
Гравитационное поле, как и
электростатическое, потенциально. Кроме того,
математическая запись закона всемирного
тяготения совпадает с записью закона Кулона.
Поэтому при исследовании электростатического
поля имеет смысл опираться на аналогию между
гравитационным и электростатическим полями.
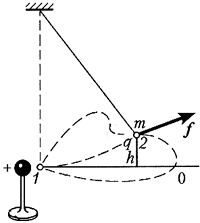
В небольшой области вблизи
поверхности Земли гравитационное поле можно
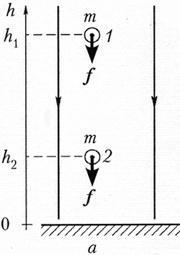
считать однородным (рис. а).
На тело массой m в этом поле действует
постоянная по модулю и направлению сила f
= тg. Если предоставленное самому себе
тело падает из положения 1 в положение 2,
то сила тяготения совершает работу A = fs
= mgs = mg (h1 – h2).
Это же самое мы можем сказать иначе.
Когда тело находилось в положении 1, система
Земля–тело обладала потенциальной энергией (т.е.
способностью совершить работу) W1 = mgh1.
Когда тело перешло в положение 2,
рассматриваемая система стала обладать
потенциальной энергией W2 = mgh2.
Совершённая при этом работа равна разности
потенциальных энергий системы в конечном и
начальном состояниях, взятой с обратным знаком: А
= – (W2 – W1).
Обратимся теперь к электрическому
полю, которое, напомним, как и гравитационное,
является потенциальным. Представим, что силы
тяжести нет, а вместо поверхности Земли имеется
плоская проводящая пластина, заряженная (для
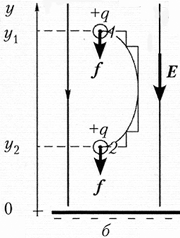
определённости) отрицательно (рис. б). Введём
координатную ось Y и над пластиной
расположим положительный заряд q. Понятно,
что, поскольку сам по себе заряд не существует,
над пластиной находится какое-то тело
определённой массы, несущее электрический заряд.
Но, поскольку мы считаем поле тяжести
отсутствующим, то и принимать во внимание массу
заряженного тела не будем.
Итак, на положительный заряд q со
стороны отрицательно заряженной плоскости
действует сила притяжения f = qE,
где E – напряжённость
электрического поля. Так как электрическое поле
однородно, то во всех его точках на заряд
действует одна и та же сила. Если заряд
перемещается из положения 1 в положение 2,
то электростатическая сила совершает над ним
работу А = fs = qE s = qE(y1
– y2).
То же самое мы можем выразить другими
словами. В положении 1 находящийся в
электростатическом поле заряд обладал
потенциальной энергией W1 = qEy1,
а в положении 2 – потенциальной энергией W2
= qEy2. При переходе заряда из положения 1
в положение 2 электрическое поле заряженной
плоскости совершило над ним работу А = –(W2
– W1).
Напомним, что потенциальная энергия
определена лишь с точностью до слагаемого: если
нулевое значение потенциальной энергии выбрать
в другом месте оси Y, то в принципе ничего не
изменится.
6.4. Потенциал однородного
электростатического поля
Если потенциальную энергию заряда в
электростатическом поле разделить на величину
этого заряда, то получим энергетическую
характеристику самого поля, которую назвали потенциалом:
Потенциал в системе СИ выражают в вольтах:
1 В = 1 Дж/1 Кл.
Если в однородном электрическом поле ось Y
направить параллельно вектору напряжённости E,
то потенциал произвольной точки поля будет
пропорционален координате точки: причём коэффициентом
пропорциональности является напряжённость
электрического поля.
6.5. Разность потенциалов
Потенциальная энергия и потенциал
определяются лишь с точностью до произвольной
постоянной, зависящей от выбора их нулевых
значений. Однако работа поля имеет вполне
определённое значение, поскольку определяется
разностью потенциальных энергий в двух точках
поля:
А = –(W2 – W1) =
–(2q –
1q) = q(
1 –
2).
Работа по перемещению электрического
заряда между двумя точками поля равна
произведению заряда на разность потенциалов
начальной и конечной точек. Разность потенциалов
иначе называют напряжением.
Напряжение между двумя точками равно
отношению работы поля при перемещении заряда из
начальной точки в конечную к этому заряду:
Напряжение, как и потенциал,
выражается в вольтах.
6.6. Разность потенциалов и
напряжённость
В однородном электрическом поле
напряжённость направлена в сторону убывания
потенциала и, согласно формуле = Еy, разность потенциалов
равна U = 1
– 2= Е(у1
– y2). Обозначив разность координат
точек у1 – y2 = d,
получаем U = Ed.
В эксперименте вместо
непосредственного измерения напряжённости
проще определять разность потенциалов и затем
вычислять модуль напряжённости по формуле
(6.1)
где d – расстояние между двумя
точками поля, близко расположенными в
направлении вектора Е. При этом в
качестве единицы напряжённости используют не
ньютон на кулон, а вольт на метр:
6.7. Потенциал произвольного
электростатического поля
Опыт показывает, что отношение работы
по перемещению заряда из бесконечности в данную
точку поля к величине этого заряда остаётся
неизменным: = А/q.
Это отношение принято называть потенциалом
данной точки электростатического поля,
принимая потенциал в бесконечности равным нулю.
6.8. Принцип суперпозиции для
потенциалов
Любое как угодно сложное
электростатическое поле можно представить в
виде суперпозиции полей точечных зарядов. Каждое
такое поле в выбранной точке имеет определённый
потенциал. Поскольку потенциал является
скалярной величиной, результирующий потенциал
поля всех точечных зарядов есть алгебраическая
сумма потенциалов 1,
2,
3, … полей отдельных
зарядов: =
1 +
2 +
3 + … Это соотношение
является прямым следствием принципа
суперпозиции электрических полей.
6.9. Потенциал поля точечного
заряда
Обратимся теперь к сферическому
(точечному) заряду. Выше показано, что
напряжённость электрического поля, созданного
равномерно распределённым по сфере зарядом Q,
не зависит от радиуса сферы. Представим, что на
некотором расстоянии r от центра сферы
находится пробный заряд q. Напряжённость
поля в точке, где находится заряд,
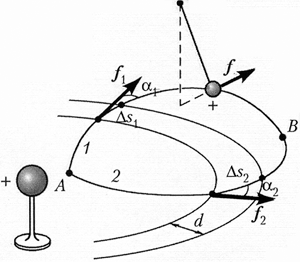
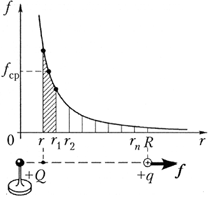
На рисунке изображён график
зависимости силы электростатического
взаимодействия между точечными зарядами от
расстояния между ними. Чтобы найти работу
электрического поля при перемещении пробного
заряда q с расстояния r до расстояния R,
разобьём этот промежуток точками r1, r2,…,
rп на равные отрезки. Средняя сила,
действующая на заряд q в пределах отрезка [rr1],
равна
Работа этой силы на этом участке:
Аналогичные выражения для работы
получатся для всех других участков. Поэтому
полная работа:
Одинаковые слагаемые с
противоположными знаками уничтожаются, и
окончательно получаем:
– работа поля над зарядом
– разность потенциалов
Теперь, чтобы найти потенциал точки
поля относительно бесконечности, устремляем R
к бесконечности и окончательно получаем:
(6.2)
Итак, потенциал поля точечного заряда
обратно пропорционален расстоянию до заряда.
6.10. Эквипотенциальные поверхности
Поверхность, в каждой точке которой
потенциал электрического поля имеет одно и то же
значение, называется эквипотенциальной.
Эквипотенциальные поверхности поля заряженного
шара нетрудно продемонстрировать подвешенным на
нити пробным зарядом, как это показано на
рисунке.
На втором рисунке электростатическое
поле двух разноимённых зарядов представлено
силовыми (сплошные) и эквипотенциальными
(пунктирные) линиями.
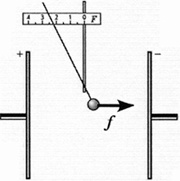
Исследование 6.1. Разность
потенциалов
Задание. Разработайте простой
опыт, позволяющий ввести понятие разности
потенциалов, или напряжения.
Вариант выполнения. Два
металлических диска на изолирующих подставках
установите параллельно друг другу на расстоянии
примерно 10 см. Диски зарядите равными по модулю и
противоположными по знаку зарядами. Зарядите
шарик электростатического динамометра зарядом,
например, q = 5 нКл (см. исследование 3.6), и
введите его в область между дисками. При этом
стрелка динамометра покажет определённое
значение силы, действующей на шарик. Зная
параметры динамометра, вычислите значение
модуля силы (см. исследование 3.6). Например, в
одном из наших опытов стрелка динамометра
показала значение х = 2 см, следовательно,
согласно формуле
модуль силы f = Kх = 17 • 10–5 Н.
Перемещая динамометр, покажите, что во
всех точках поля между заряженными дисками на
пробный заряд действует одна и та же сила.
Перемещая динамометр так, чтобы пробный заряд
прошёл путь s = 5 см в направлении действующей
на него силы, спросите учащихся: какую работу
совершает над зарядом электрическое поле?
Добейтесь понимания, что работа поля над зарядом
по модулю равна
А = fs = 8,5 • 10–6 Дж,
(6.3)
причём она положительна, если заряд
перемещается по направлению напряжённости поля,
и отрицательна, если в противоположном
направлении. Вычислите разность потенциалов
между начальным и конечным положениями шарика
динамометра: U = А/q = 1,7 • 103 В.
С одной стороны напряжённость
электрического поля между пластинами:
С другой стороны, согласно формуле (6.1),
при d = s:
Таким образом, опыт показывает, что
напряжённость электрического поля можно
определить двумя способами, которые, разумеется,
приводят к одинаковым результатам.
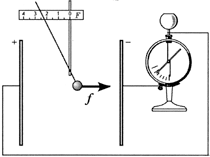
Исследование 6.2. Градуировка
электрометра по напряжению 
Задание. Разработайте
эксперимент, показывающий, что с помощью
демонстрационного стрелочного электрометра
можно измерять напряжение.
Вариант выполнения.
Экспериментальная установка схематически
изображена на рисунке. Пользуясь
электростатическим динамометром, определите
напряжённость однородного электрического поля и
по формуле U = Еd вычислите разность
потенциалов между проводящими пластинами.
Повторяя эти действия, отградуируйте
электрометр по напряжению так, чтобы получился
электростатический вольтметр.
Исследование 6.3. Потенциал поля
сферического заряда
Задание. Экспериментально
определите работу, которую нужно совершить
против электростатического поля, чтобы
переместить пробный заряд из бесконечности в
некоторую точку поля, созданного заряженной
сферой.
Вариант выполнения. На
изолирующей стойке закрепите шарик из
пенопласта, обёрнутый алюминиевой фольгой.
Зарядите его от пьезоэлектрического или иного
источника (cм. п. 1.10) и одноимённым зарядом
зарядите пробный шарик на стержне
электростатического динамометра. Пробный заряд
находится бесконечно далеко от исследуемого,
если электростатический динамометр не фиксирует
силы электростатического взаимодействия между
зарядами. В эксперименте удобно
электростатический динамометр оставить
неподвижным, а перемещать исследуемый заряд.
Постепенно приближайте заряженный
шарик на изолирующей подставке к шарику
электростатического динамометра. В первую
строку таблицы записывайте значения расстояния r
между зарядами, во вторую строку –
соответствующие им значения силы
электростатического взаимодействия. Удобно
расстояние выражать в сантиметрах, а силу – в
условных единицах, в которых отградуирована
шкала динамометра. По получившимся данным
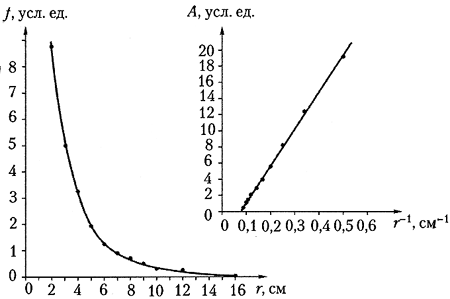
постройте график зависимости силы от расстояния.
Подобный график вы уже строили, выполняя
исследование 3.5.
Теперь найдите зависимость работы по
перемещению заряда из бесконечности в данную
точку поля. Обратите внимание на то, что в
эксперименте сила взаимодействия зарядов
становится практически равной нулю на
сравнительно небольшом удалении одного заряда
от другого.
Разбейте весь диапазон изменения
расстояния между зарядами на равные участки,
например, по 1 см. Обработку экспериментальных
данных удобнее начинать с конца графика. На
участке от 16 до 12 см среднее значение силы fср
составляет 0,13 усл. ед., поэтому элементарная
работа А
на этом участке равна 0,52 усл. ед. На участке от 12
до 10 см, рассуждая аналогичным образом, получаем
элементарную работу 0,56 усл. ед. Далее удобно
брать участки длиной по 1 см. На каждом из них
найдите среднее значение силы и умножьте его на
длину участка. Полученные значения работы поля A на всех
участках занесите в четвёртую строку таблицы.
Чтобы узнать работу А,
совершённую электрическим полем при перемещении
заряда из бесконечности на данное расстояние,
складывайте соответствующие элементарные
работы и получающиеся значения записывайте в
пятую строку таблицы. В последней строке
запишите значения величины 1/r, обратной
расстоянию между зарядами.
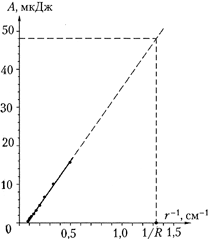
Постройте график зависимости работы
электрического поля от величины, обратной
расстоянию, и убедитесь, что получается прямая
линия (рисунок справа).
Таким образом, опыт показывает, что
работа электрического поля при перемещении
заряда из бесконечности в данную точку поля
обратно пропорциональна расстоянию от этой
точки до заряда, создающего поле.
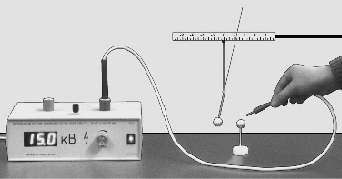
Исследование 6.4. Высоковольтный
источник напряжения
Информация. Для школьного
физического эксперимента в настоящее время
промышленность выпускает прекрасные
высоковольтные источники напряжения. Они имеют
две выходные клеммы или два высоковольтных
электрода, разность потенциалов между которыми
плавно регулируется в пределах от 0 до 25 кВ.
Встроенный в прибор стрелочный или цифровой
измеритель напряжения позволяет определять
разность потенциалов между полюсами источника.
Такие приборы повышают уровень учебного
эксперимента по электростатике.
Задание. Разработайте
доказательный учебный эксперимент,
показывающий, что потенциал заряженного шара,
экспериментально определённый в соответствии с
формулой (6.2) для точечного заряда, равен
потенциалу, сообщённому этому шару
высоковольтным источником питания.
Вариант выполнения. Вновь
соберите экспериментальную установку, состоящую
из электростатического динамометра с пробным
шариком и проводящего шара на изолирующей
подставке (см. исследования 3.4 и 6.3). Измерьте
параметры всех элементов установки.
Для определённости укажем, что в одном
из опытов мы использовали электростатический
динамометр, параметры которого указаны в
исследовании 3.4: а = 5 • 10–3 м, b = 55
• 10–3 м, с = 100 • 10–3 м, т = 0,94
• 10–3 кг, причём шарики были одинаковыми и
имели радиус R = 7,5 • 10–3 м.
Для этого динамометра градуировочный
коэффициент K, переводящий условные единицы
силы в ньютоны, даётся формулой (cм. исследование 3.6).
График работы по перемещению пробного
заряда из бесконечности в данную точку поля
представлен на рисунке на с. 31. Чтобы в этом
графике от условных единиц работы перейти к
джоулям, нужно в соответствии с формулой A = fср
r значения
расстояния в сантиметрах перевести в метры,
значения силы в усл. ед. (см) перевести в усл. ед. (м)
и умножить на K. Таким образом: A (Дж) = 10–4 K
A (уcл. ед.).
Соответствующий график зависимости
работы от величины, обратной расстоянию,
представлен ниже. Экстраполируя его до R = 7,5
мм, получаем, что работа по перемещению пробного
заряда из бесконечности до поверхности
заряженного шарика А = 57 • 10–4 K = 4,8 • 10–5 Дж.
Так как заряды шариков были одинаковы и
составляли q = 6,6 • 10–9 Кл
(см. исследование 3.6), то искомый потенциал = А/q = 7300 В.
Включите высоковольтный источник и
регулятором установите на нём выходное
напряжение, например, U = 15 кВ. Одним из
электродов поочерёдно прикоснитесь к проводящим
шарикам и выключите источник. При этом каждый из
шариков приобретает относительно Земли
потенциал =
7,5 кВ. Повторите опыт по определению зарядов
шариков методом Кулона (исследование 3.6) и вы
получите значение, близкое к 7 нКл.
Таким образом, в эксперименте двумя
независимыми способами определены заряды шаров.
Первый способ основан на непосредственном
использовании определения потенциала, второй
опирается на сообщение шарикам определённого
потенциала c помощью высоковольтного источника и
последующее измерение их заряда с помощью закона
Кулона. При этом получились совпадающие
результаты.
Конечно, никто из школьников и не
сомневается в том, что современные приборы
правильно измеряют значения физических величин.
Но теперь они убеждены, что правильно измеряются
именно те величины, которые они изучают в
простейших явлениях. Установлена прочная связь
между основами физики и современной техникой,
ликвидирована пропасть между школьными знаниями
и реальной жизнью.
Вопросы и задания для самоконтроля
1. Как экспериментально доказать, что
электростатическое поле потенциально?
2. В чём суть аналогии между
гравитационным и электростатическим полями?
3. Какова связь между напряжённостью и
разностью потенциалов электростатического поля?
4. Предложите опыт, непосредственно
обосновывающий справедливость принципа
суперпозиции для потенциалов.
5. Вычислите потенциал поля точечного
заряда, пользуясь интегральным исчислением.
Сравните сделанный вами вывод формулы с
элементарным выводом, приведённым в лекции.
6. Выясните, почему в опыте по
определению разности потенциалов между двумя
проводящими дисками (исследование 6.1) нельзя
перемещать измеритель напряжённости так, чтобы
его пробный шарик прошёл всё расстояние от
одного диска до другого.
7. Отградуировав электрометр по
напряжению (исследование 6.2), сравните
получившийся результат с теми значениями
чувствительности прибора по напряжению, которые
приводятся в паспортных данных электрометра.
8. Оцените дидактическую эффективность
учебного эксперимента по непосредственному
определению потенциала поля сферического заряда
(исследование 6.3).
9. Детально разработайте методику
формирования в сознании учащихся обоснованной
убеждённости, что введённое при изучении
электростатики понятие потенциала
электрического поля в точности соответствует
тому, которое используется современной наукой и
техникой.
Литература
Бутиков Е.И., Кондратьев А.С.
Физика: Учеб. пособие: В 3 кн. Кн. 2.
Электродинамика. Оптика. – М.: Физматлит, 2004.
Восканян А.Г., Марленский А.Д.,
Шибаев А.Ф. Демонстрация закона Кулона на
основе количественных измерений: В сб. «Учебный
эксперимент по электродинамике», вып. 7. – М.:
Школа-Пресс, 1996.
Касьянов В.А. Физика-10. – М.: Дрофа,
2003.
Мякишев Г.Я., Синяков А.З., Слободсков
Б.А. Физика: Электродинамика. 10–11 кл.: Учеб. для
угл. изучения физики. – М.: Дрофа, 2002.
Учебное оборудование для кабинетов
физики обще- образовательных учреждений: Под ред.
Г.Г.Никифорова. – М.: Дрофа, 2005.







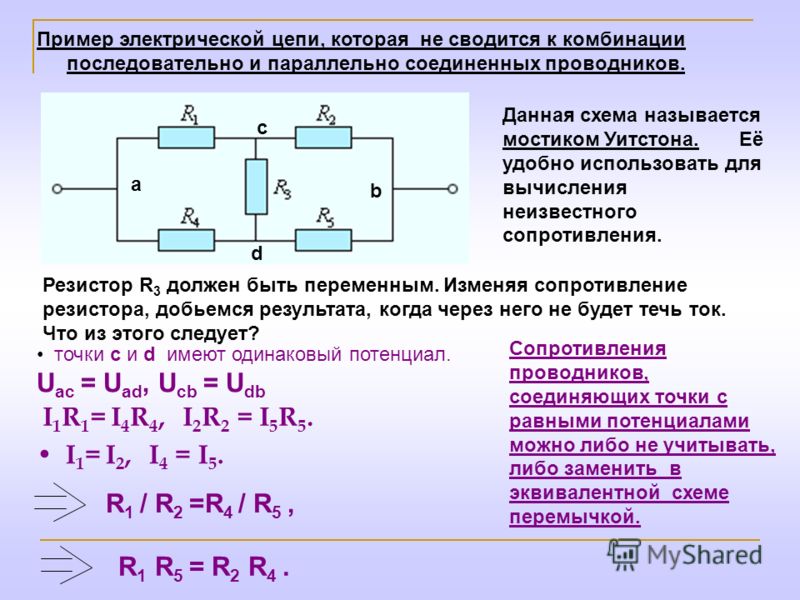


 Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен.
Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен. 
 Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.
Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.  Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.
Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.  И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось. 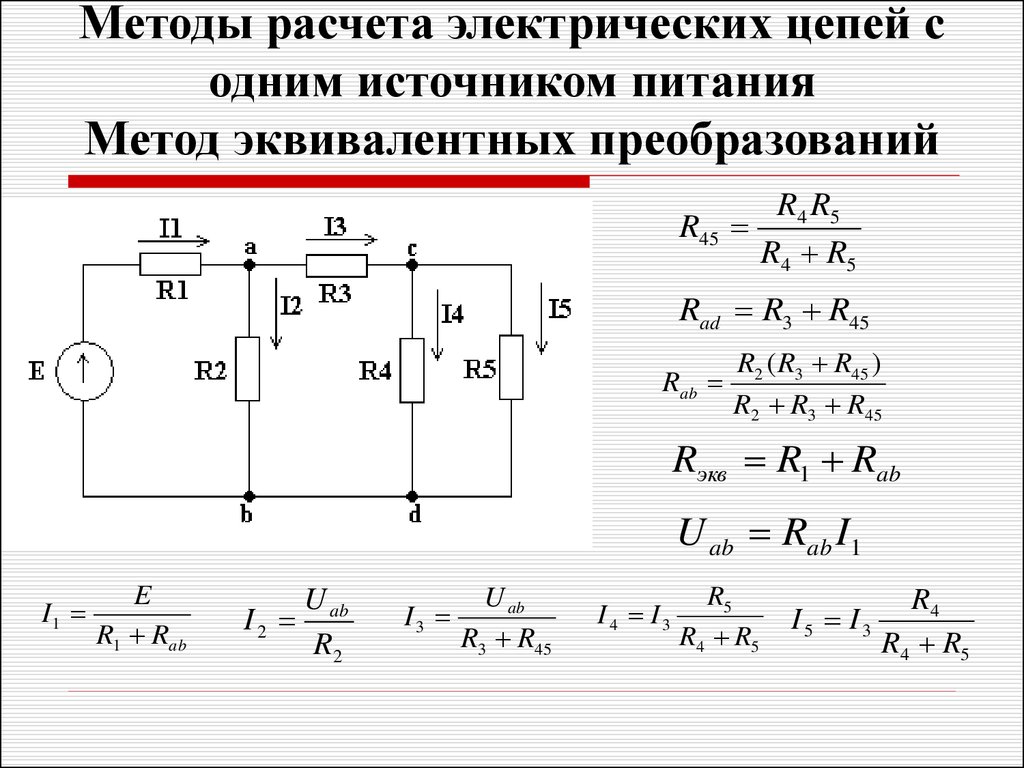 У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
У нас есть еще одно указание на то, что трудно хранить изолированные заряды.  Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку:
Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку: 
 3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
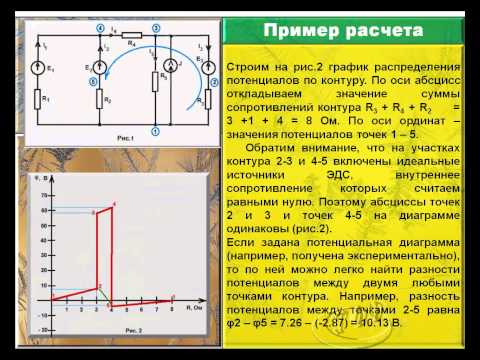 3.3)
3.3)  Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны
Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны 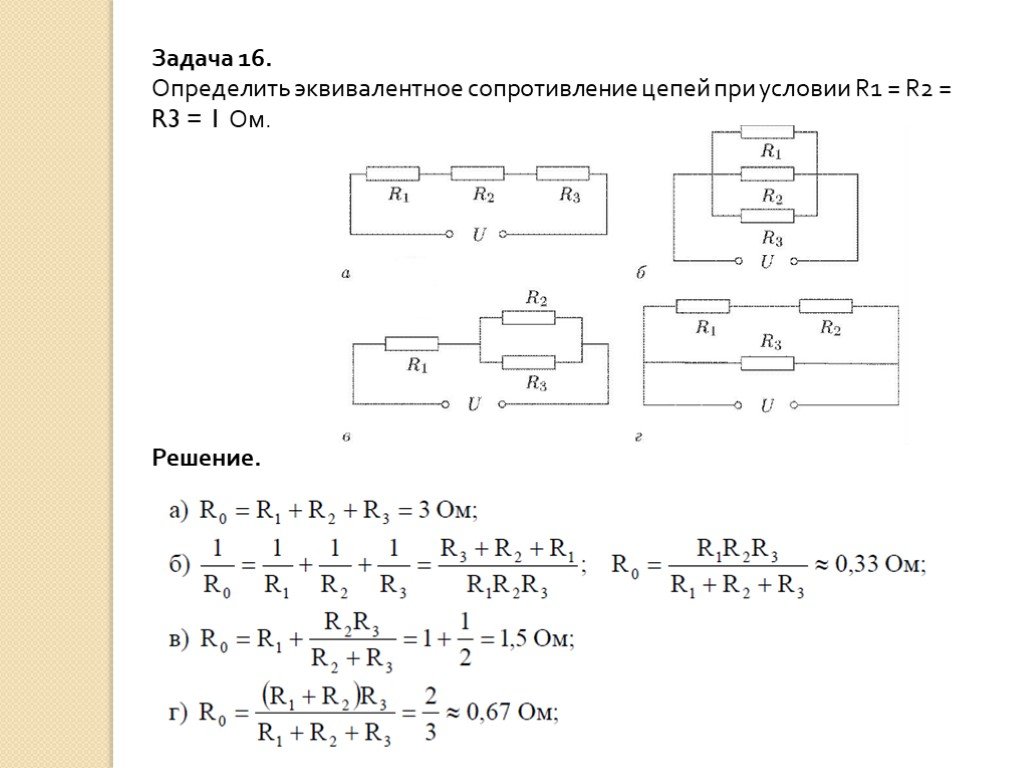
 Найти электрический потенциал в точке на оси, проходящей через центр кольца.
Найти электрический потенциал в точке на оси, проходящей через центр кольца.  Найти электрический потенциал в любой точке оси, проходящей через центр диска.
Найти электрический потенциал в любой точке оси, проходящей через центр диска.  Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.
Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.