Как найти потенциал в центре шара

2018-05-14   

Заряд $q$ распределен равномерно по объему шара радиуса $R$. Полагая диэлектрическую проницаемость всюду равной единице, найти потенциал:

а) в центре шара;

б) внутри шара как функцию расстояния $r$ от его центра.

Решение:

Из теоремы Гаусса напряженность в точке, внутри сферы на расстоянии $r$ от центра задается формулой $E_{r} = frac{ rho r}{3 epsilon_{0} }$ и вне ее, задается формулой $E_{r} = frac{1}{4 pi epsilon_{0} } frac{q}{r^{2} }$

(a) Потенциал в центре сферы,

$phi_{0} = int_{0}^{ infty} vec{E} cdot d vec{r} = int_{0}^{R} frac{ rho r}{3 epsilon_{0} } dr + int_{R}^{ infty} frac{q}{4 pi epsilon_{0} r^{2} } dr = frac{ rho}{3 epsilon_{0} } frac{R^{2} }{2} + frac{q}{4 pi epsilon_{0}R } = frac{q}{8 pi epsilon_{0}R } + frac{q}{4 pi epsilon_{0}R } = frac{3q}{8 pi epsilon_{0}R }$ (при $rho = frac{3q}{4 pi R^{3} } $)

(б) Потенциал в любой точке, внутри сферы, на расстоянии $r$ от центра $s$.

$phi (r) = int_{r}^{R} frac{ rho}{3 epsilon_{0} } rdr int_{r}^{ infty} frac{q}{4 pi epsilon_{0} } frac{dr}{r^{2} }$

При интегрировании: $phi (r) = frac{3q}{8 pi epsilon_{0}R } left [1 – frac{r^{2} }{3R^{2} } right ] = phi_{0} left [ 1 – frac{r^{2} }{3R^{2} } right ]$

§ 6. Потенциал поля точечного заряда и заряда, равномерно распределённого по сферической поверхности

Примем потенциал бесконечности равным нулю. Тогда, используя (5.2), можно вывести, что на расстоянии $$ r$$ от точечного заряда $$ Q$$ потенциал электростатического поля:

Рис. 6.1

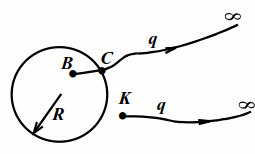
Возьмём теперь заряд $$ Q$$, равномерно распределённый по сфере радиуса $$ R$$ (рис. 6.1). 

Для нахождения потенциала на расстоянии $$ r$$ от центра сферы перенесём мысленно пробный заряд $$ q$$ из исследуемой точки в бесконечность и применим формулу (5.2). Для произвольной точки $$ K$$ вне сферы $$ {varphi }_{K}={A}_{Kinfty }/q$$, где $$ {A}_{Kinfty }$$ – работа сил поля над $$ q$$ при его перемещении из т. $$ K$$ в бесконечность. Эта работа не изменится, если весь заряд $$ Q$$ сферы поместить в  центр сферы, т. к. поля обоих зарядов $$ Q$$ при $$ r>R$$ совпадают (см. §3). Для  точечного заряда $$ Q$$ отношение $$ {A}_{Kinfty }/q$$ есть потенциал его поля в т. $$ K$$,  который находится по формуле (6.1). Итак, для сферы $$ {varphi }_{K}=kQ/r$$. В предельном случае при $$ r=R$$ получим потенциал сферы, равный `kQ//R`.

Для произвольной точки $$ B$$ внутри сферы  $$ {varphi }_{B}={A}_{BCinfty }/q={A}_{BC}+{A}_{Cinfty }/q$$.

Здесь $$ {A}_{Binfty }$$, $$ {A}_{BC}$$ и $$ {A}_{Cinfty }$$ – работа сил поля над зарядом $$ q$$ на участках $$ BCinfty $$,  `BC` и $$ Cinfty .$$ Внутри сферы поля нет, сила на $$ q$$ со стороны поля не действует и $$ {A}_{BC}=0$$. Тогда $$ {varphi }_{B}={A}_{Cinfty }/q$$. Но правая часть последнего равенства есть потенциал т. $$ C$$, т. е. потенциал сферы, равный `kQ//R`. Значит, потенциал любой точки внутри сферы равен потенциалу сферы: $$ {varphi }_{B}=kQ/R$$.

Итак, для заряда $$ Q$$, равномерно распределённого по сфере радиуса $$ R$$ потенциал поля вне сферы равен потенциалу точечного заряда, равного заряду сферы и помещённого в центре сферы (как и для напряжённости), а потенциал внутри сферы один и тот же и равен потенциалу сферы:

В двух вершинах прямоугольника со сторонами $$ a$$ и $$ 2a$$ (рис. 6.2) закреплены точечные заряды $$ Q$$ и $$ 3Q$$. Какую минимальную работу надо совершить, чтобы переместить точечный заряд $$ 4Q$$ из состояния покоя из вершины $$ B$$ в вершину $$ C$$?

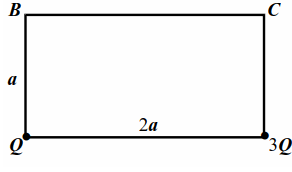Рис. 6.2

Здесь идёт речь о работе $$ A$$, которую необходимо совершить нам против электрических сил при переносе заряда $$ 4Q$$. Работа $$ A$$ в сумме с работой $$ {A}_{1}$$ сил электростатического поля над зарядом $$ 4Q$$ равна изменению кинетической энергии перемещаемого заряда:

$$ A+{A}_{1}=∆K$$

Отсюда $$ A=-{A}_{1}+∆K$$.

Работа $$ A$$ будет минимальной, если величина $$ ∆K$$ минимальна, т. е. заряд $$ 4Q$$ придёт в вершину $$ C$$ с нулевой скоростью, т. е. $$ ∆K=0.$$ Итак, $$ A=-{A}_{1}.$$ Работа сил поля над зарядом $$ {A}_{1}=4Q({varphi }_{B}-{varphi }_{C}), $$ где

$$ {varphi }_{B}=k{displaystyle frac{Q}{a}}+k{displaystyle frac{3Q}{asqrt{5}}}, {varphi }_{C}=k{displaystyle frac{Q}{asqrt{5}}}+k{displaystyle frac{3Q}{a}}$$

– потенциалы результирующего поля, созданного зарядами $$ Q$$ и $$ 3Q$$ в вершинах $$ B$$ и $$ C$$.

Окончательно 

$$ A={displaystyle frac{8(sqrt{5}-1)}{sqrt{5}}}{displaystyle frac{k{Q}^{2}}{a}}>0$$.

В центре сферы радиусом $$ R$$ находится точечный заряд $$ Q>0$$. По сфере равномерно распределён заряд $$-4Q<0$$. Найти потенциалы $$ {varphi }_{A}, {varphi }_{C}$$ на расстояниях $$ R/2$$ и $$ 2R$$ от центра сферы (рис. 6.3).

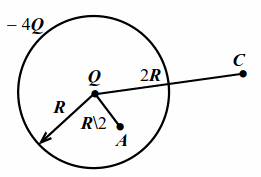Рис. 6.3

Потенциал в любой точке равен сумме потенциалов полей, созданных в этой точке зарядами $$ Q$$ и $$ -4Q$$. Для точек $$ A$$ и $$ C$$ :

$$ {varphi }_{A}=k{displaystyle frac{Q}{R/2}}+k{displaystyle frac{-4Q}{R}}=-2k{displaystyle frac{Q}{R}}$$,

$$ {varphi }_{C}=k{displaystyle frac{Q}{2R}}+k{displaystyle frac{-4Q}{2R}}=-{displaystyle frac{3}{2}}k{displaystyle frac{Q}{R}}$$.

В этой заметке разберем одну из задачек по электродинамике. Постараюсь привести максимально подробное решение, которое будет полезно учащимся 1-2 курсов физико-математических факультетов. Кто скучал по электродинамике и интегралам – ставим жирный лайк, чтоб я чаще писал про это 🙂 Доброго времени суток, друзья, мы начинаем…

Задача

Шар из однородного изотропного диэлектрика с диэлектрической проницаемостью ε и радиуса R заряжен сторонним зарядом q с объемной плотностью, линейно меняющейся от значения 0 в центре до максимального значения на поверхности шара. Считая, что шар находится в воздухе, определить потенциал во всей области изменения радиуса.

Решение:

Для начала нам нужно сделать рисунок к задаче. К любой задаче надо пытаться делать рисунок. Не потому что это нужно для кого-то или для красоты. Это нужно для того, чтобы наш мозг лучше визуализировал происходящее, строил абстрактные модели и логические цепочки.

1. По условию сказано, что плотность заряда диэлектрического шара меняется линейно, значит функционально мы можем выразить это так ( с проверкой граничных условий):

2. Нам задан именно общий заряд q, а не максимальная плотность. Поэтому эту неизвестную константу попробуем найти из условия нормировки.

3. Для начала найдем напряженность внешнего электрического поля (вне шара), а также потенциал вне шара. Для этого применим теорему Гаусса:

4. Теперь найдем напряженность электрического поля внутри шара. Для этого замкнутой поверхностью выберем сфера с радиусом r < R, центр которой будет совпадать с центром нашего шара. Симметрия подсказывает, что напряженность направленно радиально и одинакова по величине на всей поверхности. Применяем также теорему Гаусса. Учитываем, что внутри шара диэлектрик с заданной диэлектрической проницаемостью.

5. Теперь, зная внешнее и внутреннее поля, найдем потенциал внутри шара.

Первый интеграл в начале нашей формулы имеет смысл работы по переносу единичного положительного заряда из бесконечно удаленной точки в точку на поверхности шара r = R. Второй интеграл имеет смысл работы по переносу единичного положительного заряда с поверхности шара внутрь на радиус r < R. Обратим внимание, что внешний и внутренний потенциал сшиваются на границе при r = R.

Задача решена.

Понравилась заметка? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram