Векторное
поле
называется потенциальным, если работа
в этом поле не зависит от пути
интегрирования:
![]()
,
что
является условием потенциальности
поля. Из равенства нулю циркуляции
вектора
вдоль каждого замкнутого контура следует
по формуле Стокса, что
=0.
Существует
некоторая функция U(x,y,z),
для которой выражение Pdx
+ Qdy + Rdz
является полным дифференциалом:
dU
= Pdx + Qdy + Rdz.
Функция
U(М)
называется потенциалом векторного
поля:
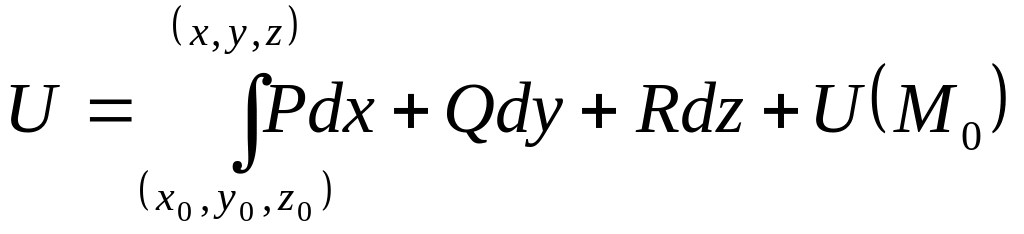
.
Для
нахождения потенциала поля по этой
формуле лучше всего интегрировать по
ломаной линии, соединяющей точки
и
,
звенья которой параллельны осям
координат.
Работа
потенциального векторного поля вдоль
любого пути равна разности значений
потенциала этого поля в конце
и начале
пути: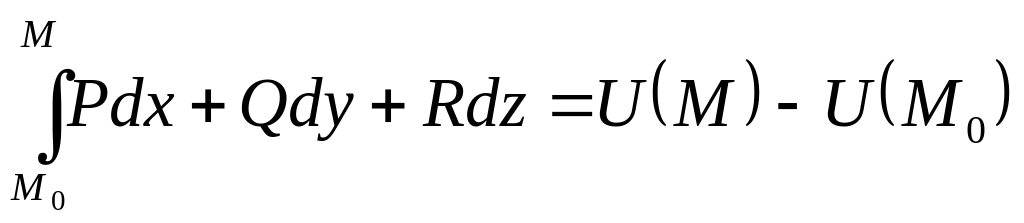
.
Пример
35.
Показать, что поле
![]()
является потенциальным и найти его
потенциал.
Решение:
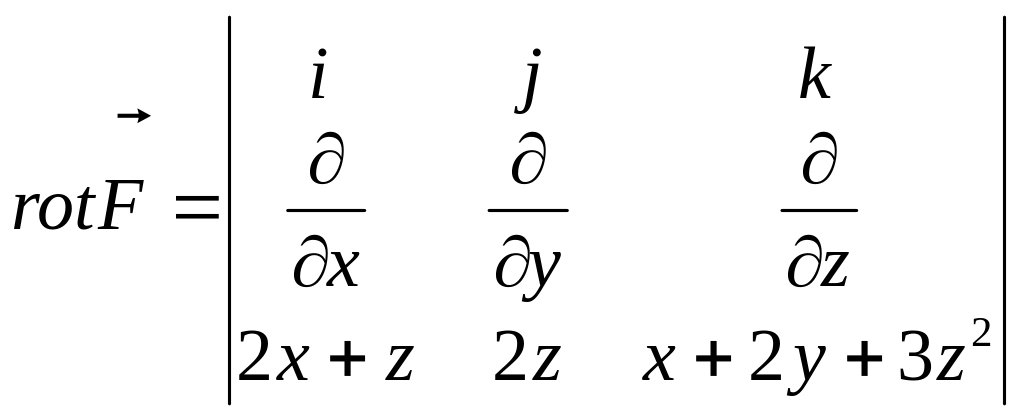
=![]()
=
=
![]()
.
Ротор равен нулю, следовательно, поле
потенциально. Возьмём
![]()
:
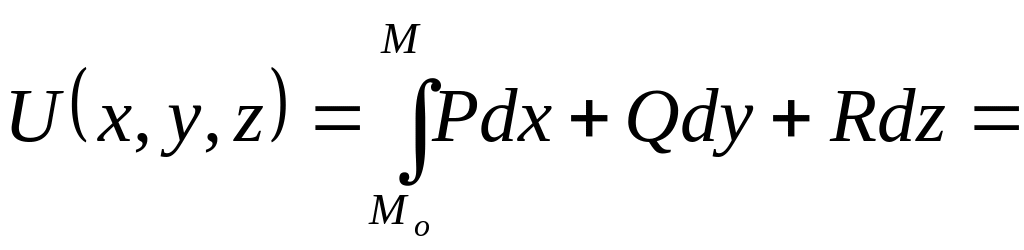
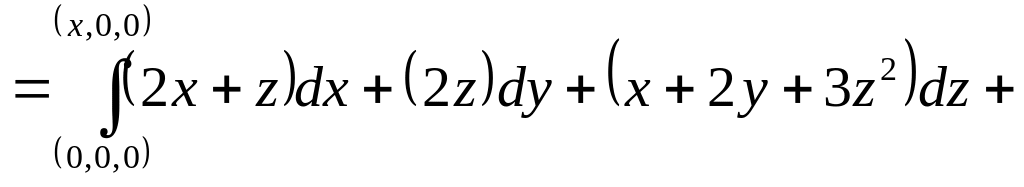
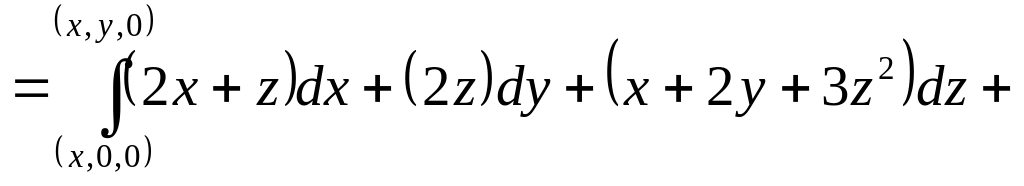
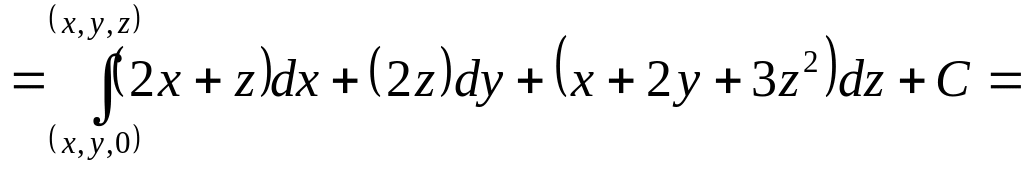
![]()
![]()
+
+![]()
=![]()
5.7. Оператор Гамильтона. Векторные операции второго порядка
Пусть
даны два поля: скалярное поле
![]()
и векторное поле
![]()
.
Для
скалярного поля можно построить векторное
– поле градиента:
![]()
,
а
по векторному полю можно построить
скалярное поле– поле дивергенции:
=
,
а
так же векторное поле – поле ротора:
.
Операции
нахождения градиента, дивергенции и
ротора называется дифференциальными
операциями первого порядка.
Для
того чтобы сделать запись менее
громоздкой, используют символический
вектор набла
![]()
,
оператор Гамильтона. При этом полагают,
что действия оператора набла подчиняются
правилам действиями с обычными векторами
при условии сохранения порядка
сомножителей. Градиент скалярной функции
получается как результат действия
оператора Гамильтона на скалярную
функцию
![]()
:
![]()
.
Дивергенция
векторного поля получается в результате
скалярного произведения векторов
![]()
и
:
![]()
![]()
.
Ротор
векторного поля получается в результате
векторного произведения векторов
и
:
![]()

.
Действие
оператора
на
![]()
,
![]()
,
![]()
даст дифференциальные операции второго
порядка над функциями
![]()
,
![]()
.
Всего таких операций пять. Рассмотрим
некоторые из них.
Операция
![]()
дает оператор
Лапласа:
=![]()
![]()
![]()
.
Таким образом, оператор Лапласа равен
![]()
![]()
.
Операция
![]()
дает
тождественный ноль, т.к. операция
представляется как векторно-скалярное
произведение:
=![]()
,
а
векторы
и
коллинеарные. Векторное поле называется
соленоидальным,
если дивергенция его равна нулю. Можно
сказать, что поле ротора соленоидально.
Операция
![]()
тоже дает тождественный ноль:
=![]()

![]()
,
так
как две строки определителя пропорциональны.
Поле называется потенциальным
или безвихревым,
если ротор поля равен нулю. Следовательно,
поле градиента – безвихревое, т.е.
потенциальное.
Операция
![]()
может быть представлена следующим
образом:
![]()
![]()
![]()
.
Операция
![]()
может представляться следующим
образом:![]()
=![]()
.
Вопросы для самопроверки
1.
Как определяются двухсторонние
поверхности?
2.
Как определяются односторонние
поверхности?
3.
Приведите пример односторонней
поверхности.
4.
Перечислите свойства поверхностного
интеграла второго рода.
5.
Каким образом поверхностный интеграл
второго рода выражается через двойные
интегралы?
6.
Как находится знак перед двойным
интегралом при
расписывании
поверхностного интеграла второго рода
в виде суммы двойных интегралов?
7.
Сформулируйте теорему Остроградского.
8.
Что такое дивергенция векторного поля?
9.
Дайте определение поля.
10.
Перечислите свойства дивергенции.
11.
Выведите формулу Стокса.
12.
Что такое ротор векторного поля?
13.
Перечислите свойства ротора векторного
поля.
14.
Когда векторное поле имеет потенциал?
15.
Каким образом дивергенция, ротор, и
градиент представляются с помощью
оператора Гамильтона?
16.
Что такое векторные операции второго
порядка?
17.
Почему
и
тожественно равны нулю?
18.
Какое векторное поле называется
соленоидальным?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
30.04.2022657.41 Кб345.doc
- #
- #
- #
- #
Имеет смысл прояснить технику расчета потенциалов для случаев сложнее одной материальной точки. Да и для нее тоже.
Пусть материальная точка массы M придает точке массы m на расстоянии r потенциал (потенциальную энергию) MmU(r). Мы ответим на два вопроса: Какой потенциал задают:
Система материальных точек;
Тело конечных размеров с заданным распределением плотности, например, вращающаяся звезда — причем пробное тело может находиться и внутри;
Шар со сферически-симметричной плотностью
Сплошная среда переменной плотности, например, межзвездный газ;
Сплошная среда с внедренными в нее материальными точками и телами конечных размеров?
И что с этим потенциалом можно делать?
Точка массой m называется пробным телом. У нее есть координаты, от которых зависит r и, следовательно, потенциал. Притягивающее тело считаем неподвижным. Если оно движется, то потенциал будет меняться во времени — техническое усложнение. Если учитываем взаимное притяжение, то будет еще сложнее — но тоже делается.
Кстати, мы уже обсуждали, что при естественных предположениях выбор потенциала U не столь и богат, точнее, выбор отсутствует: единственный вариант — это U(r)~1/r.
Потенциал удобен тем, что аддитивен: можно складывать. Поэтому две точки дадут просто сумму потенциалов. Вот и ответ на ч.1 вопроса 1: для системы материальных точек создаваемый ими потенциал равен сумме потенциалов.
Теперь обсудим тело конечных размеров. Применим идею интегрального исчисления: разделим мысленно тело на мелкие куски так, чтобы плотность каждого куска была примерно постоянной, а размеры кусков были достаточно малы, чтобы их можно было принять за материальные точки. Переход к пределу можно понимать так, что размеры эти настолько малы, насколько вам угодно. Плотность кусочка умножим на его (малый) объем, получив массу, а расстояние от кусочка до пробного тела тоже известно.
Так наше тело представлено в виде системы материальных точек, а эту задачу мы уже решили. Переход к пределу дает вместо суммы — интеграл, по объему тела. Посчитать его может быть технически сложно, но принципиально трудностей тут нет.
Обратите внимание, что, хотя мы строим приближение, разбивая тело на кусочки, интеграл дает точное значение потенциала. Если сможете интеграл этот точно вычислить))
При этом метод не имеет ограничений: пробное тело может быть снаружи, внутри, в центре, на границе… Главное — знать его координаты, чтобы выписать расстояния от любой точки тела до пробного тела.
В ряде случаев соображения симметрии позволяют значительно упростить расчеты. Например, если тело — симметричный (по плотности) шар. В этом случае ещё Ньютоном доказаны две теоремы — для потенциала U(r)=Mm/r.
Первая гласит, что шар со сферически-симметричным распределением плотности (то есть плотность в точке шара зависит только от расстояния до центра) создает такой же потенциал для тела вне себя, как материальная точка той же массы в центре.
Доказывается легко — из соображений симметрии.
Вторая гласит, что сферический слой со сферически-симметричным распределением плотности создает постоянный потенциал для тела внутри шарового слоя. Поскольку важна разность потенциалов (или градиент потенциала), можно считать его нулевым.
Доказывается тоже несложно.
Итак, в этом и только в этом частном (хотя и важном) случае есть некоторое различие между пробным телом вне гравитирующего шара и внутри него. То есть, формально различия нет, просто слои ниже и выше ведут себя по-разному по отношению к пробному телу. Если пробное вне — шар притягивает как материальная точка, и неважно, близко пробное тело или далеко. Земля, если считать ее шаром и плотность ее сферически-симметричной, притягивает нас на ее поверхности, как материальная точка той же массы в центре Земли. А звезды притягивают нас как материальные точки, потому что они слишком далеко, чтобы их размеры имели значение; но если они шары и симметричны по плотности, то их можно считать материальными точками и вблизи тоже.
Если же пробное тело внутри, то тот шарик, что ниже — притягивает как материальная точка в центре, по теореме 1. А та часть, что вне — не притягивает вообще, по теореме 2. Если пробное тело в центре, то, по теореме 2, у него нулевой потенциал: гравитация на него не действует. Ведь вся масса тела лежит выше и может быть расслоена на тонкие слои, которые не притягивают пробное тело.
Переходим к сплошной среде. Она ничем не отличается от тела конечных размеров, очевидно. Берем интеграл, и всё. Разница чисто психологическая.
Сплошная среда с материальными точками и твердыми телами — тоже не проблема. Твердые тела — просто области повышенной плотности, и не более того. Формально это то же самое. Материальные точки можно описать как плотность в виде дельта-функции и свести задачу к уже решенной. А можно посчитать создаваемый ими потенциал отдельно и прибавить к потенциалу непрерывно распределенной плотности.
Последний вопрос. Ну, нашли мы потенциал — дальше что? Ну, он — потенциал — зависит от координат пробного тела. Его градиент — вектор из производных по координатам — это сила. Можно применить второй закон Ньютона и рассчитать движение. Можно взять потенциал с обратным знаком и назвать это потенциальной энергией, и воспользоваться законом сохранения энергии. Правда, надо учитывать две вещи. Во-первых, тела и среды, которые создают потенциал, сами движутся, в том числе притягиваются пробным телом; а во-вторых, в больших масштабах гравитация Ньютона не точна и надо использовать ОТО.
Сказанное, почти все (кроме теорем Ньютона) относится к любым потенциалам, не только к гравитационному.
Последнее. Чисто про гравитацию Ньютона. Я уже рассказывал, что поле потенциальное, бездивергентное и симметричное может иметь только потенциал 1/r, с точностью до константы — и сейчас добавлю к этому немного. Смотрите, дивергенция векторного поля сил — это его источники, а для гравитации это — точечные массы (дельта-плотность) или распределение плотности ρ. Потенциальность поля означает, что вектор силы — это градиент потенциала. То есть дивергенция градиента потенциала — это распределение плотности! Получается уравнение
div grad U = 4пρ, или ∆U = 4пρ.
Это уравнение Пуассона. Решите его для какого Вам угодно распределения плотностей, возможно, с дельта-функциями, и получите потенциал. Идейно всё просто! Для одиночной дельты в правой части получится тот самый потенциал Ньютона: 1/r (с точностью до константы-множителя). Проверьте это сами — вам понравится.
Подсказка: сначала проверьте, что сумма вторых производных по x,y,z равна нулю везде (кроме начала координат, где нельзя), а потом рассмотрите шар большого радиуса с центром в нуле и докажите, что интеграл по этому шару равен константе, которая от размера шара не зависит. А это и есть дельта.
До новых встреч.
Путеводитель по каналу
Потенциальное и соленоидальное поле
Краткая теория
Векторное поле
называется потенциальным векторным полем если
оно является градиентом некоторого скалярного поля
.
Это скалярное поле
называется соответственно потенциалом векторного
поля
.
Векторное поле называется вихревым или соленоидальным векторным полем, если
через любую замкнутую поверхность S его поток равен нулю.
Пример решения задачи
Задача
Проверить,
является ли векторное поле
потенциальным и соленоидальным. В случае
потенциальности поля
найти его потенциал.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Проверка на потенциальность
Для потенциальности поля необходимо
и достаточно, чтобы
Таким образом, поле является
потенциальным.
Проверка на соленоидальность
Для соленоидальности поля:
Таким образом, поле не является
соленоидальным.
Вычисление потенциала
Потенциал можно вычислить по
формуле:
Выберем в качестве точки
точку
Нахождение потенциала
В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar { a } (mathbf { textit { M } } )$, то $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $, где $M_0 in V$ – фиксированная точка. Обычно, если в точке $mathbf { textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.
Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +intlimits_ { y_0 } ^y { Q(x,y,z_0 )dy } +intlimits_ { z_0 } ^z { R(x,y,z)dz } $.
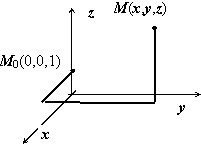
Пример 1
Доказать, что поле $bar { a } (x,y,z)=frac { ycos (xy) } { z } bar { i } +frac { xcos (xy) } { z } bar { j } -frac { sin (xy) } { z^2 } bar { k } $ потенциально и найти потенциал этого поля.
Решение
Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf { textit { V } } $, не содержащей точку $mathbf { textit { O } } (0,0,0)$. Условие безвихревости поля $bar { a } $:
$rotbar { a } (M)=left| { begin{array} { l } ,bar { i } ,,,,bar { j } ,,,bar { k } \ frac { partial } { partial x } ,,frac { partial } { partial y } ,,frac { partial } { partial z } \ ,P,,Q,,,R \ end{array} }right|=left( { frac { partial R } { partial y } -frac { partial Q } { partial z } }right)bar { i } +left( { frac { partial P } { partial z } -frac { partial R } { partial x } }right)bar { j } +left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)bar { k } =0$ в координатной форме сводится к равенствам $frac { partial R } { partial y } =frac { partial Q } { partial z } , frac { partial P } { partial z } =frac { partial R } { partial x } , frac { partial Q } { partial x } =frac { partial P } { partial y } $.
В нашем поле $P(x,y,z)=frac { ycos (xy) } { z } , Q(x,y,z)=frac { xcos (xy) } { z } ,R(x,y,z)=-frac { sin (xy) } { z^2 } $. Находим производные:
$frac { partial R } { partial y } =-frac { xcos (xy) } { z^2 } $,
$frac { partial Q } { partial z } =-frac { xcos (xy) } { z^2 } =frac { partial R } { partial y } $,
$frac { partial P } { partial z } =-frac { ycos (xy) } { z^2 } $,
$frac { partial R } { partial x } =-frac { ycos (xy) } { z^2 } =frac { partial P } { partial z } $,
$frac { partial Q } { partial x } =frac { cos (xy)-xysin (xy) } { z } $,
$frac { partial P } { partial y } =frac { cos (xy)-xysin (xy) } { z } =frac { partial Q } { partial x } $ Потенциальность поля доказана.
Ищем потенциал. Интеграл $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf { textit { M } } _ { 0 } $(0,0,1). $varphi (x,y,z)=intlimits_0^x { frac { 0cdot cos (xcdot 0) } { 1 } dx } +intlimits_0^y { frac { xcdot cos (xy) } { 1 } dy } -intlimits_1^z { frac { sin (xy) } { z^2 } dz } = =left. { sin (xy) }right|_0^y +left. { frac { sin (xy) } { z } }right|_1^z =sin (xy)+left[ { frac { sin (xy) } { z } -sin (xy) }right]=frac { sin (xy) } { z } $.
Если бы мы взяли в качестве точки $mathbf { textit { M } } _ { 0 } $ другую точку $mathbf { textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=intlimits_ { mathop { M_0 M_1 } limits^cup } { bar { a } dbar { r } } )$, поэтому $varphi (x,y,z)= frac { sin (xy) } { z } +C$.
