Как найти потенциал в точке квадрата

Электростатическое
поле точечного заряда характеризуется
не только вектором напряженности

(см. (3.1)), но и потенциалом :

. (4.1)

Из (4.1) видно,
что потенциал – это скалярная величина,
которая может быть как положительная,
так и отрицательная в зависимости от
знака заряда.

Используя
принцип суперпозиции полей, можно
найти потенциал результирующего
электрического поля в заданной точке
О как алгебраическую сумму
потенциалов полей, созданных каждым
зарядом независимо друг от друга (см.
рис. 1):

(4.2)

Задача 5.

Используя
условие задачи 4, найти потенциал 
электрического поля в точке Р.

Решение:

Подставим данные из задачи 4 в формулу
(4.2):

кВ

Ответ: _рез
= 34,1 кВ

4.1
Заряд

находится в вершине квадрата со стороной

,
а заряд

– в центре. Найти потенциал электрического
поля в точке Р, находящейся в другой
вершине этого квадрата (см. рис.).

мкКл,

мкКл,

м.

Ответ: 34,5 кВ

4.2 З
аряды

и

находятся в соседних вершинах квадрата
со стороной

.
Найти потенциал электрического поля в
точке Р, делящей сторону квадрата на
два равных отрезка (см. рис.).

мкКл,

мкКл,

м.

Ответ: 44 кВ

4.3 З
аряды

и

находятся в соседних вершинах квадрата
со стороной

.
Найти потенциал электрического поля в
точке Р, находящейся на середине
противоположной стороны квадрата (см.
рис.).

мкКл,

мкКл,

м.

Ответ: 24 кВ

4.4
Заряд

находится в вершине квадрата со стороной

,
а заряд

– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
на середине противоположной стороны
квадрата (см. рис.).

мкКл,

мкКл,

м.

Ответ: 26 кВ

4.5 З
аряд

находится в вершине квадрата со стороной

,
а заряд

– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
на середине стороны квадрата (см. рис.).

мкКл,

мкКл,

м.

Ответ: 34 кВ

4.6 З
аряд

находится в вершине квадрата со стороной

,
а заряд

– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
в противоположной вершине квадрата
(см. рис.).

мкКл,

мкКл,

м.

Ответ: 22 кВ

5. Расчет потенциала электрического поля, с озданного распределенным зарядом.

Электрическое
поле часто создается не дискретными
зарядами, а распределенными в пространстве
с плотностью

.
Тогда необходимо разбить заряженную
область на малые элементы с объемом

и зарядом

(см. рис.3). При расчете потенциала в
некоторой точке пространства О принцип
суперпозиции (4.2) для бесконечного числа
таких элементов будет выглядеть следующим
образом:

(5.1)

– где

– расстояние от малого элемента с
зарядом

до точки О.

Часто заряд
распределяется вдоль тонкой линии,
тогда заряд малого элемента длины

лучше выражать через линейную плотность
заряда

,
и уравнение (5.1) преобразуется в

(5.2)

Задача 6.

Положительный
заряд распределен по тонкому полукольцу
радиуса R = 1 м с линейной
плотностью

,
где 0< < ,

₀ = 1
мкКл/м. Определить потенциал, создаваемый
этим зарядом в центре полукольца.

Решение:

Выделим элемент
dl = Rd
на полуокружности и, учитывая, что
расстояние от элемента до точки О
равно

,
по формуле (5.2) рассчитаем потенциал в
точке О:

= 9,42 кВ

Ответ:
9,42 кВ

Задача 7

Тонкий
стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью

,
где х – координата точки на стержне,
b = 1 м – длина стержня, ₀
= 1 мкКл/м. Чему равна величина потенциала,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?

Решение:

Выделим
элементарный заряд dq
на стержне длиной dx
на расстоянии х от начала координат
О (см. рис.5). Учитывая, что r
= x, а

dq
= dx,
найдем по формуле (5.2) потенциал в точке
О:

= 4,5 кВ

Ответ: 4,5 кВ

5.1
Вдоль стержня длины

равномерно распределен заряд

.
Найти потенциал в точке

на продолжении стержня на расстоянии

от его конца (см. рис.).

м,

м,

мкКл.

Ответ: 6,2 кВ

5.2
Вдоль стержня длины

равномерно распределен заряд с линейной
плотностью

.
Найти потенциал в точке

на продолжении стержня на расстоянии

от его конца (см. рис.).

м,

м,

мкКл/м.

Ответ: 6,2 кВ

5.3 П
оложительный
заряд распределен по тонкому кольцу
радиуса

с линейной плотностью

.
Определить потенциал, создаваемый этим
зарядом в центре кольца.

R
= 1 м,

мкКл/м.

Ответ: 28 кВ

5.4. П
оложительный
заряд распределен по тонкому кольцу
радиуса

с линейной плотностью

.
Определить потенциал, создаваемый этим
зарядом в центре кольца.

R
= 1 м,

мкКл/м.

Ответ: 57 кВ

5.5
Положительный заряд распределен по
тонкому кольцу радиуса

с линейной плотностью

.
Определить потенциал, создаваемый этим
зарядом в центре кольца.

R
= 1 м,

мкКл/м.

Ответ: 75 кВ

5.6
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью

,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
потенциала, создаваемого этим зарядом
в начале координат О, совпадающем с
концом стержня?

м,

мкКл/м.

Ответ: 9 кВ

5.7 П
оложительный
заряд распределен по тонкому полукольцу
радиуса

с линейной плотностью

.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.

м,

мкКл/м.

Ответ: 14 кВ

5.8
Положительный заряд распределен по
тонкому полукольцу радиуса

с линейной плотностью

.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.

R
= 1 м,

мкКл/м.

Ответ: 14 кВ

5
.9э.
Электрон перемещается в кулоновском
поле заряженной частицы из точки А в
точку В в одном случае по траектории 1,
в другом случае по траектории 2. Как
соотносятся величины работ, совершаемых
электрическим полем над электроном, в
этих двух случаях?

а)

;
б)

;
в)

;
г)

6. Расчет напряженности электрического
поля,

созданного распределенным зарядом.

Применение
принципа суперпозиции (3.2) для нахождения
напряженности электрического поля

в векторной форме вызывает большие
трудности из-за бесконечного числа
элементарных зарядов dq,
распределенных в пространстве. В этом
случае необходимо воспользоваться не
векторным сложением вкладов полей

,
а сложением их проекций:

,

(6.1)

Задача 8

З
аряд
распределен по тонкому полукольцу
радиуса

= 1 м с линейной плотностью

.

Определить
проекцию на ось

напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца, если

мкКл/м.

Решение:

Как видно из
рис.6, проекция на ось х напряженности
электрического поля, созданного
элементарным зарядом

в точке О равна:

(6.3)

Учитывая, что

,
а

,
получим

Ответ: 4,5
кВ/м

6.1
Вдоль стержня длины

равномерно распределен заряд

.
Найти величину напряженности электрического
поля в точке

на продолжении стержня на расстоянии

от его конца (см. рис.).

м,

м,

мкКл.

Ответ: 4,5 кВ/м

6.2
Вдоль стержня длины

равномерно распределен заряд с линейной
плотностью

.
Найти величину напряженности электрического
поля в точке

на продолжении стержня на расстоянии

от его конца (см. рис.).

м,

м,

мкКл/м.

Ответ: 4,5 кВ/м

6.3
Заряд распределен по тонкому кольцу
радиуса

с линейной плотностью

.

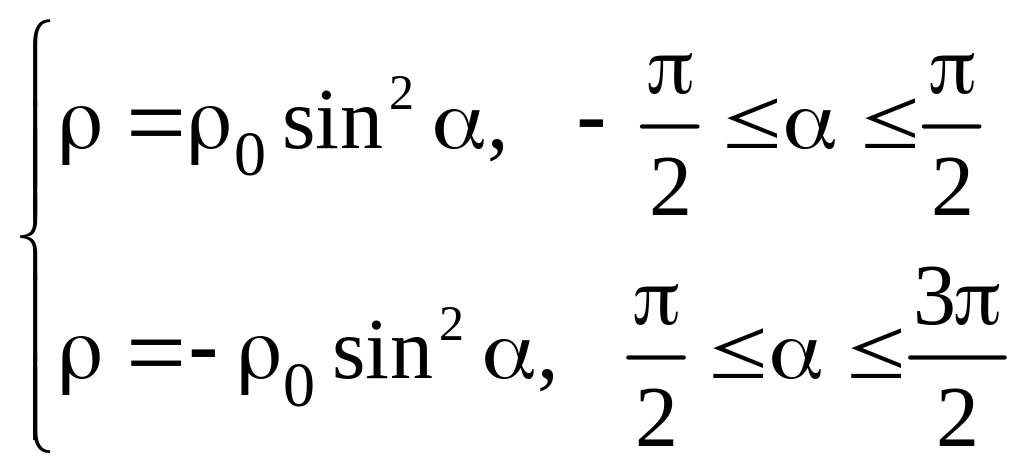
Определить
величину проекции на ось

напряженности электрического поля,
создаваемого этим зарядом в центре
кольца, если

R
= 1 м,

мкКл/м.

Ответ: 12 кВ/м

6.4
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью

,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?

м,

мкКл/м.

Ответ: 9,0 кВ/м

6.5
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью

,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?

м,

мкКл/м.

Ответ: 4,5 кВ/м

6.6
Заряд распределен по тонкому
полукольцу радиуса

с линейной плотностью

.

Определить
проекцию на ось

напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца, если R =
1 м,

мкКл/м.

Ответ: 12 кВ/м

6.7
Заряд распределен по тонкому кольцу
радиуса

с линейной плотностью

.

Определить
величину проекции на ось

напряженности электрического поля,
создаваемого этим зарядом в центре
кольца, если

R
= 1 м,

мкКл/м.

Ответ: 7,2 кВ/м

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение:


15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение: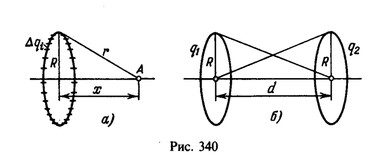

Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:


18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение: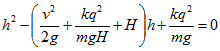

Решая его, найдем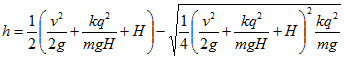

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение: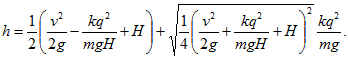


21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?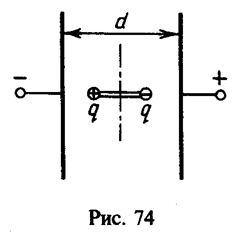

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:


28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.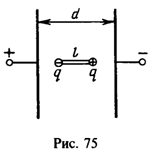

Решение: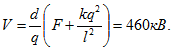


29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?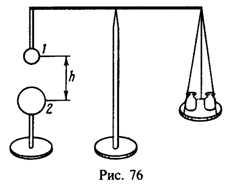

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда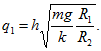
Начальный потенциал шарика 2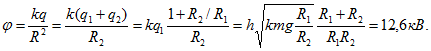

Светило науки – 16 ответов – 307 раз оказано помощи

Для начала найдите расстояние от вершин квадрата до центра – R. Оно легко находится при помощи теоремы Пифагора (диагонали квадрата пересекаются под прямым углом и делятся точкой пересечения пополам). 
Теперь подсчитаем электрическое поле от одного из зарядов, создаваемое в центре квадрата (точке пересечения диагоналей). Как известно, напряженность поля, создаваемого зарядом q в точке, отстоящей от него на расстояние r равно: 
E = k*q/r^2 
где k – коэффициент, зависящий от выбранной системы отсчета. Чему он равен в системе СИ посмотрите в справочнике. Это тот же самый коэффициент, который присутствует в законе Кулона. 
Далее, не забываем, что напряженность электрического поля – величина векторная и для нее действует принцип суперпозиции, поэтому напряженности, создаваемые каждым из зарядов складываются векторно. Но в данном случае видно, что, так, как заряды одинаковы, то векторы напряженности электрического поля, создаваемые одинаковыми зарядами одного знака, расположенными в противоположных вершинах квадрата, будут равны, но противоположны по направлении. И поэтому, их сумма будет равна 0! Остаются 2 заряда с различными знаками. Векторы напряженности электрического поля, создаваемые в центре квадрата этими зарядами будут тоже равны по модулю (т.к. заряды равны), и направлены в одну сторону, вдоль диагонали квадрата, на которой они находятся. Соответственно суммарная напряженность электрического поля в центре квадрата будет равна сумме напряженностей, создаваемых каждыми из этих зарядов, то есть удвоенной величине напряженности, создаваемой одним из зарядов: 
E = 2k*q/R^2 
где R – длина половины диагонали квадрата. 
Потенциал создаваемый зарядом q в точке, отстоящей от него на расстояние r равен: 
fi = k*q/r 
Потенциал – величина скалярная, поэтому складывается как скаляр. Так что суммарный потерциал будет равен: 
Fi = k*q1/R + k*q2/R + k*q3/R + k*q4/R = 3k*q/R – k*q/R = 2k*q/R 

2017-05-27   

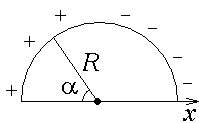
В вершинах квадрата со стороной а расположены два положительных и два отрицательных заряда, значение каждого из них $Q$ (рис. а, б). Определить напряженность электрического поля и потенциал2 в центре этого квадрата.

Решение:

Поле создано четырьмя точечными зарядами. По условию задачи требуется найти характеристики поля в точке, которая равноудалена от всех четырех зарядов и лежит с ними в одной плоскости, т. е. находится в особых условиях по отношению к источникам поля. Поэтому и потенциал, и напряженность следует определять независимо друг от друга с помощью принципа суперпозиции:

$phi = phi_{1} + phi_{2} + phi_{3} + phi_{4}$, (1)

$vec{E} = vec{E}_{1} + vec{E}_{2} + vec{E}_{3} + vec{E}_{4}$. (2)

При расчете потенциала знаки зарядов учитываются автоматически и, по-видимому, значение результирующего потенциала не зависит от порядка расположения положительных и отрицательных зарядов в вершинах квадрата. Чтобы рассчитать напряженность по равенству (2), следует показать сначала на рисунке направления всех векторов $vec{E}_{i}$, зависящие от знака заряда $Q_{i}$. Очевидно, вектор напряженности $vec{E}$ зависит от порядка расположения зарядов в вершинах квадратов.

Расстояние от любого из зарядов до рассматриваемой точки

$r = a sqrt{2}/2$.

Потенциал, создаваемый зарядом $Q_{i}$ в рассматриваемой точке, $phi_{i} = Q_{i}/(4 pi epsilon_{0} r)$. Следовательно,

$phi = sum Q_{i} / 4 pi epsilon_{0} r)$.

А так как, по условию задачи, алгебраическая сумма зарядов равна нулю, то и результирующий потенциал $phi = 0$ независимо от порядка расположения зарядов.

Рассмотрим распределение зарядов, показанное на рис. а. Напряженности $vec{E}_{2}$ и $vec{E}_{4}$ полей, созданных 2-м и 4-м зарядами в точке С, сонаправлены и равны по модулю: $| vec{E}_{2} | = | vec{E}_{4} |$. Аналогично, $| vec{E}_{1} | = | vec{E}_{3} |$. Поэтому напряженность результирующего поля

$vec{E} = 2 vec{E}_{1} + 2 vec{E}_{2}$.

Векторы $vec{E}_{1}$ и $vec{E}_{2}$ также равны по модулю и направлены ортогонально друг другу (по диагоналям квадрата), значит, результирующий вектор $vec{E}$ направлен вертикально вниз (см. рис. a) и тогда

$E = 4E_{1} cos 45^{ circ}$.

Напряженность поля, созданного каждым из зарядов,

$E_{i} = |Q_{i}| / ( 4 pi epsilon_{0} r^{2}) = |Q_{i}| / (2 pi epsilon_{0} a^{2})$.

Заряд $Q_{i}$ следует брать по модулю, так как знак каждого из зарядов был учтен при изображении соответствующего вектора $vec{E}_{i}$. Окончательно

$E = 4 | Q_{i} | cos 45^{ circ} / (2 pi epsilon_{0} a^{2}) = Q sqrt{2} /( pi epsilon_{0} a^{2})$.

При расположении зарядов, показанном на рис. б, $E = 0$.