Потенциальное и соленоидальное поле
Краткая теория
Векторное поле
называется потенциальным векторным полем если
оно является градиентом некоторого скалярного поля
.
Это скалярное поле
называется соответственно потенциалом векторного
поля
.
Векторное поле называется вихревым или соленоидальным векторным полем, если
через любую замкнутую поверхность S его поток равен нулю.
Пример решения задачи
Задача
Проверить,
является ли векторное поле
потенциальным и соленоидальным. В случае
потенциальности поля
найти его потенциал.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Проверка на потенциальность
Для потенциальности поля необходимо
и достаточно, чтобы
Таким образом, поле является
потенциальным.
Проверка на соленоидальность
Для соленоидальности поля:
Таким образом, поле не является
соленоидальным.
Вычисление потенциала
Потенциал можно вычислить по
формуле:
Выберем в качестве точки
точку
Векторное
поле
называется потенциальным, если работа
в этом поле не зависит от пути
интегрирования:
![]()
,
что
является условием потенциальности
поля. Из равенства нулю циркуляции
вектора
вдоль каждого замкнутого контура следует
по формуле Стокса, что
=0.
Существует
некоторая функция U(x,y,z),
для которой выражение Pdx
+ Qdy + Rdz
является полным дифференциалом:
dU
= Pdx + Qdy + Rdz.
Функция
U(М)
называется потенциалом векторного
поля:
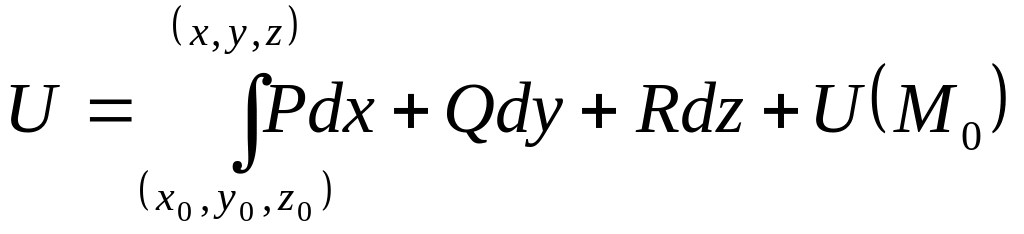
.
Для
нахождения потенциала поля по этой
формуле лучше всего интегрировать по
ломаной линии, соединяющей точки
и
,
звенья которой параллельны осям
координат.
Работа
потенциального векторного поля вдоль
любого пути равна разности значений
потенциала этого поля в конце
и начале
пути: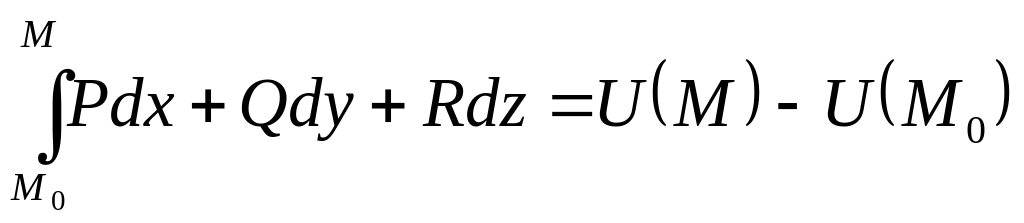
.
Пример
35.
Показать, что поле
![]()
является потенциальным и найти его
потенциал.
Решение:
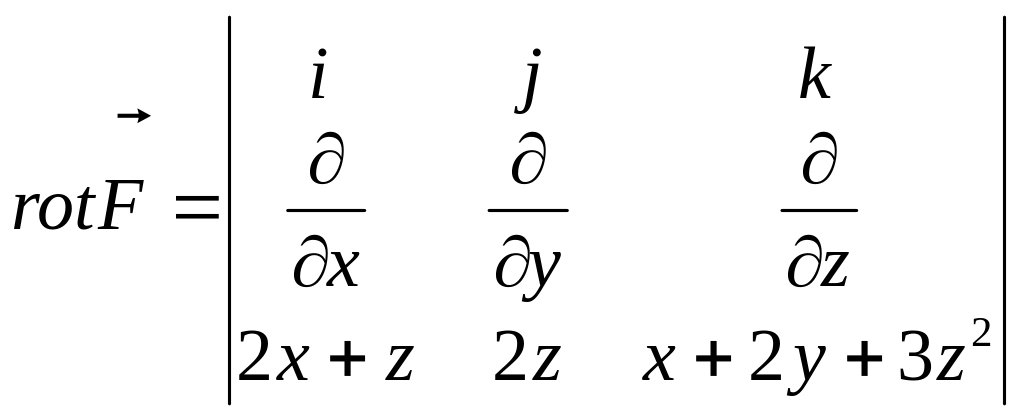
=![]()
=
=
![]()
.
Ротор равен нулю, следовательно, поле
потенциально. Возьмём
![]()
:
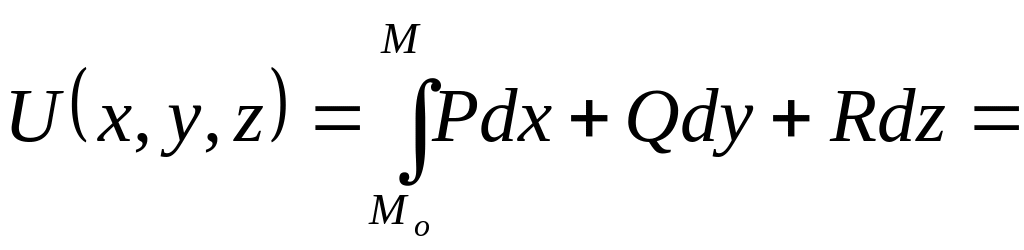
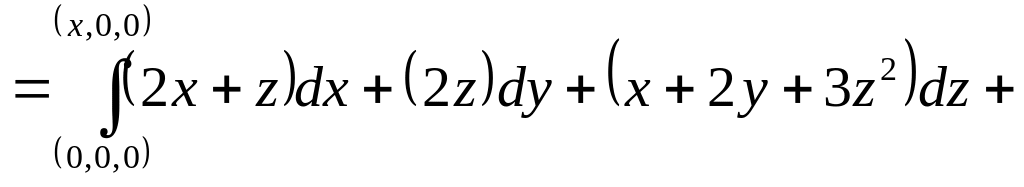
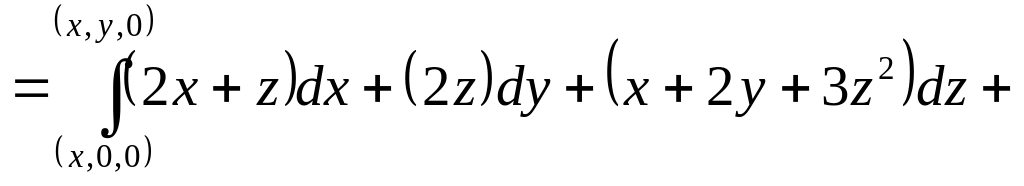
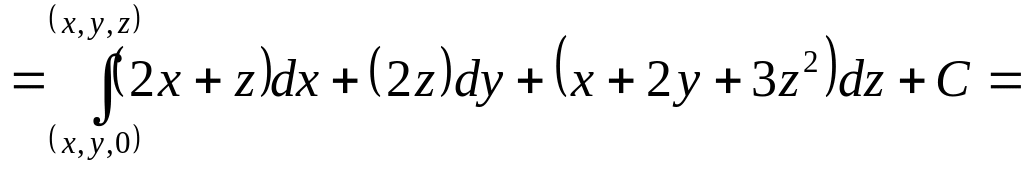
![]()
![]()
+
+![]()
=![]()
5.7. Оператор Гамильтона. Векторные операции второго порядка
Пусть
даны два поля: скалярное поле
![]()
и векторное поле
![]()
.
Для
скалярного поля можно построить векторное
– поле градиента:
![]()
,
а
по векторному полю можно построить
скалярное поле– поле дивергенции:
=
,
а
так же векторное поле – поле ротора:
.
Операции
нахождения градиента, дивергенции и
ротора называется дифференциальными
операциями первого порядка.
Для
того чтобы сделать запись менее
громоздкой, используют символический
вектор набла
![]()
,
оператор Гамильтона. При этом полагают,
что действия оператора набла подчиняются
правилам действиями с обычными векторами
при условии сохранения порядка
сомножителей. Градиент скалярной функции
получается как результат действия
оператора Гамильтона на скалярную
функцию
![]()
:
![]()
.
Дивергенция
векторного поля получается в результате
скалярного произведения векторов
![]()
и
:
![]()
![]()
.
Ротор
векторного поля получается в результате
векторного произведения векторов
и
:
![]()

.
Действие
оператора
на
![]()
,
![]()
,
![]()
даст дифференциальные операции второго
порядка над функциями
![]()
,
![]()
.
Всего таких операций пять. Рассмотрим
некоторые из них.
Операция
![]()
дает оператор
Лапласа:
=![]()
![]()
![]()
.
Таким образом, оператор Лапласа равен
![]()
![]()
.
Операция
![]()
дает
тождественный ноль, т.к. операция
представляется как векторно-скалярное
произведение:
=![]()
,
а
векторы
и
коллинеарные. Векторное поле называется
соленоидальным,
если дивергенция его равна нулю. Можно
сказать, что поле ротора соленоидально.
Операция
![]()
тоже дает тождественный ноль:
=![]()

![]()
,
так
как две строки определителя пропорциональны.
Поле называется потенциальным
или безвихревым,
если ротор поля равен нулю. Следовательно,
поле градиента – безвихревое, т.е.
потенциальное.
Операция
![]()
может быть представлена следующим
образом:
![]()
![]()
![]()
.
Операция
![]()
может представляться следующим
образом:![]()
=![]()
.
Вопросы для самопроверки
1.
Как определяются двухсторонние
поверхности?
2.
Как определяются односторонние
поверхности?
3.
Приведите пример односторонней
поверхности.
4.
Перечислите свойства поверхностного
интеграла второго рода.
5.
Каким образом поверхностный интеграл
второго рода выражается через двойные
интегралы?
6.
Как находится знак перед двойным
интегралом при
расписывании
поверхностного интеграла второго рода
в виде суммы двойных интегралов?
7.
Сформулируйте теорему Остроградского.
8.
Что такое дивергенция векторного поля?
9.
Дайте определение поля.
10.
Перечислите свойства дивергенции.
11.
Выведите формулу Стокса.
12.
Что такое ротор векторного поля?
13.
Перечислите свойства ротора векторного
поля.
14.
Когда векторное поле имеет потенциал?
15.
Каким образом дивергенция, ротор, и
градиент представляются с помощью
оператора Гамильтона?
16.
Что такое векторные операции второго
порядка?
17.
Почему
и
тожественно равны нулю?
18.
Какое векторное поле называется
соленоидальным?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
30.04.2022657.41 Кб245.doc
- #
- #
- #
- #
artem92 писал(а):
Позарез надо решение
Показать, что векторное поле [math]vec{a}=frac{2x(1-e^y)}{(1+x^2)^2},vec{i} + frac{e^y}{1+x^2},vec{j}[/math] потенциально и найти его потенциал.
Заранее огромное спасибо.
Условием потенциальности векторного поля является равенство его ротора нулю
[math]begin{aligned}mathbf{rot},vec{a}& = left(frac{partial a_z}{partial y} – frac{partial a_y}{partial z}right)vec i + left(frac{partial a_x}{partial z} – frac{partial a_z}{partial x} right)vec j + left(frac{partial a_y}{partial x} – frac{partial a_x}{partial y} right)vec k=\ &= left(frac{partial }{partial y},0 – frac{partial }{partial z}frac{e^y}{1 + x^2} right)vec i + left(frac{partial }{partial z}frac{2x(1-e^y)}{(1+x^2)^2} – frac{partial }{partial x},0right)vec j + left(frac{partial }{partial x}frac{e^y}{1 + x^2} – frac{partial}{partial y}frac{2x(1 -e^y)}{(1+x^2)^2}right)vec{k}=\ &= 0 + 0 + left(- frac{2xe^y}{(1 + x^2)^2} – frac{-2xe^y}{(1+x^2)^2}right)vec{k}=0end{aligned}[/math]
Потенциал векторного поля вычислим по формуле
[math]{color{red}boxed{{color{black}u(x,y,z)=intlimits_{x_0}^{x}a_x(x,y_0,z_0),dx+intlimits_{y_0}^{y}a_y(x,y,z_0),dy+intlimits_{z_0}^{z}a_z(x,y,z),dz+C}}}[/math]
Поскольку функции [math]a_x,,a_y[/math] и [math]a_z[/math] непрерывны во всех точках пространства, то, выбрав в качестве начальной точки пути интегрирования точку [math]M_0=(0;0;0)[/math], будем иметь
[math]u(x,y,z)= intlimits_0^xfrac{2t(1-e^0)}{(1+t^2)^2},dt+ intlimits_0^yfrac{e^t}{1+x^2},dt+ intlimits_0^z 0,dt+C= left.{frac{e^t}{1+x^2}}right|_{t=0}^{t=y}+C= frac{e^y-1}{1+x^2}+C[/math]
Пример.
1) Показать, что поле
вектора ![]() потенциально и найти его потенциал.
потенциально и найти его потенциал.
Решение.
Поле вектора ![]() будет потенциальным, если
будет потенциальным, если ![]() =0.
=0.
Найдем ![]() .
.
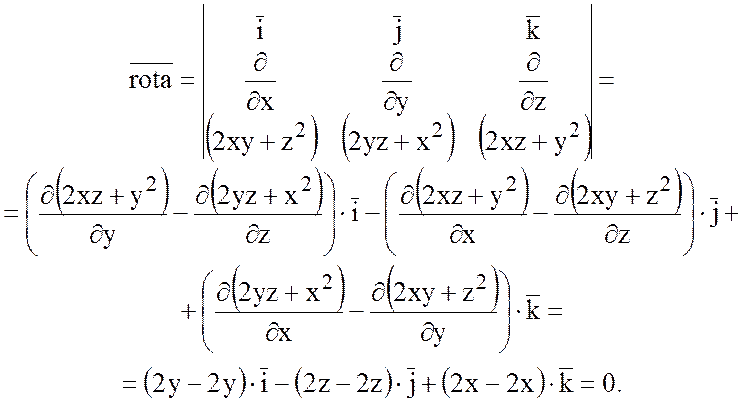
Так как ![]() =0, то поле вектора
=0, то поле вектора ![]() потенциально. Найдем потенциал. В
потенциально. Найдем потенциал. В
качестве точки ![]() возьмем (0;0;0).
возьмем (0;0;0).
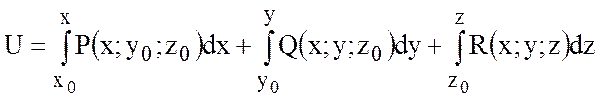 .
.
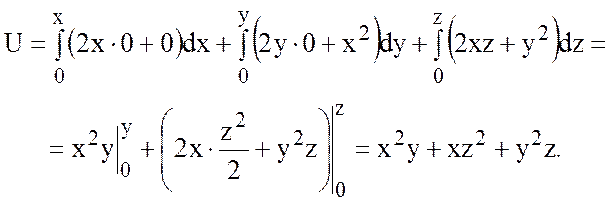
Можно проверить, что
функция U действительно является потенциалом
векторного поля вектора ![]() . Если U потенциал, то
. Если U потенциал, то 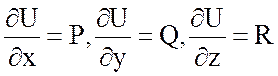 .
.
Найдем 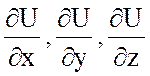 .
.
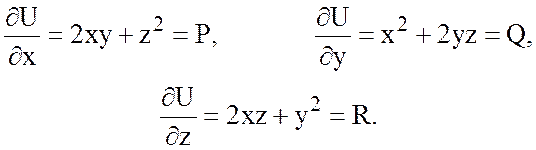
Ответ: ![]() .
.
2) Проверить, будет ли
поле вектора
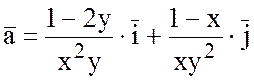 потенциальным
потенциальным
и найти его потенциал.
Решение.
Если плоское поле вектора
![]() потенциально, то
потенциально, то 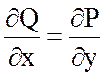 .
.
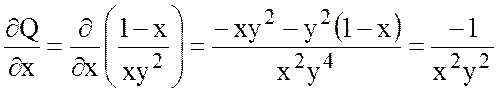 ,
,
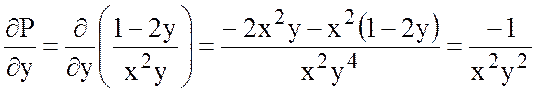 .
.
Так как 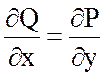 , то поле потенциально. Найдем
, то поле потенциально. Найдем
потенциал.
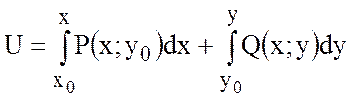 .
.
В качестве точки ![]() возьмем точку (1;1). Точку (0;0)
возьмем точку (1;1). Точку (0;0)
брать нельзя, так как в этой точке поле вектора ![]() не
не
задано, функции Р и Q не существуют в
(0;0).
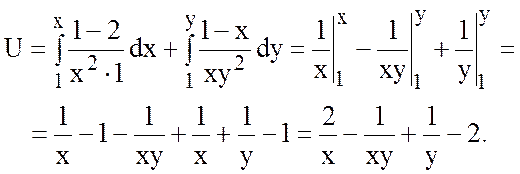
Проверка: 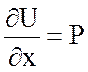 ,
, 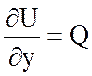 .
.
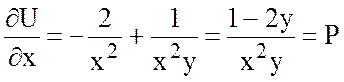 ,
,
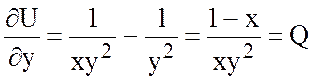 .
.
Ответ: 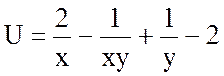 .
.
13 Циркуляция
векторного поля
Определение:Циркуляцией вектора ![]() вдоль
вдоль
замкнутого контура L называется
криволинейный интеграл по этому контуру от скалярного произведения вектора ![]() на вектор
на вектор ![]() касательной
касательной
к контуру:
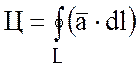 ,
,
если ![]() и
и ![]() ,
,
то
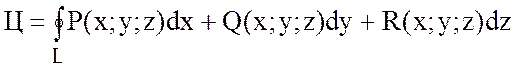 (6)
(6)
Положительным
направлением обхода замкнутой кривой L считают направление, при котором область, ограниченная этой кривой,
будет оставаться слева.
В силовом поле формула
(6) выражает работу при перемещении материальной точки вдоль линии L.
Пример.
1) Найти циркуляцию
векторного поля ![]() вдоль линии эллипса
вдоль линии эллипса 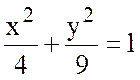
Решение.
По определению циркуляции
имеем:
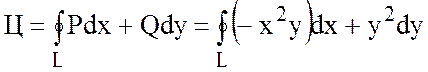 .
.
Так как 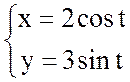 – параметрическое уравнение эллипса,
– параметрическое уравнение эллипса,
то
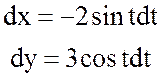 , при этом
, при этом ![]() .
.
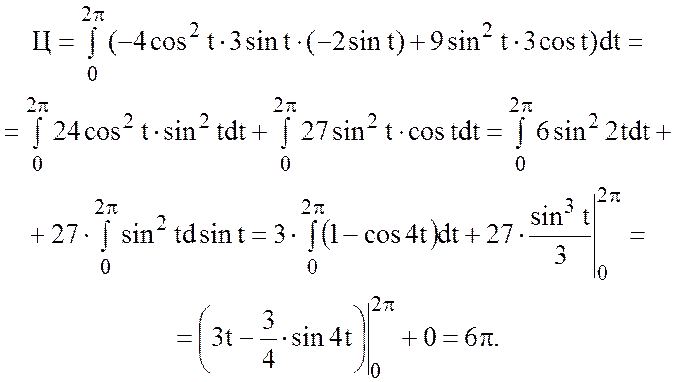
2) Найти циркуляцию
векторного поля
![]() вдоль
вдоль
линии пересечения плоскости ![]() с координатными
с координатными
плоскостями.
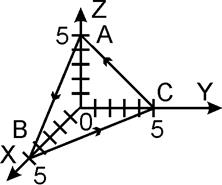
Линиями пересечения плоскости
![]() с координатными плоскостями будут
с координатными плоскостями будут
стороны треугольника АВС, т.е.
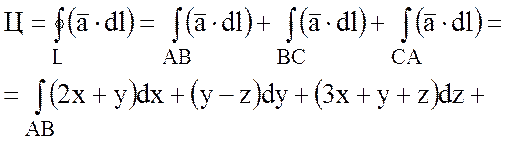
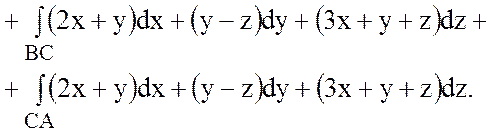
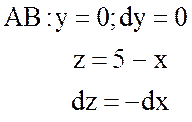 ;
; 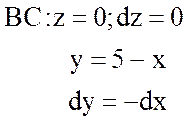 ;
;
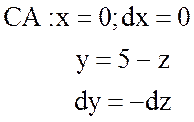 .
.
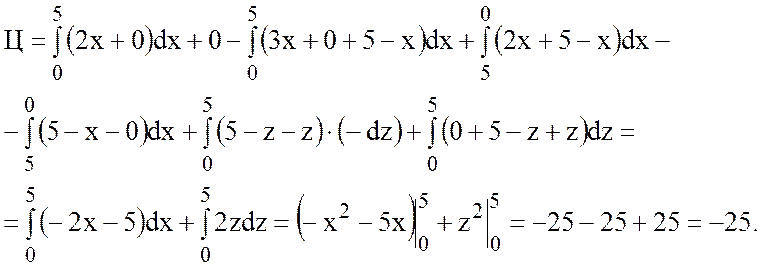
14 Формула Стокса
Пусть координаты вектора ![]() непрерывны и имеют непрерывные
непрерывны и имеют непрерывные
частные производные, тогда циркуляцию вектора ![]() по
по
замкнутому контуру L удобно вычислить
по формуле Стокса.
Теорема:Циркуляция вектора ![]() по
по
замкнутому контуру L равна потоку
ротора этого вектора через любую поверхность S, натянутую на контур L.
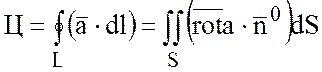 .
.
Предполагается, что
ориентация нормали ![]() к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
контура в выбранном направлении был виден совершающимся против часовой стрелки.
Так как
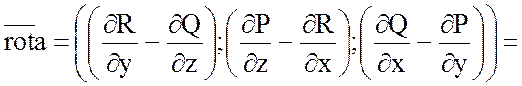
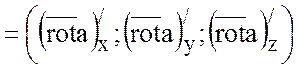 , а
, а ![]() ,
,
то
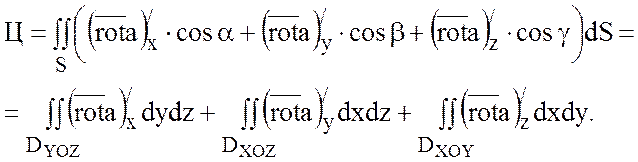
Так как
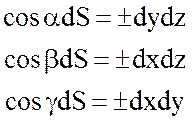 .
.
Из теоремы следует
формула Стокса:
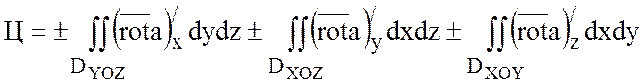 ,
,
где ![]() – проекции поверхности S на плоскости YOZ, XOZ, XOY.
– проекции поверхности S на плоскости YOZ, XOZ, XOY.
Из формулы Стокса
следует, что если поле вектора ![]() потенциально, то
потенциально, то
тогда ![]() =0 и циркуляция вектора
=0 и циркуляция вектора ![]() потенциального поля равна нулю
потенциального поля равна нулю
Частным случаем формулы
Стокса, когда поле вектора ![]() плоское, будет
плоское, будет
формула Грина.
Если поле вектора ![]() плоское, то
плоское, то
![]() ,
,
 ,
,
так как 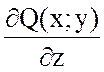 =0 и
=0 и 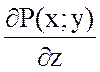 =0.
=0.
Тогда в формуле Стокса 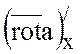 =0 и
=0 и 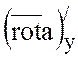 =0
=0
и
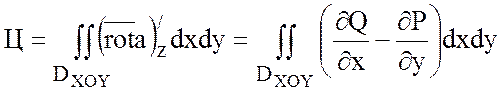 .
.
Примеры.
1) Решим второй пример из
рассмотренных ранее вторым способом по формуле Стокса.
Найти циркуляцию
векторного поля
![]() вдоль
вдоль
линии пересечения плоскости ![]() с координатными
с координатными
плоскостями.
Решение.
Найдем ![]() :
:
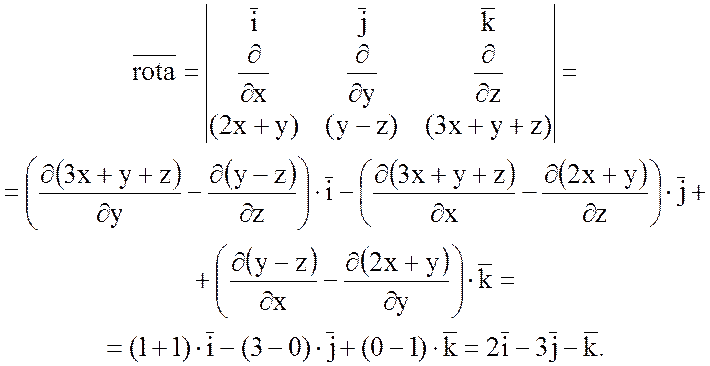
Тогда 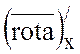 =2,
=2, 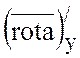 =-3,
=-3,
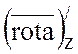 =-1.
=-1.
Найдем циркуляцию по
формуле Стокса:
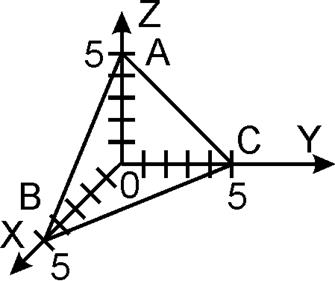
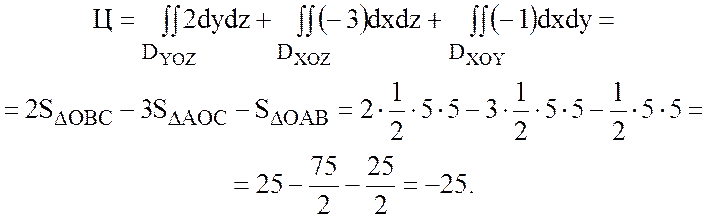
2) Вычислить циркуляцию
вектора ![]() по контуру L, образованному линиями y=x,
по контуру L, образованному линиями y=x, ![]() .
.
Решение.
Так как поле вектора ![]() плоское, то найдем циркуляцию по
плоское, то найдем циркуляцию по
формуле Грина:
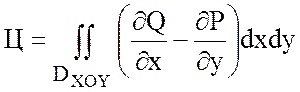 .
.
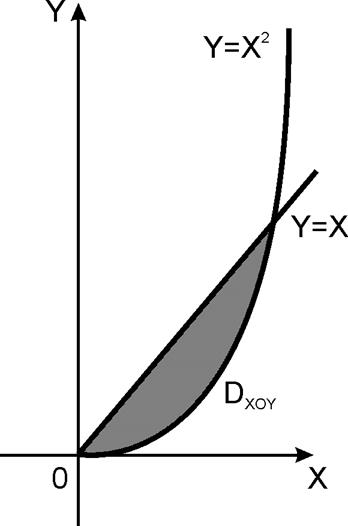
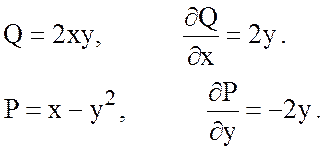
Рисунок 17
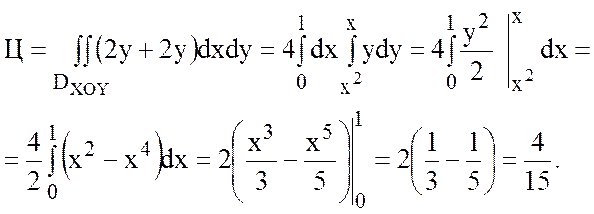
15 Оператор
Гамильтона. Векторные дифференциальные операции второго порядка
Многие операции
векторного анализа могут быть записаны в сокращенной и удобной для расчетов
форме с помощью символического оператора Гамильтона «набла».
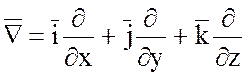 .
.
В этом операторе
соединены дифференциальные и векторные свойства. Формальное умножение ![]() на функцию U(x;y;z) понимают как частное дифференцирование
на функцию U(x;y;z) понимают как частное дифференцирование ![]() .
.
Правила действия с
оператором «набла» таковы:
1) Произведение набла –
вектора ![]() на скалярную функцию U(x;y;z) дает градиент этой функции:
на скалярную функцию U(x;y;z) дает градиент этой функции:
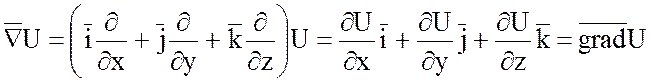 .
.
2) Скалярное произведение
набла – вектора ![]() на векторную функцию
на векторную функцию ![]() дает дивергенцию этой функции:
дает дивергенцию этой функции:
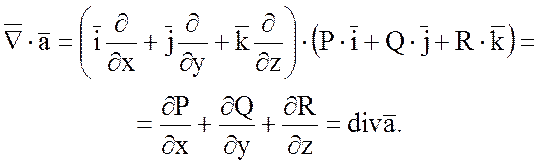
3) Векторное произведение
набла – вектора ![]() на векторную функцию
на векторную функцию ![]() дает ротор этой функции:
дает ротор этой функции:
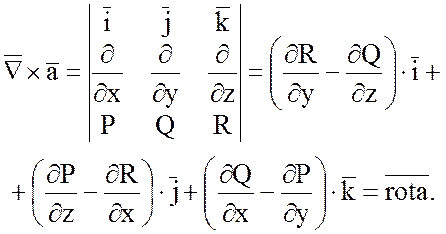
Рассмотрим теперь
векторные дифференциальные операции второго порядка.
Пусть задано скалярное
поле U(x;y;z) и нашли градиент этого поля ![]() . Поле градиента является векторным
. Поле градиента является векторным
полем и можно найти его дивергенцию и ротор, т.е. ![]() и
и
![]() .
.
а) 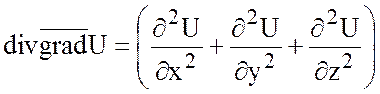 . (*)
. (*)
Действительно, 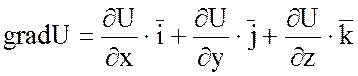 , образуя дивергенцию этого вектора,
, образуя дивергенцию этого вектора,
мы и получим данную формулу (*). Правая часть формулы (*) называется оператором
Лапласа от функции и обозначается ![]() :
:
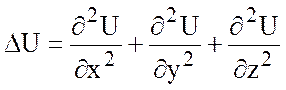 .
.
Выражение ![]() можно с помощью набла – вектора
можно с помощью набла – вектора
записать так:
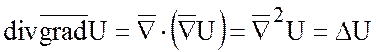 .
.
б) Пусть функция U(x;y;z) имеет непрерывные частные
производные до второго порядка включительно, тогда ![]() =0.
=0.
Это равенство проверяется
просто, так как все координаты ![]() представляют
представляют
собой разность вторых смешанных производных функции U, отличающихся лишь порядком дифференцирования, которые
равны, например:
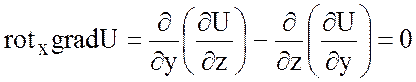 .
.
Это соотношение легко
запоминается, если записать его с помощью набла – вектора:
![]() ,
,
так как векторное
произведение одинаковых «векторов» равно нулю.
в) ![]() .
.
Образуя дивергенцию от ![]() , получим:
, получим:
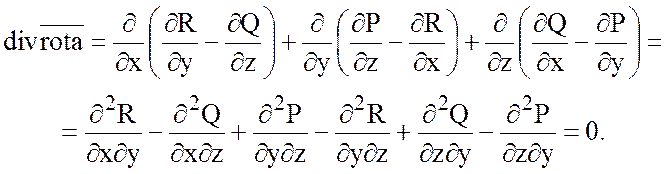
Так как вторые смешанные
производные равны, если функции P, Q, R имеют непрерывные частные производные до второго порядка
включительно.
С помощью набла – вектора
это запишется так:
![]() .
.
То есть мы имеем
смешанное произведение трех «векторов», из которых два вектора одинаковы. Такое
произведение равно нулю.
16 Семестровое задание
по теме «Теория поля»
Решение задач.
Задача 1.
а) Найти угол между
градиентами функции ![]() в точках (1;-1;0) и
в точках (1;-1;0) и
(2;1;1).
Решение.
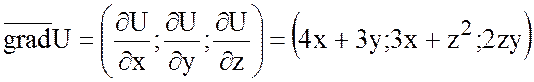 .
.
Найдем градиент функции U в точках (1;-1;0) и (2;1;1):
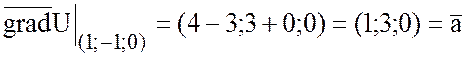 ,
,
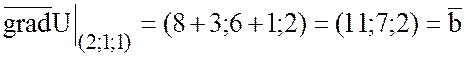 .
.
Тогда косинус угла ![]() между градиентами, т.е. между
между градиентами, т.е. между
векторами ![]() и
и ![]() найдем
найдем
по формуле:
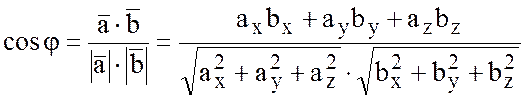 ,
,
