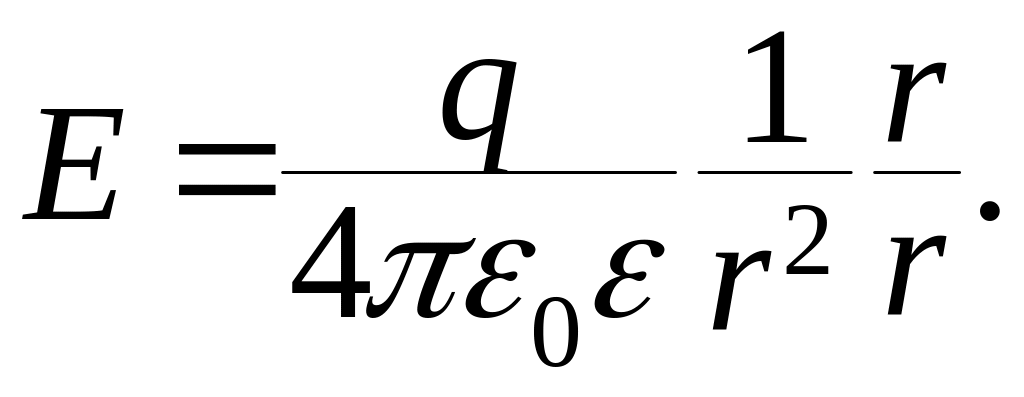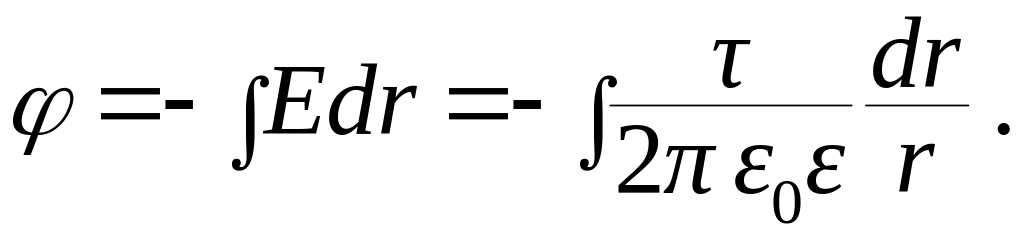Как найти потенциал внешней сферы

2021-06-21   

Две тонкие концентрические проводящие сферы радиусами $R_{1}$ и $R_{2}$ ($R_{1} < R_{2}$) несут на себе заряды $q_{1}$ и $q_{2}$ соответственно. Вычислите потенциалы сфер и энергию системы. Какой заряд останется на внутренней сфере, если ее заземлить (рис.)? Как изменится при этом энергия системы?

Решение:

Потенциал любой точки пространства можно найти по принципу суперпозиции как сумму потенциала $phi_{1} (r)$, создаваемого зарядами первой сферы, и потенциала $phi_{2}(r)$, создаваемого второй сферой. Для каждой точки во внешней области ($r geq R_{2}$) оба слагаемых надо вычислять по формуле $phi = frac{1}{4 pi epsilon_{0} } frac{q}{r}$ – получится потенциал поля точечного заряда. Значит, потенциал внешней сферы ($r = R_{2}$) равен

$phi (R_{2}) = frac{1}{4 pi epsilon_{0} } frac{q_{1} + q_{2} }{R_{2} }$. (4)

В пространстве между сферами ($R_{1} < r < R_{2}$) вклад внутренней сферы надо вычислять по формуле $phi = frac{1}{4 pi epsilon_{0} } frac{q}{r}$, а вклад внешней сферы по формуле $phi_{сф} = phi (R) = frac{1}{4 pi epsilon_{0} } frac{q}{R}$:

$phi(r) = frac{1}{4 pi epsilon_{0} } frac{q_{1} }{r} + frac{1}{4 pi epsilon_{0} } frac{q_{2} }{R_{2} }$.

Положив в этой формуле $r = R_{2}$, мы опять получим потенциал внешней сферы, а положив $r = R_{1}$, получим ответ для потенциала внутренней сферы:

$phi (R_{1} ) = frac{1}{4 pi epsilon_{0} } = frac{1}{4 pi epsilon_{0} } frac{q_{1} }{R_{1} } + frac{1}{4 pi epsilon_{0} } frac{q_{2} }{R_{2} }$. (5)

Такой же потенциал будет у всех точек при $r < R_{1}$.

Энергия этой системы зарядов равна

$W = frac{1}{2} q_{1} phi (R_{1} ) + frac{1}{2} q_{2} phi (R_{2} ) = frac{1}{ 8 pi epsilon_{0} } left ( frac{q_{1}^{2} }{R_{1} } + frac{2q_{1}q_{2} }{R_{2} } + frac{q_{2}^{2} }{R_{2} } right )$.

Первый и третий члены представляют собой собственные энергии сфер, а второй член – энергию их взаимодействия.

После заземления внутренней сферы ее потенциал станет равным нулю. Применяя формулу (5), получим уравнение для нового заряда этой сферы:

$0 = frac{1}{4 pi epsilon_{0} } frac{q_{1}^{ prime } }{R_{1} } + frac{1}{4 pi epsilon_{0} } frac{q_{2}}{R_{2} }$,

откуда найдем

$q_{1}^{ prime} = – q_{2} frac{R_{1}}{R_{2}}$.

С помощью формулы (4) найдем теперь новый потенциал внешней сферы:

$phi^{ prime } (R_{2}) = frac{1}{4 pi epsilon_{0} } frac{q_{1}^{ prime} + q_{2} }{R_{2} } = frac{1}{4 pi epsilon_{0} } frac{q_{2}(R_{2} – R_{1} ) }{R_{2}^{2} }$.

Поскольку потенциал внутренней сферы теперь равен нулю, энергия системы в конечном состоянии равна

$W^{ prime } = frac{1}{2} q_{2} phi^{ prime } (R_{2}) = frac{1}{8 pi epsilon_{0} } frac{q_{2}^{2}(R_{2} – R_{1} ) }{R_{2}^{2} }$.

Видно, что конечная энергия системы меньше начальной. Это и понятно. Уменьшение электростатической энергии системы равно тому количеству теплоты, которое выделилось при перезарядке.

Примеры решения задач по физике — концентрические проводящие сферы

Суббота, 25 февраля, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ_in (внутренней) и φ_ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ_ex складывается из двух потенциалов: внешней сферы φ₁ и собственно внутренней сферы φ₂.

Потенциал внешней сферы φ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

Потенциал внутренней сферы φ₂ определяется известным соотношением:

Тогда общий потенциал φ_in на поверхности внутренней сферы равен:

Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’₁ и собственно внешней сферы φ’₂.

Потенциал внутренней сферы φ’₁ на расстоянии R от ее центра определяется известным соотношением:

Формула, определяющая потенциал внешней сферы φ’₂ на ее поверхности, также хорошо известна:

Тогда общий потенциал на поверхности внешней сферы равен:

Задача 2. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R₂. Определите потенциал шара φ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

где q₁ и q₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q₁ + q₂. После несложных преобразований получаем:

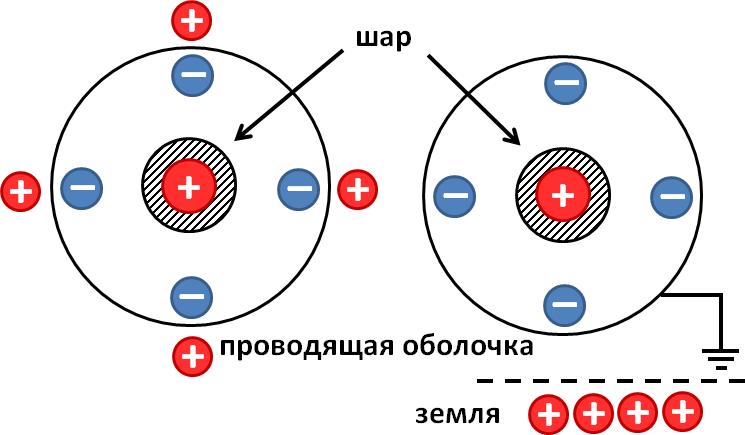
Задача 3. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R₂. Чему станет равен потенциал шара φ‘, если заземлить оболочку?

Начнем с рисунка к решению задачи:

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q₂, поскольку он притягивается к положительному заряду q₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Валерьевич

Три заряженные концентрические сферы

Продолжаю серию задач с проводящими сферами. Вот несложная задача.

Три проводящие концентрические сферы радиусов , и  имеют заряды , и  соответственно. Определите потенциал каждой из сфер и постройте график зависимости .

Решение. Рассмотрим внутреннюю сферу. Ее потенциал будет складываться из потенциалов всех трех сфер, причем потенциал поверхности будет равен потенциалу любой точки внутри нее:

Если рассмотреть пространство между внутренней и второй сферами, то потенциал каждой точки здесь зависит от ее расстояния от центра сферы и определяется по формуле:

На поверхности это величина , а при удалении от центра потенциал падает – это гипербола.

Теперь рассмотрим вторую сферу. Он также является суммой трех потенциалов:

Первое слагаемое – потенциал внутренней сферы на расстоянии , второе – потенциал самой этой сферы, третье – потенциал внешней сферы.

При удалении от поверхности этой сферы потенциал тоже будет падать, так как он будет определяться выражением:

Теперь переходим ко внешней сфере: ее потенциал складывается из потенциалов двух первых при , и потенциала самой третьей сферы.

Значит, во внешнем пространстве тоже будет нулевой потенциал.

Решение

Внутри малой проводящей сферы напряженность поля все время равна нулю. Снаружи от большой сферы поле не зависит от положения точечного заряда — его силовые линии не выходят за внутреннюю поверхность большой сферы, а заряд внешней поверхности этой сферы распределен по ней равномерно и равен . По этой причине после соединения сфер проводником при перетекании зарядов с внутренней сферы на внешнюю поле снаружи не изменится.

Найдем начальные потенциалы сфер, которые равны сумме потенциалов, создаваемых всеми зарядами системы, в том числе и наведенными. Поскольку суммарные заряды каждой из сфер вначале равны нулю, то они не дают вклада в суммарный потенциал центральной точки системы, то есть ее потенциал определяется только зарядом и равен . Таким же будет и потенциал внутренней сферы, поскольку поле внутри нее равно нулю. Потенциал внешней сферы такой же, как и потенциал точечного заряда на расстоянии от него: . Таким образом, разность потенциалов между сферами

Если соединить сферы проводником, то их потенциалы сравняются. Пусть с внутренней сферы перетек на наружную заряд . Тогда суммарный заряд большой сферы станет равным , а малой — равным . Подсчитаем потенциал малой сферы и приравняем его к потенциалу большой сферы, который в процессе перетекания зарядов не изменяется. В центре малой сферы . Отсюда находим: .  

Ответ

Разность потенциалов между сферами перетекший заряд .

Найдем
потенциал, создаваемый проводящей
заряженной сферой радиуса R. Как известно,
внутри сферы (при r
< R)
E
= 0;
вне сферы (при r
> R)

С учетом формулы (13.18), связывающей
напряженность и потенциал, находим:

1.

,
отсюда 
= const;

2.

(13.21)

Постоянную
C
выберем из условия, что

при

,
отсюда C
= 0. Потенциал внутри проводящей сферы
имеет одинаковое значение во всех точках
внутри сферы и равен потенциалу на
поверхности:

(13.22)

Потенциал
вне заряженной сферы равен потенциалу
точечного заряда, помещенного в центр
сферы.

На
рис. 13.6 приведен график зависимости
потенциала 
от расстояния до центра сферы r.

Для
проводящего шара получим тот же результат,
что и для сферы.

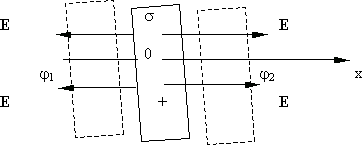
Найдем
теперь потенциал заряженной бесконечной
плоскости с поверхностной плотностью
заряда 
(рис. 13.7).

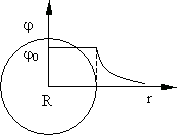
Рис.
13.6.

Напряженность
электрического поля плоскости:

.
Потенциал 
получим в виде

(13.23)

Выберем
начало отсчета потенциала так, чтобы
при x
= 0, потенциал был равен 0, тогда C
= 0.

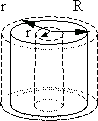
Рис.
13.7. Рис. 13.8.

Потенциал электрического поля заряженной плоскости:

171

(13.24)

Разность
потенциалов между двумя точками поля

(13.25)

Потенциал электрического поля заряженного цилиндра:

Потенциал
заряженного бесконечного цилиндра с
линейной плотностью 
найдем из соотношения:

(13.26)

Потенциал
поля внутри цилиндра (рис. 13.8) является
постоянной величиной при r
< R и равен
потенциалу на поверхности цилиндра,
т.к. E = 0
внутри цилиндра. Потенциал вне заряженного
цилиндра (r
> R):


Если принять, что потенциал j
на поверхности цилиндра (при r
= R)
равен нулю, тогда постоянная

Потенциал
вне цилиндра имеет такую же величину,
как и потенциал заряженной нити,
помещенной на оси цилиндра

(13.27)

Глава 14. Диэлектрики в электростатическом поле

14.1. Проводники и диэлектрики

По
электрическим свойствам твердые тела
можно разделить на проводники и
диэлектрики. Основным отличием
диэлектриков от проводников является
отсутствие в диэлектриках свободных
зарядов, способных перемещаться в
электрическом поле. Проводники содержат
свободные заряды, носителями которых
являются электроны, не связанные с
атомами.

Каждое
вещество может проявлять свойства
диэлектрика и проводника, в зависимости
от внешних условий и времени наблюдения.
Так, заряженный шар из диэлектрика,
например из эбонита, подвешенный на
шелковой нити, может долго сохранять
свой заряд, но через длительное время
заряд все же стечет с поверхности шара.

Если
заряженное тело находится вблизи
другого, первоначально незаряженного
тела, то в проводниках и диэлектриках
происходит электростатическая индукция,
и на соседнем теле появятся заряды
противоположного знака. В проводнике
заряд распределится по поверхности,
внутри проводника заряд будет равен
0, поэтому напряженность электрического
поля E
= 0. В диэлектрике связанные заряды
распределяются по всему объему.

Если
проводник поместить во внешнее
электростатическое поле, то на концах
проводника появятся заряды разного
знака. Если разрезать проводник на две
части, то на каждой останется заряд
одного знака.

В
диэлектрике, помещенном в электростатическое
поле, также появятся на концах разноименные
заряды, но эти заряды нельзя отделить.
В разрезанном диэлектрике суммарный
заряд каждой его части будет равен
нулю.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #