Как найти потенциальную энергию электрического поля - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Потенциал.

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

${displaystyle varphi ={frac {W_{p}}{q_{p}}}.}$

Напряжённость электростатического поля и потенциал varphi связаны соотношением^[1]

${displaystyle int limits _{A}^{B}mathbf {E} cdot mathbf {dl} =varphi (A)-varphi (B),}$

или обратно^[2]:

Здесь nabla — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ${mathbf nabla }cdot {mathbf E}={rho over varepsilon _{0}}$ , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

${displaystyle {nabla }^{2}varphi =-{rho over varepsilon _{0}},}$

где varphi — электростатический потенциал (в вольтах), rho — объёмная плотность заряда (в кулонах на кубический метр), а ${displaystyle varepsilon _{0}}$ — электрическая постоянная (в фарадах на метр).

Неоднозначность определения потенциала[править | править код]

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

${displaystyle varphi _{1}-varphi _{2}={frac {A_{f}^{q^{*}1to 2}}{q^{*}}},}$

где:

$varphi _{1}$

— потенциал в точке 1,

$varphi _{2}$

— потенциал в точке 2,

$A_{{f}}^{{q^{{*}}1to 2}}$

— работа, совершаемая полем при переносе пробного заряда $q^{{*}}$

из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произвольностью выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения[править | править код]

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Использование термина[править | править код]

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Кулоновский потенциал[править | править код]

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния ${frac 1r}$ (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

${displaystyle varphi =k{frac {q}{r}},}$

где обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

$k={frac 1{4pi varepsilon _{0}}}$

= 9·10⁹ В·м/Кл,

— величина заряда, — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

${displaystyle W=sum _{i<j}k{frac {q_{i}q_{j}}{r_{ij}}}={frac {1}{2}}sum _{ineq j}k{frac {q_{i}q_{j}}{r_{ij}}}.}$

В электродинамике[править | править код]

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ${displaystyle textstyle int _{C}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}}$ зависит от пути, потому что (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы

{displaystyle mathbf {B} =mathbf {nabla } times mathbf {A} ,,}

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

${displaystyle mathbf {F} =mathbf {E} +{frac {partial mathbf {A} }{partial t}}}$

является консервативным полем по закону Фарадея, и поэтому можно написать

${displaystyle mathbf {E} =-mathbf {nabla } V-{frac {partial mathbf {A} }{partial t}},,}$

где V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

${displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)},,}$

в отличие от электростатики.

См. также[править | править код]

Гальвани-потенциал
Вольта-потенциал
Векторный потенциал электромагнитного поля
4-потенциал
Стандартный электродный потенциал
Степень окисления
Гравитационный потенциал
Ядерный потенциал

Примечания[править | править код]

Литература[править | править код]

Алешкевич В. А. Электромагнетизм. — М.: Физматлит, 2014. — 404 с. — 700 экз. — ISBN 978-5-9221-1555-1.

Источник

Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.

Потенциальные и непотенциальные силы в электродинамике

Все силы можно разделить на потенциальные и непотенциальные.

Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.

Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))

Энергия системы заряженных тел

Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.

Изменение потенциальной энергии заряда в однородном электрическом поле

Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).

Рис. (1). Перемещение заряда в однородном поле

Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.

Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б – vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б – vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:

(A=-E_Б). ((5))

Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))

Энергия взаимодействия точечных зарядов

Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.

Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).

Рис. (2). Перемещение заряда в поле точечного заряда

Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.

В таком случае работа электрического поля на дуге (СБ) будет нулевой:

(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))

поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:

(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)

(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))

Энергия системы (n) точечных зарядов

Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.

Свойство линий напряжённости электрического поля

Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).

Рис. (3). Замкнутая линия электрического поля

Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).

Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.

Источники:

Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.

Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.

Рис. 3. Замкнутая линия электрического поля. © ЯКласс.

Источник

Electrical potential energy is the cumulative effect of the position and configuration of a charged object and its neighboring charges. The electric potential energy of a charged object governs its motion in the local electric field. Sometimes electrical potential energy is confused with electric potential, however, the electric potential at a specific point in an electric field is the amount of work required to transport a unit charge from a reference point to that specific point and electrical potential energy is the amount of energy required to move a charge against the electric field.

In this article, let’s understand the electrical potential energy, electric potential, their key concepts, applications, and solved problems.

What is Electric Potential Energy?

The electric potential energy of a system of charges or a single charge is the total work done by an external force to bring the charge or system of charges from infinity to a reference point in an electric field without any acceleration.

Definition: Electric potential energy is the total energy possessed by a charge in order to change its position in the electric field.

Overview

As electrical potential energy has only magnitude and no direction, therefore it is a scalar quantity. The SI unit of electric potential energy is Joule (J). The following table shows some important points and symbols of the electric potential energy:

Electric Potential Energy
Representation	U_E or U
Dimensions	ML²T^-2
General Formula	U_E = kq₁q₂/r
SI Unit	Joules

Two factors are majorly responsible for the electric potential energy:

The charge on the object.
The relative position of the object with another neighboring charge.

Electric Potential Energy Formula

If W is the work done in transferring a unit positive charge q from infinity to a particular point in the electric field, this work done energy will be stored in form of the electric potential energy or electrostatic potential energy. Let’s derive the expression for electric potential energy,

Consider the electrostatic field E that exists as a result of a charge arrangement. Consider the electric field E caused by a charge Q placed at the origin for simplicity. Consider moving a test charge q from a point R to a point P while resisting the charge Q’s repulsive force. If Q and q are both positive or both negative, this will happen with reference. Let’s use Q as an example, with q > 0,

A test charge q (> 0) is moved from point R to point P against the repulsive force on it by the charge Q (> 0) placed at the origin.

Assume that the test charge q is so little that it has no effect on the original configuration, specifically the charge Q at the origin (or that Q is held fixed at the origin by some unknown force). Second, apply an external force F_ext exactly enough to counter the repulsive electric force F_E (i.e. F_ext= –F_E ) as the charge q move from R to P. This means that when the charge q is transported from R to P, it experiences no net force or acceleration, implying that it is transported at an infinitesimally slow constant speed. In this case, the work done by the external force is minus the work done by the electric force, and the potential energy of the charge q is fully stored. If the external force is withdrawn when the charge reaches P, the electric force will pull the charge away from Q – the stored energy (potential energy) at P is used to provide kinetic energy to the charge q, preserving the sum of the kinetic and potential energies.

Therefore, the work done by external forces in moving a charge q from R to P can be written as,

$W_{RP}=int_{R}^{P} F_{ext}cdot{dr}$

Since, F_ext= –F_E, then we can write,

$W_{RP}=-int_{R}^{P} F_{E}cdot{dr}$

The above expression is the work done against electrostatic opposing force and gets stored as potential energy. A particle with charge q has a definite electrostatic potential energy at every location in the electric field. The work done raises its potential energy by an amount equal to the potential energy difference between points R and P. Therefore, the potential energy difference can be expressed as,

∆U = U_P – U_R = W_RP

Note that this displacement is in the inverse direction of the electric force, hence the work done by the electric field is negative, i.e., –W_RP.

As a result, the work required by an external force to move (without accelerating) charge q from one location to another for an electric field of any arbitrary charge configuration can be defined as the electric potential energy difference between two points. At this point, two key points should be made,

The work done by an electrostatic field in transferring a charge from one location to another is solely reliant on the initial and final points and is unaffected by the path used to get there. This is a conservative force’s defining attribute.
The above expression defines the difference in potential energy in terms of a physically meaningful quantity of work. Within an additive constant, potential energy is clearly uncertain. This indicates that the actual value of potential energy has no physical significance; only the change in potential energy is essential. We can always add an arbitrary constant to potential energy at any time since the potential energy difference will not change,

(U_P – β ) – (U_R – β ) = U_P– U_R

To put it another way, the point where potential energy is zero can be chosen at will. Electrostatic potential energy 0 at infinity is a convenient choice. If we take the point R at infinity with this option,

W_∞P = U_P– U_∞ = U_P– 0 = U_P

The above expression defines the potential energy of a charge q at any moment in time.

The work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that location (in the presence of field due to any charge configuration) is called potential energy of charge q at a point.

Electric Potential Energy of a Point Charge

Consider the origin of a point charge Q. Consider Q to be a positive character. We wish to find the electrical potential energy at any location P using the position vector r from the origin. To do so, we need to figure out how much work it takes to transfer a unit-positive test charge from infinity to point P. When Q > 0, the work done against the repulsive force on the test charge is positive. Because the work is independent of the path, we choose a convenient path, i.e., along the radial direction from infinity to point P.

Work done in bringing a unit positive test charge from infinity to the point P, against the repulsive force of charge Q (Q > 0), is the potential at P due to the charge Q.

The electrostatic force on a unit positive charge at some intermediate point P′ on the path equals to

$frac{Qtimes1}{4piepsilon_0r'^2}hat{r'}$

where is the unit vector along OP’, therefore, work done against this force from r′ to r′ + ∆r′ can be written as

$Delta{W}=-frac{Q}{4piepsilon_0r'^2}Delta{r'}$

The negative sign represents ∆r′ < 0, and ∆W is positive. Total work done (W) by the external force is determined by integrating the above equation on both sides, from r′ = ∞ to r′ = r,

$W=-int_{∞}^{r} frac{Q}{4piepsilon_0r'^2}d{r'}\ W=left[frac{Q}{4piepsilon_0r'}right]_∞^r\ W=frac{Q}{4piepsilon_0r}$

The potential at P due to the charge Q can be expressed as,

$V(r)=frac{Q}{4piepsilon_0r}$

Electric Potential Energy of a System of Charges

Potential at a point due to a system of charges is the sum of potentials due to individual charges.

Suppose a system of charges q₁, q₂,…, q_n with position vectors r₁, r₂,…, r_n relative to some origin. The potential V₁ at P due to the charge q₁ can be expressed as

$V_1=frac{1}{4piepsilon_0}frac{q_1}{r_{1P}}$

Where r_1P is the distance between q₁ and P.

Similarly, the potential V₂ at P due to q₂ and V₃ due to q₃ can be written as,

$V_2=frac{1}{4piepsilon_0}frac{q_2}{r_{2P}}\ V_3=frac{1}{4piepsilon_0}frac{q_3}{r_{3P}}$

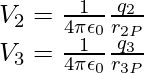
where r_2P and r_3P are the distances of P from charges q₂ and q₃, respectively, and so on for the potential due to other charges.

By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charge, that is,

V = V₁+ V₂ + V₃ +…. + V_n

The above expression can be expressed as,

$V=frac{1}{4piepsilon_0}frac{q_1}{r_{1P}}+frac{1}{4piepsilon_0}frac{q_2}{r_{2P}}+ frac{1}{4piepsilon_0}frac{q_3}{r_{3P}}+.....+frac{1}{4piepsilon_0}frac{q_n}{r_{nP}}$

$V=frac{1}{4piepsilon_0}left(frac{q_1}{r_{1P}}+frac{q_2}{r_{2P}}+frac{q_3}{r_{3P}}+...+frac{q_n}{r_{nP}}right)$

It is necessary to divide a continuous charge distribution with a charge density (r) into small volume elements of size ∆v, each carrying a charge ρ∆v. Then, for each volume element, compute the potential and add (or, more properly, integrate) all of these contributions to get the overall potential owing to the distribution.

What is Electric Potential?

The electric potential is defined as the amount of energy required to bring a unit mass object from a reference point to a specific point. If W amount of work is done to move an object of charge q from a point A to a reference point B. The formula for the electric potential can be expressed as,

$Delta V=V_B-V_A=frac{W}{q}\ frac{W}{q}=frac{U_B-U_A}{q}$

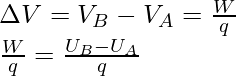
where V_B and V_Aare the electric potentials at points B and A, respectively.

In general, think about any static charge configuration. A test charge’s potential energy q is defined in terms of the work done on it. This work is obviously proportional to q because the force at any position is qE, where E is the electric field at that site due to the given charge arrangement. As a result, dividing the work by the charge q yields a quantity independent of q.

The work done by an external force to carry a unit positive charge from infinity to a specific location is equal to the electrostatic potential (V) at that point.

In other words, the electrostatic potential (V ) at any place in an area with an electrostatic field is the work needed to transport a unit positive charge from infinity to that specific location (without acceleration). Electric potential is a scalar quantity with no direction and only magnitude. It is symbolized by V and has the dimensional formula ML²T^-3A^-1.

Work done on a test charge q by the electrostatic field due to any given charge configuration is independent of the path and depends only on its initial and final positions

The same caveats that were expressed before about potential energy apply to the definition of potential. To calculate the work done per unit test charge, start with an infinitesimal test charge δq, calculate the work done δW in bringing it from infinity to the point, and divide by δq to get the δW/δq ratio. In addition, at each point along the path, the external force must be equal to and opposite to the electrostatic force acting on the test charge.

What is Electric Potential Difference?

Electric potential difference is also known as voltage. The electric potential difference is the work done per unit charge to move a unit charge from one point to another in an electric field. Electric potential difference is usually referred to as a Voltage difference. Imagine a ball sitting at some height, will there be some energy in the ball? Yes, the energy is called Potential energy, and if the ball is dropped from a point A to B height, the ball will always fall from higher gravitational potential to lower, then there will be a difference in both energies. The electrical potential difference is analogical to this concept. The energy possessed by Electric charges is known as electrical energy. A charge with higher potential will have more potential energy, and a charge with lesser potential will have less potential energy. The current always moves from higher potential to lower potential. The formula for electric potential difference:

V_xy= V_x – V_y = [W_x– W_y]/q

Solved Examples on Electric Potential Energy

Example 1: Suppose you have a 12.0 V motorcycle battery that can move 5000 C of charge and a 12.0 V car battery that can move 60,000 C of charge. How much energy does each deliver?

Solution:

Given,

The voltage of the battery is V =12.0 V.

The charge that the motorcycle battery move is Q = 5000 C.

The 12.0 V car battery can move 60,000 C of charge.

When such a battery moves charge, it puts the charge through a potential difference of 12.0 V, and the charge is given a change in potential energy equal to Δ(PE) = qΔV.

For the motorcycle battery, q = 5000 C and ΔV = 12.0 V. The total energy delivered by the motorcycle battery is

ΔPE_motorcycle = (5000 C) × (12.0 V)

ΔPE_motorcycle = 6.00 × 10⁴ J

Now, for the car battery,

ΔPE_car = (60,000 C) × (12.0 V)

ΔPE_car =7.20 × 10⁵ J

Example 2: A particle of mass 40 mg carrying a charge 5 × 10^-9C is moving directly towards a fixed positive point charge of magnitude 10^-8 C. When it is at a distance of 10 cm from the fixed point charge, it has a velocity of 50 cm/s. At what distance from the fixed point charge will the particle come momentarily to rest? Is the acceleration constant during motion?

Solution:

Given,

The mass of the particle m = 40 mg.

The charge of the particle Q = 5×10^-9C.

The fixed positive point charge of magnitude q =10^-8 C.

Velocity of the charged particle is v = 50 cm/s = 0.5 m/s

The particle comes to rest momentarily at a distance r from the fixed charge, from conservation of energy we have,

According to the law of conservation of energy, the total energy of the system = Constant

i.e., (K.E. + P.E.) = constant.

The expression for the kinetic energy can be expressed as,

$K.E= frac{1}{2}mu^2$

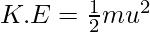
The expression for the potential energy can be expressed as,

Now,

(1/2)mu² + (1/4πε_o) × [Qq/a] = (1/4πε_o) × [Qq/r]

(1/2)mu²= (1/4πε_o) [Qq/r – Qq/a]

(1/2)mu²= (1/4πε_o) Qq[1/r – 1/a]

Substituting the values in the above equation,

1/2 × 40 × 10^-6 × (0.5)²= 9 × 10⁹× 10^-8 × 5 × 10^-9 × [ 1/r – 1/(10 × 10^-2)]

or, [1/r – 10] = (5×10^-5)/(9×5×10^-8) = 100/9

or, 1/r = (100/9) + 10

or, 1/r = 190/9 m

or r = 4.7 × 10^-2 m

Since, F = [1/4πεo] × [Qq/r²]

Therefore, acceleration = F/m ∝ 1/r² , i.e., acceleration is not constant during motion.

Example 3: A ball of mass 5 g and charge 10^-7 C moves from point A, whose potential is 500 V, to point B, whose potential is zero. What is the velocity of the ball at point A if at point B, it is 25 cm per second?

Solution:

Given,

The mass ball is 5 g.

The charge of the particle is 10^-7 C.

The potential of ball at point A is 500 V and potential at point B is zero.

Suppose u be the velocity of the ball at point A.

The work done on the charge by the field given by,

W = q × (V_A – V_B)

Substitute the value in the above expression,

W = 10^-7 C× (500 V – 0 V)

W = 5 × 10^-5 J

Therefore,

W = (1/2) mv²– (1/2) mu²

5 × 10^-5 J= (1/2) × (5/1000 )×[(1/4)² – u²]

2 × 10^-2 = 1/16 – u²

u² = (1/16) – 0.02

u² = (1- 0.32)/16

u² = 0.0425

Therefore, u =0.206 m/s

u = 20.6 cm/s.

Example 4: When a 12.0 V car battery runs a single 30.0 W headlight, how many electrons pass through it each second?

Solution:

The expression for the potential energy can be written as,

Δ(PE) = qΔV

Rearrange the above expression,

q = Δ(PE)/ΔV

Substitute the values in the above equation,

q = −30.0 J/ 12.0 V

q = −30.0 J/ 12.0 J/C

q = −2.50 C

The number of electrons n can be calculated as,

n = q/e

n = −2.50 C/(−1.60 × 10⁻¹⁹ C/e)

n = 1.56 × 10¹⁹ electrons

Example 5: How much work is required to be done in order to bring two charges of magnitude 3 C and 5 C from a separation of infinite distance to a separation of 0.5 m?

Solution:

Given,

Two charges of magnitude 3 C and 5 C.

The separation between two charges are 0.5 m.

The potential at P due to the charge Q can be expressed as

$U_{r} =frac{Qq}{4piepsilon_0r}$

∆U = U₀ – U_r

∆U = 0 J – [-(9 × 10⁹ Nm²/C²× 5 C × 3 C)/0.5 m] J = 2.7 × 10¹¹J.

Therefore, ∆U = 2.7 × 10¹¹ J.

FAQs on Electric Potential Energy

Question 1: What is electric potential energy?

Answer:

Electric potential energy of a single charge or system of charges is the energy required by an external force in moving a charge in the electric field.

Question 2: List some examples of electric potential energy.

Answer:

Some examples of electric potential energy are:

Air-conditioner system before turning on.

Vacuum cleaner after turning off.

Television before turning on.

Car’s headlights before it is turned on.

Question 3: What is the electrical potential energy formula?

Answer:

The formula for electrical potential energy is:

U_E = k (q₁q₂)/r

Where,

U_E = Electric potential energy

k = Coulomb constant

q₁, q₂ = Charges

r = Distance between charges

Источник

Подробнее о потенциальной энергии взаимодействия зарядов и потенциале точки электростатического поля

Для школьников.

Электростатическое поле обладает энергией.

Это видно из опыта, когда пробный (очень малый положительный) заряд

помещённый в точку 1 электростатического поля, созданного точечным зарядом

перемещается под действием силы Кулона :

(Когда говорим о пробном заряде, то имеем в виду, что не учитываем поле им создаваемое (оно очень слабое), а рассматриваем только поведение пробного заряда в электрическом поле заряженных тел.)

Если пробному заряду дать возможность переместиться из точки 1 поля в точку 2, то сила Кулона (электрическая сила) совершит работу

где

расстояния от пробного заряда до заряда

Работа

по переносу пробного заряда из точки 1 в точку 2 поля не зависит от траектории его движения.

Поля, обладающие таким свойством, называются потенциальными или консервативными. Для таких полей вводится понятие “потенциальная энергия”

Электрическая сила совершает работу за счёт уменьшения потенциальной энергии поля:

Сравнение уравнений для работы даёт формулу нахождения потенциальной энергии пробного заряда. Так, для точки 1 поля формула имеет такой вид:

По сути эта энергия является энергией взаимодействия зарядов

находящихся на расстоянии

друг от друга (или энергией электростатического поля).

Если пробный заряд освободить в точке 1 поля, то он под действием силы Кулона переместится в точку с потенциальной энергией, равной нулю

Эта точка условно называется бесконечно удалённой.

Теперь от потенциальной энергии перейдём к понятию потенциала точки поля.

Если в точку 1 поместить пробный заряд, равный

то потенциальная энергия увеличится в 2 раза, но отношение потенциальной энергии к величине пробного заряда останется прежним

и, следовательно, характеризует точку электростатического поля.

Эту характеристику точки поля назвали потенциалом.

Потенциал точки 1 поля равен

или

Потенциал точки 1 поля численно равен работе, совершаемой электрическим полем при переносе единичного положительного заряда из этой точки поля в бесконечность.

или

Диэлектрическую проницаемость

можно опустить, так как для воздуха она равна единице.

(Продолжение см. в следующей статье).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Как найти напряжение на конденсаторах в конденсаторной цепи, изображённой на рисунке?

Следующая запись: Нахождение потенциальной энергии электростатического поля, созданного системой точечных зарядов.

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.

Источник

Потенциальная
энергия заряда в электрическом
поле. Работу,
совершаемую силами электрического поля
при перемещении положительного точечного
заряда q из
положения 1 в положение 2, представим
как изменение потенциальной энергии
этого заряда:

где W_п1 и W_п2 –
потенциальные энергии заряда q в
положениях 1 и 2. При малом перемещении
заряда q в
поле, создаваемом положительным точечным
зарядом Q,
изменение потенциальной энергии равно

При
конечном перемещении заряда q из
положения 1 в положение 2, находящиеся
на расстояниях r₁ и r₂ от
заряда Q,

Если
поле создано системой точечных
зарядов Q₁, Q₂,¼, Q_n,
то изменение потенциальной энергии
заряда q в
этом поле:

Приведённые
формулы позволяют найти
только изменение потенциальной
энергии точечного заряда q,
а не саму потенциальную энергию. Для
определения потенциальной энергии
необходимо условиться, в какой точке
поля считать ее равной нулю. Для
потенциальной энергии точечного
заряда q,
находящегося в электрическом поле,
созданном другим точечным зарядом Q,
получим

где C –
произвольная постоянная. Пусть
потенциальная энергия равна нулю на
бесконечно большом расстоянии от
заряда Q (при r ® ¥),
тогда постоянная C =
0 и предыдущее выражение принимает вид

При
этом потенциальная энергия определяется
как работа
перемещения заряда силами поля из данной
точки в бесконечно удаленную. В
случае электрического поля, создаваемого
системой точечных зарядов, потенциальная
энергия заряда q:

Потенциальная
энергия системы точечных зарядов. В
случае электростатического поля
потенциальная энергия служит мерой
взаимодействия зарядов. Пусть в
пространстве существует система точечных
зарядов Q_i (i =
1, 2, … ,n).
Энергия взаимодействия
всех n зарядов
определится соотношением

где r_ij – расстояние
между соответствующими зарядами, а
суммирование производится таким образом,
чтобы взаимодействие между каждой парой
зарядов учитывалось один раз.

Потенциал
электростатического поля. Поле
консервативной силы может быть описано
не только векторной функцией, но
эквивалентное описание этого поля можно
получить, определив в каждой его точке
подходящую скалярную величину. Для
электростатического поля такой величиной
является потенциал
электростатического поля,
определяемый как отношение потенциальной
энергии пробного заряда q к
величине этого заряда, j = W_п / q,
откуда следует, что потенциал численно
равен потенциальной энергии, которой
обладает в данной точке поля единичный
положительный заряд. Единицей измерения
потенциала служит Вольт (1 В).

Потенциал
поля точечного заряда Q в
однородной изотропной среде с
диэлектрической проницаемостью e :

3.
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО
ПОЛЯ. Количественной
характеристикой силового действия
электрического поля на заряженные тела
служит векторная величина E,
называемая напряжённостью
электрического поля.

E = F / q_пр.

Она
определяется отношением силы F,
действующей со стороны поля на точечный
пробный заряд q_пр,
помещенный в рассматриваемую точку
поля, к величине этого заряда.

Понятие
«пробный заряд» предполагает, что этот
заряд не участвует в создании электрического
поля и так мал, что не искажает его, т.
е. не вызывает перераспределения в
пространстве зарядов, создающих
рассматриваемое поле. В системе СИ
единицей напряженности служит 1 В / м,
что эквивалентно 1 Н / Кл.

Электрическое
поле. Для
объяснения природы электрических
взаимодействий заряженных тел необходимо
допустить наличие в окружающем заряды
пространстве физического агента,
осуществляющего это взаимодействие. В
соответствии с теорией
близкодействия,
утверждающей, что силовые взаимодействия
между телами осуществляются через
посредство особой материальной среды,
окружающей взаимодействующие тела и
передающей любые изменения таких
взаимодействий в пространстве с конечной
скоростью, таким агентом является электрическое
поле.

Электрическое
поле создается как неподвижными, так и
движущимися зарядами. О наличии
электрического поля можно судить, прежде
всего, по его способности оказывать
силовое действие на электрические
заряды, движущиеся и неподвижные, а
также по способности индуцировать
электрические заряды на поверхности
проводящих нейтральных тел.

Поле,
создаваемое неподвижными электрическими
зарядами, называют стационарным
электрическим,
или электростатическим полем.
Оно представляет собой частный
случай электромагнитного
поля,
посредством которого осуществляются
силовые взаимодействия между электрически
заряженными телами, движущимся в общем
случае произвольным образом относительно
системы отсчета.

Напряженность
поля точечного заряда. Используя
закон Кулона (1.1) найдем выражение для
напряжённости электрического поля,
создаваемого точечным зарядом q в
однородной изотропной среде на
расстоянии r от
заряда:

(1.2)

В
этой формуле r –
радиус-вектор, соединяющий заряды q и q_пр.
Из (1.2) следует, что напряжённость E поля
точечного заряда q во
всех точках поля направлена радиально
от заряда при q >
0 и к заряду при q <
0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Неоднозначность определения потенциала[править | править код]

Единицы измерения[править | править код]

Использование термина[править | править код]

Кулоновский потенциал[править | править код]

В электродинамике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

What is Electric Potential Energy?

Overview

Electric Potential Energy Formula

Electric Potential Energy of a Point Charge

Electric Potential Energy of a System of Charges

What is Electric Potential?

What is Electric Potential Difference?

Solved Examples on Electric Potential Energy

FAQs on Electric Potential Energy

Question 1: What is electric potential energy?

Question 2: List some examples of electric potential energy.

Question 3: What is the electrical potential energy formula?

Вам также может понравиться

Как найти площадь четырехугольника прямого

Как найти а полезен физика

Как мне исправить свои оценки за несколько дней

Добавить комментарий Отменить ответ