Как найти потенциальную энергию электростатического поля

Для школьников.

В предыдущей статье записана формула для потенциальной энергии взаимодействия заряда, создающего электростатическое поле, и пробного заряда.

Если электростатическое поле создаётся двумя точечными зарядами

находящимися на расстоянии

друг от друга, то потенциальная энергия их взаимодействия выражается формулой:

Можно сказать так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого первым зарядом в точке нахождения второго заряда, на величину второго заряда.

Можно сказать и так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого вторым зарядом в точке нахождения первого заряда, на величину первого заряда.

Потенциальная энергия взаимодействия двух точечных зарядов – это и есть энергия электростатического поля, созданного ими.

Обладая энергией, электрическое поле может совершить работу. Энергия электростатического поля численно равна работе, которую могут совершить заряды при их удалении друг от друга в бесконечность.

Пользуясь уравнением (1) можно найти энергию электрического поля, созданного заряженным телом, так как заряд тела можно представить как сумму множества точечных зарядов.

Пользуясь уравнением (1), можно найти и выражение для энергии электрического поля конденсатора, что будет сделано в следующих статьях.

Сейчас, пользуясь уравнением (1), найдём энергию электростатического поля, созданного тремя точечными зарядами.

Задача

Подумайте над решением задачи такого содержания:

Три одинаковых заряда закреплены на одной прямой на одинаковом расстоянии друг от друга. Какую работу надо совершить, чтобы удалить средний заряд?

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Подробнее о потенциальной энергии взаимодействия зарядов и потенциале точки электростатического поля.

Следующая запись: Три одинаковых заряда закреплены на одной прямой. Какую работу надо совершить, чтобы удалить средний заряд?

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.

1. Энергия электростатического поля

1. Энергия
   системы точечных зарядов как сумма
   энергия парного взаимодействия зарядов
   ( и принцип суперпозиции)

Потенциальная
энергия заряда в электрическом
поле. Работу,
совершаемую силами электрического поля
при перемещении положительного точечного
заряда q из
положения 1 в положение 2, представим
как изменение потенциальной энергии
этого заряда:

,

где W_п1 и W_п2 –
потенциальные энергии заряда q в
положениях 1 и 2. При малом перемещении
заряда q в
поле, создаваемом положительным точечным
зарядом Q,
изменение потенциальной энергии равно

.

При
конечном перемещении заряда q из
положения 1 в положение 2, находящиеся
на расстояниях r₁ и r₂ от
заряда Q,

.

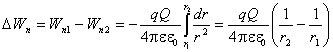Если
поле создано системой точечных
зарядов Q₁, Q₂,¼, Q_n,
то изменение потенциальной энергии
заряда q в
этом поле:

.

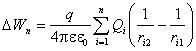Приведённые
формулы позволяют найти
только изменение потенциальной
энергии точечного заряда q,
а не саму потенциальную энергию. Для
определения потенциальной энергии
необходимо условиться, в какой точке
поля считать ее равной нулю. Для
потенциальной энергии точечного
заряда q,
находящегося в электрическом поле,
созданном другим точечным зарядом Q,
получим

,

где C –
произвольная постоянная. Пусть
потенциальная энергия равна нулю на
бесконечно большом расстоянии от
заряда Q (при r ® ¥),
тогда постоянная C =
0 и предыдущее выражение принимает вид

.

При
этом потенциальная энергия определяется
как работа
перемещения заряда силами поля из данной
точки в бесконечно удаленную. В
случае электрического поля, создаваемого
системой точечных зарядов, потенциальная
энергия заряда q:

.

Потенциальная
энергия системы точечных зарядов. В
случае электростатического поля
потенциальная энергия служит мерой
взаимодействия зарядов. Пусть в
пространстве существует система точечных
зарядов Q_i (i =
1, 2, … ,n).
Энергия взаимодействия
всех n зарядов
определится соотношением

 ,

где r_ij – расстояние
между соответствующими зарядами, а
суммирование производится таким образом,
чтобы взаимодействие между каждой парой
зарядов учитывалось один раз.

Потенциал
электростатического поля. Поле
консервативной силы может быть описано
не только векторной функцией, но
эквивалентное описание этого поля можно
получить, определив в каждой его точке
подходящую скалярную величину. Для
электростатического поля такой величиной
является потенциал
электростатического поля,
определяемый как отношение потенциальной
энергии пробного заряда q к
величине этого заряда, j = W_п / q,
откуда следует, что потенциал численно
равен потенциальной энергии, которой
обладает в данной точке поля единичный
положительный заряд. Единицей измерения
потенциала служит Вольт (1 В).

Потенциал
поля точечного заряда Q в
однородной изотропной среде с
диэлектрической проницаемостью e :

.

Принцип
суперпозиции. Потенциал
есть скалярная функция, для неё справедлив
принцип суперпозиции. Так для потенциала
поля системы точечных зарядов Q_1, Q₂¼, Q_n имеем

 ,

где r_i –
расстояние от точки поля, обладающей
потенциалом j,
до заряда Q_i.
Если заряд произвольным образом
распределен в пространстве, то

 ,

где r –
расстояние от элементарного объема dx,
dy,
dz до
точки (x, y, z),
где определяется потенциал; V –
объем пространства, в котором распределен
заряд.

Потенциал
и работа сил электрического поля. Основываясь
на определении потенциала, можно
показать, что работа сил электрического
поля при перемещении точечного заряда q из
одной точки поля в другую равна
произведению величины этого заряда на
разность потенциалов в начальной и
конечной точках пути, A = q (j₁ – j₂).
Если
по аналогии с потенциальной энергией
считать, что в точках, бесконечно
удалённых от электрических зарядов –
источников поля, потенциал равен нулю,
то работу сил электрического поля при
перемещении заряда q из
точки 1 в бесконечность можно представить
как A_¥ = q j₁.
Таким
образом, потенциал â данной точке
электростатического поля – этофизическая
величина, численно равная работе,
совершаемой силами электрического поля
при перемещении единичного положительного
точечного заряда из данной точки поля
в бесконечно удаленную: j = A_¥ / q.
В
некоторых случаях потенциал электрического
поля нагляднее определяется какфизическая
величина, численно равная работе внешних
сил против сил электрического поля при
перемещении единичного положительного
точечного заряда из бесконечности в
данную точку.
Последнее определение удобно записать
следующим образом:

 .

В
современной науке и технике, особенно
при описании явлений, происходящих в
микромире, часто используется единица
работы и энергии, называемая электрон-вольтом (эВ).
Это работа, совершаемая при перемещении
заряда, равного заряду электрона, между
двумя точками с разностью потенциалов
1 В: 1 эВ = 1,60×10^-19 Кл×1
В = 1,60×10^-19 Дж.

1. Интегральное
   представление энергии непрерывного
   распределения зарядов, cравнение
   со случаем энергии системы точечных
   зарядов

Пусть
в элементе объема находится
заряд.
Для определения энергии взаимодействия
всех элементовв
объеме V можно использовать формулу(12.4).
,
перейдя в ней от суммы к интегралу:

 (12.5)

Где –
потенциал, создаваемый всеми зарядами
в точке нахождения заряда.

На
первый заряд формулы (12.4) и (12.5) кажутся
аналогичными, тем более что (12.5) “выведена”
из (12.4). Однако между ними существует
принципиальное различие. Формула (12.4)
учитывает лишь энергию взаимодействия
между заряженными шарами, но не учитывает
энергию взаимодействия между элементами
зарядов, находящихся на каждом шаре. А
(12.5) учитывает и первое, и второе.

Учитывая
сказанное, энергию взаимодействия
зарядов можно записать в виде:

 (12.6)

Величина –
это энергия заряженных шаров, учитывающая
взаимодействие зарядов между собой на
каждом шаре. Собственная энергия зависит
от законов распределения зарядов шара
и значений зарядов. Если имеется
уединенный шар, то.

Тогда (12.7)

Это
означает, что собственная энергия
точечного заряда равна бесконечности.

Но
при .
Это приводит к серьезным трудностям
при использовании модели точечных
зарядов.

1. Электрическая
   энергия заряженных уединенного
   проводника и конденсатора

Если
уединенный проводник имеет заряд q, то
вокруг него существует электрическое
поле, потенциал которого на поверхности
проводника равен ,
а емкость – С. Увеличим заряд на величину
dq. При переносе заряда dq из бесконечности
должна быть совершена работа равная.
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю.
Тогда

При
переносе заряда dq с проводника в
бесконечность такую же работу совершают
силы электростатического поля.
Следовательно, при увеличении заряда
проводника на величину dq возрастает
потенциальная энергия поля, т.е.

Проинтегрировав
данное выражение, найдем потенциальную
энергию электростатического поля
заряженного проводника при увеличении
его заряда от нуля до q:

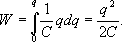
Применяя
соотношение ,
можно получить следующие выражения для
потенциальной энергии W:

(16.2)

Для
заряженного конденсатора разность
потенциалов (напряжение) равна поэтому
соотношение для полной энергии его
электростатического поля имеют вид

1. Энергия
   электростатического поля, выраженная
   в виде объемного интеграла от векторов
   напряжённости Е и электрического
   смещения D.

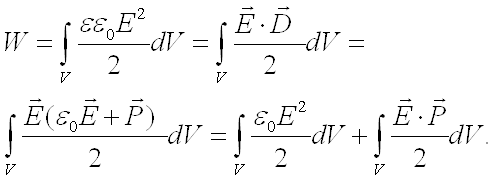
1. Выражение
   силы, действующей на проводник,
   погруженный в жидкий или газообразный
   диэлектрик, через объемную плотность
   энергии электрического поля вблизи
   проводника.

При
наличии среды вычисление сил, действующих
на проводники и диэлектрики, усложняется.

Прежде
всего выражение для объемной силыстановится
несправедливым, даже если под понимать
молекулярную плотность заряда. Это
связано с тем, чтоесть
средняя макроскопическая плотность,
которая не учитывает поляризацию
отдельных молекул.
Между тем в неоднородном электрическом поле на
поляризованную молекулу действует
сила. Можно было бы попробовать усреднить
эту силу по объему, но такая процедура
наталкивается на значительные трудности.
Воспользуемся энергетическим методом
вычисления сил.

Рассмотрим
несколько типичных задач. Найдем силу,
действующую на диэлектрический шар,
помещенный в слабо неоднородное поле.
Последнее условие означает, что поле
должно мало меняться на размере шара.
Тогда дипольный момент шара
будет приблизительно такой же, как и в
однородном поле: где
Е — внешнее поле (в отсутствие шара).
Так как момент шара пропорционален
полю, от он ведет себя как квазиупругий диполь и,
следовательно, его энергия в поле .
Произведем теперь виртуальное перемещение
шара во внешнем неоднородном поле и
запишем баланс энергии:
где —
сила, действующая на шар со стороны
поля:

(19.1)

т.
е. диэлектрик втягивается
в сильное поле. Если (слабый
диэлектрик), то выражение (19.1) справедливо
для диэлектрика произвольной формы,
так как в этом случае можно пренебречь
взаимодействием отдельных участков
диэлектрика, которые поляризуются
независимо друг друга. Тогда объемная
сила, действующая на диэлектрик,

(19.2)

т.
е. определяется изменением
плотности энергии электрического
поля при
внесении диэлектрика.

Кроме
силы, действующей в
неоднородном электрическом поле на диэлектрик как
целое, в нем возникают еще и внутренние
напряжения, называемые стрикционными
силами. Рассмотрим пластину диэлектрика,
помещенную в плоский конденсатор (рис.
11.5). Ясно, что под действием стрикционных
сил пластина несколько

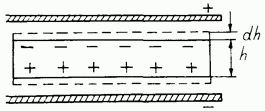
Рис.
11.5. К расчету стрикционных сил.

растянется
вдоль поля. Попробуем вычислить
стрикционные силы в этом примере.
Воспользуемся энергетическим методом.
При небольшем растяжении пластины
изменение энергии поля складывается
из двух частей. Во-первых, в слое энергия
поля в вакууме заменяется
на энергию поля в среде Здесь поле
в вакуумном зазоре, которое не изменяется
при деформации диэлектрика, поскольку
мы принимаем заряд на конденсаторе
неизменным (см. выше). Во-вторых, необходимо
учесть изменение энергии во всем объеме
вещества из-за изменения его плотности,
от которой
зависит диэлектрическая проницаемость: где .Частная производная взята
здесь при постоянной температуре, чтобы
исключить зависимость от
температуры. Полный баланс энергии на
единицу площади диэлектрика имеет вид

(19.3)

Отсюда
натяжение, действующее на диэлектрик,

(19.4)

можно
рассматривать как разность натяжений
снаружи и
изнутри диэлектрика,
где Е —электрическое поле внутри
последнего.

Обычно
стрикционным давлением называется
величина

(19.5)

Это
давление не дает вклада в силу, действующую
на диэлектрик как
целое, при условии, что он окружен
вакуумом.

Рассмотрим,
наконец, произвольную систему заряженных
тел, погруженных в однородный жидкий
диэлектрик. Как мы уже знаем , такая
среда ослабляет поле в раз,
не изменяя его конфигурации. Отсюда, в
частности, следует, что энергия поля
также в раз
меньше, чем в вакууме. Значит, и работа
по перемещению зарядов, и силы между
телами тоже уменьшаются в раз.
На первый взгляд этот вывод кажется
тривиальным: раз поле уменьшается
в раз,
то во столько же раз должна уменьшиться
и сила его воздействия на заряд. Однако
под полем в среде понимается среднее
поле, тогда как действующее на заряд
локальное поле зависит от формы полости,
т. е. от формы заряженного тела. Чтобы
разобраться, в чем здесь дело, вернемся
к предыдущему примеру. Пусть диэлектрик является
теперь жидким и заполняет весь конденсатор.
Тем не менее мы можем представить себе,
что между диэлектриком и пластиной
конденсатора существует очень

тонкая
щель, в которой поле равно так
что все предыдущее рассмотрение остается
в силе. В таком случае давление поля
непосредственно на пластину равно т.
е. такое же, как в вакууме, вместо
ожидаемого ослабления в раз.
Этот пример подтверждает, что сила,
действующая со стороны поля на заряженное
тело, действительно зависит от формы
тела.

Однако
жидкий диэлектрик имеет,
как правило, механический контакт с
телом и тоже действует на него с некоторой
силой, которая в рассматриваемом примере
дается выражением (19.4). Наконец, нужно
учесть еще дополнительное давление
в жидкости,
возникающее за счет электрического поля и
равное стрикционному давлению (19.5).
Таким образом, полное давление на
пластину

(19.6)

в
соответствии с энергетическими
соображениями.

Подчеркнем
еще раз, что такой простой результат
получается только для жидкого однородного
диэлектрика. Механический контакт
проводников с твердым диэлектриком
является, как правило, неопределенным.
Кроме того, внутренние упругие напряжения
зависят теперь не от локального
стрикционного давления, а от сил,
действующих на весь диэлектрик.

Соседние файлы в папке 1 семестр

• #
• #
• #

  16.02.201717.04 Кб8M9+.xlsx

• #

  16.02.201715.15 Кб10M9.xlsx

• #
• #
• #
• #
• #
• #

У этого термина существуют и другие значения, см. Потенциал.

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал связаны соотношением^[1]

или обратно^[2]:

Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

где  — электростатический потенциал (в вольтах),  — объёмная плотность заряда (в кулонах на кубический метр), а  — электрическая постоянная (в фарадах на метр).

Неоднозначность определения потенциала[править | править код]

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

где:

 — потенциал в точке 1,

 — потенциал в точке 2,

 — работа, совершаемая полем при переносе пробного заряда из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произвольностью выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения[править | править код]

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Использование термина[править | править код]

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Кулоновский потенциал[править | править код]

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

где обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

= 9·10⁹ В·м/Кл,

 — величина заряда,  — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
• Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

  

В электродинамике[править | править код]

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция зависит от пути, потому что (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

является консервативным полем по закону Фарадея, и поэтому можно написать

где V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

в отличие от электростатики.

См. также[править | править код]

• Гальвани-потенциал
• Вольта-потенциал
• Векторный потенциал электромагнитного поля
• 4-потенциал
• Стандартный электродный потенциал
• Степень окисления
• Гравитационный потенциал
• Ядерный потенциал

Примечания[править | править код]

Литература[править | править код]

• Алешкевич В. А. Электромагнетизм. — М.: Физматлит, 2014. — 404 с. — 700 экз. — ISBN 978-5-9221-1555-1.

На прошлых уроках мы с вами говорили о том, что на помещённый
в электростатическое поле пробный заряд действует кулоновская сила, под
действием которой пробный заряд способен перемещаться вдоль линии напряжённости
поля. Из механики мы знаем, что при перемещении тела действующая на него сила
совершает работу. Логично предположить, что и электрическое поле также будет
совершать работу по перемещению в нём заряда.

В общем случае работа сил электрического поля зависит как от
начального и конечного положений перемещаемого заряда, так и от вида
траектории, по которой он движется.

Однако электростатическое поле имеет важную особенность. Работа
сил этого поля при перемещении заряда между двумя точками зависит только от
положения этих точек и не зависит от вида траектории.

Давайте вспомним, что физические поля, работа сил которых
не зависит от формы траектории, называют потенциальными (или консервативными).
Покажем, что электростатическое поле потенциально.

Итак, пусть положительный пробный заряд находится в
однородном электростатическом поле, созданном вертикальными параллельными
пластинами, находящимися на расстоянии d друг от друга и имеющими заряды противоположных знаков.

Предположим, что под действием электрической силы,
действующей со стороны поля, заряд перемещается из точки В в точку С
вдоль линии напряжённости рассматриваемого поля. При этом сила, с которой поле
действует на пробный заряд, совершает работу.

Давайте вспомним, что в общем случае работа постоянной силы
равна произведению модуля этой силы на модуль перемещения и на косинус угла
между ними:

Модуль электрической силы мы найдём, как произведение
величины пробного заряда и модуля напряжённости электростатического поля:

Так как направления силы и перемещения заряда совпадают, то
косинус угла между нами равен единице:

А модуль перемещения заряда равен расстоянию между точками В
и С.

Тогда работа силы однородного электростатического поля по
перемещению заряда прямо пропорциональна величине этого заряда, напряжённости
поля и расстоянию, пройденному зарядом в поле под действием электрической силы:

Теперь предположим, что заряд перемещается не вдоль силовой
линии поля, а под некоторым углом к ней.

Обозначив угол между направлением вектора силы и вектора
перемещения α, запишем формулу для работы поля в общем виде:

Для определения перемещения точки воспользуемся ΔMKN. Это прямоугольный треугольник, в котором гипотенуза
— это искомое перемещение, а один из острых углов — это угол между вектором
силы и вектором перемещения. Тогда очевидно, что произведение модуля вектора
перемещения на косинус угла альфа равно длине прилежащего к углу катета М):

Следовательно, работа поля вновь равна произведению величины
заряда, напряжённости поля и расстоянию, пройденному зарядом в поле под
действием силы:

И, наконец, пусть перемещение нашего заряда из одной точки
поля в другую происходит по криволинейной траектории.

Чтобы найти работу поля, разобьём траекторию движения заряда
на такие малые участки, что бы каждый из них можно было считать прямолинейным.Тогда
работа на поля на всей траектории будет равна алгебраической сумме работ,
совершаемых полем на каждом из маленьких участочков.

А теперь заметим, что в скобках стоит сумма длин
прямолинейных участков, на которые мы разбили траекторию заряда. А это есть ни
что иное, как расстояние между пластинами d.
Таким образом мы получаем уже знакомую нам формулу:

Таким образом действительно, работа силы однородного
электростатического поля по перемещению заряда из одной точки поля в другую не
зависит от формы траектории, по которой двигался пробный заряд, а зависит
только от начального и конечного положений заряда.

Тогда становится очевидным, что в случае движения заряда по
замкнутой траектории работа поля будет равна нулю, так как начальное и конечное
положения заряда совпадают. Следовательно, однородное электростатическое
поле потенциально. Это означает, что электростатическое и гравитационное
поля имеют похожие свойства, определяемые их потенциальным характером.

Применительно к электростатическому полю эти свойства
выражаются в следующем:

Во-первых, точечный электрический заряд, находящийся в любой
точке электростатического поля, обладает потенциальной энергией взаимодействия
с этим полем, значение которой определяют относительно произвольно выбираемой
нулевой точки. В нулевой точке потенциальную энергию заряда в поле принимают
равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с
электростатическим полем равна работе, которую совершили бы силы поля при
перемещении данного заряда из указанной точки поля в нулевую точку:

А во-вторых, работа сил электростатического поля по
перемещению электрического заряда из начальной точки в конечную равна изменению
потенциальной энергии, взятому с обратным знаком:

Знак «минус» в формуле означает, что если сила
электростатического поля совершает положительную работу (подобно силе
гравитационного поля Земли при падении мяча), то потенциальная энергия
заряженного тела в поле уменьшается. Тогда, согласно закону сохранения энергии,
кинетическая энергия заряженной частицы будет увеличиваться. На этом основано
ускорение заряженных частиц электростатическим полем.

Если работа сил электростатического поля отрицательна
(подобно работе силы гравитационного поля при движении мяча, брошенного вверх),
то потенциальная энергия заряда в поле увеличивается, а кинетическая энергия
наоборот уменьшается.

Обратим внимание ещё и на то, что потенциальная энергия —
это энергия взаимодействия, и её необходимо относить не к заряженной частице
или телу, а к системе в целом. В частности, для заряженной частицы, находящейся
в электростатическом поле, это потенциальная энергия взаимодействия
заряженной частицы с другими заряженными частицами или телами, являющимися
источниками этого поля.