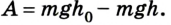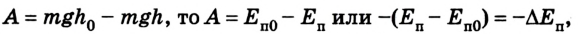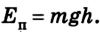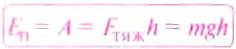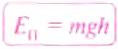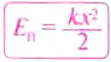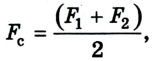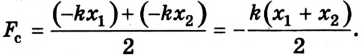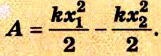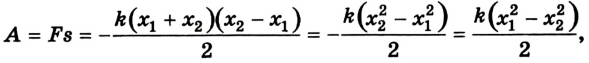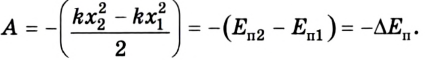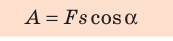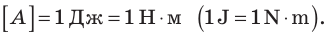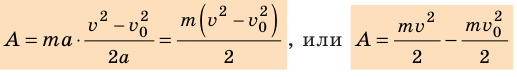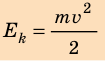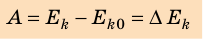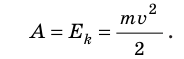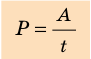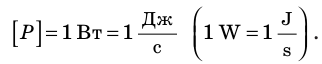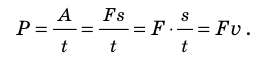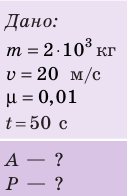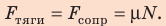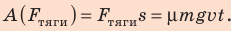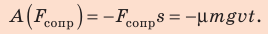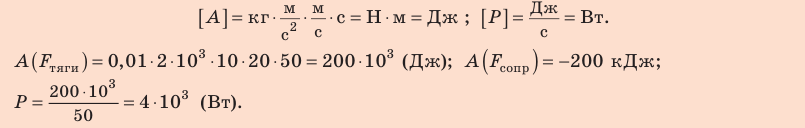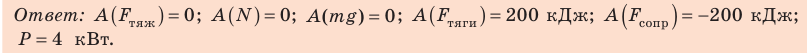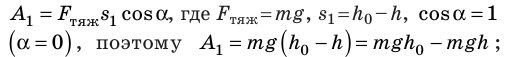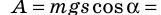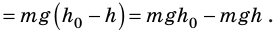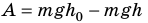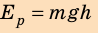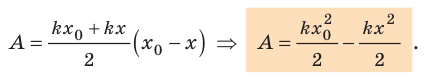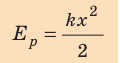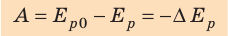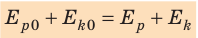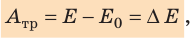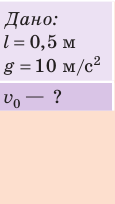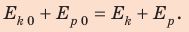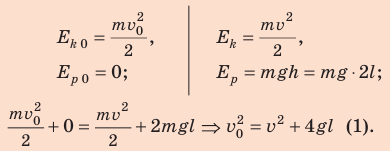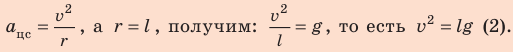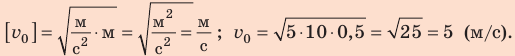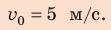Как найти потенциальную энергию если известна масса

Энергия является важнейшим понятием в механике. Данный термин определяет способность тела совершать работу. Универсальная количественная мера в физике характеризует движение и взаимодействие объектов. Она может быть двух типов: потенциальной и кинетической.

Потенциальная и кинетическая энергия

Потенциальной энергией называют энергию взаимодействия тел.

Определить потенциальную энергию тела можно, зная его массу, ускорение свободного падения и положение относительно земли. Формула для расчета имеет следующий вид:

E = m * g * h

В международной системе СИ потенциальная энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В вышеуказанной формуле m является массой тела, h представляет собой высоту, а g – ускорением свободного падения, которое приблизительно равно 9,8 м/с2.

Величина потенциальной энергии определяется выбранной системой отсчета. Это связано с тем, что отсчет высоты можно выполнять не только относительно земной поверхности, но и от какой-то точки или определенного уровня.

Кинетической энергией называют энергию, которой обладает тело во время движения.

Кинетическая энергия служит для определения запаса энергии тела, обладающего определенной скоростью. Определить кинетическую энергию можно с помощью формулы:

(E=frac{mv^{2}}{2})

В международной системе СИ кинетическая энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В уравнении m является массой тела, а v представляет собой его скорость.

Скорость тела определяется выбранной системой отсчета. Поэтому кинетическая энергия также зависит от того, каким образом рассчитывают характеристики системы, в которой движется тело.

Представленное уравнение для расчета кинетической энергии справедливо в том случае, когда рассматривают скорости, намного меньшие, чем скорость света в вакуумной среде в 300 тысяч километров в секунду. Если скорость близка к световой, то расчеты необходимо производить с учетом теории относительности, созданной Эйнштейном.

Каким законам подчиняется, формулы

Потенциальная энергия характерна не только для тела, находящегося на определенной высоте. Несколько иначе выполняют расчет потенциальной энергии упруго деформированного тела. При деформации изменяется его форма и объем, при этом объекту передается определенный запас энергии. К примеру, если растянуть пружину или, напротив, сжать ее, то такие действия меняют расстояние, на которое удалены атомы и молекулы друг от друга. Таким образом, создается потенциальная энергия.

Расчет потенциальной энергии деформированного объекта выполняют с помощью уравнения:

(E=frac{k(Delta x)^{2}}{2})

k является жесткостью пружины, (Delta x) — это изменение длины пружины.

Следует отметить, что значение потенциальной энергии пружины будет всегда положительным, так как формула содержит ее изменение в квадрате. Даже в случае, когда изменение будет иметь знак «-», потенциальная энергия в любом случае останется положительной.

Говоря об энергии, следует учитывать, что объект обладает несколькими типами энергии одновременно. К примеру, летящий на большой высоте самолет имеет запас потенциальной энергии, так как удален от поверхности земли, и кинетической энергии из-за своей скорости движения.

Ели принять земную поверхность за уровень нулевой энергии, то данное утверждение будет справедливо. В случае, когда рассматривают объект в других системах отсчета, его энергия будет отличаться.

Рассматривая качели, можно сказать, что они обладают запасом и кинетической, и потенциальной энергии. Когда конструкция максимально отклоняется от равновесного положения, энергия будет рассчитываться таким образом:

Е_п = макс

Е_к = 0, так как скорость имеет нулевое значение.

В момент, когда качели пересекают точку равновесного положения, энергия будет распределена следующим образом:

Е_к = макс

скорость качелей в этой точке будет максимальна;

Е_п = мин

высота, на которой тело находится над землей, будет минимальной.

При сложении двух видов энергии получают полную механическую энергию тела. Она включает потенциальную и кинетическую энергии.

Задачи по теме с подробными решениями

Задача 1

Самолет, масса которого составляет 50 тонн, пролетает на высоте 10 километров. Скорость транспортного средства равна 900 км/ч. Требуется рассчитать, какова полная механическая энергия самолета.

Решение

Первым шагом является перевод искомых данных, согласно системе СИ. В таком случае масса самолета составит 50 000 кг, скорость – 250 м/с, а высота – 10 000 м.

Самолет обладает запасом полной энергии, которая включает и потенциальную, и кинетическую.

E = E_п + Е_к

E_п = m * g * h

Е_к = m * v² / 2

Таким образом, полная энергия составит:

(E=mtimes gtimes htimes frac{mv^{2}}{2})

Если подставить в полученную формулу числовые значения величин из условия задачи, то получим полную энергию:

(E=6.5625times 10^{9}) Дж

Если записать ответ сокращенно, то он примет такой вид:

(Е = 6,5625) Гдж.

Ответ: в рассмотренной системе отсчета значение полной механической энергии самолета составит 6.5625 Гдж.

Однако, данную задачу можно решить, принимая за нулевой уровень отметку в 10 километров. Тогда транспортное средство будет характеризоваться лишь запасом кинетической энергии, а значение потенциальной энергии будет равно нулю.

Задача 2

Пружину закрепили к стене и поместили на гладкую поверхность. На конце пружины зафиксировали тело. Растяжение пружины, которая обладает жесткостью в 400 Н/м, происходит при воздействии силы в 80 Н. Требуется рассчитать запас энергии в пружине.

Решение

Согласно условию задачи, поверхность обладает гладкостью, что позволяет сделать вывод о нулевом значении силы трения. Таким образом, потери энергии исключены. Воздействуя на пружину, можно наблюдать ее деформацию. Весь запас энергии будет сосредоточен в ней. Найти данную величину можно по формуле:

(E=frac{k(Delta x)^{2}}{2})

Сила упругости равна произведению жесткости на изменение длины пружины:

(ktimes Delta x=F)

Деформацию пружины можно рассчитать таким образом:

(Delta x=frac{F}{k})

Используя последнее равенство, можно преобразовать формулу для расчета энергии:

(E=frac{k(frac{F}{k})^{2}}{2}=frac{kF^{2}}{2k^{2}}=frac{F^{2}}{2k})

Далее следует подставить числовые значения в полученное выражение:

(E=frac{80^{2}}{2times 400}=8) Дж

Ответ: запас энергии в пружине составляет 8 Дж.

Задача 3

Масса пули составляет 9 грамм. Ее выпустили из оружия вертикально в верхнем направлении. Скорость пули при этом составила 700 м/с. Требуется рассчитать ее кинетическую энергию.

Решение

Условия задачи удобно представить в виде рисунка.

Расчет нужно выполнить по формуле:

(E=frac{mv^{2}}{2})

Перед тем, как подставить в уравнение числовые значения, требуется перевести их в систему СИ. Тогда масса пули составит 0,009 кг. Выражение будет записано следующим образом:

(E=frac{0.009times 49times 10^{4}}{2}=2200) Дж

Ответ: запас кинетической энергии пули равен 2200 Дж.

Задача 4

Масса ракеты составляет 0,2 кг. Ее выпустили из орудия вертикально вверх. После этого ракета достигла высоты в 60 метров. Требуется рассчитать значение потенциальной энергии ракеты, характерной для этой отметки.

Решение

Условие задачи можно представить с помощью рисунка.

Для того чтобы рассчитать потенциальную энергию, требуется воспользоваться формулой:

E = m * g * h

Далее необходимо подставить в выражение числовые значения:

Е = 0,2 * 9,8 * 60 = 118 Дж

Ответ: потенциальная энергия ракеты на заданной высоте составит 118 Дж.

Задача 5

Пружину растянули на 5 мм. Коэффициент ее жесткости составляет 10000 Н/м. Требуется вычислить, какова энергия пружины.

Решение

Следует представить условия задачи на рисунке.

Уравнение, с помощью которого можно рассчитать энергию пружины, имеет такой вид:

(E=frac{k(Delta x)^{2}}{2})

Далее необходимо привести к системе СИ расстояние, на которое растянули пружину. Оно составит 0,005 м.

После преобразований можно подставить числовые значения в искомую формулу:

(E=frac{10^{4}times 25times 10^{-6}}{2}=0.125) Дж

Ответ: энергия пружины составляет 0,125 Дж.

Знание основных формул для расчета кинетической, потенциальной и полной энергии тела позволит решить задачи любой сложности. Наиболее простым способом является выполнение последовательных действий, включая запись условий задачи, графическое изображение системы, представление формул для вычисления энергии, решение уравнения с помощью подстановки числовых значений. Важно отметить, что механическая энергия представляет собой сумму потенциальной и кинетической энергии.

Если в процессе поиска решений уравнений возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.

Энергия – скалярная величина. Любую энергию в системе СИ измеряют в Джоулях.

В механике рассматривают два вида энергии тел – кинетическую энергию и потенциальную энергию.

Сумма кинетической и потенциальной энергии называется полной механической энергией

Кинетическая энергия

Кинетическая энергия – это энергия движения. Любое тело, находящееся в движении, обладает кинетической энергией.

В русском языке есть глагол «кинуть». Бросим (кинем) камень – он будет находиться в движении, то есть, будет обладать кинетической энергией.

Когда тело изменяет свою скорость, изменяется его кинетическая энергия.
Скорость увеличивается – кинетическая энергия тоже растет, скорость падает – кинетическая энергия уменьшается.
Если тело покоится, кинетической энергии нет. Математики в таком случае запишут: (E_{k}=0 ).

Рассмотрим тело, движущееся по поверхности с какой-либо скоростью (рис 1а).

Зная массу и скорость тела, можно рассчитать его кинетическую энергию с помощью формулы:

[ large boxed{ E_{k} = m cdot frac{v^{2}}{2}}]

( E_{k} left( text{Дж}right) ) – кинетическая энергия;

( m left( text{кг}right) ) – масса тела;

( v left( frac{text{м}}{c}right) ) – cскорость, с которой тело движется.

Потенциальная энергия

Любое тело, поднятое над поверхностью, обладает потенциальной возможностью упасть и совершить работу. Например, потенциальная энергия поднятого над гвоздем молотка переходит в работу по забиванию гвоздя в доску.

Физики говорят: поднятое на высоту тело обладает потенциальной энергией.

Примечание: Потенциальная энергия возникает у тела из-за притяжения Земли.

Вообще, потенциальная энергия – это энергия взаимодействия (притяжения, или отталкивания). В нашем примере – энергия притяжения тела и Земли.

Если тело изменит высоту, на которой оно находится, будет изменяться его потенциальная энергия.
Тело опускается вниз – потенциальная энергия уменьшается.
Тело поднимается выше – потенциальная энергия растет.
Когда тело находится на поверхности земли, потенциальной энергии у него нет (E_{p}=0).

Рассмотрим тело, находящееся на какой-либо высоте над поверхностью земли (рис 1б).

Можно рассчитать потенциальную энергию тела, зная его массу и высоту тела над поверхностью земли, с помощью формулы:

[ large boxed{ E_{p} = m cdot g cdot  h}]

( E_{p} left( text{Дж}right) ) – потенциальная энергия;

( m left( text{кг}right) ) – масса тела;

( h left( text{м}right) ) – высота, на которую тело подняли над поверхностью земли.

Полная механическая энергия тела

Если сложить кинетическую энергию тела с его потенциальной энергией в какой-либо момент времени, мы получим полную механическую энергию, которой тело обладало в этот момент времени.

Летящий в небе самолет (рис. 3) одновременно будет обладать и кинетической энергией – он движется, и потенциальной энергией – он находится на высоте.

Любая энергия – это скаляр (просто число).  Значит, энергия направления не имеет и ее можно складывать алгебраически.

[ large boxed{ E_{k} + E_{p} = E_{text{полн. мех}} }]

( E_{p} left( text{Дж}right) ) – потенциальная энергия тела;

( E_{k} left( text{Дж}right) ) – кинетическая энергия, которой обладает тело;

( E_{text{полн. мех}} left( text{Дж}right) ) – полная механическая энергия этого тела;

Советую далее прочитать о законе сохранения энергии

Содержание:

Потенциальная энергия:

По определению потенциальная энергия – это энергия взаимодействия. Т. е. потенциальную энергию имеют все взаимодействующие тела. Для каждого вида механического взаимодействия можно рассчитать потенциальную энергию, учитывая особенности данного взаимодействия.

Самым распространенным в природе является гравитационное взаимодействие, проявлением которого является сила тяжести. При определенных условиях эта сила может выполнять работу.

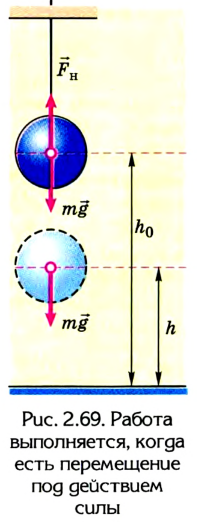
Допустим, тело массой т подвешено над полом на высоте

Если нить перерезать, то тело начнет падать под действием силы тяжести.

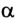
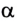
По определению работа А = Fs cos = mgs cos.

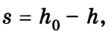
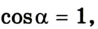
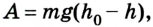
Если учесть, что a то или 

Поскольку работа равна изменению энергии, то можно считать, что выражение mgh определяет потенциальную энергию тела в поле силы тяжести Земли на высоте Л. Движение под действием силы тяжести может происходить по разным траекториям. Выясним, будет ли это влиять на значение работы.

Дадим возможность телу свободно скользить без трения по наклонной плоскости под действием силы тяжести (рис. 2.70).

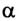
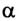
Если учитывать, что А = mgscos, s=AB, то А = mgABcos.

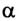
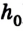
Из треугольника ABC ABcos  = ВС и вместе с тем BD = – h.

Тогда работа силы тяжести при скольжении тела без трения по наклонной плоскости будет равна А = mg(h – ).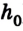

Следовательно, работа силы тяжести по перемещению тела по наклонной плоскости будет такой же, как и при его падении из точки В, расположенной на высоте 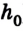, в точку D, находящуюся на высоте Л.

Таким образом, работа силы тяжести определяется положением точек начала и конца движения и не зависит от формы траектории.

В тех случаях, когда работа силы не зависит от формы траектории, а определяется начальным и конечным положением тела, пользуются понятием потенциальной энергии.

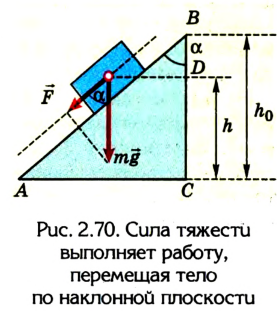
Если записать формулу для работы силы тяжести в виде

т. е. работа определяется изменением величины mgh, которая называется потенциальной энергией тела в поле силы тяжести:

Работа силы тяжести равна изменению потенциальной энергии тела с противоположным знаком. Это означает, что при падении тела, когда сила тяжести выполняет положительную работу, его потенциальная энергия уменьшается. И наоборот, при движении тела вверх, когда сила тяжести выполняет отрицательную работу, его потенциальная энергия увеличивается. Эта особенность характерна для всех случаев, когда работа силы не зависит от формы траектории.

Что такое потенциальная энергия

Потенциальная энергия (от латинского слова потенциал – возможность) – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного тела.

Поскольку любое тело и Земля притягивают друг друга, т. е. взаимодействуют, то потенциальная энергия тела, поднятого над Землей, будет зависеть от высоты подъёма h. Чем больше высота подъёма тела, тем больше его потенциальная энергия.

Опытами установлено, что потенциальная энергия тела зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела подняты на одинаковую высоту, то тело, у которого масса больше, будет иметь и ббльшую потенциальную энергию. Во время падения поднятого тела на поверхность Земли сила тяжести выполнила работу, соответствующую изменению потенциальной энергии тела со значения её на высоте И до значения на поверхности Земли. Если для удобства принять, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия поднятого тела будет равна выполненной во время падения работе:

Итак, потенциальную энергию тела, поднятого на некоторую высоту, будем определять по формуле: 

где Е_п — потенциальная энергия поднятого тела; m — масса тела; 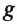= 9,81

h — высота, на которую поднято тело.

Большой запас потенциальной энергии у воды горных или равнинных рек, поднятых плотинами. Падая с высоты вниз, вода выполняет работу: приводит в движение турбины гидроэлектростанций. В Украине на Днепре построено несколько гидроэлектростанций, в которых используют энергию воды для получения электроэнергии. На рисунке 174 изображено сечение такой станции. Вода с более высокого уровня падает вниз и вращает колесо гидротурбины. Вал турбины соединён с генератором электрического тока.

Потенциальной энергией обладает самолёт, летящий высоко в небе; дождевые капли в туче; молот копра при забивании свай. Открывая двери с пружиной, мы растягиваем её, преодолевая силу упругости, т. е. выполняем работу. Вследствие этого пружина приобретает потенциальную энергию. За счёт этой энергии пружина, сокращаясь, выполняет работу – закрывает двери. Потенциальную энергию пружин используют в часах, разнообразных заводных игрушках. В автомобилях, вагонах пружины амортизаторов и буферов, деформируясь, уменьшают толчки.

Потенциальная энергия пружины зависит от её удлинения (изменения длины при сжатии или растяжении) и жёсткости (зависит от конструкции пружины и упругости материала, из которого она изготовлена). Чем больше удлинение (деформация) пружины, и чем больше её жёсткость, тем большую потенциальную энергию она приобретает при деформации. Такая зависимость свойственна любому упруго деформированному телу.

Потенциальную энергию упругодеформированного тела определяют по формуле:   

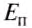
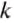
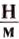
где — потенциальная энергия упруго деформированного тела (пружины); — жёсткость тела (единица жёсткости — 1 — удлинение (деформация) тела (пружины).

Но тела могут обладать энергией не только потому, что они находятся в определённом положении или деформируются, а и потому, что они находятся в движении.

Определение потенциальной энергии

В повседневной жизни можно обнаружить множество различных тел, при перемещении которых может выполняться работа. Так, выпавший из рук шарик начнет падать под действием силы притяжения, которая будет выполнять работу по перемещению шарика.

Сжатая пружина может поднять на определенную высоту груз. В этом случае сила упругости выполняет работу по перемещению груза.

Что такое энергия

Энергия – это физическая величина, показывающая, какая работа может быть выполнена при перемещении тела.

Можно привести еще много разных примеров из природы, из повседневной жизни, из техники, в которых речь идет о телах, находящихся в таком состоянии, что при определенных условиях может выполняться работа при их перемещении. О таких телах говорят, что они обладают энергией. При различных условиях результат выполнения работы может быть разным. Поэтому и энергия может иметь различные значения и может быть рассчитана.

Единицы энергии

Поскольку речь идет о возможности выполнения работы, то энергию целесообразно измерять в таких же единицах, что и работу. Поэтому единицей энергии есть 1 Дж.

Виды механической энергии

В физике выделяют два вида механической энергии: потенциальную и кинетическую. Если тело неподвижно, но па него действует определенная сила, то говорят, что оно обладает потенциальной энергией.

Потенциальной энергией обладает тело, поднятое над поверх-136 ностью Земли, сжатая пружина, сжатый газ, речная вода в водоеме и другие тела.

Как рассчитывают потенциальную энергию

Рассчитывают потенциальную энергию с учетом природы сил, действующих на эти тела. Проще всего рассчитать потенциальную энергию тела, поднятого над поверхностью Земли, поскольку сила, действующая на него, остается практически постоянной на протяжении всего времени его движения под действием этой силы.

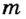
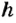
Пусть тело массой находится на высоте над землей. Если оно упадет на поверхность, то будет выполнена работа

Следовательно, о таком теле можно сказать, что оно обладает потенциальной энергией

Потенциальная энергия тела, поднятого над поверхностью Земли, пропорциональна массе тела и его высоте над поверхностью Земли.

При расчете потенциальной энергии важно помнить, что высота 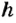является путем, который тело преодолеет в вертикальном направлении. Таким образом, всегда следует указывать, относительно какой поверхности определяется потенциальная энергия. Например, тело массой 2 кг, поднятое над столом на высоту 1,5 м, будет обладать потенциальной энергией, равной примерно 30 Дж, а потенциальная энергия этого тела, рассчитанная для высоты 3 м над полом, будет 60 Дж.

Потенциальная энергия упруго деформированного тела

Расчет работы силы упругости усложняется тем, что в ходе выполнения работы значение силы изменяется. Поскольку изменение силы упругости происходит линейно, то при расчетах работы используют среднее значение силы:

где 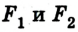– значения силы упругости в начале и в конце процесса.

Учитывая, что 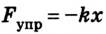(по закону Гука), то

В случае, когда 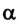 = 0, т. е. сила упругости действует вдоль прямой, по которой происходит перемещение, получим выражение для расчета работы силы упругости:

где 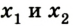– удлинение, характеризующее начальную и конечную деформации соответственно.

Для потенциальной энергии тела в поле силы тяжести можно записать:

Потенциальная энергия упруго деформированного тела зависит от его деформации.

Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятой с противоположным знаком.

Как и в случае работы силы тяжести, работа силы упругости зависит не от формы траектории, а только от начальной и конечной деформации тела.

Механическая работа и кинетическая энергия

Чтобы шли механические часы, их нужно завести — закрутить пружину; раскручиваясь, пружина совершит работу. Поднявшись на вершину горы, лыжник создаст «запас работы» и в результате сможет скатиться вниз; при этом работу совершит сила тяжести. Самый простой способ разбить окно в горящем доме — бросить в окно камень. Если скорость движения камня достаточна, он разобьет окно — совершит работу. О теле или системе тел, которые могут совершить работу, говорят, что они обладают энергией.

Когда сила совершает механическую работу

Основная задача механики — определение механического состояния тела (координат тела и скорости его движения) в любой момент времени. Механическое состояние тела не изменяется само по себе — необходимо взаимодействие, то есть наличие силы. Когда тело перемещается (изменяет свое механическое состояние) под действием силы, говорят, что данная сила совершает механическую работу.

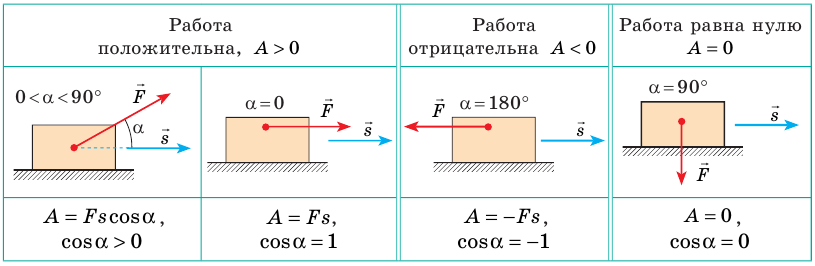
Механическая работа (работа силы) A — физическая величина, характеризующая изменение механического состояния тела и равная произведению модуля силы F, модуля перемещения s и косинуса угла a между вектором силы и вектором перемещения:

Единица работы в СИ — джоуль:

1 Дж равен механической работе, которую совершает сила 1 Н, перемещая тело на 1 м в направлении действия этой силы.

Работа силы — величина скалярная, однако она может быть положительной, отрицательной, равной нулю — в зависимости от того, куда направлена сила относительно направления движения тела (см. таблицу).

Геометрический смысл работы силы

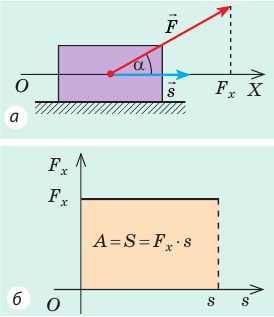
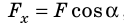
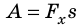
Рассмотрим силу, действующую под некоторым углом α к направлению движения тела. Найдем проекцию этой силы на направление перемещения тела, для чего ось ОХ направим в сторону движения тела (рис. 15.1, а). Из рисунка видим, что , следовательно, .

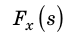
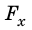
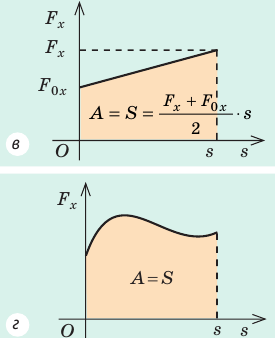
Построим график — зависимости проекции силы от модуля перемещения. Если сила, действующая на тело, постоянна, график этой зависимости представляет собой отрезок прямой, параллельной оси перемещения (рис. 15.1, б). Из рисунка видим, что произведение и s соответствует площади S прямоугольника под графиком.

Рис. 15.1. Если направление оси ОХ совпадает с направлением движения тела, то работа A силы численно равна площади S фигуры под графиком зависимости

В этом состоит геометрический смысл работы силы: работа силы численно равна площади фигуры под графиком зависимости проекции силы от модуля перемещения. Это утверждение распространяется и на случаи, когда сила переменная (рис. 15.1, в, г).

Когда тело имеет кинетическую энергию

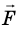
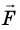
Рассмотрим тело массой m, которое под действием равнодействующей силы увеличивает скорость своего движения от v0 до v. Пусть равнодействующая не изменяется со временем и направлена в сторону движения тела. Определим работу этой силы.

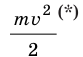
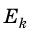
Величину называют кинетической энергией тела .

Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы m тела на квадрат скорости v его движения:

Теорема о кинетической энергии: работа равнодействующей всех сил, которые действуют на тело, равна изменению кинетической энергии тела:

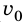
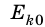
Если в начальный момент времени тело неподвижно ( = 0), то есть= 0, то теорема о кинетической энергии сводится к равенству:

Кинетическая энергия тела, движущегося со скоростью v, равна работе, которую совершает сила, чтобы придать неподвижному телу данную скорость.

Мощность

До сих пор мы говорили о работе силы. Но любая сила характеризует действие определенного тела (или поля). Поэтому работу силы часто называют работой тела (работой поля), со стороны которого действует эта сила. На практике большое значение имеет не только выполненная работа, но и время, за которое эта работа была выполнена. Поэтому для характеристики механизмов, предназначенных для совершения работы, используют понятие мощности.

Мощность P (или N) — физическая величина, характеризующая скорость выполнения работы и равная отношению работы А к интервалу времени t, за который эта работа выполнена:

Единица мощности в СИ — ватт:

(Названа в честь Джеймса Ватта (1736–1819). Как единицу мощности он ввел лошадиную силу, которую иногда используют и сейчас: 1 л. с. = 746 Вт.)

Мощность, которую развивает транспортное средство, удобно определять через силу тяги и скорость движения. Если тело движется равномерно, а направление силы тяги совпадает с направлением перемещения, тяговую мощность двигателя можно вычислить по формуле:

Обратите внимание! Данная формула справедлива для любого движения: мощность, которую развивает двигатель в данный момент времени, равна произведению модуля силы тяги двигателя на модуль его мгновенной скорости: P = Fv (рис. 15.3).

Рис. 15.3. Когда для движения автомобиля требуется большая сила тяги, водитель переходит на меньшую скорость или нажимает на газ, увеличивая таким образом мощность двигателя

Чтобы определить механическую работу и мощность, нужно знать силу, действующую на тело, перемещение тела и время его движения. Поэтому обычно решение задач на определение работы и мощности сводится к решению задач по кинематике и динамике.

Пример №1

Автомобиль массой 2 т движется равномерно со скоростью 20 м/с по горизонтальному участку дороги. Какие силы действуют на автомобиль? Найдите работу каждой силы и тяговую мощность двигателя автомобиля, если коэффициент сопротивления движению равен 0,01, а время движения — 50 с.

Решение:

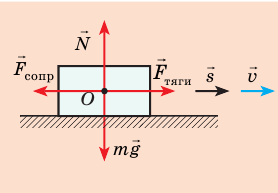
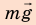
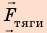
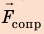
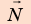
Выполним пояснительный рисунок, на котором укажем силы, действующие на автомобиль: силу тяжести , силу тяги , силу сопротивления движению , силу нормальной реакции опоры. По определению работы: A = Fscosα

Чтобы определить работу каждой силы, нужно найти::

• угол между направлением этой силы и направлением перемещения;
• модуль силы и модуль перемещения.

1. Автомобиль движется равномерно, поэтому действующие на него силы скомпенсированы: — сила тяжести уравновешена силой нормальной реакции опоры: N = mg; — сила тяги уравновешена силой сопротивления движению:

2. Перемещение автомобиля можно найти по формуле: s = vt .

3. Сила тяжести и сила нормальной реакции опоры перпендикулярны направлению движения автомобиля (α = 90°, cosα = 0). Следовательно, работа этих сил равна нулю. Сила тяги направлена в сторону движения тела: α = 0, cosα = 1, поэтому:

Сила сопротивления противоположна движению: α = 180°, cosα = −1, поэтому:

4. Тяговую мощность двигателя автомобиля определим по формуле 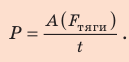Проверим единицы, найдем значения искомых величин:

Выводы:

Потенциальная энергия и закон сохранения механической энергии

Поднятый молот не обладает кинетической энергией, так как его скорость равна нулю. Но если молот отпустить, он совершит работу (расплющит металл). Натянутая тетива лука не имеет кинетической энергии, но, выпрямляясь, она придаст скорость стреле, а значит, совершит работу. И деформированное тело, и тело, поднятое над поверхностью Земли, способны совершить работу, то есть обладают энергией. Что это за энергия и как ее рассчитать?

Когда тело обладает потенциальной энергией

Механическая энергия E — физическая величина, характеризующая способность тела (системы тел) совершить работу.

Единица энергии (как и работы) в СИ — джоуль [E] = 1 Дж (J).

Любое движущееся тело может совершить работу, поскольку оно обладает кинетической энергией, или «живой силой», как ее называли раньше. Есть еще один вид механической энергии — ее называли «мертвая сила». Это — потенциальная энергия (от лат. potentia — сила, возможность), — энергия, которую имеет тело в результате взаимодействия с другими телами.

Потенциальная энергия — энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела.

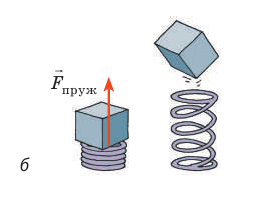
Рис. 16.1. И девочка в результате взаимодействия с Землей (а), и сжатая пружина в результате взаимодействия ее витков (б) обладают потенциальной энергией

Девочка на вершине горки (рис. 16.1, а) обладает потенциальной энергией, поскольку в результате взаимодействия с Землей может начать движение и сила тяжести совершит работу. Но как вычислить эту работу, ведь горка неровная и в течение всего времени движения угол между направлением силы тяжести и направлением перемещения будет изменяться?

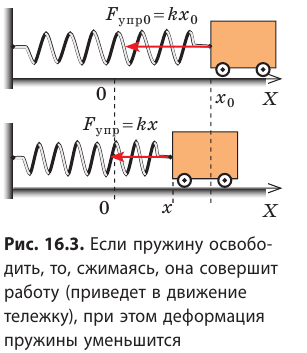
Сжатая пружина (рис. 16.1, б) тоже обладает потенциальной энергией: при распрямлении пружины сила упругости совершит работу — подбросит брусок. Но как вычислить эту работу, ведь во время действия пружины на брусок сила упругости непрерывно уменьшается?

Оказывается, все не так сложно. И сила тяжести, и сила упругости имеют одно «замечательное» свойство — работа этих сил не зависит от формы траектории. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным механическими состояниями тела (системы тел), называют потенциальными, или консервативными, силами (от лат. conservare — сохранять, охранять).

Потенциальная энергия поднятого тела

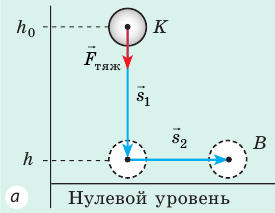
Докажем, что сила тяжести — консервативная сила. Для этого определим работу силы тяжести при движении тела из точки K в точку B по разным траекториям.

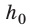
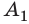
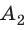
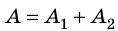
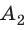
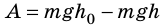
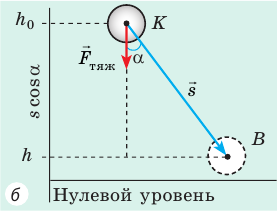
Случай 1. Пусть траектория движения тела — «ступенька» (рис. 16.2, а): сначала тело падает с некоторой высоты до высоты h и сила тяжести совершает работу , затем тело движется горизонтально и сила тяжести совершает работу . Работа — величина аддитивная, поэтому общая работа .

= 0, так как сила тяжести перпендикулярна перемещению тела. Итак: .

Случай 2. Пусть тело перемещается из точки K в точку В, скользя по наклонной плоскости (рис. 16.2, б). В этом случае работа силы тяжести равна:

Рис. 16.2. При перемещении тела с высоты 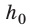до высоты h работа силы тяжести, независимо от траектории движения тела, определяется по формуле:

Тот же результат получим и для случаев перемещения тела по произвольной траектории. Следовательно, работа силы тяжести не зависит от траектории движения тела, то есть сила тяжести — консервативная сила. Величину mgh называют потенциальной энергией поднятого тела:

Потенциальная энергия поднятого тела зависит от высоты, на которой находится тело, то есть зависит от выбора нулевого уровня, — уровня, от которого будет отсчитываться высота. Нулевой уровень выбирают из соображений удобства. Так, находясь в комнате, за нулевой уровень целесообразно взять пол, определяя высоту горы — поверхность Мирового океана.

Обратите внимание! Изменение потенциальной энергии, а следовательно, и работа силы тяжести от выбора нулевого уровня не зависят.

• Заказать решение задач по физике

Потенциальная энергия упруго деформированного тела

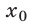
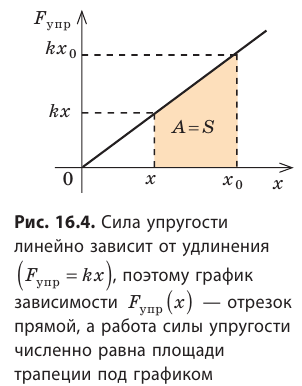
Пусть имеется упруго деформированное тело — растянутая пружина. Определим работу, которую совершит сила упругости при уменьшении удлинения пружины от до x (рис. 16.3). Воспользуемся для этого геометрическим смыслом механической работы (рис. 16.4):

Таким образом, работа силы упругости определяется только начальным и конечным состояниями пружины, то есть сила упругости — консервативная сила. Величину 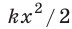называют потенциальной энергией упруго деформированного тела:

Работа силы упругости (как и силы тяжести) равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Данное выражение — математическая запись теоремы о потенциальной энергии: работа всех консервативных сил, действующих на тело, равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Состояние с меньшей потенциальной энергией является энергетически выгодным; любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна, — в этом заключается принцип минимума потенциальной энергии. Действительно, камень, выпущенный из руки, никогда не полетит вверх — он будет падать, стремясь достичь состояния с наименьшей потенциальной энергией. Недеформированная пружина никогда не станет сама растягиваться или сжиматься, а деформированная пружина стремится перейти в недеформированное состояние.

Закон сохранения полной механической энергии

Как правило, тело или система тел обладают и потенциальной, и кинетической энергиями. Сумму кинетических и потенциальных энергий тел системы называют полной механической энергией системы тел: 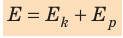(рис. 16.5).

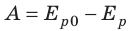
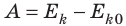
Рассмотрим замкнутую систему тел, взаимодействующих друг с другом только консервативными силами (силами тяготения или силами упругости). По теореме о потенциальной энергии работа A, совершаемая этими силами, равна: . С другой стороны, согласно теореме о кинетической энергии эта же работа равна: . Приравняв правые части равенств, получим закон сохранения и превращения полной механической энергии:

В замкнутой системе тел, взаимодействующих только консервативными силами, полная механическая энергия остается неизменной (сохраняется):

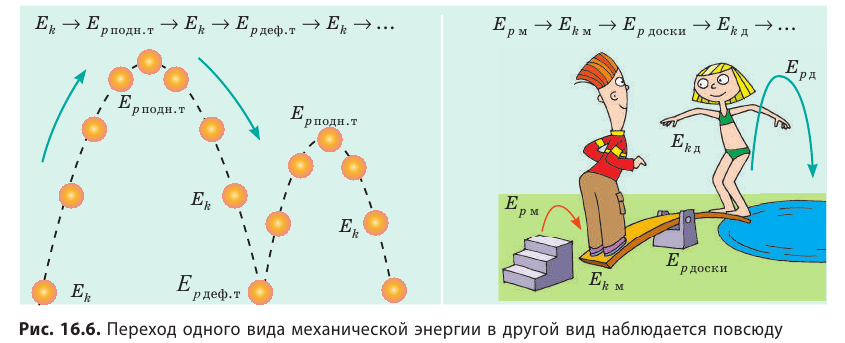
Закон сохранения полной механической энергии предполагает превращение кинетической энергии в потенциальную и наоборот (рис. 16.6). Однако сохраняется ли при этом полная механическая энергия? Наш опыт подсказывает, что нет. И действительно, закон сохранения полной механической энергии справедлив только в случаях, когда в системе отсутствует трение. Однако в природе не существует движений, не сопровождающихся трением. Сила трения всегда направлена против движения тела, поэтому при движении она совершает отрицательную работу, при этом полная механическая энергия системы уменьшается:

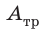
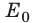
где — работа силы трения; E, — полная механическая энергия системы в конце и в начале наблюдения соответственно.

Потери энергии наблюдаются и в случае неупругого удара. Так что, при наличии трения или при неупругой деформации энергия бесследно исчезает? Казалось бы, да. Однако измерения показывают, что в результате и трения, и неупругого удара температуры взаимодействующих тел увеличиваются, то есть увеличиваются внутренние энергии тел. Значит, кинетическая энергия не исчезает, а переходит во внутреннюю энергию.

Энергия никуда не исчезает и ниоткуда не появляется: она только переходит из одного вида в другой, передается от одного тела к другому.

Алгоритм решения задач с применением закона сохранения механической энергии

1. Прочитайте условие задачи. Выясните, является ли система замкнутой, можно ли пренебречь действием сил сопротивления. Запишите краткое условие задачи.
2. Выполните пояснительный рисунок, на котором укажите нулевой уровень, начальное и конечное состояния тела (системы тел).
3. Запишите закон сохранения механической энергии. Конкретизируйте запись, воспользовавшись данными условия задачи и соответствующими формулами для определения энергии.
4. Решите полученное уравнение относительно неизвестной величины.
5. Проверьте единицу, найдите значение искомой величины.
6. Проанализируйте результат, запишите ответ.

Пример №2

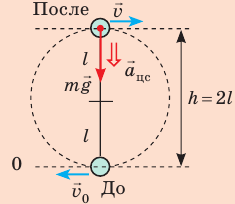
Какую минимальную скорость нужно сообщить шарику, подвешенному на нити длиной 0,5 м, чтобы он смог совершить полный оборот в вертикальной плоскости? Сопротивлением воздуха пренебречь.

Анализ физической проблемы

• Сопротивлением воздуха пренебрегаем, поэтому система «шарик — нить — Земля» является замкнутой и можно воспользоваться законом сохранения механической энергии.
• За нулевой уровень примем самое низкое положение шарика.
• В самой высокой точке траектории шарик имеет некоторую скорость, иначе он не продолжил бы вращаться, а стал бы падать вертикально вниз.
• Для определения скорости движения шарика в наивысшей точке траектории воспользуемся определением центростремительного ускорения и вторым законом Ньютона.
• Нужно найти минимальную скорость движения шарика в момент толчка, поэтому понятно, что в наивысшей точке траектории нить натянута не будет, то есть сила ее натяжения будет равна нулю.

Решение:

На рисунке отметим положения шарика в самой нижней и самой верхней точках траектории; силы, действующие на шарик в верхней точке; направление ускорения. По закону сохранения механической энергии:

Согласно второму закону Ньютона: .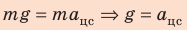

Поскольку

Подставим выражение (2) в выражение (1): 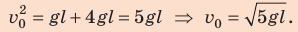Проверим единицу, найдем значение искомой величины:

Ответ:

Выводы: