Как найти потенциальную энергию гравитационного взаимодействия

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2022 года; проверки требуют 3 правки.

Виды энергии:
	Механическая	Потенциальная Кинетическая
‹♦›	Внутренняя
	Электромагнитная	Электрическая Магнитная
	Химическая
	Ядерная
	Гравитационная
	Вакуума
Гипотетические:
	Тёмная
См. также: Закон сохранения энергии

Гравитациóнная энéргия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением.

Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

Гравитационная энергия играет очень важную роль на заключительных этапах эволюции звёзд, при их превращении в нейтронные звёзды и сверхновые^[1].

Гравитационно-связанные системы[править | править код]

Гравитациóнно-свя́занная систéма — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).

Земля, которая, как и любое небесное тело, сама является гравитационно-связанной системой, является также частью следующих гравитационно-связанных систем:

Система Земля — Луна,
Солнечная система,
Галактика Млечный Путь,
Местная группа,
Ланиакея.

В классической механике[править | править код]

Для двух тяготеющих точечных тел с массами M и m гравитационная энергия ${displaystyle U_{g}}$ равна:

${displaystyle U_{g}=-G{Mm over R},}$

где:

— гравитационная постоянная;

— расстояние между центрами масс тел.

Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид

${displaystyle F_{g}=G{Mm over R^{2}},}$

где:

$F_{g}$

— сила гравитационного взаимодействия

С другой стороны согласно определению потенциальной энергии

${displaystyle F_{g}={frac {dU_{g}}{dR}}.}$

Тогда:

${displaystyle U_{g}=const-G{Mm over R}.}$

Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, ${displaystyle U_{g}}$ стремилось к нулю.

Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным ${displaystyle h+R_{M}}$ , где ${displaystyle R_{M}}$ — радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M.

На поверхности тела M имеем:

${displaystyle U_{g}=-G{Mm over R_{M}},}$

Если размеры тела много больше размеров тела , то формулу гравитационной энергии можно переписать в следующем виде:

${displaystyle U_{g}=-G{Mm over R_{M}+h}=-mG{frac {M}{R_{M}}}{frac {1}{1+h/R_{M}}}approx -mG{frac {M}{R_{M}}}left(1-{frac {h}{R_{M}}}right)=mgh-m{frac {GM}{R_{M}}},}$

где величину ${displaystyle g={frac {GM}{R_{M}^{2}}}}$ называют ускорением свободного падения. При этом член ${displaystyle m{frac {GM}{R_{M}}}}$ не зависит от высоты поднятия тела над поверхностью и может быть исключён из выражения путём выбора соответствующей константы. Таким образом для малого тела, находящегося на поверхности большого тела справедлива следующая формула

${displaystyle U_{g}=mgh.}$

В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли.

Отрицательность потенциальной энергии здесь вызвана тем, что невозможно принять за точку отсчета геометрический центр тела (то есть R = 0 ) одновременно с принятием гипотезы о том, что тело представляет собой материальную точку. В этом случае потенциальная энергия будет стремится к бесконечности в центре (образуется сингулярность). По этому за точку отсчета потенциальной энергии принято считать бесконечно удаленную точку. Знак «минус» при этом просто говорит, что потенциальная энергия увеличивается при отдалении от тело.

Однако, при необходимости, сингулярности можно избежать, приняв, что вся масса большего тела не сосредоточена в точке, а равномерно распределена в шаре с радиусом $R_{M}$ . При этом масса тела с его радиусом будет связана соотношением

${displaystyle M={frac {4}{3}}pi rho R_{M}^{3},}$

где rho – средняя плотность тела. Оказывается, что в этом случае сила притяжения внутри тела будет описываться линейной зависимостью относительно (то есть она представляет собой силу упругости), а снаружи как и прежде — пропорционально обратному квадрату.

${displaystyle F_{g}=mgcdot left{{begin{matrix}{bar {R}}&,{bar {R}}leq 1\{bar {R}}^{-2}&,{bar {R}}>1end{matrix}}right.,}$

где — ускорение свободного падения у поверхности большего тела; ${displaystyle {bar {R}}=R/R_{M}}$ — нормированное расстояние от центра большего тела, при этом соответствует уровню поверхности, — положению под поверхностью, а положению над поверхностью.

Потенциальная энергия при этом, если принять, что в центре тела она равна нулю, будет описываться как

${displaystyle U_{g}=U_{s}cdot left{{begin{matrix}{bar {R}}^{2}&,{bar {R}}leq 1\3-{frac {2}{bar {R}}}&,{bar {R}}>1end{matrix}}right.,}$

где ${displaystyle U_{s}={frac {mgR_{M}}{2}}={frac {GMm}{2R_{M}}}={frac {2pi }{3}}Grho R_{M}^{2}m}$ — потенциальная энергия у поверхности тела. Потенциальная энергия в бесконечно удаленной точке равна

${displaystyle U_{infty }=3U_{s}={frac {3GMm}{2R_{M}}}=2pi Grho R_{M}^{2}m}$ .

Сравнив потенциальную энергию на поверхности и в бесконечности с кинетической энергией, можно определить характерные для рассматриваемого тела скорости:

${displaystyle v_{1}={sqrt {gR_{M}}}={sqrt {frac {GM}{R_{M}}}}=2R_{M}{sqrt {{frac {pi }{3}}Grho }}}$ — минимально необходимая скорость малого тела для того, чтобы достичь поверхности большего тела из его центра. Или максимальная скорость малого тела, брошенного вниз в вертикальный тоннель. Она же в точности равняется скорости движения по круговой орбите у поверхности большего тела (первая космическая скорость).

${displaystyle v_{2}={sqrt {2gR_{M}}}={sqrt {frac {2GM}{R_{M}}}}=2R_{M}{sqrt {{frac {2pi }{3}}Grho }}}$ — Минимальная скорость убегания малого тела в бесконечность с поверхности большого тела (вторая космическая скорость).

${displaystyle v_{20}={sqrt {3gR_{M}}}={sqrt {frac {3GM}{R_{M}}}}=2R_{M}{sqrt {pi Grho }}}$ — Минимальная скорость убегания малого тела в бесконечность из центра большого тела (аналог второй космической скорости при «стрельбе» малым телом из центра большего тела).

Если сравнить силу тяготения с центробежной силой, то можно получить величину требуемой скорости малого тела для движения по круговой орбите вокруг центра большего тела

${displaystyle v_{o}=v_{1}cdot left{{begin{matrix}{bar {R}}&,{bar {R}}leq 1\{bar {R}}^{-{frac {1}{2}}}&,{bar {R}}>1end{matrix}}right.}$ .

Из особенности тяготения внутри большего тела, малое тело движется внутри него так, как будто бы подцепленно за конец воображаемой пружины, другой конец которой прикреплён к центру тела. Если бросить с поверхности такое тело вертикально вниз в воображаемый вакуумный тоннель, проходящий через центр планеты насквозь, то оно будет совершать гармонические колебания с периодом

${displaystyle T_{g}=2pi {sqrt {frac {R_{M}}{g}}}=2pi {sqrt {frac {R_{M}^{3}}{GM}}}={sqrt {frac {3pi }{Grho }}}}$ ,

что для Земли равняется 5064 с или 1 час, 24 минуты, 24 секунды. Максимальная скорость при пролёте через центр тела равна первой космической. Жёсткость такой воображаемой пружины равняется

${displaystyle k_{g}={frac {mg}{R_{M}}}={frac {GMm}{R_{M}^{3}}}={frac {4pi }{3}}Grho m}$ .

В ОТО[править | править код]

В общей теории относительности наряду с классическим отрицательным компонентом гравитационной энергии связи появляется положительная компонента, обусловленная гравитационным излучением, то есть полная энергия гравитирующей системы убывает во времени за счёт такого излучения.

См. также[править | править код]

Потенциальная энергия
Кинетическая энергия
Первая космическая скорость
Вторая космическая скорость
Гравитационный потенциал

Примечания[править | править код]

↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М., Наука, 1972. — c. 553—557

Литература[править | править код]

Tsokos, K. A. Physics for the IB Diploma Full Colour. — revised. — Cambridge University Press, 2010. — P. 143. — ISBN 978-0-521-13821-5.
MacDougal, Douglas W. Newton’s Gravity: An Introductory Guide to the Mechanics of the Universe. — illustrated. — Springer Science & Business Media, 2012. — P. 10. — ISBN 978-1-4614-5444-1.
For a demonstration of the negativity of gravitational energy, see Alan Guth, The Inflationary Universe: The Quest for a New Theory of Cosmic Origins (Random House, 1997), ISBN 0-224-04448-6, Appendix A—Gravitational Energy.

Ссылки[править | править код]

Fitzpatrick Richard. Gravitational potential energy. farside.ph.utexas.edu. The University of Texas at Austin (2 февраля 2006).

Источник

Потенциальная энергия гравитационного
взаимодействия системы двух материальных
точек с массами m и М, находящихся
на расстоянии r одна от другой, равна

.
(11)

где G – гравитационная постоянная,
а нуль отсчета потенциальной энергии
(Е_p = 0) принят при r = ∞.

Потенциальная энергия гравитационного
взаимодействия тела массой m с
Землей, где h – высота тела над
поверхностью Земли, M_e – масса
Земли, R_e – радиус Земли, а нуль
отсчета потенциальной энергии выбран
при h = 0.

.
(12)

При том же условии выбора нуля отсчета
потенциальная энергия гравитационного
взаимодействия тела массой m с Землей
для малых высот h (h « R_e)
равна

где

–
модуль ускорения свободного падения
вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой
упругости при изменении деформации
(удлинения) пружины от некоторого
начального значения x₁ до
конечного значения x₂ (рис. 4,
б, в).

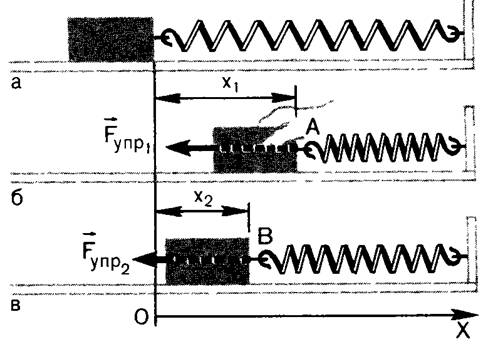
Рис. 4

Сила упругости изменяется в процессе
деформации пружины. Для нахождения
работы силы упругости можно взять
среднее значение модуля силы (т.к. сила
упругости линейно зависит от x) и
умножить на модуль перемещения:

,
(13)

где

.
Отсюда

или

.
(14)

Физическая величина, равная половине
произведения жесткости тела на квадрат
его деформации, называется потенциальной
энергией упруго деформированного
тела:

.
(15)

Из формул (14) и (15) следует, что работа
силы упругости равна изменению
потенциальной энергии упруго
деформированного тела, взятому с
противоположным знаком:

.
(16)

Если x₂ = 0 и x₁ = х,
то, как видно из формул (14) и (15),

7.Закон сохранения механической энергии системы. Из уравнения (10.15) следует,

Полная механическая энергия замкнутой консервативной системы не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии системы.

Заметим, что в процессе движения тел
системы один вид энергии может переходить
в другой.

Причины
изменения механической энергии системы.
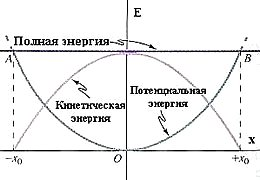
Полной механической энергией системы
тел называется сумма кинетической и
потенциальной энергий:

E = E_к
+ E_п.

Какие причины могут изменить полную
механическую энергию?

Полная механическая энергия может
изменяться в результате следующих
причин:

	внешнего воздействия на систему (толчки, приближение из вне магнита, заряженных тел и т.п.);
	наличия внутренних неконсервативных сил. Например, силы сопротивления вызывают уменьшение механической энергии системы “шар, Земля, воздух, нить”.

9-10.Моментом инерции механической
системы относительно
неподвижной оси («осевой момент инерции»)
называется величина J_a,
равная сумме произведений масс всех n
материальных
точек системы на квадраты их
расстояний до оси:

где:

m_i — масса i-й точки,
r_i — расстояние от i-й
точки до оси.

Осевой момент инерции тела J_a
является мерой инертности тела во
вращательном
движении вокруг оси подобно
тому, как масса
тела является мерой его инертности в
поступательном
движении.

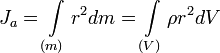
где:

dm = ρdV — масса малого элемента
объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV
до оси a.

Если тело однородно, то есть его плотность
всюду одинакова, то

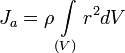
11.Теоре́ма Гю́йгенса — Ште́йнера,
или просто теорема Штейнера (названа
по имени швейцарского математика Якоба
Штейнера и голландского
математика, физика и астронома Христиана
Гюйгенса): момент
инерции тела J относительно
произвольной оси равен сумме момента
инерции этого тела J_C
относительно параллельной ей оси,
проходящей через центр масс тела, и
произведения массы тела m на квадрат
расстояния d между осями:

где

J_C — известный момент
инерции относительно оси, проходящей
через центр масс тела,

J — искомый момент инерции относительно
параллельной оси,

m — масса тела,

d — расстояние между указанными
осями.

Вывод

Момент инерции, по определению:

Радиус-вектор

можно
расписать как разность двух векторов:

где

—
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:

Вынося за сумму

,
получим:

Поскольку старая ось проходит через
центр масс, то суммарный импульс тела
будет равен нулю:

Тогда:

Откуда и следует искомая формула:

где J_C — известный момент
инерции относительно оси, проходящей
через центр масс тела.

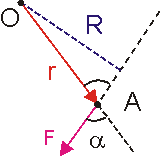
Момент
силы, действующей на материальную точку.
Пусть частица A
движется произвольным образом относительно
точки О под действием
силы F (см. рис. 6.2).
Моментом силы частицы относительно
закрепленной точки называется величина,
равная векторному произведению:

M =
[r·F],
(6.3)

где r
– радиус вектор точки приложения силы
F.

кинетическая
энергия твердого тела при вращательном
движении. Кинетическая энергия
твердого тела складывается из кинетических
энергий его частей E_i.
Рассчитаем значение E_iдля элементов твердого тела.

E_i
= m_i·v_i²/2
= m_i·w²·r_i²/2.

Кинетическая энергия твердого тела
будет равна:

E_к
= w²/2·m_i·r_i²
= I·w²/2.
(8.13)

Заметим, что формула для расчета E_кпохожа на выражение для определения
кинетической энергии поступательного
движения тела, только роль меры инертности
в этом случае играет момент инерции, а
не масса и характеристикой движения
является угловая, а не линейная скорость
твердого тела.

Момент импульса

частицы
относительно некоторого начала отсчёта
определяется векторным
произведением её радиус-вектора
и импульса:

где

—
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта,

—
импульс частицы.

Для нескольких частиц момент импульса
определяется как (векторная) сумма таких
членов:

где

—
радиус-вектор и импульс каждой частицы,
входящей в систему, момент импульса
которой определяется.

(В пределе количество частиц может быть
бесконечным, например, в случае твердого
тела с непрерывно распределенной массой
или вообще распределенной
системы это может быть записано
как

где

–
импульс бесконечно малого точечного
элемента системы).

В системе СИ
момент импульса измеряется в единицах
джоуль–секунда;
Дж·с.

Из определения момента импульса следует
его аддитивность:
как, для системы частиц в частности, так
и для системы, состоящей из нескольких
подсистем, выполняется:

Закон
изменения момента импульса.

Рассмотрим
произвольную систему тел. Моментом
импульса системы назовем величину
L, равную
векторной сумме моментов импульсов
отдельных ее частей L_i,
взятых относительно одной и той же точки
выбранной системы отсчета.

L
= ΣL_i.

Найдем скорость
изменения момента импульса системы.
Проведя рассуждения, аналогичные
описанию вращательного движения твердого
тела, получим, что

скорость
изменения момента импульса системы
равна векторной сумме моментов внешних
сил M, действующих на части этой системы.

dL/dt
=
M.

Причем вектора L
и M
задаются относительно одной и той же
точки O в
выбранной СО. Уравнение (21) представляет
собой закон
изменения момента импульса системы.

Причиной изменения
момента импульса является действующий
на систему результирующий момент внешних
сил. Изменение момента импульса за
конечный промежуток времени можно
найти, воспользовавшись выражением

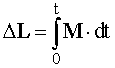
Приращение момента
импульса системы равно импульсу
результирующего момента внешних сил,
действующих на нее.

В неинерциальной
системе к моменту внешних сил необходимо
прибавить момент сил инерции относительно
выбранной точки O.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Физика > Гравитационная потенциальная энергия

Гравитационная энергия – потенциальная энергия, связанная с гравитационной силой.

Задача обучения

Вычислить гравитационную потенциальную энергию для двух масс.

Основные пункты

Если объект падает от одной точки к другой внутри гравитационного поля, то сила тяжести проделает положительную работу над объектом, а гравитационная потенциальная энергия уменьшится на ту же величину.
Возле земной поверхности работа, осуществляемая при поднятии объекта на высоту h выступает как mgh, поэтому U = mgh.
Гравитационная потенциальная энергия (U) системы масс (m₁ и M₂) на дистанции r при использовании гравитационной постоянной G равняется:

Термины

Потенциальная энергия – энергия объекта в его позиции или химическом состоянии.
Затон тяготения Ньютона – каждая точечная вселенская масса притягивает другую при помощи силы, выступающей прямо пропорциональной их массам и обратно пропорциональной квадрату их дистанции.
Сила тяжести – результирующая сила наземной поверхности, притягивающая объекты к центру. Создается вращением.

Пример

Какой будет гравитационная потенциальная энергия 1-килограммовой книги на высоте в 1 м? Так как положение установлено близко к земной поверхности, то гравитационное ускорение будет постоянным (g = 9.8 м/с²), а энергия гравитационного потенциала (mgh) достигает 1 кг ⋅ 1 м ⋅ 9.8 м/с². Это можно проследить и в формуле:

, если добавить массу и земной радиус.

Гравитационная энергия отображает собою потенциальную, связанную с силой гравитации, потому что необходимо преодолеть земное притяжение, чтобы выполнить работу над поднятием предметов. Если объект падает от одной точки к другой внутри гравитационного поля, то сила тяжести выполнит положительную работу, а гравитационная потенциальная энергия уменьшится на ту же величину.

Допустим у нас есть книга, оставленная на столе. Когда мы переносим ее с пола на вершину стола, определенное внешнее вмешательство работает против гравитационной силы. Если же она упадет, то это работа гравитации. Поэтому процесс падения отображает потенциальную энергию, ускоряющую массу книгу и трансформирующуюся в кинетическую. Как только книга коснется пола, кинетическая энергия станет теплом и звуком.

На гравитационную потенциальную энергию влияют высота относительно конкретной точки, масса и сила гравитационного поля. Так что книга на столе уступает по гравитационной потенциальной энергии более тяжелой книга, расположенной ниже. Запомните, что высота не может применяться в вычислении гравитационной потенциальной энергии, если гравитация не выступает постоянной.

Локальное приближение

На силу гравитационного поля влияет расположение. Если изменение дистанции незначительное, то им можно пренебречь, а силу тяжести сделать постоянной (g = 9.8 м/с²). Тогда для вычисления используем простую формулу: W = Fd. Восходящая сила приравнивается к весу, поэтому работа соотносится с mgh, выливающихся в формуле: U = mgh (U – потенциальная энергия, m – масса объекта, g – ускорение силы тяжести, h – высота объекта). Значение выражается в джоулях. Изменение потенциальной энергии передается как

ΔU = mgΔh

Общая формула

Однако, если мы сталкиваемся с серьезными переменами в дистанции, то g не может оставаться постоянной и приходится применять исчисление и математическое определение работы. Чтобы рассчитать потенциальную энергию, можно интегрировать гравитационную силу относительно дистанции между телами. Тогда получим формулу гравитационной энергии:

U = -G + K, где К – постоянная интегрирования и приравнивается к нулю. Здесь потенциальная энергия превращается в ноль, когда r – бесконечна.

Требушет применяет гравитационную потенциальную энергию противовеса для выброса снарядов на большие дистанции

Источник

Гравитационно-связанные системы[править | править код]

В классической механике[править | править код]

В ОТО[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Потенциальная энергия упруго деформированного тела

7.Закон сохранения механической энергии системы. Из уравнения (10.15) следует,

Задача обучения

Основные пункты

Термины

Пример

Локальное приближение

Общая формула

Вам также может понравиться

Как найти свой дом в списках капремонта

Как найти гугл плей на телефоне хонор

Как составить комплексный план программы

Добавить комментарий Отменить ответ