Условие задачи:
Найти потенциальную энергию математического маятника массой 200 г в положении, соответствующем углу отклонения нити от вертикали 10°, если частота колебаний маятника 0,5 Гц. В положении равновесия потенциальную энергию считать равной нулю.
Задача №9.4.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=200) г, (alpha=10^circ), (nu=0,5) Гц, (E_п-?)
Решение задачи:
Если считать, что в положении равновесия потенциальная энергия груза равна нулю, то искомую потенциальную энергию (E_п) следует искать по формуле:
[{E_п} = mgh;;;;(1)]
В этой формуле (h) – высота груза относительно положения равновесия при угле отклонении нити, равном (alpha), которое можно найти по формуле:
[h = lleft( {1 – cos alpha } right);;;;(2)]
Подставим выражение (2) в формулу (1), тогда получим:
[{E_п} = mglleft( {1 – cos alpha } right);;;;(3)]
Чтобы узнать длину нити маятника (nu), запишем формулу для определения частоты колебаний (nu) математического маятника:
[nu = frac{1}{{2pi }}sqrt {frac{g}{l}} ;;;;(1)]
Здесь (l) – длина маятника, (g) – ускорение свободного падения (при решении задач можно принимать (g=10) м/с2).
Возведем обе части в квадрат, тогда:
[{nu ^2} = frac{g}{{4{pi ^2}l}}]
Выразим отсюда длину нити:
[l = frac{g}{{4{pi ^2}{nu ^2}}};;;;(4)]
Осталось только подставить выражение (4) в формулу (3), окончательно имеем:
[{E_п} = frac{{m{g^2}left( {1 – cos alpha } right)}}{{4{pi ^2}{nu ^2}}}]
Подставим численные данные задачи в формулу и посчитаем численный ответ:
[{E_п} = frac{{0,2 cdot {{10}^2} cdot left( {1 – cos 10^circ } right)}}{{4 cdot {{3,14}^2} cdot {{0,5}^2}}} = 0,031;Дж]
Ответ: 0,031 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.4.2 Во сколько раз изменится полная механическая энергия колеблющегося маятника
9.4.4 Груз массой 0,2 кг колеблется на пружине жесткостью 500 Н/м. Чему равна полная
9.4.5 Смещение груза, подвешенного на пружине, в зависимости от времени задается законом
Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Рассмотрим превращения энергии при колебаниях математического маятника.
Выберем систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
Рис. (1). Схема колебательного движения математического маятника
При колебаниях математического маятника (рис. (1)) изменяется высота (h) грузика относительно положения равновесия и изменяется его скорость (υ).
Причём при максимальных смещениях высота достигает максимального значения
hmax
, а скорость становится равной нулю, в положении равновесия — наоборот: высота тела равна нулю, а скорость достигает максимального значения
vmax
.
Так как высота тела определяет его потенциальную энергию
а скорость — кинетическую энергию
то вместе с изменением высоты и скорости будут изменяться и энергии.
Когда маятник находится в точке, где его смещение от положения равновесия максимально (крайняя левая или крайняя правая точка траектории его движения — точка (A)), то кинетическая энергия маятника равна минимально возможному значению — нулю:
а потенциальная энергия максимальна и равна:
Таким образом, полная механическая энергия маятника в крайних левой и правой точках равна:
Когда маятник находится в какой-либо промежуточной точке между крайней левой или правой точками (точками, где смещение маятника от положения равновесия максимально) и положением равновесия (точка (B)), то его полная механическая энергия (E) равна:
При этом потенциальная и кинетическая энергии принимают некоторые промежуточные значения, большие (0) и меньшие максимального значения:
Когда маятник проходит положение равновесия (точка (O)), то его кинетическая энергия максимальна и равна
а потенциальная энергия принимает нулевое значение
Тогда полная механическая энергия в точке равновесия равна:
Таким образом, можно составить цепочку превращений одного вида энергии в другой при движении математического маятника от крайней левой точки до положения равновесия:
точка (A)
→
точка (B)
→
точка (O),
При движении математического маятника от положения равновесия до крайней правой точки происходит обратное превращение энергии: кинетическая энергия уменьшается от своего максимального значения до нуля, а потенциальная увеличивается от нуля до своего максимального значения.
Обрати внимание!
Полная механическая энергия математического маятника в любой точке траектории его движения постоянна.
Источники:
Рис. 1. Схема колебательного движения математического маятника. . © ЯКласс.
|
Колебания математического маятника. |
|
|
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити (физическая модель). |
|
|
Будем рассматривать движение маятника при условии, что угол отклонения мал, тогда, если измерять угол в радианах, справедливо утверждение: |
|
|
На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную, меняющую ускорение по величине, и нормальную, меняющую ускорение по направлению (центростремительное ускорение, тело движется по дуге). |
|
|
Т.к. угол мал, то тангенциальная составляющая равна проекции силы тяжести на касательную к траектории: |
|
|
Сравним полученное уравнение с уравнением колебательного движения Видно, что |
|
|
Период колебаний |
Формула Галилея |
|
Важнейший вывод: период колебаний математического маятника не зависит от массы тела! |
|
|
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна |
|
|
Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: Т.к. производная от постоянной величины равна нулю, то Производная суммы равна сумме производных: |
|
|
Следовательно: |
тела
совершающего гармонические колебания
Выражение для
потенциальной энергии тела при
гармонических колебаниях следует из
определения потенциальной энергии
![]()
или
![]() .
.
В рассматриваемом случае имеем:
![]() ,
,
а
![]() .
.
Поэтому
![]() .
.
Полагая, что в
состоянии равновесия (![]() )
)
потенциальная энергия тела, совершающего
колебания, равна нулю, имеем:
![]() .
.
Кинетическая
энергия тела при гармонических колебаниях
определяется скоростью его движения
(![]()
) и определяется величиной:
![]() .
.
Полная энергия
тела, совершающего гармонические
колебания, равна сумме полученных
выражений для потенциальной и кинетической
энергий:
![]() .
.
Выражения
представленные выше показывают, что
при колебательном движении кинетическая
энергия преобразуется в потенциальную
и наоборот. При этом полная энергия
колебаний, не зависит от времени
(замкнутая система) и пропорциональна
квадрату амплитуды и квадрату частоты.
3.3. Пружинный, математический, физический и крутильный маятники
Пружинный
маятник
Пружинный
маятник представляет собой систему,
состоящую из пружины и тела, подвешенного
на этой пружине, систему, способную
совершать колебательное движение в
поле действия гравитационных сил или
сил инерции.
Уравнение,
описывающее движение пружинного маятника
в поле тяжести Земли имеет вид (см. рис.
3.1):
![]()
Преобразуем
это уравнение к виду:
![]()
и,
сделав замену переменных:
![]() ,
,
получим:
![]() .
.
Как
было показано выше, решением этого
уравнения являются гармонические
колебания
![]()
Возвращаясь
к переменной
![]() ,
,
получаем:
![]()
или,
с учетом собственной длины пружины
![]() ,
,
имеем:
![]() .
.
На
рисунке, представленном ниже,
![]() .
.

Следует отметить,
что в колебательном процессе участвует
не только тело массой![]() ,
,
подвешенное на пружине, но и сама пружина.
Таким образом, возникает вопрос о влиянии
массы пружины (![]() )
)
на частоту колебаний пружинного маятника.
Заметим, что если тело массой
![]()
в полной мере участвует в колебательном
движении, то различные части пружины
имеют различную амплитуду колебаний.
Таким образом, следует ожидать, что в
выражении для частоты колебаний войдет
не вся
![]() ,
,
а только ее часть. Расчеты показывают,
что это действительно так, и в этом
случае выражение для частоты колебаний
пружинного маятника имеет вид:

Математический
маятник
Математический
маятник состоит из подвешенной на
невесомой нерастяжимой нити материальной
точки, которая может совершать
колебательное движение в поле действия
гравитационных сил или в поле действия
сил инерции.

Для того, что бы
реализовать эту модель на практике
должны выполняться следующие условия:
-
размер
тела должен быть много меньше длины
нити
 ,
, -
масса
тела должна быть много больше массы
нити
 ,
, -
происходящее
во время колебаний изменение длины
нити должно быть много меньше длины
самой нити
 .
.
Остановимся на последнем более подробно.
При максимальном
отклонении маятника от состояния
равновесия сила натяжения нити
![]() ,
,
где
![]()
– угол максимального отклонения. При
прохождении телом положения равновесия
сила натяжения нити определяется как
силой тяжести, так и центробежной силой
![]() ,
,
где величина центробежной силы может
быть найдена следующим образом. Согласно
закону сохранения энергии запишем
![]() ,
,
![]()
откуда
следует:
![]() .
.
Итак, величина
![]() определяет
определяет
значение
![]() ,
,
которое должно быть много меньше
![]() .
.
Расчет показывает, что это условие
выполняется, когда
![]() .
.
Из полученного
выражения следует, что подбором амплитуды
колебаний (угла максимального отклонения)
это условие может быть всегда выполнено.
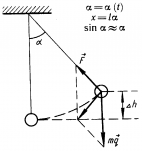
Теперь
рассмотрим движение самого маятника.
Возвращающая сила, действующая вдоль
оси «х» определяется силой натяжения
нити
![]() ,
,
где
![]() ,
,
а
![]()
-угол отклонения
![]() .
.
Воспользуемся законом сохранения
энергии и получим выражение для
центростремительной силы
![]() ,
,
где
![]()
соответствует отклонению маятника на
максимальный угол
![]() ,
,
а
![]() .
.
После
подстановки соответствующих величин
в выражение для
![]() получим:
получим:
![]()
Если угол отклонения
маятника настолько мал, что
![]() ,
,
то
![]()
Сравнивая
это выражение с выражением для силы,
определяющей гармонические колебания,
видим, что частота колебаний математического
маятника
![]() ,
,
а
период колебаний составляет величину:
![]() .
.
Период
колебаний математического маятника
зависит от его длины и от характеристики
поля, в котором он находится.
Физический
маятник
Физическим
маятником называется твердое тело,
способное совершать колебательное
движение в поле действия гравитационных
сил или сил инерции (см. рис. 3.3).
Ранее было показано,
что законы вращательного движения тела
формально не отличаются от законов
движения материальной точки, с той
разницей, что производится замена
величин
![]() ,
,
![]() ,
,
![]() .
.

В данном случае
(см. рисунок) момент силы действующий
на физический маятник равен:
![]() .
.
Если
амплитуда колебаний мала, то и углы
отклонения маятника от состояния
равновесия (![]() )
)
малы, поэтому
![]() .
.
В этом случае можем записать:
![]() .
.
Видим, что
![]() ~
~![]()
и что в рассматриваемом случае роль
коэффициента жесткости играет величина
![]() .
.
По
аналогии с выражением
![]()
можно написать выражение для частоты
колебаний физического маятника в виде:
 .
.
Замечание.
Если в полученное выражение для частоты
колебания физического маятника подставить
значение момента инерции, соответствующее
материальной точке находящейся на
расстоянии
![]()
от точки подвеса (![]() ),
),
то полученное выражение будет
соответствовать частоте колебаний
математического маятника, длиной
![]() .
.
Сравнивая
формулу для частоты колебаний физического
маятника, с соответствующей формулой
для математического маятника
![]() ,
,
мы видим, что частота колебаний физического
маятника будет равна частоте колебаний
математического, если его длина будет
составлять величину
![]() .
.
Это,
так называемая, приведенная
длина физического маятника.
Так как
![]() ,
,
где
![]()
– момент инерции тела относительно оси,
проходящей через центр инерции
![]() ,
,
выражение для приведенной длины мы
можем записать в виде:
![]() .
.
Из
этого выражения следует, что периоды
колебаний физического маятника,
подвешенного на параллельных осях,
отстоящих друг от друга на расстояние
![]()
равны. В самом деле, отложим на прямой
ОС отрезок
![]() .
.
Подвесим маятник на ось, проходящую
через точку
![]() .
.
Тогда приведенная длина будет
![]() ,
,
где
![]() .
.
Но
![]() .
.
Подставим это в выражение для
![]() и
и
получим:
 .
.
Итак:
приведенные длины, а значит и периоды
(частоты) колебаний физических маятников,
подвешенных на параллельных осях,
отстоящих друг от друга на величину
равную приведенной длине равны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
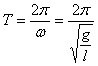 или
или 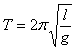 (формула Галилея).
(формула Галилея).