Как найти потенциальную энергию стержня

Потенциальной
энергиейназывается энергия,
накапливаемая в образце при его упругих
деформациях. Потенциальная энергия
численно равняется работе внешних сил,
приложенных к телу, на вызванных ими
перемещениях. За счет потенциальной
энергии восстанавливаются первоначальная
форма и размеры образца при снятии
нагрузки.

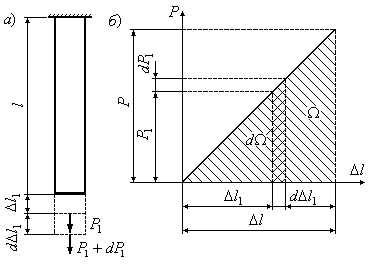
Рассмотрим
стержень, растянутый силой
на величину.
Растягивающая сила в процессе деформации
медленно росла от 0 дои совершала работу, которая в переделах
упругих деформаций численно равняется
потенциальной энергии деформации:

.

Пусть
в процессе деформации сила
приняла некоторое значение.
При этом удлинение стержня стало равным(Рис.3.15,а).
Дадим силеприращение,
тогда удлинение вырастет на величину.
Элементарная работа силына этом преремещении будет равна:

.

Рис.3.15

Пренебрегая
величиной второго порядка малости
выражение для элементарной работы
получаем в виде:

.

На
рис.3.15,б приведена диаграмма растяжения
стержня в зоне упругих деформаций. Из
рисунка видно, что величина
равна площади узкой заштрихованной
полоски диаграммы:

.
(3.17)

Всю
работу на упругой деформации вычислим,
проинтегрировав выражение (3.17) по всей
площади диаграммы:

.

Таким
образом, работа и, следовательно,
потенциальная энергия равны площади
диаграммы растяжения, которая в пределах
упругих деформаций имеет вид треугольника:

.
(3.18)

Подставляя
в формулу (3.18) вместо силы
равное ей внутреннее усилиеи удлинение (3.7), получим:

.
(3.19)

Анализируя
выражение (3.19), приходим к выводу, что
потенциальная энергия всегда будет
положительной. Вследствие нелинейности
функции (3.19) при вычислении потенциальной
энергии нельзя пользоваться принципом
независимости действия сил. Непосредственно
выражением (3.19) можно пользоваться для
вычисления потенциальной энергии лишь
в том случае, если продольная сила
на участке будет иметь постоянное
значение. Если же площади поперечного
сечения и продольные силы на участках
стержня будут разными, то при скачкообразном
изменении этих величин потенциальную
энергию вычисляют на каждом участке
отдельно, а результаты подсчетов
складывают:

.
(3.20)

Если
же площадь поперечного сечения или
продольное усилие меняются по длине
постепенно в соответствии с каким-либо
законом, то сначала записывают выражение
для потенциальной энергии бесконечно
малого отрезка стержня длиной
,
на протяжении которого и площадь
поперечного сечения и продольное усилие
могут считаться постоянными:

,

а
затем интегрируют это выражение по
длине стержня. Тогда вся потенциальная
энергия, накапливаемая в стержне, будет
равна:

.
(3.21)

Энергия,
затраченная на деформацию единицы
объема материала в пределах упругости,
называется удельной потенциальной
энергиейи обозначается буквой.
Для стержня, растягиваемого силой(Рис.3.15,а), удельная потенциальная энергия
равна:

,
(3.22)

где
объем образца перед
началом нагружения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для растянутого стержня потенциальная энергия  [c.487]

Вычислим Пд. При статической деформации стержня потенциальная энергия Пс, как известно, численно равна половине произведения действующей силы на соответствующую деформацию.  [c.310]

Мы видели, что решение задач о кручении в каждом частном случае сводится к определению функции напряжений, удовлетворяющей дифференциальному уравнению (150) и граничному условию (152). При выводе приближенного решения задачи полезно вместо обращения к дифференциальному уравнению определять функцию напряжений из условия минимума некоторого интеграла, ) который можно получить, рассматривая потенциальную энергию скручиваемого стержня. Потенциальная энергия скручиваемого стержня, приходящаяся на единицу длины, согласно выражению (136), определяется формулой  [c.322]

Продольная сила М изменяется в.доль каждого стержня по линейному закону. Поэтому эпюры Л/ строятся весьма просто по значениям концевых ординат, которые определяются узловыми нагрузками или усилиями опорных стержней. Погонные касательные усилия q между стержнями и стенкой имеют постоянное значение для каждого прямоугольного поля и равны тангенсам углов наклона эпюр продольных сил к осям стержней. Потенциальная энергия  [c.380]

Пример 2.2 (к 2.1…2.3, 2.5…2.8). Стальной стержень площадью поперечного сечения Е= 2 см закреплен верхним концом и находится под действием собственного веса (рис. 2.32, а). Найти наибольшую, допустимую по условию прочности длину стержня /, потенциальную энергию деформации этого стержня, а также перемещение его нижнего конца и сечения / — /.  [c.75]

При разгрузке стержня потенциальная энергия деформации расходуется на восстановление его первоначальных формы и размеров, то есть на возвращение его в первоначальное не деформированное состояние.  [c.67]

Это явление имеет место и при кручении. Если упругий стержень в пределах упругости закрутить на некоторый угол, то после удаления внешних сил он будет раскручиваться и может произвести работу за счет накопившейся в стержне потенциальной энергии кручения. Пренебрегая необратимыми потерями (нагревание, внутреннее трение и т. п.), мы должны считать, что обнаруживаемая таким образом работа внутренних сил, определяемая количеством потенциальной энергии упругой деформации U, равна работе внешних сил А.  [c.175]

При расчете пружин иногда заданной является не сила, сжимающая или растягивающая пружину, а энергия Т, которая должна быть ею поглощена. Подобно тому, как это было при растяжении или сжатии стержня, потенциальная энергия деформации пружины U измеряется работой внешних сил.  [c.180]

Учет поперечных сдвигов и инерции поперечных сечений. Когда длина волны поперечных колебаний соизмерима с размерами поперечного сечения стержня, применяют уточненные уравнения, в которых учтены поперечные сдвиги и инерция поворота сечений. В уточненной теории Тимошенко введено предположение поперечные сечения остаются плоскими, но не перпендикулярными к деформированной оси стержня. Потенциальная энергия деформации  [c.333]

Решение. Примем в качестве нулевого верхнее вертикальное положение стержня. Потенциальная энергия системы имеет вид  [c.381]

Здесь Э — кинетическая энергия падающего груза, которую он набрал к моменту соприкосновения с торцом стержня — потенциальная энергия, накапливаемая деформируемым телом при статическом воздействии этого груза. В итоге формула для коэффициента динамичности представляется в виде  [c.208]

Чтобы определить относительный угол закручивания тонкостенного стержня, рассмотрим потенциальную энергию деформации, накопленную в элементарном объеме тонкостенного стержня с размерами ds, dx, б. Учитывая, что при кручении имеет место чистый сдвиг, на основании формулы (8.12) имеем  [c.226]

Энергия Т при ударе согласно закону сохранения энергии и будет трансформирована в потенциальную энергию деформации упругого стержня. Поэтому полученное выражение (22.30) и должно быть подставлено вместо То в формулу (22.15) для определения коэффициента динамичности, т. е.  [c.637]

Величина потенциальной энергии деформации под действием сил инерции в элементе стержня длиной dx на расстоянии х может быть выражена следующим образом  [c.638]

Определять напряжения и деформации стержней, находящихся под действием скручивающих ударных нагрузок, как и при растяжении или сжатии, целесообразно из рассмотрения потенциальной энергии деформации скручиваемого стержня.  [c.640]

Потенциальная энергия деформации стержня при скручивающем ударе может быть представлена в виде  [c.640]

При изгибе, так же как и при других деформациях, работа, производимая внешними силами, затрачивается на изменение потенциальной энергии деформированного стержня.  [c.162]

Полная потенциальная энергия стержня  [c.282]

Приравняем работу падающего груза потенциальной энергии деформации стержня.  [c.290]

Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммирование.м по участкам г (рис. 25). Для элементарного участка  [c.39]

Далее, определяем значение потенциальной энергии для каждого стержня  [c.176]

Положим, что стержень (рис. 512) сжат силой Р, меньшей критического значения, В этом случае он находится и устойчивом положении равновесия. Его можно изогнуть, прикладывая к нему поперечную нагрузку (сила Р ). При переходе стержня от прямолинейной формы равновесия к криволинейной силы Р и Р совершат работу, и результате чего увеличится потенциальная энергия изгиба стержня. Энергетический баланс системы можно выразить в виде следующего уравнения  [c.441]

Определим потенциальную энергию стержня в иоле сил тяжести  [c.333]

Потенциальную- энергию рассматриваемой механической системы определим как сумму потенциальной энергии стержня в поле сил тяжести [1q и потенциальной энергии деформированной пружины Пр.  [c.334]

За обобщенную координату нельзя выбрать высоту центра масс, потому что обобщенная координата должна однозначно определять положение системы, а каждому положению центра масс соответствуют два положения системы. Угол поворота стержня вокруг вертикальной оси можно принять за обобщенную координату, но удобнее в качестве таковой выбрать угол наклона нитей к вертикали, так как через этот угол легко выразить потенциальную энергию системы. Построим прямоугольную систему координат, как показано на рисунке. Пусть в произвольное мгновение i угол поворота стержня был а, а угол наклона нитей O (рис. 135, б). Спроецируем стержень на горизонтальную плоскость кОу (рис. 135, в). Равнобедренный треугольник M”OMi и прямоугольный треугольник NiM M (рис, 135, б) имеют равные стороны М М =  [c.286]

Пусть р — плотность стержня, <т — площадь его поперечного сечения. Дифференциал (1х при малых иЦ,х) отождествим с элементом длины дуги деформированного стержня. Кинетическая энергия Т и потенциальная энергия П упругой изгибной деформации имеют вид  [c.614]

Груз 2 прикреплен к стержню J и движется в вертикальной плоскости. Потенциальная энергия маятника П = 9,81(1 os

кинетическая энергия Т 0,8 . Определить кинетический потенциал в момент времени, когда угол V = 60° и угловая скорость tp = 1 рад/с.  [c.331]

S — площадь сечения стержня). Среднюю полную энергию можно найти как удвоенную потенциальную энергию  [c.186]

В этом случае потенциальная энергия упруго деформированного тела пропорциональна квадрату величины, характеризующей перемещение из натурального состояния. Точно так же потенциальная энергия скрученного стержня определяется формулой  [c.225]

Потенциальная энергия изогнутого стержня равна  [c.227]

Составим выражение потенциальной энергии системы, пренебрегая весом стержней по сравнению с весом груза М-.  [c.342]

Пример 59. Определить величину потенциальной энергии деформации, нако 1-ленную в шарнирно-стержнеаой системе (рис. 386), нагруженной в узле В вертикальной силой Р. Стержни АВ н ВС имеют одинаковые размеры и изготовлены т ОДНОГО материала.  [c.387]

Удар стержня о жесткую плиту.В некоторых случаях приходится определять напряжения в ударяющем теле, в частности, рассчитывая шток ковочного молота. При этом наиболее опасным для прочности штока является момент окончания ковки,когда проковываемое изделие почти не деформируется и вся энергия удара поглощается штоком. Схематически этот случай показан на рис. 588, где некоторый призматический стержень длиной I поперечного сечения F и веса Q падает с высоты Н и ударяется о жесткую плиту А. Поскольку плита не деформируется, то весь запас кинетической энергии Tq = QH, накогг лен1Юй падающим стержнем к моменту соударения, целиком перейдет в потенциальную энергию деформации падающего стержня.  [c.638]

Поэтому для определения потенциальной энергии деформации воспользуемся фopмy l i iи потенциальной энергии в стержне, нагруженном равномерно распределенной нагрузкой  [c.648]

Потенциальная энергия деформации стержней ОВ и ВС равна и = М111/А, + тк/А2)/2Е.  [c.66]

Решение. Выберем в качестве обобщенной координаты системы малый угол ф1 отклонения стержня 1 от равновесного положения. При таком отклонении, очевидно, Д д= Д8д= Д5д. Следовательно, 2Ф2= l< >I и Гзфз=71ф1, где гд — радиус диска. Кроме того, удлинение горизонтальной пружины Xi=X r+ASy4= = ст+ 1ф1. а удлинение вертикальной пружины А,2= А5д=/2ф2= 1ф1 Тогда для потенциальной энергии системы, принимая во внимание ( мулы (64) н (64 )  [c.391]

Решение. Система имеет одну степень свободы. За обобщенную координату системы примем угол ф отклоиепия стержня от еер-тикали. Составим выражение для потенциальной энергии системы  [c.457]

Естественно ожидать, что в таком случае угол кручения т постоянен вдоль длины стержня. В этом можно убедиться, например, из условия минимума полной свободной энергии стержня в равновесии. Полная энергия деформированного стержня равна сумме F T + У, где U — потенциальная энергия, обусловленг ная действием внешних сил. Подставляя в (16,14) т = d(f/dz н варьируя по углу ф, находим  [c.91]

В последнем члене слева берется разность значений на пределах интегрирования, т. е. на концах стержня. Один из этих концов, скажем нижний, закреплен так, что на нем бф = 0. Что касается вариации 6U потенциальной энергии, то, взятая с обратным знаком, она представляет собой работу внешних сил при повороте на. угол бф. Как известно из механики, работа пары сил при таком повороте равна произведению Мбф угла поворота на момент пары. Поскольку никаких других внешних сил нет, то 8U = —уИбф, и мы получаем  [c.91]

---