Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
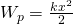
Потенциальная энергия упруго деформированного тела зависит от взаимного положения частей тела относительно друг друга, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины.
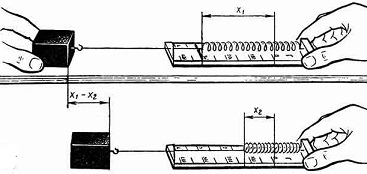
Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем потенциальную энергию растянутой пружины.
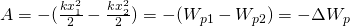
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Обозначения:
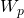 — потенциальная энергия тела
— потенциальная энергия тела
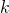 — коэффициент жесткости (или просто жесткость) пружины
— коэффициент жесткости (или просто жесткость) пружины
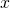 — абсолютная деформация (удлинение или сжатие пружины)
— абсолютная деформация (удлинение или сжатие пружины)
A — работа, которую совершает растянутая пружина
Содержание:
Потенциальная энергия:
По определению потенциальная энергия – это энергия взаимодействия. Т. е. потенциальную энергию имеют все взаимодействующие тела. Для каждого вида механического взаимодействия можно рассчитать потенциальную энергию, учитывая особенности данного взаимодействия.
Самым распространенным в природе является гравитационное взаимодействие, проявлением которого является сила тяжести. При определенных условиях эта сила может выполнять работу.
Допустим, тело массой т подвешено над полом на высоте 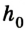
Если нить перерезать, то тело начнет падать под действием силы тяжести.
По определению работа А = Fs cos = mgs cos
= mgs cos .
.
Если учесть, что 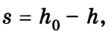 a
a 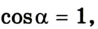 то
то 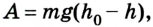 или
или 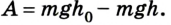
Поскольку работа равна изменению энергии, то можно считать, что выражение mgh определяет потенциальную энергию тела в поле силы тяжести Земли на высоте Л. Движение под действием силы тяжести может происходить по разным траекториям. Выясним, будет ли это влиять на значение работы.
Дадим возможность телу свободно скользить без трения по наклонной плоскости под действием силы тяжести (рис. 2.70).
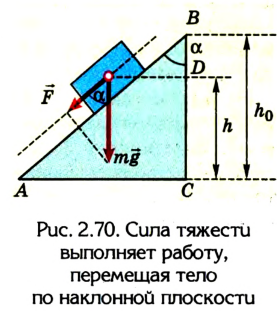
Если учитывать, что А = mgscos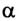 , s=AB, то А = mgABcos
, s=AB, то А = mgABcos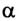 .
.
Из треугольника ABC ABcos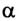 = ВС и вместе с тем BD =
= ВС и вместе с тем BD = 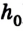 – h.
– h.
Тогда работа силы тяжести при скольжении тела без трения по наклонной плоскости будет равна А = mg(h – 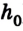 ).
).
Следовательно, работа силы тяжести по перемещению тела по наклонной плоскости будет такой же, как и при его падении из точки В, расположенной на высоте 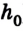 , в точку D, находящуюся на высоте Л.
, в точку D, находящуюся на высоте Л.
Таким образом, работа силы тяжести определяется положением точек начала и конца движения и не зависит от формы траектории.
В тех случаях, когда работа силы не зависит от формы траектории, а определяется начальным и конечным положением тела, пользуются понятием потенциальной энергии.
Если записать формулу для работы силы тяжести в виде
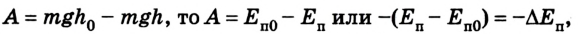
т. е. работа определяется изменением величины mgh, которая называется потенциальной энергией тела в поле силы тяжести: 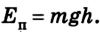
Работа силы тяжести равна изменению потенциальной энергии тела с противоположным знаком. Это означает, что при падении тела, когда сила тяжести выполняет положительную работу, его потенциальная энергия уменьшается. И наоборот, при движении тела вверх, когда сила тяжести выполняет отрицательную работу, его потенциальная энергия увеличивается. Эта особенность характерна для всех случаев, когда работа силы не зависит от формы траектории.
Что такое потенциальная энергия
Потенциальная энергия (от латинского слова потенциал – возможность) – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного тела.
Поскольку любое тело и Земля притягивают друг друга, т. е. взаимодействуют, то потенциальная энергия тела, поднятого над Землей, будет зависеть от высоты подъёма h. Чем больше высота подъёма тела, тем больше его потенциальная энергия.
Опытами установлено, что потенциальная энергия тела зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела подняты на одинаковую высоту, то тело, у которого масса больше, будет иметь и ббльшую потенциальную энергию. Во время падения поднятого тела на поверхность Земли сила тяжести выполнила работу, соответствующую изменению потенциальной энергии тела со значения её на высоте И до значения на поверхности Земли. Если для удобства принять, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия поднятого тела будет равна выполненной во время падения работе: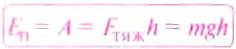
Итак, потенциальную энергию тела, поднятого на некоторую высоту, будем определять по формуле: 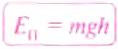
где Еп — потенциальная энергия поднятого тела; m — масса тела; 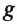 = 9,81
= 9,81
h — высота, на которую поднято тело.
Большой запас потенциальной энергии у воды горных или равнинных рек, поднятых плотинами. Падая с высоты вниз, вода выполняет работу: приводит в движение турбины гидроэлектростанций. В Украине на Днепре построено несколько гидроэлектростанций, в которых используют энергию воды для получения электроэнергии. На рисунке 174 изображено сечение такой станции. Вода с более высокого уровня падает вниз и вращает колесо гидротурбины. Вал турбины соединён с генератором электрического тока.
Потенциальной энергией обладает самолёт, летящий высоко в небе; дождевые капли в туче; молот копра при забивании свай. Открывая двери с пружиной, мы растягиваем её, преодолевая силу упругости, т. е. выполняем работу. Вследствие этого пружина приобретает потенциальную энергию. За счёт этой энергии пружина, сокращаясь, выполняет работу – закрывает двери. Потенциальную энергию пружин используют в часах, разнообразных заводных игрушках. В автомобилях, вагонах пружины амортизаторов и буферов, деформируясь, уменьшают толчки.
Потенциальная энергия пружины зависит от её удлинения (изменения длины при сжатии или растяжении) и жёсткости (зависит от конструкции пружины и упругости материала, из которого она изготовлена). Чем больше удлинение (деформация) пружины, и чем больше её жёсткость, тем большую потенциальную энергию она приобретает при деформации. Такая зависимость свойственна любому упруго деформированному телу.
Потенциальную энергию упругодеформированного тела определяют по формуле: 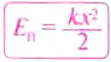

где 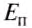 — потенциальная энергия упруго деформированного тела (пружины);
— потенциальная энергия упруго деформированного тела (пружины); 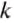 — жёсткость тела (единица жёсткости — 1
— жёсткость тела (единица жёсткости — 1 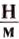 — удлинение (деформация) тела (пружины).
— удлинение (деформация) тела (пружины).

Но тела могут обладать энергией не только потому, что они находятся в определённом положении или деформируются, а и потому, что они находятся в движении.
Определение потенциальной энергии
В повседневной жизни можно обнаружить множество различных тел, при перемещении которых может выполняться работа. Так, выпавший из рук шарик начнет падать под действием силы притяжения, которая будет выполнять работу по перемещению шарика.
Сжатая пружина может поднять на определенную высоту груз. В этом случае сила упругости выполняет работу по перемещению груза.
Что такое энергия
Энергия – это физическая величина, показывающая, какая работа может быть выполнена при перемещении тела.
Можно привести еще много разных примеров из природы, из повседневной жизни, из техники, в которых речь идет о телах, находящихся в таком состоянии, что при определенных условиях может выполняться работа при их перемещении. О таких телах говорят, что они обладают энергией. При различных условиях результат выполнения работы может быть разным. Поэтому и энергия может иметь различные значения и может быть рассчитана.
Единицы энергии
Поскольку речь идет о возможности выполнения работы, то энергию целесообразно измерять в таких же единицах, что и работу. Поэтому единицей энергии есть 1 Дж.
Виды механической энергии
В физике выделяют два вида механической энергии: потенциальную и кинетическую. Если тело неподвижно, но па него действует определенная сила, то говорят, что оно обладает потенциальной энергией.
Потенциальной энергией обладает тело, поднятое над поверх-136 ностью Земли, сжатая пружина, сжатый газ, речная вода в водоеме и другие тела.
Как рассчитывают потенциальную энергию
Рассчитывают потенциальную энергию с учетом природы сил, действующих на эти тела. Проще всего рассчитать потенциальную энергию тела, поднятого над поверхностью Земли, поскольку сила, действующая на него, остается практически постоянной на протяжении всего времени его движения под действием этой силы.
Пусть тело массой 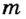 находится на высоте
находится на высоте 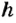 над землей. Если оно упадет на поверхность, то будет выполнена работа
над землей. Если оно упадет на поверхность, то будет выполнена работа

Следовательно, о таком теле можно сказать, что оно обладает потенциальной энергией

Потенциальная энергия тела, поднятого над поверхностью Земли, пропорциональна массе тела и его высоте над поверхностью Земли.
При расчете потенциальной энергии важно помнить, что высота 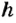 является путем, который тело преодолеет в вертикальном направлении. Таким образом, всегда следует указывать, относительно какой поверхности определяется потенциальная энергия. Например, тело массой 2 кг, поднятое над столом на высоту 1,5 м, будет обладать потенциальной энергией, равной примерно 30 Дж, а потенциальная энергия этого тела, рассчитанная для высоты 3 м над полом, будет 60 Дж.
является путем, который тело преодолеет в вертикальном направлении. Таким образом, всегда следует указывать, относительно какой поверхности определяется потенциальная энергия. Например, тело массой 2 кг, поднятое над столом на высоту 1,5 м, будет обладать потенциальной энергией, равной примерно 30 Дж, а потенциальная энергия этого тела, рассчитанная для высоты 3 м над полом, будет 60 Дж.
Потенциальная энергия упруго деформированного тела
Расчет работы силы упругости усложняется тем, что в ходе выполнения работы значение силы изменяется. Поскольку изменение силы упругости происходит линейно, то при расчетах работы используют среднее значение силы:
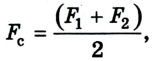
где 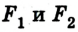 – значения силы упругости в начале и в конце процесса.
– значения силы упругости в начале и в конце процесса.
Учитывая, что 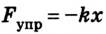 (по закону Гука), то
(по закону Гука), то
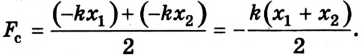
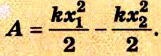
В случае, когда 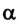 = 0, т. е. сила упругости действует вдоль прямой, по которой происходит перемещение, получим выражение для расчета работы силы упругости:
= 0, т. е. сила упругости действует вдоль прямой, по которой происходит перемещение, получим выражение для расчета работы силы упругости:
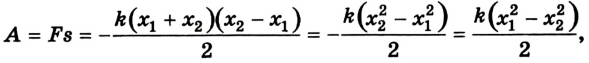
где 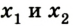 – удлинение, характеризующее начальную и конечную деформации соответственно.
– удлинение, характеризующее начальную и конечную деформации соответственно.
Для потенциальной энергии тела в поле силы тяжести можно записать:
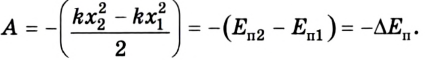
Потенциальная энергия упруго деформированного тела зависит от его деформации.
Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятой с противоположным знаком.
Как и в случае работы силы тяжести, работа силы упругости зависит не от формы траектории, а только от начальной и конечной деформации тела.
Механическая работа и кинетическая энергия
Чтобы шли механические часы, их нужно завести — закрутить пружину; раскручиваясь, пружина совершит работу. Поднявшись на вершину горы, лыжник создаст «запас работы» и в результате сможет скатиться вниз; при этом работу совершит сила тяжести. Самый простой способ разбить окно в горящем доме — бросить в окно камень. Если скорость движения камня достаточна, он разобьет окно — совершит работу. О теле или системе тел, которые могут совершить работу, говорят, что они обладают энергией.
Когда сила совершает механическую работу
Основная задача механики — определение механического состояния тела (координат тела и скорости его движения) в любой момент времени. Механическое состояние тела не изменяется само по себе — необходимо взаимодействие, то есть наличие силы. Когда тело перемещается (изменяет свое механическое состояние) под действием силы, говорят, что данная сила совершает механическую работу.
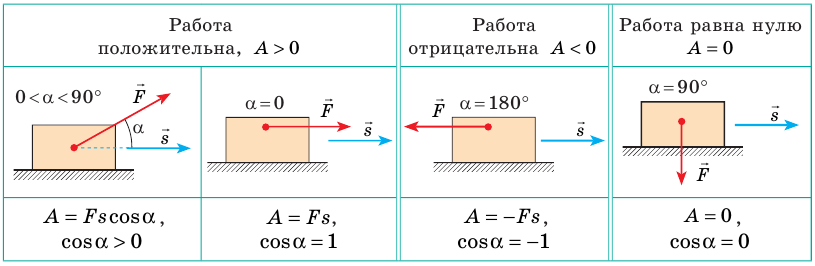
Механическая работа (работа силы) A — физическая величина, характеризующая изменение механического состояния тела и равная произведению модуля силы F, модуля перемещения s и косинуса угла a между вектором силы и вектором перемещения:
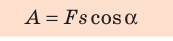
Единица работы в СИ — джоуль: 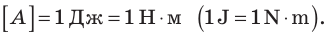
1 Дж равен механической работе, которую совершает сила 1 Н, перемещая тело на 1 м в направлении действия этой силы.
Работа силы — величина скалярная, однако она может быть положительной, отрицательной, равной нулю — в зависимости от того, куда направлена сила относительно направления движения тела (см. таблицу).
Геометрический смысл работы силы
Рассмотрим силу, действующую под некоторым углом α к направлению движения тела. Найдем проекцию этой силы на направление перемещения тела, для чего ось ОХ направим в сторону движения тела (рис. 15.1, а). Из рисунка видим, что 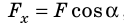 , следовательно,
, следовательно, 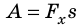 .
.
Построим график 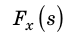 — зависимости проекции силы от модуля перемещения. Если сила, действующая на тело, постоянна, график этой зависимости представляет собой отрезок прямой, параллельной оси перемещения (рис. 15.1, б). Из рисунка видим, что произведение
— зависимости проекции силы от модуля перемещения. Если сила, действующая на тело, постоянна, график этой зависимости представляет собой отрезок прямой, параллельной оси перемещения (рис. 15.1, б). Из рисунка видим, что произведение 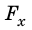 и s соответствует площади S прямоугольника под графиком.
и s соответствует площади S прямоугольника под графиком.
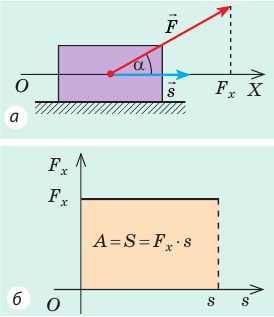
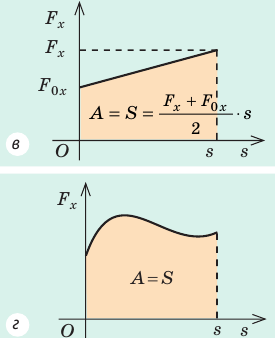
Рис. 15.1. Если направление оси ОХ совпадает с направлением движения тела, то работа A силы численно равна площади S фигуры под графиком зависимости 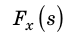
В этом состоит геометрический смысл работы силы: работа силы численно равна площади фигуры под графиком зависимости проекции силы от модуля перемещения. Это утверждение распространяется и на случаи, когда сила переменная (рис. 15.1, в, г).
Когда тело имеет кинетическую энергию
Рассмотрим тело массой m, которое под действием равнодействующей силы 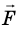 увеличивает скорость своего движения от v0 до v. Пусть равнодействующая
увеличивает скорость своего движения от v0 до v. Пусть равнодействующая 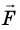 не изменяется со временем и направлена в сторону движения тела. Определим работу этой силы.
не изменяется со временем и направлена в сторону движения тела. Определим работу этой силы.
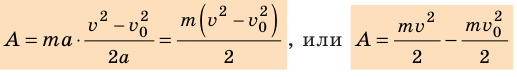
Величину 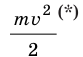 называют кинетической энергией тела
называют кинетической энергией тела 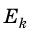 .
.
Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы m тела на квадрат скорости v его движения:
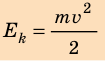
Теорема о кинетической энергии: работа равнодействующей всех сил, которые действуют на тело, равна изменению кинетической энергии тела:
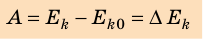
Если в начальный момент времени тело неподвижно (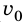 = 0), то есть
= 0), то есть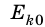 = 0, то теорема о кинетической энергии сводится к равенству:
= 0, то теорема о кинетической энергии сводится к равенству:
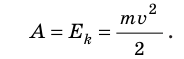
Кинетическая энергия тела, движущегося со скоростью v, равна работе, которую совершает сила, чтобы придать неподвижному телу данную скорость.
Мощность
До сих пор мы говорили о работе силы. Но любая сила характеризует действие определенного тела (или поля). Поэтому работу силы часто называют работой тела (работой поля), со стороны которого действует эта сила. На практике большое значение имеет не только выполненная работа, но и время, за которое эта работа была выполнена. Поэтому для характеристики механизмов, предназначенных для совершения работы, используют понятие мощности.
Мощность P (или N) — физическая величина, характеризующая скорость выполнения работы и равная отношению работы А к интервалу времени t, за который эта работа выполнена:
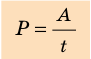
Единица мощности в СИ — ватт:
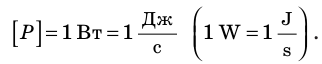
(Названа в честь Джеймса Ватта (1736–1819). Как единицу мощности он ввел лошадиную силу, которую иногда используют и сейчас: 1 л. с. = 746 Вт.)
Мощность, которую развивает транспортное средство, удобно определять через силу тяги и скорость движения. Если тело движется равномерно, а направление силы тяги совпадает с направлением перемещения, тяговую мощность двигателя можно вычислить по формуле:
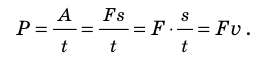
Обратите внимание! Данная формула справедлива для любого движения: мощность, которую развивает двигатель в данный момент времени, равна произведению модуля силы тяги двигателя на модуль его мгновенной скорости: P = Fv (рис. 15.3).

Рис. 15.3. Когда для движения автомобиля требуется большая сила тяги, водитель переходит на меньшую скорость или нажимает на газ, увеличивая таким образом мощность двигателя
Чтобы определить механическую работу и мощность, нужно знать силу, действующую на тело, перемещение тела и время его движения. Поэтому обычно решение задач на определение работы и мощности сводится к решению задач по кинематике и динамике.
Пример №1
Автомобиль массой 2 т движется равномерно со скоростью 20 м/с по горизонтальному участку дороги. Какие силы действуют на автомобиль? Найдите работу каждой силы и тяговую мощность двигателя автомобиля, если коэффициент сопротивления движению равен 0,01, а время движения — 50 с.
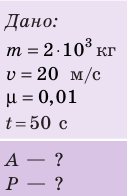
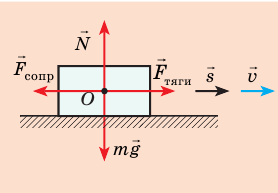
Решение:
Выполним пояснительный рисунок, на котором укажем силы, действующие на автомобиль: силу тяжести 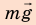 , силу тяги
, силу тяги 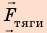 , силу сопротивления движению
, силу сопротивления движению 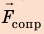 , силу
, силу 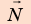 нормальной реакции опоры. По определению работы: A = Fscosα
нормальной реакции опоры. По определению работы: A = Fscosα
Чтобы определить работу каждой силы, нужно найти::
- угол между направлением этой силы и направлением перемещения;
- модуль силы и модуль перемещения.
1. Автомобиль движется равномерно, поэтому действующие на него силы скомпенсированы: — сила тяжести уравновешена силой нормальной реакции опоры: N = mg; — сила тяги уравновешена силой сопротивления движению: 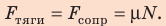
2. Перемещение автомобиля можно найти по формуле: s = vt .
3. Сила тяжести и сила нормальной реакции опоры перпендикулярны направлению движения автомобиля (α = 90°, cosα = 0). Следовательно, работа этих сил равна нулю. Сила тяги направлена в сторону движения тела: α = 0, cosα = 1, поэтому:
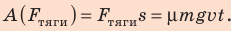
Сила сопротивления противоположна движению: α = 180°, cosα = −1, поэтому:
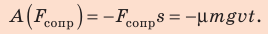
4. Тяговую мощность двигателя автомобиля определим по формуле 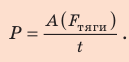 Проверим единицы, найдем значения искомых величин:
Проверим единицы, найдем значения искомых величин:
Выводы:
Потенциальная энергия и закон сохранения механической энергии
Поднятый молот не обладает кинетической энергией, так как его скорость равна нулю. Но если молот отпустить, он совершит работу (расплющит металл). Натянутая тетива лука не имеет кинетической энергии, но, выпрямляясь, она придаст скорость стреле, а значит, совершит работу. И деформированное тело, и тело, поднятое над поверхностью Земли, способны совершить работу, то есть обладают энергией. Что это за энергия и как ее рассчитать?
Когда тело обладает потенциальной энергией
Механическая энергия E — физическая величина, характеризующая способность тела (системы тел) совершить работу.
Единица энергии (как и работы) в СИ — джоуль [E] = 1 Дж (J).
Любое движущееся тело может совершить работу, поскольку оно обладает кинетической энергией, или «живой силой», как ее называли раньше. Есть еще один вид механической энергии — ее называли «мертвая сила». Это — потенциальная энергия (от лат. potentia — сила, возможность), — энергия, которую имеет тело в результате взаимодействия с другими телами.
Потенциальная энергия — энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела.

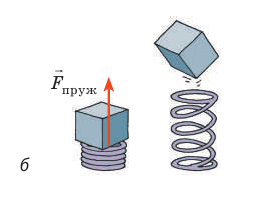
Рис. 16.1. И девочка в результате взаимодействия с Землей (а), и сжатая пружина в результате взаимодействия ее витков (б) обладают потенциальной энергией
Девочка на вершине горки (рис. 16.1, а) обладает потенциальной энергией, поскольку в результате взаимодействия с Землей может начать движение и сила тяжести совершит работу. Но как вычислить эту работу, ведь горка неровная и в течение всего времени движения угол между направлением силы тяжести и направлением перемещения будет изменяться?
Сжатая пружина (рис. 16.1, б) тоже обладает потенциальной энергией: при распрямлении пружины сила упругости совершит работу — подбросит брусок. Но как вычислить эту работу, ведь во время действия пружины на брусок сила упругости непрерывно уменьшается?
Оказывается, все не так сложно. И сила тяжести, и сила упругости имеют одно «замечательное» свойство — работа этих сил не зависит от формы траектории. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным механическими состояниями тела (системы тел), называют потенциальными, или консервативными, силами (от лат. conservare — сохранять, охранять).
Потенциальная энергия поднятого тела
Докажем, что сила тяжести — консервативная сила. Для этого определим работу силы тяжести при движении тела из точки K в точку B по разным траекториям.
Случай 1. Пусть траектория движения тела — «ступенька» (рис. 16.2, а): сначала тело падает с некоторой высоты  до высоты h и сила тяжести совершает работу
до высоты h и сила тяжести совершает работу 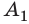 , затем тело движется горизонтально и сила тяжести совершает работу
, затем тело движется горизонтально и сила тяжести совершает работу 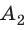 . Работа — величина аддитивная, поэтому общая работа
. Работа — величина аддитивная, поэтому общая работа 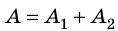 .
.
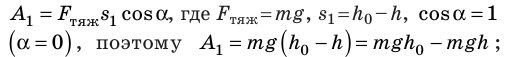
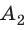 = 0, так как сила тяжести перпендикулярна перемещению тела. Итак:
= 0, так как сила тяжести перпендикулярна перемещению тела. Итак: 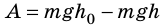 .
.
Случай 2. Пусть тело перемещается из точки K в точку В, скользя по наклонной плоскости (рис. 16.2, б). В этом случае работа силы тяжести равна: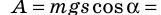
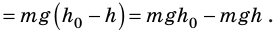
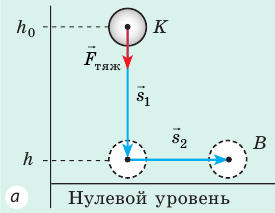
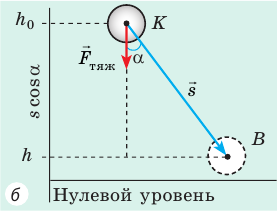
Рис. 16.2. При перемещении тела с высоты 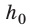 до высоты h работа силы тяжести, независимо от траектории движения тела, определяется по формуле:
до высоты h работа силы тяжести, независимо от траектории движения тела, определяется по формуле: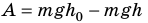
Тот же результат получим и для случаев перемещения тела по произвольной траектории. Следовательно, работа силы тяжести не зависит от траектории движения тела, то есть сила тяжести — консервативная сила. Величину mgh называют потенциальной энергией поднятого тела:
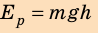
Потенциальная энергия поднятого тела зависит от высоты, на которой находится тело, то есть зависит от выбора нулевого уровня, — уровня, от которого будет отсчитываться высота. Нулевой уровень выбирают из соображений удобства. Так, находясь в комнате, за нулевой уровень целесообразно взять пол, определяя высоту горы — поверхность Мирового океана.
Обратите внимание! Изменение потенциальной энергии, а следовательно, и работа силы тяжести от выбора нулевого уровня не зависят.
- Заказать решение задач по физике
Потенциальная энергия упруго деформированного тела
Пусть имеется упруго деформированное тело — растянутая пружина. Определим работу, которую совершит сила упругости при уменьшении удлинения пружины от  до x (рис. 16.3). Воспользуемся для этого геометрическим смыслом механической работы (рис. 16.4):
до x (рис. 16.3). Воспользуемся для этого геометрическим смыслом механической работы (рис. 16.4):
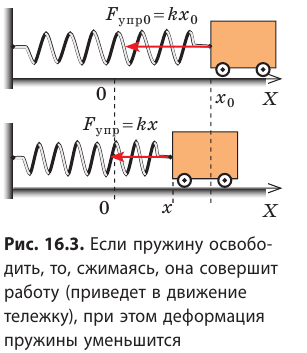
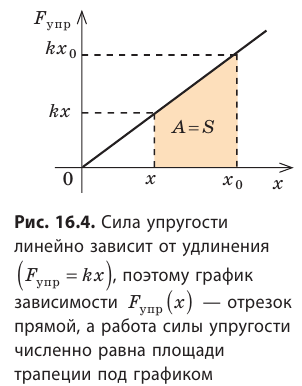
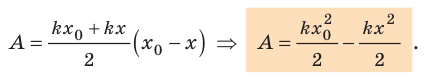
Таким образом, работа силы упругости определяется только начальным и конечным состояниями пружины, то есть сила упругости — консервативная сила. Величину 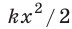 называют потенциальной энергией упруго деформированного тела:
называют потенциальной энергией упруго деформированного тела:
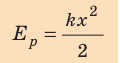
Работа силы упругости (как и силы тяжести) равна изменению потенциальной энергии тела, взятому с противоположным знаком:
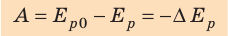
Данное выражение — математическая запись теоремы о потенциальной энергии: работа всех консервативных сил, действующих на тело, равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Состояние с меньшей потенциальной энергией является энергетически выгодным; любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна, — в этом заключается принцип минимума потенциальной энергии. Действительно, камень, выпущенный из руки, никогда не полетит вверх — он будет падать, стремясь достичь состояния с наименьшей потенциальной энергией. Недеформированная пружина никогда не станет сама растягиваться или сжиматься, а деформированная пружина стремится перейти в недеформированное состояние.
Закон сохранения полной механической энергии
Как правило, тело или система тел обладают и потенциальной, и кинетической энергиями. Сумму кинетических и потенциальных энергий тел системы называют полной механической энергией системы тел: 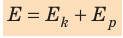 (рис. 16.5).
(рис. 16.5).

Рассмотрим замкнутую систему тел, взаимодействующих друг с другом только консервативными силами (силами тяготения или силами упругости). По теореме о потенциальной энергии работа A, совершаемая этими силами, равна: 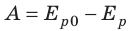 . С другой стороны, согласно теореме о кинетической энергии эта же работа равна:
. С другой стороны, согласно теореме о кинетической энергии эта же работа равна: 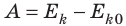 . Приравняв правые части равенств, получим закон сохранения и превращения полной механической энергии:
. Приравняв правые части равенств, получим закон сохранения и превращения полной механической энергии:
В замкнутой системе тел, взаимодействующих только консервативными силами, полная механическая энергия остается неизменной (сохраняется):
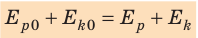
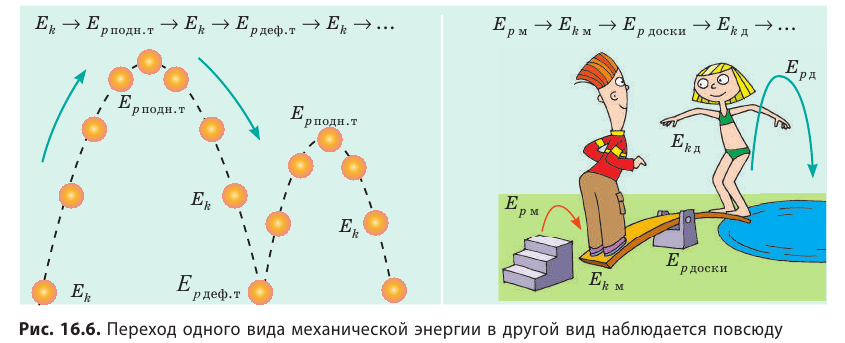
Закон сохранения полной механической энергии предполагает превращение кинетической энергии в потенциальную и наоборот (рис. 16.6). Однако сохраняется ли при этом полная механическая энергия? Наш опыт подсказывает, что нет. И действительно, закон сохранения полной механической энергии справедлив только в случаях, когда в системе отсутствует трение. Однако в природе не существует движений, не сопровождающихся трением. Сила трения всегда направлена против движения тела, поэтому при движении она совершает отрицательную работу, при этом полная механическая энергия системы уменьшается:
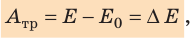
где 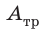 — работа силы трения; E,
— работа силы трения; E, 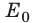 — полная механическая энергия системы в конце и в начале наблюдения соответственно.
— полная механическая энергия системы в конце и в начале наблюдения соответственно.
Потери энергии наблюдаются и в случае неупругого удара. Так что, при наличии трения или при неупругой деформации энергия бесследно исчезает? Казалось бы, да. Однако измерения показывают, что в результате и трения, и неупругого удара температуры взаимодействующих тел увеличиваются, то есть увеличиваются внутренние энергии тел. Значит, кинетическая энергия не исчезает, а переходит во внутреннюю энергию.
Энергия никуда не исчезает и ниоткуда не появляется: она только переходит из одного вида в другой, передается от одного тела к другому.
Алгоритм решения задач с применением закона сохранения механической энергии
- Прочитайте условие задачи. Выясните, является ли система замкнутой, можно ли пренебречь действием сил сопротивления. Запишите краткое условие задачи.
- Выполните пояснительный рисунок, на котором укажите нулевой уровень, начальное и конечное состояния тела (системы тел).
- Запишите закон сохранения механической энергии. Конкретизируйте запись, воспользовавшись данными условия задачи и соответствующими формулами для определения энергии.
- Решите полученное уравнение относительно неизвестной величины.
- Проверьте единицу, найдите значение искомой величины.
- Проанализируйте результат, запишите ответ.
Пример №2
Какую минимальную скорость нужно сообщить шарику, подвешенному на нити длиной 0,5 м, чтобы он смог совершить полный оборот в вертикальной плоскости? Сопротивлением воздуха пренебречь.
Анализ физической проблемы
- Сопротивлением воздуха пренебрегаем, поэтому система «шарик — нить — Земля» является замкнутой и можно воспользоваться законом сохранения механической энергии.
- За нулевой уровень примем самое низкое положение шарика.
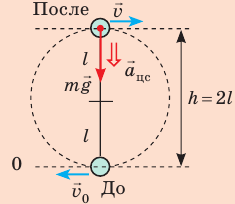
- В самой высокой точке траектории шарик имеет некоторую скорость, иначе он не продолжил бы вращаться, а стал бы падать вертикально вниз.
- Для определения скорости движения шарика в наивысшей точке траектории воспользуемся определением центростремительного ускорения и вторым законом Ньютона.
- Нужно найти минимальную скорость движения шарика в момент толчка, поэтому понятно, что в наивысшей точке траектории нить натянута не будет, то есть сила ее натяжения будет равна нулю.
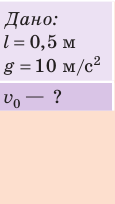
Решение:
На рисунке отметим положения шарика в самой нижней и самой верхней точках траектории; силы, действующие на шарик в верхней точке; направление ускорения. По закону сохранения механической энергии: 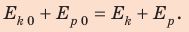
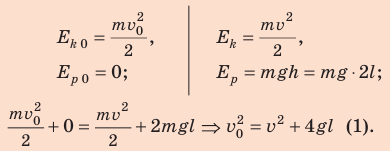
Согласно второму закону Ньютона: 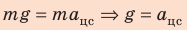 .
.
Поскольку 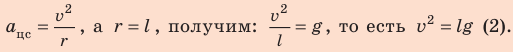
Подставим выражение (2) в выражение (1): 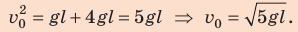 Проверим единицу, найдем значение искомой величины:
Проверим единицу, найдем значение искомой величины: 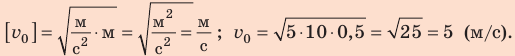
Ответ: 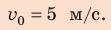
Выводы:
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Движение и силы
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
Совершение работы телом не проходит бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.
Если тело или система тел могут совершить работу, говорят, что они обладает механической энергией.
Определение
Механическая энергия — скалярная физическая величина, являющаяся единой мерой всех форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Механическая энергия обозначается буквой E. Единица изменения энергии — Джоуль (Дж).
Виды механической энергии
В механике состояние системы определяется положением тел и их скоростями. Поэтому в ней выделяют два вида энергии: потенциальную и кинетическую.
Определение кинетической энергии
Кинетическая энергия — это энергия, которой обладает движущееся тело. Она обозначается как Ek. Кинетическая энергия тела зависит от его массы и скорости. Численно она равна половине произведения массы тела на квадрат его скорости:
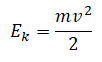
Определение потенциальной энергии
Потенциальная энергия — это энергия взаимодействующих тел. Она обозначается как Ep.
Потенциальная энергия в поле тяготения Земли численно равна произведению массы тела на его высоту (расстояние от поверхности планеты) и на ускорение свободного падения:
Ep=mgh
Потенциальная энергия упруго деформированного тела определяется формулой:
Ep=kx22
k — жесткость пружины, x — ее удлинение.
Пример №1. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м. Определить его потенциальную и кинетическую энергию в верхней точке.
Потенциальная энергия мяча в поле тяготения Земли равна:
Ep = mgh = 0,4∙10∙3 = 12 (Дж)
В верхней точке полета скорость мяча равна нулю. Следовательно, кинетическая энергия мяча в этой точке тоже будет равна нулю:
Ek = 0 (Дж).
Теорема о кинетической энергии
Теорема о кинетической энергии
Изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело:
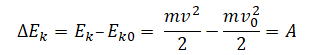
Эта теорема справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести.
Пример №2. Скорость движущегося автомобиля массой 1 т изменилась с 10 м/с до 20 м/с. Чему равна работа равнодействующей силы?
Сначала переведем единицы измерения в СИ: 1 т = 1000 кг. Работа равна изменения кинетической энергии, следовательно:
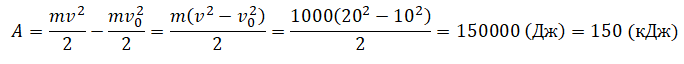
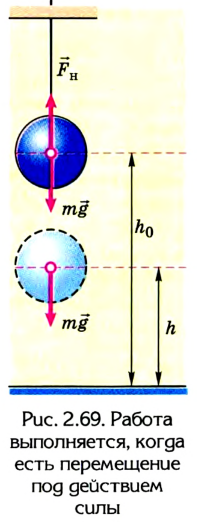
Работа и потенциальная энергия тела, поднятого над Землей
Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.
Работа силы тяжести
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
A = – ∆Ep = –(mgh – mgh0) = mg(h0 – h)
Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.
Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30о. Определить работу, совершенную силой тяжести.
Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:
A = mg(h0 – h) = 0,1∙10(2∙sin30o – 0) =2∙0,5 = 1 (Дж)
Потенциальная энергия протяженного тела
Работа силы тяжести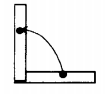
Потенциальная энергия протяженного тела выражается через его центр масс. К примеру, чтобы поднять лом длиной l и массой m, нужно совершить работу равную:
A = mgh
где h — высота центра массы лома над поверхностью Земли. Так как лом однородный по всей длине, его центр масс будет находиться посередине между его концами, или:
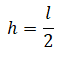
Отсюда работа, которую необходимо совершить, чтобы поднять этот лом, будет равна:
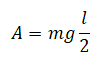
Пример №4. Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?
Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:
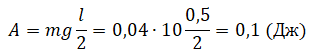
Работа и изменение потенциальной энергии упруго деформированного тела
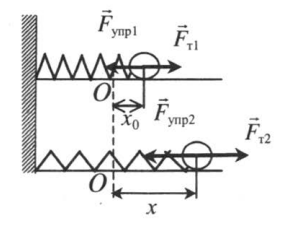
Вспомним, что работа определяется формулой:
A = Fs cosα
Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:![]()
Модуль силы тяги равен по модулю силе упругости, поэтому:
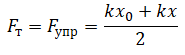
Перемещение определяется формулой:
s = x – x0
Следовательно, работа силы тяги по сжатию или растяжению пружины равна:
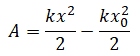
Но известно, что потенциальная энергия упруго деформированного тела равна:
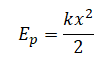
Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:
Задание EF18117
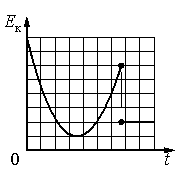 На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?
Ответ:
а) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.
б) Тело брошено под углом к горизонту с поверхности Земли и упало на Землю.
в) Тело брошено под углом к горизонту с поверхности Земли и упало на балкон.
г) Тело брошено вертикально вверх с балкона и упало на Землю.
Алгоритм решения
1.Описать изменение кинетической энергии в течение всего времени движения тела.
2.Установить характер движения тела в течение этого времени.
3.Проанализировать все ситуации и выбрать ту, которая не противоречит установленному характеру движения тела.
Решение
Согласно графику, кинетическая энергия тела сначала уменьшалась, а затем увеличилась. Затем она резко уменьшилась до некоторого значения и осталась постоянной.
Кинетическая энергия тела определяется формулой:
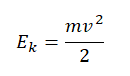
Кинетическая энергия зависит прямо пропорциональной от квадрата скорости. Следовательно, когда уменьшается кинетическая энергия, скорость тоже уменьшается. Когда она возрастает — скорость тоже возрастает. Когда она постоянная — скорость тоже постоянна и не равна нулю.
Если тело брошено под углом к горизонту, скорость сначала будет уменьшаться, так как ускорение свободного падения направлено вниз. Если тело бросить вертикально вверх, скорость тоже сначала будет уменьшаться. Но в этом случае при достижении верхней точки траектории на момент скорость тела будет равна нулю. Следовательно, график зависимости кинетической энергии от времени в этот момент тоже должен быть равен нулю. Но это не так. Поэтому последний вариант ответа не подходит.
Если бы тело упало на неподвижный объект, его скорость относительно Земли стала бы равной нулю. Но так как его кинетическая энергия не равна нулю и является постоянной, тело начало двигаться с постоянной скоростью. Это возможно только в случае, если тело упало на объект, движущийся с постоянной скоростью. Поэтому из всех вариантов ответа подходит только первый, когда тело падает в проезжающий мимо грузовик.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18192
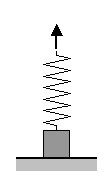 К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
Ответ:
а) 40 мДж
б) 20 мДж
в) 80 мДж
г) 200 мДж
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, указать силы, действующие на пружину, выбрать систему отсчета.
3.Записать формулу для вычисления потенциальной энергии в пружине.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса бруска: m = 4 кг.
• Удлинение пружины: ∆l = 2 см.
Переведем сантиметры в метры:
2 см = 0,02 м
Выполним рисунок. Для описания ситуации нам понадобится только одна ось: Oy.
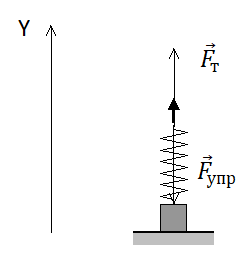
Потенциальная энергия деформированной пружины определяется формулой:
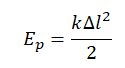
Так как брусок поднимают за прикрепленную к нему пружину медленно, можно считать, что это движение равномерное (и прямолинейное). Поэтому, согласно второму закону Ньютона:
Fт = Fупр
Чтобы оторвать брусок от поверхности стола, модуль силы тяги должен быть равен модулю силы тяжести. Поэтому:
Fт = Fтяж =Fупр
Или:
mg = k∆l
Теперь можем выразить жесткость пружины:
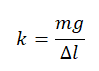
Подставим жесткость пружины в формулу потенциальной энергии и сделаем вычисления:
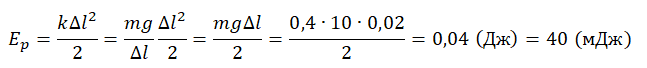
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18553
 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t2(все величины выражены в СИ).
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t2(все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.3k
Любое
упруго деформированное тело обладает
потенциальной энергией,
так как
изменяется взаимное расположение
отдельных частей тела. Рассмотрим случай
растяжения пружины.
Растяжение
будем производить очень медленно, чтобы
силу
![]() ,
,
с которой мы действуем на пружину, можно
было считать все время равной по модулю
упругой силе![]() .
.
Тогда![]() гдек, х –
гдек, х –
соответственно жесткость и удлинение
пружины. Тогда работа, которую нужно
совершить, чтобы вызвать удлинение (или
сокращение) х
пружины,
равна
![]() (8.12)
(8.12)
Эта
работа идет на увеличение потенциальной
энергии пружины. Следовательно,
зависимость потенциальной энергии
пружины от удлинения х
имеет вид
![]() , (8.13)
, (8.13)
если
считать, что потенциальная энергия
недеформированной пружины равна нулю.
Потенциальная энергия упруго деформированного стержня равна
![]() ,
,
(8.14)
где
![]() –
–
объем стержня.
Отношение
энергии
![]() к тому объему
к тому объему![]() ,
,
в котором она заключена, называетсяплотностью
энергии u.
Тогда
![]()
– плотность энергии упругой деформации
при растяжении (или сжатии).
Аналогично
нетрудно получить, что плотность энергии
деформации при сдвиге равна
![]() .
.
6. Кручение
Деформации
кручения и изгиба являются деформациями
неоднородными. Это значит, что в этих
случаях деформации внутри тела меняются
от точки к точке.
Возьмем
однородную проволоку, верхний конец ее
закрепим, а к нижнему концу приложим
закручивающие силы. Они создадут
вращающий момент относительно продольной
оси проволоки. При этом каждый радиус
нижнего основания повернется вокруг
продольной оси на угол
![]() .
.
Такая деформация называется кручением.
Закон Гука для деформации кручения
имеет вид
![]() , (8.15)
, (8.15)
где
![]() – модуль кручения, постоянная для данной
– модуль кручения, постоянная для данной
проволоки. Модуль кручения зависит не
только от материала, но и от геометрических
размеров проволоки.
Выведем
выражение для модуля кручения.
Пусть
имеется цилиндрическая трубка радиуса
![]() .
.
Причем толщина ее![]() очень
очень
мала по сравнению с радиусом. Площадь
сечения трубки равна
![]() .
.
Обозначим через![]() касательное напряжение в том же основании.
касательное напряжение в том же основании.
Тогда момент сил, действующий на это
основание, будет![]() .
.
При закручивании совершается работа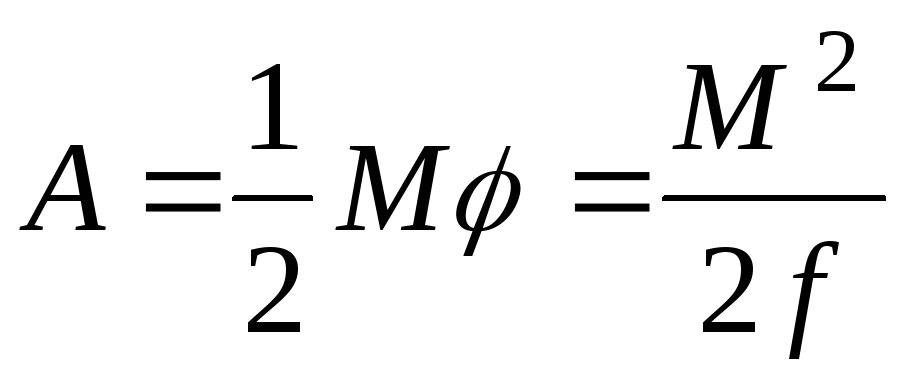 .
.
Разделим
ее на объем трубки
![]() .
.
Найдем плотность упругой энергии при
деформации кручения
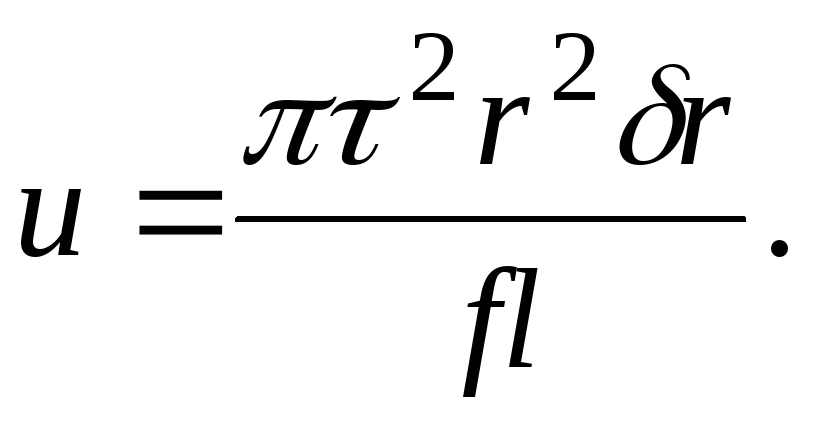 (8.16)
(8.16)
Найдем
эту же величину иначе.
Мысленно
вырежем из трубки бесконечно короткую
часть (рис.8.5).
|
|
Рис. |
В
результате кручения бесконечно малый
элемент трубки ABDC
перейдет в положение
![]() .
.
Это есть сдвиг. Таким образом, деформацию
кручения можно рассматривать как
неоднородный сдвиг. Плотность упругой
энергии при сдвиге равна
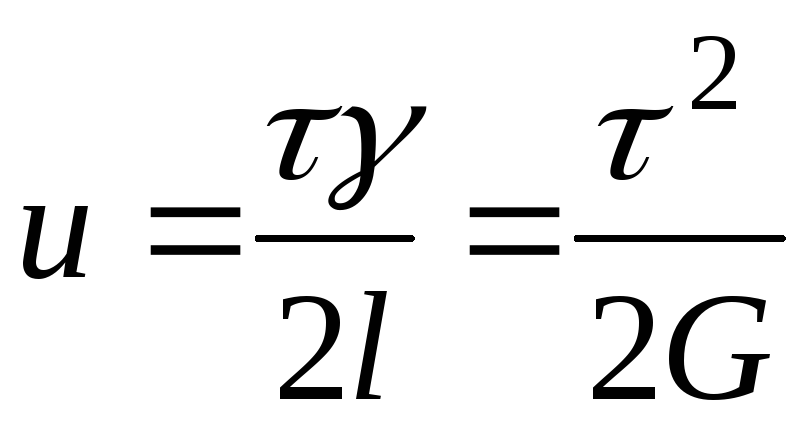 (8.17)
(8.17)
Приравнивая
его выражению (8.16), находим искомое
соотношение
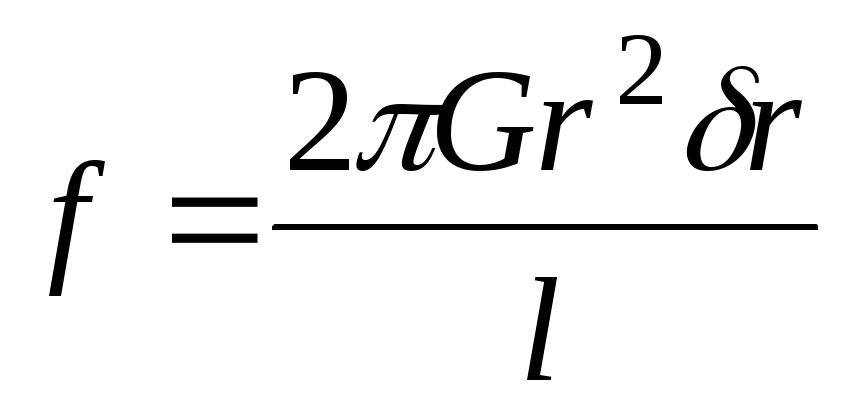 (8.18)
(8.18)
Если
стенка трубки имеет конечную толщину,
то модуль
![]() найдется интегрированием последнего
найдется интегрированием последнего
выражения по![]() .
.
Это дает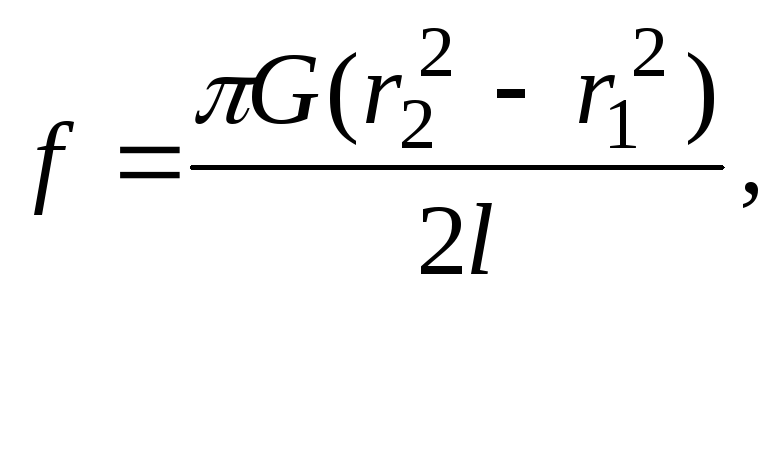
где
![]() – внутренний радиус трубки,
– внутренний радиус трубки,![]() – внешний радиус трубки.
– внешний радиус трубки.
Для
сплошной проволоки радиуса
![]() модуль
модуль
кручения
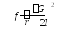 .
.
Контрольные вопросы
-
Что
называется деформацией? Какие деформации
называются упругими? Приведите примеры
упругих деформаций. -
Какова физическая
сущность упругих сил? -
Сформулируйте
закон Гука? Когда он справедлив? -
Дайте
объяснение качественной диаграмме
напряжений. Что такое предел
пропорциональности, упругости и
прочности? -
Что такое упругий
гистерезис и упругое последействие? -
Каков физический
смысл модуля Юнга и модуля сдвига? -
Что такое упругое
последействие? -
Выведите выражения
для деформаций при всестороннем
растяжении. -
Что называется
коэффициентом Пуассона? -
Определите энергию
деформированного тела. -
Что называется
плотностью упругой энергии? Получите
формулы этой энергии при растяжении и
сдвиге. -
Какой вид имеет
закон Гука при кручении. -
Выведите выражение
для модуля кручения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Видеоурок 1: Потенциальная энергия. Работа силы тяжести
Видеоурок 2: Потенциальная энергия. Работа силы упругости
Лекция: Потенциальная энергия. Потенциальная энергия упруго деформированного тел
 Работа силы тяжести и потенциальная энергия
Работа силы тяжести и потенциальная энергия
Давайте представим себе тело, которое падает с некоторой высоты. Для перемещения этого тела сила тяжести совершает некоторую работу. При этом перемещение равно высоте, на которой находилось тело в начальный момент времени.
Если в формулу работы вместо силы, подставить формулу силы тяжести, а вместо перемещения – высоту на которой находилось тело, то полученная формула будет соответствовать разности потенциальных энергий, в начальный и конечный момент наблюдения за телом, которое падает.
Потенциальная энергия – это энергия, определяющая взаимное положение тел или их частей в пространстве.

При этом работа, которую выполняет сила тяжести, по модулю равна изменению потенциальной энергии тела.
 Работа силы упругости и потенциальная энергия
Работа силы упругости и потенциальная энергия
Так как уже было сказано, что потенциальная энергия определяет взаимное положение частей тела в пространстве, то можно сделать вывод: если во время растяжения пружины происходит изменение взаимного положения её частей, то происходит изменение потенциальной энергии. Поэтому имеет место говорить о потенциальной энергии упруго деформированного тела.

Эта величина зависит от рода вещества, из которого изготовлена пружина, а также от степени её растяжения.
Изменение потенциальной энергии упруго деформированного тела равно работе сил упругости.
Потенциальную энергию имеют любые тела, на которые действуют консервативные силы.
Консервативными называются те силы, которые не влияют на скорость движения тела, а определяются взаимным расположением их частей.