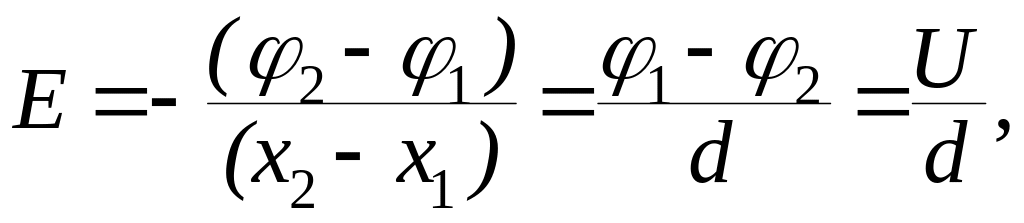Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.
Потенциальные и непотенциальные силы в электродинамике
Все силы можно разделить на потенциальные и непотенциальные.
Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.
Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))
Энергия системы заряженных тел
Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.
Изменение потенциальной энергии заряда в однородном электрическом поле
Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).
Рис. (1). Перемещение заряда в однородном поле
Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.
Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б – vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б – vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:
(A=-E_Б). ((5))
Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))
Энергия взаимодействия точечных зарядов
Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.
Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).
Рис. (2). Перемещение заряда в поле точечного заряда
Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.
В таком случае работа электрического поля на дуге (СБ) будет нулевой:
(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))
поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:
(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)
(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))
Энергия системы (n) точечных зарядов
Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.
Свойство линий напряжённости электрического поля
Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).
Рис. (3). Замкнутая линия электрического поля
Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).
Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.
Источники:
Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.
Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.
Рис. 3. Замкнутая линия электрического поля. © ЯКласс.
Для школьников.
Если электростатическое поле создаётся двумя точечными зарядами
находящимися на расстоянии
друг от друга, то потенциальная энергия их взаимодействия выражается формулой:
Можно сказать так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого первым зарядом в точке нахождения второго заряда, на величину второго заряда.
Можно сказать и так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого вторым зарядом в точке нахождения первого заряда, на величину первого заряда.
Потенциальная энергия взаимодействия двух точечных зарядов – это и есть энергия электростатического поля, созданного ими.
Обладая энергией, электрическое поле может совершить работу. Энергия электростатического поля численно равна работе, которую могут совершить заряды при их удалении друг от друга в бесконечность.
Для получения формулы, по которой можно найти энергию электрического поля, созданного неподвижным заряженным проводником, применяют уравнение
есть потенциал, создаваемый всеми остальными зарядами в точке нахождения одного из зарядов.
Он одинаков для всех точек проводника, так как поверхность проводника является эквипотенциальной поверхностью.
Заряд всего проводника можно представить как сумму множества точечных зарядов. Тогда, пользуясь формулой (1) (см. Занятие 55), можно получить выражения для энергии поля уединённого проводника.
Что произойдёт после этого соединения?
Таким образом, получены формулы, по которым можно рассчитать энергию электростатического поля заряженного проводника.
На примере показано, что если электрическое поле создаётся несколькими проводниками, то энергия поля складывается из собственных энергий проводников и энергий их взаимодействия.
Общая энергия соединённых заряженных проводников уменьшается, так как при прохождении зарядов по проволоке выделяется энергия в виде тепла.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Три одинаковых заряда закреплены на одной прямой. Какую работу надо совершить, чтобы удалить средний заряд?
Следующая запись: Более чётко о нахождении энергии электростатического поля. Поле конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Для
потенциального поля справедливо
соотношение между силой F
и
потенциальной энергией:
(13.10)
Найдем
потенциальную энергию точечного заряда
q’
в поле другого точечного заряда q:
(13.11)
Эта
энергия определяется с точностью до
константы C, выбор которой может быть
сделан произвольно. Энергию W
можно рассматривать как потенциальную
энергию взаимодействия точечных зарядов
q
и q’.
Единица измерения энергии [W]
= Дж.
Работа,
совершаемая силами электростатического
поля, равна разности потенциальной
энергии взаимодействия зарядов q’ и q в
точках 1 и 2:
(13.12)
Выберем
точку отсчета, в которой W
= 0. Так, если при r
W
®
0, то отсюда следует, что C
= 0.
13.3. Электрический потенциал
Потенциал
определяется как электрическая
потенциальная энергия единичного
положительного заряда, помещенного в
данную точку поля:
(13.13)
Потенциал
поля, создаваемого зарядом q,
не зависит от величины пробного заряда
q’,
помещенного в это поле:
(13.14)
Потенциал,
также, как и энергия, определяется
неоднозначно и зависит от выбора
постоянной C.
Электрический
потенциал численно равен работе, которую
необходимо совершить, чтобы перенести
единичный заряд q’ из бесконечности на
расстояние r от точечного заряда q.
Пусть
при
,
тогда положим С
= 0.
Потенциал
точечного заряда будет иметь вид:
(13.15)
На
рис. 13.2 показана зависимость потенциала
точечного заряда
от расстояния r
до
заряда. Единица измерения потенциала
Вольт,
[]
= В, 1В = 1Дж/1Кл.

Рис.
13.2.
Напряжением
U называется разность потенциалов между
двумя точками, численно равная работе,
которую необходимо затратить для
перемещения единичного заряда из точки
1 в точку 2:
(13.16)
Е
166
диница измерения напряжения –
Вольт, [U] = В.
Вольта
Алессандро (1745 – 1827),
итальянский физик, химик и физиолог,
родился в Комо. Учился в школе ордена
иезуитов. Сконструировал первый источник
электрического тока – вольтов столб.
Открыл взаимную электризацию разнородных
металлов при их контакте. Построил
электроскоп, конденсатор.

Рис.
13.3.
Е
157
сли каждой точке поля сопоставить
вектор напряженности E,
то получим векторное поле, если же в
каждой точке пространства задать
определенное число ,
то образуется скалярное поле. В скалярном
поле можно провести поверхности, которые
называются эквипотенциальными. В каждой
точке эквипотенциальной поверхности
потенциал имеет постоянную величину,
= const. Поверхности эти проводят так, чтобы
разность потенциалов на соседних
поверхностях составляла:
.

Рис.
13.4.
На
рис. 13.3 изображены силовые линии
положительного точечного заряда и
перпендикулярные к ним эквипотенциальные
сферические поверхности с потенциалами
,
.
На рис. 13.4 изображены силовые линии и
эквипотенциальные поверхности
электрического поля, создаваемого двумя
разноименно заряженными плоскостями.
Поверхность
заряженного проводника имеет одинаковый
потенциал во всех его точках, поэтому
эквипотенциальные поверхности повторяют
форму проводника (рис. 13.5).

Рис.
13.5.
Потенциал
изменяется от точки к точке пространства.
Это изменение можно характеризовать с
помощью векторной величины, называемой
градиентом потенциала. В декартовой
системе координат
где
– частные производные от потенциала по
координатам x,
y, z;
– единичные векторы вдоль осей координат
х,
y,
z.
Если
потенциал зависит только от одной
координаты, например, от радиуса r, тогда
Зная
распределение потенциала в пространстве,
можно определить напряженность
электрического поля:
(13.18)
В
случае однородного поля напряженность
связана с напряжением соотношением:
(13.19)
где
U
–
напряжение;
d
– расстояние между двумя точками в
пространстве.
Электрическое
поле между обкладками плоского
конденсатора является однородным, также
как и поле в проводниках. Если напряженность
зависит только от одной координаты x
,
то связь между напряженностью и
потенциалом имеет вид:
(13.20)
Знак
минус в формуле указывает, что электрическое
поле направлено в сторону уменьшения
потенциала.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Сила Кулона.
;
– диэлектрическая
проницаемость.
;
- Потенциальная (электростатическая) энергия
взаимодействия зарядов.
– может быть и
положительной и отрицательной.
Если есть система электрических точечных
зарядов qi…….qg, то
.
Методические указания по решению задач.
Решая задачи целесообразно использовать
следующие методические указания.
- Вникнув в условие задачи, сделать краткую
запись условия, выразить все данные в СИ и, где
это только возможно, сделать схематичный чертеж
или рисунок, поясняющий содержание задачи. - Выяснив, какие физические законы лежат в основе
данной задачи, решить ее в общем виде, т.е.
выразить искомую физическую величину через
заданные в задаче величины (в буквенных
обозначениях, без подстановки числовых значений
в промежуточные формулы). - Проверив правильность общего решения,
подставить числа в окончательную формулу и
указать единицу искомой величины, проверив
правильность ее размерности. Проверить
достоверность ответа.
1. Два разноименных заряда q1= 2*10-9Кл
и q2= -3*10-9Кл находятся на расcтоянии r1=1м.
Какую работу необходимо совершить, чтобы
раздвинуть эти заряды на r2= 2м.
2.Четыре точечных положительных заряда
находятся в вершинах квадрата со стороной а.
Найдите потенциальную энергию Wвсей системы.
3. Два отрицательных и два положительных
заряда находятся в вершинах квадрата со стороной
а, как показано на рисунке. Найдите
потенциальную энергию всей системы.
4. Какую работу необходимо совершить, чтобы
три положительных заряда q, находящиеся в
вакууме на одной прямой, на расстоянии а друг
от друга, расположить в вершинах равностороннего
треугольника.
5. Определить работу, которую нужно совершить,
чтобы три положительных заряда q, находящиеся
в вакууме на одной прямой, на расстоянии а
друг от друга, расположить в вершинах
равностороннего треугольника со стороной а/2.
6. Три маленьких положительно заряженных
шарика заряда q каждый удерживаются вдоль
прямой на расстоянии а друг от друга двумя
нитями. Какую максимальную кинетическую энергию
приобретет крайний шарик, если обе нити
одновременно пережечь.
7. Три маленьких положительно заряженных
шарика, массой m и зарядом q каждый
соединены нитями и находятся на расстоянии а
друг от друга. Определить максимальную скорость
крайнего шарика №1, если одну из нитей пережечь.
|
Дано |
Рисунок |
Решение |
| q
m a |
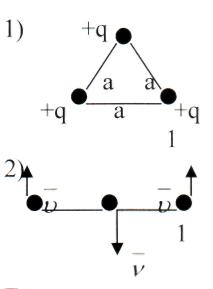
Если продолжить наблюдать процесс, то увидим колебательную систему. |
По закону сохранения импульса общий импульс системы равен нулю и до и после пережигания нити: 2m
По закону сохранения энергии: Е Е Е 3k
|
| Ответ: V |
8. Четыре точечных положительных
заряда q расположены на расстоянии а на
одной прямой. Определите полную потенциальную
энергию системы.
Понятие о потенциальной энергии взаимодействия зарядов
Содержание
- 1 Потенциальная энергия
- 2 Потенциальная энергия электрозаряда
- 3 Определение нулевого уровня ПЭ
- 4 Суть электрического потенциала
- 5 Что называют разностью потенциалов
- 6 ПЭ взаимодействия точечных электрозарядов
- 7 Видео по теме
Взаимодействуя друг с другом, заряженные тела отталкиваются или притягиваются. Перемещение заряженных объектов (тел или частиц) под действием на них электрополя приводит к совершению работы. По аналогии с механикой это свидетельствует о том, что система обладает потенциальной энергией (ПЭ). Если напряженность электрополя является его силовой характеристикой, то потенциал отражает его энергетические возможности.
Потенциальная энергия
Понятие силового поля в физике считается базовым. Оно проявляет себя в виде действия на материальные объекты (тела, молекулы, атомы, элементарные частицы), приводящего к их перемещению, то есть, к совершению работы. Основные признаки (свойства) потенциального поля:
- На работу, совершаемую при движении тела из одного пункта в другой, не влияет форма траектории.
- Если траектория передвижения тела в силовом поле является замкнутой (начальная точка совпадает с конечной), то работа, совершаемая данным телом, равняется нулю.
Поля, удовлетворяющие этим условиям, называются потенциальными, а силы — консервативными. Первым примером такого поля может служить гравитационное. Его определение было сформулировано Исааком Ньютоном (1643-1727) после открытия им закона всемирного тяготения.
Хорошо известна из школьного курса физики формула для потенциальной энергии Eg тела массы m, поднятого на высоту h над поверхностью Земли:
Позднее было обнаружено, что электрополе также является потенциальным, но имеет некоторое отличие от гравитационного. Если в последнем присутствует лишь сила притяжения, то в электрическом одноименные заряды отталкиваются друг от друга.
Потенциальная энергия электрозаряда
Так как траектория не оказывает влияния на работу, то величина A равна изменению ПЭ, взятому с противоположным знаком:
Если электрополе однородное (такое присутсвует между обкладками плоского конденсатора), то на заряд q будет действовать сила F, величину которой можно определить по формуле:
Тогда изменение ПЭ при перемещении заряда на расстояние d будет равняться:
Данная формула похожа на формулу для ПЭ в гравитационном поле. Разница заключается в том, что электрозаряд может иметь и положительный, и отрицательный знак, а масса только положительный.
Определение нулевого уровня ПЭ
В потенциальном поле нулевой уровень выбирается произвольно, поскольку в зависимости от точки отсчета он может быть разным. По аналогии с формулой для гравитационного поля, где за нулевой принимается уровень поверхности Земли, в электростатике физический смысл имеет не абсолютная величина ПЭ, а разность ее значений, задаваемая работой, которая совершается электрополем при передвижении электрозаряда из начального расположения в конечное.
Суть электрического потенциала
Потенциальная энергия взаимодействия электрических зарядов прямо пропорционально зависит от величины данных электрозарядов. Это экспериментальный факт, который является справедливым и для однородного, и для неоднородного электрополя. Следовательно, можно сделать вывод, что отношение потенциальной энергии заряда к этому заряду не зависит от величины заряда в электрическом поле. На основании этого введена специальная характеристика, которую называют потенциалом.
Напряжённость электрополя — векторная величина, характеризующая его силовые возможности, а электропотенциал φ — величина скалярная и определяет энергетические возможности единичного электрического заряда в поле.
Что называют разностью потенциалов
По аналогии с ПЭ значение электропотенциала в конкретной точке зависит от точки отсчёта нулевого уровня. Поэтому на практике значение имеет не сам электропотенциал в какой-либо точке, а его изменение Δφ. Следовательно, формулу для работы A можно записать так:
Таким образом, разность потенциалов (электронапряжение U) между двумя точками электрополя определяется по формуле:
ПЭ взаимодействия точечных электрозарядов
На картинке ниже схематично показаны силовые линии полей точечных электрозарядов (положительного и отрицательного), каждый из которых создаёт собственное электрополе.
Французский учёный Ш. О. Кулон (1736-1806) открыл закон, который назван в его честь. Согласно ему сила взаимодействия F двух точечных электрозарядов q1 и q2 равна произведению их модулей, делённому на квадрат расстояния r между ними.
Следствием формулы для силы взаимодействия электрозарядов является выражение для ПЭ двух взаимодействующих электрозарядов:
При взаимодействии электрозарядов с одинаковым знаком возникает положительная ПЭ. Ее величина будет тем больше, чем меньше расстояние от одного заряженного тела до другого. Если же взаимодействуют заряды с разными знаками, то энергия отрицательна. Работа, совершаемая силами притяжения при сближении электрозарядов, будет тем больше, чем больше расстояние между электрозарядами.