Лекция № 7
Потери мощности и электроэнергии в элементах сети
План.
-
Потери мощности
в элементах сети. -
Расчет потерь
мощности в линиях электропередач. -
Расчет потерь
мощности в ЛЕП с равномерно распределенной
нагрузкой. -
Расчет потерь
мощности в трансформаторах. -
Приведенные и
расчетные нагрузки потребителей. -
Расчет потерь
электроэнергии. -
Мероприятия по
снижению потерь мощности.
Потери мощности в элементах сети
Для
количественной характеристики работы
элементов электрической сети
рассматриваются ее рабочие режимы.
Рабочий
режим
– это установившееся электрическое
состояние, которое характеризуется
значениями токов, напряжений, активной,
реактивной и полной мощностей.
Основной целью
расчета режимов является определение
этих параметров, как для проверки
допустимости режимов, так и для обеспечения
экономичности работы элементов сетей.
Определение
значений токов в элементах сети и
напряжений в ее узлах начинается с
построения картины распределения полной
мощности по элементу, т.е. с определения
мощностей в начале и конце каждого
элемента. Такую картину называют
потокораспределением.
Рассчитывая
мощности в начале и в конце элемента
электрической сети, учитывают потери
мощности в сопротивлениях элемента и
влияние его проводимостей.
Расчет потерь мощности в линиях электропередач
Потери активной
мощности на участке ЛЕП (см. рис. 7.1)
обусловлены активным сопротивлением
проводов и кабелей, а также несовершенством
их изоляции. Мощность, теряемая в активных
сопротивлениях трехфазной ЛЕП и
расходуемая на ее нагрев, определяется
по формуле:

![]()
![]()
![]() ,
,
где
![]() полный,
полный,
активный и реактивный токи в ЛЕП;
P, Q, S
– активная, реактивная и полная
мощности в начале или конце ЛЕП;
U– линейное напряжение в начале или
конце ЛЕП;
R
– активное сопротивление одной
фазы ЛЕП.
Потери активной
мощности в проводимостях ЛЕП обусловлены
несовершенством изоляции. В воздушных
ЛЕП – появлением короны и, в очень
незначительной степени, утечкой тока
по изоляторам. В кабельных ЛЕП –
появлением тока проводимости а его
абсорбции. Рассчитываются потери по
формуле:
![]() ,
,
где U– линейное напряжение в начале или
конце ЛЕП;
G
– активная проводимость ЛЕП.
При проектировании
воздушных ЛЕП потери мощности на корону
стремятся свести к нулю, выбирая такой
диаметр провода, когда возможность
возникновения короны практически
отсутствует.
Потери реактивной
мощности на участке ЛЕП обусловлены
индуктивными сопротивлениями проводов
и кабелей. Реактивная мощность, теряемая
в трехфазной ЛЕП, рассчитывается
аналогично мощности, теряемой в активных
сопротивлениях:
![]()
Генерируемая
емкостной проводимостью зарядная
мощность ЛЕП рассчитывается по формуле:
![]() ,
,
где U– линейное напряжение в начале или
конце ЛЕП;
B
– реактивная проводимость ЛЕП.
Зарядная мощность
уменьшает реактивную нагрузку сети и
тем самым снижает потери мощности в
ней.
Расчет потерь мощности в леп с равномерно распределенной нагрузкой
В линиях местных
сетей (![]() )
)
потребители одинаковой мощности могут
располагаться на одинаковом расстоянии
друг от друга (например, источники
света). Такие ЛЕП называются линиями с
равномерно распределенной нагрузкой
(см. рис. 7.2).
В равномерно
нагруженной линии трехфазного переменного
тока длиной L
с суммарной токовой нагрузкойIплотность тока на единицу длины составитI/L. При погонном
активном сопротивленииr0
потери активной мощности составят:
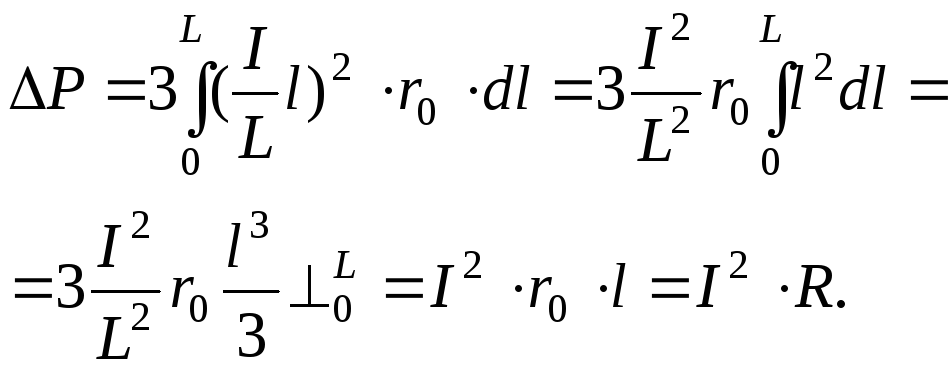
Если бы нагрузка
была сосредоточена в конце, то потери
мощности определялись бы как:
![]() .
.
Сравнивая приведенные
выражения, видим, что потери мощности
в линии с равномерно распределенной
нагрузкой в 3 раза меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

При передаче электрической энергии от генераторов электростанций до потребителя около 12-18% всей вырабатываемой электроэнергии теряется в проводниках воздушных и кабельных линий, а также в обмотках и стальных сердечниках силовых трансформаторов.
При проектировании нужно стремиться к уменьшению потерь электроэнергии на всех участках энергосистемы, поскольку потери электроэнергии ведут к увеличению мощности электростанций, что в свою очередь влияет на стоимость электроэнергии.
В сетях до 10кВ потери мощности в основном обусловлены нагревом проводов от действия тока.
Потери мощности в линии.
Потери активной мощности (кВт) и потери реактивной мощности (кВАр) можно найти по следующим формулам:
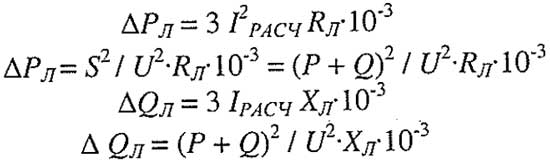
Формулы для расчета потери мощности в линии
где Iрасч – расчетный ток данного участка линии, А;
Rл – активное сопротивление линии, Ом.
Потери мощности в трансформаторах.
Потери мощности в силовых трансформаторах состоят из потерь, не зависящих и зависящих от нагрузки. Потери активной мощности (кВт) в трансформаторе можно определить по следующей формуле:
Потери активной мощности в трансформаторе
где ?Рст – потери активной мощности в стали трансформатора при номинальном напряжении. Зависят только от мощности трансформатора и приложенного к первичной обмотке трансформатора напряжения. ?Рст приравнивают ?Рх;
?Рх— потери холостого хода трансформатора;
?Роб – потери в обмотках при номинальной нагрузке трансформатора, кВт; ?Роб приравнивают ?Рк.
?Рк– потери короткого замыкания;
?=S/Sном – коэффициент загрузки трансформатора равен отношению фактической нагрузки трансформатора к его номинальной мощности;
Потери реактивной мощности трансформатора (кВАр) можно определить по следующей формуле:
![]()
Потери реактивной мощности в трансформаторе
где ?Qст – потери реактивной мощности на намагничивание, кВАр. ?Qст приравнивают ?Qх.
?Qх – намагничивающая мощность холостого хода трансформатора;
?Qрас – потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке.
Значения ?Рст(?Рх) и ?Роб(?Рк) приведения в каталогах производителей силовых трансформаторов. Значения ?Qст(?Qх) и ?Qрас определяют по данным каталогов из следующих выражений:
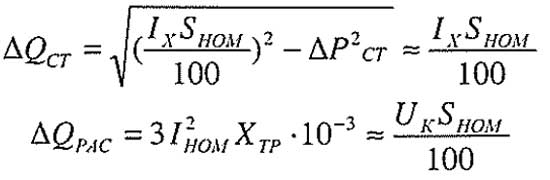
Формулы для расчета потери реактивной мощности
где Iх – ток холостого хода трансформатора, %;
Uк – напряжение короткого замыкания, %;
Iном – номинальный ток трансформатора, А;
Xтр – реактивное сопротивление трансформатора;
Sном – номинальная мощность трансформатора, кВА.
Потери электроэнергии.
На основании потерь мощности можно посчитать потери электроэнергии. Здесь следует быть внимательными. Нельзя посчитать потери электроэнергии умножив потери мощности при какой либо определенной нагрузке на число часов работы линии. Этого делать не стоит, т.к в течение суток или сезона потребляемая нагрузка изменяется и таким образом мы получим необоснованно завышенное значение.
Чтобы правильно посчитать потери электроэнергии используют метод, основанный на понятиях времени использования потерь и времени использовании максимума нагрузки.
Время максимальных потерь ? – условное число часов, в течение которых максимальный ток, протекающий в линии, создает потери энергии, равные действительным потерям энергии в год.
Временем использования максимальной нагрузки или временем использования максимума Тмах называют условное число часов, в течение которых линия, работая с максимальной нагрузкой, могла бы передать потребителю за год столько энергии, сколько при работе по действительному переменному графику. Пусть W(кВт*ч) – энергия переданная по линии за некоторый промежуток времени, Рмах(кВт) -максимальная нагрузка, тогда время использования максимальной нагрузки:
Тмах=W/Рмах
На основании статистических данных для отдельных групп электроприемников были получены следующие значения Тмах:
- Для внутреннего освещения – 1500—2000 ч;
- Наружного освещения – 2000—3000 ч;
- Промышленного предприятия односменного – 2000—2500 ч;
- Двухсменного – 3000—4500 ч;
- Трехсменного – 3000—7000 ч;
Время потерь ? можно найти по графику, зная Тмах и коэффициент мощности.
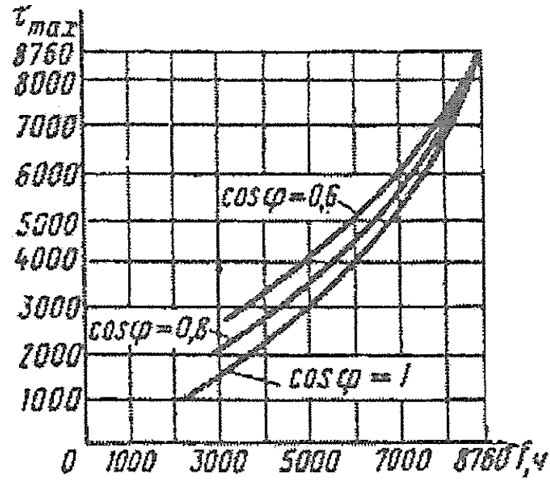
Зависимость времени максимальных потерь от продолжительности использования максимума нагрузки
Теперь зная ? можно посчитать потери электроэнергии в линии и в трансформаторе.
Потери энергии в линии:
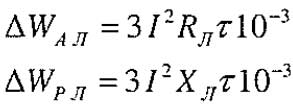
Потери энергии в линии
Потери энергии в трансформаторе:
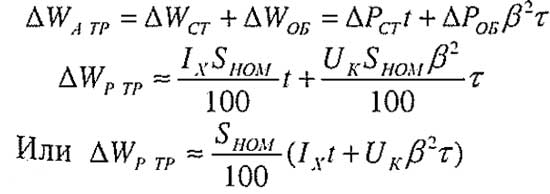
Потери энергии в трансформаторе
где ?Wатр –общая потеря активной энергии (кВт*ч) в трансформаторе;
?Wртр –общая потеря реактивной энергии (кВАр*ч) в трансформаторе.
Советую почитать:
Потери мощности в трансформаторе определяются по формулам:
потери активной мощности![]()
потери реактивной мощности![]()
где ![]() — потери холостого хода трансформатора (потери в стали), квт;
— потери холостого хода трансформатора (потери в стали), квт;![]() — потери к. з. трансформатора (потери в обмотках) при номинальной нагрузке, квт;
— потери к. з. трансформатора (потери в обмотках) при номинальной нагрузке, квт;![]() — ток холостого хода трансформатора, %;
— ток холостого хода трансформатора, %;![]() — падение напряжения в реактивном сопротивлении трансформатора, %;
— падение напряжения в реактивном сопротивлении трансформатора, %;![]() — номинальная мощность трансформатора, ква;
— номинальная мощность трансформатора, ква;![]() — коэффициент загрузки трансформатора;
— коэффициент загрузки трансформатора;![]()
где S — фактическая нагрузка трансформатора, ква.
Формула (9-4) для определения потерь реактивной мощности в трансформаторе может быть представлена в виде:
![]()
где ![]() — потери реактивной мощности в трансформаторе при холостом ходе (потери на намагничивание), квар:
— потери реактивной мощности в трансформаторе при холостом ходе (потери на намагничивание), квар:
![]()
![]() — потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке, квар:
— потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке, квар:![]()
Падение напряжения в реактивном сопротивлении трансформатора определяется по формуле
![]()
где Uк — напряжение к. з. трансформатора, %;
Ur — падение напряжения в активном сопротивлении трансформатора, определяемое из выражения
![]()
Для трансформаторов мощностью более 10 Мва можно принять
![]()
Некоторые значения величин ![]() для понижающих трансформаторов приведены в табл. 9-2. В табл. 9-2 уровень Б потерь активной мощности холостого хода относится к трансформаторам, в которых использована электротехническая сталь толщиной 0,35 мм марки Э 330 А по ГОСТ 802-58 с жаростойким покрытием и отжигом пластин. В табл. 9-2 даны значения активных и реактивных сопротивлений трансформаторов, приведенные по отношению к номинальному напряжению обмотки ВН.
для понижающих трансформаторов приведены в табл. 9-2. В табл. 9-2 уровень Б потерь активной мощности холостого хода относится к трансформаторам, в которых использована электротехническая сталь толщиной 0,35 мм марки Э 330 А по ГОСТ 802-58 с жаростойким покрытием и отжигом пластин. В табл. 9-2 даны значения активных и реактивных сопротивлений трансформаторов, приведенные по отношению к номинальному напряжению обмотки ВН.
| Таблица 9-2 Технические данные трехфазных двухобмоточных силовых масляных трансформаторов общего назначения (ГОСТ 12022-66) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Номинальная мощность, ква | Верхний предел номиналього напряжения обмотки, кв | Схема и группа соединений обмоток | Потери активной мощности, квт | Напряжение к.з., % | Ток холостого хода | Сопротивления обмоток трансформатора, ом | Потери реактивной мощности, квар | ||||
| холостого хода | к.з. | ||||||||||
| уровень А | уровень Б | активное | реактивное | холостого хода | к.з. | ||||||
| 25 | 10 10 |
У/Ун-0 У/Zн-11 |
0,105 0,105 |
0,125 0,125 |
0,6 0,69 |
4,5 4,7 |
3,2 3,2 |
96,0 110 |
152 152 |
0,80 0,80 |
0,95 0,95 |
| 40 | 10 10 |
У/Ун-0 У/Zн-11 |
0,15 0,15 |
0,18 0,18 |
0,88 1,0 |
4,5 4,7 |
3,0 3,0 |
55,0 62,5 |
98,1 99,5 |
1,20 1,20 |
1,57 1,59 |
| 63 | 10 10 20 20 |
У/Ун-о У/Zн-11 У/Ун-0 У/Zн-11 |
0,22 0,22 0,245 0,245 |
0,265 0,265 0,29 0,29 |
1,28 1,47 1,28 1,47 |
4,5 4,7 5,0 5,3 |
2,8 2,8 2,8 2,8 |
32,3 37,0 129 148 |
63,7 64,8 290 302 |
1,76 1,76 1,76 1,76 |
2,53 2,57 2,88 3,00 |
| 100 | 10 10 35 35 |
У/Ун-0 У/Zн-11 У/Ун-0 У/Zн-11 |
0,31 0,31 0,39 0,39 |
0,365 0,365 0,465 0,465 |
1,97 2,27 1,97 2,27 |
4,5 4,7 6,5 6,8 |
2,6 2,6 2,6 2,6 |
19,7 22,7 241 278 |
40,5 41,2 759 785 |
2,60 2,60 2,60 2,60 |
4,05 4,12 6,19 6,41 |
| 160 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,46 0,46 0,46 0,56 0,56 0,56 |
0,54 0,54 0,54 0,66 0,66 0,66 |
2,65 2,65 3,1 2,65 2,65 3,1 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,4 2,4 2,4 2,4 2,4 2,4 |
10,4 10,4 12,1 127 127 148 |
26,2 26,2 26,8 481 481 499 |
3,84 3,84 3,84 3,84 3,84 3,84 |
6,69 6,69 6,85 10,1 10,1 10,4 |
| 250 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,66 0,66 0,66 0,82 0,82 0,82 |
0,78 0,78 0,78 0,96 0,96 0,96 |
3,7 3,7 4,2 3,7 3,7 4,2 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,3 2,3 2,3 2,3 2,3 2,3 |
5,92 5,92 6,72 72,5 72,5 82,3 |
17,0 17,0 17,6 310 310 322 |
7,25 5,75 5,75 5,75 5,75 5,75 |
10,6 10,6 11,0 15,8 15,8 16,5 |
| 400 | 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Д-11 |
0,62 0,92 0,92 1,15 1,15 |
1,08 1,08 1,08 1,35 1,35 |
5,5 5,5 5,9 5,5 5,5 |
4,5 4,5 4,5 6,5 6,5 |
2,1 2,1 2,1 2,1 2,1 |
3,44 3,44 3,69 42,1 42,1 |
10,7 10,7 10,6 195 195 |
8,40 8,40 8,40 8,40 8,40 |
17,1 17,1 17,0 25,4 25,4 |
| 630 | 10 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Ун-0 У/Д-11 |
1,42 1,42 1,42 1,42 1,7 1,7 |
1,68 1,68 1,68 1,68 2,0 2,0 |
7,6 7,6 8,5 8,5 7,6 7,6 |
5,5 5,5 5,5 5,5 6,5 6,5 |
2,0 2,0 2,0 2,0 2,0 2,0 |
1,91 1,91 2,14 2,14 23,5 23,5 |
8,52 8,52 8,46 8,46 124 124 |
12,6 12,6 12,6 12,6 12,6 12,6 |
33,8 33,8 33,6 33,6 40,2 40,2 |
Для других номинальных напряжений обмоток сопротивления пересчитываются по формулам:
где Uн — номинальное напряжение обмотки, указанное в табл. 9-2, кв;![]() — номинальное напряжение обмотки, по отношению к которому пересчитываются сопротивления, кв;
— номинальное напряжение обмотки, по отношению к которому пересчитываются сопротивления, кв;
R и X — соответственно активное и реактивное сопротивления трансформатора, определяемые по табл. 9-2, ом.
Потери электроэнергии в сети определяются по формуле
![]()
где ![]() — наибольшие потери мощности в сети, кет;
— наибольшие потери мощности в сети, кет;![]() — число часов максимальных потерь, определенное в зависимости от годового графика нагрузки.
— число часов максимальных потерь, определенное в зависимости от годового графика нагрузки.
Потери электроэнергии в трансформаторе определяются по формуле
![]()
где tТ — число часов работы трансформатора.
Число часов максимальных потерь, если известен годовой график нагрузки, может быть определено по формуле
![]()
где ![]() — сумма произведений квадратов полных нагрузок на годовую продолжительность каждой из них, вычисленная для всего годового графика нагрузок рассматриваемого элемента сети;
— сумма произведений квадратов полных нагрузок на годовую продолжительность каждой из них, вычисленная для всего годового графика нагрузок рассматриваемого элемента сети;
Sб — наибольшая полная нагрузка элемента сети. Для типичного графика, имеющего сниженные нагрузки ночью и утренний и вечерний максимумы, число часов максимальных потерь согласно в зависимости от числа часов использования максимума может определяться по табл. 9-7.
| Таблица 9-7 Число часов максимальных потерь | |||||
|---|---|---|---|---|---|
| Число часов использования максимума | 3000 | 3500 | 4000 | 4500 | 5000 |
| Число часов максимальных потерь | 1300 | 1650 | 2000 | 2500 | 3000 |
| Число часов использования максимума | 5500 | 6000 | 6500 | 7000 | 7500 |
| Число часов максимальных потерь | 3650 | 4300 | 5000 | 5700 | 6450 |
Пример 9-1.
Определить годовые потери электроэнергии в трансформаторе типа ТМ мощностью 6,3 Мва с напряжением высшей стороны 10 кв, если трансформатор включен постоянно и годовой график его нагрузки представлен на рис. 9-1.
Решение.
Годовые потери электроэнергии в трансформаторе определяем по (9-10).
По справочным данным находим потери активной мощности в трансформаторе при холостом ходе для уровня Б: ΔРс=9 квт
и нагрузочные потери (потери к. з.) при номинальной нагрузке трансформатора: ΔРк.з=46,5 квт
По условию примера годовое число часов работы трансформатора tТ = 8 760.
Коэффициент загрузки трансформатора при наибольшей нагрузке составляет:![]()
Число часов максимальных потерь определяем из графика на рис. 9-1, подставив в (9-11) значения нагрузок трансформатора в мегавольт-амперах и соответствующие им продолжительности работы в тысячах часов:
![]()
Подставив числовые значения в (9-10), определим годовые потери энергии в трансформаторе:
![]()

Рис. 9-1.
Годовой график нагрузки
Пример 9-2.
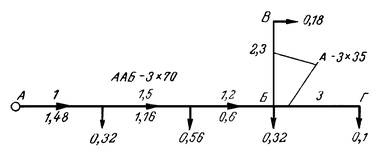
На рис. 9-2 представлена схема линии 6 кв с указанием длин участков линии (км) и расчетных (наибольших) нагрузок (Мва). Магистраль АБ выполнена кабелем с алюминиевыми жилами сечением 3X70 мм.кв, а ответвления БВ и БГ — воздушной линией с алюминиевыми проводами сечением 35 мм.кв.
Определить годовые потери электроэнергии в сопротивлениях проводов и кабелей линии, если годовая продолжительность использования максимума нагрузок составляет 3000 ч и график нагрузок является типичным (имеются утренний и вечерний максимумы и снижение нагрузки в ночное время).
Решение.
Наибольшие потери мощности в сопротивлениях проводов и кабелей линии находим по (9-1), в которой значение коэффициента определяется из табл. 9-1:![]()
Удельные сопротивления участков линии находим по табл. 5-1: для алюминиевого кабеля сечением 70 мм.кв — 0,46 ом/км; для алюминиевого провода сечением 35 мм.кв — 0,92 ом/км.
Определяем значение величины N для магистрали АБ:
![]()
для ответвлений БВ и БГ
![]()
Из (9-1) находим наибольшие потери мощности в сети:
![]()
По табл. 9-7 в зависимости от продолжительности использования максимума Т=3000 ч находим значение числа часов максимальных потерь τ=1300. Величину потерь электроэнергии определяем по (9-9):
![]()
В статье представлен пример оценки потерь мощности в электроэнергетической системе.
В составе статьи представлены расчёты, описывающие следующие подходы:
- Оценка потерь мощности по средствам расчёта потокораспределения сети в установившемся режиме.
- Приближенный анализ величины потерь мощности с использованием числа часов максимальных нагрузок (потерь).
Содержание
- 1 Описание примера
- 2 Исходные данные
- 3 Расчёт схемы замещения
- 4 Оценка потерь мощности
- 4.1 Оценка потерь мощности при расчёте установившегося режима
- 4.1.1 Интервал 1 (0 — 8 часов)
- 4.1.2 Интервал 2 (8 — 16 часов)
- 4.1.3 Интервал 3 (16 — 24 часов)
- 4.1.4 Потери в сети
- 4.2 Оценка потерь мощности по графику нагрузки для суток
- 4.3 Оценка потерь мощности по графику нагрузки для года
- 4.3.1 Расчёт по графикам нагрузок
- 4.3.2 Расчёт по эмпирическим коэффициентам
- 4.1 Оценка потерь мощности при расчёте установившегося режима
Описание примера
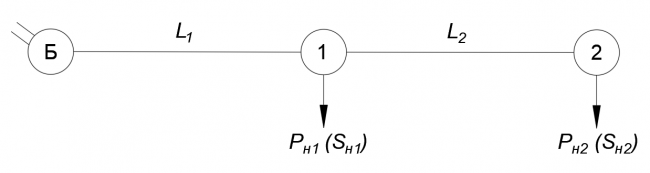
Рисунок 1. Схема исследуемой сети
В данном примере производится последовательная реализация следующих этапов:
- Выбор объекта исследования.
- Подготовка исходных данных.
- Формирование и расчёт схемы замещения исследуемой сети.
- Оценка интервальных потерь мощности и суммарных потерь энергии:
- оценка потерь мощности при расчёте установившегося режима;
- оценка потерь мощности по графику нагрузки для суток с использванием числа часов максимальной нагрузки;
- оценка потерь мощности по графику нагрузки для года с использванием числа часов максимальной нагрузки.
Исходные данные
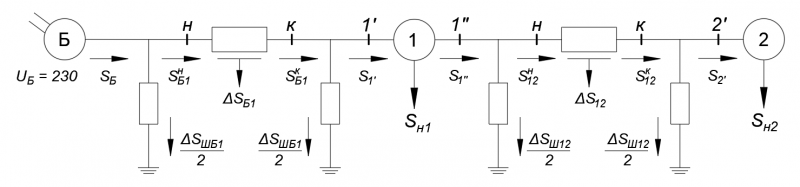
Рисунок 2. Схема замещения исследуемой сети
,
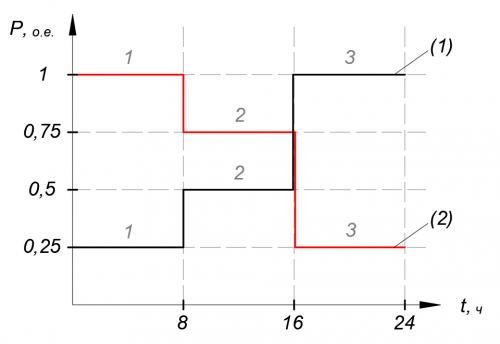
Рисунок 3. Графики нагрузок узлов 1 и 2 в относительных единицах
На рисунке 1 представлена электрическая сеть, в составе которой присутствуют два узла нагрузки (1,2) и базисный узел (Б).
Свзязь между узлами выплолнена линиями электропередачи [math]displaystyle L_{text{1}}[/math] и [math]displaystyle L_{text{2}}[/math].
На рисунке 2 представлена схема замещения исследуемой сети.
В составе исходных данных задано:
- Напряжение базисного узла [math]displaystyle U_{text{Б}}=230 text{ кВ}[/math].
- Линии электропередачи (воздушные) [math]displaystyle L_{text{1}}[/math] и [math]displaystyle L_{text{2}}[/math] имеют следующие аналогичные характеристики:
- марка провода: AC-400;
- длина провода: [math]displaystyle L = 100[/math] км;
- удельные сопротивления: [math]displaystyle R_{text{0}} = 0.075[/math] Ом/км, [math]displaystyle X_{text{0}} = 0.42[/math] Ом/км;
- удельная реактивная проводимость: [math]displaystyle b_{text{0}} = 2.7 cdot 10^{-6} [/math] См/км;
- удельные потери мощности на корону максимальные:[math]displaystyle Delta P^{max}_{text{кор}} = 1.7 text{ кВт/км }[/math];
- удельные потери мощности на корону минимальные:[math]displaystyle Delta P^{min}_{text{кор}} = 1.3 text{ кВт/км }[/math];
- Значение максимальной активной мощности нагрузки:
- узел 1: [math]displaystyle P_{text{1}} = text{ 80 МВт }[/math];
- узел 2: [math]displaystyle P_{text{2}} = text{ 100 МВт }[/math];
- Коэффициент мощности нагрузки [math]displaystyle cos{phi} = text{ 0.9 о.е. }[/math].
На рисунке 3 представлены графики нагрузок узлов 1 и 2 в относительных единицах.
Графики нагрузки узлов 1 и 2 в абсолютных единицах:
| Интервал | 1 | 2 | 3 |
| [math]displaystyle P_{text{, } text{o.e.}}[/math] | 0.25 | 0.5 | 1 |
| [math]displaystyle P_{text{, } text{МВт}}[/math] | 20 | 40 | 80 |
| [math]displaystyle t_{text{, ч}}[/math] | 0-8 | 8-16 | 16-24 |
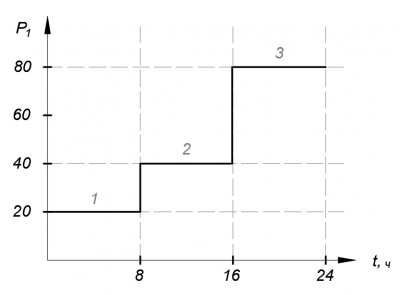
Рисунок 4. График нагрузки узла 1 в абсолютных единицах
| Интервал | 1 | 2 | 3 |
| [math]displaystyle P_{text{, } text{o.e.}}[/math] | 1 | 0.75 | 0.25 |
| [math]displaystyle P_{text{, } text{МВт}}[/math] | 25 | 75 | 100 |
| [math]displaystyle t_{text{, ч}}[/math] | 0-8 | 8-16 | 16-24 |
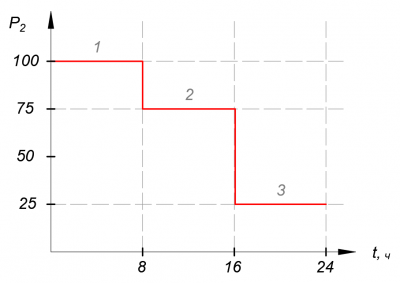
Рисунок 5. График нагрузки узла 2 в абсолютных единицах
Складывая соответствующие интервальные нагрузки узлов, получаем суммарный график нагрузки. Суммарный график нагрузки узлов 1 и 2 представлен на рисунке 6:
-
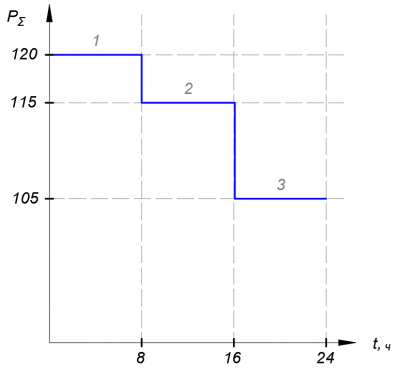
Рисунок 6. Суммарный график нагрузки узлов
-
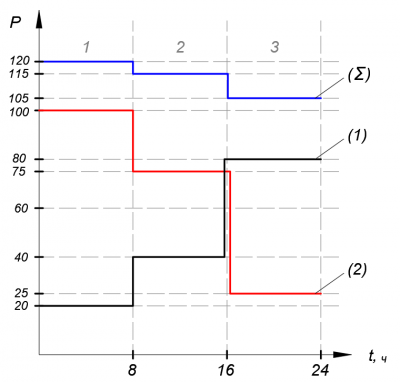
Рисунок 7. Все графики нагрузки узлов в абсолютных единицах
Расчёт схемы замещения
Проводимость шунтов ЛЭП:
- [math]displaystyle frac{Y_{text{Б1}}}{2} = frac{Y_{text{12}}}{2} = frac{Y_{text{L}}}{2} = frac{1}{2} cdot jb_{text{0}} cdot l cdot n = frac{1}{2} cdot j2.7 cdot 10^{-6} cdot 100 cdot 1 = j1.35 cdot 10^{-4} text{ См }[/math].
Комплексное сопротивление ЛЭП:
- [math]displaystyle Z_{text{Б1}} = Z_{text{12}} = Z_{text{L}} = (R_{text{0}} + jX_{text{0}}) cdot l cdot frac{1}{n} = (0.075 + j0.42) cdot 100 cdot 1 = 7.5 + j42 text{ Ом }[/math].
Полные потери в линиях на корону:
- [math]displaystyle Delta P_{text{кор.ср.}} = frac{P^{max}_{text{кор}} + P^{min}_{text{кор}}}{2} = frac{1.7 + 1.3}{2} = 1.5 text{ кВт/км }[/math];
- [math]displaystyle Delta P_{text{кор.L}} = Delta P_{text{кор.ср.}} cdot l cdot n = 1.5 cdot 10^{-3} cdot 100 cdot 1 = 0.15 text{ МВт }[/math] (Для одной линии);
- [math]displaystyle Delta P_{text{кор.}Sigma} = Delta P_{text{кор.L}} cdot 2 = 0.15 cdot 2 = 0.3 text{ МВт }[/math] (Для двух линий).
Полные постоянные потери мощности в линиях:
- [math]displaystyle Delta P_{text{ш.}L} = Delta P_{text{кор.L}} + Delta P_{text{ут.}Sigma} = 0.15 text{ МВт }[/math] (Для одной линии),
-
- где [math] Delta P_{text{ут.}Sigma} = 0 text{ МВт }[/math] — потери мощности на утечки в изоляторах;
-
- [math]displaystyle Delta P_{text{ш.}Sigma} = Delta P_{text{ш.}L} cdot 2 = 0.15 cdot 2 = 0.3 text{ МВт }[/math] (Для двух линии).
Максимальная реактивная мощность нагрузки:
- [math]displaystyle Q_{text{1}} = P_{text{1}} cdot tan{(arccos{(0.9)})} = 80 cdot tan{(arccos{(0.9)})} = 38.75 text{ Мвар }[/math];
- [math]displaystyle Q_{text{2}} = P_{text{2}} cdot tan{(arccos{(0.9)})} = 100 cdot tan{(arccos{(0.9)})} = 48.43 text{ Мвар }[/math].
Оценка потерь мощности
Оценка потерь мощности при расчёте установившегося режима
Расчёт установишегося режима производится для каждого из заданных интервалов времени. В соответствии с методикой, определяются потокораспределение и величины потерь в элементах сети.
Для упрощения вычислений зададимся допущением о неизменности напряжения в узлах 1 и 2 на всех интервалах времени. Пусть значение напряжения в узлах составляет:
- [math] U1 = 220 text{ кВ }[/math];
- [math] U2 = 210 text{ кВ }[/math];
Интервал 1 (0 — 8 часов)
Определение комплексной нагрузки в узлах согласно исходным данным:
Активные мощности
- [math]displaystyle P1_{text{1}} = 0.25 cdot P1 = 20 text{ МВт }[/math];
- [math]displaystyle P2_{text{1}} = 1 cdot P2 = 100 text{ МВт }[/math].
Рективные мощности
- [math]displaystyle Q1_{text{1}} = P1_{text{1}} cdot tan{(arccos{(0.9)})} = 9.68 text{ Мвар }[/math];
- [math]displaystyle Q2_{text{1}} = P2_{text{1}} cdot tan{(arccos{(0.9)})} = 48.43 text{ Мвар }[/math].
Полные мощности
- [math]displaystyle Sн1_{text{1}} = P1_{text{1}} + jQ1_{text{1}} = 20 + j9.68 text{ МВА }[/math];
- [math]displaystyle Sн2_{text{1}} = P2_{text{1}} + jQ2_{text{1}} = 100 + j48.43 text{ МВА }[/math].
В точке [math]2^{‘}[/math] (конец линии 1-2, рисунок 2), смежной с узлом 2, значение потока мощности, втекающего в узел 2 [math]displaystyle S2^{‘}_{text{1}}[/math]:
- [math]displaystyle S2^{‘}_{text{1}} = Sн2_{text{1}} = 100 + j48.43 text{ МВА }[/math].
Потери в шунте на участке 1-2:
- [math]displaystyle frac{Delta Sш12_{text{1}}}{2} = frac{Y12}{2} cdot (U2)^{2} = – j2.9768 text{ МВА }[/math].
Поток мощности в конце линии 1-2:
- [math]displaystyle S12^{к}_{text{1}} = S2^{‘}_{text{1}} + frac{Delta Sш12_{text{1}}}{2} = 100 + j45.455 text{ МВА }[/math].
Потери мощности в линии 1-2:
- [math]displaystyle Delta S12_{text{1}} = frac{ Re(S12^{к}_{text{1}})^{2} + Im(S12^{к}_{text{1}})^{2} }{(U2)^2} cdot Z_{text{L}} = 2.052 + j11.492 text{ МВА }[/math].
Поток мощности в начале линии 1-2:
- [math]displaystyle S12^{н}_{text{1}} = S12^{к}_{text{1}} + Delta S12_{text{1}} = 102.052 + j56.947 text{ МВА }[/math].
В точке [math]1^{”}[/math] (начало линии 1-2, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{”}_{text{1}}[/math]:
- [math]displaystyle S1^{”}_{text{1}} = S12^{н}_{text{1}} + frac{Delta Sш12_{text{1}}}{2} = 100 + j53.970 text{ МВА }[/math].
В точке [math]1^{‘}[/math] (конец линии Б-1, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{‘}_{text{1}}[/math]:
- [math]displaystyle S1^{‘}_{text{1}} = S1^{”}_{text{1}} + Sн1_{text{1}} = 122.052 + j63.658 text{ МВА }[/math].
Потери в шунте на участке Б-1:
- [math]displaystyle frac{Delta SшБ1_{text{1}}}{2} = frac{YБ1}{2} cdot (U1)^{2} = – j3.267 text{ МВА }[/math].
Поток мощности в конце линии Б-1:
- [math]displaystyle SБ1^{к}_{text{1}} = S1^{‘}_{text{1}} + frac{Delta SшБ1_{text{1}}}{2} = 122 + j60.389 text{ МВА }[/math].
Потери мощности в линии Б-1:
- [math]displaystyle Delta SБ1_{text{1}} = frac{ Re(SБ1^{к}_{text{1}})^{2} + Im(SБ1^{к}_{text{1}})^{2} }{(U1)^2} cdot Z_{text{L}} = 2.873 + j16.091 text{ МВА }[/math].
Поток мощности в начале линии Б-1:
- [math]displaystyle SБ1^{н}_{text{1}} = SБ1^{к}_{text{1}} + Delta SБ1_{text{1}} = 124.926 + j76.481 text{ МВА }[/math].
Таким образом, поток мощности из источника составляет:
- [math]displaystyle SБ_{text{1}} = SБ1^{н}_{text{1}} + frac{Delta SшБ1_{text{1}}}{2} = 124.926 + j73.214 text{ МВА }[/math].
Интервал 2 (8 — 16 часов)
Определение комплексной нагрузки в узлах согласно исходным данным:
Активные мощности
- [math]displaystyle P1_{text{2}} = 0.5 cdot P1 = 40 text{ МВт }[/math];
- [math]displaystyle P2_{text{2}} = 0.75 cdot P2 = 75 text{ МВт }[/math].
Рективные мощности
- [math]displaystyle Q1_{text{2}} = P1_{text{2}} cdot tan{(arccos{(0.9)})} = 19.373 text{ Мвар }[/math];
- [math]displaystyle Q2_{text{2}} = P2_{text{2}} cdot tan{(arccos{(0.9)})} = 36.324 text{ Мвар }[/math].
Полные мощности
- [math]displaystyle Sн1_{text{2}} = P1_{text{2}} + jQ1_{text{2}} = 40 + j19.373 text{ МВА }[/math];
- [math]displaystyle Sн2_{text{2}} = P2_{text{2}} + jQ2_{text{2}} = 75 + j36.324 text{ МВА }[/math].
В точке [math]2^{‘}[/math] (конец линии 1-2, рисунок 2), смежной с узлом 2, значение потока мощности, втекающего в узел 2 [math]displaystyle S2^{‘}_{text{2}}[/math]:
- [math]displaystyle S2^{‘}_{text{2}} = Sн2_{text{2}} = 75 + j36.324 text{ МВА }[/math].
Потери в шунте на участке 1-2:
- [math]displaystyle frac{Delta Sш12_{text{2}}}{2} = frac{Y12}{2} cdot (U2)^{2} = – j2.9768 text{ МВА }[/math].
Поток мощности в конце линии 1-2:
- [math]displaystyle S12^{к}_{text{2}} = S2^{‘}_{text{2}} + frac{Delta Sш12_{text{2}}}{2} = 75 + j33.347 text{ МВА }[/math].
Потери мощности в линии 1-2:
- [math]displaystyle Delta S12_{text{2}} = frac{ Re(S12^{к}_{text{2}})^{2} + Im(S12^{к}_{text{2}})^{2} }{(U2)^2} cdot Z_{text{L}} = 1.146 + j6.416 text{ МВА }[/math].
Поток мощности в начале линии 1-2:
- [math]displaystyle S12^{н}_{text{2}} = S12^{к}_{text{2}} + Delta S12_{text{2}} = 76.146 + j39.764 text{ МВА }[/math].
В точке [math]1^{”}[/math] (начало линии 1-2, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{”}_{text{2}}[/math]:
- [math]displaystyle S1^{”}_{text{2}} = S12^{н}_{text{2}} + frac{Delta Sш12_{text{2}}}{2} = 76.146 + j36.787 text{ МВА }[/math].
В точке [math]1^{‘}[/math] (конец линии Б-1, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{‘}_{text{2}}[/math]:
- [math]displaystyle S1^{‘}_{text{2}} = S1^{”}_{text{2}} + Sн1_{text{2}} = 116.146 + j56.159 text{ МВА }[/math].
Потери в шунте на участке Б-1:
- [math]displaystyle frac{Delta SшБ1_{text{2}}}{2} = frac{YБ1}{2} cdot (U1)^{2} = – j3.267 text{ МВА }[/math].
Поток мощности в конце линии Б-1:
- [math]displaystyle SБ1^{к}_{text{2}} = S1^{‘}_{text{2}} + frac{Delta SшБ1_{text{2}}}{2} = 116.146 + j52.893 text{ МВА }[/math].
Потери мощности в линии Б-1:
- [math]displaystyle Delta SБ1_{text{2}} = frac{ Re(SБ1^{к}_{text{2}})^{2} + Im(SБ1^{к}_{text{2}})^{2} }{(U1)^2} cdot Z_{text{L}} = 2.524 + j14.134 text{ МВА }[/math].
Поток мощности в начале линии Б-1:
- [math]displaystyle SБ1^{н}_{text{2}} = SБ1^{к}_{text{2}} + Delta SБ1_{text{2}} = 118.669 + j67.026 text{ МВА }[/math].
Таким образом, поток мощности из источника составляет:
- [math]displaystyle SБ_{text{2}} = SБ1^{н}_{text{2}} + frac{Delta SшБ1_{text{2}}}{2} = 118.669 + j63.759 text{ МВА }[/math].
Интервал 3 (16 — 24 часов)
Определение комплексной нагрузки в узлах согласно исходным данным:
Активные мощности
- [math]displaystyle P1_{text{3}} = 1 cdot P1 = 80 text{ МВт }[/math];
- [math]displaystyle P2_{text{3}} = 0.25 cdot P2 = 25 text{ МВт }[/math].
Рективные мощности
- [math]displaystyle Q1_{text{3}} = P1_{text{3}} cdot tan{(arccos{(0.9)})} = 38.746 text{ Мвар }[/math];
- [math]displaystyle Q2_{text{3}} = P2_{text{3}} cdot tan{(arccos{(0.9)})} = 12.108 text{ Мвар }[/math].
Полные мощности
- [math]displaystyle Sн1_{text{3}} = P1_{text{3}} + jQ1_{text{3}} = 80 + j38.746 text{ МВА }[/math];
- [math]displaystyle Sн2_{text{3}} = P2_{text{3}} + jQ2_{text{3}} = 25 + j12.108 text{ МВА }[/math].
В точке [math]2^{‘}[/math] (конец линии 1-2, рисунок 2), смежной с узлом 2, значение потока мощности, втекающего в узел 2 [math]displaystyle S2^{‘}_{text{3}}[/math]:
- [math]displaystyle S2^{‘}_{text{3}} = Sн2_{text{3}} = 25 + j12.108 text{ МВА }[/math].
Потери в шунте на участке 1-2:
- [math]displaystyle frac{Delta Sш12_{text{3}}}{2} = frac{Y12}{2} cdot (U2)^{2} = – j2.9768 text{ МВА }[/math].
Поток мощности в конце линии 1-2:
- [math]displaystyle S12^{к}_{text{3}} = S2^{‘}_{text{3}} + frac{Delta Sш12_{text{3}}}{2} = 25 + j9.131 text{ МВА }[/math].
Потери мощности в линии 1-2:
- [math]displaystyle Delta S12_{text{3}} = frac{ Re(S12^{к}_{text{3}})^{2} + Im(S12^{к}_{text{3}})^{2} }{(U2)^2} cdot Z_{text{L}} = 0.121 + j0.675 text{ МВА }[/math].
Поток мощности в начале линии 1-2:
- [math]displaystyle S12^{н}_{text{3}} = S12^{к}_{text{3}} + Delta S12_{text{3}} = 25.121 + j9.806 text{ МВА }[/math].
В точке [math]1^{”}[/math] (начало линии 1-2, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{”}_{text{3}}[/math]:
- [math]displaystyle S1^{”}_{text{3}} = S12^{н}_{text{3}} + frac{Delta Sш12_{text{3}}}{2} = 25.121 + j6.829 text{ МВА }[/math].
В точке [math]1^{‘}[/math] (конец линии Б-1, рисунок 2), смежной с узлом 1, значение потока мощности, вытекающего из узла 1 [math]displaystyle S1^{‘}_{text{3}}[/math]:
- [math]displaystyle S1^{‘}_{text{3}} = S1^{”}_{text{3}} + Sн1_{text{3}} = 105.121 + j45.575 text{ МВА }[/math].
Потери в шунте на участке Б-1:
- [math]displaystyle frac{Delta SшБ1_{text{3}}}{2} = frac{YБ1}{2} cdot (U1)^{2} = – j3.267 text{ МВА }[/math].
Поток мощности в конце линии Б-1:
- [math]displaystyle SБ1^{к}_{text{3}} = S1^{‘}_{text{3}} + frac{Delta SшБ1_{text{3}}}{2} = 105.121 + j42.308 text{ МВА }[/math].
Потери мощности в линии Б-1:
- [math]displaystyle Delta SБ1_{text{3}} = frac{ Re(SБ1^{к}_{text{3}})^{2} + Im(SБ1^{к}_{text{3}})^{2} }{(U1)^2} cdot Z_{text{L}} = 1.989 + j11.142 text{ МВА }[/math].
Поток мощности в начале линии Б-1:
- [math]displaystyle SБ1^{н}_{text{3}} = SБ1^{к}_{text{3}} + Delta SБ1_{text{3}} = 107.110 + j53.450 text{ МВА }[/math].
Таким образом, поток мощности из источника составляет:
- [math]displaystyle SБ_{text{3}} = SБ1^{н}_{text{3}} + frac{Delta SшБ1_{text{3}}}{2} = 107.110 + j50.183 text{ МВА }[/math].
Потери в сети
Потери мощности на расчётных интервалах времени составили:
- [math]displaystyle Delta S_{text{сумм.1}} = Delta S12_{text{1}} + Delta SБ1_{text{1}} = 4.956 + j27.583 text{ МВА }[/math];
- [math]displaystyle Delta S_{text{сумм.2}} = Delta S12_{text{2}} + Delta SБ1_{text{2}} = 3.669 + j20.55 text{ МВА }[/math];
- [math]displaystyle Delta S_{text{сумм.3}} = Delta S12_{text{3}} + Delta SБ1_{text{3}} = 2.110 + j11.817 text{ МВА }[/math].
Величина расчётного интервала [math]displaystyle Delta t = 8 text{ ч }[/math].
Таким образом, потери энергии за исследуемый период составят:
- [math]displaystyle Delta Э_{text{пер.реж.}} = Delta S_{text{сумм.1}} cdot Delta t + Delta S_{text{сумм.2}} cdot Delta t + Delta S_{text{сумм.3}} cdot Delta t = 85.643 + j479.602 text{ МВА} cdot text{ч}[/math].
Оценка потерь мощности по графику нагрузки для суток
Максимальные значения активной мощности нагрузки для узлов 1 и 2 составляют:
- [math]displaystyle P1 = 80 text{ МВт }[/math];
- [math]displaystyle P2 = 100 text{ МВт }[/math].
Расчётные интервалы внутри суток предполагаются равными и составляют:
- [math]displaystyle Delta t = 8 text{ ч }[/math].
Согласно суммарному графику нагрузки (рисунок 6), максимальное значение нагрузки определяется на 1 интервале времени (0 — 8 часов). Для данного интервала в предыдущем примере были расчитаны суммарные потери мощности:
- [math]displaystyle Delta S_{text{сумм.1}} = 4.956 + j27.583 text{ МВА }[/math].
Для оценки суточных потерь воспользуемся методом расчёта с применением числа часов максимальной мощности для каждого узла.
- [math]displaystyle T1_{text{max}} = frac{P1_{1} cdot Delta t + P1_{2} cdot Delta t + P1_{3} cdot Delta t}{P1} = 14 text{ ч }[/math];
- [math]displaystyle T2_{text{max}} = frac{P2_{1} cdot Delta t + P2_{2} cdot Delta t + P2_{3} cdot Delta t}{P1} = 16 text{ ч }[/math].
Средневзвешанное значение числа часов использования максимальной мощности для схемы составит:
- [math]displaystyle T^{ср.взв.}_{text{max}} = frac{P1 cdot T1_{text{max}} + P2 cdot T2_{text{max}}}{P2} = 27.2 text{ ч }[/math].
Рассчитаем число часов масимальных потерь для каждого узла.
- [math]displaystyle tau1 = frac{(frac{P1_{1}}{cos{phi}})^{2} cdot Delta t + (frac{P1_{2}}{cos{phi}})^{2} cdot Delta t + (frac{P1_{3}}{cos{phi}})^{2} cdot Delta t}{(frac{P1}{cos{phi}})^{2}} = 10.5 text{ ч }[/math];
- [math]displaystyle tau2 = frac{(frac{P2_{1}}{cos{phi}})^{2} cdot Delta t + (frac{P2_{2}}{cos{phi}})^{2} cdot Delta t + (frac{P2_{3}}{cos{phi}})^{2} cdot Delta t}{(frac{P2}{cos{phi}})^{2}} = 13 text{ ч }[/math].
Средневзвешанное значение числа часов максимальных потерь для схемы составит:
- [math]displaystyle tau^{ср.взв.} = frac{frac{P1}{cos{phi}} cdot tau1 + frac{P2}{cos{phi}} cdot tau2}{frac{P2}{cos{phi}}} = 21.4 text{ ч }[/math];
Таким образом, потери энергии в сети для суток будут определяться как произведение средневзвешанного числа часов максимальных потерь и максимального значения потерь (интервал 1):
- [math]displaystyle Delta Э_{text{пер.}tau} = tau^{ср.взв.} cdot Delta S_{text{сумм.1}} = 105.407 + j590.280 text{ МВА} cdot text{ч}[/math].
Расчетные потери энергии при интервальной оценке режимов на аналогичном периоде составляют (для сравнения):
- [math]displaystyle Delta Э_{text{пер.реж.}} = 85.643 + j479.602 text{ МВА} cdot text{ч}[/math].
Оценка потерь мощности по графику нагрузки для года
Для оценки потерь мощности за год используется два подхода. Первый подход основан на анализе графиков нагрузок и, в целом, аналогичен рассмотренному ранее при расчет потерь за сутки. Второй подход также опирается на значение числа часов использования максимумов, однако предполагает применение эмпирических коэффициентов для расчета числа часов масимальных потерь. Далее рассмотрим более подробно каждый из них.
Максимальные значения активной мощности нагрузки для узлов 1 и 2 составляют:
- [math]displaystyle P1 = 80 text{ МВт }[/math];
- [math]displaystyle P2 = 100 text{ МВт }[/math].
Разделим год на три условных интервала. Расчётные интервалы для данной задачи:
- [math]displaystyle Delta t_{1} = 121 text{ суток }[/math];
- [math]displaystyle Delta t_{2} = 121 text{ суток }[/math];
- [math]displaystyle Delta t_{3} = 123 text{ суток }[/math].
Пусть на указанных интервалах значение мощности нагрузки совпадает с суточными графиками нагруки, а именно:
для узла 1:
- [math]displaystyle P1_{1} = 20 text{ МВт }[/math];
- [math]displaystyle P1_{2} = 40 text{ МВт }[/math];
- [math]displaystyle P1_{3} = 80 text{ МВт }[/math].
для узла 2:
- [math]displaystyle P2_{1} = 100 text{ МВт }[/math];
- [math]displaystyle P2_{2} = 75 text{ МВт }[/math];
- [math]displaystyle P2_{3} = 25 text{ МВт }[/math].
Согласно суммарному графику нагрузки (рисунок 6), максимальное значение нагрузки определяется на 1 интервале времени. Для данного интервала в предыдущем примере были расчитаны суммарные потери мощности:
- [math]displaystyle Delta S_{text{сумм.1}} = 4.956 + j27.583 text{ МВА }[/math].
Определим значения числа часов использования масимума за год для каждого узла:
- [math]displaystyle T1_{text{max.год}} = frac{P1_{1} cdot Delta t_{1} + P1_{2} cdot Delta t_{2} + P1_{3} cdot Delta t_{3}}{P1} = 213.75 text{ суток }[/math];
- [math]displaystyle T2_{text{max.год}} = frac{P2_{1} cdot Delta t_{1} + P2_{2} cdot Delta t_{2} + P2_{3} cdot Delta t_{3}}{P2} = 242.5 text{ суток }[/math].
Средневзвешанное значение числа часов использования максимальной мощности для схемы составит:
- [math]displaystyle T^{ср.взв.}_{text{max.год}} = frac{P1 cdot T1_{text{max.год}} + P2 cdot T2_{text{max.год}}}{P2} = 413.5 text{ суток }[/math].
Расчёт по графикам нагрузок
Рассчитаем число часов масимальных потерь (по графикам нагрузки) для каждого узла и средневзвешанное значение.
- [math]displaystyle tau1_{text{год}} = frac{(frac{P1_{1}}{cos{phi}})^{2} cdot Delta t_{1} + (frac{P1_{2}}{cos{phi}})^{2} cdot Delta t_{2} + (frac{P1_{3}}{cos{phi}})^{2} cdot Delta t_{3}}{(frac{P1}{cos{phi}})^{2}} = 160.81 text{ суток }[/math];
- [math]displaystyle tau2_{text{год}} = frac{(frac{P2_{1}}{cos{phi}})^{2} cdot Delta t_{1} + (frac{P2_{2}}{cos{phi}})^{2} cdot Delta t_{2} + (frac{P2_{3}}{cos{phi}})^{2} cdot Delta t_{3}}{(frac{P2}{cos{phi}})^{2}} = 196.75 text{ суток }[/math];
- [math]displaystyle tau^{ср.взв.}_{text{год}} = frac{frac{P1}{cos{phi}} cdot tau1_{text{год}} + frac{P2}{cos{phi}} cdot tau2_{text{год}}}{frac{P2}{cos{phi}}} = 325.4 text{ суток }[/math].
Потери энергии в сети для года будут определяться как:
- [math]displaystyle Delta Э^{text{гр.н}}_{text{пер.}tautext{ год}} = tau^{ср.взв.}_{text{год}} cdot Delta S_{text{сумм.1}} = 1602.781 + j8975.573 text{ МВА} cdot text{сутки}[/math].
Расчёт по эмпирическим коэффициентам
Рассчитаем число часов масимальных потерь (по эмпирическим коэффициентам) для каждого узла и средневзвешанное значение.
- [math]displaystyle tau1_{text{ф}} = (0.124 + T1_{text{max.год}} cdot (10)^{-4})^{2} cdot 8760 = 137.75 text{ суток }[/math];
- [math]displaystyle tau2_{text{ф}} = (0.124 + T2_{text{max.год}} cdot (10)^{-4})^{2} cdot 8760 = 138.19 text{ суток }[/math];
- [math]displaystyle tau^{ср.взв.}_{text{ф}} = frac{frac{P1}{cos{phi}} cdot tau1_{text{ф}} + frac{P2}{cos{phi}} cdot tau2_{text{ф}}}{frac{P2}{cos{phi}}} = 248.394 text{ суток }[/math].
Потери энергии в сети для года будут определяться как:
- [math]displaystyle Delta Э^{text{ф}}_{text{пер.}tautext{ год}} = tau^{ср.взв.}_{text{ф}} cdot Delta S_{text{сумм.1}} = 1223.483 + j6851.504 text{ МВА} cdot text{сутки}[/math].
Расчетные потери энергии при интервальной оценке режимов на аналогичном периоде (для года) составлят (для сравнения):
- [math]displaystyle Delta Э_{text{пер.реж.год}} = Delta S_{text{сумм.1}} cdot Delta t_{1} + Delta S_{text{сумм.2}} cdot Delta t_{2} + Delta S_{text{сумм.3}} cdot Delta t_{2} = 1299.574 + j7277.613 text{ МВА} cdot text{сутки}[/math].
Многие СНТ, оплачивающие электроэнергию по общему счётчику, стоят перед вопросом, а не слишком ли много потерь во внутренней электросети им приходится оплачивать? Может, приходится оплачивать не только технологические потери, но и воровство ушлых соседей?
Потери вполне можно оценить расчётом, и сейчас я расскажу, как это сделать. Существует несколько методов теоретического расчёта. Наиболее простым и доступным для широкого круга потребителей мне видится метод расчёта по формулам, изложенным в книге Ю.С. Железко, А.В. Артемьев, О.В. Савченко «Расчёт, анализ и нормирование потерь электроэнергии в электрических сетях», Москва, ЗАО «Издательство НЦЭНАС», 2008 (приложение 2). Его и рассмотрим в этой статье.
О расчёте потерь в однофазных отводах и линиях я рассказывал в предыдущей статье. Сейчас я расскажу о том, как правильно оценить потери в трёхфазных магистральных линиях и трёхфазных отводах. Как и в прошлый раз, расчёт будет включать в себя 4 этапа.
Расчёт сопротивления провода
Сначала посчитаем сопротивление провода (Ом/м) по формуле:
Предположим, магистральная линия селана СИПом сечением 35 мм². СИП — алюминиевый провод. Итого получаем 0,0287 / 35 = 0,00082 Ом/м.
При желании в удельное сопротивление материала провода можно ввести поправку на его температуру под нагрузкой. В данном случае взято сопротивление материала при 20°С.
Расчёт эквивалентного сопротивления линии
Поскольку магистральные линии имеют распределённую нагрузку, то рассчитывается не настоящее сопротивление линии, а эквивалентное, учитывающее эту неравномерность:
Предположим, длина магистральной линии от трансформатора до последней опоры равна 340 метров. Пусть коэффициент распределения нагрузки будет 2,5 (трансформатор стоит чуть в стороне, и от него до первого отвода есть метров 80-90).
Таким образом, эквивалентное сопротивление такой линии будет:
0,00082 * 340 / 2,5 = 0,112 Ом
Замечу, что для трёхфазной линии мы рассчитываем сопротивление только одного провода, а не суммируем длины всех четырёх проводов. Эти особенности учтены в последующих формулах расчёта.
Расчёт квадрата коэффициента формы графика нагрузки
Квадрат коэффициента формы графика нагрузки — это промежуточный параметр, который также потребуется нам в итоговой расчётной формуле.
При отсутствии исходных данных о коэффициенте заполнения графика нагрузки, в промышленных сетях допускается использовать коэффициент 0,5. Однако в СНТ ввиду сезонного и других факторов этот коэффициент может достигать значений 0,1 и даже менее (низкая плотность, высокие нагрузки).
В нашем случае используем коэффициент 0,2. Тогда квадрат коэффициента будет равен (1 + 2 * 0,2) / (3 * 0,3) = 2,33.
Расчёт потерь за расчётный период
Теперь осталось посчитать потери за расчётный период (Вт*ч):
Давайте посчитаем годовые потери в магистральной линии. Пусть годовое потребление по этой линии равно 51000 кВт*ч, а коэффициент мощности в сети 0,9 (при этом tg φ = 0,48):
(51000² * (1 + 0,48²) * 2,33) / (24 * 365 * 0,4²) * 0,112 = 600 кВт*ч
600 кВт*ч — это 1,2% от годового потребления 51000 кВт*ч (600 / 51000 * 100).
Таким образом, потери в магистральной линии составляют 1,2% от электроэнергии, отданной в неё.
Заключение
Внимание! Никакой теоретический расчёт, конечно, не может являться точным. Он может быть лишь оценочным, для приблизительного представления самого порядка технологических потерь.
Повысить точность расчёта можно, например, введя температурную поправку на удельное сопротивление материала провода в связи с его повышенной температурой при работе под нагрузкой. Также можно более точно подогнать коэффициент заполнения графика нагрузок именно под ваше СНТ, хотя это не всегда осуществимо.
Для облегчения расчётов мною написана специальная программа под Windows для расчёта электропотерь:
Скачать её можно с официальной страницы:
http://макс.мск.рус/products/losses/losses.html
На последней вкладке имеется подробная встроенная справка. Также в программе можно произвести расчёт потерь в однофазных отводах (вторая вкладка). На третьей вкладке имеется калькулятор эквивалентной длины провода. Надеюсь, программа окажется вам полезной.
Спасибо за то, что дочитали статью до конца. Если вы посчитаете информацию полезной, отметьте её, пожалуйста, лайком! Напишите свои мысли в комментариях. Подписывайтесь на мой канал. Спасибо и удачи!
