
При передаче электрической энергии от генераторов электростанций до потребителя около 12-18% всей вырабатываемой электроэнергии теряется в проводниках воздушных и кабельных линий, а также в обмотках и стальных сердечниках силовых трансформаторов.
При проектировании нужно стремиться к уменьшению потерь электроэнергии на всех участках энергосистемы, поскольку потери электроэнергии ведут к увеличению мощности электростанций, что в свою очередь влияет на стоимость электроэнергии.
В сетях до 10кВ потери мощности в основном обусловлены нагревом проводов от действия тока.
Потери мощности в линии.
Потери активной мощности (кВт) и потери реактивной мощности (кВАр) можно найти по следующим формулам:
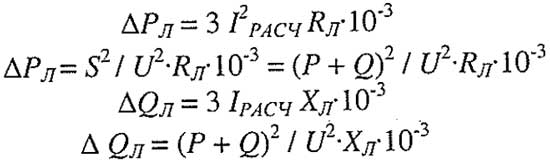
Формулы для расчета потери мощности в линии
где Iрасч – расчетный ток данного участка линии, А;
Rл – активное сопротивление линии, Ом.
Потери мощности в трансформаторах.
Потери мощности в силовых трансформаторах состоят из потерь, не зависящих и зависящих от нагрузки. Потери активной мощности (кВт) в трансформаторе можно определить по следующей формуле:
Потери активной мощности в трансформаторе
где ?Рст – потери активной мощности в стали трансформатора при номинальном напряжении. Зависят только от мощности трансформатора и приложенного к первичной обмотке трансформатора напряжения. ?Рст приравнивают ?Рх;
?Рх— потери холостого хода трансформатора;
?Роб – потери в обмотках при номинальной нагрузке трансформатора, кВт; ?Роб приравнивают ?Рк.
?Рк– потери короткого замыкания;
?=S/Sном – коэффициент загрузки трансформатора равен отношению фактической нагрузки трансформатора к его номинальной мощности;
Потери реактивной мощности трансформатора (кВАр) можно определить по следующей формуле:
![]()
Потери реактивной мощности в трансформаторе
где ?Qст – потери реактивной мощности на намагничивание, кВАр. ?Qст приравнивают ?Qх.
?Qх – намагничивающая мощность холостого хода трансформатора;
?Qрас – потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке.
Значения ?Рст(?Рх) и ?Роб(?Рк) приведения в каталогах производителей силовых трансформаторов. Значения ?Qст(?Qх) и ?Qрас определяют по данным каталогов из следующих выражений:
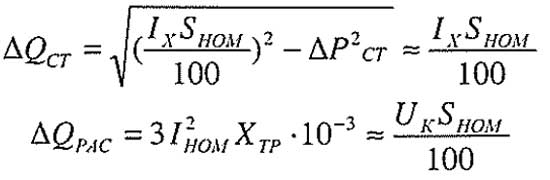
Формулы для расчета потери реактивной мощности
где Iх – ток холостого хода трансформатора, %;
Uк – напряжение короткого замыкания, %;
Iном – номинальный ток трансформатора, А;
Xтр – реактивное сопротивление трансформатора;
Sном – номинальная мощность трансформатора, кВА.
Потери электроэнергии.
На основании потерь мощности можно посчитать потери электроэнергии. Здесь следует быть внимательными. Нельзя посчитать потери электроэнергии умножив потери мощности при какой либо определенной нагрузке на число часов работы линии. Этого делать не стоит, т.к в течение суток или сезона потребляемая нагрузка изменяется и таким образом мы получим необоснованно завышенное значение.
Чтобы правильно посчитать потери электроэнергии используют метод, основанный на понятиях времени использования потерь и времени использовании максимума нагрузки.
Время максимальных потерь ? – условное число часов, в течение которых максимальный ток, протекающий в линии, создает потери энергии, равные действительным потерям энергии в год.
Временем использования максимальной нагрузки или временем использования максимума Тмах называют условное число часов, в течение которых линия, работая с максимальной нагрузкой, могла бы передать потребителю за год столько энергии, сколько при работе по действительному переменному графику. Пусть W(кВт*ч) – энергия переданная по линии за некоторый промежуток времени, Рмах(кВт) -максимальная нагрузка, тогда время использования максимальной нагрузки:
Тмах=W/Рмах
На основании статистических данных для отдельных групп электроприемников были получены следующие значения Тмах:
- Для внутреннего освещения – 1500—2000 ч;
- Наружного освещения – 2000—3000 ч;
- Промышленного предприятия односменного – 2000—2500 ч;
- Двухсменного – 3000—4500 ч;
- Трехсменного – 3000—7000 ч;
Время потерь ? можно найти по графику, зная Тмах и коэффициент мощности.
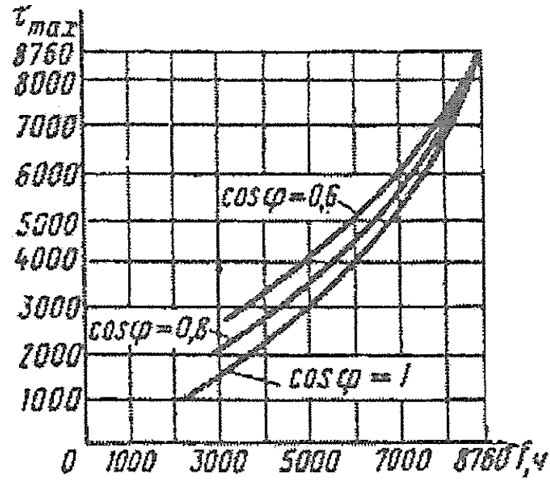
Зависимость времени максимальных потерь от продолжительности использования максимума нагрузки
Теперь зная ? можно посчитать потери электроэнергии в линии и в трансформаторе.
Потери энергии в линии:
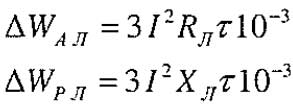
Потери энергии в линии
Потери энергии в трансформаторе:
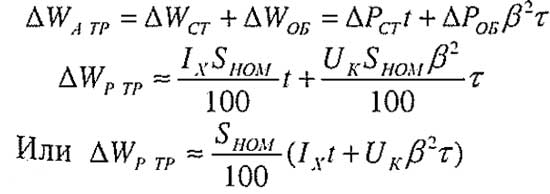
Потери энергии в трансформаторе
где ?Wатр –общая потеря активной энергии (кВт*ч) в трансформаторе;
?Wртр –общая потеря реактивной энергии (кВАр*ч) в трансформаторе.
Советую почитать:
Лекция № 7
Потери мощности и электроэнергии в элементах сети
План.
-
Потери мощности
в элементах сети. -
Расчет потерь
мощности в линиях электропередач. -
Расчет потерь
мощности в ЛЕП с равномерно распределенной
нагрузкой. -
Расчет потерь
мощности в трансформаторах. -
Приведенные и
расчетные нагрузки потребителей. -
Расчет потерь
электроэнергии. -
Мероприятия по
снижению потерь мощности.
Потери мощности в элементах сети
Для
количественной характеристики работы
элементов электрической сети
рассматриваются ее рабочие режимы.
Рабочий
режим
– это установившееся электрическое
состояние, которое характеризуется
значениями токов, напряжений, активной,
реактивной и полной мощностей.
Основной целью
расчета режимов является определение
этих параметров, как для проверки
допустимости режимов, так и для обеспечения
экономичности работы элементов сетей.
Определение
значений токов в элементах сети и
напряжений в ее узлах начинается с
построения картины распределения полной
мощности по элементу, т.е. с определения
мощностей в начале и конце каждого
элемента. Такую картину называют
потокораспределением.
Рассчитывая
мощности в начале и в конце элемента
электрической сети, учитывают потери
мощности в сопротивлениях элемента и
влияние его проводимостей.
Расчет потерь мощности в линиях электропередач
Потери активной
мощности на участке ЛЕП (см. рис. 7.1)
обусловлены активным сопротивлением
проводов и кабелей, а также несовершенством
их изоляции. Мощность, теряемая в активных
сопротивлениях трехфазной ЛЕП и
расходуемая на ее нагрев, определяется
по формуле:

![]()
![]()
![]() ,
,
где
![]() полный,
полный,
активный и реактивный токи в ЛЕП;
P, Q, S
– активная, реактивная и полная
мощности в начале или конце ЛЕП;
U– линейное напряжение в начале или
конце ЛЕП;
R
– активное сопротивление одной
фазы ЛЕП.
Потери активной
мощности в проводимостях ЛЕП обусловлены
несовершенством изоляции. В воздушных
ЛЕП – появлением короны и, в очень
незначительной степени, утечкой тока
по изоляторам. В кабельных ЛЕП –
появлением тока проводимости а его
абсорбции. Рассчитываются потери по
формуле:
![]() ,
,
где U– линейное напряжение в начале или
конце ЛЕП;
G
– активная проводимость ЛЕП.
При проектировании
воздушных ЛЕП потери мощности на корону
стремятся свести к нулю, выбирая такой
диаметр провода, когда возможность
возникновения короны практически
отсутствует.
Потери реактивной
мощности на участке ЛЕП обусловлены
индуктивными сопротивлениями проводов
и кабелей. Реактивная мощность, теряемая
в трехфазной ЛЕП, рассчитывается
аналогично мощности, теряемой в активных
сопротивлениях:
![]()
Генерируемая
емкостной проводимостью зарядная
мощность ЛЕП рассчитывается по формуле:
![]() ,
,
где U– линейное напряжение в начале или
конце ЛЕП;
B
– реактивная проводимость ЛЕП.
Зарядная мощность
уменьшает реактивную нагрузку сети и
тем самым снижает потери мощности в
ней.
Расчет потерь мощности в леп с равномерно распределенной нагрузкой
В линиях местных
сетей (![]() )
)
потребители одинаковой мощности могут
располагаться на одинаковом расстоянии
друг от друга (например, источники
света). Такие ЛЕП называются линиями с
равномерно распределенной нагрузкой
(см. рис. 7.2).
В равномерно
нагруженной линии трехфазного переменного
тока длиной L
с суммарной токовой нагрузкойIплотность тока на единицу длины составитI/L. При погонном
активном сопротивленииr0
потери активной мощности составят:
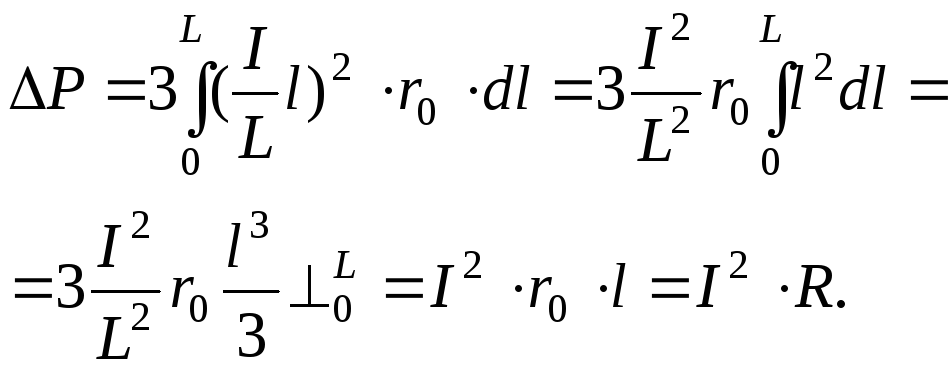
Если бы нагрузка
была сосредоточена в конце, то потери
мощности определялись бы как:
![]() .
.
Сравнивая приведенные
выражения, видим, что потери мощности
в линии с равномерно распределенной
нагрузкой в 3 раза меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Потери мощности в трансформаторе определяются по формулам:
потери активной мощности![]()
потери реактивной мощности![]()
где ![]() — потери холостого хода трансформатора (потери в стали), квт;
— потери холостого хода трансформатора (потери в стали), квт;![]() — потери к. з. трансформатора (потери в обмотках) при номинальной нагрузке, квт;
— потери к. з. трансформатора (потери в обмотках) при номинальной нагрузке, квт;![]() — ток холостого хода трансформатора, %;
— ток холостого хода трансформатора, %;![]() — падение напряжения в реактивном сопротивлении трансформатора, %;
— падение напряжения в реактивном сопротивлении трансформатора, %;![]() — номинальная мощность трансформатора, ква;
— номинальная мощность трансформатора, ква;![]() — коэффициент загрузки трансформатора;
— коэффициент загрузки трансформатора;![]()
где S — фактическая нагрузка трансформатора, ква.
Формула (9-4) для определения потерь реактивной мощности в трансформаторе может быть представлена в виде:
![]()
где ![]() — потери реактивной мощности в трансформаторе при холостом ходе (потери на намагничивание), квар:
— потери реактивной мощности в трансформаторе при холостом ходе (потери на намагничивание), квар:
![]()
![]() — потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке, квар:
— потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке, квар:![]()
Падение напряжения в реактивном сопротивлении трансформатора определяется по формуле
![]()
где Uк — напряжение к. з. трансформатора, %;
Ur — падение напряжения в активном сопротивлении трансформатора, определяемое из выражения
![]()
Для трансформаторов мощностью более 10 Мва можно принять
![]()
Некоторые значения величин ![]() для понижающих трансформаторов приведены в табл. 9-2. В табл. 9-2 уровень Б потерь активной мощности холостого хода относится к трансформаторам, в которых использована электротехническая сталь толщиной 0,35 мм марки Э 330 А по ГОСТ 802-58 с жаростойким покрытием и отжигом пластин. В табл. 9-2 даны значения активных и реактивных сопротивлений трансформаторов, приведенные по отношению к номинальному напряжению обмотки ВН.
для понижающих трансформаторов приведены в табл. 9-2. В табл. 9-2 уровень Б потерь активной мощности холостого хода относится к трансформаторам, в которых использована электротехническая сталь толщиной 0,35 мм марки Э 330 А по ГОСТ 802-58 с жаростойким покрытием и отжигом пластин. В табл. 9-2 даны значения активных и реактивных сопротивлений трансформаторов, приведенные по отношению к номинальному напряжению обмотки ВН.
| Таблица 9-2 Технические данные трехфазных двухобмоточных силовых масляных трансформаторов общего назначения (ГОСТ 12022-66) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Номинальная мощность, ква | Верхний предел номиналього напряжения обмотки, кв | Схема и группа соединений обмоток | Потери активной мощности, квт | Напряжение к.з., % | Ток холостого хода | Сопротивления обмоток трансформатора, ом | Потери реактивной мощности, квар | ||||
| холостого хода | к.з. | ||||||||||
| уровень А | уровень Б | активное | реактивное | холостого хода | к.з. | ||||||
| 25 | 10 10 |
У/Ун-0 У/Zн-11 |
0,105 0,105 |
0,125 0,125 |
0,6 0,69 |
4,5 4,7 |
3,2 3,2 |
96,0 110 |
152 152 |
0,80 0,80 |
0,95 0,95 |
| 40 | 10 10 |
У/Ун-0 У/Zн-11 |
0,15 0,15 |
0,18 0,18 |
0,88 1,0 |
4,5 4,7 |
3,0 3,0 |
55,0 62,5 |
98,1 99,5 |
1,20 1,20 |
1,57 1,59 |
| 63 | 10 10 20 20 |
У/Ун-о У/Zн-11 У/Ун-0 У/Zн-11 |
0,22 0,22 0,245 0,245 |
0,265 0,265 0,29 0,29 |
1,28 1,47 1,28 1,47 |
4,5 4,7 5,0 5,3 |
2,8 2,8 2,8 2,8 |
32,3 37,0 129 148 |
63,7 64,8 290 302 |
1,76 1,76 1,76 1,76 |
2,53 2,57 2,88 3,00 |
| 100 | 10 10 35 35 |
У/Ун-0 У/Zн-11 У/Ун-0 У/Zн-11 |
0,31 0,31 0,39 0,39 |
0,365 0,365 0,465 0,465 |
1,97 2,27 1,97 2,27 |
4,5 4,7 6,5 6,8 |
2,6 2,6 2,6 2,6 |
19,7 22,7 241 278 |
40,5 41,2 759 785 |
2,60 2,60 2,60 2,60 |
4,05 4,12 6,19 6,41 |
| 160 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,46 0,46 0,46 0,56 0,56 0,56 |
0,54 0,54 0,54 0,66 0,66 0,66 |
2,65 2,65 3,1 2,65 2,65 3,1 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,4 2,4 2,4 2,4 2,4 2,4 |
10,4 10,4 12,1 127 127 148 |
26,2 26,2 26,8 481 481 499 |
3,84 3,84 3,84 3,84 3,84 3,84 |
6,69 6,69 6,85 10,1 10,1 10,4 |
| 250 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,66 0,66 0,66 0,82 0,82 0,82 |
0,78 0,78 0,78 0,96 0,96 0,96 |
3,7 3,7 4,2 3,7 3,7 4,2 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,3 2,3 2,3 2,3 2,3 2,3 |
5,92 5,92 6,72 72,5 72,5 82,3 |
17,0 17,0 17,6 310 310 322 |
7,25 5,75 5,75 5,75 5,75 5,75 |
10,6 10,6 11,0 15,8 15,8 16,5 |
| 400 | 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Д-11 |
0,62 0,92 0,92 1,15 1,15 |
1,08 1,08 1,08 1,35 1,35 |
5,5 5,5 5,9 5,5 5,5 |
4,5 4,5 4,5 6,5 6,5 |
2,1 2,1 2,1 2,1 2,1 |
3,44 3,44 3,69 42,1 42,1 |
10,7 10,7 10,6 195 195 |
8,40 8,40 8,40 8,40 8,40 |
17,1 17,1 17,0 25,4 25,4 |
| 630 | 10 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Ун-0 У/Д-11 |
1,42 1,42 1,42 1,42 1,7 1,7 |
1,68 1,68 1,68 1,68 2,0 2,0 |
7,6 7,6 8,5 8,5 7,6 7,6 |
5,5 5,5 5,5 5,5 6,5 6,5 |
2,0 2,0 2,0 2,0 2,0 2,0 |
1,91 1,91 2,14 2,14 23,5 23,5 |
8,52 8,52 8,46 8,46 124 124 |
12,6 12,6 12,6 12,6 12,6 12,6 |
33,8 33,8 33,6 33,6 40,2 40,2 |
Для других номинальных напряжений обмоток сопротивления пересчитываются по формулам:
где Uн — номинальное напряжение обмотки, указанное в табл. 9-2, кв;![]() — номинальное напряжение обмотки, по отношению к которому пересчитываются сопротивления, кв;
— номинальное напряжение обмотки, по отношению к которому пересчитываются сопротивления, кв;
R и X — соответственно активное и реактивное сопротивления трансформатора, определяемые по табл. 9-2, ом.
Потери электроэнергии в сети определяются по формуле
![]()
где ![]() — наибольшие потери мощности в сети, кет;
— наибольшие потери мощности в сети, кет;![]() — число часов максимальных потерь, определенное в зависимости от годового графика нагрузки.
— число часов максимальных потерь, определенное в зависимости от годового графика нагрузки.
Потери электроэнергии в трансформаторе определяются по формуле
![]()
где tТ — число часов работы трансформатора.
Число часов максимальных потерь, если известен годовой график нагрузки, может быть определено по формуле
![]()
где ![]() — сумма произведений квадратов полных нагрузок на годовую продолжительность каждой из них, вычисленная для всего годового графика нагрузок рассматриваемого элемента сети;
— сумма произведений квадратов полных нагрузок на годовую продолжительность каждой из них, вычисленная для всего годового графика нагрузок рассматриваемого элемента сети;
Sб — наибольшая полная нагрузка элемента сети. Для типичного графика, имеющего сниженные нагрузки ночью и утренний и вечерний максимумы, число часов максимальных потерь согласно в зависимости от числа часов использования максимума может определяться по табл. 9-7.
| Таблица 9-7 Число часов максимальных потерь | |||||
|---|---|---|---|---|---|
| Число часов использования максимума | 3000 | 3500 | 4000 | 4500 | 5000 |
| Число часов максимальных потерь | 1300 | 1650 | 2000 | 2500 | 3000 |
| Число часов использования максимума | 5500 | 6000 | 6500 | 7000 | 7500 |
| Число часов максимальных потерь | 3650 | 4300 | 5000 | 5700 | 6450 |
Пример 9-1.
Определить годовые потери электроэнергии в трансформаторе типа ТМ мощностью 6,3 Мва с напряжением высшей стороны 10 кв, если трансформатор включен постоянно и годовой график его нагрузки представлен на рис. 9-1.
Решение.
Годовые потери электроэнергии в трансформаторе определяем по (9-10).
По справочным данным находим потери активной мощности в трансформаторе при холостом ходе для уровня Б: ΔРс=9 квт
и нагрузочные потери (потери к. з.) при номинальной нагрузке трансформатора: ΔРк.з=46,5 квт
По условию примера годовое число часов работы трансформатора tТ = 8 760.
Коэффициент загрузки трансформатора при наибольшей нагрузке составляет:![]()
Число часов максимальных потерь определяем из графика на рис. 9-1, подставив в (9-11) значения нагрузок трансформатора в мегавольт-амперах и соответствующие им продолжительности работы в тысячах часов:
![]()
Подставив числовые значения в (9-10), определим годовые потери энергии в трансформаторе:
![]()

Рис. 9-1.
Годовой график нагрузки
Пример 9-2.
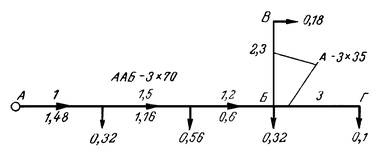
На рис. 9-2 представлена схема линии 6 кв с указанием длин участков линии (км) и расчетных (наибольших) нагрузок (Мва). Магистраль АБ выполнена кабелем с алюминиевыми жилами сечением 3X70 мм.кв, а ответвления БВ и БГ — воздушной линией с алюминиевыми проводами сечением 35 мм.кв.
Определить годовые потери электроэнергии в сопротивлениях проводов и кабелей линии, если годовая продолжительность использования максимума нагрузок составляет 3000 ч и график нагрузок является типичным (имеются утренний и вечерний максимумы и снижение нагрузки в ночное время).
Решение.
Наибольшие потери мощности в сопротивлениях проводов и кабелей линии находим по (9-1), в которой значение коэффициента определяется из табл. 9-1:![]()
Удельные сопротивления участков линии находим по табл. 5-1: для алюминиевого кабеля сечением 70 мм.кв — 0,46 ом/км; для алюминиевого провода сечением 35 мм.кв — 0,92 ом/км.
Определяем значение величины N для магистрали АБ:
![]()
для ответвлений БВ и БГ
![]()
Из (9-1) находим наибольшие потери мощности в сети:
![]()
По табл. 9-7 в зависимости от продолжительности использования максимума Т=3000 ч находим значение числа часов максимальных потерь τ=1300. Величину потерь электроэнергии определяем по (9-9):
![]()
Содержание
- Расчёт потерь напряжения в кабеле
- Доступна Windows-версия программы расчёта потерь напряжения
- Пояснения к расчёту
- Последствия при падении напряжения по длине кабеля и расчет потерь
- Результат понижения напряжения
- Причины падения напряжения
- Расчет с применением формулы
- Проведение сложных расчетов
- Использование готовых таблиц
- Применение сервис-калькулятора
- Как сократить потери
Расчёт потерь напряжения в кабеле
Потеря напряжения в кабеле — величина, равная разности между установившимися значениями действующего напряжения, измеренными в двух точках системы электроснабжения (по ГОСТ 23875-88). Этот параметр необходимо знать при производстве любых электромонтажных работ — начиная от видеонаблюдения и ОПС и заканчивая системами электроснабжения промышленных объектов.
При равенстве сопротивлений Zп 1 =Zп 2 =Zп 3 и Zн 1 =Zн 2 =Zн 3 ток в нулевом проводе отсутствует (Рис.1), поэтому для трёхфазных линий потери напряжения рассчитываются для одного проводника.
В двух- и однофазных линиях, а также в цепи постоянного тока, ток идёт по двум проводникам (Рис.2), поэтому вводится коэффициент 2 (при условии равенства Zп 1 =Zп 2 ).
Доступна Windows-версия программы расчёта потерь напряжения
Пояснения к расчёту
Расчёт потерь линейного (между фазами) напряжения в кабеле при трёхфазном переменном токе производится по формулам:
Расчёт потерь фазного (между фазой и нулевым проводом) напряжения в кабеле производится по формулам:
Для расчёта потерь линейного напряжения U=380 В; 3 фазы.
Для расчёта потерь фазного напряжения U=220 В; 1 фаза.
P — активная мощность передаваемая по линии, Вт;
Q — реактивная мощность передаваемая по линии, ВАр;
R — удельное активное сопротивление кабельной линии, Ом/м;
X — удельное индуктивное сопротивление кабельной линии, Ом/м;
L — длина кабельной линии, м;
Uл — линейное напряжение сети, В;
Uф — фазное напряжение сети, В.
Пожелания, замечания, рекомендации по улучшению раздела расчётов на нашем сайте просьба присылать по электронной почте support@ivtechno.ru
Разрешается копирование java-скриптов при условии ссылки на источник.
Источник
Последствия при падении напряжения по длине кабеля и расчет потерь
Линии электропередач транспортируют ток от распределительного устройства к конечному потребителю по токоведущим жилам различной протяженности. В точке входа и выхода напряжение будет неодинаковым из-за потерь, возникающих в результате большой длины проводника.
Падение напряжения по длине кабеля возникает по причине прохождения высокого тока, вызывающего увеличение сопротивления проводника.
На линиях значительной протяженности потери будут выше, чем при прохождении тока по коротким проводникам такого же сечения. Чтобы обеспечить подачу на конечный объект тока требуемого напряжения, нужно рассчитывать монтаж линий с учетом потерь в токоведущем кабеле, отталкиваясь от длины проводника.

Результат понижения напряжения
Согласно нормативным документам, потери на линии от трансформатора до наиболее удаленного энергонагруженного участка для жилых и общественных объектов должны составлять не более девяти процентов.
Допускаются потери 5 % до главного ввода, а 4 % — от ввода до конечного потребителя. Для трехфазных сетей на три или четыре провода номинальное значение должно составлять 400 В ± 10 % при нормальных условиях эксплуатации.
Отклонение параметра от нормированного значения может иметь следующие последствия:
- Некорректная работа энергозависимых установок, оборудования, осветительных приборов.
- Отказ работы электроприборов при сниженном показателе напряжения на входе, выход оборудования из строя.
- Снижение ускорения вращающего момента электродвигателей при пусковом токе, потери учитываемой энергии, отключение двигателей при перегреве.
- Неравномерное распределение токовой нагрузки между потребителями на начале линии и на удаленном конце протяженного провода.
- Работа осветительных приборов на половину накала, за счет чего происходят недоиспользование мощности тока в сети, потери электроэнергии.

В рабочем режиме наиболее приемлемым показателем потерь напряжения в кабеле считается 5 %. Это оптимальное расчетное значение, которое можно принимать допустимым для электросетей, поскольку в энергетической отрасли токи огромной мощности транспортируются на большие расстояния.
К характеристикам линий электропередач предъявляются повышенные требования. Важно уделять особое внимание потерям напряжения не только на магистральных сетях, но и на линиях вторичного назначения.
Причины падения напряжения
Каждому электромеханику известно, что кабель состоит из проводников — на практике используются жилы с медными или алюминиевыми сердечниками, обмотанные изоляционным материалом. Провод помещен в герметичную полимерную оболочку — диэлектрический корпус.
Поскольку металлические проводники расположены в кабеле слишком плотно, дополнительно прижаты слоями изоляции, при большой протяженности электромагистрали металлические сердечники начинают работать по принципу конденсатора, создающего заряд с емкостным сопротивлением.

Падение напряжения происходит по следующей схеме:
- Проводник, по которому пущен ток, перегревается и создает емкостное сопротивление как часть реактивного сопротивления.
- Под воздействием преобразований, протекающих на обмотках трансформаторов, реакторах, прочих элементах цепи, мощность электроэнергии становится индуктивной.
- В результате резистивное сопротивление металлических жил преобразуется в активное сопротивление каждой фазы электрической цепи.
- Кабель подключают на токовую нагрузку с полным (комплексным) сопротивлением по каждой токоведущей жиле.
- При эксплуатации кабеля по трехфазной схеме три линии тока в трех фазах будут симметричными, а нейтральная жила пропускает ток, приближенный к нулю.
- Комплексное сопротивление проводников приводит к потерям напряжения в кабеле при прохождении тока с векторным отклонением за счет реактивной составляющей.
Графически схему падения напряжения можно представить следующим образом: из одной точки выходит прямая горизонтальная линия — вектор силы тока. Из этой же точки выходит под углом к силе тока вектор входного значения напряжения U1 и вектор выходного напряжения U2 под меньшим углом. Тогда падение напряжения по линии равно геометрической разнице векторов U1 и U2.
Рисунок 1. Графическое изображение падения напряжения

На представленном рисунке прямоугольный треугольник ABC отражает падение и потери напряжения на линии кабеля большой длины. Отрезок AB — гипотенуза прямоугольного треугольника и одновременно падение, катеты AC и BC показывают падение напряжения с учетом активного и реактивного сопротивления, а отрезок AD демонстрирует величину потерь.
Производить подобные расчеты вручную довольно сложно. График служит для наглядного представления процессов, протекающих в электрической цепи большой протяженности при прохождении тока заданной нагрузки.
Расчет с применением формулы
На практике при монтаже линий электропередач магистрального типа и отведения кабелей к конечному потребителю с дальнейшей разводкой на объекте используется медный или алюминиевый кабель.
Удельное сопротивление для проводников постоянное, составляет для меди р = 0,0175 Ом*мм2/м, для алюминиевых жил р = 0,028 Ом*мм2/м.
Зная сопротивление и силу тока, несложно вычислить напряжение по формуле U = RI и формуле R = р*l/S, где используются следующие величины:
- Удельное сопротивление провода — p.
- Длина токопроводящего кабеля — l.
- Площадь сечения проводника — S.
- Сила тока нагрузки в амперах — I.
- Сопротивление проводника — R.
- Напряжение в электрической цепи — U.
Использование простых формул на несложном примере: запланировано установить несколько розеток в отдельно стоящей пристройке частного дома. Для монтажа выбран медный проводник сечением 1,5 кв. мм, хотя для алюминиевого кабеля суть расчетов не изменяется.

Поскольку ток по проводам проходит туда и обратно, нужно учесть, что расстояние длины кабеля придется умножать вдвое. Если предположить, что розетки будут установлены в сорока метрах от дома, а максимальная мощность устройств составляет 4 кВт при силе тока в 16 А, то по формуле несложно сделать расчет потерь напряжения:
Если сравнить полученное значение с номинальным для однофазной линии 220 В 50 Гц, получается, что потери напряжения составили: 220-14,93 = 205,07 В.
Такие потери в 14,93 В — это практически 6,8 % от входного (номинального) напряжения в сети. Значение, недопустимое для силовой группы розеток и осветительных приборов, потери будут заметны: розетки будут пропускать ток неполной мощности, а осветительные приборы — работать с меньшим накалом.
Мощность на нагрев проводника составит P = UI = 14,93*16 = 238,9 Вт. Это процент потерь в теории без учета падения напряжения на местах соединения проводов, контактах розеточной группы.

Проведение сложных расчетов
Для более детального и достоверного расчета потерь напряжения на линии нужно принимать во внимание реактивное и активное сопротивление, которое вместе образует комплексное сопротивление, и мощность.
Для проведения расчетов падения напряжения в кабеле используют формулу:
∆U = (P*r0+Q*x0)*L/ U ном
В этой формуле указаны следующие величины:
- P, Q — активная, реактивная мощность.
- r0, x0 — активное, реактивное сопротивление.
- U ном — номинальное напряжение.
Чтобы обеспечить оптимальную нагрузку по трехфазных линиям передач, необходимо нагружать их равномерно. Для этого силовые электродвигатели целесообразно подключать к линейным проводам, а питание на осветительные приборы — между фазами и нейтральной линией.
Есть три варианта подключения нагрузки:
- от электрощита в конец линии;
- от электрощита с равномерным распределением по длине кабеля;
- от электрощита к двум совмещенным линиям с равномерным распределением нагрузки.

Пример расчета потерь напряжения: суммарная потребляемая мощность всех энергозависимых установок в доме, квартире составляет 3,5 кВт — среднее значение при небольшом количестве мощных электроприборов. Если все нагрузки активные (все приборы включены в сеть), cosφ = 1 (угол между вектором силы тока и вектором напряжения). Используя формулу I = P/(Ucosφ), получают силу тока I = 3,5*1000/220 = 15,9 А.
Дальнейшие расчеты: если использовать медный кабель сечением 1,5 кв. мм, удельное сопротивление 0,0175 Ом*мм2, а длина двухжильного кабеля для разводки равна 30 метров.
По формуле потери напряжения составляют:
∆U = I*R/U*100 %, где сила тока равна 15,9 А, сопротивление составляет 2 (две жилы)*0,0175*30/1,5 = 0,7 Ом. Тогда ∆U = 15,9*0,7/220*100% = 5,06 %.
Полученное значение незначительно превышает рекомендуемое нормативными документами падение в пять процентов. В принципе, можно оставить схему такого подключения, но если на основные величины формулы повлияет неучтенный фактор, потери будут превышать допустимое значение.
Что это значит для конечного потребителя? Оплата за использованную электроэнергию, поступающую к распределительному щиту с полной мощностью при фактическом потреблении электроэнергии более низкого напряжения.

Использование готовых таблиц
Как домашнему мастеру или специалисту упростить систему расчетов при определении потерь напряжения по длине кабеля? Можно пользоваться специальными таблицами, приведенными в узкоспециализированной литературе для инженеров ЛЭП. Таблицы рассчитаны по двум основным параметрам — длина кабеля в 1000 м и величина тока в 1 А.
В качестве примера представлена таблица с готовыми расчетами для однофазных и трехфазных электрических силовых и осветительных цепей из меди и алюминия с разным сечением от 1,5 до 70 кв. мм при подаче питания на электродвигатель.
Таблица 1. Определение потерь напряжения по длине кабеля
| Площадь сечения, мм2 | Линия с одной фазой | Линия с тремя фазами | |||||
|---|---|---|---|---|---|---|---|
| Питание | Освещение | Питание | Освещение | ||||
| Режим | Пуск | Режим | Пуск | ||||
| Медь | Алюминий | Косинус фазового угла = 0,8 | Косинус фазового угла = 0,35 | Косинус фазового угла = 1 | Косинус фазового угла = 0,8 | Косинус фазового угла = 0,35 | Косинус фазового угла = 1 |
| 1,5 | 24,0 | 10,6 | 30,0 | 20,0 | 9,4 | 25,0 | |
| 2,5 | 14,4 | 6,4 | 18,0 | 12,0 | 5,7 | 15,0 | |
| 4,0 | 9,1 | 4,1 | 11,2 | 8,0 | 3,6 | 9,5 | |
| 6,0 | 10,0 | 6,1 | 2,9 | 7,5 | 5,3 | 2,5 | 6,2 |
| 10,0 | 16,0 | 3,7 | 1,7 | 4,5 | 3,2 | 1,5 | 3,6 |
| 16,0 | 25,0 | 2,36 | 1,15 | 2,8 | 2,05 | 1,0 | 2,4 |
| 25,0 | 35,0 | 1,5 | 0,75 | 1,8 | 1,3 | 0,65 | 1,5 |
| 35,0 | 50,0 | 1,15 | 0,6 | 1,29 | 1,0 | 0,52 | 1,1 |
| 50,0 | 70,0 | 0,86 | 0,47 | 0,95 | 0,75 | 0,41 | 0,77 |
Таблицы удобно использовать для расчетов при проектировании линий электропередач. Пример расчетов: двигатель работает с номинальной силой тока 100 А, но при запуске требуется сила тока 500 А. При нормальном режиме работы cos ȹ составляет 0,8, а на момент пуска значение равно 0,35. Электрический щит распределяет ток 1000 А. Потери напряжения рассчитывают по формуле ∆U% = 100∆U/U номинальное.
Двигатель рассчитан на высокую мощность, поэтому рационально использовать для подключения провод с сечением 35 кв. мм, для трехфазной цепи в обычном режиме работы двигателя потери напряжения равны 1 вольт по длине провода 1 км. Если длина провода меньше (к примеру, 50 метров), сила тока равна 100 А, то потери напряжения достигнут:
∆U = 1 В*0,05 км*100А = 5 В
Потери на распределительном щите при запуске двигателя равны 10 В. Суммарное падение 5 + 10 = 15 В, что в процентном отношении от номинального значения составляет 100*15*/400 = 3,75 %. Полученное число не превышает допустимое значение, поэтому монтаж такой силовой линии вполне реальный.

На момент пуска двигателя сила тока должна составлять 500 А, а при рабочем режиме — 100 А, разница равна 400 А, на которые увеличивается ток в распределительном щите. 1000 + 400 = 1400 А. В таблице 1 указано, что при пуске двигателя потери по длине кабеля 1 км равны 0,52 В, тогда
∆U при запуске = 0,52*0,05*500 = 13 В
∆U щита = 10*1400/100 = 14 В
∆U суммарные = 13+14 = 27 В, в процентном отношении ∆U = 27/400*100 = 6,75 % — допустимое значение, не превышает максимальную величину 8 %. С учетом всех параметров монтаж силовой линии приемлем.
Применение сервис-калькулятора
Расчеты, таблицы, графики, диаграммы — точные инструменты для вычисления падения напряжения по длине кабеля. Упростить работу можно, если выполнить расчеты с помощью онлайн-калькулятора. Преимущества очевидны, но стоит проверить данные на нескольких ресурсах и отталкиваться от среднего полученного значения.

Как это работает:
- Онлайн-калькулятор разработан для быстрого выполнения расчетов на основе исходных данных.
- В калькулятор нужно ввести следующие величины — ток (переменный, постоянный), проводник (медь, алюминий), длина линии, сечение кабеля.
- Обязательно вводят параметры по количеству фаз, мощности, напряжению сети, коэффициенту мощности, температуре эксплуатации линии.
- После введения исходных данных программа определяет падение напряжения по линии кабеля с максимальной точностью.
- Недостоверный результат можно получить при ошибочном введении исходных величин.
Пользоваться такой системой можно для проведения предварительных расчетов, поскольку сервис-калькуляторы на различных ресурсах показывают не всегда одинаковый результат: итог зависит от грамотной реализации программы с учетом множества факторов.
Тем не менее, можно провести расчеты на трех калькуляторах, взять среднее значение и отталкиваться от него на стадии предварительного проектирования.

Как сократить потери
Очевидно, что чем длиннее кабель на линии, тем больше сопротивление проводника при прохождении тока и, соответственно, выше потери напряжения.
Есть несколько способов сократить процент потерь, которые можно использовать как самостоятельно, так и комплексно:
- Использовать кабель большего сечения, проводить расчеты применительно к другому проводнику. Увеличение площади сечения токоведущих жил можно получить при соединении двух проводов параллельно. Суммарная площадь сечения увеличится, нагрузка распределится равномерно, потери напряжения станут ниже.
- Уменьшить рабочую длину проводника. Метод эффективный, но его не всегда можно использовать. Сократить длину кабеля можно при наличии резервной длины проводника. На высокотехнологичных предприятиях вполне реально рассмотреть вариант перекладки кабеля, если затраты на трудоемкий процесс гораздо ниже, чем расходы на монтаж новой линии с большим сечением жил.
- Сократить мощность тока, передаваемую по кабелю большой протяженности. Для этого можно отключить от линии несколько потребителей и подключить их по обходной цепи. Данный метод применим на хорошо разветвленных сетях с наличием резервных магистралей. Чем ниже мощность, передаваемая по кабелю, тем меньше греется проводник, снижаются сопротивление и потери напряжения.
Внимание! При эксплуатации кабеля в условиях повышенной температуры проводник нагревается, падение напряжения растет. Сократить потери можно при использовании дополнительной теплоизоляции или прокладке кабеля по другой магистрали, где температурный показатель существенно ниже.
Расчет потерь напряжения — одна из главных задач энергетической отрасли. Если для конечного потребителя падение напряжения на линии и потери электроэнергии будут практически незаметными, то для крупных предприятий и организаций, занимающихся подачей электроэнергии на объекты, они впечатляющие. Снизить падение напряжения можно, если правильно выполнить все расчеты.
Источник
Многие СНТ, оплачивающие электроэнергию по общему счётчику, стоят перед вопросом, а не слишком ли много потерь во внутренней электросети им приходится оплачивать? Может, приходится оплачивать не только технологические потери, но и воровство ушлых соседей?
Потери вполне можно оценить расчётом, и сейчас я расскажу, как это сделать. Существует несколько методов теоретического расчёта. Наиболее простым и доступным для широкого круга потребителей мне видится метод расчёта по формулам, изложенным в книге Ю.С. Железко, А.В. Артемьев, О.В. Савченко «Расчёт, анализ и нормирование потерь электроэнергии в электрических сетях», Москва, ЗАО «Издательство НЦЭНАС», 2008 (приложение 2). Его и рассмотрим в этой статье.
О расчёте потерь в однофазных отводах и линиях я рассказывал в предыдущей статье. Сейчас я расскажу о том, как правильно оценить потери в трёхфазных магистральных линиях и трёхфазных отводах. Как и в прошлый раз, расчёт будет включать в себя 4 этапа.
Расчёт сопротивления провода
Сначала посчитаем сопротивление провода (Ом/м) по формуле:
Предположим, магистральная линия селана СИПом сечением 35 мм². СИП — алюминиевый провод. Итого получаем 0,0287 / 35 = 0,00082 Ом/м.
При желании в удельное сопротивление материала провода можно ввести поправку на его температуру под нагрузкой. В данном случае взято сопротивление материала при 20°С.
Расчёт эквивалентного сопротивления линии
Поскольку магистральные линии имеют распределённую нагрузку, то рассчитывается не настоящее сопротивление линии, а эквивалентное, учитывающее эту неравномерность:
Предположим, длина магистральной линии от трансформатора до последней опоры равна 340 метров. Пусть коэффициент распределения нагрузки будет 2,5 (трансформатор стоит чуть в стороне, и от него до первого отвода есть метров 80-90).
Таким образом, эквивалентное сопротивление такой линии будет:
0,00082 * 340 / 2,5 = 0,112 Ом
Замечу, что для трёхфазной линии мы рассчитываем сопротивление только одного провода, а не суммируем длины всех четырёх проводов. Эти особенности учтены в последующих формулах расчёта.
Расчёт квадрата коэффициента формы графика нагрузки
Квадрат коэффициента формы графика нагрузки — это промежуточный параметр, который также потребуется нам в итоговой расчётной формуле.
При отсутствии исходных данных о коэффициенте заполнения графика нагрузки, в промышленных сетях допускается использовать коэффициент 0,5. Однако в СНТ ввиду сезонного и других факторов этот коэффициент может достигать значений 0,1 и даже менее (низкая плотность, высокие нагрузки).
В нашем случае используем коэффициент 0,2. Тогда квадрат коэффициента будет равен (1 + 2 * 0,2) / (3 * 0,3) = 2,33.
Расчёт потерь за расчётный период
Теперь осталось посчитать потери за расчётный период (Вт*ч):
Давайте посчитаем годовые потери в магистральной линии. Пусть годовое потребление по этой линии равно 51000 кВт*ч, а коэффициент мощности в сети 0,9 (при этом tg φ = 0,48):
(51000² * (1 + 0,48²) * 2,33) / (24 * 365 * 0,4²) * 0,112 = 600 кВт*ч
600 кВт*ч — это 1,2% от годового потребления 51000 кВт*ч (600 / 51000 * 100).
Таким образом, потери в магистральной линии составляют 1,2% от электроэнергии, отданной в неё.
Заключение
Внимание! Никакой теоретический расчёт, конечно, не может являться точным. Он может быть лишь оценочным, для приблизительного представления самого порядка технологических потерь.
Повысить точность расчёта можно, например, введя температурную поправку на удельное сопротивление материала провода в связи с его повышенной температурой при работе под нагрузкой. Также можно более точно подогнать коэффициент заполнения графика нагрузок именно под ваше СНТ, хотя это не всегда осуществимо.
Для облегчения расчётов мною написана специальная программа под Windows для расчёта электропотерь:
Скачать её можно с официальной страницы:
http://макс.мск.рус/products/losses/losses.html
На последней вкладке имеется подробная встроенная справка. Также в программе можно произвести расчёт потерь в однофазных отводах (вторая вкладка). На третьей вкладке имеется калькулятор эквивалентной длины провода. Надеюсь, программа окажется вам полезной.
Спасибо за то, что дочитали статью до конца. Если вы посчитаете информацию полезной, отметьте её, пожалуйста, лайком! Напишите свои мысли в комментариях. Подписывайтесь на мой канал. Спасибо и удачи!
