В
электрических сетях следует различать
падение
напряжения и потери
напряжения.
ПС-1
ПС-2

![]()
![]()
I
Раз
протекает ток, то имеет место падение
напряжения
![]()
![]()
,
где
Zл
– сопротивление линии

I Rл
Xл
Iном
![]()
![]()
В
комплексной форме фазное напряжение в
конце линии
![]()
Где
ΔUФ
– падение напряжения в линии. Аналогично
можно записать для линейных напряжений
![]()
.
Чаще
всего в сетях 6, 10, 35, 110 кВ углы между
![]()
– единицы градусов.
Пользоваться
комплексной записью падения напряжения
неудобно. Тем более что при эксплуатации
интерес представляет не комплексы
напряжений. а их действующие значения.
Поэтому удобнее определять напряжение
в конце линии не в комплексной форме. а
в арифметической форме
U2
=Г1–
ΔU/
Где
ΔU
– называют потеря напряжения.
Таким
образом, потеря напряжения в линии ΔU-
это арифметическая разность напряжений
в начале и в конце линии
ΔU=
Г1–
U2.
Найдем
выражение для потери напряжения через
ток и сопротивления линии. Построим
упрощенную векторную диаграмму. За
основу возьмем напряжение в конце линии
.
Тогда
![]()
.
По этому уравнению
построим диаграмму:
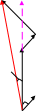
U1
![]()
U2
![]()
I
Ток
отстает от напряжения на какой-то угол
.
–
угол нагрузки
![]()
–
угол расхождения по фазе напряжений в
начале и в конце линии.
Для
линий 6, 10, 35 кВ угол
– единицы градусов; для 110 кВ – 15 -20о.
Для
линий до 35 кВ можно принять
=0.
Тогда U1
и U2
будут совпадать по фазе и для потери
напряжения можно записать
![]()
.
Перейдем к линейным
напряжениям и получим
![]()
(1)
или
![]()
,
(2)
где
lл
– длина линии;
Ro
– удельное активное сопротивление на
один км длины;
Xo
– удельное индуктивное сопротивление
на один км длины.
Умножив
и разделив (1) на U,
получим
активная мощность
Р, передаваемая по линии
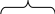
![]()
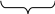
реактивная
мощностьQ,
передаваемая по линии
Т.
о. получаем
![]()
,
где
P
и Q
– расчетные мощности,
U
– напряжение в конце линии.
При
расчетах предполагается, что U
в конце линии равно номинальному
напряжению сети Uном.,.
Как выполнять
проверку линии по потерям напряжения?
Нормативных
требований к потерям напряжения нет.
Нормируется уровень напряжения на
зажимах потребителя
Требования
к
зависят от требований к напряжению и
возможности регулирования напряжения
U1,
т. е.
![]()
f(U2
и регулирование U1).
Предположим,
что мы расчетным путем для заданной
схемы мы нашли допустимую потерю
напряжения
![]()
. Подчеркнем еще раз, что
–
это расчетная величина. Ее нужно
рассчитывать конкретно для каждой сети.
В
практике проектирования и тем более в
учебной практике
часто принимают. При этом лучше принимать
на основании отраслевых документов. Но
можно пользоваться и рекомендациями
справочников или учебной литературы.
Обычно
=5-8%.
Рекомендации
относятся не к линии, а к совокупности,
цепочки линий одного напряжения от шин
приемной подстанции до вводов
электроприемников.
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
 |
Учебник “Онлайн Электрик” | > |  |
Содержание |  Расчет | Пример | Расчет | Пример | Источники | Источники | 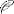 Теория Теория |
Пример расчета потерь напряжения в линии электропередачи
Определить потери напряжения на участках воздушной линии электропередачи
6 кВ. Исходные данные приведены в таблице 1.
Таблица 1
Исходные данные
|
Наименование |
Расчетный ток, А |
Длина, м |
cosφ |
R0, мОм/м |
X0, мОм/м |
|
Участок 1 |
90 |
2000 |
0,94 |
0,329 |
0,4 |
|
Участок 2 |
70 |
1500 |
0,92 |
0,447 |
0,4 |
|
Участок 3 |
45 |
2000 |
0,89 |
0,447 |
0,4 |
Решение:
Потери напряжения в трехфазной линии электропередачи определяется по
формуле:
![]() ,
,
где IР – расчетный ток линии, А; L – длина линии, м; R0 – удельное активное сопротивление линии, мОм/м; X0 – удельное индуктивное сопротивление линии, мОм/м; cos![]() – коэффициент мощности нагрузки; n – число параллельно проложенных
– коэффициент мощности нагрузки; n – число параллельно проложенных
проводников; UНОМ –
номинальное напряжение сети, В.
Подставляя известные данные в формулу, получаем для первого участка ЛЭП:
ΔUР=![]() %.
%.
![]() Результаты
Результаты
расчетов для других участков сведены в таблицу 2.
Таблица 2
Результаты расчета потерь напряжения
на участках ЛЭП
|
Наименование |
ΔU, В |
ΔU, % |
|
Участок 1 |
138,96 |
2,3 |
|
Участок 2 |
103,30 |
1,7 |
|
Участок 3 |
90,45 |
1,5 |
|
Итого по ЛЭП |
332,71 |
5,5 |
[Расчет]
Описание:
В разделе сайта продемонстрирован наглядный пример, в котором содержится наглядный пример расчета потерь напряжения в линии электропередачи.
Ключевые слова:
Пример расчета потерь напряжения в линиях электропередач
| Библиографическая ссылка на ресурс “Онлайн Электрик”: |
|
Алюнов, А.Н. Онлайн Электрик : Интерактивные расчеты систем электроснабжения / А. Н. Алюнов. – Москва : Всероссийский научно-технический информационный центр, 2010. – EDN XXFLYN. |
Линии электропередач транспортируют ток от распределительного устройства к конечному потребителю по токоведущим жилам различной протяженности. В точке входа и выхода напряжение будет неодинаковым из-за потерь, возникающих в результате большой длины проводника.
Падение напряжения по длине кабеля возникает по причине прохождения высокого тока, вызывающего увеличение сопротивления проводника.
На линиях значительной протяженности потери будут выше, чем при прохождении тока по коротким проводникам такого же сечения. Чтобы обеспечить подачу на конечный объект тока требуемого напряжения, нужно рассчитывать монтаж линий с учетом потерь в токоведущем кабеле, отталкиваясь от длины проводника.

Содержание
- Результат понижения напряжения
- Причины падения напряжения
- Расчет с применением формулы
- Проведение сложных расчетов
- Использование готовых таблиц
- Применение сервис-калькулятора
- Как сократить потери
Результат понижения напряжения
Согласно нормативным документам, потери на линии от трансформатора до наиболее удаленного энергонагруженного участка для жилых и общественных объектов должны составлять не более девяти процентов.
Допускаются потери 5 % до главного ввода, а 4 % — от ввода до конечного потребителя. Для трехфазных сетей на три или четыре провода номинальное значение должно составлять 400 В ± 10 % при нормальных условиях эксплуатации.
Отклонение параметра от нормированного значения может иметь следующие последствия:
- Некорректная работа энергозависимых установок, оборудования, осветительных приборов.
- Отказ работы электроприборов при сниженном показателе напряжения на входе, выход оборудования из строя.
- Снижение ускорения вращающего момента электродвигателей при пусковом токе, потери учитываемой энергии, отключение двигателей при перегреве.
- Неравномерное распределение токовой нагрузки между потребителями на начале линии и на удаленном конце протяженного провода.
- Работа осветительных приборов на половину накала, за счет чего происходят недоиспользование мощности тока в сети, потери электроэнергии.

В рабочем режиме наиболее приемлемым показателем потерь напряжения в кабеле считается 5 %. Это оптимальное расчетное значение, которое можно принимать допустимым для электросетей, поскольку в энергетической отрасли токи огромной мощности транспортируются на большие расстояния.
К характеристикам линий электропередач предъявляются повышенные требования. Важно уделять особое внимание потерям напряжения не только на магистральных сетях, но и на линиях вторичного назначения.
Причины падения напряжения
Каждому электромеханику известно, что кабель состоит из проводников — на практике используются жилы с медными или алюминиевыми сердечниками, обмотанные изоляционным материалом. Провод помещен в герметичную полимерную оболочку — диэлектрический корпус.
Поскольку металлические проводники расположены в кабеле слишком плотно, дополнительно прижаты слоями изоляции, при большой протяженности электромагистрали металлические сердечники начинают работать по принципу конденсатора, создающего заряд с емкостным сопротивлением.

Падение напряжения происходит по следующей схеме:
- Проводник, по которому пущен ток, перегревается и создает емкостное сопротивление как часть реактивного сопротивления.
- Под воздействием преобразований, протекающих на обмотках трансформаторов, реакторах, прочих элементах цепи, мощность электроэнергии становится индуктивной.
- В результате резистивное сопротивление металлических жил преобразуется в активное сопротивление каждой фазы электрической цепи.
- Кабель подключают на токовую нагрузку с полным (комплексным) сопротивлением по каждой токоведущей жиле.
- При эксплуатации кабеля по трехфазной схеме три линии тока в трех фазах будут симметричными, а нейтральная жила пропускает ток, приближенный к нулю.
- Комплексное сопротивление проводников приводит к потерям напряжения в кабеле при прохождении тока с векторным отклонением за счет реактивной составляющей.
Графически схему падения напряжения можно представить следующим образом: из одной точки выходит прямая горизонтальная линия — вектор силы тока. Из этой же точки выходит под углом к силе тока вектор входного значения напряжения U1 и вектор выходного напряжения U2 под меньшим углом. Тогда падение напряжения по линии равно геометрической разнице векторов U1 и U2.
Рисунок 1. Графическое изображение падения напряжения

На представленном рисунке прямоугольный треугольник ABC отражает падение и потери напряжения на линии кабеля большой длины. Отрезок AB — гипотенуза прямоугольного треугольника и одновременно падение, катеты AC и BC показывают падение напряжения с учетом активного и реактивного сопротивления, а отрезок AD демонстрирует величину потерь.
Производить подобные расчеты вручную довольно сложно. График служит для наглядного представления процессов, протекающих в электрической цепи большой протяженности при прохождении тока заданной нагрузки.
Расчет с применением формулы
На практике при монтаже линий электропередач магистрального типа и отведения кабелей к конечному потребителю с дальнейшей разводкой на объекте используется медный или алюминиевый кабель.
Удельное сопротивление для проводников постоянное, составляет для меди р = 0,0175 Ом*мм2/м, для алюминиевых жил р = 0,028 Ом*мм2/м.
Зная сопротивление и силу тока, несложно вычислить напряжение по формуле U = RI и формуле R = р*l/S, где используются следующие величины:
- Удельное сопротивление провода — p.
- Длина токопроводящего кабеля — l.
- Площадь сечения проводника — S.
- Сила тока нагрузки в амперах — I.
- Сопротивление проводника — R.
- Напряжение в электрической цепи — U.
Использование простых формул на несложном примере: запланировано установить несколько розеток в отдельно стоящей пристройке частного дома. Для монтажа выбран медный проводник сечением 1,5 кв. мм, хотя для алюминиевого кабеля суть расчетов не изменяется.

Поскольку ток по проводам проходит туда и обратно, нужно учесть, что расстояние длины кабеля придется умножать вдвое. Если предположить, что розетки будут установлены в сорока метрах от дома, а максимальная мощность устройств составляет 4 кВт при силе тока в 16 А, то по формуле несложно сделать расчет потерь напряжения:
U=(р*L*2)/(s*I), где
- p – удельное сопротивление материала жилы кабеля;
- L – длина кабеля;
- s – сечение жилы кабеля;
- I – сила тока в амперах.
Пример расчета:
U = 0,0175*40*2/1,5*16
U = 14,93 В
Если сравнить полученное значение с номинальным для однофазной линии 220 В 50 Гц, получается, что потери напряжения составили: 220-14,93 = 205,07 В.
Такие потери в 14,93 В — это практически 6,8 % от входного (номинального) напряжения в сети. Значение, недопустимое для силовой группы розеток и осветительных приборов, потери будут заметны: розетки будут пропускать ток неполной мощности, а осветительные приборы — работать с меньшим накалом.
Мощность на нагрев проводника составит P = UI = 14,93*16 = 238,9 Вт. Это процент потерь в теории без учета падения напряжения на местах соединения проводов, контактах розеточной группы.

Проведение сложных расчетов
Для более детального и достоверного расчета потерь напряжения на линии нужно принимать во внимание реактивное и активное сопротивление, которое вместе образует комплексное сопротивление, и мощность.
Для проведения расчетов падения напряжения в кабеле используют формулу:
∆U = (P*r0+Q*x0)*L/ U ном
В этой формуле указаны следующие величины:
- P, Q — активная, реактивная мощность.
- r0, x0 — активное, реактивное сопротивление.
- U ном — номинальное напряжение.
Чтобы обеспечить оптимальную нагрузку по трехфазных линиям передач, необходимо нагружать их равномерно. Для этого силовые электродвигатели целесообразно подключать к линейным проводам, а питание на осветительные приборы — между фазами и нейтральной линией.
Есть три варианта подключения нагрузки:
- от электрощита в конец линии;
- от электрощита с равномерным распределением по длине кабеля;
- от электрощита к двум совмещенным линиям с равномерным распределением нагрузки.

Пример расчета потерь напряжения: суммарная потребляемая мощность всех энергозависимых установок в доме, квартире составляет 3,5 кВт — среднее значение при небольшом количестве мощных электроприборов. Если все нагрузки активные (все приборы включены в сеть), cosφ = 1 (угол между вектором силы тока и вектором напряжения). Используя формулу I = P/(Ucosφ), получают силу тока I = 3,5*1000/220 = 15,9 А.
Дальнейшие расчеты: если использовать медный кабель сечением 1,5 кв. мм, удельное сопротивление 0,0175 Ом*мм2, а длина двухжильного кабеля для разводки равна 30 метров.
По формуле потери напряжения составляют:
∆U = I*R/U*100 %, где сила тока равна 15,9 А, сопротивление составляет 2 (две жилы)*0,0175*30/1,5 = 0,7 Ом. Тогда ∆U = 15,9*0,7/220*100% = 5,06 %.
Полученное значение незначительно превышает рекомендуемое нормативными документами падение в пять процентов. В принципе, можно оставить схему такого подключения, но если на основные величины формулы повлияет неучтенный фактор, потери будут превышать допустимое значение.
Что это значит для конечного потребителя? Оплата за использованную электроэнергию, поступающую к распределительному щиту с полной мощностью при фактическом потреблении электроэнергии более низкого напряжения.

Использование готовых таблиц
Как домашнему мастеру или специалисту упростить систему расчетов при определении потерь напряжения по длине кабеля? Можно пользоваться специальными таблицами, приведенными в узкоспециализированной литературе для инженеров ЛЭП. Таблицы рассчитаны по двум основным параметрам — длина кабеля в 1000 м и величина тока в 1 А.
В качестве примера представлена таблица с готовыми расчетами для однофазных и трехфазных электрических силовых и осветительных цепей из меди и алюминия с разным сечением от 1,5 до 70 кв. мм при подаче питания на электродвигатель.
Таблица 1. Определение потерь напряжения по длине кабеля
| Площадь сечения, мм2 | Линия с одной фазой | Линия с тремя фазами | |||||
|---|---|---|---|---|---|---|---|
| Питание | Освещение | Питание | Освещение | ||||
| Режим | Пуск | Режим | Пуск | ||||
| Медь | Алюминий | Косинус фазового угла = 0,8 | Косинус фазового угла = 0,35 | Косинус фазового угла = 1 | Косинус фазового угла = 0,8 | Косинус фазового угла = 0,35 | Косинус фазового угла = 1 |
| 1,5 | 24,0 | 10,6 | 30,0 | 20,0 | 9,4 | 25,0 | |
| 2,5 | 14,4 | 6,4 | 18,0 | 12,0 | 5,7 | 15,0 | |
| 4,0 | 9,1 | 4,1 | 11,2 | 8,0 | 3,6 | 9,5 | |
| 6,0 | 10,0 | 6,1 | 2,9 | 7,5 | 5,3 | 2,5 | 6,2 |
| 10,0 | 16,0 | 3,7 | 1,7 | 4,5 | 3,2 | 1,5 | 3,6 |
| 16,0 | 25,0 | 2,36 | 1,15 | 2,8 | 2,05 | 1,0 | 2,4 |
| 25,0 | 35,0 | 1,5 | 0,75 | 1,8 | 1,3 | 0,65 | 1,5 |
| 35,0 | 50,0 | 1,15 | 0,6 | 1,29 | 1,0 | 0,52 | 1,1 |
| 50,0 | 70,0 | 0,86 | 0,47 | 0,95 | 0,75 | 0,41 | 0,77 |
Таблицы удобно использовать для расчетов при проектировании линий электропередач. Пример расчетов: двигатель работает с номинальной силой тока 100 А, но при запуске требуется сила тока 500 А. При нормальном режиме работы cos ȹ составляет 0,8, а на момент пуска значение равно 0,35. Электрический щит распределяет ток 1000 А. Потери напряжения рассчитывают по формуле ∆U% = 100∆U/U номинальное.
Двигатель рассчитан на высокую мощность, поэтому рационально использовать для подключения провод с сечением 35 кв. мм, для трехфазной цепи в обычном режиме работы двигателя потери напряжения равны 1 вольт по длине провода 1 км. Если длина провода меньше (к примеру, 50 метров), сила тока равна 100 А, то потери напряжения достигнут:
∆U = 1 В*0,05 км*100А = 5 В
Потери на распределительном щите при запуске двигателя равны 10 В. Суммарное падение 5 + 10 = 15 В, что в процентном отношении от номинального значения составляет 100*15*/400 = 3,75 %. Полученное число не превышает допустимое значение, поэтому монтаж такой силовой линии вполне реальный.

На момент пуска двигателя сила тока должна составлять 500 А, а при рабочем режиме — 100 А, разница равна 400 А, на которые увеличивается ток в распределительном щите. 1000 + 400 = 1400 А. В таблице 1 указано, что при пуске двигателя потери по длине кабеля 1 км равны 0,52 В, тогда
∆U при запуске = 0,52*0,05*500 = 13 В
∆U щита = 10*1400/100 = 14 В
∆U суммарные = 13+14 = 27 В, в процентном отношении ∆U = 27/400*100 = 6,75 % — допустимое значение, не превышает максимальную величину 8 %. С учетом всех параметров монтаж силовой линии приемлем.
Применение сервис-калькулятора
Расчеты, таблицы, графики, диаграммы — точные инструменты для вычисления падения напряжения по длине кабеля. Упростить работу можно, если выполнить расчеты с помощью онлайн-калькулятора. Преимущества очевидны, но стоит проверить данные на нескольких ресурсах и отталкиваться от среднего полученного значения.

Как это работает:
- Онлайн-калькулятор разработан для быстрого выполнения расчетов на основе исходных данных.
- В калькулятор нужно ввести следующие величины — ток (переменный, постоянный), проводник (медь, алюминий), длина линии, сечение кабеля.
- Обязательно вводят параметры по количеству фаз, мощности, напряжению сети, коэффициенту мощности, температуре эксплуатации линии.
- После введения исходных данных программа определяет падение напряжения по линии кабеля с максимальной точностью.
- Недостоверный результат можно получить при ошибочном введении исходных величин.
Пользоваться такой системой можно для проведения предварительных расчетов, поскольку сервис-калькуляторы на различных ресурсах показывают не всегда одинаковый результат: итог зависит от грамотной реализации программы с учетом множества факторов.
Тем не менее, можно провести расчеты на трех калькуляторах, взять среднее значение и отталкиваться от него на стадии предварительного проектирования.

Как сократить потери
Очевидно, что чем длиннее кабель на линии, тем больше сопротивление проводника при прохождении тока и, соответственно, выше потери напряжения.
Есть несколько способов сократить процент потерь, которые можно использовать как самостоятельно, так и комплексно:
- Использовать кабель большего сечения, проводить расчеты применительно к другому проводнику. Увеличение площади сечения токоведущих жил можно получить при соединении двух проводов параллельно. Суммарная площадь сечения увеличится, нагрузка распределится равномерно, потери напряжения станут ниже.
- Уменьшить рабочую длину проводника. Метод эффективный, но его не всегда можно использовать. Сократить длину кабеля можно при наличии резервной длины проводника. На высокотехнологичных предприятиях вполне реально рассмотреть вариант перекладки кабеля, если затраты на трудоемкий процесс гораздо ниже, чем расходы на монтаж новой линии с большим сечением жил.
- Сократить мощность тока, передаваемую по кабелю большой протяженности. Для этого можно отключить от линии несколько потребителей и подключить их по обходной цепи. Данный метод применим на хорошо разветвленных сетях с наличием резервных магистралей. Чем ниже мощность, передаваемая по кабелю, тем меньше греется проводник, снижаются сопротивление и потери напряжения.
Внимание! При эксплуатации кабеля в условиях повышенной температуры проводник нагревается, падение напряжения растет. Сократить потери можно при использовании дополнительной теплоизоляции или прокладке кабеля по другой магистрали, где температурный показатель существенно ниже.
Расчет потерь напряжения — одна из главных задач энергетической отрасли. Если для конечного потребителя падение напряжения на линии и потери электроэнергии будут практически незаметными, то для крупных предприятий и организаций, занимающихся подачей электроэнергии на объекты, они впечатляющие. Снизить падение напряжения можно, если правильно выполнить все расчеты.
В данной статье я буду рассматривать 2 примера определения потери напряжения в воздушной линии 10 кВ, когда нагрузка подключена в конце линии и с несколькими нагрузками вдоль линии.
Пример 1 – Определение потери напряжения, когда нагрузка подключена в конце линии
Определить потерю напряжения в трехфазной воздушной линии с номинальным напряжением Uном.=10 кВ протяженностью l = 2 км, питающей электрооборудование коммунального предприятия мощностью Р=100 кВт. Коэффициент мощности нагрузки cosϕ = 0,8. Линия выполнена алюминиевыми проводами марки А-25 сечением 25 мм2, расстояние между фазами 600 мм.
Решение.
1. Определяем активное сопротивление провода марки А-25:
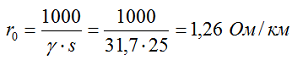
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
Также вы можете встретить в тех. литературе еще одну формулу по определению активного сопротивления провода (кабеля):
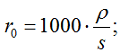
где:
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
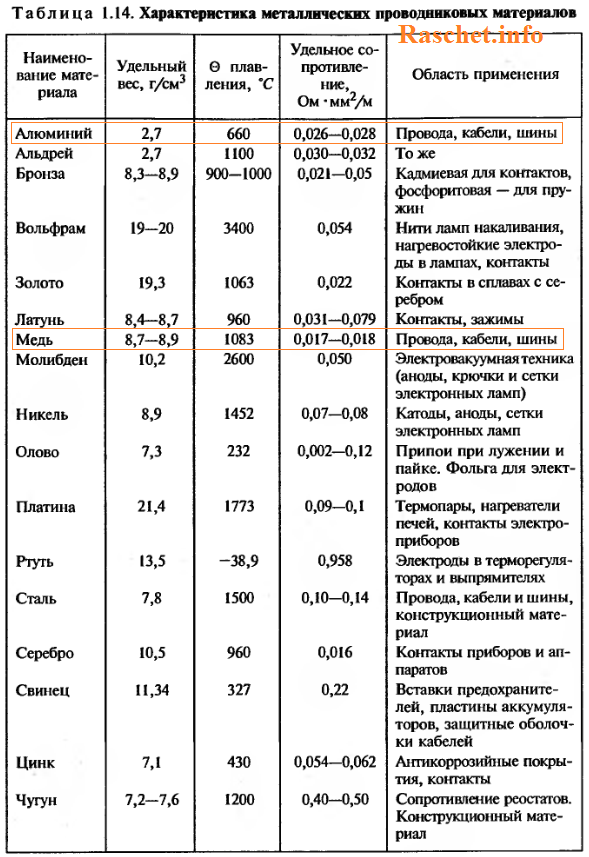
2. Определяем индуктивное сопротивление для провода марки А-25 [Л1.с.420]:
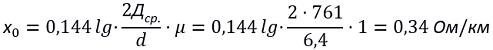
где:
- Дср. – среднее геометрическое расстояние между осями проводов, мм;
- d = 6,40 мм – диаметр провода, для марки провода А-25. Значение диаметра провода можно определить по ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. В данном расчете я привожу значение диаметра провода, только для провода марки А, для остальных марок проводов значения диаметров проводов вы сможете найти непосредственно в самом ГОСТе;
- µ — относительная магнитная проницаемость для цветных металлов (немагнитных) равна 1, для стальных проводов µ может достигать значений 103 и даже больше.
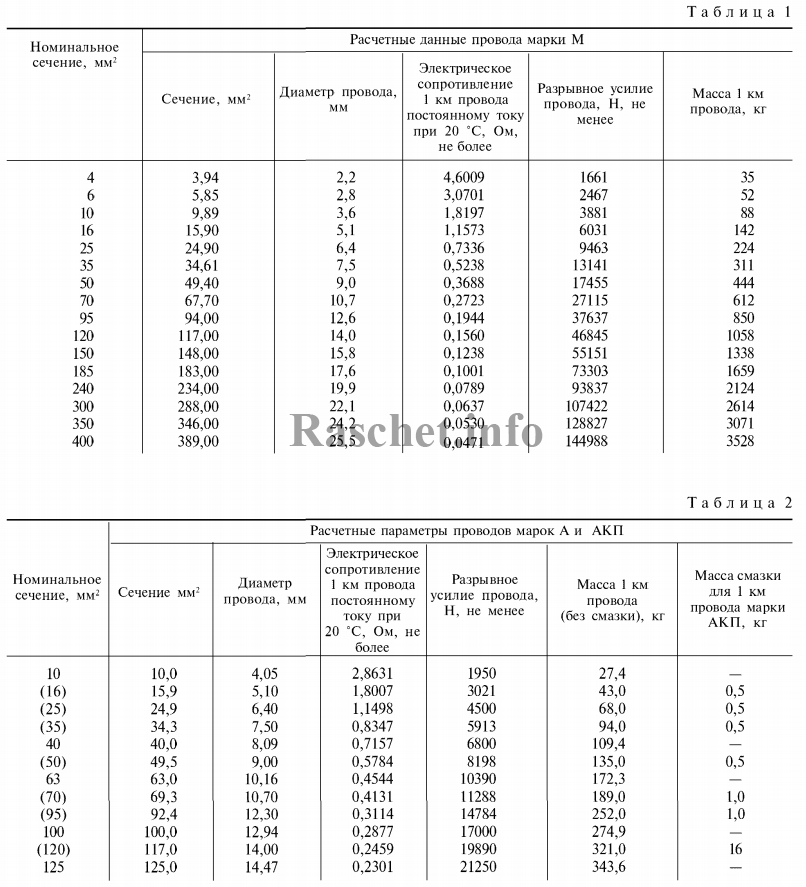
2.1 Определяем среднее геометрическое расстояние между осями трех проводов проложенных в одной плоскости [Л1.с.419]:
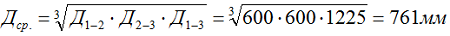
где: расстояние между проводами первой и второй фазы Д1-2= 600 мм, между второй и третью Д2-3 = 600 мм, между первой и третью Д1-3= 600 + 25 + 600 = 1225 мм.
3. Определяем коэффициент мощности tgϕ, зная cosϕ:
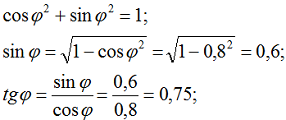
4. Определяем потерю напряжения в линии [Л1.с.422]:
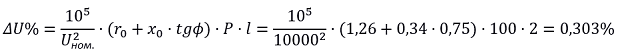
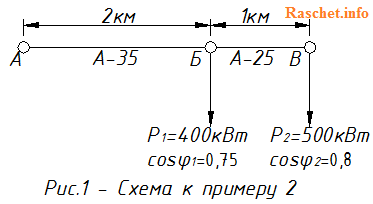
Пример 2 – Определение потери напряжения с несколькими нагрузками вдоль линии
Определить потерю напряжения в трехфазной сети 10 кВ, изображенной на рис.1. Сеть выполнена воздушной линией с алюминиевыми проводами марки А-35 сечением 35 мм2 на участке А-Б и проводами марки А-25 сечением 25 мм2 на участке Б-В. Расстояние между фазами равно 600 мм. Соответствующая нагрузка, коэффициент мощности cosϕ в ответвлениях, а также длины участков сети указаны на схеме.
Решение.
1. Определяем активное сопротивление провода марки А-35 на участке А-Б:
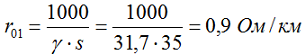
2. Определяем индуктивное сопротивление для провода марки А-35 [Л1.с.420]:

2.1 Определяем среднее геометрическое расстояние между осями трех проводов проложенных в одной плоскости [Л1.с.419]:
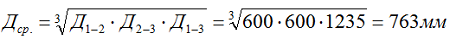
где: расстояние между проводами первой и второй фазы Д1-2= 600 мм, между второй и третью Д2-3 = 600 мм, между первой и третью Д1-3= 600 + 35 + 600 = 1235 мм.
3. Определяем коэффициент мощности tgϕ1, зная cosϕ1:
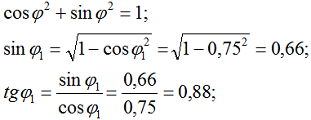
4. Значения активного и индуктивного сопротивления для марки провода А-25 берем из примера 1: r02 = 1,26 Ом/км; х02 = 0,256 Ом/км; tgϕ2 = 0,75.
5. Определяем суммарную потерю напряжения в линии 10 кВ [Л1.с.422] :
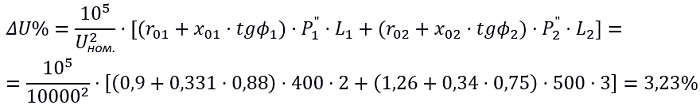
где:
- Uном. – номинальное напряжение, В;
- r01, x01, r02, x02 – активные и индуктивные сопротивления трехфазных линий, Ом/км;
- Р1,Р2 – мощности в ответвлениях, кВт;
- L1,L2 – длины от начала линии до соответствующего ответвления, км;
- tgϕ1, tgϕ2 – коэффициент мощности;
Литература:
1. Основы проектирования систем электроснабжения. Маньков В.Д. 2010 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Разность между напряжениями начала и конца линии называют падением напряжения
ΔU = U1 – U2,
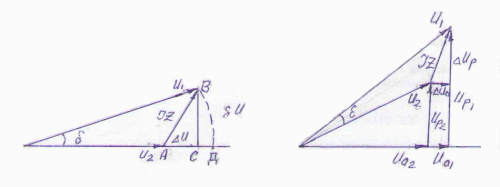
причем эта разность есть геометрическая. В учебниках различают еще так называемую алгебраическую разность напряжений в начале и конце линии, которую называют потерей напряжения. Эту потерю напряжения определяют из неудачно построенной векторной диаграммы. По оси абсцисс (вещественной оси) откладывают напряжение конца линии, определяют падение напряжения, напряжение начала линии, от конца вектора U1 делают циркулем засечку на вещественной оси, получают отрезок АД (Рис. 6.5.1), потерю напряжения U принимают равным приближенно продольной составляющей падения напряжения, которая есть проекция падения напряжения на действительную ось.
Необходимо отметить, что эти два понятия падение и потеря напряжения часто вводят путаницу. Мы предлагаем отказаться от понятия потеря напряжения, в этом нет никакой необходимости. Мы предлагаем изображать векторную диаграмму как общепринято в электротехнике: по вещественной оси откладывать активную составляющую напряжения, реактивную составляющую как принято под углом 90о, тогда отпадает необходимость в применении понятия потеря напряжения. При таком построении векторной диаграммы, она становится проще, нагляднее и самое главное соблюдаются общепринятые в электротехнике правила построения векторных диаграмм (Рис. 6.5.2). Необходимо отметить еще один существенный момент в определении падения напряжения необходимо учитывать баланс реактивных мощностей. По существующей методике напряжение в конце линии получалось всегда меньше, чем в начале. При небольших нагрузках напряжение в конце радиальной линии бывает больше, чем в начале. Это хорошо видно в векторных диаграммах расчета линии по предложенной нами методике с учетом баланса реактивных мощностей (см. выше).

Рис. 6.5.1 Рис. 6.5.2
Содержание главы:
Содержание книги:
Статьи и книги по теме:
