Как найти потери общества - Сайт, где вы сможете решить свои вопросы

Функция спроса населения на данный товар имеет вид:

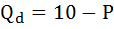
Функция предложения данного товара:

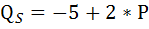
Предположим, что на данный товар введён налог, уплачиваемый продавцом, в размере 3 ден. ед. за штуку.

Определить величину чистых потерь, обусловленных введением налога.

Решение:

Найдём параметры равновесия до введения налога. Приравняв функции спроса и предложения, рассчитаем равновесную цену

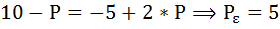
Подставив значение цены, например, в функцию спроса, получим равновесный объём:

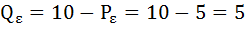
Найдём параметры равновесия после введения налога.

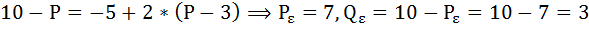
Определим величину чистых потерь, обусловленных введением налога:

Источник

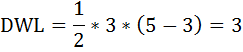
Потери общества от монополизации рынка

1. Оценка чистых
потерь монополии

2. Альтернативные
издержки монополизации

3. X
– неэффективность монополии

Литература

Основная:

1. Авдашева С.Б.,
Розанова Н.М., Теория организации
отраслевых рынков. М., 1998., Гл. 3. С. 71-80.

2. Шерер Ф.М., Росс
Д. Структура отраслевых рынков. М., 1997.
С. 654-678.

3. Тироль Ж. Рынки
и рыночная власть СПб., 1996. Гл. 1. С.97-118.

Дополнительная:

1. Лейбенстайн Х.
Аллокативная эффективность в сравнении
с “X-неэффективностью”
/ Теория фирмы. СПб., 1995. С. 477-506.

2. Хэй Д., Моррис Д.
Теория организации промышленности.
СПб., 1999. Т.2. Гл. 16. С. 433-456.

1. Оценка чистых потерь монополии

Условие максимизации
прибыли для монополии также записывается
уравнением MR=MC.
Но MR
не равно P,
т. к. кривая спроса имеет отрицательный
наклон.

Поэтому определим,
на какую величину отличается MR
от P.

Приравняв, MR=MC,
получим:

Из приведенного
выражения следует, что монополист будет
действовать только на эластичном участке
кривой спроса.

Следовательно,
надбавка к предельным издержкам в цене
должна быть тем меньше, чем выше
эластичность спроса.

Монополист
назначает цену, превышающую предельные
издержки на величину обратно
пропорциональную эластичности спроса.
Если спрос чрезвычайно эластичен, то
цена будет близка к предельным издержкам,
и следовательно монополизированный
рынок будет похож на рынок совершенной
конкуренции. Исходя из этого, положения
А. Лернер предложил в 1934 году индекс,
определяющий монопольную власть:

В условиях свободной
конкуренции достигается оптимальное
(по Парето) размещение ресурсов между
альтернативными возможностями
использования. Когда же на рынке
устанавливается монополия, условие
равенства цен предельным издержкам не
выполняется, так как цена монополии
всегда выше предельных издержек.

Если бы в отрасли
была свободная конкуренция, то объем
выпуска отрасли достиг бы значения Qc
– величины, соответствующей условию
равенства цены предельным издержкам.
В условиях монополии объем производства
в отрасли соответствует значению Qm
– такому, когда предельная выручка
монополиста равна его предельным
издержкам. Чистые потери от монополии
треугольник EMC
обозначаются как DWL
(deadweight
loss)
– омертвелые затраты.

Величина чистых
потерь от монополии определяется как:

Величина мертвого
груза монополии (DWL)
в рамках представленной модели
зависит от того, насколько действия
монополиста повышают цену и сокращают
объем продаж по сравнению с рынком
совершенной конкуренции:

(1)

Можно выразить
чистые потери от монополизации через
индекс Лернера

Если ценовая
эластичность равна
откуда
можно выразить зависимость сокращения
объема продаж от ценовой эластичности
спросаподставив
в (1) получимпреобразуя,
помножив наполучим
необходимую зависимость:т.к.а,

(2)

Таким образом
чистые потери от монополии тем выше,
чем:

• чем выше
эластичность спроса при цене, которую
назначает монополист;

• чем выше общая
выручка монополиста;

• чем выше индекс
Лернера монопольной власти, отражающий
долю прибыли в цене.

Эта формула активно
используется в эмпирических исследованиях,
так как она позволяет определять чистые
потери на основе объективных данных,
характеризующих рыночный спрос и
экономическое положение продавца.

Потери общества
от монопольной власти можно определить,
используя и другой показатель положения
продавца – сумму экономической прибыли.

(3)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

�� 17. ��

��, ��

��, �� 

� �� 1 � 2, �� , �� , �� . �� , �� – ��, �� ; �� .

� �� 10 �� , �� . �� .

�� . �� , �� . � �� . ��. 8, �� , �� 10.

��. 8. ��

�� S (�� ) �� , �� ; S₁ – �� , �� , �� , – �� . �� S₁, �� S �� (��).

�� E₀ � �� E₁; �� Q₀ �� Q₁, ��, �� , �� ₀ �� P^D₁, � �� – �� ₀ �� P^S₁.

�� -�� , � �� . �� -�� , �� , � ��-�� , �� , � �� , ��, �� . �� , �� , �� P₀P^D₁E₁E₀.

�� , �� , � � �� ; �� , ��, �� . �� . 8 �� P^S₁P^D₁E₁E₀E^S₁.

�� , �� – �� . �� TQ₁ � �� P^S₁P^D₁E₁E^S₁. �� : �� E^S₁E₁E₀ (�� ) �� . �� – �� , �� .

�� . �� , �� , � � �� . �� , �� , – �� , �� Q₀ � Q₁; �� P^D₁ – P₀ � P₀ – P^S₁. �� , � �� (�� ). ��

DW^D = [(Q₀ + Q₁)(P₀ – P^D₁)]/2

(3)

��

DW^S = [(Q₀ + Q₁)(P^S₁ – P₀)]/2

(4)

�� , �� , ��

�� E^S₁E₁E₀. �� E^S₁E₁ �� , �� Q₀ – Q₁, � ��, �.�. �� , –

L = ½T(Q₀ – Q₁) = -½TDQ₁

(6)

�� 5

��

�� (��. 8)

��

P₀P^D₁E₁E₀

P₀P^S₁E^S₁E₀

[(Q₀ + Q₁)(P₀ – P^D₁)]/2

[(Q₀ + Q₁)(P^S₁ – P₀)]/2

��

P^S₁P^D₁E₁E₀E^S₁

– [(Q₀ + Q₁)T]/2

��

P^S₁P^D₁E₁E^S₁

E^S₁E₁E₀

Q₁T

(Q₀ – Q₁)T/2

��

P^S₁P^D₁E₁E₀E^S₁

T(Q₀ + Q₁)/2

�� DQ₁ = Q₁ + Q₀ – �� (��, ��, ��). �� . 5. �� , �� P^D₁ – P^S₁ = T, ��

M₁ + L = – (DM^D + DM^S)

�� . �� “��” �� . �� , �� ; � ��, �� . �� , �� . �� , ��, �� 100 %-�� , �� . �� , �� (6), �� . � �� , �� , �� DQ �� :

�� . �� , �� , �� , �� :

�� 10, �� , �� , �� , �� . �� , ��-�� . �� :

Q – Q₀ = –b(P – P₀), Q – Q₀ = �(P – P₀).

�� –b � � – �� (�� ); � �� , �� , � � �� – ��, �� . �� , � �� :

{

DQ = –b(P^D₁ – P₀),

DQ = c(P^D₁ – T – P₀).

�� ; �� , ��

DP^D = P^D₁ – P₀ = cT/(b + c),

��

DP^S = P^S₁ – P₀ = P^D₁ – P₀ – T,

��

DP^S = bT/(b + c).

�� , �� b � �; �� (3) � (4), �� :

|DW^D|/|DW^S| = |DP^D|/|DP^S| = c/b.

�� , �� , �� 10. ��

DQ = –bcT/(b + c).

�� , �� (7), ��

a = bc/(b + c) = 1/(1/c + 1/b).

�� .

��, �� 

�� , �� . ��, �� V ��. �� , �� (�� ). �� . 9. �� (S₂) �� (S) �� V �� , �� E₀ � �� E₂.

��. 9. ��

�� : �� , �� . �� “�� ” �� . �� – �� . �� (3)-(6) �� , �� –V, � �� 1 – �� 2. �� “��” � �� ₂ = –VQ₂ �� , �� , � � �� . �� . 6.

�� 6.

��

�� (��. 9)

��

P^D₂P₀E₀E₂

P₀P^S₂E^S₂E₀

[(Q₀ + Q₂)(P₀ – P^D₂)]/2

[(Q₀ + Q₂)(P^S₂ – P₀)]/2

��

P^D₂P^S₂E^S₂E₀E₂

– V(Q₀ + Q₂)/2

�� (-)

��

P^D₂P^S₂E^S₂E₂

E₂E₀E^S₂

-Q₂V

(Q₂ – Q₀)V/2

��

P^D₂P^S₂E^S₂E₀E₂

–V(Q₀ + Q₂)/2

�� . �� , �� ; �� , ��, �� . � � ��, � � �� . �� E₀E^S₂E₂, �� . 9 ��. �� –V � �� (8) �� , � ��

�� a – �� . �� (9).

�� 

��, � �� , � �� . �� , �� (8) � (10). �� , �� , �� , �� .

�� . �� , �� Q �� TU(Q). �� , �� TC(Q). �� , �� . �� , �� , ��

�� -�� , � � �� , �� , �� “�� ”, �� . �� �� .

�� Q. �� , � �� ; �� , �� , �� . �� , �� :

dI(Q)/dQ = dTU(Q)/dQ – dTC(Q)/dQ = 0,

��, ��,

�� MU(Q), MC(Q) -�� . �� . �� 4, �� 2 – �� , � �� – � �� . �� , �� -�� Q₀, �� , �.�. �� , �� “�� ”. �� “��” �� (� �� ), �� Q₀ �� , �.�. � ��. �� , �� .

� �� , ��, �� , �� , �� , �� . �� , �� , �� . �� , � �� . �� -�� “��” �� “��” �� .

�� , �� , �� . �� , �� , �� , � �� . �� , �� , �� , �� .

�� . �� . �� , �� “��” � �� “��” (�� ) ��.

�� .

1. �� , �� , � �� , �� (��, �� .) �� , �� .

2. �� , �� .

Источник

Определение безвозвратных убытков

Безвозвратные потери относятся к издержкам, которые несет общество, когда существует дисбаланс между спросом и предложением. Это неэффективность рынка, вызванная неправильным распределением ресурсов.

В сценарии свободного рынка цена товаров и услуг в основном зависит от спроса и предложения на них. Но иногда неэффективность рынка вызвана внешней силой — государственными законами, налогообложением, субсидиями, монополией, минимальными или максимальными ценами. На таком рынке товары либо переоценены, либо недооценены.

Оглавление

Определение безвозвратных убытков
- Объяснение безвозвратных потерь
- Причины безвозвратных потерь
  - # 1 — Ценовой потолок
  - # 2 — Ценовой этаж
  - №3 – Монополия
  - #4 – Налогообложение
  - № 5 – Субсидия
  - # 6 — Излишек продукта
- Рассчитать безвозвратные потери
- Пример
- График безвозвратных потерь
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Безвозвратные потери — это экономические издержки, которые несет общество. Это неэффективность рынка, вызванная дисбалансом между потреблением и распределением ресурсов.
Безвозвратная неэффективность продукта никогда не может быть отрицательной; может быть ноль. Безвозвратные потери равны нулю, когда спрос абсолютно эластичен или когда предложение совершенно неэластично.
Эта неэффективность рынка представлена следующей формулой:
Безвозвратные потери = ½ * (новая цена – первоначальная цена) * (исходное количество
— Новое количество)

Объяснение безвозвратных потерь

Безвозвратная потеря – это неэффективность рынка, вызванная несоответствием между потреблением товаров и спросом. Из-за неэффективности продукты либо переоценены, либо занижены.

В таких сценариях спрос и предложение не зависят от рыночных сил. Вместо этого спрос и предложение двигаются искусственно — такими факторами, как налогообложение, субсидии, излишки продукта, потребительские излишки, монополия, олигополия, потолок и минимальная цена. Высокоэластичные товары склонны к такой неэффективности. Изменения цен существенно влияют на спрос на высокоэластичный товар.

Безвозвратные потери также возникают при наличии положительного внешнего эффекта. В таких сценариях предельная выгода от продукта выше предельных социальных издержек. Безвозвратные потери не наблюдаются на эффективном рынке, где рынком управляет честная конкуренция.

Хотя стоимость безвозвратных потерь продукта никогда не может быть отрицательной, она может равняться нулю. Безвозвратные потери равны нулю, когда спрос абсолютно эластичен или когда предложение совершенно неэластично.

Причины безвозвратных потерь

Безвозвратная неэффективность возникает, когда рынок неестественно контролируется правительствами или внешними силами. Неэффективность рынка безвозвратным грузом вызвана следующими причинами:

# 1 — Ценовой потолок

Правительство устанавливает максимальную цену на продукты, чтобы не допустить завышения цены. Однако потолки цен отпугивают продавцов, поскольку ограничивают возможность получения высокой прибыли. Таким образом, потолки цен снижают предложение товаров.

# 2 — Ценовой этаж

Часто правительство устанавливает минимальную цену продажи товаров. Это увеличивает цены на продукты. Точно так же правительства часто устанавливают минимальную заработную плату для рабочих и служащих. Но высокая заработная плата приводит к потере работы для некомпетентных сотрудников.

№3 – Монополия

Когда монопольным игроком на рынке является единственный игрок, регулирование цены и предложения товаров неестественно. Цена продажи, устанавливаемая монополистом, значительно выше предельных издержек — рынок становится неэффективным. Кроме того, если клиенты не могут позволить себе продукт или услугу, спрос падает.

#4 – Налогообложение

Когда правительство повышает налоги на определенные товары или услуги, оно влияет на цену и спрос на этот продукт. Когда налоги повышают цену товара, спрос на него начинает падать. Но это сокращает прибыль производителей.

№ 5 – Субсидия

Правительства предоставляют субсидии на определенные товары или услуги, снижая цены. В результате спрос на продукцию возрастает. Однако этот искусственно созданный спрос побуждает потребителей покупать конкретный товар в большем количестве.

# 6 — Излишек продукта

Когда рынок переполнен товарами в избытке, а спрос на них низок, создается излишек продукта. Когда спрос низок, цена товара падает. Производители несут убытки из-за разрыва между спросом и предложением.

Рассчитать безвозвратные потери

Для расчетов безвозвратные потери равны половине изменения цены, умноженной на изменение спроса. Он рассчитывается по следующей формуле:

На приведенном выше графике кривая спроса пересекается с кривой предложения в точке «Е», т. е. в точке равновесия. Равновесие — это сценарий, при котором потребление и распределение товаров равны.

Однако из-за потолка цен кривая спроса сдвигается влево — новой ценой является P2. Точно так же Q2 — это новое требуемое количество. Субсидии также сдвигают кривую спроса влево. Напротив, минимальные цены и налоги сдвигают кривую спроса вправо.

Часто задаваемые вопросы (FAQ)

Что такое безвозвратные потери?

Безвозвратная неэффективность — это экономические издержки, которые несет общество, когда существует дисбаланс спроса и предложения. Это может быть неэффективное распределение ресурсов, вызванное вмешательством государства, монополией, сговором, излишком или дефицитом продукта.

Как рассчитать безвозвратные потери?

Он рассчитывается как половина стоимости, полученной путем умножения изменения цены продукта на разницу в величине спроса. Если ∆P — разница в цене, а ∆Q — разница в объеме спроса, безвозвратная неэффективность рассчитывается по следующей формуле:
Безвозвратные потери = ½ * (новая цена – первоначальная цена) * (исходное количество
— Новое количество)

Почему монополия приносит безвозвратные убытки?

Когда единственный участник рынка обладает монополией, монополист регулирует цены на товары и предложение. Когда предложение низкое, с потребителей взимается непомерная плата, значительно превышающая предельные издержки. Когда потребители теряют покупательную способность, спрос падает.

Могут ли безвозвратные потери быть отрицательными?

Это не может быть отрицательное значение. Но может быть и ноль. Это происходит, когда спрос совершенно эластичен или когда предложение совершенно неэластично.

Решение:

Потери общества от монополизации рынка

1. Оценка чистых потерь монополии

Определение безвозвратных убытков

Объяснение безвозвратных потерь

Причины безвозвратных потерь

Рассчитать безвозвратные потери

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Вам также может понравиться

Как найти винторез шрама

Как исправить неработающие кнопки на клавиатуре

Как найти массовую долю алкана формула

Добавить комментарий Отменить ответ