Как найти потерю энергии при ударе

Из-за
остаточных деформаций и нагревания тел
при ударе проис­ходит частичная потеря
начальной кинетической энергии
соударяющихся тел. Определим потерю
кинетической энергии при упругом ударе
тел, имеющих коэффициент восстановления
k.
Начальная кинетическая энергия тел

.

Кинетическая энергия тел в конце удара

.

Потеря кинетической энергии тел за время удара

.
(3.41)

В этом
выражении величины (v₁–u₁)
и (v₂–u₂)
представляют собой скорости, потерянные
телами при ударе. Обозначим кинетическую
энергию тел, соответствующую их
потерян­ным скоростям, Т*.
Если числовая величина

,
(3.42)

тогда выражение (3.41),
определяющее потерю кинетической
энергии тел при ударе, примет вид

Таким
образом, кинетическая энергия, потерянная
телами при упругом ударе, равна
произведению коэффициента (1-k)/(1+k)
на кинетическую энергию тел Т*,
соответствующую их потерянным ско­ростям.
При неупругом ударе, когда k=0
и и₁=и₂=и,
формула (3.41) принимает вид

.
(3.43)

Формула
(3.43) выражает теорему Карно: кинетическая
энергия, потерянная телами при неупругом
ударе, равна кинетической энергии тел,
соответствующей их потерянным скоростям.

15.5. Теорема об изменении кинетического момента

механической
системы при ударе

Теорема
об изменении кинетического момента
механической системы при ударе: изменение
кинетического момента механической
системы относительно любого неподвижного
центра при ударе равно геометрической
сумме моментов всех внешних ударных
импульсов, приложенных к точкам системы,
относительно того же центра.

.
(3.44)

Здесь

– кинетический момент системы относительно
центра О
в момент окончания действия ударных
сил;

– кинетический момент системы относительно
центра О в
момент начала действия ударных сил;


– главный
момент всех внешних ударных импульсов,
приложенных к точкам системы, относи­тельно
центра О.

Из
уравнения (3.44) при отсутствии внешних
ударных импульсов, т.е.
при

имеем

.

Таким
образом, если
к точкам
механической системы приложены только
внутренние ударные импульсы, то
кинетический момент системы относительно
любого центра не изменяется.

Векторному уравнению (3.44) соответствуют
три уравнения в проекциях на оси
координат:

т.
е. изменение
кинетического момента механической
системы относи­тельно любой оси при
ударе равно сумме моментов всех внешних
ударных импульсов, приложенных к точкам
системы относительно той же оси.

15.6. Действие ударных сил на твердое тело, вращающееся вокруг неподвижной оси и совершающее плоское движение

Вращение
тела вокруг неподвижной оси.
Предположим, что твердое тело вращается
вокруг неподвижной оси z.
В момент, когда оно имело угловую скорость
ω₀,
на него подей­ствовали внешние ударные
силы. Определим изменение угловой
скорости тела под действием этих сил.
Для этого воспользуемся уравнением

.

Кинетический
момент твердого тела относительно оси
вращения равен произведению момента
инерции тела относительно этой оси на
угловую скорость тела , т. е.

.

Подставим эти
значения в уравнение:

,

откуда

.

Таким
образом, изменение
угловой скорости твердого тела,
вращаю­щегося вокруг неподвижной
оси, под действием внешних ударных сил
равно сумме моментов импульсов этих
сил относительно той же оси.

Плоское
движение тела. Выясним
влияние внешних ударных сил на плоское
движение твердого тела. Рассмотрим это
движение тела как совокупность двух
движений: поступательного движения
вместе с центром масс и враще­ния
вокруг оси,
проходящей
через центр
масс перпендикулярно той плоскости, в
которой он
движется. В плоскости движения центра
масс проведем оси х
и у.
Предполо­жим, что в момент начала
действия ударных сил скорость центра
масс была

а угловая скорость –

Обозначим скорость центра масс в момент
конца действия ударных сил

а угловую скорость тела — ω.
Изменение проекций скорости центра
масс определяют два уравнения:

,
(3.45)

где

– проекции внешнего ударного импульса

на оси х
и у.

Так
как dL_ζr/dt
= dL_r/dt,
то изменение угловой скорости тела
определяет уравнение:

,
(3.46)

где

– момент инерции тела относительно
подвижной оси ζ,
проходя­щей через центр тяжести
перпендикулярно плоскости ху;

– момент внешнего ударного импульса

относительно той же оси.

Таким
образом, внешние
ударные силы, действующие на
твердое
тело,
совершающее
плоское
движение,
вызывают конечное изменение скорости
центра масс тела, определяемое уравнениями
(3.45), и конечное
изменение угловой скорости тела,
определяемое уравнением
(3.46).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Потеря кинетической энергии при ударе двух тел

• Из-за неупругого воздействия 2 гелей происходит потеря кинетической энергии, которая расходуется на постоянную деформацию и нагрев тела. Частичное упругое воздействие 2-х объектов на первом этапе, а при увеличении деформации кинетическая энергия переходит в другие формы энергии. Второй этап процесса восстановления В постоянном состоянии кинетическая энергия вновь приобретается. При частичном упругом ударе потери кинетической энергии меньше, чем в случае соответствующего неупругого удара. За счет упругого удара полностью восстанавливается состояние полной недеформации, поэтому потери кинетической энергии сравнимы с пулей.

Кинетическая энергия системы в начале удара, 7 — кинетическая энергия
системы в момент удара, ТХ, и масса сталкивающегося объекта, и скорость
объекта в начале удара, к— Потеря кинетической энергии вследствие
прямого Центрального частичного упругого воздействия 2 поступательно
движущихся объектов Вычисляется по формуле Неупругое воздействие, так
как a 0, — m, t В случае упругого удара k-1, следовательно, , −7 0.
Если 2-й объект был неподвижен до столкновения, т. е.

Таким образом, в реальных условиях движение материальной точки в тех случаях, когда действием па нее сил можно пренебречь, про-исходит без ускорения, т.
Людмила Фирмаль

То кинетическая энергия системы в начале столкновения равна 7 — Потеря кинетической энергии при столкновении задается формулой Решение задачи расчета потерь кинетической энергии при столкновении двух объектов должно осуществляться по приведенной выше формуле. Задача 439. А каково соотношение массы молота и наковальни, кто должен стремиться ковать металл б при ударе колом, к какому соотношению сваи и массы сваи следует стремиться Раствор, а следующий — молотковая масса, t. 2-mass. To Бревно и кованые изделия, Т -Скорость молота в начале удара, скорость молота в начале удара равна нулю.

Потери кинетической энергии рассчитываются по формуле 1 Требуется
большая потеря кинетической энергии, так как желательно получить большую
остаточную деформацию кованого металла при ковке. Для этого значение
дроби- То есть масса наковальни и кованого изделия должна быть
значительно больше массы молота. Коэффициент полезного действия молотка м
— это отношение полезной работы, затраченной на деформацию металла, и
работы, затраченной на подъем молотка, то есть отношение.

• Потеря кинетической энергии в случае Лар против кинетической энергии системы в начале удара. Используя выражение i, вы можете видеть, что yach t9 следовательно, если молот весит 2 тонны, то вес кованой наковальни равен 40 тоннам, а коэффициент восстановления равен a 0, 6, то КПД равен 0, 61. 6 обозначим следующее m масса копры, м3-масса забитой сваи. Скорость v сваи в начале удара равна zero. So можно воспользоваться формулой 1.

При ударе о сваю необходимо приложить усилия, чтобы уменьшить
деформацию сваи, поэтому необходима небольшая потеря кинетической
энергии. По этой причине, дробное значение- — — — — должно быть близко к
нулю. Средний балл То есть масса сваи должна быть значительно меньше
массы сваи. Семь КПД при забивке свай равен t. Удобно хранить
кинетическую энергию. Кинетическая энергия остается в системе в конце
удара. Задача 440. Вес а 2 кг.

Материальная точка назы-вается изолированной в том случае, когда действиями на нее всех прочих материальных тел можно пренебречь (это понятие является, конечно, абстракцией).
Людмила Фирмаль

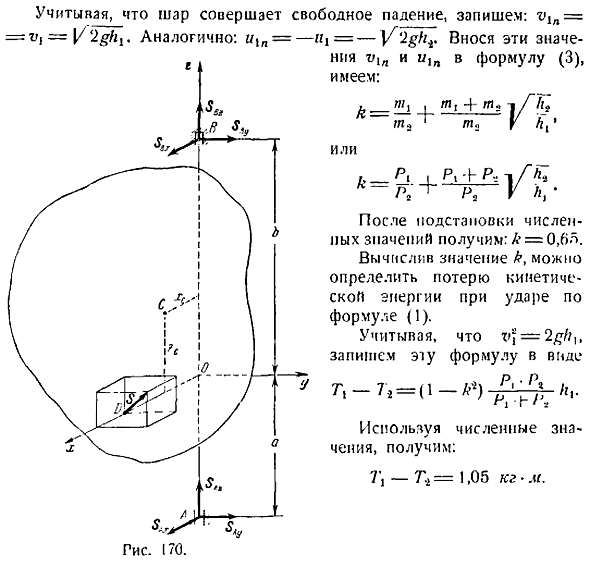
Мяч падает с высоты. Плита без веса 1 м Р2 20 кг, подпрыгивающая до высоты 88 25 см. Рассчитайте потери кинетической энергии при столкновении. Решение. Потеря кинетической энергии при столкновении объекта с неподвижной плоскостью рассчитывается по следующей формуле Т, -Т, 1-а — тг 11 — 1 Для расчета по Формуле 1 необходимо сначала найти значение коэффициента Восстановление k. Точка оси n перпендикулярна неподвижной плоскости. Проекция скорости шара рассчитывается по оси n по формуле ЛН nl4 блока. Цель 440. Где проекция полной скорости и оси n равна Т1 1П 4-Т1 9Н Т Потому что пластина m m т. -КТ.

Откуда т т и 1П л не двигался в начале удара, то есть r n 0 Где выражение 2 принимает вид 3 Если мяч падает свободно, мы напишем следующее. T 2 1. Аналогично s1y ГИС. 170. 111 — 2 kg если ввести эти значения p1l и s1l в уравнение 3 Если вы назначаете число, вы получаете k 0. 65. Вычисляя значение k, уравнение 1 позволяет определить потери кинетической энергии при столкновении.

Смотрите также:

Предмет теоретическая механика

Из рассуждений, приведенных в § 153, следует, что при неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшей эта потеря будет при абсолютно неупругом ударе. Подсчитаем, какую кинетическую энергию теряет система при абсолютно неупругом ударе двух тел.

Считая, что соударяющиеся тела движутся поступательно, и обозначая их общую скорость после абсолютно неупругого удара через и, получим для кинетической энергии системы в начале и в конце удара значения:

(162)

Потерянная при ударе кинетическая энергия равна Представим эту разность в виде

Так как из формулы (160) следует, что

то отсюда

Подставляя в правую часть равенства (163) вместо их значения из формул (162), а вместо правую часть выражения (164), получим:

или

Разности показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел. Их можно назвать потерянными при ударе скоростями. Тогда из формулы (165) вытекает следующая теорема Карно кинетическая энергия, потерянная системой тел при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями.

Если удар не является абсолютно неупругим то аналогичными преобразованиями можно найти, что кинетическая энергия, потерянная при ударе двух тел, определяется равенством

Рассмотрим частный случай абсолютно неупругого удара по первоначально неподвижному телу. В этом случае и

Тогда

или

Формула (166) показывает, какая энершя остается у системы после удара. Отметим два интересных предельных случая.

Рис. 380

1. Масса ударяющего тела много больше массы ударяемого . В этом случае можно считать и формула (166) дает

Следовательно, хотя удар и является абсолютно нспругим, потеря кинетической энергии при ударе почти не происходит, и система после удара начнет двигаться почти с той же кинетической энергией, которая у нее была в начале удара.

На практике такой результат нужно, очевидно, получать при забивании гвоздей, свай и т. п. Следовательно, в этом случае нужно, чтобы масса молотка была намного больше массы гвоздя (рис. 380, а).

2. Масса ударяемого тела много больше массы ударяющего . В этом случае можно считать и формула (166) дает . Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел, по окончании удара тела можно считать неподвижными.

Практически такой результат нужно, очевидно, получать при ковке, клепке и т. п. Следовательно, в этих случаях нужно, чтобы масса поковки вместе с наковальней (или масса заклепки вместе с поддержкой) была много больше массы молота (рис. 380, б).