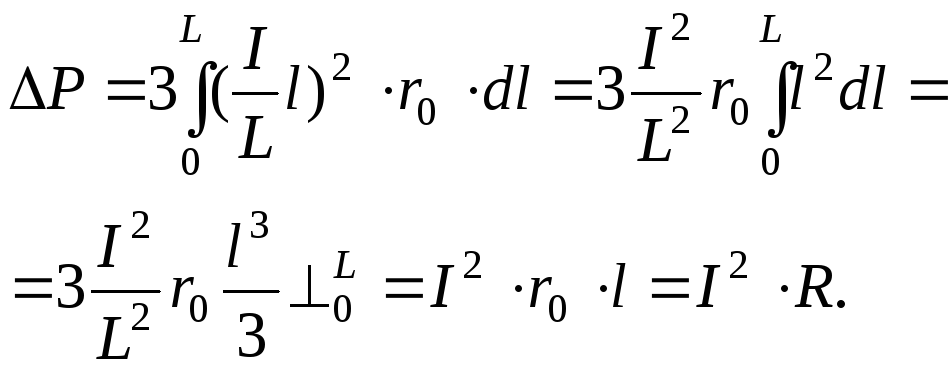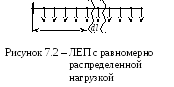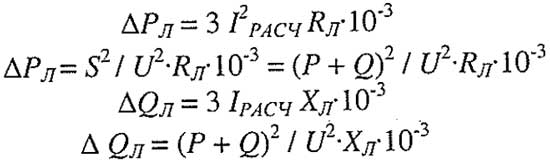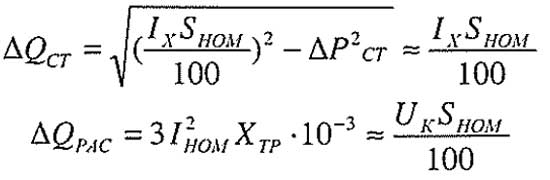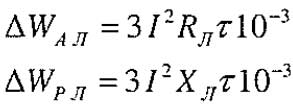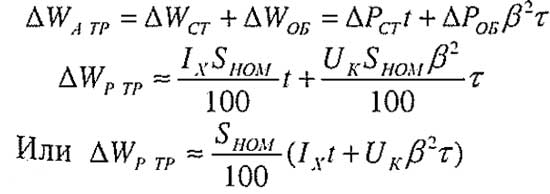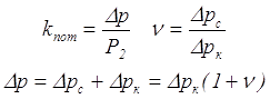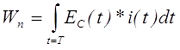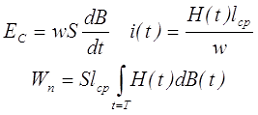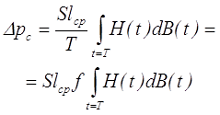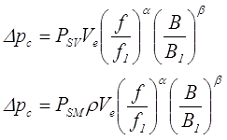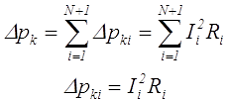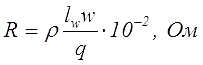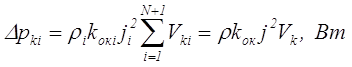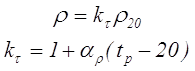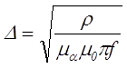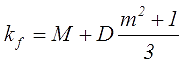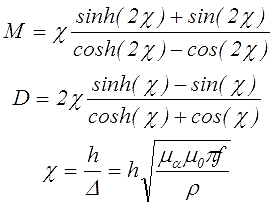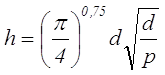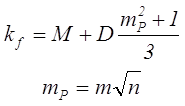Лекция № 7
Потери мощности и электроэнергии в элементах сети
План.
-
Потери мощности
в элементах сети. -
Расчет потерь
мощности в линиях электропередач. -
Расчет потерь
мощности в ЛЕП с равномерно распределенной
нагрузкой. -
Расчет потерь
мощности в трансформаторах. -
Приведенные и
расчетные нагрузки потребителей. -
Расчет потерь
электроэнергии. -
Мероприятия по
снижению потерь мощности.
Потери мощности в элементах сети
Для
количественной характеристики работы
элементов электрической сети
рассматриваются ее рабочие режимы.
Рабочий
режим
– это установившееся электрическое
состояние, которое характеризуется
значениями токов, напряжений, активной,
реактивной и полной мощностей.
Основной целью
расчета режимов является определение
этих параметров, как для проверки
допустимости режимов, так и для обеспечения
экономичности работы элементов сетей.
Определение
значений токов в элементах сети и
напряжений в ее узлах начинается с
построения картины распределения полной
мощности по элементу, т.е. с определения
мощностей в начале и конце каждого
элемента. Такую картину называют
потокораспределением.
Рассчитывая
мощности в начале и в конце элемента
электрической сети, учитывают потери
мощности в сопротивлениях элемента и
влияние его проводимостей.
Расчет потерь мощности в линиях электропередач
Потери активной
мощности на участке ЛЕП (см. рис. 7.1)
обусловлены активным сопротивлением
проводов и кабелей, а также несовершенством
их изоляции. Мощность, теряемая в активных
сопротивлениях трехфазной ЛЕП и
расходуемая на ее нагрев, определяется
по формуле:
,
где
полный,
активный и реактивный токи в ЛЕП;
P, Q, S
– активная, реактивная и полная
мощности в начале или конце ЛЕП;
U– линейное напряжение в начале или
конце ЛЕП;
R
– активное сопротивление одной
фазы ЛЕП.
Потери активной
мощности в проводимостях ЛЕП обусловлены
несовершенством изоляции. В воздушных
ЛЕП – появлением короны и, в очень
незначительной степени, утечкой тока
по изоляторам. В кабельных ЛЕП –
появлением тока проводимости а его
абсорбции. Рассчитываются потери по
формуле:
,
где U– линейное напряжение в начале или
конце ЛЕП;
G
– активная проводимость ЛЕП.
При проектировании
воздушных ЛЕП потери мощности на корону
стремятся свести к нулю, выбирая такой
диаметр провода, когда возможность
возникновения короны практически
отсутствует.
Потери реактивной
мощности на участке ЛЕП обусловлены
индуктивными сопротивлениями проводов
и кабелей. Реактивная мощность, теряемая
в трехфазной ЛЕП, рассчитывается
аналогично мощности, теряемой в активных
сопротивлениях:
Генерируемая
емкостной проводимостью зарядная
мощность ЛЕП рассчитывается по формуле:
,
где U– линейное напряжение в начале или
конце ЛЕП;
B
– реактивная проводимость ЛЕП.
Зарядная мощность
уменьшает реактивную нагрузку сети и
тем самым снижает потери мощности в
ней.
Расчет потерь мощности в леп с равномерно распределенной нагрузкой
В линиях местных
сетей ()
потребители одинаковой мощности могут
располагаться на одинаковом расстоянии
друг от друга (например, источники
света). Такие ЛЕП называются линиями с
равномерно распределенной нагрузкой
(см. рис. 7.2).
В равномерно
нагруженной линии трехфазного переменного
тока длиной L
с суммарной токовой нагрузкойIплотность тока на единицу длины составитI/L. При погонном
активном сопротивленииr0
потери активной мощности составят:
Если бы нагрузка
была сосредоточена в конце, то потери
мощности определялись бы как:
.
Сравнивая приведенные
выражения, видим, что потери мощности
в линии с равномерно распределенной
нагрузкой в 3 раза меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При передаче электрической энергии от генераторов электростанций до потребителя около 12-18% всей вырабатываемой электроэнергии теряется в проводниках воздушных и кабельных линий, а также в обмотках и стальных сердечниках силовых трансформаторов.
При проектировании нужно стремиться к уменьшению потерь электроэнергии на всех участках энергосистемы, поскольку потери электроэнергии ведут к увеличению мощности электростанций, что в свою очередь влияет на стоимость электроэнергии.
В сетях до 10кВ потери мощности в основном обусловлены нагревом проводов от действия тока.
Потери мощности в линии.
Потери активной мощности (кВт) и потери реактивной мощности (кВАр) можно найти по следующим формулам:
Формулы для расчета потери мощности в линии
где Iрасч – расчетный ток данного участка линии, А;
Rл – активное сопротивление линии, Ом.
Потери мощности в трансформаторах.
Потери мощности в силовых трансформаторах состоят из потерь, не зависящих и зависящих от нагрузки. Потери активной мощности (кВт) в трансформаторе можно определить по следующей формуле:
Потери активной мощности в трансформаторе
где ?Рст – потери активной мощности в стали трансформатора при номинальном напряжении. Зависят только от мощности трансформатора и приложенного к первичной обмотке трансформатора напряжения. ?Рст приравнивают ?Рх;
?Рх— потери холостого хода трансформатора;
?Роб – потери в обмотках при номинальной нагрузке трансформатора, кВт; ?Роб приравнивают ?Рк.
?Рк– потери короткого замыкания;
?=S/Sном – коэффициент загрузки трансформатора равен отношению фактической нагрузки трансформатора к его номинальной мощности;
Потери реактивной мощности трансформатора (кВАр) можно определить по следующей формуле:
Потери реактивной мощности в трансформаторе
где ?Qст – потери реактивной мощности на намагничивание, кВАр. ?Qст приравнивают ?Qх.
?Qх – намагничивающая мощность холостого хода трансформатора;
?Qрас – потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке.
Значения ?Рст(?Рх) и ?Роб(?Рк) приведения в каталогах производителей силовых трансформаторов. Значения ?Qст(?Qх) и ?Qрас определяют по данным каталогов из следующих выражений:
Формулы для расчета потери реактивной мощности
где Iх – ток холостого хода трансформатора, %;
Uк – напряжение короткого замыкания, %;
Iном – номинальный ток трансформатора, А;
Xтр – реактивное сопротивление трансформатора;
Sном – номинальная мощность трансформатора, кВА.
Потери электроэнергии.
На основании потерь мощности можно посчитать потери электроэнергии. Здесь следует быть внимательными. Нельзя посчитать потери электроэнергии умножив потери мощности при какой либо определенной нагрузке на число часов работы линии. Этого делать не стоит, т.к в течение суток или сезона потребляемая нагрузка изменяется и таким образом мы получим необоснованно завышенное значение.
Чтобы правильно посчитать потери электроэнергии используют метод, основанный на понятиях времени использования потерь и времени использовании максимума нагрузки.
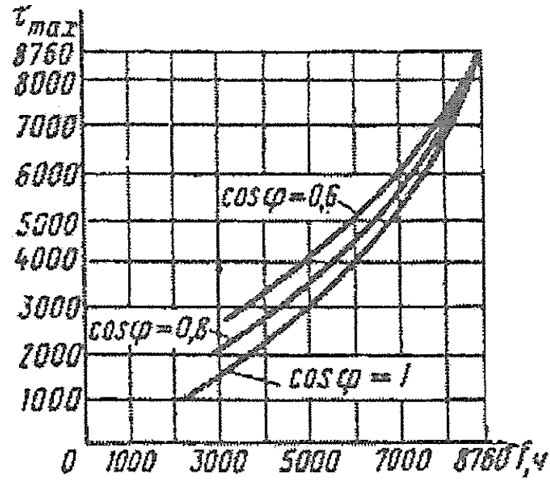
Время максимальных потерь ? – условное число часов, в течение которых максимальный ток, протекающий в линии, создает потери энергии, равные действительным потерям энергии в год.
Временем использования максимальной нагрузки или временем использования максимума Тмах называют условное число часов, в течение которых линия, работая с максимальной нагрузкой, могла бы передать потребителю за год столько энергии, сколько при работе по действительному переменному графику. Пусть W(кВт*ч) – энергия переданная по линии за некоторый промежуток времени, Рмах(кВт) -максимальная нагрузка, тогда время использования максимальной нагрузки:
Тмах=W/Рмах
На основании статистических данных для отдельных групп электроприемников были получены следующие значения Тмах:
- Для внутреннего освещения – 1500—2000 ч;
- Наружного освещения – 2000—3000 ч;
- Промышленного предприятия односменного – 2000—2500 ч;
- Двухсменного – 3000—4500 ч;
- Трехсменного – 3000—7000 ч;
Время потерь ? можно найти по графику, зная Тмах и коэффициент мощности.
Зависимость времени максимальных потерь от продолжительности использования максимума нагрузки
Теперь зная ? можно посчитать потери электроэнергии в линии и в трансформаторе.
Потери энергии в линии:
Потери энергии в линии
Потери энергии в трансформаторе:
Потери энергии в трансформаторе
где ?Wатр –общая потеря активной энергии (кВт*ч) в трансформаторе;
?Wртр –общая потеря реактивной энергии (кВАр*ч) в трансформаторе.
Советую почитать:
Потери мощности в трансформаторе определяются по формулам:
потери активной мощности
потери реактивной мощности
где — потери холостого хода трансформатора (потери в стали), квт;
— потери к. з. трансформатора (потери в обмотках) при номинальной нагрузке, квт;
— ток холостого хода трансформатора, %;
— падение напряжения в реактивном сопротивлении трансформатора, %;
— номинальная мощность трансформатора, ква;
— коэффициент загрузки трансформатора;
где S — фактическая нагрузка трансформатора, ква.
Формула (9-4) для определения потерь реактивной мощности в трансформаторе может быть представлена в виде:
где — потери реактивной мощности в трансформаторе при холостом ходе (потери на намагничивание), квар:
— потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке, квар:
Падение напряжения в реактивном сопротивлении трансформатора определяется по формуле
где Uк — напряжение к. з. трансформатора, %;
Ur — падение напряжения в активном сопротивлении трансформатора, определяемое из выражения
Для трансформаторов мощностью более 10 Мва можно принять
Некоторые значения величин для понижающих трансформаторов приведены в табл. 9-2. В табл. 9-2 уровень Б потерь активной мощности холостого хода относится к трансформаторам, в которых использована электротехническая сталь толщиной 0,35 мм марки Э 330 А по ГОСТ 802-58 с жаростойким покрытием и отжигом пластин. В табл. 9-2 даны значения активных и реактивных сопротивлений трансформаторов, приведенные по отношению к номинальному напряжению обмотки ВН.
| Таблица 9-2 Технические данные трехфазных двухобмоточных силовых масляных трансформаторов общего назначения (ГОСТ 12022-66) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Номинальная мощность, ква | Верхний предел номиналього напряжения обмотки, кв | Схема и группа соединений обмоток | Потери активной мощности, квт | Напряжение к.з., % | Ток холостого хода | Сопротивления обмоток трансформатора, ом | Потери реактивной мощности, квар | ||||
| холостого хода | к.з. | ||||||||||
| уровень А | уровень Б | активное | реактивное | холостого хода | к.з. | ||||||
| 25 | 10 10 |
У/Ун-0 У/Zн-11 |
0,105 0,105 |
0,125 0,125 |
0,6 0,69 |
4,5 4,7 |
3,2 3,2 |
96,0 110 |
152 152 |
0,80 0,80 |
0,95 0,95 |
| 40 | 10 10 |
У/Ун-0 У/Zн-11 |
0,15 0,15 |
0,18 0,18 |
0,88 1,0 |
4,5 4,7 |
3,0 3,0 |
55,0 62,5 |
98,1 99,5 |
1,20 1,20 |
1,57 1,59 |
| 63 | 10 10 20 20 |
У/Ун-о У/Zн-11 У/Ун-0 У/Zн-11 |
0,22 0,22 0,245 0,245 |
0,265 0,265 0,29 0,29 |
1,28 1,47 1,28 1,47 |
4,5 4,7 5,0 5,3 |
2,8 2,8 2,8 2,8 |
32,3 37,0 129 148 |
63,7 64,8 290 302 |
1,76 1,76 1,76 1,76 |
2,53 2,57 2,88 3,00 |
| 100 | 10 10 35 35 |
У/Ун-0 У/Zн-11 У/Ун-0 У/Zн-11 |
0,31 0,31 0,39 0,39 |
0,365 0,365 0,465 0,465 |
1,97 2,27 1,97 2,27 |
4,5 4,7 6,5 6,8 |
2,6 2,6 2,6 2,6 |
19,7 22,7 241 278 |
40,5 41,2 759 785 |
2,60 2,60 2,60 2,60 |
4,05 4,12 6,19 6,41 |
| 160 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,46 0,46 0,46 0,56 0,56 0,56 |
0,54 0,54 0,54 0,66 0,66 0,66 |
2,65 2,65 3,1 2,65 2,65 3,1 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,4 2,4 2,4 2,4 2,4 2,4 |
10,4 10,4 12,1 127 127 148 |
26,2 26,2 26,8 481 481 499 |
3,84 3,84 3,84 3,84 3,84 3,84 |
6,69 6,69 6,85 10,1 10,1 10,4 |
| 250 | 10 10 10 35 35 35 |
У/Ун-0 У/Д-11 У/Zн-11 У/Ун-0 У/Д-11 У/Zн-11 |
0,66 0,66 0,66 0,82 0,82 0,82 |
0,78 0,78 0,78 0,96 0,96 0,96 |
3,7 3,7 4,2 3,7 3,7 4,2 |
4,5 4,5 4,7 6,5 6,5 6,8 |
2,3 2,3 2,3 2,3 2,3 2,3 |
5,92 5,92 6,72 72,5 72,5 82,3 |
17,0 17,0 17,6 310 310 322 |
7,25 5,75 5,75 5,75 5,75 5,75 |
10,6 10,6 11,0 15,8 15,8 16,5 |
| 400 | 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Д-11 |
0,62 0,92 0,92 1,15 1,15 |
1,08 1,08 1,08 1,35 1,35 |
5,5 5,5 5,9 5,5 5,5 |
4,5 4,5 4,5 6,5 6,5 |
2,1 2,1 2,1 2,1 2,1 |
3,44 3,44 3,69 42,1 42,1 |
10,7 10,7 10,6 195 195 |
8,40 8,40 8,40 8,40 8,40 |
17,1 17,1 17,0 25,4 25,4 |
| 630 | 10 10 10 10 35 35 |
У/Ун-0 Ун/Д-11 Д/Ун-11 У/Ун-0 У/Ун-0 У/Д-11 |
1,42 1,42 1,42 1,42 1,7 1,7 |
1,68 1,68 1,68 1,68 2,0 2,0 |
7,6 7,6 8,5 8,5 7,6 7,6 |
5,5 5,5 5,5 5,5 6,5 6,5 |
2,0 2,0 2,0 2,0 2,0 2,0 |
1,91 1,91 2,14 2,14 23,5 23,5 |
8,52 8,52 8,46 8,46 124 124 |
12,6 12,6 12,6 12,6 12,6 12,6 |
33,8 33,8 33,6 33,6 40,2 40,2 |
Для других номинальных напряжений обмоток сопротивления пересчитываются по формулам:
где Uн — номинальное напряжение обмотки, указанное в табл. 9-2, кв; — номинальное напряжение обмотки, по отношению к которому пересчитываются сопротивления, кв;
R и X — соответственно активное и реактивное сопротивления трансформатора, определяемые по табл. 9-2, ом.
Потери электроэнергии в сети определяются по формуле
где — наибольшие потери мощности в сети, кет;
— число часов максимальных потерь, определенное в зависимости от годового графика нагрузки.
Потери электроэнергии в трансформаторе определяются по формуле
где tТ — число часов работы трансформатора.
Число часов максимальных потерь, если известен годовой график нагрузки, может быть определено по формуле
где — сумма произведений квадратов полных нагрузок на годовую продолжительность каждой из них, вычисленная для всего годового графика нагрузок рассматриваемого элемента сети;
Sб — наибольшая полная нагрузка элемента сети. Для типичного графика, имеющего сниженные нагрузки ночью и утренний и вечерний максимумы, число часов максимальных потерь согласно в зависимости от числа часов использования максимума может определяться по табл. 9-7.
| Таблица 9-7 Число часов максимальных потерь | |||||
|---|---|---|---|---|---|
| Число часов использования максимума | 3000 | 3500 | 4000 | 4500 | 5000 |
| Число часов максимальных потерь | 1300 | 1650 | 2000 | 2500 | 3000 |
| Число часов использования максимума | 5500 | 6000 | 6500 | 7000 | 7500 |
| Число часов максимальных потерь | 3650 | 4300 | 5000 | 5700 | 6450 |
Пример 9-1.
Определить годовые потери электроэнергии в трансформаторе типа ТМ мощностью 6,3 Мва с напряжением высшей стороны 10 кв, если трансформатор включен постоянно и годовой график его нагрузки представлен на рис. 9-1.
Решение.
Годовые потери электроэнергии в трансформаторе определяем по (9-10).
По справочным данным находим потери активной мощности в трансформаторе при холостом ходе для уровня Б: ΔРс=9 квт
и нагрузочные потери (потери к. з.) при номинальной нагрузке трансформатора: ΔРк.з=46,5 квт
По условию примера годовое число часов работы трансформатора tТ = 8 760.
Коэффициент загрузки трансформатора при наибольшей нагрузке составляет:
Число часов максимальных потерь определяем из графика на рис. 9-1, подставив в (9-11) значения нагрузок трансформатора в мегавольт-амперах и соответствующие им продолжительности работы в тысячах часов:
Подставив числовые значения в (9-10), определим годовые потери энергии в трансформаторе:

Рис. 9-1.
Годовой график нагрузки
Пример 9-2.
На рис. 9-2 представлена схема линии 6 кв с указанием длин участков линии (км) и расчетных (наибольших) нагрузок (Мва). Магистраль АБ выполнена кабелем с алюминиевыми жилами сечением 3X70 мм.кв, а ответвления БВ и БГ — воздушной линией с алюминиевыми проводами сечением 35 мм.кв.
Определить годовые потери электроэнергии в сопротивлениях проводов и кабелей линии, если годовая продолжительность использования максимума нагрузок составляет 3000 ч и график нагрузок является типичным (имеются утренний и вечерний максимумы и снижение нагрузки в ночное время).
Решение.
Наибольшие потери мощности в сопротивлениях проводов и кабелей линии находим по (9-1), в которой значение коэффициента определяется из табл. 9-1:
Удельные сопротивления участков линии находим по табл. 5-1: для алюминиевого кабеля сечением 70 мм.кв — 0,46 ом/км; для алюминиевого провода сечением 35 мм.кв — 0,92 ом/км.
Определяем значение величины N для магистрали АБ:
для ответвлений БВ и БГ
Из (9-1) находим наибольшие потери мощности в сети:
По табл. 9-7 в зависимости от продолжительности использования максимума Т=3000 ч находим значение числа часов максимальных потерь τ=1300. Величину потерь электроэнергии определяем по (9-9):
Всем доброго времени суток! В прошлой статье я рассказал об эквивалентной схеме трансформатора. В данной статье я расскажу, как рассчитать потери мощности в трансформаторе. От потерь мощности в трансформаторе зависит температура его нагрева, поэтому они значительно влияют на расчётные параметры. При расчёте трансформатора следует ограничивать потери мощности путем правильного выбора параметров и величин, влияющих на потери.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Составляющие потерь мощности в трансформаторе
Полные или суммарные потери мощности в трансформаторе ∆р состоят в основном из двух частей: потерь в сердечнике ∆рс и потерь в катушках ∆рк. Присутствующие потери мощности в элементах конструкций трансформатора имеют достаточно малое значение и обычно не учитываются.
При расчёте трансформатора, кроме вышеназванных величин, важное значение имеет соотношение потерь мощности ν и отношение суммарных потерь мощности ∆р к выходной мощности Р2, называемое коэффициентом потерь kпот
Довольно часто потери мощности ∆рс и ∆рк называют потерями «в стали» и потерями «в меди», однако это не совсем правильно, так как в качестве материала сердечника используются не только стали, но и различные сплавов, а в качестве материала проводов обмоток – не только медные, но и алюминий.
Потери мощности в катушках ∆рк, кроме основной части – потерь в обмотках – включает в себя потери в диэлектрике: изоляции проводника, межслоевой и межобмоточной ∆рд. Однако, данный компонент потерь мощности начинает влиять на общие потери, только у высоковольтных высокочастотных трансформаторов. Рассмотрим составляющие потерь мощности трансформатора.
Потери мощности в сердечнике трансформатора
В сердечнике ∆рс трансформатора потери мощности обусловлены затратами энергии магнитного поля на перемагничивание материала из которого сделан сердечник.
Энергия магнитного поля в общем случае определяется следующим выражением
где EC(t) – изменение напряжения за один период,
i(t) – изменение тока за один период.
В соответствие с законом электромагнитной индукции и теоремой о циркуляции вектора напряженности магнитного поля получим
где S – площадь поперечного сечения магнитопровода,
lcp – средняя длина магнитной силовой линии.
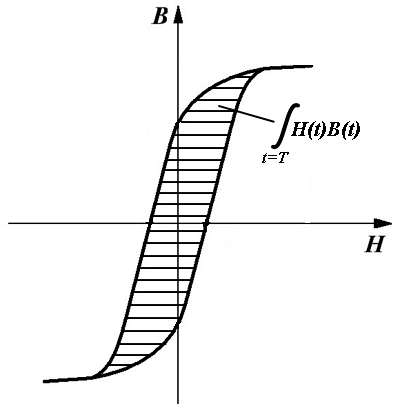
Так как ферромагнитные сердечники обладают гистерезисом, то однозначной функциональной зависимости между напряженностью Н и индукцией В магнитного поля в нем не существует. Однако при перемагничивании сердечника от –Нmax до Нmax можно считать, что любой величине напряженности магнитного поля Н соответствует только два значения магнитной индукции В: на восходящей и нисходящей ветвях. То есть, после полного цикла перемагничивания ферромагнетик вернётся в тоже состояние, из которого начинался процесс. Тогда подынтегральное выражение имеет физический смысл теплоты, отданной сердечником за один цикл перемегничивания.
Физический смысл магнитных потерь в сердечнике.
Так как потери мощности в сердечнике ∆рс определяется, как работа за единицу времени, то преобразовав предыдущую формулу, получим выражение для вычисления потерь мощности в сердечнике
где f – частота перемагничивания магнитопровода.
Подынтегральное выражение численно равно площади заштрихованного участка петли гистерезиса. Таким образом, вычисление данного интеграла является вычислением удельных потерь.
На практике нет необходимости в вычислении удельных потерь, так как для разработанных ферромагнитных материалов существуют справочные данные. Поэтому используют различные формулы в зависимости от известных справочных данных.
Достаточно широко распространено следующее выражение для высокочастотных материалов, где удельные потери имеют размерность Вт/(см3Гц)
PSV – удельные объемные потери в магнитопроводе,
Ve – эквивалентный объем сердечника магнитопровода,
f – частота перемагничивания.
Так для отечественных ферритов значение удельных объемных потерь составляют
| Марка феррита | PSV, мкВт/(см3*Гц), на частоте 10-20кГц | При индукции В, Тл | ||
| Т, °С | ||||
| +25 | +100 | +120 | ||
| 2500НМС1 | 10,5 | 8,7 | — | 0,2 |
| 2500НМС2 | 8,5 | 6 | — | 0,2 |
| 2500НМС5 | 9,0 | 7,6 | — | 0,2 (при 100 кГц) |
| 3000НМС | 2,5 | — | 2,5 | 0,1 |
Кроме данного выражения существуют более сложные способы вычисления потерь мощности в сердечнике трансформатора. Часто в справочниках приводятся удельные объемные потери PSV в Вт/см3 или удельные массовые потери PSM в Вт/кг. В этом случае потери мощности рассчитываются по следующим выражениям
где ρ – плотность материала,
f1, B1 – базовые расчётные параметры, при которых были измерены потери мощности в сердечнике,
α и β – степенные параметры, зависящие от конкретного материала, их значение можно найти в справочниках.
| Материал | PSV Вт/см3 | α | β |
| 2000НМ-А | 0,142 | 1,2 | 2,4 |
| 2000НМ-17 | 0,272 | 1,2 | 2,8 |
| 3000НМ-А | 0,208 | 1,2 | 2,8 |
| 1500НМ3 | 0,093 | 1,2 | 2,2 |
| 2000НМ3 | 0,178 | 1,3 | 2,7 |
Для данных материалов В1 = 1 Тл, f1 = 1 кГц.
| Материал | Толщина, мм | PSM, Вт/кг | α | β |
| 34НКМП | 0,1 | 2,2 | 1,65 | 1,7 |
| 40НКМП | 0,05 | 2,8 | 1,5 | 1,3 |
| 50НП | 0,1 | 5 | 1,4 | 1,5 |
| 79НМ | 0,1 | 1,4 | 1,65 | 2,0 |
| 68НМП | 0,05 | 2,2 | 1,55 | 1,7 |
| 80НХС | 0,05 | 1,2 | 1,5 | 2,0 |
Для данных материалов В1 = 0,5 Тл, f1 = 1 кГц.
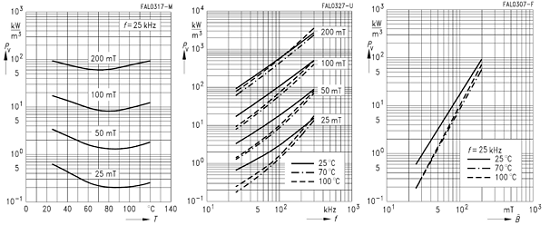
Для ферритов иностранного производства выпускаются довольно подробные справочные материалы. Для расчета потерь в сердечниках из этих ферритов используется коэффициент удельных объемных потерь PV (Relative core losses) измеряемый в кВт/м3. Для этого параметра приводятся подробные графические зависимости от частоты f, магнитной индукции В и температуры Т.
Зависимость удельных потерь PV для феррита N72 от различных параметров.
Поэтому для нахождения потерь мощности для сердечников из таких материалов достаточно воспользоваться следующим выражением
где PV – удельные объемные потери в конкретных условиях,
Ve – эффективный объем сердечника.
Как рассчитать потери мощности в наборных сердечниках?
Удельные потери магнитного материала в наборных сердечниках превышают аналогичные у прессованных. Причиной увеличения потерь является негативное влияние технологических операций при изготовлении сердечников. Для учета данного влияния вводят коэффициент увеличения потерь kp:
где Рсн – удельные потери мощности в наборном (ленточном или шихтованном) сердечнике,
РV/ – удельные потери материала, из которого изготовлены пластины или ленты сердечника,
kp – коэффициент увеличения потерь.
Значения данного коэффициента зависят от технологии изготовления, вида материала, рабочей частоты и вида сердечника. Так для наборных сердечников (ЛС и ШС) из электротехнической стали определяется следующим выражением
А для разрезных ленточных сердечников из железоникелевых сплавов
где ψа – параметр учитывающий тип сердечника. Для разъёмных сердечников (СТ, БТ) ψа = 3, а для замкнутых (ТТ) составляет ψа = 1.
В таблице ниже приведены типовые значения коэффициента увеличения потерь
| Тип сердечника | Материал | Значения kp при частоте в Гц | ||||
| Вид | Толщина | 50 | 400 | 2000 | 10000 | |
| ШС и замкнутые ЛС | Стали и сплавы | 0,15-0,35 | 1,15 | 1,2 | 1,25 | 1,3 |
| 0,05 | — | 1,25 | 1,35 | 1,4 | ||
| Разрезные ЛС | Эл. тех. стали | 0,15-0,35 | 1,3 | 1,4 | 1,5 | 1,6 |
| 0,05 | — | 1,5 | 1,6 | 1,7 | ||
| 50Н, 33НКМС | 0,05-0,1 | — | 1,7 | 1,8 | 1,9 | |
| 80НХС, 79НМ | 0,05-0,1 | — | 2,5 | 2,8 | 3 |
Значение коэффициента добавочных потерь kp даны для сердечников средних размеров (несколько десятков Вт). Для сердечников меньших размеров значение данного коэффициента необходимо увеличить в 1,2 – 1,3 раза, а для больших сердечников уменьшить в 1,2 – 1,3 раза.
Как рассчитать потери мощности в обмотках трансформатора?
Потери мощности в обмотках трансформатора ∆рк напрямую зависят от их активного сопротивления Ri. Кроме того необходимо учитывать увеличение сопротивления из-за дополнительных факторов (увеличение температуры и скин-эффект). В общем случае потери мощности в обмотках определяются следующим выражением
где N – количество вторичных обмоток,
рki – потери в i-й обмотке,
Ii – сила тока в i-й обмотке,
Ri – сопротивление i-й обмотки.
Сопротивление обмотки рассчитывается по известной формуле, через удельное сопротивление
где lw – средняя длина витка обмотки, см,
w – число витков обмотки,
q – сечение проводника, мм2,
ρ – удельное сопротивление материала проводника, Ом*мм2/м.
Данное выражение достаточно неудобно использовать на практике. Чаще всего известны размеры сердечника, а также его основные параметры (площади и объёмы). Поэтому можно использовать следующее выражение для потерь мощности в обмотках трансформатора
где koki – коэффициент заполнения окна для i-й обмотки,
Vki – геометрический объем, занятый i-й обмоткой, см3,
ji – плотность тока для i-й обмотки, а/мм2,
Soki – площадь сечения i-й обмотки, мм2,
Если параметры ρ, j, kok одинаковы для всех обмоток либо взяты их средние значения, то получим следующее выражение
где Vk – геометрический объем, занятый всей катушкой, см3.
Как уже было сказано, при работе трансформатор нагревается. Вместе с этим изменяется активное сопротивление обмоток. Рассчитать удельное сопротивление проводника при увеличении температуры можно по следующим выражениям
где kτ — коэффициент учитывающий увеличение сопротивления из-за роста температуры,
ρ20 – удельное сопротивление проводника при температуре 20°С,
αρ – температурный коэффициент сопротивления, для меди и алюминия αρ = 0,004 1/°С,
tp – рабочая температура трансформатора, °С.
Так как в большинстве случаев в справочниках указывают удельное сопротивление материалов при температуре 20°С, то выражение можно упростить
где τ – перегрев трансформатора.
Влияние температуры на сопротивление обмотки трансформатора необходимо всегда учитывать при расчете падения напряжения на них.
Как влияет переменное напряжение на потери мощности в обмотках?
При протекании переменного электрического тока по проводнику возбуждаются вихревые токи или токи Фуко. Они направленны так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате переменный ток оказывается неравномерно распределённым по сечению провода – он как бы вытесняется на поверхность проводника. Данное явление называется скин-эффектом или поверхностным эффектом.
Вследствие этого эффекта плотность тока у поверхности проводника максимальна, а на глубине ∆ становится меньше в е раз (примерно на 70%). Глубину скин-слоя можно определить по следующему выражению
где ρ – удельное сопротивление проводника, для меди ρ = 0,0172 Ом*мм2/м,
μα — абсолютная магнитная проницаемость проводника, для меди μα = 4*π*10-7 Гн/м,
μ0 — относительная магнитная проницаемость проводника, для меди μ0 ≈ 1,
f – частота переменного тока.
Кроме скин-эффекта в проводниках, в обмотках трансформатора, проявляется так называемый катушечный эффект и эффект близости проводников, заключающегося в том что переменное напряжение за счет токов Фуко вытесняется во внешнюю часть обмотки. Данные эффекты также увеличивают сопротивление обмотки трансформатора. Для учета данный факторов вводят поправочный коэффициент kf
где m – число слоёв в обмотке.
Для определения коэффициентов M и D необходимо воспользоваться следующими выражениями
где χ – высота одного слоя обмотки, отнесённая к глубине скин-слоя,
∆ — глубина скин-слоя,
h – высота проводника,
sinh и cosh – гиперболические синус и косинус, соответственно.
Высота проводника h не эквивалентна его диаметру d. Только если производится намотка фольгой, параметр высота проводника h равен толщине фольги, в случае круглого провода высота проводника h равна
где d – диаметр проводника,
р – расстояние между центрами соседних проводников.
При использовании многожильного обмоточного провода (литцендрата), выражение для поправочного коэффициента kf будет иметь следующий вид
где mР – приведённое количество слоев обмотки,
m – реальное количество слоев обмотки,
n – количество элементарных жил в «литцендрате».
Кроме рассмотренных потерь при высокочастотном напряжении в обмотках, необходимо учитывать, что из-за наличия зазоров в сердечнике происходит искривление магнитного поля, что вызывает дополнительные вихревые токи в проводниках
Сравнение потерь в однофазной и трехфазной линиях при одинаковом токе. Потеря мощности в проводах однофазной линии передачи равна 
Действительно, потеря мощности для такой трехфазной равномерно нагруженной линии, очевидно, будет равна 
Однако при трехфазном токе общая передаваемая мощность будет в 1,732 раза больше, если напряжения между проводами и токи в проводах в случае однофазной и трехфазной линий будут одинаковы.
Сравнение потерь в однофазной и трехфазной линиях при одинаковой передаваемой мощности. Если же, не изменяя напряжения, довести мощность однофазной линии до мощности трехфазной линии, то ток в однофазной линии должен быть увеличен в 1,732 раза.
Потери в проводах при этом возрастут [формула (Б)] в 3 раза, т. е. будут в 2 раза больше потерь в трехфазной линии.

Рис. 7.10. Однофазная передача к трем лампам

Рис. 7.11. Трехфазная передача. Следует обратить внимание на то, что здесь нагрузка соединена треугольником
Пример. Определить потерю мощности в медных проводах, имеющих сечение 4 мм2, по которым на расстояние 100 м (длина линии) передается энергия, необходимая для питания трех 500-ваттных ламп при напряжении на лампах 120 В.
Предположим сначала, что энергия передается однофазным переменным током (рис. 7.10).
Общая мощность ламп 


Сопротивление каждого из проводов определим по формуле

(полагая удельное сопротивление 
Мощность, теряемая в проводах, при этом

Предположим теперь, что согласно, схеме, представленной на рис. 7.11, передача энергии к тем же трем лампам производится трехфазным током по трехпроводной линии при помощи проводов того же сечения. –
В этом случае мощность Р, ток I (линейный) и напряжение U (линейное, равное напряжению в лампах) будут связаны уравнением

Следовательно, при той же. мощности Р=1500 Вт и при том же напряжении 

Сопротивление проводов нам известно: для каждого провода 
А так как потеря мощности теперь происходит в трех проводах, то находим, что общая потеря мощности составляет

Таким образом, при передаче трехфазным током потеря мощности будет в 2 раза меньше, чем при передаче однофазным током.
Преимущества трехфазных систем. Из рассмотренных примеров достаточно отчетливо видим преимущества трехфазного тока при передаче электрической энергии по проводам. Но самым существенным достоинством трехфазных систем является их удобство для устройства электрических двигателей.