Как найти поток через боковую поверхность

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.

Найти поток вектора через боковую поверхность

        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6

        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12

    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18

    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24

    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30

        7.14 Найти поток векторного поля         через замкнутую поверхность    
.

Решение

        Поверхность         ограничивает конус, у которого радиус равен         , а высота         .
        Воспользуемся формулой Гаусса-Остроградского

. Здесь

– дивергенция векторного поля.

        Тогда поток

        Где

– объём конуса.
        Поэтому

Ответ:     .

Поток векторного поля: теория и примеры

Понятие потока векторного поля и его вычисление как поверхностного интеграла

Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.

Пусть в некоторой области пространства задано векторное поле

и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора – непрерывные функции координат x, y, z точки M.

Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл

.

Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода

.

.

поток векторного поля можно вычислить и как поверхностный интеграл второго рода

.

Направление и интенсивность потока векторного поля

Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.

Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля – это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.

Если поток векторного поля – поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k – коэффициент теплопроводности, а u(M) – температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .

Вычисление потока векторного поля: примеры

Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy – треугольник AOB .

Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:

.

Длина вектора нормали:

.

Единичный вектор нормали:

.

Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .

Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:

Выразим переменную “зет”:

Продолжаем вычислять интеграл и, таким образом, поток векторного поля:

Получили ответ: поток векторного поля равен 64.

2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем

.

Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:

Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:

Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:

Осталось только сложить все три интеграла:

.

Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.

Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.

1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:

.

Длина этого вектора:

,

единичный вектор нормали (орт):

.

Скалярное произведение векторного поля и единичного нормального вектора:

Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода

.

Выразим “зет” и продифференцируем то, что уже можно продифференцировать:

2) Представим поток векторного поля в виде поверхностного интеграла второго рода:

.

Первый и второй интегралы берём со знаком “минус”, так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.

Вычисляем первый интеграл:

Вычисляем второй интеграл:

Вычисляем третий интеграл:

Складываем три интеграла и получаем тот же самый результат:

.

Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .

Поток векторного поля представим в виде поверхностного интеграла второго рода:

Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:

Вычисляем второй интеграл:

В сумме получаем искомый поток векторного поля:

.

[spoiler title=”источники:”]

http://www.kvadromir.com/kuznecov_vector_analiz_7.html

http://function-x.ru/fields_stream.html

[/spoiler]

2.1.1. Вычисление методом проектирования на одну

из координатных
плоскостей

Пусть поверхность

задана уравнением

.

Единичный вектор
нормали

,
но, как известно,

.
Следовательно,

.

Знак в правой части
берется так, чтобы получить нормальный
вектор

именно к выбранной стороне поверхности.

Если поверхность
задана уравнением

,
то

.

Знак «+» соответствует
выбору верхней стороны поверхности,
нормаль к которой образует острый угол
с осью

и, следовательно, направляющий косинус
положителен.

Известно также,
что

и

.

Пусть поверхность

взаимно однозначно проектируется на
плоскость

в область

,
тогда вычисление потока векторного
поля через поверхность

сводится к вычислению двойного интеграла

по области

:

.
(2.2)

Аналогично, если
поверхность

взаимно однозначно проектируется на
плоскость

или

,
то поток вычисляется по формулам

;

.

Пример 2.1. Найти
поток векторного поля

через поверхность конуса

и плоскость

.

Решение. Обозначим
потоки векторного поля:

через

боковую
поверхность конуса

и

через плоскость

.

Тогда
весь поток П=П₁
+П₂ =

.

Вычислим

.
Уравнение

:

.

Проекция вектора

на ось

отрицательна.

;

.

Из выражения для
(2.2.) найдем

.

.

Вычислим

.
Уравнения поверхности

:

,

,

(На поверхности

),

.

Следовательно,

.

Пример 2.2. Найти
поток векторного поля

через верхнюю сторону треугольника с
вершинами в точках

,

,

.

Решение. Уравнение
плоскости

составим как уравнение

плоскости,
проходящей через три точки

.
Следовательно,

,

.

.

Пример 2.3. Вычислить
поток векторного поля

через внешнюю
сторону однополостного гиперболоида

,ограниченного плоскостями

.

Решение. Данная
поверхность проектируется взаимно
однозначно на плоскость

в область

,
ограниченную окружностями

и

.

Находим внешнюю
нормаль

:


.

Т
.к.

образует с осью

тупой угол

(рис.2.4),
то берем знак минус и, значит,

.

Находим скалярное
произведение


.

Применяя формулу

,

получим

Рис.2.4

.

Переходя к полярным
координатам

,
,
будем иметь

2.1.2. Вычисление потока методом проектирования

на все
три координатные плоскости

Пусть поверхность

взаимно однозначно проектируется на
все три координатные плоскости:

Тогда поток
векторного поля

равен

(2.3.)

где знак перед
каждым из двойных интегралом берется
соответственно таким, каков знак

,

,

на поверхности

.

Пример 2.3. Найти
поток векторного поля

через треугольник, получаемый при
пересечении плоскости

с координатными плоскостями (выбор
указан на рис. 2.5).

Р
ешение.
Найдем

.
P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z

(выразили
из уравнения плоскости)

.

По
формуле (2.3) получим

Рис. 2.5

.

При вычислении
потока векторного поля через боковую
поверхность кругового цилиндра или
через сферу удобно пользоваться
соответственно цилиндрическими или
сферическими координатами.

Пример 2.4. Найти
поток векторного поля

через часть
сферической поверхности

,
расположенную в первом октанте.

Решение. Найдем
вектор- градиент

,

тогда единичный
вектор

;

.

По условию задачи
поверхность находится в первом октанте,
т.е.

,

,
элемент площади в сферических координатах
равен

.
Следовательно, поток через часть сферы
вычисляется по формуле

.

2.1.3. Вычисление
потока методом введения

криволинейных
координат на поверхности

В некоторых случаях
при вычислении потока векторного поля
через данную поверхность
S
возможно выбрать на самой поверхности
простую систему координат, в которой
удобно вычислять поток, не применяя
проектирования на координатные плоскости.

Рассмотрим частные
случаи.

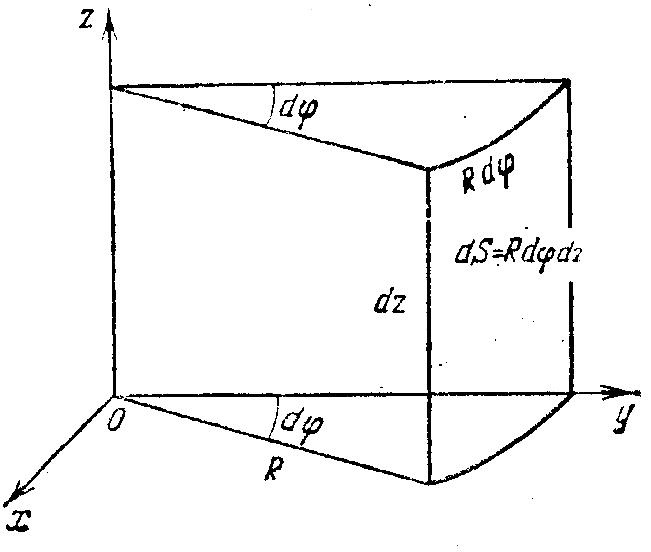
Случай 1). Пусть
поверхность S
является частью кругового цилиндра

,
ограниченного поверхностями

и

.

Полагая

,
будем иметь для данной поверхности

,

, а для элемента
площади dS
получаем следующее выражение (рис.
2.6.):

.

Тогда поток
векторного поля a

через
внешнюю сторону поверхности S

вычисляется по
формуле

,
(2.4)

где

Рис. 2.6

Пример 2.5. Вычислить
поток радиуса-вектора

через боковую
поверхность кругового цилиндра

,
ограниченного снизу плоскостью

,
а сверху – плоскостью

.

Р
ешение.
В данном случае (рис. 2.7) имеем

.

Переходя
к координатам на цилиндре

,
будем иметь

,

Согласно
формуле (2.4) поток вектора r

будет
равен

Но
так как на цилиндре

Рис.
2.7

то

и,
следовательно,

Случай 2). Пусть
поверхность S является
частью сферы

,
ограниченной коническими поверхностями,
уравнения которых в сферических
координатах имеют вид

и
полуплоскостями

.

Положим для точек
данной сферы

г
де

.

Тогда для элемента
площади dS
полу- чим (рис. 2.7)

.

В этом случае поток
векторного поля а
через внешнюю часть S
сферы вычисляется по формуле

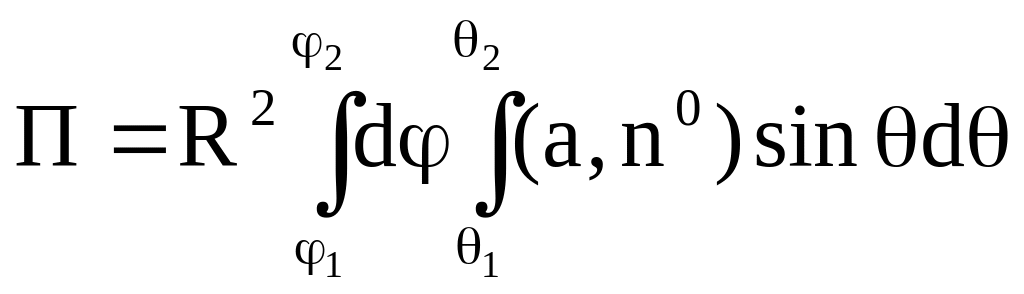
, ( 2.5)

Рис. 2.8
где

Пример 2.6. Найти
поток вектора

через
часть поверхности сферы

,
расположенную в первом октанте, в
область, где

.

Решение. В данном
случае имеем

,

,

Введем
на сфере

координаты

и

так, что

Тогда
будет иметь

и,
применяя формулу (2.5), получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание книги

Предыдующая страница

§7. Механика жидкости и газа

7.3 Поток жидкости.

Пусть нам известно поле скоростей движущейся жидкости. Рассчитаем объем жидкости, протекающей в единицу времени через некоторую воображаемую площадку, часто эту характеристику называют расход, или поток жидкости Ф. Проще всего решить данную задачу для однородного потока жидкости.

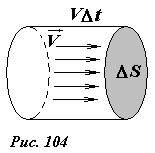
Пусть воображаемая площадка, площадью ΔS расположена перпендикулярно однородному потоку жидкости, движущейся со скоростью (~vec V) (рис. 104). За промежуток времени Δt через площадку пройдет жидкость, находящаяся на расстоянии меньшем, чем VΔt, объем этой жидкости будет равен VΔt·ΔS . Итак, в единицу времени, через площадку пройдет объем жидкости равный

(~Delta Phi = V Delta S) . (1)

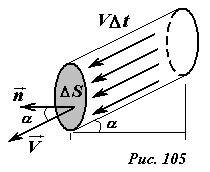
Пусть площадка расположена под некоторым углом к набегающему потоку жидкости, который, по-прежнему, считаем однородным (рис. 105). Ориентацию площадки удобно задавать, указывая вектор нормали к этой площадке (~vec n) – модуль, которого равен единице, а направлен перпендикулярно площадке. Пусть вектор скорости жидкости (~vec V) образует угол α с вектором нормали (~vec n) к площадке, площадью ΔS. Объем жидкости, протекающей через площадку за время Δt, может быть найден по формуле VΔtcos α·ΔS. Следовательно, расход (поток) жидкости через площадку определяется выражениями

(~Delta Phi = V cos alpha Delta S = (vec V cdot vec n) Delta S = V_n Delta S) . (2)

где (~(vec V cdot vec n) = V cos alpha) – скалярное произведение векторов (~vec V) и (~vec n) ; (~V_n) – нормальная к площадке компонента вектора скорости. Отметим, что согласно определению поток может быть как положительным, так и отрицательным. Знак потока определяется выбором направление нормали к поверхности, в конце концов, этот произвол, обусловлен выбором положительного направления движения жидкости.

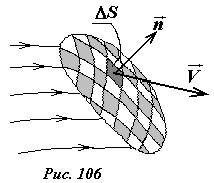
Наконец, в произвольном поле скоростей, объем жидкости, протекающий в единицу времени через произвольную поверхность, подсчитаем следующим образом (рис. 106): разобьем поверхность на малые площадки ΔS (которые будем считать плоскими), определим вектор скорости жидкости (~vec V) на этой площадке (который в пределах площадки будем считать постоянным), запишем выражение (2) для расхода жидкости через площадку, просуммируем по всем площадкам рассматриваемой поверхности.

(~Phi = Delta Phi_1 + Delta Phi_2 + Delta Phi_3 + ldots = sum_{i} {Delta Phi_i} = sum_{i} {V_i cos alpha_i Delta S_i}) . (3)

Эта сумма называется потоком вектора скорости через заданную поверхность.

Подобную сумму в некоторых случаях можно вычислить достаточно просто, иногда ее вычисление может быть громоздким. Заметьте, что скорость жидкости мы определяем в каждой точке (говорят, что это точечная характеристика), поток через поверхность определяется движением жидкости в некоторой части пространства, поэтому эта характеристика является интегральной, описывающей свойства движения обобщенно, усреднено для этой части пространства.

Оказывается, что некоторые законы движения жидкости могут быть сформулированы как теоремы для потока жидкости. С использованием таких теорем можно решать многочисленные и сложные задачи.

Приведем примеры таких «очевидных» теорем.

«Первая теорема о потоке несжимаемой жидкости»: Если в некоторой области движущейся несжимаемой жидкости отсутствуют источники и стоки, то поток жидкости, через любую замкнутую поверхность равен нулю Ф = 0.

Конечно, все реальные жидкости могут изменять свой объем, под действием внешних сил. Однако изменение объема жидкостей обычно настолько мало, что им можно пренебречь, именно такое приближение используется в модели несжимаемой жидкости.

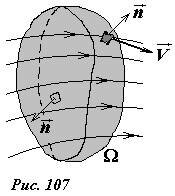
Для замкнутой поверхности положительной принимается внешняя нормаль, направленная наружу от объема, ограниченного рассматриваемой поверхностью (рис. 107). В этом случае на одних частях поверхности поток будет положительным (там, где жидкость вытекает из ограниченного объема), на других отрицательным (там, где жидкость втекает внутрь объема). Так как объем жидкости внутри поверхности остается постоянным, то количество жидкости втекающей внутрь равно количеству жидкости вытекающей наружу – вот смысл сформулированной теоремы.

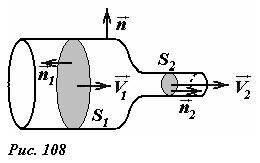
Применим эту теорему к жидкости, протекающей по трубе переменного сечения, сочлененной из двух труб, площадь поперечного сечения первой S₁, второй S₂ (рис. 108). В качестве поверхности, к которой применим теорему о потоке жидкости, выберем часть боковой поверхности в месте сочленения и две плоских площадки перпендикулярных оси трубы, находящиеся в широкой и узкой части. Скорость жидкости в широкой части обозначим V₁, а в узкой части V₂. Поток через боковую поверхность равен нулю Ф_b = 0, так как здесь векторы скорости и нормали взаимно перпендикулярны, поток через площадку в широкой части трубы равен Ф₁ = –V₁S₁ (знак минус появился, так как векторы направлены в противоположные стороны), поток через площадку в узкой части трубы Ф₂ = V₂S₂. Таким образом, поток через оговоренную поверхность равен

(~Phi = Phi_1 + Phi_b + Phi_2 = – V_1 S_1 + V_2 S_2 = 0) .

Из этого соотношения получим уравнение, связывающее скорости в разных частях трубы V₁S₁ = V₂S₂ . Это уравнение является частным случаем уравнения неразрывности, смысл которого очевиден: «сколько влилось, столько вылилось». Можно сказать, что теорема о потоке несжимаемой жидкости выражает общий случай уравнения неразрывности.

Обобщим данную теорему. Пусть в некоторой области движущейся жидкости имеются источники (и стоки) жидкости. В качестве характеристики источника будем использовать его расход q: количество (объем) жидкости, вытекающей из источника в единицу времени. Будем считать, что «сток» тоже источник, расход которого отрицателен. Из источника жидкость вытекает, в сток стекает: математическая же характеристика для них едина, но отличается знаком.

«Вторая теорема о потоке несжимаемой жидкости»: Поток несжимаемой жидкости через любую замкнутую поверхность равен сумме расходов источников, находящихся внутри поверхности Ф = q . Смысл и доказательство этой теоремы аналогичны предыдущей: «сколько вливается, столько же выливается». Заметим, что если внутри рассматриваемой поверхности находятся источники, то поток жидкости через поверхность не зависит от расположения источников. Подчеркнем – распределение скоростей (то есть скорости в разных точках), конечно, зависит от положения источников, но суммарный поток через поверхность полностью определяется суммарным расходом источников. Если же источник находится вне рассматриваемой поверхности, то он изменяет распределение скоростей, но не изменяет суммарный поток через рассматриваемую поверхность.

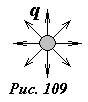
Применим эту теорему к следующей задаче. Пусть внутри очень большого объема жидкости находится точечный изотропный источник, расход которого равен q. Найдем распределение скоростей жидкости возле источника. Изотропным называется источник, посылающий жидкость во все стороны одинаково. Реально такой источник можно представить в виде сферы с большим числом маленьких отверстий, через которые вытекает жидкость (рис. 109). Понятно, что жидкость будет растекаться от источника во все стороны одинаково, то есть изотропно. Иными словами, скорость течения жидкости по модулю одинакова во всех точках, находящихся на одинаковом расстоянии r от источника, вектор скорости направлен во всех точках радиально от источника. Эти соображения позволяют нам найти зависимость скорости жидкости от расстояния до источника.

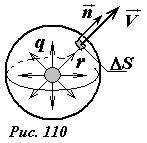
В качестве поверхности, к которой применим теорему о потоке, используем сферу, радиуса r, в центре которой находится источник (рис. 110). Выделим на поверхности сферы небольшую площадку площадью ΔS. На поверхности сферы направление вектора скорости совпадает с направлением внешней нормали, поэтому поток жидкости через эту площадку равен ΔФ = VΔS. Далее, заметим, что на всех участках сферы, модуль скорости одинаков. Поэтому суммирование потоков через все участки сферы сводится к суммированию площадей этих площадок. Таким образом, суммарный поток через поверхность сферы равен произведению модуля скорости на площадь сферы Ф = 4πr²V. С другой стороны, по теореме о потоке, эта величина равна расходу источника Ф = q. Приравнивая эти выражения 4πr²V = q, получим искомое выражение для скорости жидкости

(~V(r) = frac{q}{4 pi r^2}) . (4)

Отметим, важное обстоятельство: сформулированная теорема о потоке жидкости справедлива для любой поверхности. Успех в решении этой задачи обусловлен правильным выбором ^[1] поверхности: во всех точках сферы модуль скорости постоянен, а угол между скоростью и нормалью равен нулю, именно эти обстоятельства позволили выразить суммарный поток простой формулой. Для другой поверхности теорема о потоке также будет выполняться, но в разных точках этой поверхности могут быть разные скорости, разные углы – поэтому получить выражение для скорости в разных точках невозможно.

Заметим, что сформулированные теоремы не являются математическими, так как они явным образом используют физические свойства жидкости, а именно, ее слабую сжимаемость (т.е. возможностью использовать модель несжимаемой жидкости). Для газов, приведенные теоремы использовать нельзя, так объемы газов могут изменяться в широких пределах, поэтому для формулировки подобных теорем необходимо привлекать физические свойства газов – например, зависимость плотности газа от температуры и давления.

Таким образом, мы показали, что понятие потока оказывается полезным для описания векторного поля. В дальнейшем мы будем широко использовать эту математическую конструкцию над векторным полем для описания физических свойств других реальных полей. В общем случае, если задано векторное поле, то есть в любой точке пространства с координатами (x,y,z) определен некоторый вектор (~vec A), то потоком вектора через малую площадку ΔS с нормалью (~vec n) называется величина (~Delta Phi_{vec A} = (vec A cdot vec n) Delta S = A Delta S cos alpha) , где α – угол между вектором поля и нормалью к площадке.

В случае поля скоростей движения несжимаемой жидкости поток этого поля имеет наглядный смысл – объем жидкости, протекающий через поверхность в единицу времени. Для других полей найти смысл потока может быть затруднительно, в таких случаях к потоку следует относиться как к полезной математической величине.

Примечания

1. ↑ Произволом в выборе надо пользоваться с умом.

Следующая страница