Как найти поток энергии через поверхность

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 ноября 2016 года; проверки требуют 5 правок.

Поток энергии
Размерность	L2MT−3
Единицы измерения
СИ	Вт
СГС	эрг·с−1

Пото́к эне́ргии — количество энергии, переносимое за единицу времени через рассматриваемую поверхность. В СИ измеряется в ваттах. Стандартного обозначения данной величины не существует, могут использоваться буквы , и другие.

Поток находится как сумма (интеграл) элементарных, то есть через бесконечно малые участки поверхности, потоков:

Каждый из таких элементарных вкладов равен произведению прошедшей за единицу времени через малый участок энергии на единичный вектор в направлении переноса энергии и на единичный вектор нормали к площадке (при этом , где — векторный элемент площадки):

.

Если речь идёт об энергии, переносимой оптическим излучением, то вместо термина «поток энергии» используют эквивалентный для такого случая термин «поток излучения»^[1][2].

Если речь идёт о переносе тепла, используется термин «тепловой поток» — количество теплоты, проходящее через изотермическую поверхность в единицу времени.

Говоря о потоке энергии, иногда имеют в виду другую величину, а именно плотность потока энергии, измеряемую в Вт/м², причём эту плотность потока рассматривают как вектор, направленный по направлению переноса энергии в данной точке. Например, для теплового потока его плотность направлена противоположно градиенту температуры, а по величине равна потоку тепла через изотермическую поверхность единичной площади. Иные названия этой же величины: удельный тепловой поток, тепловая нагрузка^[3].

Строго, вектор плотности потока энергии и поток энергии связаны соотношением

,

где вид выражения для следует из представленной выше формулы для . Аналогичным образом связываются плотность потока и поток любой физической величины, не только энергии.

См. также[править | править код]

• Мощность
• Плотность потока энергии
• Поток излучения

Примечания[править | править код]

_{Рассмотрим
плоскую
продольную волну,
распространяющуюся в направление оси
Х.}

_{Пусть
волна является бегущей,
т.е. ее
распространение связанно с распространением
в пространстве энергии колебаний.}

<sub>Уравнение
волны

(2.8)</sub>

_{Выделим
в среде элементарный
объем
настолько малый, что скорости движения
и деформации во всех его точках одинаковы.}

_{Выделенный
объем
обладает кинетической энергией}

_{где
–масса объема,
–скорость.}

_{Разделив
эту энергию
на величину объема, получим объемную
плотность кинетической энергии}

_(2.9)

_{Рассматриваемый
элемент объема обладает потенциальной
энергией упругой деформации.}

_{Чтобы
найти эту энергию,}

• _{представим
  выделенный объем в виде стержня с
  площадью поперечного сечения S
  и длиной
  ..}

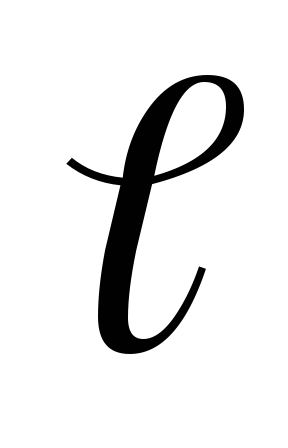• _{Один
  конец стержня закреплен, ко второму
  приложим растягивающую силу
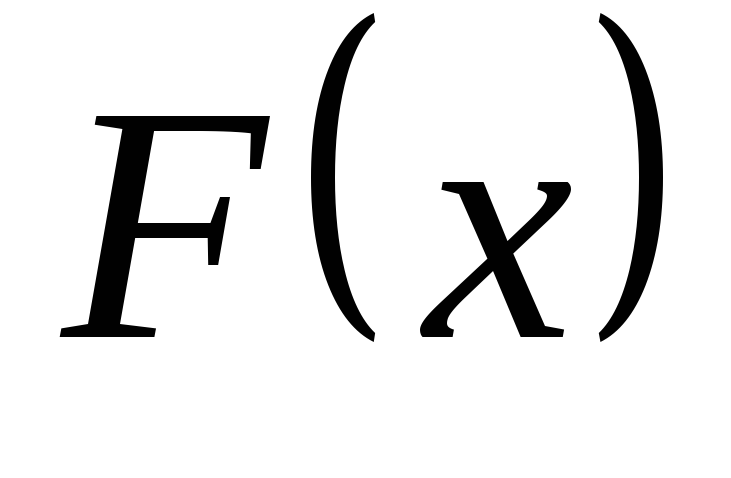  и будем медленно увеличивать ее от 0
  до.}

• _{Удлинение
  стержня будет при этом меняться от 0 до
  х.}
  

• _{По
  закону Гука
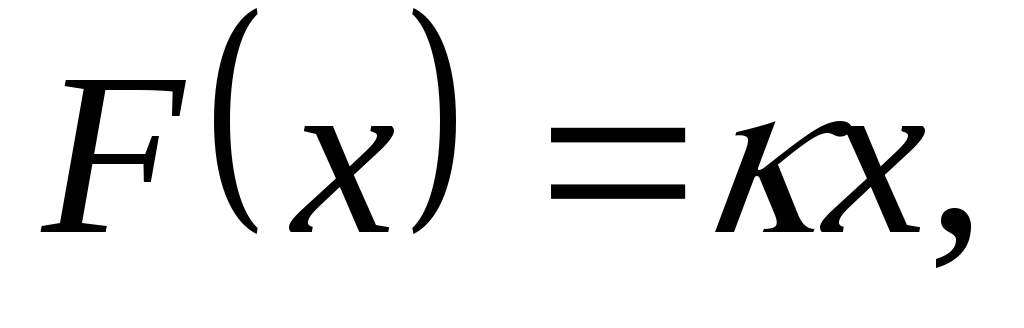  где–коэффициент
  упругости.}
  

• _{Работа
  силы упругости в этом процессе}
  

_{Эта
работа идет
на увеличение упругой энергии
U
. т.е.}

_{Плотность
этой энергии
(2.10)}

_{где
–напряжение,
Е –
модуль Юнга,
–относительная
деформация.}

_{Так
как фазовая
скорость
волны
,
то,
и}

_{объемная
плотность потенциальной энергии
равна}

Под объемной
плотностью энергии упругих волн понимают
объемную плотность
механической
энергии среды, обусловленную
распространением этих волн:

(2.11)

Продифференцируем
уравнение (2.8) сначала по времени, а затем
по координате х

Подставив в (4) и
заменив
,
имеем

– в каждой точке
среды, охваченной волновым движением,
объемные плотности кинетической и
потенциальной энергий являются
одинаковыми функциями времени.

Объемная плотность
энергии волныизменяется
с течением времени, это связанно с
процессами распространения волн, так
как волновой процесс сопровождается
переносом энергии при вовлечении в
колебательное движение все новых частиц.
Поэтому объемная плотность энергии
волн зависит как от координат, так и от
времени.

Среднее за период
значение объемной плотности энергии.

Плотность
энергии волны и ее среднее значение
пропорциональны плотности среды
,
квадрату частотыи квадрату амплитуды.

Таким образом,
среда, в которой распространяется
волна, обладает дополнительной энергией,
которая доставляется от источника
колебаний в различные т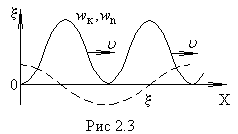очки
среды самой волной, т.е. волна переносит
с собой энергию. Скорость переноса
энергии волной равна скорости перемещения
в пространстве поверхности, соответствующей
максимальному значению объемной
плотности энергии волны. Для синусоидальных
волн эта скорость равна фазовой скорости(рис 2.3).

Количество
энергии, переносимое волной через
некоторую поверхность в единицу времени,
называется потоком энергии через
эту поверхность.

Если через данную
поверхность за время dt
переносится энергияdW,

то поток энергии
Фравен

Поток энергии в
разных точках различен.

Для характеристики
значения энергии в разных точках
пространства вводится вектор плотности
потока энергии (вектор
Умова):

• численно равен
  потоку энергии через единичную площадку,
  помещенную в данной точке перпендикулярно
  к направлению переноса энергии

• направлен в
  сторону переноса энергии: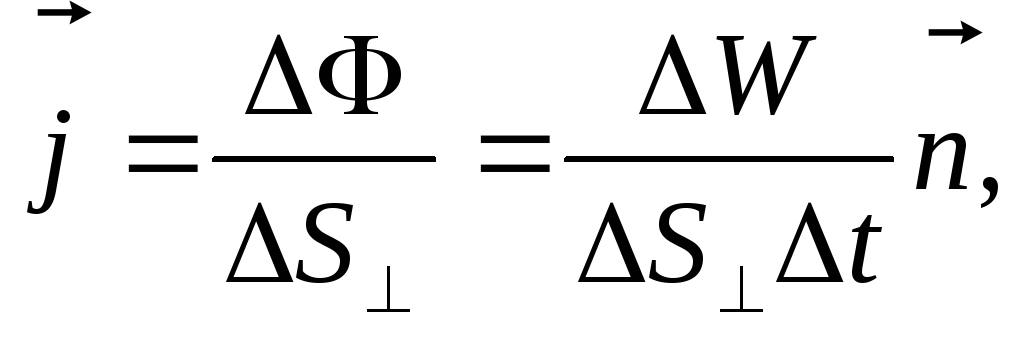

где
–единичный вектор, совпадающий по
направлению с распространением волны.

Очевидно, за время
через площадкубудет перенесена энергия,
заключенная в объеме цилиндра с основаниеми высотой,
где– фазовая скорость волны,

Тогда плотность
потока энергии

здесь
–вектор, численно равный фазовой
скорости и направленный в сторону
переноса энергии волной.

Интенсивностью
волны I
называется модуль среднего значения
вектора Умова.Интенсивность
волны численно равна энергии, переносимой
волной за единицу времени сквозь единицу
площади поверхности, нормальной к
направлению распространения волны.

Для синусоидальной
волны

Поток энергиичерез некоторую поверхность S
равен потоку вектора
через эту поверхность

Среднее значение
потока энергии через произвольную
волновую поверхность незатухающей
сферической волны( в каждой точке
поверхности векторыисовпадают):

где r
–радиус волновой поверхности.

Энергия волны
не поглощается средой, поэтому средний
поток энергии через сферу любого радиуса
должен иметь одинаковое значение, т.е.
выполняется соотношение

– амплитуда
незатухающей сферической волны обратно
пропорциональна расстояниюrот источника волны.

Тогда средняя
плотность потока энергии пропорциональна
квадрату расстояния от источника.

В случае плоской
затухающей волны

• амплитуда
  убывает с расстоянием по закону,

• средняя
  плотностьпотока энергии (т.е.
  интенсивность) убывает по закону,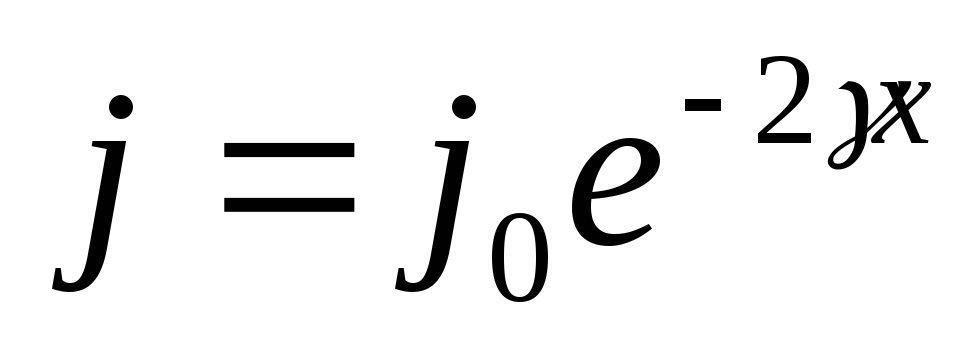

где
–коэффициент поглощения волны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  08.03.2015302.08 Кб81Л3.doc

• #

  08.03.2015387.07 Кб60Л4.doc
• #

  08.03.2015440.83 Кб40Л5.doc

• #

  08.03.2015302.59 Кб71Л6.doc

• #
• #
• #
• #

Мы уже много раз показывали, что электромагнитное поле обладает энергией. Значит, распространение электромагнитных волн связано с переносом энергии (подобно тому, как распространение упругих волн в веществе связано с переносом механической энергии). Сама возможность обнаружения ЭМВ указывает на то, что они переносят энергию.

Для характеристики переносимой волной энергии русским ученым Н.А. Умовым были введены понятия о скорости и направлении движения энергии, о потоке энергии. Спустя десять лет после этого, в 1884 г., английский ученый Джон Пойнтинг описал процесс переноса энергии с помощью вектора плотности потока энергии.

Введем вектор – приращение плотности электромагнитной энергии, где сама величина w определяется интегралом:

.

Объемная плотность энергии w электромагнитной волны складывается из объемных плотностей и электрического и магнитного полей:

.

Учитывая, что , получим, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова, т.е. . Поэтому

.

Умножив плотность энергии w на скорость υ распространения волны в среде, получим модуль плотности потока энергии – поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени:

Так как векторы и взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ ] совпадает с направлением переноса энергии, а модуль этого вектора равен EH (рис. 6.8).

Вектор плотности потока электромагнитной энергии называется вектором Умова–Пойнтинга:

Вектор направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

В сферической электромагнитной волне, излучаемой ускоренно двигающимися зарядами, векторы направлены по параллелям, векторы – по меридианам, а поток энергии – по нормали (рис. 6.9).

Векторы Умова–Пойнтинга зависят от пространства и времени, так как от них зависят модули векторов напряженности электрического и магнитного полей. Поэтому часто пользуются параметром, называемым интенсивностью – модуль среднего значения вектора Умова–Пойнтинга:

Интенсивность пропорциональна квадрату амплитуды:

Зависимость интенсивности излучения от направления называют диаграммой направленности. Такая диаграмма для линейного излучателя показана на рис. 6.10.

Как доказал Герц, диполь сильнее всего излучает в направлении перпендикулярном по отношению к собственному направлению.

Ускоренно двигающиеся заряды излучают электромагнитную энергию в окружающее пространство. Вектор направлен вдоль радиуса и убывает обратно пропорционально r 2 . Излучение максимально в направлении, перпендикулярном вектору , и отсутствует вдоль этого вектора. Поэтому диаграмма направленности диполя имеет вид двух симметричных лепестков, как показано на рис. 6.10.

Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление ЭМВ объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля действию силы. Однако, значение этого давления ничтожно мало.

Давление света и электромагнитный импульс настолько малы, что непосредственное их измерение затруднительно. Так, зеркало, расположенное на расстоянии 1 м от источника света в миллион свечей (кандел), испытывает давление 10 – 7 Н/м 2 . Давление излучения Солнца на поверхность Земли равно 4,3×10 – 6 Н/м 2 , а общее давление излучения Солнца на Землю равно 6×10 8 Н, что в 10 13 раз меньше силы притяжения Солнца.

Световое давление было впервые обнаружено и измерено в 1899 г. в Москве русским ученым П.Н. Лебедевым (1866-1912). Его результаты, как и более точные измерения последующих исследователей, согласуются с теорией в пределах ошибок опыта – до 2 %.

На рис. 6.11 изображен прибор, с помощью которого было измерено давление света, – радиометр. Свет, отраженный посеребренной поверхностью каждой лопасти 2, 3, передает вдвое больший импульс по сравнению со светом, поглощенным зачерненной поверхностью 1, 4. Вследствие этого лопасти начинают вращаться по часовой стрелке.

Давление света можно рассчитать по формуле:

,

где J – интенсивность света, K – коэффициент отражения.

Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой ЭМВ.

Давление света играет существенную роль в двух противоположных по масштабу областях явлений.

Так, например, гравитационное притяжение верхних слоев звезд к центру в значительной мере уравновешивается силой давления светового потока, идущего от центра звезды наружу. В атомных процессах существенной является отдача, испытываемая возбужденным атомом при излучении им света в силу малости массы атома. Световое давление может создавать ускорение атомов до , где g – ускорение свободного падения.

Впервые гипотеза о световом давлении была высказана в 1619 г. немецким ученым И. Кеплером (1571-1630) для объяснения отклонения хвостов комет, пролетающих вблизи Солнца (рис. 6.12).

Возможными областями физического применения светового давления могут служить процессы разделения смеси изотопов газов, ускорение микрочастиц и создание условий для протекания управляемой термоядерной реакции.

Электромагнитная масса и импульс

Существование давления ЭМВ приводит к выводу о том, что электромагнитному полю присущ механический импульс.

Выражая импульс как (поле в вакууме распространяется со скоростью света с), получим

,

Это соотношение между массой и энергией ЭМП является универсальным законом природы, справедливым для любых тел независимо от их внутреннего строения.

Импульс электромагнитного поля, связанного с движущейся частицей, – электромагнитный импульс – оказался пропорциональным скорости частицы υ, что имеет место и в выражении для обычного импульса mυ, где m – инертная масса заряженной частицы. Поэтому коэффициент пропорциональности в полученном выражении для импульса называют электромагнитной массой:

где е – заряд движущейся частицы, а – ее радиус.

И даже если тело не обладает никакой иной массой, оказывается, что между импульсом и скоростью заряженной частицы существует соотношение:

Это соотношение как бы раскрывает происхождение массы – это электродинамический эффект. Движение заряженной частицы сопровождается возникновением магнитного поля. Магнитное поле сообщает телу дополнительную инертность – при ускорении затрачивается работа на создание магнитного поля, при торможении –работа против затормаживающих сил индукционного происхождения. По отношению к движущемуся заряду электромагнитное поле является средой, неотделимой от заряда.

В общем случае можно записать, что полный импульс равен сумме механического и электромагнитного импульсов; возможно, что другие поля вносят и иные вклады в полную массу частицы, но, определенно, в полной массе есть электромагнитная часть:

, .

Если учесть релятивистские эффекты сокращения длины и преобразования электрических и магнитных полей, то для электромагнитного импульса получается также релятивистски инвариантная формула:

Таким же образом изменяется релятивистский механический импульс.

Плотность энергии электромагнитной волны. Вектор Пойнтинга. Опыт Лебедева

Электромагнитные волны переносят в пространстве энергию. Энергия электромагнитного поля W — это количественная характеристика электромагнитного взаимодействия:

где iv — объемная плотность энергии поля. Объемная плотность w энергии электромагнитного поля складывается из объемных плотностей w_e и w_m электрического и магнитного полей и, если среда не содержит сегнето- электриков и ферромагнетиков, определяется так:

I

где Е и Н — соответственно напряженности электрического и магнитного полей волны в произвольный момент времени в данной точке пространства.

Так как из выражения (20.4), то

Формулы (20.8) и (20.9) характеризуют плотность энергии электромагнитной волны в любой момент времени в любой точке пространства.

Вектор П плотности потока энергии электромагнитной волны называется вектором Пойнтинга (Умова — Пойнтинга):

По модулю вектор П определяет энергию, переносимую волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны:

где v — фазовая скорость волны, равная скорости переноса энергии (при отсутствии дисперсии). Направление вектора П совпадает с направлением переноса энергии, т.е. с направлением распространения электромагнитной волны.

Единица плотности потока энергии электромагнитной волны в СИ —

ватт на метр в квадрате (Вт/м 2 ).

Если исходить из представлений о локализации электромагнитной энергии в пространстве, то можно заключить, что она будет изменяться в данном объеме V как за счет ее вытекания из объема через поверхность S, так и за счет того, что поле передает свою энергию веществу (заряженным частицам), т.е. производит работу над веществом.

Согласно теореме Пойнтинга, убыль энергии W электромагнитного поля, заключенного в объеме V, за единицу времени определяется как

где П – вектор Пойнтинга; И — наружная нормаль к поверхности S; dS и dV — элементы поверхности и объема соответственно; j — плотность тока; Ё — напряженность электрического поля. Интеграл фп-яй^ опре-

деляет поток энергии, переносимый электромагнитным полем сквозь замкнутую поверхность S, ограничивающую рассматриваемый объем V.

Интеграл J j ? EdV описывает работу, совершаемую сторонними ЭДС над

токами проводимости, и джоулевы потери — потери энергии электромагнитного поля за счет ее преобразования в энергию теплового движения среды.

Скалярная величина /, равная модулю среднего значения вектора Пойнтинга, называется интенсивностью электромагнитной волны:

Из (20.11) следует, что интенсивность плоской гармонической электромагнитной волны пропорциональна квадрату амплитуды ее электрической составляющей:

Опыт Лебедева. Максвелл теоретически показал, что электромагнитные волны, отражаясь или поглощаясь в телах, на которые они падают, оказывают на них давление. Это давление возникает в результате воздействия магнитного поля волны на электрические токи, возбуждаемые электрическим полем той же волны. Давление электромагнитной волны на тело определяется выражением

где р — коэффициент отражения электромагнитной волны’, это отношение интенсивности отраженной волны к интенсивности падающей (при полном отражении р = 1, при полном поглощении р = 0); (w) — среднее за период волны значение объемной плотности энергии электромагнитного поля. Если волна падает на поверхность тела наклонно, под углом 0 к нормали, то (w) = (7cos0)/c.

Давление электромагнитного излучения обычно очень мало. Например, давление солнечного излучения на Земле составляет около К)- 6 Па, что в 10 10 раз меньше атмосферного давления. Экспериментальное доказательство существования давления электромагнитных волн, подтвердившее теорию Максвелла, было получено П. Н. Лебедевым. В 1899 г. он обнаружил и измерил давление света на твердые тела, а в 1910 г. — на газы. В эксперименте, выполненном в 1899 г., объект исследования имел вид подвижного крылышка. Лебедев обнаружил поворот этого крылышка под действием падающего на него света. Величина светового давления оказалась соответствующей формуле (20.15).

Давление света играет большую роль в астрофизике и атомных явлениях. Например, наряду с давлением газа давление света обеспечивает стабильность звезд, противодействуя силам гравитации.

Лекция №10. Механические волны

6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность

Пусть в некоторой среде распространяется в направлении оси 0х плоская продольная волна $$S=Acos(ωt-kx+φ)$$ . Выделим в среде элементарный объем ΔV , настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными. Выделенный объем обладает кинетической энергией $$K=<1 over 2>mv^2$$ . Если масса $$m=ρΔV$$ , а $$v=<∂S over ∂t>$$ , то

Потенциальная энергия упругой деформации рассматриваемого объема

где $$k=$$ ; $$l_0$$ − первоначальная длина рассматриваемого объема; $$ε=<Δl over l_0>$$ − относительная деформация объема; $$ΔV=$$ − первоначальный объем. Используя формулу (6.4.8) и, учитывая, что $$ε=<∂S over ∂x>$$ , получим

Тогда полная энергия упругой волны

Определим плотность энергии, разделив (6.5.4) на объем ΔV

Продифференцируем уравнение плоской продольной волны (6.2.8) по времени t и по координате х и подставим выражения в формулу (6.5.5) учтя, что $$k^2υ^2=ω^2$$

Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно

Таким образом, плотность энергии и среднее значение плотности энергии пропорциональны плотности среды ρ , квадрату частоты ω и квадрату амплитуды волны А .

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии Ф через данную поверхность равен энергии dW переносимой за время dt

Ф измеряется в ваттах.

Для характеристики распространения энергии в разных точках пространства вводится векторная величина, называема плотностью потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку ΔS , помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Если через площадку ΔS , перпендикулярную к направлению распространения волны, переносится энергия ΔW за время Δt , то плотность потока энергии равна

Рассмотрим объем цилиндра с основанием ΔS и высотой υΔt ( υ − фазовая скорость волны). В случае малого объема цилиндра, плотность энергии во всех точках цилиндра можно было считать одинаковой и поэтому энергию можно найти как произведение плотности энергии ω на объем ΔV=ΔSυΔt

Подставив выражение (6.5.10) в последнее выражение, получим

где j − вектор плотности потока энергии, называемый вектором Умова.

Интенсивность волны равна

Данное выражение справедливо для волны любого вида.

Определим поток энергии через поверхность S . Для этого разобьем поверхность на элементарные участки dS . За время dt через площадку dS пройдет энергия dW . Объем цилиндра, где вычисляется энергия, равен $$dV = υdtdScosϕ$$ . Тогда в этом объеме содержится энергия

где d S = n dS ; n − единичный вектор нормали к поверхности dS .

Поток энергии через элементарную поверхность dS

Поток энергии через поверхность S равен

6.6. Фазовая и групповая скорости волн

Скорость распространения волны есть скорость перемещения фазы и называется фазовой скоростью. Фазовая скорость равна

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, и к ним применим принцип суперпозиции волн: при распространении в линейной среде (т. е. среде снеизменяющимися свойствами) нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

Используя принципа суперпозиции, любая волна может быть представлена в виде волнового пакета. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Простейший волновой пакет двух распространяющихся вдоль положительного направления оси Х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем

Эта волна отличается от гармонической тем, что ее амплитуда

медленно изменяющаяся функция координаты х и времени t .

За скорость распространения волнового пакета принимают скорость перемещения максимума амплитуды волны. При условии, что $$tdω-xdk=const$$ , получим

где υ_гр – групповая скорость. Рассмотрим связь между групповой и фазовой скоростями. Учитывая, что волновое число $$k=<2π over λ>$$ и $$dk=-<2π over λ^2>dλ=-dλ$$ , получим

В теории относительности доказывается, что групповая скорость υ_гр ≤ c , в то время как для фазовой скорости ограничений не существует.

6.7. Интерференция упругих волн

Для того чтобы рассмотреть интерференцию волн, введем понятие когерентности . Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связано с понятием когерентности. Волны называются когерентными , если разность их фаз остается постоянной во времени. При наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн, и заключается в том, что колебания в одних точках усиливают, а в других ослабляют друг друга.

Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками $$S_1$$ и $$S_2$$ , колеблющимися с одинаковыми амплитудой, частотой, нулевой начальной фазой и постоянной разностью фаз. Запишем уравнения колебаний:

где $$r_1$$ и $$r_2$$ − расстояния от источников волн до рассматриваемой точки.

Амплитуда результирующей волны равна (сложение одинаково направленных колебаний)

Так как разность начальных фаз $$(ϕ_1-ϕ_2)=<2π over λ>(r_2-r_1)=<2π over λ>Δ=const$$ , то результат наложения двух волн в различных точках зависит от величины $$Δ=r_2-r_1$$ , называемой разностью хода волн.

В точках, где выполняется условие

Так как квадрат амплитуды колебаний пропорционален интенсивности волны, то получаем

То есть наблюдается усиление интенсивности (увеличение амплитуду) результирующей волны или интерференционный максимум.

2) В точках, где выполняется условие

То есть наблюдается ослабление интенсивности (уменьшение амплитуды) результирующей волны или интерференционный минимум.

Таким образом, в результате наложения двух когерентных волн в среде возникают колебания, амплитуда которых различна в разных точках среды, при этом в каждой точке среды получается или максимум амплитуды, или минимум амплитуды, или ее промежуточное значение − в зависимости от значения разности расстояний точки до когерентных источников. Интерференция света приводит к перераспределению энергии волны между соседними областями, хотя в среднем для больших областей энергия остается неизменной.

6.8. Стоячие волны

Рассмотрим интерференцию стоячих волн. Стоячие волны − это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Запишем уравнение двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях

Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны

Из данного уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда зависит от координаты х

Точки, в которых амплитуда колебаний достигает максимального значения и координаты которых удовлетворяют условию

где m = 0, 1, 2, … называются пучностями стоячей волны.

Точки, в которых амплитуда колебаний обращается в нуль и координаты которых удовлетворяют условию

где m = 0, 1, 2, … называются узлами стоячей волны.

[spoiler title=”источники:”]

http://studref.com/504911/matematika_himiya_fizik/plotnost_energii_elektromagnitnoy_volny_vektor_poyntinga_opyt_lebedeva

http://physics.belstu.by/mechanics_lk/mechanics_lk10.html

[/spoiler]

Макеты страниц