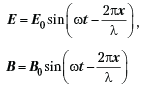Занятия 15, 16.
№5.278
Точечный изотропный
источник испускает свет с
![]() .
.
Световая мощность источника
![]() .
.
Найти:
а) среднюю плотность
потока фотонов на расстоянии
![]() ;
;
б) расстояние от
источника до точки, где средняя
концентрация фотонов
![]() ;
;
Решение:
а )
)
По определению плотность потока фотонов
находится по формуле:
![]() ,
,
где
![]()
– концентрация фотонов. Найдем ее. Так
как источник обладает постоянной
мощностью, в любом шаровом слое толщиной
![]() (именно
(именно
такое расстояние проходит фотон за
время
![]() )
)
суммарная энергия фотонов будет
выражаться по формуле:
![]() .
.
Зная что, средняя плотность фотонов в
таком слое
![]() ,
,
объем такого слоя
![]()
и энергия одного фотона
![]() ,
,
можно найти суммарную энергию фотонов
в таком слое:
![]() .
.
Приравняв значения
![]()
и вспомнив, что
![]() ,
,
получим
![]() ,
,
тогда
![]() .
.
б) Из ![]()
![]()
![]()
№5.280
Лазер
излучил в импульсе длительностью
![]()
пучок света с энергией
![]() .
.
Найти среднее давление такого светового
импульса, если его сфокусировать в
пятнышко диаметром
![]()
на поверхность, перпендикулярную к
пучку, с коэффициентом отражения
![]() .
.
Решение:
По определению, давление ищется по
формуле
![]() ,
,
где
![]()
– сила, действующая на преграду, а
![]()
– площадь поверхности, на которую падает
пучок. Из условия ясно, что площадь
поверхности равна:
![]() .
.
Сила давления возникает за счет изменения
импульса пучка при столкновении, тогда
импульс пучка до столкновения
![]() ,
,
а после столкновения
![]()
(потому что отразилась только
![]()
часть пучка). С учетом того, что импульсы
направлены в противоположные стороны,
получаем
![]() .
.
Тогда
![]()
![]()
![]() .
.
№ 5.283
5.283
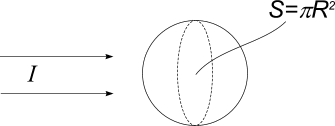
Плоская световая
волна интенсивности
![]()
освещает шар с абсолютно зеркальной
поверхностью. Радиус шара
![]() .
.
Найти с помощью корпускулярных
представлений силу светового давления,
испытываемую пластинкой.
Решение:
Э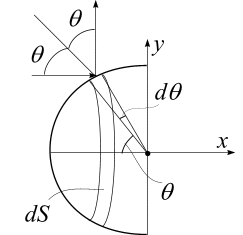 нергия
нергия
волны, падающей на поверхность шара за
время
![]()
будет выражаться по формуле
![]() .
.
Волна будет давить на шар за счет
изменения импульса фотонов. Так как
поверхность симметричная, и волна
освещает шар равномерно, то можно не
учитывать
![]() –
–
составляющую импульса отраженных частиц
(суммарный импульс вдоль оси
![]() после
после
отражения будет равняться 0, а сила будет
направлена вдоль оси
![]() ).
).
Поскольку поверхность абсолютно
зеркальная и имеет шарообразную форму,
то изменение импульса одного фотона
вдоль оси
![]()
при ударе о кольцо на шаре площади
![]()
расположенного под углом
![]()
и шириной
![]() будет
будет
иметь вид:
![]() .
.
Известно, что импульс одного фотона
вычисляется по формуле
![]() .
.
За время
![]()
на наше кольцо площадью
![]()
падает
![]()
фотонов. Площадь кольца
![]()
будет равняться произведению длины
окружности
![]()
на ширину полоски
![]() :
:
![]() .
.
Для нахождения результирующей силы
проинтегрируем по половине поверхности
шара:
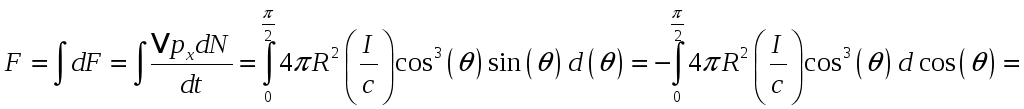
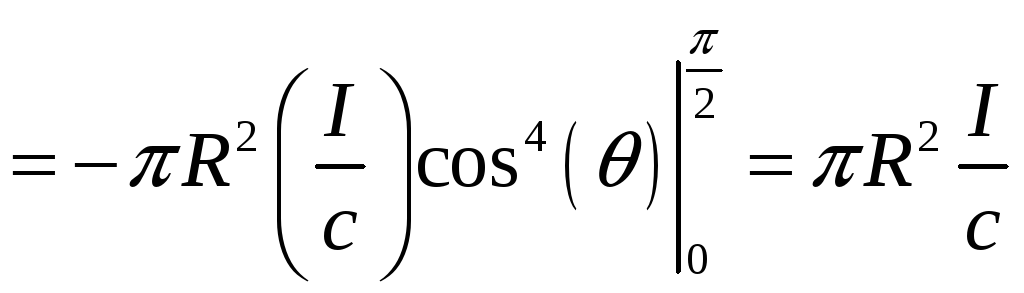 .
.
№5.290
Найти длину волны
коротковолновой границы сплошного
рентгеновского спектра, если скорость
электронов, подлетающих к антикатоду
трубки,
![]() ,
,
где с – скорость света.
Решение:
Причина рентгеновского спектра: электрон,
подлетая к антикатоду, тормозит, т.е.
движется с ускорением. А любая частица,
движущаяся с ускорением, излучает.
Причем длину волны коротковолновой
границы будем наблюдать в том случае,
когда электрон затормозит перед самой
границей антикатода. Значит, кинетическая
энергия электронов в трубке из
релятивистских соображений:

,
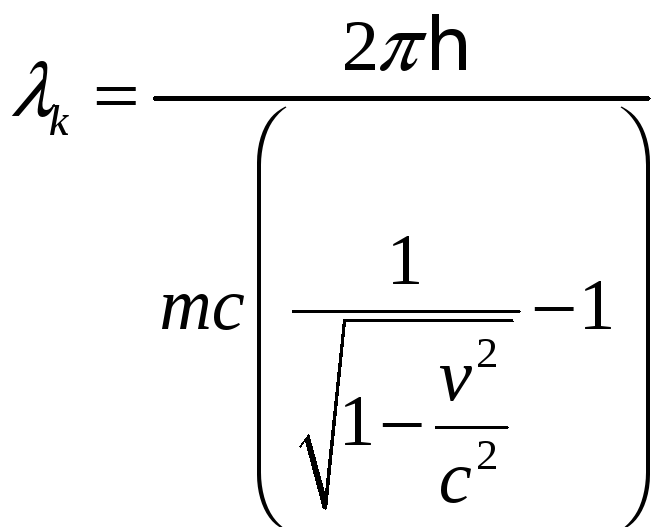
или из волновых свойств частиц:
![]() ,
,
тогда приравняв эти два выражения:

![]()
№5.293
При поочередном
освещении поверхности некоторого
металла светом с длинами волн
![]()
и
![]()
обнаружили, что соответствующие
максимальные скорости фотоэлектронов
отличаются друг от друга в
![]()
раза. Найти работу выхода с поверхности
этого металла.
Решение:
Энергия фотона уходит на то, чтобы выбить
электрон и сообщить ему какую-то скорость:
![]() ,
,
где
![]()
![]()
Тогда при освещении светом с двумя
разными длинами волн:
![]() и
и ![]()
Подставляя второе в первое и вспоминая,
что такое
![]() ,
,
получаем:

![]()
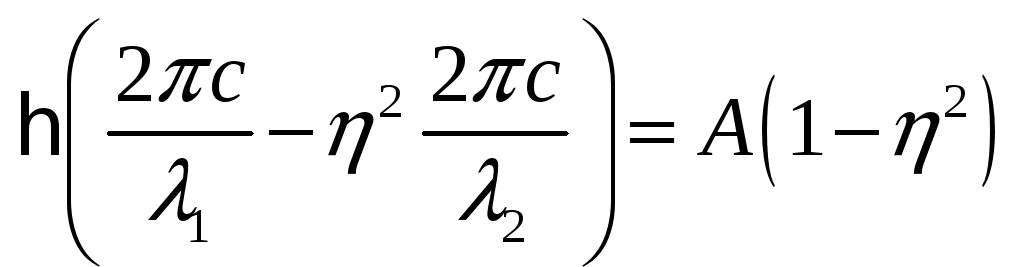
![]()

![]()
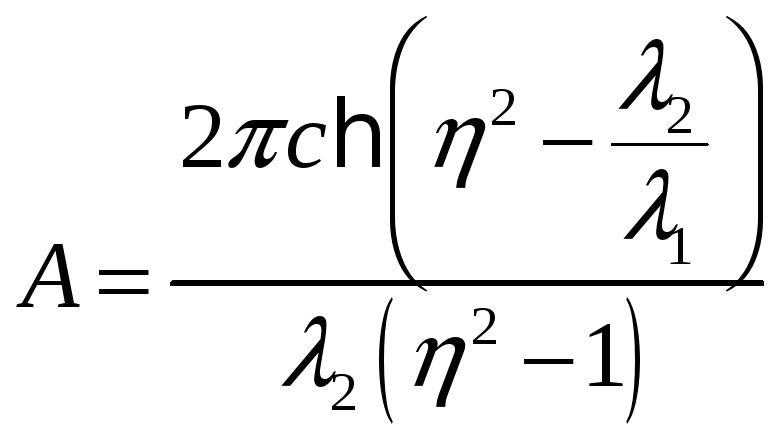
№ 5.298
5.298
Фототок,
возникающий в цепи вакуумного фотоэлемента
при освещении цинкового электрода
электромагнитным излучением с длиной
волны
![]()
прекращается, если подключить внешнее
задерживающее напряжение
![]() .
.
Найти величину и полярность внешней
контактной разности потенциалов
фотоэлемента.
Решение:
Для того чтобы внешнее задерживающее
напряжение было > 0, система должна
выглядеть так, как изображено на рисунке.
Т.е. энергия падающих фотонов полностью
расходуется на работу выхода электронов
из металла и на противодействие внешнему
напряжению, т.е.
![]() ,
,
где
![]()
– максимальная энергия, которую может
получить электрон; с учетом того, что
она полностью гасится внешним полем,
можно записать:
![]() ,
,
где
![]()
– разность потенциалов между катодом и
анодом, возникающая в результате
фотоэффекта; контактная разность
потенциалов – разность потенциалов,
возникающая между двумя разнородными
проводниками при их соприкосновении,
т.е. его тоже нужно скомпенсировать
внешним напряжением:
![]()
![]()
![]()
![]()
О направлении контактного напряжения
можно судить по ее знаку, полученному
после подсчетов. Если получим знак «+»
– оно сонаправлено с
![]() ,
,
т.е. противонаправлено внешнему напряжению
(судя по ответу, так и есть).
№5.304
Фотон с длиной
волны
![]()
рассеялся под прямым углом на покоившемся
свободном электроне. Найти:
а) частоту
рассеянного фотона;
б) кинетическую
энергию электрона отдачи;
Решение:
а) Из формулы эффекта Комптона,
![]() ,
,
где
![]() ;
;
в нашей задаче
![]() ,
,
тогда
![]()
![]()
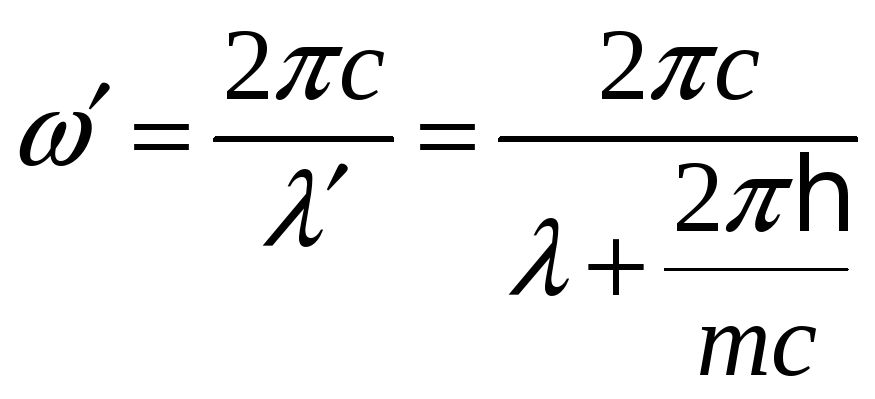
б) Кинетическая энергия электрона отдачи
– это разница между его полной энергией
после рассеяния на нем фотона (эта
энергия включает в себя энергию
![]() )
)
и той самой энергией
![]() ,
,
которой обладал покоящийся электрон:
![]() .
.
Из закона сохранения энергии:
![]()
![]()
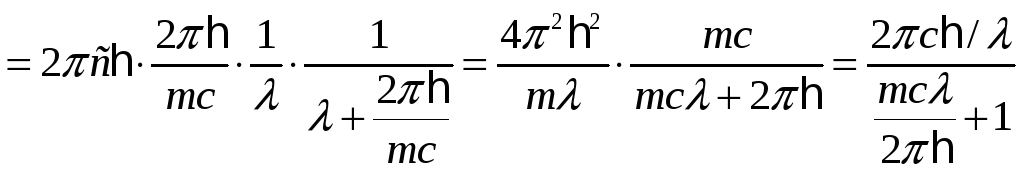
Соседние файлы в папке 11
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Фотоны:
В конце XIX в. многие ученые считали, что развитие физики завершилось. Законы механики и теория всемирного тяготения были известны более 200 лет. Максвеллом была завершена теория электромагнетизма. Установлены законы сохранения энергии, импульса, электрического заряда.
Однако к началу XX в. возникли проблемы, касающиеся физической природы излучения и вещества, а также их взаимодействия. В рамках классической физики возникали непреодолимые противоречия при объяснении экспериментальных данных дня процессов поглощения и испускания света атомами, закономерностей испускания электромагнитного излучения нагретыми телами, фотоэффекта и т. п.
Анализ этих противоречий привел к научной революции, и в течение последующих 30 лет были заложены основы квантовой физики. Квантовая физика пришла на смену классической при рассмотрении явлений на атомном и субатомном уровнях.
Тепловое излучение и квантовая гипотеза Планка
Существует три способа теплопередачи: теплопроводность, конвекция и излучение. Спектр — распределение энергии, излучаемой или поглощаемой веществом, по частотам или длинам волн.
Опыт показывает, что все нагретые тела испускают тепловое (электромагнитное) излучение, интенсивность которого зависит от температуры тела. При комнатных температурах мы не ошущаем электромагнитного излучения, испускаемого телами, из-за его слабой интенсивности. Однако по мере повышения температуры интенсивность теплового излучения возрастает, в результате чего мы начинаем ощущать тепло. Нагревание происходит в результате поглощения энергии излучения и ее превращения (трансформации) во внутреннюю энергию тела.
При нагревании тугоплавкое вещество сначала раскаляется докрасна (при температуре ~ 1000 К), затем становится оранжево-красным (при температуре ~ 1500 К), и, наконец, при температуре ~2000 К приобретает бело-желтый цвет.
Любое тело состоит из множества частиц — атомов, молекул, ионов и свободных электронов. Эти частицы в телах непрерывно участвуют в поступательном, вращательном, колебательном движениях. Согласно законам классической электромагнитной теории света любой ускоренно движущийся заряд излучает электромагнитные волны. Излучение, испускаемое телами, содержит волны различных частот, так как частицы совершают колебания, представляющие собой суперпозиции большого числа гармонических колебаний. Кроме того, и интенсивность излучаемых волн на разных частотах различна.
Эксперименты показали, что спектр теплового излучения тел является непрерывным. В волновой теории света испускание и поглощение электромагнитных волн любой частоты рассматривается как непрерывный процесс, в результате которого энергия источника или приемника волн изменяется также непрерывно.
Нагретое тело, согласно электромагнитной теории света, непрерывно излучая электромагнитные волны, теряет энергию, и, следовательно, должно было бы охлаждаться до абсолютного нуля. Следовательно, невозможно было бы тепловое равновесие между веществом и излучением. Однако эксперименты показали, что нагретое тело не расходует всю свою энергию на излучение.
Сточки зрения классической теории, все частоты равноправны. Следовательно, на каждый интервал частот в спектре в условиях равновесия должна приходиться в среднем одна и та же доля энергии. Значит, при перемещении по спектру от его красной области к фиолетовой энергия излучения должна была бы непрерывно расти. Рост энергии излучения тела привел бы к полной потере им энергии, т. е. к «ультрафиолетовой катастрофе».
Эксперименты показали, что в спектре излучения каждого теплового источника имеется максимум, положение которого зависит от температуры источника (рис. 77, а). При температуре 4000 °С максимум находится в инфракрасной области спектра и при нагревании перемещается в видимую область спектра.
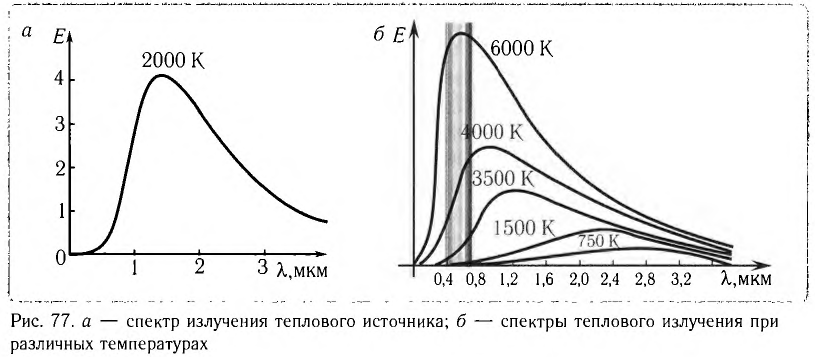
При температуре абсолютно черного тела 2000 К в видимое излучение переходит только 0,3 % излучаемой энергии, а при температуре 3000 К — 3 %. Выгоднее всего «работает» абсолютно черное тело при температуре 6000 К — температуре поверхности Солнца. Но даже в этом случае в видимое излучение переходит только 13 % излучаемой энергии.
Распределение энергии излучения по частотам (E) для абсолютно черных тел приведено на рисунке 77, б. Если считать Солнце абсолютно черным телом, то температура его поверхности составляет около 6000 К. Для излучателей, не полностью поглощающих падающий на них свет, спектральные кривые располагаются ниже.
Для объяснения распределения энергии в спектре излучения 14 декабря 1900 г. Макс Планк в докладе на заседании немецкого физического общества выдвинул революционную гипотезу, что атомы излучают энергию не непрерывно, а отдельными порциями — квантами световой энергии. В соответствии с этой гипотезой энергия любой колебательной системы (атома, молекулы), имеющей частоту собственных колебаний v, может принимать лишь определенные значения, отличающиеся на целое число п элементарных порций — квантов энергии:
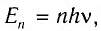
где n — целое положительное число, h — коэффициент пропорциональности, который называют постоянной Планка. Это — фундаментальная постоянная. Ее значение
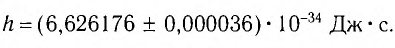
Приближенное значение постоянной Планка, применяемое при решении задач,
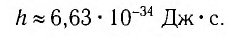
Планк поэтически назвал новую фундаментальную постоянную «таинственным послом из реального мира».
Слово «квант» происходит от латинского слова quantum — «сколько», или «как много». Это слово вообще обозначает часть, долю или разделенную порцию.
Представление о квантах световой энергии объяснило свойства теплового излучения и позволило рассчитывать спектр излучения абсолютно черного тела дня любых температур. Для температуры поверхности Солнца 6000 °К максимум кривой соответствует длине волны 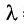 = 0,483 мкм, т. е. сине-зеленой области спектра.
= 0,483 мкм, т. е. сине-зеленой области спектра.
Фотоэффект и экспериментальные законы внешнего фотоэффекта
Свет — электромагнитные волны, обладающие энергией и импульсом и распространяющиеся в вакууме со скоростью с = 3,0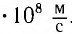
Наше зрительное восприятие физических явлений в окружающем мире определяется взаимодействием света с веществом. Воздействие света на вещество состоит в сообщении ему энергии, приносимой световой волной, т. е. первичным процессом является поглощение света. Такое взаимодействие, например в сетчатке глаза, приводит к зрительным ощущениям. Для прозрачной среды, например стекла, при падении на него световой волны главным результатом взаимодействия является ее отражение и преломление, а поглощением электромагнитной энергии в видимом диапазоне можно пренебречь.
При падении света на поверхность непрозрачного предмета часть излучения, преломляясь, проникает в него и поглощается, другая часть отражается от поверхности, и мы видим предмет в отраженном свете. Доля отраженного от поверхности света зависит от длины волны. Более темные поверхности поглощают свет сильнее, чем более светлые.
Мы видим не только тела, которые отражают или рассеивают свет, но и тела, которые светятся сами, например Солнце, другие звезды, пламя. Электромагнитное излучение испускают все тела, причем его интенсивность зависит от температуры их поверхности. В видимом диапазоне спектра излучение достаточной интенсивности, позволяющее видеть предмет, возникает, если температура поверхности предмета намного больше комнатной.
Взаимодействие электромагнитных волн с веществом приводит и к другим физическим явлениям, изучение которых помогло выяснить природу света.
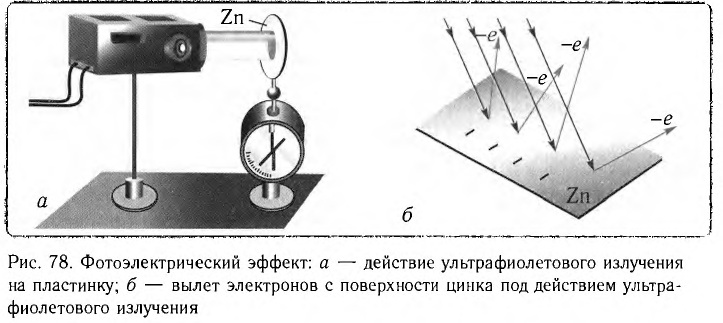
В 1887 г. Генрих Герц обнаружил, что пробой воздушного промежутка между электродами искрового разрядника происходит при меньшем напряжении, если освещать отрицательно заряженный электрод ультрафиолетовым излучением. Дальнейшие эксперименты показали, что отрицательно заряженная цинковая пластинка при облучении ультрафиолетовым излучением (рис. 78, а) разряжается. Оба эти явления можно объяснить, предполагая, что под действием падающего излучения из металла вылетают отрицательно заряженные частицы — электроны (рис. 78, б). Это явление получило название фотоэффекта.
Фотоэффектом (фотоэлектрическим эффектом) называется явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения полностью передается электронам вещества.
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним фотоэффектом.
Испускание веществом каких-либо частиц называется эмиссией. Поэтому внешний фотоэффект называют также фотоэлектронной эмиссией (фотоэмиссией).
«Фото 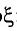 » по-гречески означает «свет».
» по-гречески означает «свет».
Систематическое изучение фотоэффекта было проведено в 1888—1889 гг. русским физиком Александром Григорьевичем Столетовым.
Установка для изучения внешнего фотоэффекта представлена на рисунке 79, а. В экспериментах Столетова в электрическую цепь был включен конденсатор, одна из обкладок которого была изготовлена из медной сетки, а вторая представляла собой цинковую пластинку. Медная сетка была заряжена положительно, а цинковая пластинка — отрицательно.
Наблюдения показали, что даже при отсутствии напряжения между пластинами под действием падающего ультрафиолетового излучения в цепи возникал электрический ток. Этот ток назвали фототоком (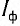 ).
).
Изменяя напряжение U между пластинами А и В с помощью реостата R (рис. 79, б), Столетов получил зависимость силы фототока 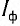 от напряжения U (вольт-амперную характеристику).
от напряжения U (вольт-амперную характеристику).
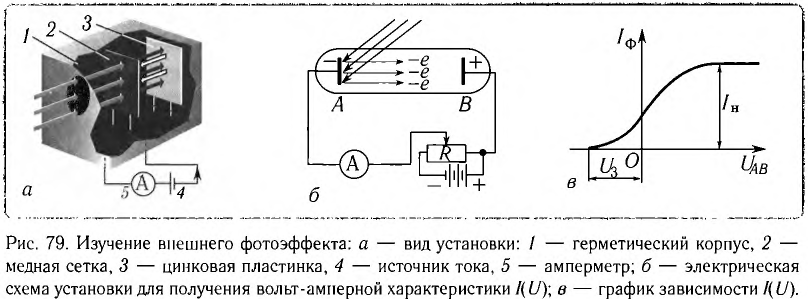
Как видно из зависимости, представленной на рисунке 79, в, при увеличении напряжения 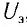 сила фототока растет до некоторого значения
сила фототока растет до некоторого значения 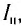 которое называется фототоком насыщения. Дальнейшее увеличение напряжения не приводит к росту фототока. Изменение полярности напряжения приводит к исчезновению фототока при напряжении которое называется задерживающим напряжением.
которое называется фототоком насыщения. Дальнейшее увеличение напряжения не приводит к росту фототока. Изменение полярности напряжения приводит к исчезновению фототока при напряжении которое называется задерживающим напряжением.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового излучения. Однако некоторые металлы, например литий, натрий и калий, испускают электроны и при облучении видимым светом.
Экспериментально установлены следующие законы внешнего фотоэффекта:
1. Сила фототока насыщения 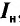 , определяемая максимальным числом фотоэлектронов, вырываемых из катода за единицу времени, прямо пропорциональна интенсивности I падающего излучения (первый закон фотоэффекта).
, определяемая максимальным числом фотоэлектронов, вырываемых из катода за единицу времени, прямо пропорциональна интенсивности I падающего излучения (первый закон фотоэффекта).
Вольт-амперная характеристика фотоэффекта показана на рисунке 80, а, а зависимость силы фототока насыщения 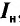 от интенсивности падающего излучения I — на рисунке 80, б.
от интенсивности падающего излучения I — на рисунке 80, б.
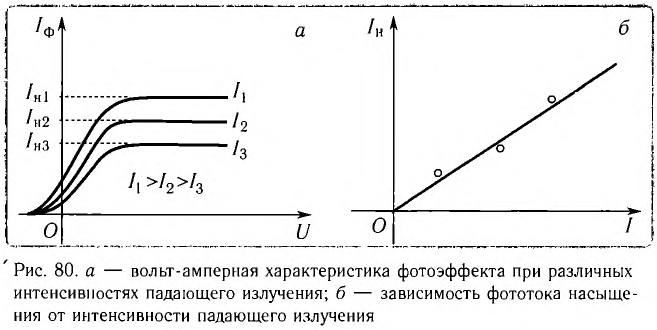
Из графика зависимости 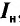 от I видно, что сила фототока насыщения равна нулю только при отсутствии излучения (I = 0). Иными словами, фотоэффект наблюдается даже при малых значениях интенсивности падающего излучения.
от I видно, что сила фототока насыщения равна нулю только при отсутствии излучения (I = 0). Иными словами, фотоэффект наблюдается даже при малых значениях интенсивности падающего излучения.
2. Максимальная кинетическая энергия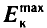 фотоэлектронов не зависит от интенсивности I падающего излучения и линейно возрастает с увеличением частоты v падающего излучения (второй закон фотоэффекта).
фотоэлектронов не зависит от интенсивности I падающего излучения и линейно возрастает с увеличением частоты v падающего излучения (второй закон фотоэффекта).
Подчеркнем, что фотоэлектроны не имеют фиксированной кинетической энергии при вылете из фотокатода: она меняется в некотором диапазоне от нуля до 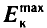 , так как фотоэлектроны могут часть своей энергии, полученной от падающего излучения, передать частицам вещества перед вылетом с поверхности.
, так как фотоэлектроны могут часть своей энергии, полученной от падающего излучения, передать частицам вещества перед вылетом с поверхности.
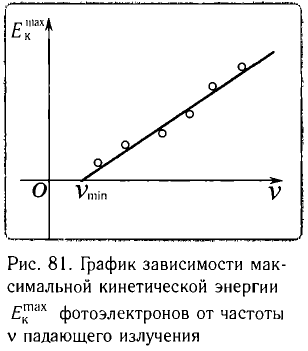
На рисунке 81 представлен график зависимости максимальной кинетической энергии 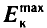 от частоты v падающего излучения.
от частоты v падающего излучения.
3. Для каждого вещества существует граничная частота  , такая, что излучение меньшей частоты не может вырывать электроны (третий закон фотоэффекта).
, такая, что излучение меньшей частоты не может вырывать электроны (третий закон фотоэффекта).
Эта минимальная частота  называется красной границей фотоэффекта. Такое название связано с тем, что минимальной частоте излучения соответствует максимальная длина волны. А поскольку максимальная длина волны в видимом диапазоне соответствует красному цвету, то граница и получила название «красной».
называется красной границей фотоэффекта. Такое название связано с тем, что минимальной частоте излучения соответствует максимальная длина волны. А поскольку максимальная длина волны в видимом диапазоне соответствует красному цвету, то граница и получила название «красной».
Красная граница для различных веществ совсем не обязательно соответствует красному цвету. Например, для рубидия она соответствует желтому цвету, для кальция — синему, а для некоторых веществ может вообще находиться в инфракрасной или ультрафиолетовой областях спектра.
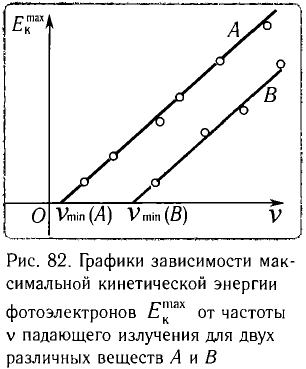
На рисунке 82 приведены графики зависимости максимальной кинетической энергии 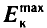 фотоэлектронов от частоты v падающего излучения для двух различных веществ А и В. Точки пересечения графиков с осью абсцисс (частот) определяют красные границы фотоэффекта для каждого из них:
фотоэлектронов от частоты v падающего излучения для двух различных веществ А и В. Точки пересечения графиков с осью абсцисс (частот) определяют красные границы фотоэффекта для каждого из них: 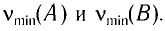
При частотах, больших  , излучение даже очень малой интенсивности вызывает фотоэффект. Кроме того, между моментом включения источника излучения и вылетом электронов фактически нет задержки во времени: электроны вылетают из вещества через промежуток времени порядка
, излучение даже очень малой интенсивности вызывает фотоэффект. Кроме того, между моментом включения источника излучения и вылетом электронов фактически нет задержки во времени: электроны вылетают из вещества через промежуток времени порядка 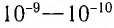 с после начала облучения.
с после начала облучения.
Следует заметить, что к моменту открытия фотоэффекта в 1887 г. еще ничего не было известно об электронах, открытых английским физиком Джозефом Джоном Томсоном только в 1897 г.
В 1898 г. Ф. Ленардом и Дж. Дж. Томсоном было определено отношение ! заряда q частицы, вылетающей с поверхности металла при фотоэффекте, к ее массе т (так называемый удельный заряд 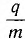 ) по ее отклонению в электрическом и магнитном полях. Эти измерения дали значение
) по ее отклонению в электрическом и магнитном полях. Эти измерения дали значение 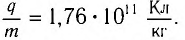 Таким образом, было доказано, что выбиваемые светом заряженные частицы — электроны.
Таким образом, было доказано, что выбиваемые светом заряженные частицы — электроны.
За работы по определению удельного заряда 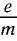 , приведшие к открытию первой элементарной частицы — электрона, Дж. Дж. Томсон в 1906 г. был удостоен Нобелевской премии по физике.
, приведшие к открытию первой элементарной частицы — электрона, Дж. Дж. Томсон в 1906 г. был удостоен Нобелевской премии по физике.
На основе волновой теории можно объяснить только 1-й закон фотоэффекта: чем больше энергия падающего света, тем больше электронов вылетает из вещества. Объяснить 2-й и 3-й законы фотоэффекта в рамках классической теории излучения не удалось. Например, непонятно, почему максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения. Невозможно также объяснить существование красной границы фотоэффекта. Действительно, даже при малой частоте падающего излучения, но при длительном воздействии электронам можно сообщить энергию, необходимую для выхода из вещества. Следовательно, красная граница фотоэффекта не должна существовать. Все эти противоречия были сняты квантовой теорией.
Фотон
Электронвольт — энергия, которую приобретет частица с зарядом, равным элементарному, при перемещении между двумя точками с разностью потенциалов 1 В (1,0 эВ =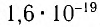 Дж).
Дж).
Изменение энергии 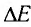 системы связано с изменением ее массы
системы связано с изменением ее массы 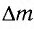 уравнением Эйнштейна:
уравнением Эйнштейна: 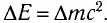
Длина волны 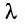 связана с ее частотой v соотношением
связана с ее частотой v соотношением 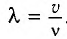 , где v — скорость волны.
, где v — скорость волны.
После выдвижения гипотезы Планка началось интенсивное развитие квантовой физики, которая сравнительно быстро превратилась в стройную и законченную теорию, открывшую «новую эру» в развитии физики.
Развивая идеи Планка, Эйнштейн в 1905 г. для объяснения экспериментальных законов внешнего фотоэффекта выдвинул гипотезу, что свет не только излучается и поглощается, но и распространяется в виде отдельных порций (квантов). Таким образом, свет имеет квантовую структуру и является совокупностью движущихся элементарных частиц (корпускул).
Корпускула — от латинского corpusculum — маленькая частица.
Назвать эти частицы фотонами предложил в 1928 г. американский физик Артур Комптон.
По гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой v представляет собой поток фотонов. Каждый фотон движется со скоростью света с и несет квант энергии E = hv. При взаимодействии с веществом фотон ведет себя подобно частице и передает свою энергию не веществу в целом и даже не атому, а только отдельным электронам в веществе. Последний забирает всю энергию фотона, который с этого мгновения больше не существует. В этом случае говорят, что электрон в веществе поглотил фотон.
Энергия фотона может быть выражена через длину волны 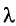 :
:
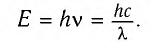
Из определения релятивистского импульса 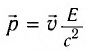 для фотона (v = с) следует, что модуль его импульса определяется выражениями
для фотона (v = с) следует, что модуль его импульса определяется выражениями
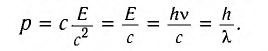
Оказывается, фотон — удивительная частица, которая обладает энергией E = hv, импульсом 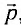 , но вследствие того, что скорость его движения всегда равна скорости света, его масса равна нулю (m = 0). Такие частицы называют безмассовыми. Энергия фотона связана с его импульсом соотношением Е = рс. Таким соотношением описываются частицы, масса которых равна нулю.
, но вследствие того, что скорость его движения всегда равна скорости света, его масса равна нулю (m = 0). Такие частицы называют безмассовыми. Энергия фотона связана с его импульсом соотношением Е = рс. Таким соотношением описываются частицы, масса которых равна нулю.
Таким образом, фотом является элементарной частицей, только в отличие от других элементарных частиц он не имеет массы, а потому «обречен» всегда двигаться со скоростью света.
Фотон обладает следующими свойствами:
Уравнение Эйнштейна для фотоэффекта
Рассмотрим объяснение экспериментальных законов фотоэффекта на основе квантовых представлений, предложенное Эйнштейном. Электрон одного из атомов внутри металла после поглощения одного фотона получает квант энергии hv и стремится выйти за пределы кристаллической решетки, т. е. покинуть облучаемое твердое тело.
Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю. Именно поэтому вольт-амперная характеристика фотоэффекта при напряжении, ..равном нулю, не проходит через нуль (см. рис. 80, а).
Часть энергии, полученной при поглощении фотона, электрон расходует на совершение работы по преодолению сил притяжения, удерживающих его внутри вещества. Соответственно остаток энергии будет равен кинетической энергии электрона:
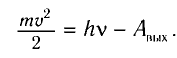
Здесь 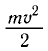 — кинетическая энергия электрона массой m, вылетевшего под действием света с поверхности металла и движущегося со скоростью v (
— кинетическая энергия электрона массой m, вылетевшего под действием света с поверхности металла и движущегося со скоростью v (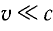 ). Величина
). Величина 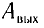 > 0 представляет собой работу, которую необходимо совершить против сил электрического поля для того, чтобы электрон вылетел из вещества. Она называется работой выхода.
> 0 представляет собой работу, которую необходимо совершить против сил электрического поля для того, чтобы электрон вылетел из вещества. Она называется работой выхода.
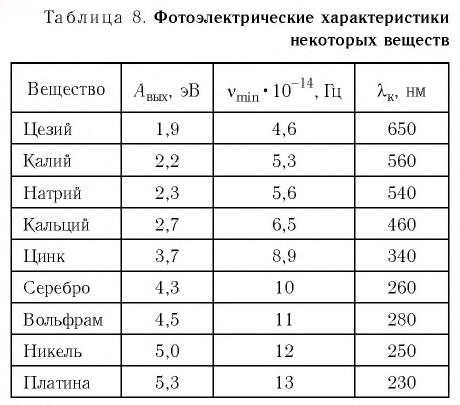
Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решетки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт (табл. 8).
Таблица 8
Фотоэлектрические характеристики некоторых веществ
| Вещество | 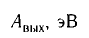 |
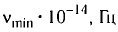 |
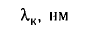 |
| Цезий | 1,9 | 4,6 | 650 |
| Калий |
2,2 | 5,3 | 560 |
| Натрий |
2,3 | 5,6 | 540 |
| Кальций |
2,7 | 6,5 | 460 |
| Цинк |
3,7 | 8,9 | 340 |
| Серебро |
4,3 | 10 | 300 |
| Вольфрам |
4,5 | 11 | 270 |
| Никель |
5,0 | 12 | 250 |
| Платина | 5,3 | 13 | 230 |
С появлением мощных монохроматических источников света (лазеров) удалось наблюдать процессы многофотонного поглощения. В таких процессах прежде чем покинуть вещество, электрон поглощает не один, а несколько фотонов. В этом случае формула Эйнштейна для фотоэффекта записывается в виде
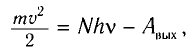
где N — число фотонов.
Таким образом, уравнение Эйнштейна для внешнего фотоэффекта является следствием закона сохранения и превращения энергии в этом процессе:
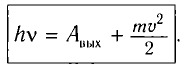 (1)
(1)
Отметим, что 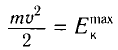 — это максимальная кинетическая энергия электрона (
— это максимальная кинетическая энергия электрона (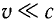 ), которой он может обладать, вылетев из вещества. Из-за различных потерь энергия электрона может быть меньше расчетного значения.
), которой он может обладать, вылетев из вещества. Из-за различных потерь энергия электрона может быть меньше расчетного значения.
В релятивистском случае (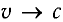 ) для кинетической энергии необходимо использовать выражение
) для кинетической энергии необходимо использовать выражение
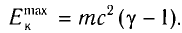
Используя уравнение Эйнштейна, можно объяснить экспериментальные законы фотоэффекта.
Первый закон фотоэффекта: сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени. Число таких фотоэлектронов пропорционально числу фотонов, падающих на поверхность за это же время. Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают из металла больше электронов.
Второй закон фотоэффекта: при увеличении частоты v падающего света максимальная кинетическая энергия 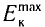 возрастает линейно согласно формуле
возрастает линейно согласно формуле
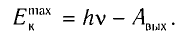
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, затрудняющее вылет электронов, то сила тока уменьшится, так как теперь фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
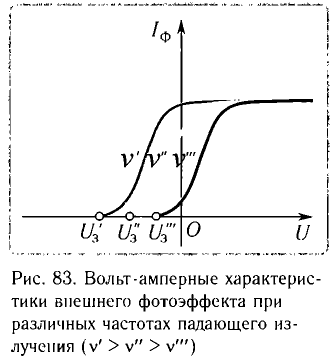
При некотором отрицательном напряжении 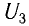 электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи будет равна нулю (рис. 83). Величину
электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи будет равна нулю (рис. 83). Величину 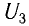 называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетичеcкая энергия электронов выражается через задерживающее напряжение следующим образом:
называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетичеcкая энергия электронов выражается через задерживающее напряжение следующим образом:
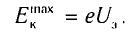 (2)
(2)
Третий закон фотоэффекта: если частота падающего света v меньше граничной частоты 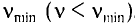 , при которой
, при которой 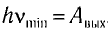 , то испускания электронов не происходит.
, то испускания электронов не происходит.
Таким образом, красную границу фотоэффекта можно найти из соотношения
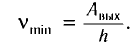 (3)
(3)
Ока зависит только от работы выхода электронов, т. е. определяется строением металла и состоянием его поверхности. Длина волны 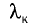 излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения
излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения
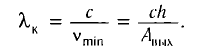
Подставив в уравнение Эйнштейна (1) выражения (2) и (3), найдем зависимость задерживающего напряжения от частоты падающего света:
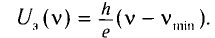 (4)
(4)
Построим графики зависимости задерживающего напряжения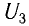 от частоты v падающего света для двух различных металлов. Получаются параллельные прямые (рис. 84).
от частоты v падающего света для двух различных металлов. Получаются параллельные прямые (рис. 84).

По тангенсу угла наклона а этих прямых из соотношения (4) можно вычислить постоянную Планка, так как
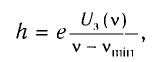
а по точкам пересечения графиков с осями — найти работу выхода 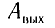 и красную границу
и красную границу 
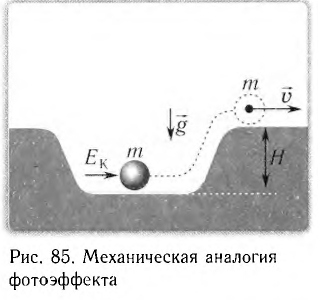
В качестве механической аналогии объяснения явления фотоэффекта рассмотрим шарик массой m, покоящийся на дне ямы глубиной Н (рис. 85). Если шарику сообщить достаточную начальную кинетическую энергию 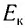 , он поднимется из ямы и покатится по поверхности земли с некоторой скоростью v. Закон сохранения и превращения энергии для такого процесса имеет вид
, он поднимется из ямы и покатится по поверхности земли с некоторой скоростью v. Закон сохранения и превращения энергии для такого процесса имеет вид
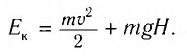
В этом выражении mgH является работой выхода шарика из ямы, а сообщенная ему кинетическая энергия 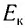 аналогична энергии фотона. Иначе говоря: шарику необходимо преодолеть потенциальный барьер для того, чтобы оказаться на поверхности земли.
аналогична энергии фотона. Иначе говоря: шарику необходимо преодолеть потенциальный барьер для того, чтобы оказаться на поверхности земли.
В 1921 г. при присуждении Альберту Эйнштейну Нобелевской премии в решении Нобелевского комитета указывалось, что «премией особенно отмечается объяснение законов фотоэлектрического эффекта».
- Заказать решение задач по физике
Пример №1
Монохроматический свет длиной волны 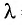 = 450 нм падает на поверхность натрия. Определите:
= 450 нм падает на поверхность натрия. Определите:
а) энергию Е фотона этого света;
б) модуль импульса р фотона падающего света;
в) красную границу 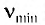 фотоэффекта для натрия;
фотоэффекта для натрия;
г) максимальную кинетическую энергию 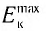 фотоэлектронов.
фотоэлектронов.
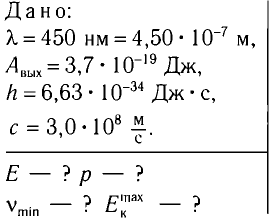
Решение
а) Энергия фотона определяется из соотношения E = hv = $-.
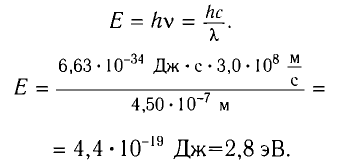
б) Модуль импульса фотона падающего света определяется из соотношения
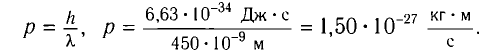
в) Красная граница связана с работой выхода соотношением
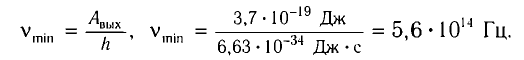
г) Согласно уравнению Эйнштейна электрон поглощает фотон и приобретает дополнительную энергию E = hv. Для того чтобы выйти за пределы металла, электрон должен отдать часть энергии на выполнение работы 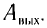 При этом его максимальная кинетическая энергия
При этом его максимальная кинетическая энергия
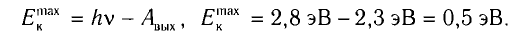
Ответ: 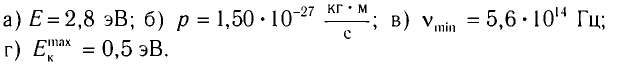
Пример №2
Под действием света длиной волны 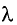 = 400 нм с поверхности металла вылетают электроны, при этом их энергия равна половине энергии фотонов, вызывающих фотоэффект. Определите длину волны
= 400 нм с поверхности металла вылетают электроны, при этом их энергия равна половине энергии фотонов, вызывающих фотоэффект. Определите длину волны 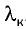 соответствующую красной границе фотоэффекта.
соответствующую красной границе фотоэффекта.
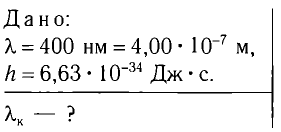
Ре ш е н и е
Запишем уравнение Эйнштейна для фотоэффекта:
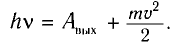
Красную границу фотоэффекта определим из соотношения
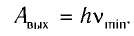
По условию задачи
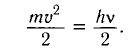
Тогда 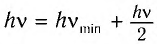 , откуда следует, что
, откуда следует, что 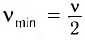 . Так как длина волны
. Так как длина волны 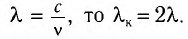
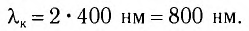
Ответ: 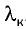 = 800 нм.
= 800 нм.
Давление света
Давлением называется скалярная физическая величина, численно равная отношению силы, действующей по нормали к площадке, к ее площади 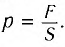
В СИ единицей давления является паскаль (Па): 1 Па = 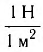 .
.
Из законов механики следует, что тело при ударе о поверхность оказывает механическое на нее давление, обусловленное изменением импульса тела. Причем давление оказывается в случае как упругого удара, так и неупругого. А будет ли возникать подобный эффект при отражении и поглощении света некоторой поверхностью? Иными словами, оказывает ли свет давление на поверхность, с которой взаимодействует? После завершения построения волновой теории света Максвеллом ответы на эти вопросы стали очевидными. Свет как электромагнитная волна обладает энергией и импульсом и поэтому оказывает давление на поверхность, на которую он падает.
В 1873 г. Максвелл вычислил световое давление, используя разработанную им теорию электромагнитного поля. Он показал, что если за промежуток времени 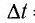 = 1 с перпендикулярно зеркальной площадке площадью S = 1 м2 падает свет с энергией то он оказывает на площадку давление р:
= 1 с перпендикулярно зеркальной площадке площадью S = 1 м2 падает свет с энергией то он оказывает на площадку давление р:
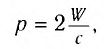
где с — скорость света.
Модуль силы давления, с которой солнечные лучи действуют на S= 1 м2 черной поверхности при нормальном падении: 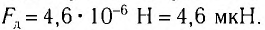
Объяснить давление света можно следующим образом. Электрическое поле 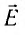 электромагнитной волны, падающей на поверхность проводника, вызывает движение электронов вещества в направлении, противоположном
электромагнитной волны, падающей на поверхность проводника, вызывает движение электронов вещества в направлении, противоположном 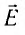 . Магнитное поле
. Магнитное поле 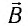 волны действует на уже движущиеся частицы с силой Лоренца
волны действует на уже движущиеся частицы с силой Лоренца 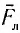 которая в данном случае направлена внутрь вещества (рис. 87) и совпадает с направлением распространения света. Суммарная сила, действующая на все электроны со стороны электромагнитной волны, и есть сила давления света.
которая в данном случае направлена внутрь вещества (рис. 87) и совпадает с направлением распространения света. Суммарная сила, действующая на все электроны со стороны электромагнитной волны, и есть сила давления света.
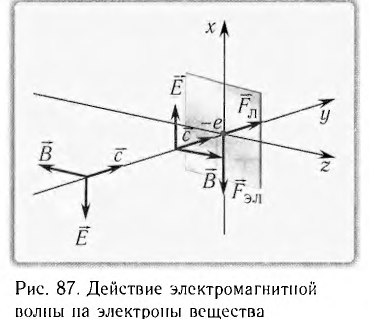
Это явление можно объяснить и с квантовой точки зрения. Рассмотрим свет как поток фотонов частотой v, падающих нормально на поверхность (рис. 88, а), и приносящий за промежуток времени 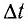 =1 с на площадь S = 1 м2 энергию, равную W. Число n фотонов определяется из условия nhv = W т. е.
=1 с на площадь S = 1 м2 энергию, равную W. Число n фотонов определяется из условия nhv = W т. е.
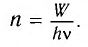
Так как каждый фотон обладает импульсом, модуль которого 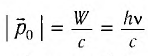 (рис. 88, б), то поглощающей поверхности (неупругий удар частицы) он сообщает импульс, модуль которого |
(рис. 88, б), то поглощающей поверхности (неупругий удар частицы) он сообщает импульс, модуль которого |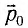 |, а полностью отражающей поверхности (абсолютно упругий удар) — импульс, модуль которого 2 |
|, а полностью отражающей поверхности (абсолютно упругий удар) — импульс, модуль которого 2 |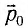 |.
|.
Следовательно, модуль импульса, сообщаемого абсолютно поглощающей (абсолютно черной) поверхности площадью S =1 м2 поверхности потоком фотонов за промежуток времени 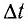 = 1 с, определяется по формуле:
= 1 с, определяется по формуле:
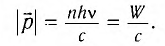
Это и есть изменение модуля импульса потока фотонов:
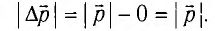
Согласно второму закону Ньютона изменение импульса приводит к возникновению силы 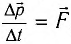 , которая по модулю равна силе давления
, которая по модулю равна силе давления 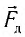 , но противоположно направлена. По определению давление на поверхность площадью S равно
, но противоположно направлена. По определению давление на поверхность площадью S равно 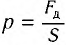 . Это приводит к окончательному результату:
. Это приводит к окончательному результату: 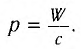 В случае полностью отражающей поверхности
В случае полностью отражающей поверхности 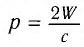 , что находится в согласии с формулой Максвелла.
, что находится в согласии с формулой Максвелла.
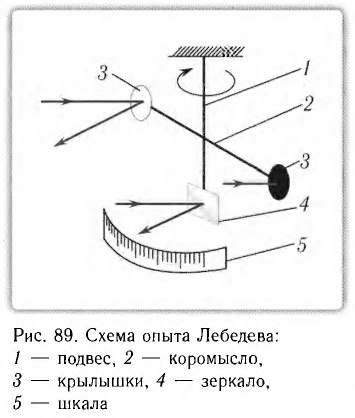
Пусть из полного числа n фотонов, падающих на единичную поверхность за 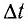 = 1 с, отражается Rn фотонов (R — коэффициент отражения), а (1 -R)n фотонов поглощается. Тогда сообщаемый единице поверхности импульс, численно равный давлению, находится по формуле
= 1 с, отражается Rn фотонов (R — коэффициент отражения), а (1 -R)n фотонов поглощается. Тогда сообщаемый единице поверхности импульс, численно равный давлению, находится по формуле
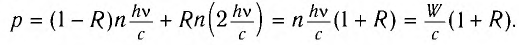
Русский физик Петр Николаевич Лебедев в 1899 г. впервые измерил световое давление. Он подвесил на тонкой нити коромысло с парой крылышек на концах (рис. 89): поверхность у одного из них была зачерненной, обеспечивая почти полное поглощение (R = 0), а у другого — зеркальной (/?=!)■
Свет практически полностью отражался от зеркальной поверхности, и его давление на зеркальное крылышко было вдвое больше, чем на зачерненное. Вследствие этого создавался момент сил, поворачивающий коромысло (см. рис. 89). Измеряя угол поворота коромысла, можно было судить о силе, действовавшей на крылышки, а следовательно, определить световое давление.
О сложности и тщательности подготовки и проведения измерений говорит тот факт, что при освещении крылышек светом в обычных условиях возникают силы, которые по величине превосходят силу давления света в тысячи раз. Одна из таких сил возникает в газе вследствие разности температур освещенной и неосвещенной сторон крылышка. Это действие Лебедеву удалось свести к минимуму, изготовив крылышки из тонкой, хорошо проводящей тепло фольги и поместив их в вакуум.
Измерения Лебедева дали величину светового давления, согласующуюся с теорией Максвелла с погрешностью до 20 %. В 1923 г. немецкий физик-экспериментатор Вальтер Герлах, используя более совершенные методы получения вакуума, повторил опыты Лебедева. Ему удалось получить результаты, согласующиеся с теоретическими значениями с погрешностью до 2%.
Факт существования светового давления имеет большое значение, так как доказывает наличие у света не только энергии, но и импульса. Это свидетельствует о материальности электромагнитных волн, представляющих собой еще одну форму существования материи — в виде поля.

Несмотря на сравнительно малое значение, световое давление играет существенную роль в природе: препятствует гравитационному сжатию звезд, ориентирует хвосты комет в сторону от Солнца, сокращает срок службы искусственных спутников Земли. Сегодня активно обсуждаются и реализуются проекты космических кораблей — «парусников», которые приводятся в движение «солнечным ветром».
В 1604 г. немецкий астроном Иоганн Кеплер объяснил изогнутую форму хвоста кометы действием сил светового давления со стороны Солнца (рис. 90), поскольку хвост всегда направлен от Солнца. Однако на доказательство этого факта потребовалось значительное время.
Корпускулярно-волновой дуализм
Когерентными называются волны одинаковой частоты, разность фаз колебаний которых в некоторой точке пространства остается постоянной с течением времени.
Интерференция — явление взаимодействия двух или более когерентных волн в пространстве, приводящее к увеличению или уменьшению амплитуды результирующего колебания в зависимости от разности хода волн. Дифракция — явление отклонения распространения волн от прямолинейного вблизи краев препятствий и огибания волнами препятствий.
Еще со времен Ньютона и Гюйгенса (XVII в.) представления о природе света были противоречивы. Одни ученые, во главе с Ньютоном, считали свет потоком частиц — корпускул, другие, вслед за Гюйгенсом, полагали, что свет представляет собой волны.
До начала XIX в. обе точки зрения отстаивались с переменным успехом. Так, исходя из гипотезы о корпускулах, можно было объяснить законы прямолинейного распространения и отражения света, а такие явления, как интерференция, дифракция и поляризация света, объяснялись только его волновыми свойствами.
Однако в XX в. было установлено, что в целом ряде явлений, таких, как, например, фотоэффект, свет ведет себя как совокупность частиц с определенной энергией и импульсом. Одновременное наличие у объекта волновых и корпускулярных свойств получило название корпускулярно-волнового дуализма.
В одних процессах проявляются волновые свойства света, в других — корпускулярные. Долгое время природа этого дуализма была совершенно непонятна, и он казался искусственным объединением противоречивых свойств материи.
Для преодоления этого противоречия датский физик Нильс Бор сформулировал принцип дополнительности, который утверждал, что для полного понимания природы света необходимо учитывать как волновые, так и корпускулярные свойства света: они взаимно дополняют друг друга.
Однако для объяснения конкретного эксперимента следует использовать либо волновые, либо корпускулярные представления о природе света, но не те и другие одновременно. Только после создания квантовой механики выяснилось, что «раздвоение личности» света закономерно и представляет собой проявление специфических свойств, присущих микромиру.
В 1923 г. французский физик Луи де Бройль свою диссертацию на соискание ученой степени доктора философии начал словами: «История оптических теорий показывает, что научные взгляды долгое время колебались между механической и волновой концепциями света, однако эти две точки зрения, вероятно, менее противоречат одна другой, чем думали раньше».
Далее он высказал смелое предположение: раз корпускулярно-волновой дуализм имеет место для световых квантов, он должен быть справедлив и для всех других частиц.
В частности движущемуся электрону должна соответствовать некоторая вол-
на, характеризуемая частотой v и длиной волны XR. Как и в случае фотона, частота v должна быть связана с энергией частицы Е соотношением E = hv. В настоящее время с каждой материальной частицей связывают волну, распространяющуюся в направлении движения частицы, которую называют волной де Бройля, а длину этой волны — дебройлевской длиной волны.
Дe Бройль определил, что модуль импульса частицы р должен выражаться через ее длину волны 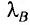 следующим образом:
следующим образом:
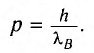 (I)
(I)
По этому соотношению всякому объекту, имеющему импульс 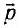 , независимо от его природы ставится в соответствие волновой процесс с длиной волны
, независимо от его природы ставится в соответствие волновой процесс с длиной волны
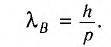 (2)
(2)
Формула де Бройля позволяет определить, в каких явлениях существенны волновые свойства, а в каких — корпускулярные. Вспомним, что волновые свойства — интерференция и дифракция — проявляются только тогда, когда размеры предметов или щелей сравнимы с длиной волны. Для частицы массой m, движущейся со скоростью и, длина волны де Бройля 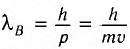 обратно пропорциональна массе частицы и ее скорости
обратно пропорциональна массе частицы и ее скорости 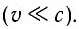 Таким образом, чем меньше масса частицы, движущейся с фиксированной скоростью, тем больше соответствующая ей длина волны
Таким образом, чем меньше масса частицы, движущейся с фиксированной скоростью, тем больше соответствующая ей длина волны 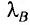 и тем более отчетливо обнаруживаются волновые свойства данной частицы. Следовательно, у электронов волновые свойства при движении проявляются наиболее отчетливо по сравнению с другими частицами.
и тем более отчетливо обнаруживаются волновые свойства данной частицы. Следовательно, у электронов волновые свойства при движении проявляются наиболее отчетливо по сравнению с другими частицами.
Для большинства движущихся макроскопических объектов (например, песчинка, теннисный шарик, футбольный мяч, Луна и т. д.) модуль импульса р, как правило, очень велик. В этом случае длина волны 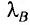 намного меньше размеров окружающих тел, и, соответственно, волновые свойства подобных макрообъектов становятся несущественными.
намного меньше размеров окружающих тел, и, соответственно, волновые свойства подобных макрообъектов становятся несущественными.
Для подобных предметов эта длина волны не превышает величины 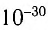 м, поэтому обнаружить их волновые свойства не удается. При сравнении этой величины с размером атома (
м, поэтому обнаружить их волновые свойства не удается. При сравнении этой величины с размером атома (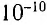 м) или даже атомного ядра (
м) или даже атомного ядра (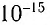 м) становится очевидной невозможность определения волн де Бройля такой длины.
м) становится очевидной невозможность определения волн де Бройля такой длины.
Таким образом, соотношение де Бройля 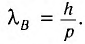 — особенно важно в следующих отношениях.
— особенно важно в следующих отношениях.
Во-первых, оно «узаконило» корпускулярно-волновой дуализм. Всякому телу, движущемуся с импульсом 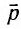 , сопоставляется теперь волновой процесс с длиной волны
, сопоставляется теперь волновой процесс с длиной волны 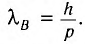
Во-вторых, из него видно, в каких явлениях волновые свойства существенны, а в каких — нет. Для макроскопических объектов их импульс, как правило, очень велик. Соответственно, в этом случае длина волны мала — много меньше размеров самого тела, и волновые свойства становятся незаметными.
Гипотеза де Бройля о наличии волновых свойств у электрона и других микрочастиц была проверена экспериментально.
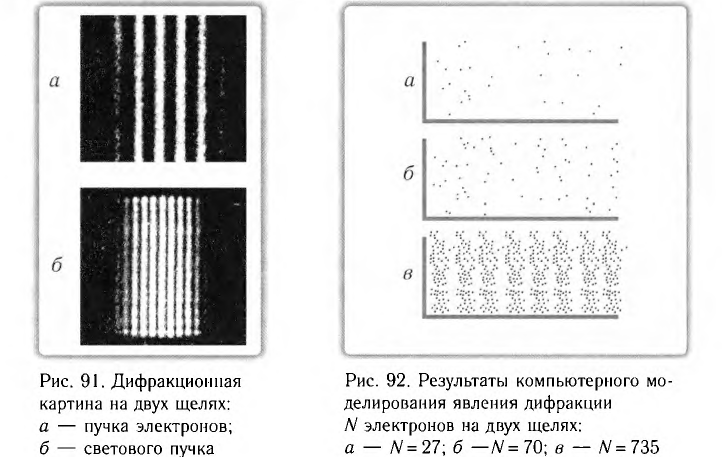
Поскольку дифракция света наблюдается на решетках, период d которых сравним с длиной волны 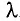 , то для наблюдения дифракции электронов следует выбирать решетки с соответствующим периодом. Например, каждому из электронов в пучке, прошедшем между обкладками конденсатора, заряженного до напряжения U = 150 В, соответствует энергия W= 150 эВ и длина волны
, то для наблюдения дифракции электронов следует выбирать решетки с соответствующим периодом. Например, каждому из электронов в пучке, прошедшем между обкладками конденсатора, заряженного до напряжения U = 150 В, соответствует энергия W= 150 эВ и длина волны 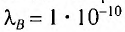 . Таким образом, в качестве дифракционной решетки следует выбрать кристалл какого-либо вещества, поскольку именно его кристаллическая решетка имеет период
. Таким образом, в качестве дифракционной решетки следует выбрать кристалл какого-либо вещества, поскольку именно его кристаллическая решетка имеет период 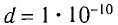 м, необходимый для обнаружения волновых свойств электронов.
м, необходимый для обнаружения волновых свойств электронов.
На рисунке 91 представлена фотография дифракционной картины на двух щелях: дня пучка электронов (рис. 91, а) и для светового пучка (рис. 91, б).
Компьютерное моделирование позволяет «увидеть» процесс образования ; дифракционной картины при последовательном увеличении числа электронов, прошедших через щель (рис. 92).
Способность к интерференции и дифракции была обнаружена не только у электронов, но и у других частиц — протонов, нейтронов и а-частиц.
Волновые свойства частиц нашли свое применение в электронной оптике, занимающейся исследованием, построением и использованием в практических целях электронных пучков.
Так использование волновых свойств пучка электронов позволило создать новое поколение микроскопов — электронные микроскопы (рис. 93), значительно превосходящие по степени увеличения оптические микроскопы.

Уже первый электронный просвечивающий микроскоп (Э. Руска, 1933 г.) позволял изучать детали в десять раз меньшие, чем те, которые способны разрешать самые «мощные» оптические микроскопы. Дальнейшие исследования позволили сотрудникам лаборатории фирмы IBM в Цюрихе (Швейцария) Г. Биннингу и Г. Рореру в 1981 г. создать электронный сканирующе-туннельный микроскоп, позволяющий рассмотреть даже «отдельный» атом.
Таким образом, корпускулярно-волновой дуализм относится не только к частицам, но и к любым материальным телам. На них также распространяется принцип дополнительности, и используются как волновое, так и корпускулярное представления, в зависимости от конкретной ситуации.
В 1929 г. Луи де Бройль за открытие волновой природы электрона был удостоен Нобелевской премии.
В 1986 г. Герду Биннингу и Генриху Рореру совместно с Эрнстом Руска была присуждена Нобелевская премия по физике за создание электронного микроскопа.
Пример №3
Вычислите длину волны де Бройля 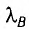 для футбольного мяча массой m = 400 г, летящего со скоростью v = 20
для футбольного мяча массой m = 400 г, летящего со скоростью v = 20 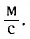
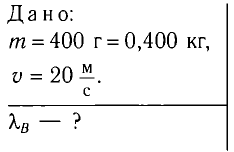
Решение
Длина волны де Бройля 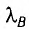 определяется по формуле
определяется по формуле
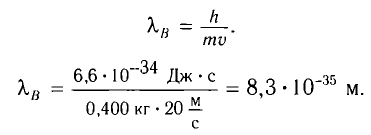
Ответ: 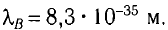
Химическое действие света
В веществах под действием света могут происходить химические реакции, которые без освещения (если все остальные условия остаются неизменными) не происходят. Такие реакции называются фотохимическими.
Примерами фотохимических реакций являются реакции фотосинтеза и реакции разложения (диссоциации).
Реакция фотосинтеза заключается в том, что под действием света происходит образование углеводов и выделение кислорода в растениях:

Фотосинтез — основа жизни на Земле. Это единственный процесс, в результате которого «органический мир» за счет энергии излучения Солнца пополняет запасы кислорода, расходуемые в процессе жизнедеятельности. По современным представлениям, весь кислород в атмосфере Земли образовался и постоянно пополняется за счет фотосинтеза в листьях растений и зеленых водорослях. Кроме того, эта реакция обеспечивает круговорот углерода в природе, без которого было бы невозможно длительное существование органической жизни на Земле.
Реакция разложения приводит к образованию более простых молекул и атомов под действием света. Например: разложение бромистого серебра
Химическое действие света
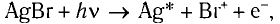
диссоциация молекул хлора
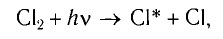
разложение углекислого газа
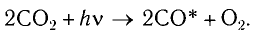
(В реакциях разложения значком (*) обозначены энергетически возбужденные атомы, которые в химии называются активными радикалами.)
Классическая физика не могла объяснить экспериментально установленные закономерности фотохимических реакций. В квантовой физике они нашли четкое объяснение. В 1912 г. Эйнштейн, используя квантовые представления, дал объяснения фотохимических явлений и сформулировал два закона фотохимических реакций.
- Каждый поглощенный веществом фотон вызывает превращение одной поглотившей свет молекулы (закон эквивалентности).
- Молекула вступает в фотохимическую реакцию под действием фотона лишь в том случае, когда энергия фотона не меньше определенного значения (энергии активации D):
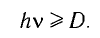
Атомы внутри молекулы удерживаются химическими связями, которые при поглощении молекулой фотона с энергией Е разрываются, и в результате молекула распадается. Однако если энергия фотона меньше энергии, необходимой для разрыва молекулярных связей, то фотохимическая реакция не произойдет. Вследствие этого для каждой фотохимической реакции существует «красная граница», т. е. минимальная частота, при которой свет еще химически активен.
Химическим действием света обусловлены реакции фотосинтеза хлоропласта в зеленых частях растений, появление загара у человека, выцветание тканей на солнце, разложение молекул бромистого серебра в светочувствительном слое фотопластинки и т. д. Большую роль играют фотохимические превращения, лежащие в основе зрительного восприятия человека и животных.
Фотохимические реакции лежат в основе фотографического процесса (фотография — светопись) — одного из величайших достижений нашей цивилизации. Он состоит из четырех основных этапов:
- фотосъемка — распад молекул бромистого серебра в фотопленке под действием света;
- проявление фотопленки — выделение серебра, образовавшегося при световом воздействии;
- закрепление фотопленки — удаление бромистого серебра с фотослоя и таким образом предохранение фотослоя от дальнейших изменений под действием света;
- копирование — перенос изображения с фотопленки на фотобумагу.
Самое первое упоминание о фотографии на стекле (медная гравюра с изображением папы Пия VII), снятой в Грасе (Франция), содержится в письме французского ученого Жозефа Нисефора Ньепса от 19 июля 1822 г. 7 января 1839 г. принято считать датой рождения фотографии. В этот день на заседании Парижской академии наук ее секретарь Доменик Франсуа Араго доложил об изобретении художника Луи Жака Дагера. «Благодаря стараниям Луи Дагера человечество вознаграждено за настойчивость: свет стал послушным рисовальщиком».
Самая первая фотография с воздуха выполнена в 1858 г. Гаспаром Феликсом Турнашоном с воздушного шара над окраиной Парижа. Самой маленькой является круглая японская камера «Petal» диаметром 2,9 см и толщиной 1,65 см. Ее фокусное расстояние равно 12 мм.
Итоги:
Начало квантовой теории было положено гипотезой Планка, согласно которой излучение и поглощение света веществом происходит не непрерывно, а порциями, или квантами.
Наименьшая порция энергии (квант энергии), которую несет излучение частотой v, определяется по формуле
Е = hv,
где постоянная h — фундаментальная постоянная (постоянная Планка). Ее значение
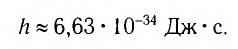
Эйнштейн развил гипотезу Планка, представив, что свет является совокупностью движущихся фотонов.
Модуль импульса фотона определяется соотношением
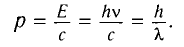
Явление испускания электронов веществом под действием падающего на него света получило название внешнего фотоэффекта. Испускание веществом каких-либо частиц называется эмиссией. Поэтому внешний фотоэффект называют также фотоэлектронной эмиссией (фотоэмиссией), а вылетающие электроны — фотоэлектронами.
Экспериментально установлены следующие законы внешнего фотоэффекта:
- Сила фототока насыщения
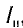 определяемая максимальным числом фотоэлектронов, вырываемых из катода за единицу времени, прямо пропорциональна интенсивности l падающего излучения.
определяемая максимальным числом фотоэлектронов, вырываемых из катода за единицу времени, прямо пропорциональна интенсивности l падающего излучения. - Максимальная кинетическая энергия
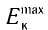 фотоэлектронов не зависит от интенсивности l падающего излучения и линейно возрастает с увеличением частоты v падающего излучения.
фотоэлектронов не зависит от интенсивности l падающего излучения и линейно возрастает с увеличением частоты v падающего излучения. - Для каждого вещества существует граничная частота vmin такая, что излучение меньшей частоты не может вырывать электроны.
Формула, предложенная Эйнштейном для объяснения внешнего фотоэффекта, имеет вид:
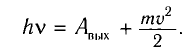
Красная граница фотоэффекта — наименьшая частота излучения, при которой наблюдается фотоэффект:
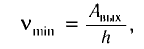
зависит только от работы выхода электронов для данного вещества (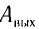 > 0), т. е. определяется химической природой вещества и состоянием его поверхности.
> 0), т. е. определяется химической природой вещества и состоянием его поверхности.
Под корпускулярно-волновым дуализмом понимают совокупность волновых и корпускулярных свойств, присущих всем объектам в природе.
Химическое действие света (фотохимические реакции) — химические превращения, происходящие в веществах в результате поглощения света.
Фотоны и действия света
В конце XIX в. многие ученые считали, что развитие физики завершилось. Законы механики и теория всемирного тяготения были известны более 200 лет. К этому времени была развита и стала общепризнанной теория электромагнитного поля, основы которой были заложены Дж. Максвеллом.
Однако к началу XX в. возникли проблемы, касающиеся физической природы излучения и вещества, а также их взаимодействия. В рамках классической физики возникали непреодолимые противоречия при объяснении экспериментальных данных для процессов поглощения и испускания света атомами, закономерностей испускания электромагнитного излучения нагретыми телами, фотоэффекта и т. п.
Анализ этих противоречий привел физиков в начале XX в. к научной революции, которая коренным образом изменила взгляды ученых на объекты микромира — атом, его ядро и элементарные частицы. В течение последующих 30 лет были заложены основы современной квантовой физики, пришедшей на смену классической физике при рассмотрении явлений на атомном и внутриатомном (субатомном) уровнях. В следующих двух главах (5-й и 6-й) рассматриваются основные вопросы квантовой физики.
Экспериментальные законы внешнего фотоэффекта и квантовая гипотеза Планка
Сила тока 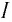 — скалярная физическая величина, равная отношению заряда
— скалярная физическая величина, равная отношению заряда 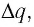 прошедшего за промежуток времени
прошедшего за промежуток времени 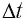 через поперечное сечение проводника, к этому промежутку:
через поперечное сечение проводника, к этому промежутку: 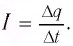
Наше зрительное восприятие физических явлений в окружающем мире определяется взаимодействием света с веществом. Воздействие света на вещество состоит в поглощении им световой энергии, приносимой излучением, т. е. первичным процессом является поглощение света. Такое взаимодействие, например в сетчатке глаза, приводит к зрительным ощущениям.
При падении света на поверхность непрозрачного предмета часть излучения проникает в него и поглощается, другая часть отражается от поверхности, и мы видим предмет в отраженном свете. Более темные поверхности поглощают свет сильнее, чем более светлые. Доля отраженного от поверхности света зависит от длины волны.
Для прозрачной среды, например стекла, при падении на него световой волны главным результатом взаимодействия является ее отражение и преломление, а поглощением электромагнитной энергии в видимом диапазоне можно пренебречь. Именно поэтому среда и воспринимается зрительно как прозрачная.
Мы видим не только тела, которые отражают или рассеивают свет, но и тела, которые светятся сами, например Солнце, другие звезды, пламя. Электромагнитное излучение испускают все тела, причем его интенсивность зависит от температуры их поверхности. В видимом диапазоне спектра излучение достаточной интенсивности, позволяющее видеть предмет, возникает, если температура поверхности предмета намного больше комнатной.
Взаимодействие электромагнитных волн с веществом приводит и к другим физическим явлениям, изучение которых помогло выяснить природу света.
В 1887 г. Генрих Герц обнаружил, что пробой воздушного промежутка между электродами искрового разрядника происходит при меньшем напряжении, если освещать отрицательно заряженный электрод ультрафиолетовым излучением. Дальнейшие эксперименты показали, что отрицательно заряженная цинковая пластинка при облучении ультрафиолетовым излучением (рис. 107, а) разряжается. Оба эти явления можно объяснить, предполагая, что под действием падающего излучения из металла вылетают отрицательно заряженные частицы — электроны (рис. 107, б). Это явление получило название фотоэффекта.
Фотоэффектом (фотоэлектрическим эффектом) называется явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передается электронам вещества, что приводит к разрыву связей электронов и ядер в атомах.
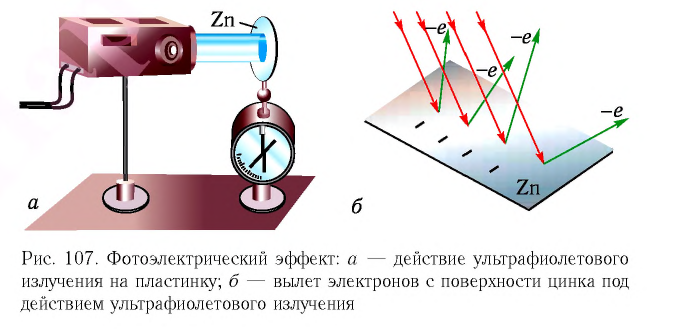
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним фотоэффектом. При внутреннем фотоэффекте часть электронов, находящихся в веществе в связанном состоянии, переходят в свободное состояние, увеличивая концентрацию носителей тока.
Испускание веществом каких-либо частиц называется эмиссией. Поэтому внешний фотоэффект называют также фотоэлектронной эмиссией (фотоэмиссией).
 (фотос) по-гречески означает «свет».
(фотос) по-гречески означает «свет».
Систематическое изучение фотоэффекта было проведено в 1888—1889 гг. русским физиком Александром Григорьевичем Столетовым.
Установка для изучения внешнего фотоэффекта представлена на рисунке 108, а. В экспериментах Столетова в электрическую цепь был включен конденсатор, одна из обкладок которого была изготовлена из медной сетки, а вторая — представляла собой цинковую пластинку. Медная сетка была заряжена положительно, а цинковая пластинка — отрицательно. Наблюдения показали, что под действием падающего ультрафиолетового излучения в цепи возникает электрический ток. Этот ток называется фототоком.
Изменяя напряжение 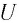 между пластинами
между пластинами 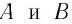 с помощью реостата (рис. 108,6), Столетов исследовал зависимость силы фототока
с помощью реостата (рис. 108,6), Столетов исследовал зависимость силы фототока 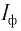 от напряжения
от напряжения 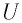 (вольт-амперную характеристику). Как видно из представленной на рисунке 108, в зависимости, даже при отсутствии разности потенциалов между пластинами в цепи проходит фототок. Так как скорости электронов, испускаемых катодом, различны как по модулю, так и по направлению, то не все они при малых значениях напряжения могут достигнуть анода.
(вольт-амперную характеристику). Как видно из представленной на рисунке 108, в зависимости, даже при отсутствии разности потенциалов между пластинами в цепи проходит фототок. Так как скорости электронов, испускаемых катодом, различны как по модулю, так и по направлению, то не все они при малых значениях напряжения могут достигнуть анода.
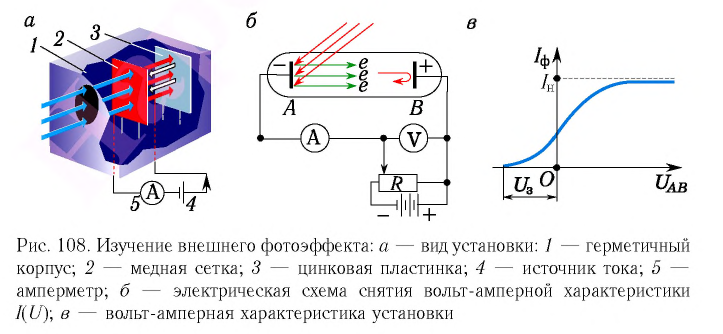
При увеличении напряжения сила фототока растет до некоторого максимального значения 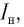 которое называется фототоком насыщения. Оно определяется при таком значении напряжения, при котором все электроны, испускаемые катодом, достигают анода. Дальнейшее увеличение напряжения не приводит к росту силы фототока. Изменение полярности напряжения приводит к исчезновению фототока при напряжении
которое называется фототоком насыщения. Оно определяется при таком значении напряжения, при котором все электроны, испускаемые катодом, достигают анода. Дальнейшее увеличение напряжения не приводит к росту силы фототока. Изменение полярности напряжения приводит к исчезновению фототока при напряжении 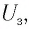 которое называется задерживающим напряжением.
которое называется задерживающим напряжением.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового излучения. Однако некоторые металлы, например литий, натрий и калий, испускают электроны и при их облучении видимым светом.
Экспериментально установлены следующие законы внешнего фотоэффекта.
1. Сила фототока насыщения 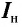 прямо пропорциональна интенсивности
прямо пропорциональна интенсивности 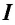 падающего излучения (первый закон фотоэффекта).
падающего излучения (первый закон фотоэффекта).
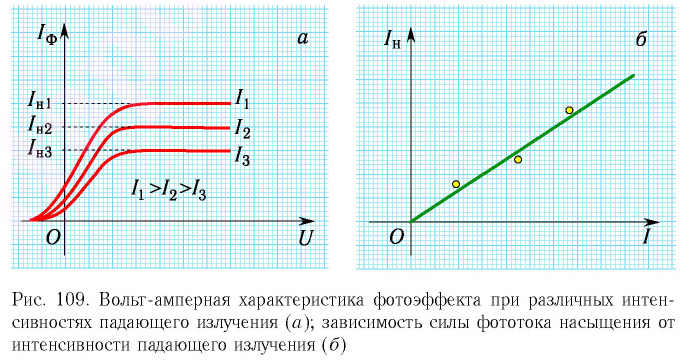
Вольт-амперная характеристика фотоэффекта показана на рисунке 108, в и 109, а, а зависимость силы фототока насыщения 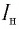 от интенсивности падающего излучения
от интенсивности падающего излучения 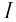 — на рисунке 109, б.
— на рисунке 109, б.
Из графика зависимости 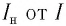 (график выходит из начала координат), приведенного на рисунке 109, б, видно, что сила фототока насыщения равна нулю
(график выходит из начала координат), приведенного на рисунке 109, б, видно, что сила фототока насыщения равна нулю 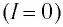 только при отсутствии излучения. Иными словами, фотоэффект наблюдается даже при малых значениях интенсивности падающего излучения.
только при отсутствии излучения. Иными словами, фотоэффект наблюдается даже при малых значениях интенсивности падающего излучения.
2. Максимальная кинетическая энергия 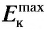 фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты v падающего излучения (второй закон фотоэффекта).
фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты v падающего излучения (второй закон фотоэффекта).
Подчеркнем, что кинетическая энергия фотоэлектронов, вылетающих из фотокатода, изменяется в некотором диапазоне от нуля до 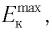 так как фотоэлектроны часть своей энергии, полученной от падающего излучения, передают частицам вещества до вылета с его поверхности.
так как фотоэлектроны часть своей энергии, полученной от падающего излучения, передают частицам вещества до вылета с его поверхности.
На рисунке 110 представлена зависимость 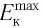 от частоты падающего излучения.
от частоты падающего излучения.
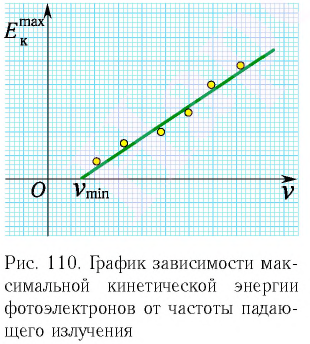
3. Для каждого вещества существует граничная частота 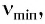 такая, что излучение меньшей частоты не может вырывать электроны из его поверхности (третий закон фотоэффекта).
такая, что излучение меньшей частоты не может вырывать электроны из его поверхности (третий закон фотоэффекта).
Эта минимальная частота 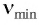 называется красной границей фотоэффекта. Такое название связано с тем, что минимальной частотой излучения в видимом диапазоне обладает излучение, соответствующее красному цвету.
называется красной границей фотоэффекта. Такое название связано с тем, что минимальной частотой излучения в видимом диапазоне обладает излучение, соответствующее красному цвету.
Красная граница фотоэффекта для различных веществ совсем не обязательно соответствует красному цвету. Например, для рубидия она соответствует желтому цвету, для кальция — синему, а для некоторых веществ может вообще находиться в инфракрасной или ультрафиолетовой областях спектра.
На рисунке 111 приведены экспериментальные зависимости максимальной кинетической энергии фотоэлектронов 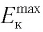 от частоты падающего излучения для цезия, рубидия, магния и серебра. Как видно из рисунка 111, экспериментальные прямые параллельны друг другу, причем точки пересечения графиков с осью абсцисс (частот) определяют красные границы фотоэффекта для каждого из них.
от частоты падающего излучения для цезия, рубидия, магния и серебра. Как видно из рисунка 111, экспериментальные прямые параллельны друг другу, причем точки пересечения графиков с осью абсцисс (частот) определяют красные границы фотоэффекта для каждого из них.
При частотах, больших 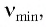 излучение даже очень малой интенсивности вызывает фотоэффект. Кроме того, между
излучение даже очень малой интенсивности вызывает фотоэффект. Кроме того, между
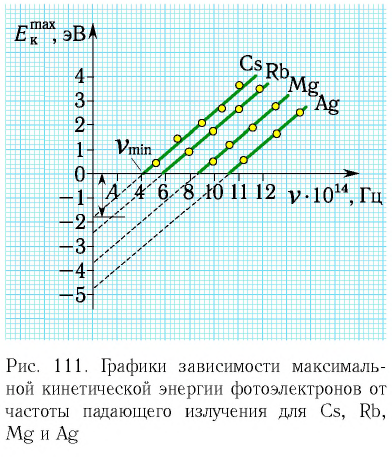
моментом включения источника излучения и вылетом электронов фактически нет задержки во времени: электроны вылетают из вещества через промежуток времени порядка 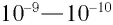 с после начала облучения.
с после начала облучения.
Следует заметить, что к моменту открытия фотоэффекта в 1887 г. еще ничего не было известно об электронах, открытых Дж. Томсоном только в 1897 г.
В 1898 г. Филиппом Ленардом и Джозефом Джоном Томсоном было определено отношение заряда 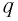 частицы, вылетающей с поверхности металла при фотоэффекте, к ее массе
частицы, вылетающей с поверхности металла при фотоэффекте, к ее массе 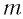 (так называемый удельный заряд —
(так называемый удельный заряд — 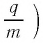 по ее отклонению в электрическом и магнитном полях. Эти измерения дали то же
по ее отклонению в электрическом и магнитном полях. Эти измерения дали то же
значение, что и отношение заряда электрона к его массе 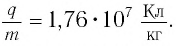
Таким образом, было доказано, что выбиваемые светом заряженные частицы — электроны.
За работы по определению удельного заряда электрона 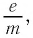 приведшие к открытию первой элементарной частицы — электрона, Дж. Томсон в 1906 г. был удостоен Нобелевской премии по физике.
приведшие к открытию первой элементарной частицы — электрона, Дж. Томсон в 1906 г. был удостоен Нобелевской премии по физике.
Установленные экспериментально законы фотоэффекта невозможно объяснить на основе представлений о том, что свет — это электромагнитная волна. На основе этих представлений можно объяснить только первый из приведенных экспериментальных законов фотоэффекта: чем больше энергия падающего света, тем больше электронов вылетает из вещества. Объяснить 2-й и 3-й законы фотоэффекта в рамках классической теории излучения невозможно.
Так, например, непонятно, почему максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения. Невозможно также объяснить существование красной границы фотоэффекта. Действительно, даже при малой частоте падающего излучения, но при длительном воздействии электромагнитной волны на электрон ему можно сообщить энергию, необходимую для выхода из вещества. Следовательно, красная граница фотоэффекта не должна существовать. Все эти противоречия были сняты квантовой теорией.
Квантовые представления были впервые введены немецким физиком Максом Планком при разработке теории теплового излучения. Планк сделал фундаментальное предположение, что энергия любой колебательной системы, совершающей гармонические колебания с частотой 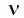 (осциллятора), может принимать лишь определенные дискретные значения, отличающиеся на целое число элементарных порций — квантов энергии:
(осциллятора), может принимать лишь определенные дискретные значения, отличающиеся на целое число элементарных порций — квантов энергии:
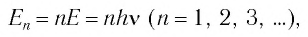
где 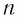 — целое положительное число,
— целое положительное число, 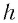 — коэффициент пропорциональности, который называют постоянной Планка. Это фундаментальная постоянная. Ее значение:
— коэффициент пропорциональности, который называют постоянной Планка. Это фундаментальная постоянная. Ее значение:
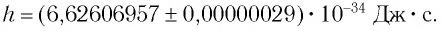
Приближенное значение постоянной Планка, применяемое при решении задач:
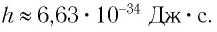
Слово квант происходит от латинского слова «quantum» — «сколько» или «как много». Это слово, вообще, обозначает часть, долю или неделимую порцию. Планк поэтически назвал новую фундаментальную постоянную 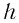 «таинственным послом из реального мира».
«таинственным послом из реального мира».
Следовательно, отдельный осциллятор может обладать не любой энергией, а лишь энергией, кратной 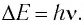 Таким образом впервые появилась идея о квантовании энергии.
Таким образом впервые появилась идея о квантовании энергии.
14 декабря 1900 г. Планк доложил свои результаты на заседании Немецкого физического общества. Этот день и считают днем рождения квантовых представлений. Появился квант энергии как дискретная порция энергии. Планк относил дискретность энергии к свойствам вещества, а излучение рассматривалось как электромагнитные волны.
После выдвижения гипотезы Планком (1900 г.) началось интенсивное развитие квантовых представлений в физике, которые к 1925—1928 гг. превратились в стройную и логичную квантовую теорию, открывшую «новую эру» в развитии физики.
Фотон и уравнение Эйнштейна для фотоэффекта
Электронвольт — энергия, которую приобретет частица с зарядом, равным элементарному, при перемещении между двумя точками с ускоряющей разностью потенциалов 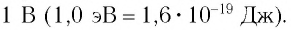
Развивая идеи М. Планка, А. Эйнштейн в 1905 г. для объяснения экспериментальных законов внешнего фотоэффекта выдвинул гипотезу о дискретности самого электромагнитного излучения — свет излучается, поглощается и распространяется в виде отдельных порций (квантов). Он рассмотрел элементарные процессы поглощения и испускания этих квантов.
По гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой 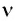 обладает не только волновыми свойствами, но и свойствами, характерными для потока частиц. Каждая такая частица движется со скоростью света
обладает не только волновыми свойствами, но и свойствами, характерными для потока частиц. Каждая такая частица движется со скоростью света 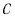 и несет квант энергии
и несет квант энергии 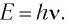 Назвать эти частицы фотонами предложил в 1928 г. американский физик Артур Комптон.
Назвать эти частицы фотонами предложил в 1928 г. американский физик Артур Комптон.
Энергия фотона может быть выражена через длину волны 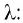
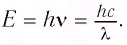
Как следует из формул (2) § 25, 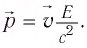 Тогда модуль импульса фотона
Тогда модуль импульса фотона 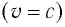 определяется выражением:
определяется выражением:
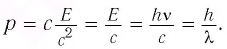
Следовательно, для фотона:
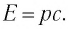
Но согласно СТО (см. § 25) энергия и импульс любой частицы связаны соотношением:
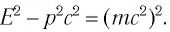
При подстановке в эту формулу энергии фотона 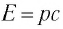 находим, что масса фотона равна нулю
находим, что масса фотона равна нулю 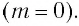
Оказывается, что фотон — это удивительная частица, которая обладает энергией 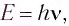 импульсом
импульсом 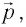 но вследствие того, что скорость его движения всегда равна скорости распространения света, его масса равна нулю
но вследствие того, что скорость его движения всегда равна скорости распространения света, его масса равна нулю 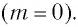 Такие частицы называют безмассовыми.
Такие частицы называют безмассовыми.
Фотон является элементарной частицей, только в отличие от других элементарных частиц он не имеет массы, а потому «обречен» всегда двигаться со скоростью распространения света.
Таким образом, фотон обладает следующими свойствами:
существует только в движении;
- является без массовой частицей
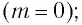
- электрически нейтрален
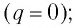
- модуль его скорости движения равен модулю скорости распространения света в вакууме
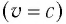 во всех ИСО;
во всех ИСО; - его энергия пропорциональна частоте соответствующего электромагнитного излучения
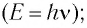
- модуль импульса фотона равен отношению его энергии к модулю скорости движения
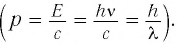
Рассмотрим объяснение экспериментальных законов фотоэффекта, предложенное Эйнштейном на основе квантовых представлений. При освещении электрода электромагнитным излучением (см. рис. 109) происходит взаимодействие фотонов с электронами вещества. Если энергия фотона 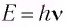 достаточно велика, то какой-либо из электронов после поглощения фотона может получить энергию, достаточную для того, чтобы покинуть облучаемое тело. Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю. Именно поэтому вольт-амперная характеристика фотоэффекта при напряжении, равном нулю, не проходит через нуль (см. рис. 109, а).
достаточно велика, то какой-либо из электронов после поглощения фотона может получить энергию, достаточную для того, чтобы покинуть облучаемое тело. Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю. Именно поэтому вольт-амперная характеристика фотоэффекта при напряжении, равном нулю, не проходит через нуль (см. рис. 109, а).
Для того чтобы покинуть вещество, электрон должен совершить работу против сил связи электрона с атомами вещества. Она называется работой выхода и обозначается 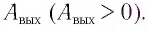 Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решетки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт (табл. 8).
Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решетки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт (табл. 8).
Оставшаяся часть энергии поглощенного кванта составляет кинетическую энергию освободившегося электрона. Наибольшей кинетической энергией
будут обладать те электроны, которые поглотят кванты света вблизи поверхности металла и вылетят из него, не успев потерять энергию при столкновениях с другими частицами в металле.
На основе закона сохранения энергии можно записать следующее уравнение для фотоэлектрона:
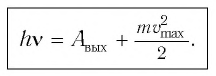
Это соотношение называют уравнением Эйнштейна для внешнего фотоэффекта.
Отметим, что 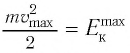 — это максимальная кинетическая энергия электрона
— это максимальная кинетическая энергия электрона 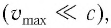 которой он может обладать, вылетев из вещества. Из-за различных потерь энергия электрона может быть меньше расчетного значения.
которой он может обладать, вылетев из вещества. Из-за различных потерь энергия электрона может быть меньше расчетного значения.
Если энергия фотонов очень велика (для рентгеновского или 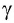 -излучения), то скорости фотоэлектронов сравнимы со скоростью света
-излучения), то скорости фотоэлектронов сравнимы со скоростью света 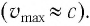 В этом случае для кинетической энергии фотоэлектрона необходимо использовать релятивистское выражение:
В этом случае для кинетической энергии фотоэлектрона необходимо использовать релятивистское выражение:
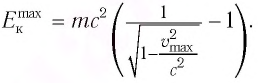
Используя уравнение Эйнштейна, можно объяснить экспериментальные законы фотоэффекта.
Объяснение первого закона фотоэффекта
Сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени. Число таких фотоэлектронов пропорционально числу фотонов, падающих на поверхность за это же время. Именно пропорционально, а не равно, так как часть квантов света поглощается кристаллической решеткой, и их энергия переходит во внутреннюю энергию металла. Увеличение интенсивности падающего света приводит к росту числа фотоэлектронов, покидающих поверхность металла.
Объяснение второго закона фотоэффекта
Фотоэлектрон вырывается из катода за счет действия одного кванта падающего излучения. Поэтому кинетическая энергия фотоэлектрона зависит не от полной энергии волны, а от энергии одного кванта, т. е. частоты 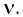 При увеличении частоты
При увеличении частоты 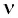 падающего света максимальная кинетическая энергия
падающего света максимальная кинетическая энергия 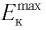 фотоэлектронов возрастает линейно, как следует из уравнения Эйнштейна для фотоэффекта (3), согласно соотношению:
фотоэлектронов возрастает линейно, как следует из уравнения Эйнштейна для фотоэффекта (3), согласно соотношению:
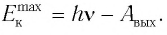
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то сила тока уменьшится, так как теперь фотоэлектронам, кроме работа выхода, придется совершать дополнительную работу против сил электрического поля.
При некотором отрицательном значении напряжения 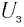 электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи при этом будет равна нулю (рис. 112). Величину
электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи при этом будет равна нулю (рис. 112). Величину 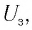 при которой сила тока в цепи равна нулю, называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетическая энергия электронов выражается через задерживающее напряжение следующим образом:
при которой сила тока в цепи равна нулю, называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетическая энергия электронов выражается через задерживающее напряжение следующим образом:
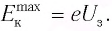
Объяснение третьего закона фотоэффекта
Если частота 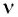 падающего излучения меньше граничной частоты
падающего излучения меньше граничной частоты 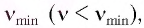 при которой
при которой 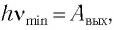 то испускания электронов не происходит. Таким образом, фотоэффект отсутствует, если частота излучения оказывается меньше некоторой характерной для данного вещества величины
то испускания электронов не происходит. Таким образом, фотоэффект отсутствует, если частота излучения оказывается меньше некоторой характерной для данного вещества величины 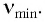
Следовательно, красную границу фотоэффекта можно найти из условия:
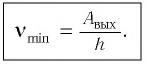
Она зависит только от работы выхода электронов, т. е. определяется строением металла и состоянием его поверхности.
Длина волны 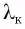 излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения:
излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения:
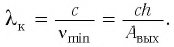
Подставляя в уравнение (3) выражения (5) и (6), найдем зависимость задерживающего напряжения от частоты падающего света:
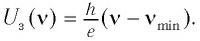
Находя тангенс угла наклона 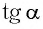 прямых линий на рисунке 111, можно из соотношения (8) с учетом (5) вычислить постоянную Планка:
прямых линий на рисунке 111, можно из соотношения (8) с учетом (5) вычислить постоянную Планка:
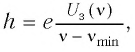
а по точкам пересечения продолжения графиков с осями 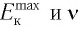 — найти работу выхода
— найти работу выхода 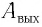 и красную границу
и красную границу 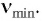
В 1921 г. при присуждении Альберту Эйнштейну Нобелевской премии в решении Нобелевского комитета указывалось, что «премией особенно отмечается объяснение законов фотоэлектрического эффекта».
Пример №4
Монохроматический свет длиной волны 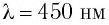 падает на поверхность натрия. Определите: а) энергию
падает на поверхность натрия. Определите: а) энергию 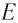 фотона этого света; б) модуль импульса
фотона этого света; б) модуль импульса 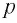 фотона падающего света; в) красную границу
фотона падающего света; в) красную границу 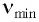 фотоэффекта для натрия; г) максимальную кинетическую энергию
фотоэффекта для натрия; г) максимальную кинетическую энергию 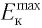 фотоэлектронов.
фотоэлектронов.
Дано:
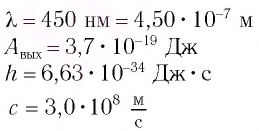
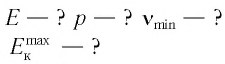
Решение а) Энергия фотона:
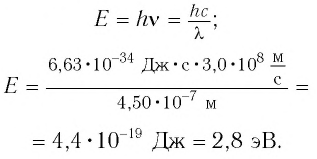
б) Модуль импульса фотона:
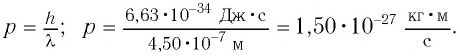
в) Красная граница связана с работой выхода соотношением:
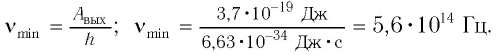
г) Из уравнения Эйнштейна для внешнего фотоэффекта находим, что максимальная кинетическая энергия вылетевшего электрона:
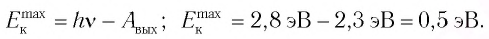
Ответ: 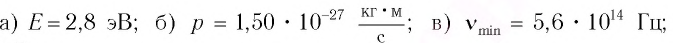
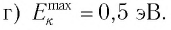
Давление света и корпускулярно-волновой дуализм
Словечко громкое всегда Из затрудненья вас выводит! И. Гете «Фауст»
Давлением называется скалярная физическая величина, численно равная отношению модуля силы, действующей по нормали к площадке, к ее площади 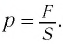 В СИ единицей давления является 1 паскаль (Па):
В СИ единицей давления является 1 паскаль (Па): 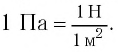
Из законов механики следует, что тело при ударе о некоторую поверхность оказывает на нее механическое давление, обусловленное изменением импульса тела. Причем давление тела на поверхность оказывается в случае как упругого, так и не упругого удара. А будет ли возникать подобный эффект при отражении и поглощении света некоторой поверхностью? Иными словами, оказывает ли свет давление на поверхность, с которой взаимодействует? После завершения построения Дж. Максвеллом волновой теории света ответы на эти вопросы стали очевидными. Свет как электромагнитная волна обладает энергией и импульсом и поэтому оказывает давление на поверхность, на которую он падает.
Объяснить давление света можно следующим образом. Электрическое поле напряженностью 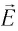 электромагнитной волны, падающей на поверхность проводника, вызывает движение электронов вещества под действием электрической силы в направлении, противоположном
электромагнитной волны, падающей на поверхность проводника, вызывает движение электронов вещества под действием электрической силы в направлении, противоположном 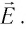 Магнитное поле волны индукцией
Магнитное поле волны индукцией 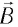 действует на движущиеся частицы с силой Лоренца
действует на движущиеся частицы с силой Лоренца 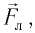 которая в данном случае будет направлена внутрь вещества (рис. 114) и совпадает с направлением распространения света. Суммарная сила, действующая на все электроны со стороны электромагнитной волны, и есть сила давления света.
которая в данном случае будет направлена внутрь вещества (рис. 114) и совпадает с направлением распространения света. Суммарная сила, действующая на все электроны со стороны электромагнитной волны, и есть сила давления света.
В 1873 г. Максвелл вычислил световое давление, используя разработанную им теорию электромагнитного поля. Он показал, что если свет, падающий перпендикулярно на зеркальную поверхность площадью 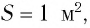 приносит за промежуток времени
приносит за промежуток времени 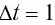 с энергию
с энергию 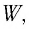 то он оказывает на данную поверхность давление:
то он оказывает на данную поверхность давление:
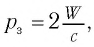
где 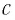 — модуль скорости распространения света. Поскольку для солнечного излучения
— модуль скорости распространения света. Поскольку для солнечного излучения 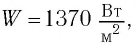 то модуль силы давления, с которой солнечное излучение действует при нормальном падении на зеркальную поверхность площадью
то модуль силы давления, с которой солнечное излучение действует при нормальном падении на зеркальную поверхность площадью 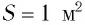
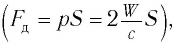 равен
равен 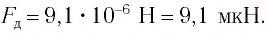
При нормальном падении света на черную (поглощающую) поверхность модуль соответствующей силы давления 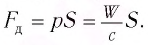 Следовательно, сила, с которой солнечное излучение действует на черную поверхность площадью
Следовательно, сила, с которой солнечное излучение действует на черную поверхность площадью 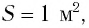 в два раза меньше, чем на зеркальную, и составляет
в два раза меньше, чем на зеркальную, и составляет 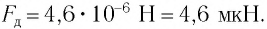
Давление света можно объяснить и с квантовой точки зрения. Рассмотрим свет как поток фотонов энергией 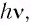 падающих нормально на зеркальную поверхность (рис. 115, а) и приносящих за промежуток времени
падающих нормально на зеркальную поверхность (рис. 115, а) и приносящих за промежуток времени 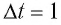 с на площадь
с на площадь 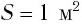 энергию, равную
энергию, равную 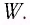
Число 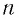 этих фотонов определяется из условия
этих фотонов определяется из условия 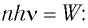
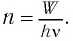
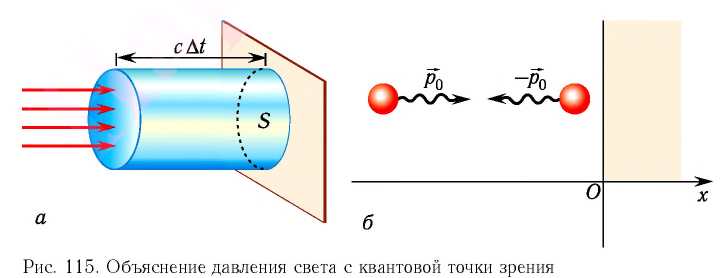
При отражении от зеркала фотон испытывает «упругий» удар, при котором происходит изменение направления импульса фотона на противоположное (рис. 115, б). Модуль этого изменения:
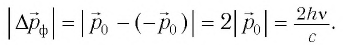
Соответственно, модуль изменения импульса потока фотонов, падающих на зеркало площадью 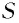 за промежуток времени
за промежуток времени 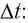
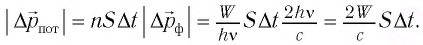
Изменение импульса потока фотонов вызвано силой 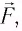 действующей на фотоны со стороны зеркала. Модуль этой силы и модуль силы, действующей со стороны потока фотонов (т. е. света) на зеркало, находится из закона изменения импульса:
действующей на фотоны со стороны зеркала. Модуль этой силы и модуль силы, действующей со стороны потока фотонов (т. е. света) на зеркало, находится из закона изменения импульса:
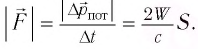
Следовательно, давление света на зеркало:
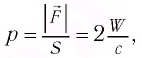
что совпадает с результатом, полученным Максвеллом.
При падении света на полностью поглощающую (черную) поверхность изменение импульса фотона будет в 2 раза меньше, так как
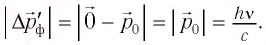
Соответственно, и давление света в этом случае будет в 2 раза меньше:
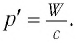
Пусть из полного числа 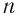 фотонов, падающих на единичную поверхность за
фотонов, падающих на единичную поверхность за 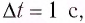 отражается
отражается 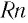 фотонов
фотонов 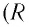 называется коэффициентом отражения), а
называется коэффициентом отражения), а 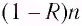 фотонов поглощается. Тогда сообщаемый ими единице поверхности импульс, численно равный давлению, находится по формуле:
фотонов поглощается. Тогда сообщаемый ими единице поверхности импульс, численно равный давлению, находится по формуле:
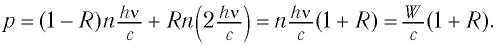
Русский физик Петр Николаевич Лебедев в 1899 г. впервые измерил световое давление. Он подвесил на тонкой нити коромысло с парой крылышек на концах (рис. 116), поверхность у одного из которых была зачерненной, обеспечивая почти полное поглощение 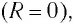 а у другого — зеркальной
а у другого — зеркальной 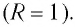 Подвес с крылышками образовал чувствительные крутильные весы, которые помещались в сосуд, воздух из которого был откачан.
Подвес с крылышками образовал чувствительные крутильные весы, которые помещались в сосуд, воздух из которого был откачан.
В опытах свет поочередно направлялся на каждое из крылышек коромысла. При этом он практически полностью отражался от зеркальной поверхности и практически полностью поглощался зачерненной поверхностью. Вследствие этого, давление света на зеркальное крылышко было примерно вдвое больше, чем на зачерненное. Соответственно, больше был и момент сил, поворачивающий коромысло при падении света на зеркальную поверхность (см. рис. 116). Измеряя угол поворота коромысла под действием света в обоих случаях, можно было судить о силе, действовавшей на крылышки, а следовательно, определить световое давление.
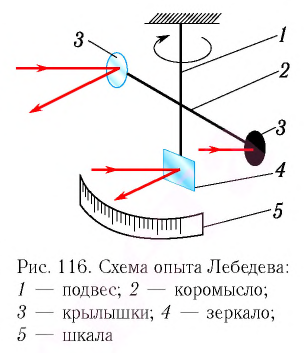
О сложности и тщательности подготовки и проведения измерений говорит тот факт, что при освещении крылышек светом в обычных условиях возникают силы, которые по величине превосходят силу давления света в тысячи раз. Основными являются силы, возникающие вследствие действия конвекционных потоков газа, и радиометрического действия.
Радиометрическое действие возникает вследствие разности температур освещенной и неосвещенной сторон крылышка в разреженном газе. Молекулы газа, остающиеся в баллоне, отражаются от более нагретой стороны с большей скоростью, и вследствие отдачи крылышки стремятся повернуться в том же направлении, что и под действием светового давления. Радиометрическое действие уменьшается, если применять очень тонкие металлические крылышки для уменьшения разности температур и увеличить разрежение газа в баллоне.
Измерения Лебедева дали величин}’ светового давления, согласующуюся с теорией Максвелла с погрешностью до 20 %. В 1923 г. немецкий физик Вальтер Герлах, используя более совершенные методы получения вакуума, повторил опыты Лебедева. Ему удалось получить результаты, согласующиеся с теоретическими значениями с погрешностью до 2 %.
Факт существования светового давления имеет большое значение, так как доказывает наличие у света не только энергии, но и импульса. Это свидетельствует о материальности электромагнитного излучения, представляющего собой еще одну форму существования материи — в виде электромагнитного поля.
Несмотря на сравнительно малое значение в обычных условиях, световое давление играет существенную роль в природе: препятствует гравитационному сжатию звезд, ориентирует хвосты комет в сторону от Солнца (рис. I 17), сокращает срок службы искусственных спутников Земли вследствие постепенного уменьшения радиуса их орбиты. Еще в 1604 г. немецкий астроном Иоганн Кеплер объяснил изогнутую форму хвоста кометы действием сил светового давления со стороны Солнца.
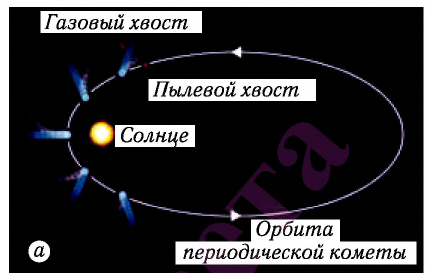

В настоящее время активно обсуждаются и реализуются проекты космических кораблей — «парусников», которые приводятся в движение «солнечным ветром».
Еще со времен Исаака Ньютона и Христиана Гюйгенса (XVII в.) представления о природе света были противоречивы. Одни ученые, во главе с Ньютоном, считали свет потоком частиц — корпускул, другие, вслед за Гюйгенсом, полагали, что свет представляет собой не что иное, как волны.
«Корпускула» от латинского слова corpusculum — маленькая частица.
До начала XIX в. обе точки зрения отстаивались с переменным успехом. Так, исходя из гипотезы о корпускулах, можно было объяснить законы прямолинейного распространения и отражения света, а такие явления, как интерференция и дифракция, объяснялись только его волновыми свойствами.
Однако в XX в. было установлено, что в целом ряде явлений, таких как, например, фотоэффект, свет ведет себя как совокупность частиц с определенной энергией и импульсом. Одновременное наличие у объекта волновых и корпускулярных свойств получило название корпускулярно-волнового дуализма.
В одних процессах в большей мере проявляются волновые свойства света, в других — корпускулярные. Долгое время природа этого дуализма была совершенно непонятна, и он казался искусственным объединением противоречивых свойств материи.
Только после создания квантовой механики выяснилось, что «раздвоение личности» света закономерно и представляет собой проявление специфических свойств, присущих микромиру в целом.
Французский физик Луи де Бройль в 1923 г. высказал смелое предположение, что корпускулярно-волновой дуализм должен иметь место для всех микрообъектов.
В своей теоретической статье «Кванта света, дифракция и интерференция» (1923 г.) де Бройль уверенно предсказал, что «Дифракционные явления обнаружатся и в потоке электронов, проходящих сквозь достаточно малое отверстие».
В квантовой физике с каждой материальной частицей связывают волну, распространяющуюся в направлении движения частицы, которую называют волной де Бройля, а длину этой волны называют дебройлевской длиной волны. Частота 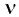 связана с энергией
связана с энергией 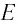 частицы соотношением
частицы соотношением 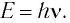 Де Бройль нашел, что модуль импульса
Де Бройль нашел, что модуль импульса 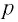 частицы должен выражаться через ее длину волны
частицы должен выражаться через ее длину волны 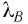 так же, как у света:
так же, как у света:
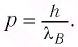
Это соотношение «узаконивает» корпускулярно-волновой дуализм, поскольку всякому объекту, имеющему импульс 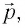 независимо от его природы ставят в соответствие волновой процесс с длиной волны
независимо от его природы ставят в соответствие волновой процесс с длиной волны
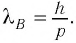
Оно также позволяет определить, в каких явлениях волновые свойства существенны, а в каких — нет. Для макроскопических объектов их модуль импульса как правило очень велик. Соответственно, в этом случае длина волны мала — много меньше размеров самого тела, и волновые свойства становятся незаметными.
Гипотеза де Бройля о наличии волновых свойств у электрона и других микрочастиц была проверена экспериментально.
Поскольку дифракция света наблюдается на решетках, период которых сравним с длиной волны 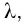 то для наблюдения дифракции электронов следует выбирать решетки с соответствующим периодом. Например, каждому из электронов в пучке, прошедшем между обкладками конденсатора, заряженного до напряжения
то для наблюдения дифракции электронов следует выбирать решетки с соответствующим периодом. Например, каждому из электронов в пучке, прошедшем между обкладками конденсатора, заряженного до напряжения 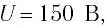 соответствует энергия
соответствует энергия 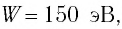 и его дебройлевская длина волны
и его дебройлевская длина волны 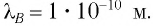 Поэтому для обнаружения волновых свойств электронов необходимо в качестве дифракционной решетки использовать кристаллы, представляющие собой упорядоченные структуры, расстояния между атомами которых
Поэтому для обнаружения волновых свойств электронов необходимо в качестве дифракционной решетки использовать кристаллы, представляющие собой упорядоченные структуры, расстояния между атомами которых 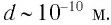
В 1927 г. американские физики Клинтон Дэвиссон и Люстер Джермер впервые наблюдали дифракцию электронов на кристалле никеля. На рисунке 118 представлена фотография дифракционной картины электронов на слюде.
Современные эксперименты позволяют наблюдать процесс образования дифракционной картины при последовательном увеличении числа электронов, проходящих через щель, а компьютерное моделирование этого процесса представлено на рисунке 119.

Способность к интерференции и дифракции была обнаружена не только у электронов, но и у других частиц — протонов, нейтронов и альфа-частиц.
Волновые свойства частиц нашли свое применение в электронной оптике, занимающейся исследованием, построением и использованием электронных пучков для получения изображений.
Так, использование волновых свойств пучка электронов позволило создать новое поколение микроскопов — электронные микроскопы (рис. 120), значительно превосходящие по степени увеличения оптические микроскопы вследствие того, что дебройлевская длина волны электронов гораздо меньше длины волны видимого света.

Уже первый электронный просвечивающий микроскоп (Э. Руска, 1933 г.) позволял изучать детали в десять раз меньшие, чем те, которые способны разрешать самые «мощные» оптические микроскопы. Дальнейшие исследования позволили сотрудникам лаборатории фирмы IBM в Цюрихе (Швейцария) Г. Биннингу и Г. Рореру в 1981 г. создать электронный сканирующий туннельный микроскоп, позволяющий рассмотреть даже «отдельный» атом.
В мае 2013 г. международная группа ученых (Германия, Греция, Нидерланды, США, Франция) с помощью фотоионизационного микроскопа сумела «сфотографировать» отдельный атом водорода. Ученым удалось получить прямое изображение самого легкого и самого маленького из всех атомов (рис. 121).
Датский физик Нильс Бор сформулировал принцип дополнительности, который утверждал, что для описания свойств материи (как поля, так и вещества) необходим учет как волновых, так и корпускулярных свойств.
Таким образом, корпускулярно-волновой дуализм присущ не только электромагнитному излучению, но и элементарным частицам. На них также распространяется и принцип дополнительности, в соответствии с которым используются как волновые, так и корпускулярные представления в зависимости от конкретной ситуации.
В 1929 г. Луи де Бройль за открытие волновой природы электрона был удостоен Нобелевской премии.
В 1986 г. Герду Биннингу и Гейнриху Рореру совместно с Эрнстом Руска была присуждена Нобелевская премия по физике за создание электронного микроскопа.
Итоги:
Раздел физики, описывающий физические явления на атомном и внутриатомном (субатомном) уровнях, называется квантовой физикой.
Энергия колебательной системы (осциллятора), совершающей гармонические колебания с частотой 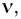 может, согласно гипотезе Планка, принимать лишь определенные дискретные значения, отличающиеся на целое число элементарных порций — квантов энергии.
может, согласно гипотезе Планка, принимать лишь определенные дискретные значения, отличающиеся на целое число элементарных порций — квантов энергии.
Эйнштейн развил гипотезу Планка, представив, что свет излучается, поглощается и распространяется в виде отдельных порций (квантов).
Наименьшая порция (квант) энергии, которую несет излучение частотой 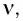 определяется по формуле:
определяется по формуле:
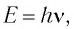
где постоянная 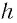 — фундаментальная постоянная — постоянная Планка. Ее. приближенное значение:
— фундаментальная постоянная — постоянная Планка. Ее. приближенное значение:
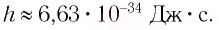
Модуль импульса фотона определяется соотношением:
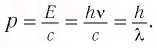
Явление испускания электронов веществом под действием падающего на него света получило название внешнего фотоэффекта. Испускание веществом каких-либо частиц называется эмиссией. Поэтому внешний фотоэффект называют также фотоэлектронной эмиссией (фотоэмиссией), а вылетающие электроны — фотоэлектронами.
Экспериментально установлены следующие законы внешнего фотоэффекта.
- Сила фототока насыщения
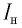 прямо пропорциональна интенсивности
прямо пропорциональна интенсивности 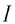 падающего излучения.
падающего излучения. - Максимальная кинетическая энергия
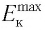 фотоэлектронов не зависит от интенсивности
фотоэлектронов не зависит от интенсивности 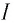 падающего излучения и линейно возрастает с увеличением частоты
падающего излучения и линейно возрастает с увеличением частоты 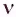 падающего излучения.
падающего излучения. - Для каждого вещества существует граничная частота
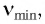 такая, что излучение меньшей частоты не может вырывать электроны из его поверхности.
такая, что излучение меньшей частоты не может вырывать электроны из его поверхности.
Формула Эйнштейна дня внешнего фотоэффекта:
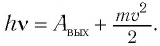
Красная граница фотоэффекта — наименьшая частота излучения, при которой наблюдается фотоэффект 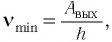 зависит только от работы выхода электронов для данного вещества
зависит только от работы выхода электронов для данного вещества 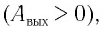 т. е. определяется химической природой вещества и состоянием его поверхности.
т. е. определяется химической природой вещества и состоянием его поверхности.
Под корпускулярно-волновым дуализмом понимают тот факт, что всем объектам в природе присущи как волновые, так и корпускулярные свойства. В одних условиях в большей мере проявляются волновые, в других — корпускулярные свойства объектов.
Принцип дополнительности утверждает, что для описания свойств материи (как поля, так и вещества) необходим учет как волновых, так и корпускулярных свойств.
- Зеркала и изображение в плоском зеркале
- Световой луч и световой пучок
- Разложение белого света на цвета и образование цветов
- Давление света в физике
- Источники света
- Скорость света
- Отражение света
- Спектральный состав естественного света
Фотон
Фотон — это частица света или квант света; частица с которой можно делать расчёты.
Фотоны всегда находятся в движении и в вакууме движутся с постоянной скоростью 2,998 x 10^8 м/с (это называется скоростью света и обозначается буквой c).
В марте 1905 года Эйнштейн создал квантовую теорию света, это была идея о том, что свет существует в виде крошечных частиц, которые он назвал фотонами.
Позже в том же году была расширена специальная теория относительности, в которой Эйнштейн доказал, что энергия (E) и материя (масса – m) связаны, и это соотношение стало самым знаменитым в физике: E=mc²; (напомним: c — скорость света).
Формулы фотона
Эти формулы являются наиболее важными.
Формула энергии кванта/фотона (формула Планка или Энергия кванта)
Энергия — это постоянная Планка, умноженная на частоту колебаний

E = h×v
Где:
- E — энергия фотона/кванта (в Дж – джоуль),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц).
Масса фотона

m = hv/c² = h/cλ
Где:
- m — масса фотона (в кг),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц),
- c = 3.10^8 (это скорость света в м/с),
- λ — длина световой волны (в метрах).
Примечание:
Фотоны всегда движутся со скоростью света. В состоянии покоя фотоны не существуют (т.е. можно сказать, что масса покоя равна нулю).
Формула массы фотона (m = h/cλ) была выведена из формулы эквивалентности массы и энергии (E = mc²), при этом было использовано также равенство с энергией Кванта (E = h×v).
Импульс фотона

p = hv/c = h/λ
Где:
- p — импульс фотона (в Н•с – ньютон-секунда),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц),
- c = 3.10^8 (это скорость света в м/с),
- λ — длина световой волны (в метрах).
Длина волны света, период и частота
Это ещё одно соотношение, которое может быть полезным в расчётах.

λ = cT = c/v
Где:
- λ — длина световой волны (в метрах),
- c = 3.10^8 (это скорость света в м/с),
- T — период световых колебаний (в секундах),
- ν — частота колебаний света (в Гц – герц).
Пример решения задачи с данными формулами
Определите энергию фотонов красного (λк = 0,76 мкм) света.
Известно:
λк = 0,76 мкм = 0,76 × 10^(–6) м
Решение:
Формула энергии фотонов: E = h×v
Где:
h — постоянная Планка,
v — частота света; из равенства λ = c/v выходит, что v = с/λ.
Таким образом, составляем равенство:
E = h × (с/λ) = hc / λ
Вспоминаем другие данные:
c = 3.10^8 (это скорость света в м/с)
h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду)
E = hc / λ = ((6,6.10^(–34) Дж.с) × (3.10^8 м/с)) / (0,76 × 10^(–6) м) = 2,6 × 10^(–19) Дж
Фотон является волной?
Фотон является одновременно частицей и волной. Согласно квантовой теории света Эйнштейна, энергия фотонов (E) равняется их частоте колебаний (v), умноженной на постоянную Планка (h); т.е. эта формула выглядит так: E = h×v.
Так он доказал, что:
- свет — это поток фотонов,
- энергия этих фотонов — это высота их частоты колебаний,
- интенсивность света соответствует количеству фотонов.
Таким образом, учёный объяснил, что поток фотонов действует и как волна, и как частица.
Узнайте также про:
- Нейтрино
- Теорию относительности
- Магнитную индукцию
- Полимер
- Теорию струн
Фотон в современной физике считается разновидностью элементарных частиц. В частности, он представляет собой квант электромагнитного излучения (квант — неделимая частица чего-либо).
Энергия и импульс фотона
Фотоны обладают определенной энергией и импульсом. Когда свет испускается или поглощается, он ведет себя подобно не волне, а потоку частиц, имеющих энергию Е = hν, которая зависит от частоты. Оказалось, что порция света по своим свойствам напоминает то, что принято называть частицей. Поэтому свойства света, обнаруживаемые при его излучении и поглощении, стали называть корпускулярными. Сама же световая частица была названа фотоном, или квантом электромагнитного излучения.
Как частица, фотон обладает определенной порцией энергии, которая равна hν. Энергию фотона часто выражают не через частоту v, а через циклическую частоту:ω = 2πν
При этом в формуле для энергии фотона в качестве коэффициента пропорциональности (постоянной Планка) используется другая величина, обозначаемая ℏ и равная:
ℏ=h2π≈1,0545726·10−34 (Дж·с)
Учитывая это, формула для определения энергии фотона примет вид:
Е=ℏω
Согласно теории относительности, энергия частиц связана с массой следующим соотношением:
Е=mс2
Так как энергия фотона равна hν, то, следовательно, его масса m получается равной:
m=hνс2
У фотона нет собственной массы, поскольку он не может существовать в состоянии покоя. Появляясь, он уже имеет скорость света. Поэтому формула выше показывает только массу движущегося фотона.
По известной массе и скорости фотона можно найти его импульс:
p=mc=hνc=hλ
Внимание! Вектор импульса фотона всегда совпадает с направлением распространения луча света.
Чем больше частота ν, тем больше энергия Е и импульс р фотона и тем отчетливее свет проявляет свои корпускулярные свойства. Из-за того что постоянная Планка мала, энергия фотонов видимого излучения крайне незначительна. К примеру, фотоны, свойственные зеленому свету, имеют энергию, равную всего 4∙10–19 Дж. Несмотря на это, человеческий глаз способен различать изменение освещенности, даже если оно измеряется единичными квантами.
Пример №1. Каков импульс фотона, если длина световой волны λ = 5∙10–7 м?
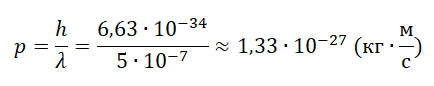
Корпускулярно-волновой дуализм
Законы теплового излучения и фотоэффекта объясняются только при условии, если начать считать свет потоком частиц. Однако нельзя отрицать тот факт, что свету присущи такие явления как интерференция и дифракция света. Но эти явления встречаются только у волновых процессов. Поэтому в современной физике принято считать свет с дуализмом, иначе — двойственностью свойств.
Когда свет распространяется в средах, он проявляет волновые свойства. Когда он начинает взаимодействовать с веществом (поглощаться или излучаться), проявляются корпускулярные свойства (свойства частицы).
Гипотеза де Бройля
Длительное время электромагнитное поле представлялось как материя, которая распределена в пространстве непрерывно. Электроны же представлялись как очень маленькие частицы материи. Не нет ли здесь ошибки, обратной той, которая была допущена при определении света? Может быть, электрон и другие частицы тоже обладают волновыми свойствами. Такую мысль высказал в 1923 г. французский ученый Луи де Бройль.
Он предположил, что с движением частиц связано распространение некоторых волн. И ученому удалось найти длину волны этих волн. Связь длины волны с импульсом частицы оказалась точно такой же, как и у фотонов. Если длину волны обозначить через λ, а импульс — через р, то получится, что:
λ=hp
Эта формула носит название формулы де Бройля, которая является одной из основных в разделе квантовой физики.
В будущем волновые свойства частиц, о которых предположил де Бройль, были обнаружены экспериментально. Так, удалось получить дифракцию электронов и других частиц на кристаллах. В этих случаях получалась почти такая же картина, как в случае с рентгеновскими и другими лучами. И формула де Бройля также нашла экспериментальное доказательство. Волновые свойства микрочастиц описываются квантовой механикой.
Квантовая механика — раздел физики, изучающий теорию движения микрочастиц.
Внимание! Законы Ньютона в квантовой физике в большинстве случаем не могут быть применены.
Давление света
В 1873 г. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствия. Предсказанное Максвеллом существование светового давления было экспериментально подтверждено Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Оно оказалось чрезвычайно малым, около 4∙10-7 Па.
Световое давление, обусловленное солнечным излучением у поверхности Земли, составляет менее 0,0001 Па. Этим и объясняется тот факт, что в обычных условиях давление света заметным образом себя не проявляет. Но давлением света объясняет следующие факты:
- хвосты комет направлены от ядра кометы в сторону, противоположную Солнцу;
- изменение орбит искусственных спутников Земли.
Свет — это поток фотонов с импульсом:
p=mc
При поглощении веществом фотон перестает существовать, но импульс его, по закону сохранения импульса, не может исчезнуть бесследно. Он предается телу, значит, на тело действует сила.
Приведенное рассуждение будет абсолютно верным, если считать, что свет только веществом поглощается. Но разве это всегда так, свет еще может отражаться телами, а если тело прозрачно, то может проходить сквозь него. В реальных условиях свет частично отражается телом, частично поглощается, а если это, например, стекло, то свет проходит сквозь него. Как будет обстоять дело, если поверхность зеркальная? Возникает световое давление в данном случае?
Для простоты предположим, что свет падает перпендикулярно к поверхности зеркала. Мы знаем, что при абсолютном ударе какого-либо тела о стенку она получает импульс, модуль которого равен удвоенному модулю импульса тела, то есть 2mv. Отражаясь, фотон летит с той же скоростью, но в противоположном направлении. Значит, при отражении фотона от зеркала его импульс изменяется на 2mc. Такое же изменение импульса, но в противоположном направлении, получит зеркало. Импульс, получаемый телом при отражении фотона, будет в 2 раза больше импульса, получаемого телом при поглощении фотона.
Задание EF17985
За время t=4 с детектор поглощает N=6⋅105 фотонов падающего на него монохроматического света. Поглощаемая мощность P=5⋅10−14 Вт. Какова длина волны падающего света?
Ответ:
а) 0,4 мкм
б) 0,6 мкм
в) 520 нм
г) 780 нм
Алгоритм решения
1.Записать исходные данные.
2.Установить взаимосвязь между энергией фотонов и поглощаемой детектором мощностью.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Количество фотонов: N = 6∙105 шт.
• Поглощенная мощность: P = 5∙10–14 Вт.
Вся энергия фотонов будет поглощена детектором. Согласно закону сохранения энергии:
Nhν=Pt
Длина волны определяется формулой:
λ=cν
Отсюда частота равна:
ν=cλ
Подставим это выражение в записанный закон сохранения энергии:
Nhcλ=Pt
Отсюда длина волны равна:
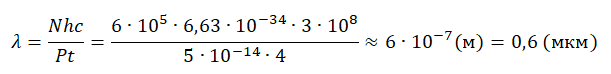
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17986
При изучении давления света проведены два опыта с одним и тем же лазером. В первом опыте свет лазера направляется на пластинку, покрытую сажей, а во втором – на зеркальную пластинку такой же площади. В обоих опытах пластинки находятся на одинаковом расстоянии от лазера и свет падает перпендикулярно поверхности пластинок.
Как изменится сила давления света на пластинку во втором опыте по сравнению с первым? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
Алгоритм решения
1.Описать процессы, происходящие во время обоих опытов.
2.С помощью физических формул установить, как изменяется сила давления света.
Решение
В обоих опытах происходит поглощение световой волны. Этот процесс можно рассматривать как поглощение за время t большого числа световых квантов — N >>1 (фотонов). Фотоны поглощаются пластинкой. Причем каждый фотон передает этой пластинке свой импульс, равный:
pф=hνc
Поэтому импульс пластинки становится равным сумме импульсу всех поглощенных фотонов:
pп=Nhνc
В результате поглощения света пластинкой, покрытой сажей, она приобретает за время t импульс pп в направлении распространения света от лазера. Согласно закону изменения импульса, тела в инерциальной системе отсчета скорость изменения импульса тела равна силе, действующей на него со стороны других тел или полей:
F1=pпt=Nthνc
В результате отражения света от зеркальной пластины отраженный фотон имеет импульс, противоположный импульсу фотона падающей волны:
pф=∣∣−pфп∣∣
Поэтому отраженная волна будет иметь импульс:
pов=−N´pф=−N´hνc
N´ — количество отраженных фотонов.
В итоге за время t импульс волны под действием зеркальной пластинки изменился. Это изменение будет равно разности импульса отраженной волны и импульса пластинки:
Δp=pов−pп=−Npф−N´pф=−(N+N´)pф
Согласно закону сохранения импульса, импульс системы, состоящей из световой волны и зеркальной пластинки, сохраняется:
Δ(pп+pпл)=0
Отсюда:
Δpпл=Δpп
Но изменение импульса тела в инерциальной системе отсчета происходит только под действием других тел или полей и характеризуется силой:
F2=pплt=N+N´thνc
Если зеркала отражает хорошо, то N ≈ N´. Тогда:
F2≈2F1
Отсюда видно, что сила давления света увеличится вдвое.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18201
Излучением лазера с длиной волны 3,3⋅10−7 м за время 1,25⋅104 с был расплавлен лёд массой 1 кг, взятый при температуре 0 °С, и полученная вода была нагрета на 100 °С. Сколько фотонов излучает лазер за 1 с? Считать, что 50% излучения поглощается веществом.
Алгоритм решения
1.Записать исходные данные.
2.Установить, какое количество тепла было сообщено льду для его расплавления и нагревания до температуры кипения.
3.Установить, какая энергия была выделена лазером при условии, что лишь половина этой энергии была сообщена льду.
4.Из полученного выражения выразить количество фотонов, излученных лазером за время t.
5.Записать формулу для количества фотонов, выделяемых за время 1 с.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем не только те данные, что есть в условии задачи, но и табличные данные, которые нам понадобятся в ходе решения задачи:
• Удельная теплота плавления льда: λльда = 3,4∙105 Дж/кг.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙оС).
• Начальная температура льда/воды: t1 = 0 оС.
• Конечная температура воды: t2 = 100 оС.
• Коэффициент полезного действия: η = 50%.
• Длина световой волны: λсвета = 3,3∙10–7.
• Время проведения всего опыта: t = 1,25∙104.
Чтобы лед расплавился, а образовавшаяся вода нагрелась до температуры кипения, нужно сообщить ему следующее количество энергии:
Q=Q1+Q2=mλльда+mc(t2−t1)
Так как КПД равен 50% (0,5), то это количество теплоты равно половине энергии, выделенной лазером:
Q=ηE
mλльда+mc(t2−t1)=ηE
Энергия, выделенная лазером, равна сумме энергий каждого из излученных фотонов, количество которых будет равно N:
E=Nhν
Но частота световой волны равна:
ν=cλсвета
Тогда:
E=Nhcλсвета
Отсюда:
Nhcλсвета
Теперь мы можем записать:
mλльда+mc(t2−t1)=ηNhcλсвета
Выразим количество излученных фотонов за все время:
N=λсвета(mλльда+mc(t2−t1))ηhc
Если разделить это выражение на время проведения опыта, то мы найдем количество фотонов, излученных за 1 секунду:
N1с=λсвета(mλльда+mc(t2−t1))ηhct
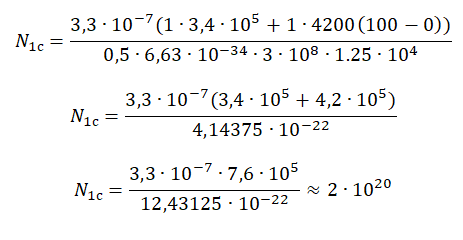
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 2.7k
Конкурс “Я иду на урок”
И. Н.
Дубова,
СОШ № 2, г. Гагарин, Смоленская обл.
Корпускулярно-волновой дуализм
Урок на трудную тему. 11й класс
Учитель. К уроку вы готовили
материал § 90 [1], т.е. изучали свойства фотона,
волновые свойства электрона, решали задачи.
Прежде чем приступить к изучению нового
материала, давайте закрепимся на завоёванных
позициях. Вот перед вами часть шпаргалки одного
ученика (в увеличенном виде, конечно).
|
Свет |
Электрон, нейтрон |
|
1. Интерференция |
1. Интерференция |
|
2. Дифракция |
2. Дифракция |
|
3. Дисперсия |
3. Волновая характеристика: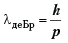 |
|
4. Поляризация |
4. Частицы локализованы в пространстве |
|
5. , |
5. Корпускулярные характеристики: |
|
6. Волна непрерывна |
|
|
7. I ~ E02; I0 ~ B02 |
|
|
8. Волновые характеристики:
|
|
|
9. Фотоэффект, эффект |
|
|
10. Корпускулярные характеристики:
|
Ученики 1го ряда изложат вслух мысли,
рождённые первым столбиком, 2го ряда – вторым, а
ученики 3го ряда, выслушают всех и сделают
заключение.
Учащиеся. Интерференция, дифракция,
поляризация, дисперсия объясняются наличием
волновых свойств у света. Например,
интерференционную картину можно объяснить
сложением волн с учётом разности хода.
Интенсивность волн I ~ E2,
I ~ B2. Уравнение
волны для электрической и магнитных составляющих – … (см.
табл.). Волновыми характеристиками света
являются амплитуда, частота, длина волны, фаза,
период. Волна непрерывна.
В фотоэффекте, Комптон-эффекте и других
явлениях проявляются корпускулярные свойства
света. Световая частица, электрон, протон,
нейтрон локализованы в пространстве,
характеризуются импульсом, энергией. При их
прохождении через кристалл на экране образуется
дифракционная картина. Потому все эти частицы
имеют ещё волновую характеристику – длину волны.
Таким образом, материя обладает двойственностью
свойств.
Учитель. Вот теперь я вас спрошу: что
было не совсем ясно в домашнем задании, какие
возникли вопросы?
Учащиеся. Что колеблется в волне де
Бройля? Как сочетать протяжённость волн с
конечным размером частиц? Где запрятаны волновые
свойства классических частиц?
Учитель. На эти и, возможно, новые
вопросы постараемся найти ответ. Поэтому тема
сегодняшнего урока «Корпускулярноволновой
дуализм». Слушая, не только вникайте в суть, но и
старайтесь 2–3 предложения из каждого ответа
записать. Специально выделяю на это время.
Волна де Бройля не похожа на материальную
волну. В звуковой волне колеблются молекулы
среды. В электромагнитной волне колеблются
напряжённость электрического поля и индукция
магнитного поля. Но в обоих случаях волну
образуют колебания материальных объектов. Волна
де Бройля – волна вероятности, описывающая
поведение микрообъекта, она не материальна. В
свободном состоянии поведение микрообъекта
описывается плоской монохроматической волной де
Бройля. В общем случае движение частицы в силовом
поле описывается волновой функцией
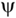
(r, t),
называемой пси-функцией. Это
функция координат и времени. Она подчиняется
уравнению Шрёдингера, играющему в квантовой
механике такую же роль, какую играют законы
Ньютона в классической физике.
Отбор решений идёт так, что
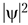
имеет
смысл плотности вероятности обнаружения частицы
в данной точке пространства, а величина
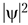 dV
dV
– cмысл абсолютной вероятности обнаружения
частицы в объёме dv.
Функция 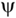 не наблюдается, а
не наблюдается, а
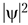 – величина, связанная с
– величина, связанная с
вероятностью обнаружения объекта, – наблюдается
[2].
Переведём дух, подкрепимся. Для тех, кто не знал
или забыл, что такое вероятность события. Пусть в
коробке карамель: смородина – С, малина – М,
вишня – В. Соответственно 60, 30, 10 штук. Всего 100
штук. Вероятность события вытаскивания
смородиновой карамели 60/100 = 6/10, малиновой – 3/10,
вишнёвой – 1/10 (6/10 + 3/10 + 1/10 = 1 – вероятность
события вытащить хоть какую-нибудь конфету).
Хорошо перемешаем, а после каждого вытаскивания
и съедания конфеты я восстанавливаю
первоначальную картину. Кладовщиком, ведущим
учёт расходов, будет Сидоров. Из 30 вытащенных
конфет должно быть теоретически С –18, М – 9, В – 3.
Вытаскивание конфетки определённого сорта –
случайное событие. Но подсчитанная заранее
вероятность отражает реальную картину
распределения конфет. Хотя возможны и
флуктуации, т.е. отклонения, которые тем меньше (в
относительной шкале), чем больше событий. (Проводится
«эксперимент».)
Вернёмся к микрочастицам. Их особенностью
является случайный характер движения. Поэтому
если известна вероятность обнаружения частицы в
какойто точке, легко объяснить и интерференцию
частиц, как объясняли раньше (см. шпаргалку).
Учащиеся. Надо сложить амплитуды
волновых функций.
Учитель. А квадрат суммарной
амплитуды даст наблюдаемую интерференционную
картину, т.к. связан с интенсивностью
распределения (см. шпаргалку). Так что получается
интерференция без волн [3]!
Как разрешить напрашивающийся вопрос о разнице
в объяснении интерференции световых волн и
вероятностных? В одном случае за неё отвечают
материальные волны, а в другом – воображаемые.
Физики объясняют это так: световые частицы,
фотоны, принадлежат к группе частиц бозонов,
способным накапливаться в одном состоянии. При
достаточно большом числе они образуют световую
волну. Её характеристики совпадают с
соответствующими характеристиками волновой
функции фотона (они одинаковы). Классическая
волна – это коллективный эффект. Для электронов,
которые принадлежат к фермионам и способны
заселять состояние лишь поодиночке,
коллективный эффект невозможен [3]. Продолжим
рассуждение: если это так, то интерференцию света
можно объяснить наличием волновой функции у
фотонов. Да, оказывается, это так. Увеличивая
время экспозиции, можно на экране получить
интерференционную картину при сколь угодно
малой интенсивности светового пучка, когда через
отверстие проходят отдельные фотоны. Таким
образом, в основе волновых свойств частиц лежит
вероятностный характер поведения микрообъектов
[4].
Впервые о корпускулярно-волновом дуализме
заявил Эйнштейн. Используя законы излучения
абсолютно чёрного тела и методы статистической
физики, он получил значение флуктуаций светового
давления и плотности энергии, пропорциональные
друг другу. Формулы содержат сумму двух членов:
первый, квантовый, соответствовал
представлениям о свете как о потоке дискретных
частиц – фотонов, второй – волновой,
был связан с электромагнитной волной.
Существенно, что только сумма этих двух членов
даёт правильное значение флуктуаций энергии и
светового давления. Когда регистрируются
результаты воздействия мощных (по меркам
микромира) световых потоков в течение
сравнительно больших промежутков времени, то
наблюдается волновая картина. В потоке воды
можно не учитывать молекулярный состав воды. Но
если рассматривать взаимодействие на межатомном
уровне, то дискретная структура проявляется.
Такая же картина и у классических частиц. Пока
идёт взаимодействие на межмолекулярном уровне,
т.е. волна де Бройля сравнима с характерными
размерами, – квантовые эффекты существенны, нет
– спокойно описывайте поведение объекта
законами классической физики, не учитывая
вероятностных проявлений [5].
Итак, противоречия разрешены. Природа
рассматриваемых объектов такова, что для них
(фотонов, нейтронов и др.) нельзя придумать
ситуацию, где одновременно проявлялись бы и
корпускулярные, и волновые свойства. Нельзя и не
нужно представлять электрон или фотон и
частицей, и волной одновременно. Под
корпускулярно-волновым дуализмом мы будем
понимать то, что микрообъекты обладают
потенциальной возможностью проявлять либо
волновые, либо корпускулярные свойства, но
никогда не проявляют их одновременно. Эти
свойства дополняют друг друга, и только их
сочетание даёт полное представление об объекте.
Исторически сложилось так, что свет и электроны
изучались в классическом варианте, и только по
мере изучения материи оказалось, что они не так
просты. Границы проявления вероятностного
поведения микрообъектов не очерчены чётко,
так что можно привести примеры вторжения
квантовых эффектов в область, кажущуюся
абсолютно классической (сверхпроводимость,
сверхтекучесть) [6].
Вернёмся к началу урока.
Помните, были вопросы? Интересно, добавите ли вы
теперь к тому единственному предложению о связи
волновых и корпускулярных свойств микрообъектов
ещё чтото? (Ученики,
используя записи, воспроизводят основные идеи
изложенного на уроке.)
А теперь проверим, как теория претворяется в
решении задач.
Задача 1
Не
Не
t = 27 °С
Т = 0,01 К
р = 105
Па
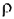 = 0,15
= 0,15
г/см3
Газ
Жидкость
Какое описание – классическое или квантовое –
применимо для описания атомов гелия в
представленных случаях?
Решение. Можно ожидать, что
квантовые эффекты будут играть роль, если длина
волны де Бройля больше среднего расстояния между
атомами. В противоположном случае годится
классическое описание. Содержимое баллона с
классических позиций – это некоторое количество
«бильярдных шаров», непрерывно сталкивающихся
друг с другом, тогда как с точки зрения квантовой
механики это совокупность взаимодействующих
волн.
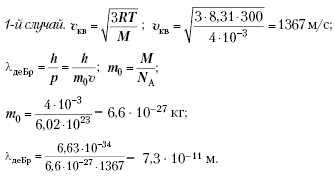
Межмолекулярное расстояние найдём из
известной формулы 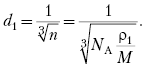
Для газа легко получить:

(Применение формулы оправдано, т.к. мы
рассматриваем состояние газа как предельное.)
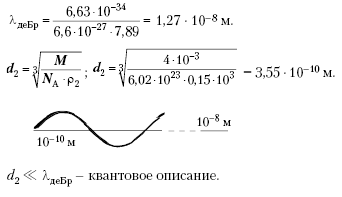
Задача 2. Параллельный поток
электронов, ускоренных разностью потенциалов U = 25 В, падает на
диафрагму с двумя узкими щелями, расстояние
между которыми d = 50 мкм. Определите
расстояние между соседними максимумами
дифракционной картины на экране, расположенном
на расстоянии D = 100 см от щелей.
Решение. Образование дифракционной
картины объясняется наличием волновых свойств у
электронов. Длина волны де Бройля
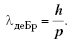 Из
Из
закона сохранения энергии следует:
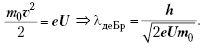
Условие наблюдения максимумов:
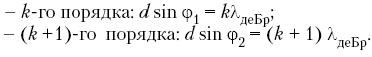
C учётом малости углов:
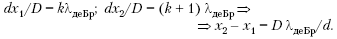
Подставляя сюда выражение для
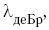 получаем:
получаем:
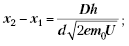
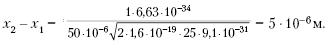
Задача 3. Пучок света имеет вид
конуса с углом раствора 10–4 рад мощностью 3
мВт и длиной волны 630 нм. На каком максимальном
расстоянии R можно видеть свет, если
глаз способен «регистрировать» поток фононов не
менее 100 фотонов в секунду? Диаметр зрачка d
= 0,5 см.
Решение. Будем рассматривать
световой поток как поток фотонов энергией hn = hc/l. Вычислим
число фотонов N, испуcкаемых
источником мощностью Р? за время t:
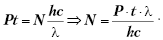
Отношение числа фотонов, прошедших через
зрачок и через основание заданного в условии
конуса высотой R, равно отношению их
площадей: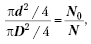 т.е.
т.е.
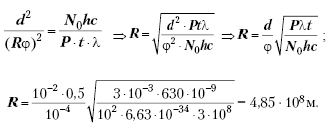
Задача 4.
Найдите длину волны коротковолновой границы
сплошного рентгеновского спектра, если скорость
электронов, подлетающих к антикатоду трубки, v = 0,85с.
Решение. Будем считать, что энергия
электрона при торможении переходит в энергию
фотона, т.е. идёт взаимодействие на уровне частиц:
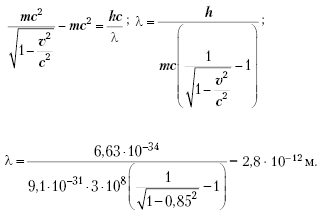
Домашнее задание. На основе
услышанного и записанного в тетради, решённых
задач и дополнительной литературы подготовьте
сообщение о корпускулярно-волновом дуализме и
решите задачи.
• Параллельный поток электронов падает
нормально на диафрагму с узкой прямоугольной
щелью шириной
b = 1 мкм. Определите скорость этих
электронов, если на экране, отстоящем от щели на
расстояние D = 50 см, ширина
центрального максимума ? x = 0,36 мм.
• Точечный изотропный источник испускает свет
длиной волны ? = 589 нм. Мощность источника
P = 10 Вт. Найдите среднюю плотность
потока фотонов на расстоянии 2 м от источника
(число фотонов, пролетающих за 1 с через 1 м2
площади).
Решения
• Условие 1-го минимума на щели: bsin
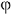 =
= 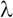 деБр.
деБр.
Так как 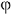 мал, то
мал, то 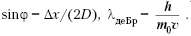
Тогда 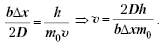
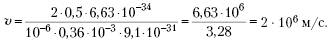
Литература
- Мякишев Г.Я., Буховцев Б.Б. Физика11.
– М.: Просвещение, 2004. - Сивухин Д.В. Общий курс физики. – М.:
Наука, 1986, т. V, с. 117. - Тарасов Л.В. Современная физика в
средней школе. – М.: Просвещение, 2001, с. 142. - Тарасов Л.В. Мир, построенный на
вероятности. – М.: Просвещение, 1984, с. 129. - Пинский А.А. Физика11. – М.: Просвещение,
2000, с. 266. - Бутиков Е.И. и др. Физика. Т. 3:
Строение и свойства вещества. – М.–СПб, 2001, с. 66.
Задачи взяты из сборников:
- Взоров Н.Н и др. Сборник задач по общей
физике. – М.: Наука, 1968. - Вихман Э. Квантовая физика, т. 4. – М.:
Наука, 1974, с. 218. - Делеков А.П., Третьяков О.Н. Физика.
– М.: Высшая школа, 2001. - Кириллов В.М. Решение задач по физике. –
М., 2006. - Пономарёв Л.И. Под знаком кванта. – М.:
Советская Россия, 1984.