Проводимость канала определяет его способность транспортировать газ. Она выражается в единицах объема газа, проходящего через данное сечение в единицу времени. Зависимости для расчета проводимости элемента, работающего в различных условиях, являются весьма сложными и зависят от режима течения, а также от геометрических параметров канала и свойств его поверхности. Расчеты проводимости и потока газа при турбулентном режиме течения трудно трактовать аналитически. Количественное определение параметров вязкостного потока также представляет трудности, поскольку зависит не только от формы канала, но и от давления газа. Однако при тех диапазонах давлений, которые имеют место в условиях высокого вакуума, поток является молекулярным, а не вязкостным.
Уравнения для расчета параметров вязкостного потока
В общем случае уравнения для расчета проводимости и потока газа при вязкостном режиме течения получены для трубопроводов и каналов, имеющих сечение простой геометрической формы – круглое или прямоугольное. Эти выражения используются, например, для расчета времени, необходимого для откачки сосуда через трубопровод, имеющий круглое или прямоугольное поперечное сечение.
Течение в трубопроводах круглого сечения
Поток газа по прямому трубопроводу круглого сечения в условиях вязкостного режима определяется уравнением Пуазейля:
$$frac{Q}{P_{1}-P_{2}}=K frac{d^{4}P}{eta L}, (60)$$
где d – диаметр трубы; L – длина трубопровода; η – динамическая вязкость газа; р – среднее давление в трубопроводе; р1 и р2 – давления на противоположных концах трубы.
Для сухого воздуха при 20 °С данное уравнение приобретает вид:
$$Q= frac{750d^{4}bar{P}}{L}(P_{1}-P_{2}), (61)$$
где Q – поток газа, Торр – л/с; d – диаметр трубопровода, см; L – длина трубопровода, см; р – это давление, Торр.
Проводимость круглого трубопровода, л/с, для воздуха при 20 °С приведено ниже:
$$C= frac{2,94pd^{4}}{L}, (62)$$
Течение в прямоугольных каналах
Уравнение Пуазейля для потока воздуха при 20 °С, текущего по прямоугольному каналу с большей стороной сечения а и меньшей b, имеет следующий вид, л/с:
$$C= frac{30a2b2KP}{L}, (63)$$
где К — это коэффициент формы, значение которого зависит от b/а.
Как можно видеть, проводимость прямоугольной диафрагмы (отверстия) быстро увеличивается при переходе сечения от прямоугольной щели к квадрату.
Так же, как и в случае круглого трубопровода, выражение для С позволяет получить соотношение для объемного потока газа в зависимости от перепада давлений в канале.
$$C= frac{pK}{Delta p}, (64)$$
где
$$F= frac{Cp}{Delta p}, (64)$$
Таким образом,
$$K= frac{30a_{2}b_{2}K}{L} cdot Delta p, (65)$$
л/с.
Уравнения для расчета параметров молекулярного потока
При низких значениях давления межмолекулярные столкновения происходят реже, чем столкновения со стенкой, поэтому последние определяют параметры газового потока по каналу. Проводимость канала в условиях молекулярного потока зависит от двух факторов:
- Скорости, с которой молекулы поступают в канал.
- Вероятности прохождения молекул по системе.
Первый фактор зависит от площади сечения входа в систему, а последний определяется последующей серией столкновений со стенками, в результате которых молекула в конечном итоге перемещается по каналу или отбрасывается обратно в откачиваемый сосуд.
Рассмотрим вначале случай очень тонкой диафрагмы в пластине. В данном случае для определения проводимости диафрагмы нас интересует ее площадь А, а не свойства стенок канала. Объем газа, проходящего через диафрагму – ее проводимость – составляет:
$$C_{a}= frac{1}{4}AV=(frac{2}{p})^{-1} – V^{0}A, (66)$$
если молекулы имеют распределение скоростей по Максвеллу. Значения проводимости зависят от молекулярной массы и кинетической энергии. Случай, когда столкновения молекул со стенками трубопровода являются более важными, чем проводимость отверстия, рассмотрен ниже.
Формула Кнутсена
Проводимость СΥотрезка длинной трубы длиной L с переменной площадью сечения А и периметром Н была рассчитана Кнудсеном и составляет:
$$C_{Upsilon} = frac{4}{3} sqrt{ frac{H( delta)}{A^{2} L} cdot de }. (67)$$
Были приняты следующие допущения:
- Длина трубопровода значительно больше диаметра.
- Направление движения отскочивших молекул после столкновения со стенками не зависит от направления их движения до столкновения.
- Угловое распределение отскочивших молекул подчиняется закону косинуса.
Допущение 1 предполагает, что влияние отверстия является незначительным, а величина проводимости, получаемая из уравнения (67), относится к молекулам внутри трубы, удаленным от отверстия. Для получения приближенных выражений для проводимости всей трубы нужно включить последовательную проводимость отверстий. Карлсон приводит формулу для трубопровода с периметром Н, площадью Л и длиной L:
$$C_{a}=1+ frac{3}{16} cdot 9 frac{LH}{A}). (58)$$
Коэффициент Клаузинга
Проводимость длинного трубопровода связана с проводимостью входного отверстия коэффициентом [1 +3/16(LH/A)]-1 Ca. Этот коэффициент можно интерпретировать как вероятность случайного входа молекулы в отверстие и ее прохождения до самого конца трубопровода.
Целесообразно рассматривать проводимость с точки зрения проводимости отверстия и соответствующей вероятности прохождения молекулы (коэффициента Клаузинга), поэтому
$$C=CA cdot P_{1 to 2}= 1/4vA_{1}P_{1to 2}. (69)$$
Так как проводимость не зависит от направления движения молекул,
$$A_{1}P_{1 to 2} = A_{2} P_{1 to 2}. (70)$$
Примеры. Выражение для потока газа по длинному прямому трубопроводу было дано Кнудсеном:
$$Q= frac{ pi d^{3/2}}{L}$$
$$Q=( pi d^{3/2}/L)n_{a}(P_{1}-P_{2}), (71)$$
где d – диаметр трубопровода; L – длина трубопровода; nа – средняя скорость молекулы; р1 и р2 – давления на противоположных концах трубопровода.
Для сухого воздуха при 20 °С d и L, выраженных в дюймах, а р – в Торр, данное уравнение принимает следующий вид:
$$Q=(80d^{3}/L)n_{a}(p_{1}-p_{2}), (72)$$
Приблизительные значения некоторых вероятностей прохождения имеют точность в пределах + 10%. Это разнообразные методы, которые включают аналитические методы, расчеты по методу пробной частицы Монте-Карло и методу вариаций. Карлсон исследовал различные геометрические формы и ссылается на соответствующие источники. Примеры числовых расчетов можно найти в работе Карлсона.
Методы измерения газовых потоков
Газовый поток — это масса газа, проходящая в единицу времени через заданное поперечное сечение элемента вакуумной системы. В Международной системе единицей газового потока является кг/с. Потоки индивидуальных веществ можно измерять также количеством молекул газа, проходящих через заданное сечение элемента вакуумной системы в единицу времени.
При постоянной температуре газа часто используют внесистемную единицу газового потока м3-Па/с. Для воздуха при То — =273 К 1 м3-Па = 1,3-10-5 кг. Стационарный поток газа, выраженный в м3-Па/с, можно записать в виде
где U—проводимость вакуумной системы. Уравнение (8.1) может быть использовано для измерения стационарных газовых потоков методом двух манометров по перепаду давления на вакуумном элементе известной проводимости.
Другое выражение для определения как стационарных, так и нестационарных газовых потоков можно записать в дифференциальной форме:
В соответствии с уравнением (8.2) для измерения газовых потоков используют два метода: постоянного давления и постоянного объема. При /?=const поток газа Q = Vdp/dt, а его измерение осуществляется по скорости изменения давления в камере постоянного объема. При V=const поток газа Q=Vdp/dt, а его измерение осуществляется по скорости изменения объема газа при постоянном давлении.
Описанные методы считаются абсолютными. Косвенные методы— тепловые, радиоизотопные, ионизационные — нуждаются в градуировке по абсолютным методам.
Метод двух манометров. Метод двух манометров основан на измерении перепада давлений на элементе с известной проводимостью в соответствии с уравнением (8.1) и применяется для измерения стационарных или медленно изменяющихся во времени газовых потоков.
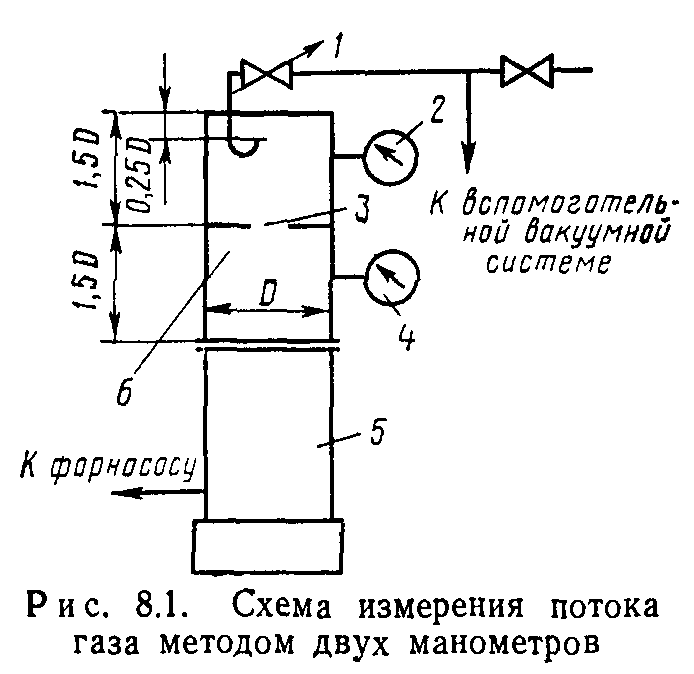
На рис. 8.1 показана схема измерения производительности и быстроты действия вакуумных насосов методом двух манометров. Поток газа, откачиваемый насосом 5, измеряется по перепаду давления на диафрагме 3 известной проводимости U. Диафрагма
установлена в измерительном колпаке 6, рекомендуемые размеры которого показаны на рисунке. Давления pi и ра измеряются соответственно манометрами 2 и 4. Регулировка потока газа осуществляется с помощью натекателя /, подключенного к вспомогательной вакуумной системе. Рабочее давление вспомогательной вакуумной системы больше, чем основной. Производительность насоса или газовый поток, проходящий через его входной патрубок, рассчитывается по уравнению (8.1), а быстрота откачки
Для расширения пределов измерения проводимость диафрагмы можно изменять непрерывно, например с помощью конструкции ирисовой диафрагмы, применяемой в фотоаппаратах, или ступенчато, используя поворотные диски с отверстиями различных диаметров.
Для элементов с малой проводимостью вместо отверстий, изготовление которых сопровождается технологическими трудностями обеспечения формы, используют длинный трубопровод — капилляр.
Метод постоянного давления. Схема измерения газового потока методом постоянного давления, использующая жидкостную бюретку, показана на рис. 8.2, а. Давление в измерительном объеме 5 жидкостной бюретки 6
гце рв — давление внешней среды; р — плотность жидкости в бюретке; h — разность уровней жидкости в измерительном объеме и внешнем цилиндре бюретки. Если выполняется условие, что ~^>pgh, то можно считать, что рИЗм~ const и требование постоянства давления выполняется. Тогда газовый поток согласно (8.2) определяют по уравнению
здесь Л/г и ЛУ— изменения уровня жидкости и величины объема измерительного цилиндра бюретки за время Л/; Кб— постоянная бюретки; Кб=л/?2изм; £изм — радиус измерительного объема.
Кран 4 необходим для опускания жидкости в бюретке и повторения экспериментов. Натекатель 3 предназначен для регулирова-
ния потока газа. Бюретка обычно заполняется вакуумным маслом, имеющим низкое давление насыщенного пара при комнатной температуре.
Схема измерения газового потока методом постоянного давления, использующая образование газовых пузырей, показана на рис. 8.2, б. При вытекании газа из объема 2 в объем 1 при Рг>р1 газовый поток может быть рассчитан по скорости dNJdt возникновения и объему Уп газовых пузырей 4, возникающих в жидкости 3:
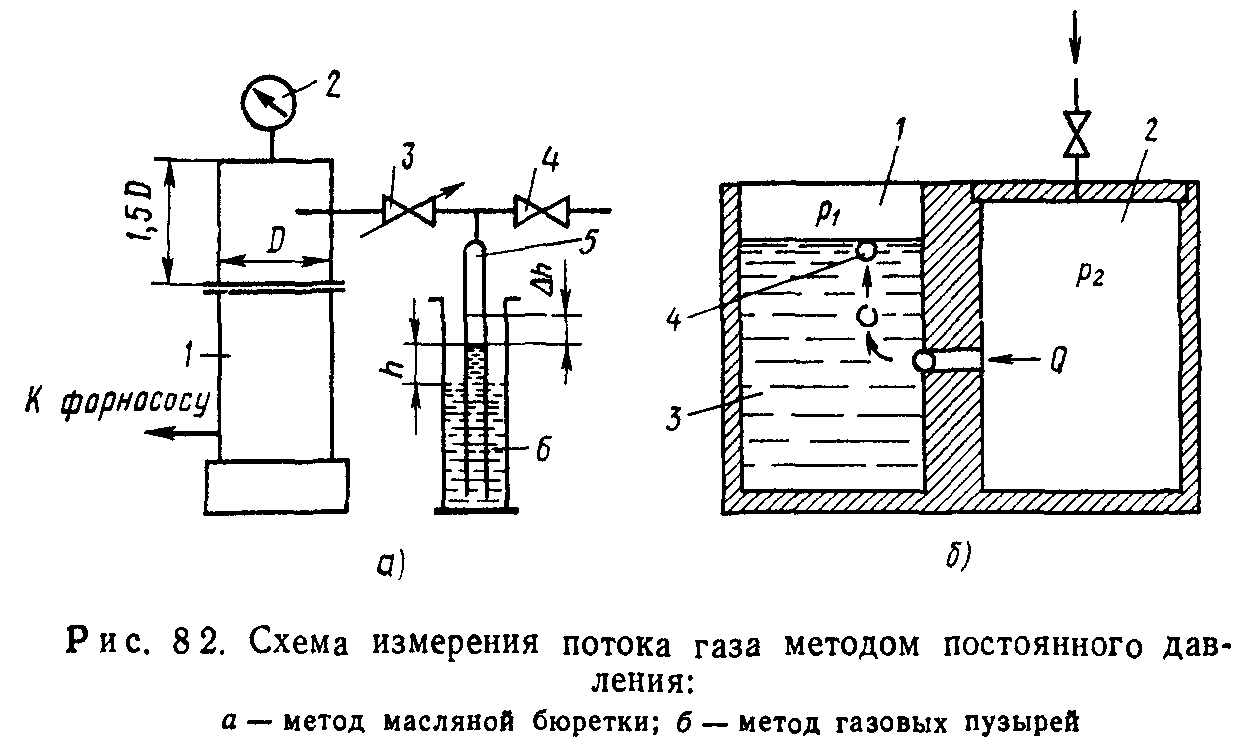
Вакуумирование пространства над жидкостью увеличивает чувствительность измерения, так как сопровождается увеличением объема пузырьков.
Примером использования метода постоянного давления является определение газового потока по известному значению быстроты откачки вакуумной камеры So. Вакуумный насос 7 (рис. 8-2, а) через клапан или диафрагму 2 подключается к откачиваемому объекту 2, давление р в котором измеряется вакуумметром 2. Поток газа регулируется клапаном 4 и натекателем 3.
Быстрота откачки камеры в соответствии с основным уравнением вакуумной техники
где U — проводимость вакуумной системы от насоса до откачиваемого объекта; SB — быстрота откачки насоса.
Измерения удобно проводить в молекулярном режиме, когда проводимость U зависит только от рода газа и температуры, но не зависит от давления. Нестабильностью быстроты откачки насоса можно пренебречь, если тогда
из (8.7) So^U. Так как50 = бГ/(1/, то, согласно (8.2), величина газового потока
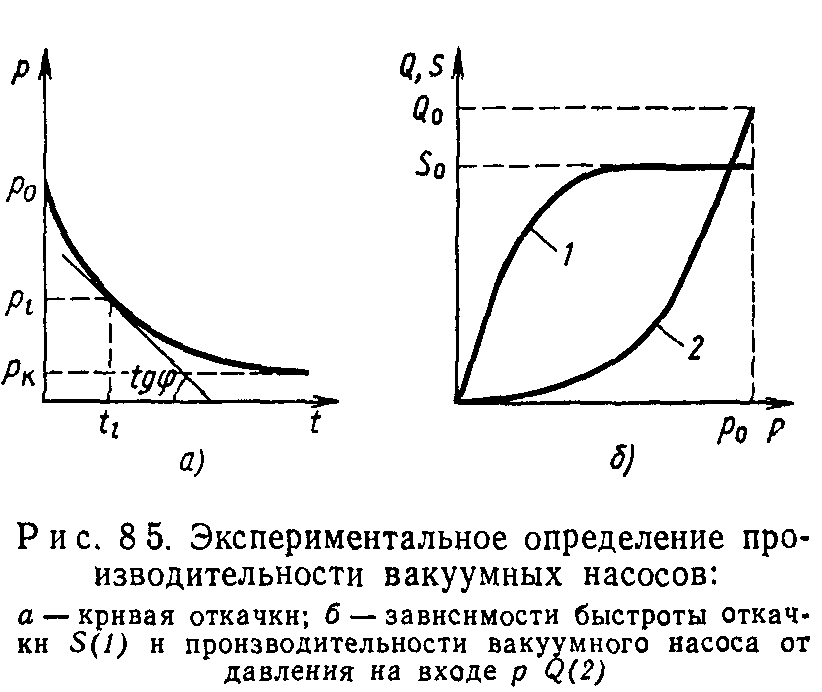
лучения вакуума в объеме 3. В процессе измерения клапан 2 закрывается. Газ из баллона 6 через натекатель 4, поступающий в объем 3, вызывает увеличение давления р. Если поток газа постоянен, то происходит линейное повышение давления (кривая 2 на рис. 8.3, б). По скорости повышения давления определяют газовый поток:
В момент прекращения откачки вакуумной камеры (/=0) в ней возникает газовыделение адсорбированных газов, приводящее к нелинейному повышению давления (кривая 3 на рис. 8.3, б). Суммарное изменение давления происходит согласно кривой 1 (рис. 8.3, б). Для надежного измерения потока методом постоянного объема газовыделение должно быть мало по сравнению с измеряемым газовым потоком. Этого можно достичь длительной предварительной откачкой вакуумной камеры.
Метод постоянного объема. Для определения газового потока методом постоянного объема можно использовать схему на рис. 8.3, а. В этом случае насос / и клапан 2 используются в качестве вспомогательной вакуумной системы для по-
Косвенные методы определения газовых потоков. Методы измерения газовых потоков, точность которых может быть обеспечена только после предварительной градуировки, называются косвенными. Чувствительность по потоку приборов для косвенных измерений где а — показания прибора в делениях самой чувствительной шкалы; Q — газовый поток, определенный абсолютным методом.
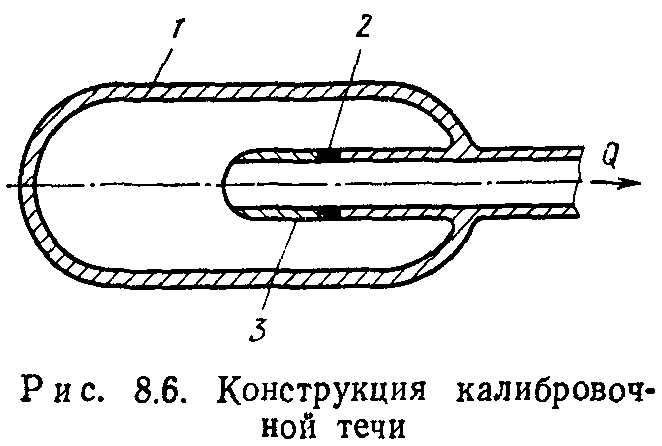
В процессе градуировки определяется диапазон потоков, в котором сохраняется линейность градуировочной характеристики. Проверка градуировки в процессе эксплуатации осуществляется с помощью калиброванных течей, одна из конструкций которых показана на рис. 8.6. Она представляет собой стеклянный баллон 1, заполненный гелием при давлении 105 Па. В баллон впаяна через переход 2 кварцевая трубка 3. Гелий диффундирует сквозь плавленый кварц. Для потоков 10—6… 10—9 м3-Па/с проверка течей может производиться один раз в год.
Примером косвенного метода измерения газовых потоков является тепловой метод. Теплопередача в области низкого вакуума при вынужденной конвекции зависит от скорости течения газа, а температура нагретой нити следовательно, от потока газа. В связи с тем что точный расчет зависимости между температурой и газовым потоком выполнить сложно, градуируют тепловой потокомер по абсолютному прибору.
«Методы измерения
вакуума. Средства создания и измерения
вакуума»
Расчетные
соотношения
В
гидромеханике массовый
расход
газа G
принято измерять в единицах
u
= [кг/с].
В
вакуумной технике речь идет о маленьких
расходах, поскольку среда находится
при низких давлениях (давление p
10 … 10–8
Па), измеряют расход не в кг/с, с помощью
специальной единицы. Это есть внесистемная
единица газового потока Q,
которая имеет размерность u
= [V][P]/[t]
u
=
.
Возможность
ввести данную единицу измерения Q
объясняется тем, что во всей области
давлений, используемых в вакуумной
технике (давления от атмосферного и
ниже), рабочая среда – воздух является
газом, заполняющий элементы вакуумной
установки. Это рабочее тело можно с
хорошей точностью считать ИДЕАЛЬНЫМ.
Уравнение состояния идеального газа
имеет вид
, (1)
где
m
– масса газа
в объеме V,
M
– молекулярная
масса газа, R
– универсальная
газовая постоянная.
Если
процесс откачки принят изотермическим
(T=const),
то поток газа, который равен массе,
удаленной за единицу времени, можно
записать в виде
.
(2)
Как
видно из формулы (2), есть основания
измерять газовый поток в единицах
комплекса
,
то есть использовать размерность u
=
для Q.
Перевод в привычные единицы массового
расхода u
= [кг/с] осуществляется с использованием
константы k
.
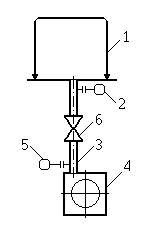
Рис. 1. Простейшая
вакуумная система
1 – рабочий объем
Vк
(в нем давление равно p1),
2, 5 – датчики давления, 2 измеряет
p1
– давление в камере, 5 измеряет p2
– давление на входе
в насос, 3 – трубопровод, 4 –вакуумный
насос.
Рассмотрим
простейшую вакуумную систему (Рис. 1),
содержащую рабочую
камеру объемом Vк
.
Поток
газа Q
из откачиваемого объема 1
определяется
выражением
,
где
VК
– объем вакуумной камеры.
Так
как объем камеры не меняется, то
справедливо выражение
.
Поток
газа можно контролировать по давлению
p(T),
то есть
по показанию манометра 2,
подсоединенного к вакуумной камере 1
(Рис. 1). Примем, что поток газа постоянен
вдоль трубопровода 3,
соединяющего откачиваемый объем и насос
4
Q
= const.
Это
допущение справедливо при вязкостном
режиме
течения газа и становится весьма грубым
при молекулярном
режиме.
В более точном приближении следует
учитывать:
-
газовыделение
адсорбированных газов с поверхности
трубопровода, -
натекание газа
извне через элементы конструкций.
Давление
газа в вакуумной камере p1
превышает давление на входе в насос p2
(эти давления измеряются манометрами
2 и 5)
на величину (p1–p2)
p1
>
p2
.
Причина
возникающей разности давлений — наличие
в вакуумной системе элементов (трубопровод
3,
вентиль 6
и другие), которые оказывают сопротивление
потоку газа. Сопротивление элементов
трубопровода зависит от режима течения
газа, длины соединяющих труб, величины
поперечных площадей сечений и т.д. Чем
выше сопротивление трубопровода, тем
больше разность давлений, требуемая
для прохождения газового потока заданной
величины Q.
Сопротивление
трубопровода W
можно представить как коэффициент
пропорциональности в выражении
Q
= W (p1
–
p2) (1)
.
(2)
Величина
U
обратная сопротивлению называется
пропускной
способностью трубопровода
или его проводимостью
. (3)
Если трубопроводы
соединены последовательно, то их полное
сопротивление
равно сумме сопротивлений, а при
параллельном соединении их полная
пропускная способность
равна сумме пропускных способностей
отдельных трубопроводов:
;
,
;
.
Пропускная
способность трубопровода может быть
рассчитана теоретически (методы и
примеры расчета приведены в [1,2]) или
определена экспериментально с помощью
соотношения (3).
Поток
газа Q
можно рассчитать, зная характеристику
насоса – производительность или быстроту
откачки насоса Sн,
которая представляет собой объем газа,
проходящий через сечение впускного
патрубка насоса в единицу времени при
впускном
давлении, pвх
,
на входе в насос
. (4)
где
Vн
– объем
насоса.
Отметим,
что механический вакуумный насос
осуществляет циклические процессы
отбора газа из рабочего объема 1 (рис.
1). За один цикл объем
насоса Vн
меняется
от 0 до Vн
, при этом
длительность
цикла составляет Δtцикл
.
Производительность
Sн
можно представить как
Sн
= Vн
/
Δtцикл
.
Производительность
Sн
(м3/с)
находится
по известным величинам (объем Vн,
частота циклов f)
и приводится как техническая характеристика
насоса в его техпаспорте. Sн
имеет единицу измерения [м3/с]
или [л/с]. Быстрота откачки насоса не
является постоянной величиной и обычно
уменьшается с уменьшением входного
давления, хотя в определенном диапазоне
давлений может оставаться постоянной.
Качество насоса тем лучше, чем шире
диапазон давлений, в пределах которого
быстрота откачки насоса мало изменяется.
Поток газа Q
может быть определен через параметры
насоса
,
где
p2
= pвх
– давление на входе в насос.
Если
за время dt
давление p2(t)
const,
то
. (5)
Эффективная
быстрота откачки Sэф
вакуумной камеры вводится в форме
,
где
p1
– давление в откачиваемом объеме.
Введение
величины Sэф,
как мы увидим ниже, оказывается полезным
при расчете параметров вакуумных систем.
Опыт
показывает, что при наличии вентиля
или иного
элемента, который расположен между
откачиваемым объектом и насосом и
оказывает
сопротивление
потоку, эффективная
быстрота откачки
Sэф
значительно отличается от быстроты
откачки насоса
Sн.
Рассмотрим
выражение, где используется Sэф
.
Из
него получим однозначную связь между
Sэф
и Sн
:
. (6)
Как
уже отмечалось выше, давление p2
всегда меньше давления в камере p1,
следовательно, Sэф
< Sн.
Разность давлений (p1
– p2)
и их отношение p2/p1
определяется суммарным сопротивлением
всех элементов трубопровода W.
Рассмотрим
задачу:
оценить
вакуум p1*
в рабочем объем
Vк
при известных характеристиках вакуумной
системы – производительности насоса Sн
и пропускной способности трубопровода
U.
Минимальное
давление p2*
насоса,
которое должно создать и поддерживать
на входном патрубке, отличается от
давления p1*.
Согласно выражению
(6)
. (7)
Выражение
(7) мало информативно, так как в нем
присутствует величина Sэф,
которая не задается явно в отличие от
быстроты откачки насоса Sн,.
Путем преобразований [3] можно получить
следующее соотношение, называемое
«основным
уравнением вакуумной техники»:
. (8)
Выражение
(8) позволяет выразить эффективную
быстроту откачки объекта Sэф
через известные характеристики вакуумной
системы: производительность насоса Sн
и пропускную способность трубопровода
U
:
. (9)
В итоге
. (10)
Если проводимость
трубопровода велика, то выполняется
условие
при U.
В этом случае
присутствие трубопровода практически
не влияет на выбор необходимого насоса,
параметры которого подбираются из
условия
.
В
случае конечной проводимости трубопровода
оценку величины p2*
необходимо проводить согласно уравнению
(10), причем, как это уже неоднократно
отмечалось,
,
и, следовательно, нам понадобится более
технически совершенный насос, чем для
случая U.
Все это означает дополнительные
материальные затраты, величина которых
определяется параметром U.
Выражение (10) можно
представить в виде
, (11)
где
KИ
– коэффициент использования насоса.
Величина
KИ
показывает, насколько эффективно
используются возможности данного насоса
в данной вакуумной системе.
Казалось бы, на
практике мы должны стремиться достичь
условия KИ1.
Необходимо учитывать стоимость
высокопроизводительных энергоемких
вакуумных насосов. Оптимальное значение
KИ
зависит от схемы вакуумной установки
и может изменяться от 0.1 до 1.0; с методиками
его оценки можно ознакомиться в
специальной литературе [2].
Замечание.
В техпаспорте вакуумного насоса задается,
как правило, не давление p2
– минимальное давление,
которое может поддерживать насос в
течение длительного
времени
работы, сохраняя при этом наибольшую
производительность откачки, а давление
pпр
– предельное давление насоса.
Предельное давление насоса – давление,
которое устанавливается в цилиндрах
насоса при закрытом впускном патрубке.
Предельное
давление большинства вакуумных насосов
определяется вторичным потоком газа:
1) газовыделением
материалов,
из которых изготовлен насос, и 2) натеканием
газа
через зазоры и места уплотнения. При
достижении предельного давления быстрота
откачки насоса Sн
становится равной нулю – насос перестает
откачивать массу газа из откачиваемого
объема, а удаляет только вторичный поток
газа. На практике для определения p2
можно пользоваться простым эмпирическим
правилом: величина p2
на порядок выше pпр.
Оценка
времени откачки
Оценим
время
откачки
заданного объема VК
от начального давления p1/
до конечного давления p1//.
Поток газа из откачиваемого объема VК
рассчитывается как
. (12)
Знак
«минус» в выражении (12) является
необходимым для того, чтобы уравнять
между собой знак потока Q
– величины по определению положительной,
и комплекса
– величины отрицательной в данной
задаче.
Произведя необходимые
преобразования, получим
.
Необходимое
время откачки t*
определяется следующей формулой
. (13)
Сделаем ряд
замечаний по поводу вывода уравнения
(13).
1)
Уравнение (13) справедливо для случая,
когда в системе отсутствует дополнительный
приток массы в объем V
за счет газовыделения адсорбированных
газов с поверхности вакуумной камеры
и натекания. В действительности приток
массы существует всегда, и выражение
(12) следует записывать в виде
,
(14)
где
– газовый поток, удаляемый насосом,
– газовый
поток, поступающий в камеру.
В
уравнении (14) предполагается условие
<
.
Время
откачки t*
необходимо рассчитывать по соотношению
.
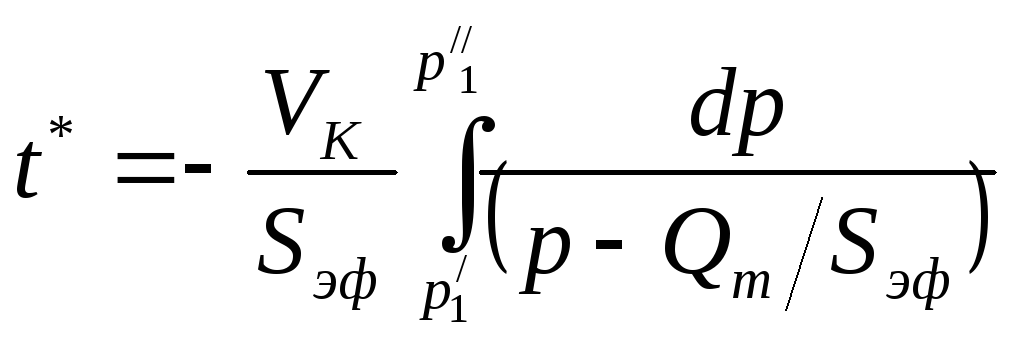Если
,
то получается следующая формула для
времени откачки
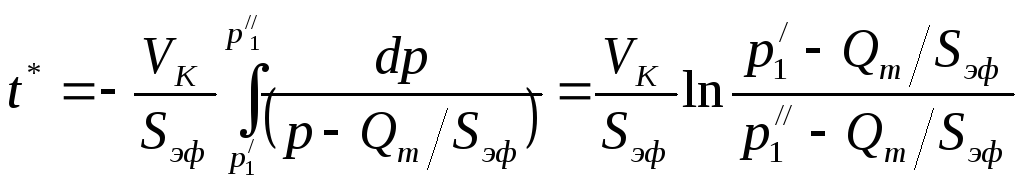. (15)
ЛИТЕРАТУРА
1.
Пипко А.И.,
Плисковский В.Я., Пенчко Е.А.
Конструирование и расчет вакуумных
систем. М.: Энергия, 1970. 504 с.
2.
Розанов Л.Н.
Вакуумная техника. М.: Высш. шк., 1990. 320 с.
3.
Буринский
В.В. Способы
создания и измерения давлений в
теплофизическом эксперименте. М.: Изд
– во МЭИ, 1992. 92 с.
4.
Комов А.Т.,
Федорович С.Ф.
Методы получения и измерения высокого
и сверхвысокого вакуума. М.: Изд–во МЭИ,
2000. 63 с.
Соседние файлы в папке ЭМИ – Лекции
- #
- #
- #
13.03.2016646.89 Кб39Эми2-Авдонина-2.xmcd
- #
13.03.2016629.07 Кб29Эми2-Авдонина.xmcd
- #
- #
- #
Лекции по гидравлике
Методы предотвращения негативных явлений гидравлического удара и его использование
Резкое увеличение давления, сопровождающее гидравлический удар – явление крайне негативное, т.к. гидравлический удар может разрушить трубопровод или какие-либо элементы гидравлических машин, испытывающие эффекты гидравлического удара. По этой причине разрабатываются методы предотвращения гидравлических ударов или уменьшить его негативное влияние. Поскольку мощность гидравлического удара напрямую зависит от массы движущийся жидкости, то для предотвращения гидравлического удара следует максимально уменьшить массу жидкости, которая будет участвовать в гидравлическом ударе. Для этого необходимо запорную арматуру монтировать в непосредственной близости к резервуару. В качестве меры уменьшения негативных последствий гидравлического удара используют замену прямого гидравлического удара на непрямой. Для этого достаточно запорную арматуру на напорных трубопроводах сделать медленно закрывающейся, что позволит уменьшить силу удара. Другой мерой борьбы с
явлением гидравлического удара является установка на напорных линиях, работающих в условиях
циклической нагрузки специальных компенсаторов с воздушной подушкой, которая принимает на себя удар
Однако в ряде случаев явление гидравлического удара успешно используется. К таким случаям использования гидравлического удара относятся производственные процессы по разрушению материалов и др. Известна специальная конструкция водоподъёмника, базирующаяся на использовании гидравлического удара.
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются весьма малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства практических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости. При движении газа таких допущений делать нельзя. Поскольку изучение общих решений уравнений газодинамики не является предметом настоящего курса, рассмотрим лишь частные задачи, встречающиеся в практике работы специалистов горных отраслей промышленности. К числу таких первоочередных задач относится изучение движения газов, включая воздух по газопроводам (воздуховодам).
Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных потерь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наиболее простой случай газопровода (воздуховода) собранного из труб одинакового диаметра (простой газопровод S = const
) при установившемся движении газа. Тогда в соответствии с уравнением неразрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной= const.
При этом объёмный расход газа будет меняться от одного сечения газопровода к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется.
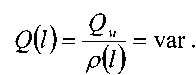
Тогда скорость движения газа также будет меняться вдоль длины газопровода:
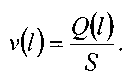
При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движение газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = const
и= const.
При таких условиях будет посто-
янным для всего потока и число Рейнольдса, и как следствие будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
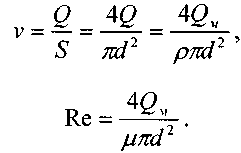
Отметим, что в последнем выражении все величины, входящие в правую часть равенства являются величинами постоянными, отсюда: Re = const
и /I = const.
По этой причине для определения величины потерь напора и расхода газа можно воспользоваться обычным уравнением Бернулли.
10.2. Основные уравнения газодинамики
для установившегося движения газа в простом газопроводе
Запишем уравнение Бернулли в дифференциальной форме:
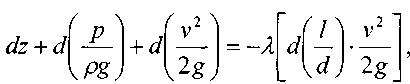
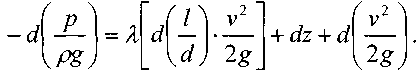
Последний член уравнения весь мал и его величиной можно пренебречь, тогда для горизонтального газопровода (z = const
) можно записать:
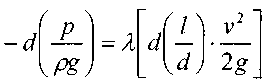
Подставив в последнее уравнение значение средней скорости движения газа, выразив её через массовый расход, получим:
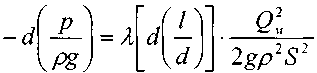
По принятым выше условиям процесс движения газа по газопроводу является изотермическим, тогда подставив в последнее уравнение значение из уравнения Бойля-Мариотта:
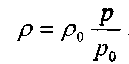, получим:
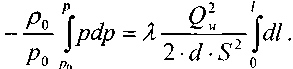
Решая последнее уравнение, получим основные расчётные формулу для определения потерь давления в газопроводе и формулу для определения массового расхода газа в газопроводе.
>
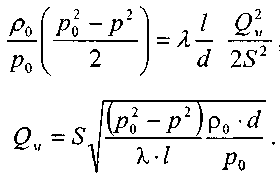Величина коэффициента трения Л
определяется по формулам для жидкости в зависимости от режима её движения или же можно воспользоваться эмпирической формулой ВННИИГаза:
*
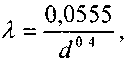где d-
диаметр газопровода в сантиметрах.
Для приближенного расчета движения жидкости или газа по трубам можно отвлечься от весьма сложных деталей этого движения (об этом будет сказано в заключительных главах) и удовольствоваться следующей упрощенной схемой. Примем поток за одномерный, т. е. будем пренебрегать изменением величины и направления скорости, а также изменениями других элементов потока (давления, плотности, температуры и др.) по сечению, перпендикулярному к оси потока; будем лишь учитывать изменение средних по сечениям величин и др. в зависимости от координаты х, определяющей положение сечения вдоль оси трубы. Площадь сечения А будем считать заданной функцией х. Отвлечемся от сил трения внутри жидкости и жидкости о стенку, а также от теплопроводности; иными словами, как повсюду в настоящей главе, будем считать жидкость идеальной.
Начнем с простейшего случая – движения несжимаемой жидкости.
В этом случае из уравнения неразрывности сразу следует
где средняя скорость в некотором начальном сечении с площадью иными словами, средняя скорость движения жидкости в любом сечении трубы обратно пропорциональна площади этого сечения.
Отсюда вытекает общеизвестное свойство движения несжимаемой жидкости по трубе переменного сечения: в сужающейся трубе жидкость движется ускоренно, в расширяющейся – замедленно.
Это очевидное свойство одномерного движения теряет свою силу при движении сжимаемого газа со сверхзвуковыми скоростями, в чем легко убедиться, составив основные уравнения одномерного стационарного движения газа:
а) уравнение Эйлера:
б) уравнение неразрывности:
Вспоминая определение местной скорости звука
перепишем уравнение Эйлера (83) в виде:
Составляя логарифмический дифференциал от обеих частей равенства (84), получим:
Исключая – из уравнений (85) и (86), найдем:
или, вводя местное число
Из этого простого уравнения вытекают важные следствия:
1. Если знак противоположен знаку т. е. при дозвуковом движении газа сохраняется то же свойство движения, что и в случае несжимаемой жидкости: с возрастанием площади сечения трубы скорость в одномерном движении уменьшается и, наоборот, при уменьшении сечения – скорость увеличивается.
2. Если знак одинаков со знаком т. е. при сверхзвуковом движении газа в сужающейся трубе движение замедляется, в расширяющейся трубе – ускоряется. Этот парадоксальный на первый взгляд результат объясняется тем, что при расширении газа плотность его настолько сильно уменьшается, что произведение в равенстве (84), несмотря на увеличение площади А, все же уменьшается и приводит к возрастанию скорости и.
3. Если Сечение трубы, в котором число достигает значения единицы, называется критическим сечением, так как в нем скорость движения и равна местной скорости звука а. Из равенства (87) следует, что критическое сечение может быть максимальным, так и минимальным по сравнению со смежными сечениями. Легко сообразить, что критическое сечение будет минимальным, так как при подходе к максимальному сечению дозвуковой поток замедляется, а сверхзвуковой ускоряется, что никак не может привести к течению со скоростью звука в критическом сечении.
Если и сечение экстремально (максимально или минимально), то по (87) либо следовательно, это сечение –
критическое, либо В последнем случае, каково бы ни было движение – дозвуковое или сверхзвуковое – скорость в экстремальном сечении принимает также экстремальное значение; при дозвуковом течении газа – минимальное в максимальном сечении и максимальное в минимальном сечении, при сверхзвуковом течении, наоборот, в максимальном сечении скорость максимальна, в минимальном – минимальна.
Переходя к более детальному изучению одномерного адиабатического и изэнтропического движения газа, заметим, что к нему применимы все ранее выведенные соотношения, связывающие между собою термодинамические параметры газа и скорость движения или число Необходимо только установить связь между одним каким-нибудь из этих параметров и сечением трубы А.
Примем за основную, например, связь между Чтобы вывести уравнение этой связи возьмем уравнение
получаемое логарифмическим дифференцированием равенства
и уравнение Бернулли в форме (47):
которое после дифференцирования дает
или, после делении обеих частей на и замены
Подставляя это значение в (88), получим
Сравнивая это уравнение с уравнением (87), будем иметь:
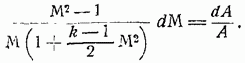
Уравнение это нетрудно проинтегрировать и получить искомое уравнение связи между числом и площадью сечения А:
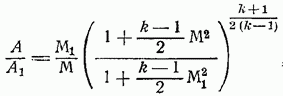
где произвольное начальное сечение трубы и число в этом сечении.
Предположим, что роль начального сечения играет критическое сечение т. е. такое сечение, в котором тогда равенство (89) приводится к более простому виду:
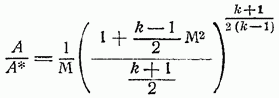
На рис. 47 приведен график этой важной зависимости для воздуха График подтверждает ранее отмеченный факт: в дозвуковом потоке для увеличения числа сечение А следует уменьшать, в сверхзвуковом потоке наоборот, увеличивать; вместе с тем график показывает количественное соотношение между изменениями чисел
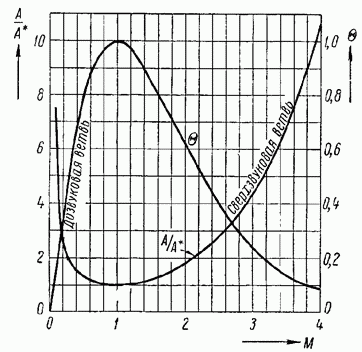
Так, например, из рис. 47 следует, что для повышения числа от 0,2 до 0,8 газ должен пройти через участок суживающейся трубы-конфузора с сечением, уменьшающимся в три раза; чтобы увеличить число от значения 1 в критическом сечении до 3,2, необходимо построить расширяющуюся трубу-диффузор – с площадью на выходе, в пять раз превышающей площадь критического сечения.
Присоединим к формуле (90) известные уже по предыдущему формулы (69), (70), (66) изэнтропической связи давления, плотности и температуры с числом которые, в силу (51) и (52) полезно
переписать в виде:
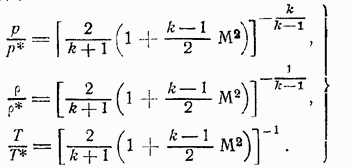
Совокупность равенств (90) и (91) представляет полное решение задачи об одномерном стационарном адиабатическом и изэнтропическом движении газа по трубе переменного сечения; решение это представлено в удобном параметрическом виде, причем роль параметра играет число Задавшись законом изменения площади сечения трубы определим по (90), а затем и искомые по (91).
Из уравнения неразрывности или сохранения массы (84) следует, что при наличии в одномерном потоке критического сечения будет существовать соотношение
где величина
представляет отношение массового расхода газа через единицу площади сечения трубы к его критическому значению. Этот безразмерный массовый расход данного газа является функцией только числа согласно (90), равен:
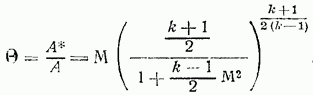
График зависимости от для воздуха приведен на том же рис. 47.
В качестве первого примера приложения выведенных формул рассмотрим классическую задачу об изэнтропическом истечении газа из резервуара (котла) очень большой вместимости.
Предположим сначала, что сопло, из которого происходит истечение, имеет вид конфузора, т. е. канала с уменьшающимся вниз по потоку сечением. Обозначим через термодинамические параметры газа в котле, где газ, в силу большой вместимости котла, может рассматриваться как покоящийся через соответствующие параметры в выходном сечении, площадь которого
пусть будет А, и через давление в среде, куда происходит истечение; это давление в теории истечения называют противодавлением.
Определим прежде всего основную характеристику одномерного потока в целом – секундный массовый расход газа одинаковый для всех сечений потока и равный
или, на основании формул (52):
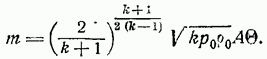
При заданных параметрах газа в котле и геометрической форме сопла секундный массовый расход газа является функцией только числа в выходном сечении, определяемой выражением в формуле (93). Что касается выходного числа то оно, в силу принятой наперед адиабатичности и изэнтропичности потока, определяется заданием давления на выходе согласно известной формуле (69):
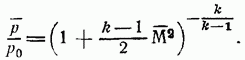
Определяя отсюда в функции от и подставляя это значение в выражение в, получим после простых приведений формулу:
представляющую, очевидно, простое приложение ранее указанной формулы Сен-Венана и Ванцеля [(67) гл. III].
Пользуясь одновременно формулами (94) и (95), легко исследовать изменение секундного массового расхода истечения в функции отпротиводавления которое при совпадает практически с или числа в выходном сечении.
При
движении газа на каждый его объем будут
действовать
не только те силы, которые характерны
для статики,
но и другие, сильно усложняющие как
явление в целом, так и его математическое
описание. Для движения идеального
газа этими дополнительными силами будут
силы инерции, а для реального газа –
силы инерции и трения (вязкости). В
механике сплошных сред большое внимание
уделяется
выводу и использованию соответствующих
математических уравнений, описывающих
движение идеальных (уравнения
Эйлера) и реальных сред (уравнения Навье
– Стокса). Уравнения Навье – Стокса
настолько сложны, что
к настоящему времени решены лишь для
крайне ограниченного
числа случаев. Эта сложность вызвана
сильным влиянием
вязкости среды на различные аспекты
процесса движения.
В силу этого в допустимых случаях
прибегают к
решению уравнений Эйлера для движения
идеальных сред
с введением необходимых поправок и
уточнений. Таким образом, получено одно
из важнейших уравнений гидро-
и аэродинамики – уравнение (закон)
Бернулли.
Уравнение
Бернулли.
В
практических условиях распространенным
является движение в трубах и каналах,
когда
газ через боковые стенки не расходуется.
В таких случаях
для расчетов применяется уравнение
Бернулли, полученное
для струйки тока (трубка тока), характерной
тем,
что расход газа в любом ее сечении
остается неизменным
(обмен газом между всем потоком и струйкой
тока через
ее боковые границы отсутствует).
Для
несжимаемого газа ()
уравнение Бернулли
при условии, что все его члены отнесены
к единице объема,
имеет вид
В
соответствии с этим величина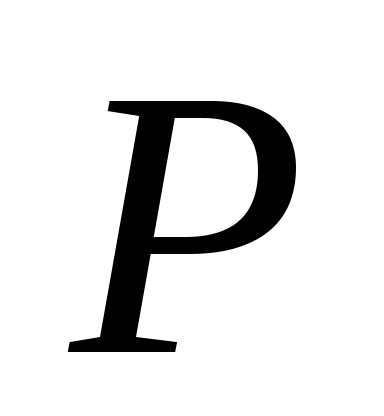 
является пьезометрическим
давлением, величина
–
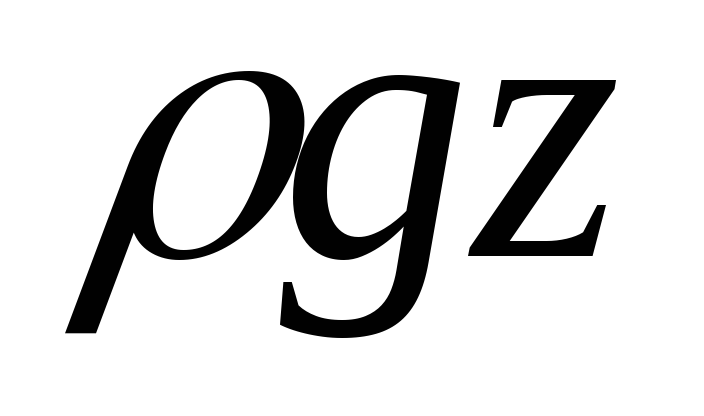геометрическим давлением, величина
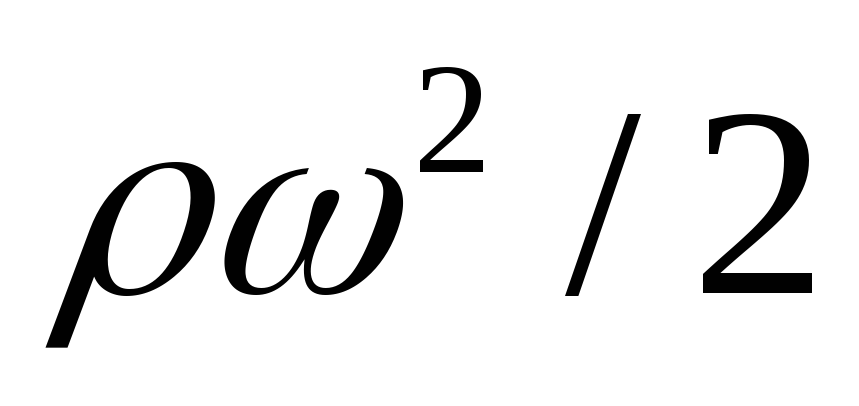
– скоростным давлением.
Уравнение
Бернулли представляет собой закон
сохранения
энергии, поскольку сумма
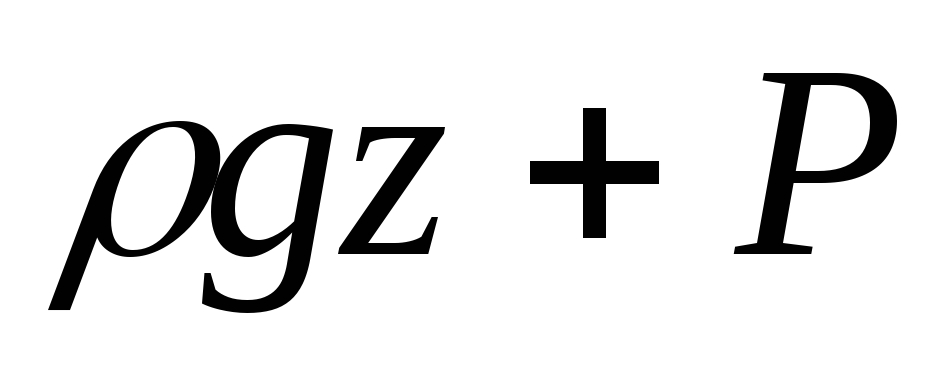характеризует
потенциальную, а
величина
–
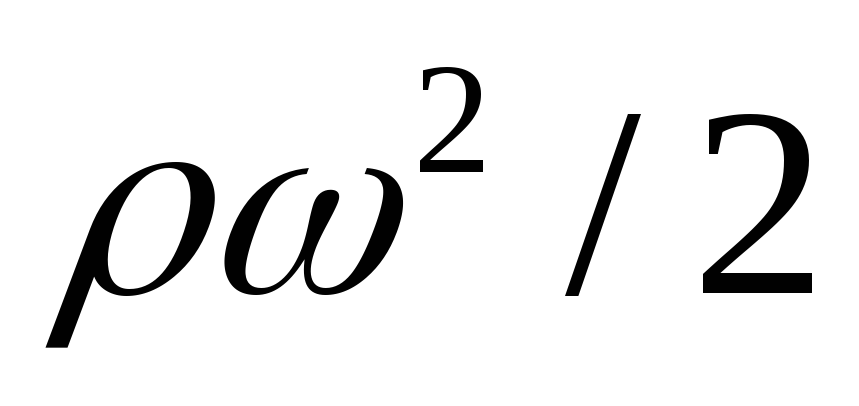кинетическую энергию.
В
металлургической теплотехнике
в большинстве случаев пользуются
давлением, избыточным
над атмосферным. Необходимо уравнение
Бернулли привести к такому виду, при
котором все члены
его были бы выражены в избыточных
давлениях. Для
этого представим себе канал, окруженный
воздухом плотностью
,
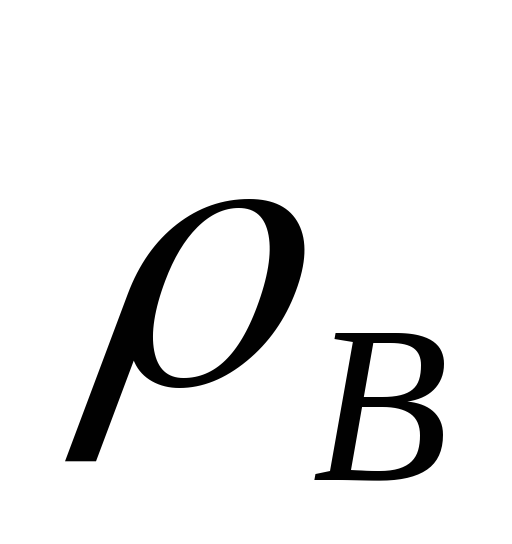по которому движется газ плотностью
.
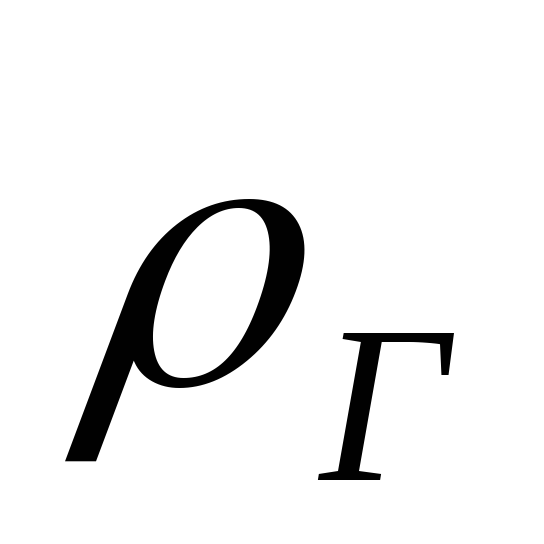Принимая
плотности газа и воздуха неизменными,
напишем
уравнение Бернулли и для газа и воздуха
применительно к
сечениям канала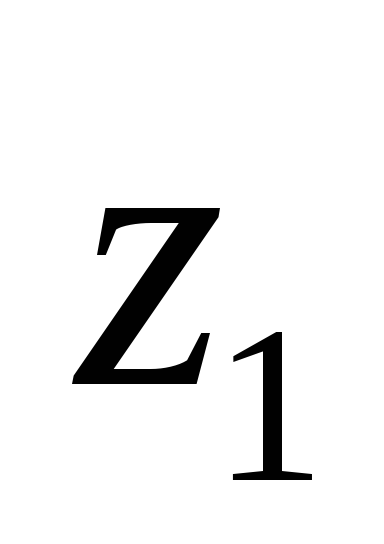 
и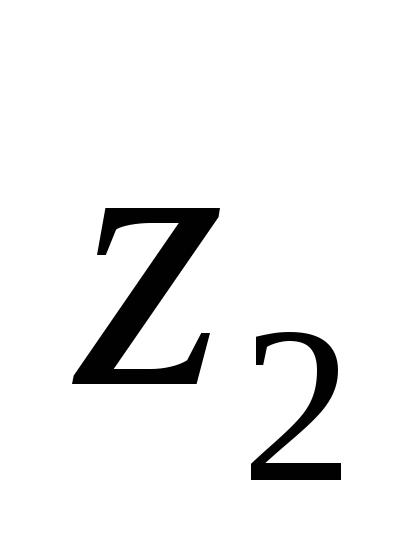 
.
Уравнение
для газа
Уравнение
для воздуха (считаем, что воздух находится
в спокойном состоянии)
Вычитая
из первого второе, получаем уравнение
Бернулли
для газа в избыточных давлениях:
.
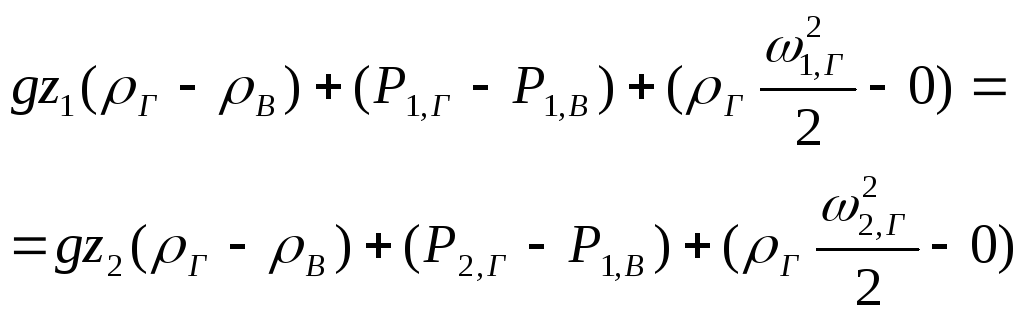(11)
Уравнение
можно переписать в таком виде:
Однако
равенство
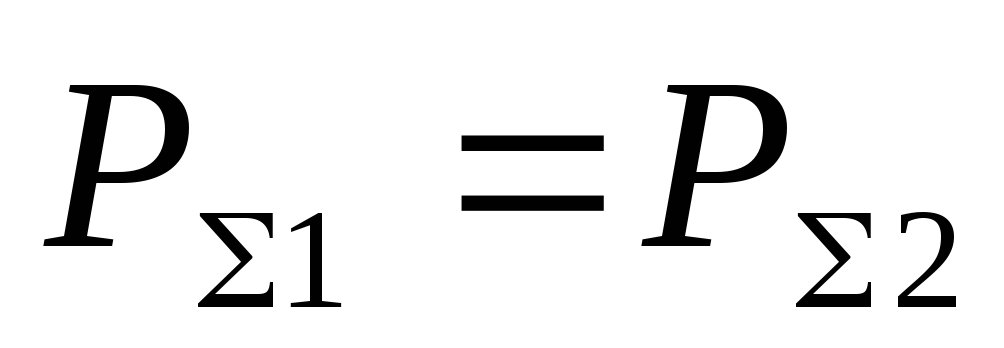
строго
справедливо лишь для
идеальной среды, полностью лишенной
вязкости. Если
по каналу перемещается реальная (вязкая)
жидкость
(газ), то часть энергии тратится на
преодоление трения и различных
сопротивлений и происходит потеря
энергии.
В этом
случае при движении от сечення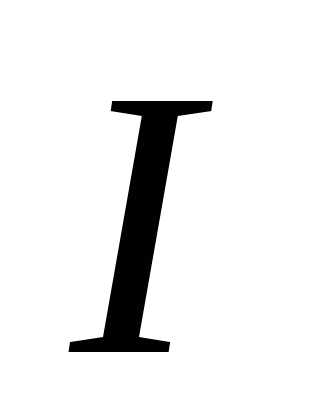 
к сечению
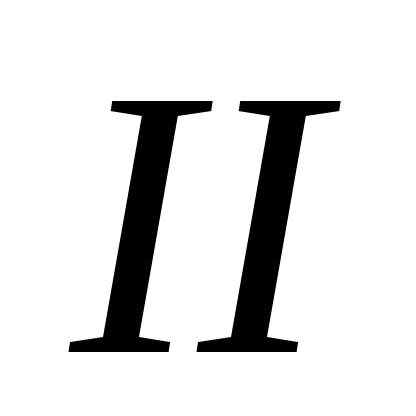
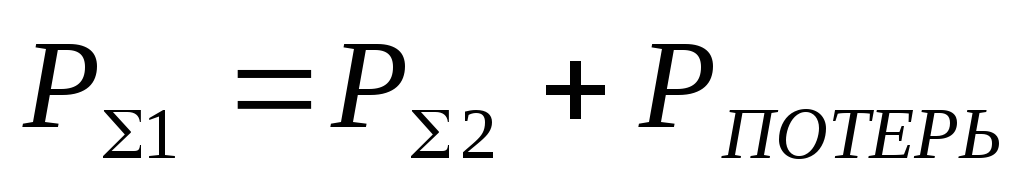(12)
и
окончательно закон Бернулли формулируется
следующим образом: «При установившемся
течении несжимаемой жидкости
(газа) для различных сечений канала
сумма давлений
всех видов является постоянной».
Рассмотрим,
что представляет собой потерянное
давление,
входящее в уравнение Бернулли.
При
движении реального газа часть его
энергии расходуется
на преодоление трения и различных
сопротивлений.
Потери
на местные сопротивления возникают
при резком изменении величины и
направления скорости, при резком
изменении сечения канала, при повороте
канала или усложнении его сечения, при
соударении потоков.
Величину потерь энергии выражают в
долях скоростного
давления.
Потери
на трение
,(Па)
можно определить по формуле
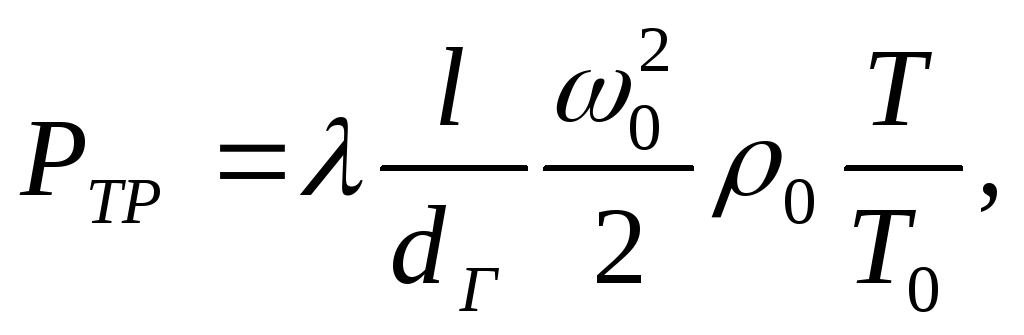(13)
где 
– коэффициент трения;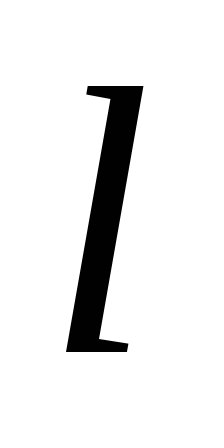 
– длина канала, м;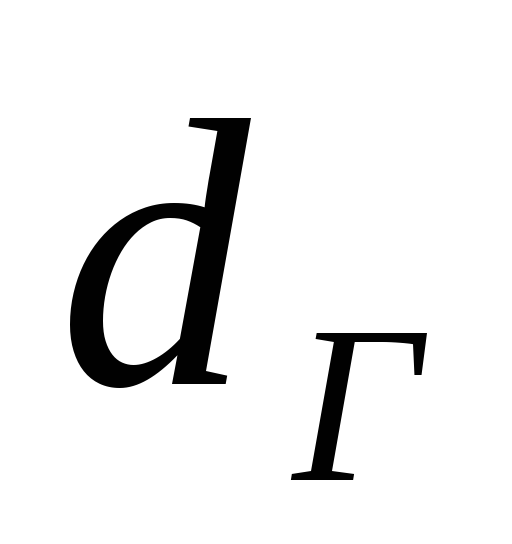 
– гидравлический
диаметр канала, м;
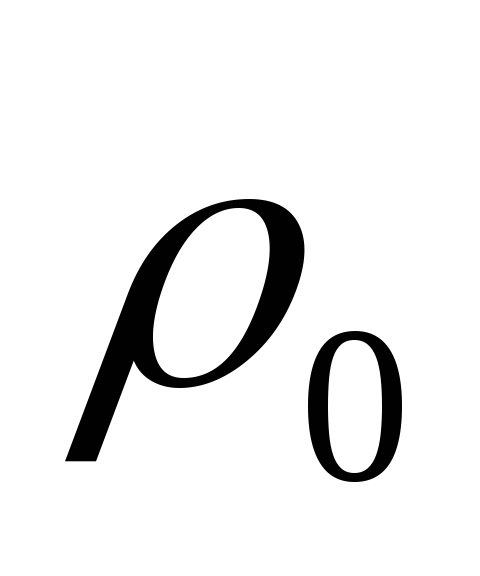
и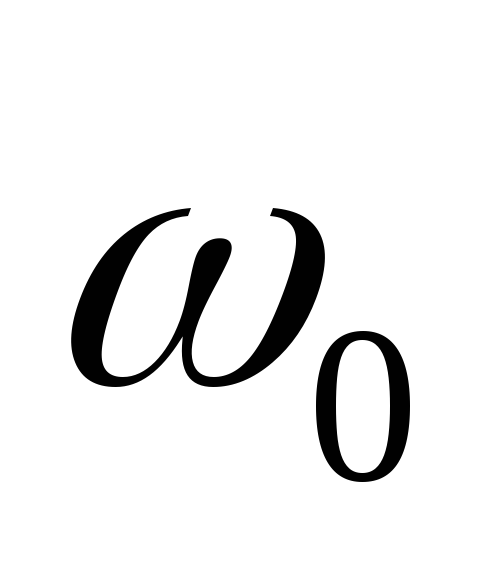 
– плотность и скорость
жидкости
(газа) при нормальных условиях, т.е. при
атмосферном давлении
и температуре Т
о
,
равной 273 К; Т
– действительная
температура жидкости или газа, К.
При
ламинарном движении (Rе<2300)
коэффициент трения
зависит от критерия Rе
.
(14)
При
турбулентном движении коэффициент
трения зависит не
только от критерия Re,
но и от относительной шероховатости
стенки канала (
),
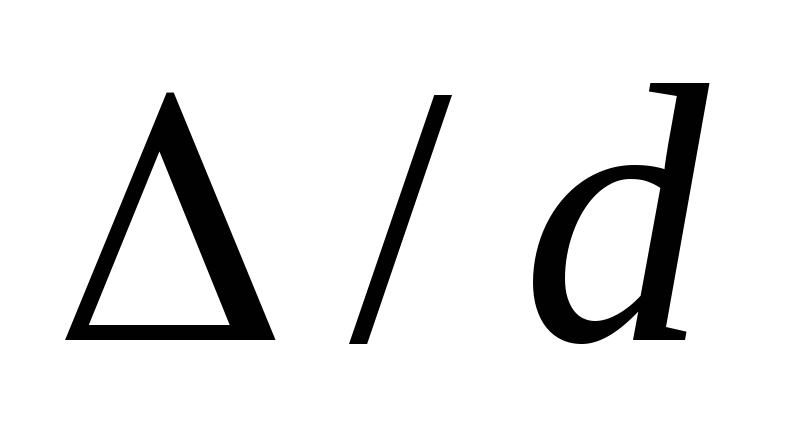равной
отношению абсолютной
шероховатости 
(в мм) к диаметру канала 
:
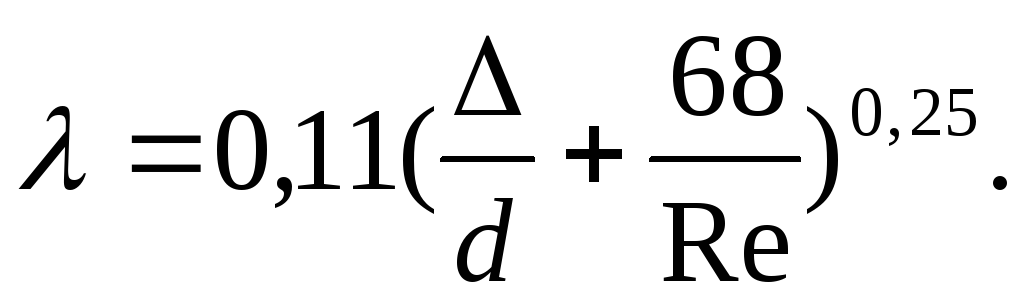
При
приближенных практических расчетах
коэффициент трения
можно принимать
постоянным и равным для кирпичных
каналов 0,05, для металлических 0,04.
Потери
на преодоление местных сопротивлений
(Па),
определяются
по формуле
,
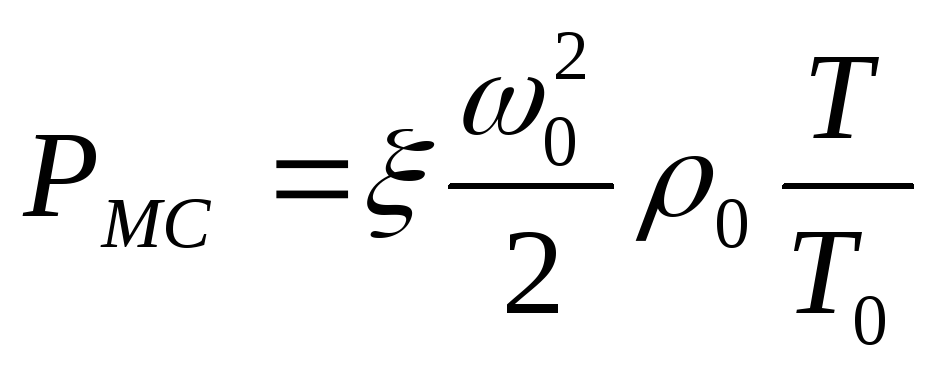где 
– коэффициент местного сопротивления.
Его величина
зависит от формы местного сопротивления,
как правило,
определена опытным путем и приведена
в справочной литературе.
Важнейшим
расчетом, который выполняется для
подавляющего
большинства печей, является определение
суммарных
потерь давления на пути движения дымовых
газов
от печи до дымовой трубы. Суммарные
потери используются
при определении размеров дымовой трубы,
которая
рассчитывается из условия, что разрежение,
создаваемое
дымовой трубой, должно быть по абсолютной
величине больше
суммы всех сопротивлений, возникающих
в дымовом
тракте печи.
Таким
образом, уравнение (закон) Бернулли
находит очень
широкое применение. Наряду с уравнением
Бернулли
важную роль в гидро- и аэродинамике
играют также уравнение
сплошности (или неразрывности течения)
и уравнение импульсов Эйлера.
Уравнение
сплошности.
В
практических условиях наиболее
распространенными являются такие
процессы, при которых
масса газа, протекающая по какому-то
объему, остается
неизменной. При этом, естественно, масса
газа, втекающая
в объем в единицу времени, должна быть
равна
массе вытекающего газа.
Следовательно,
можно написать, что
,
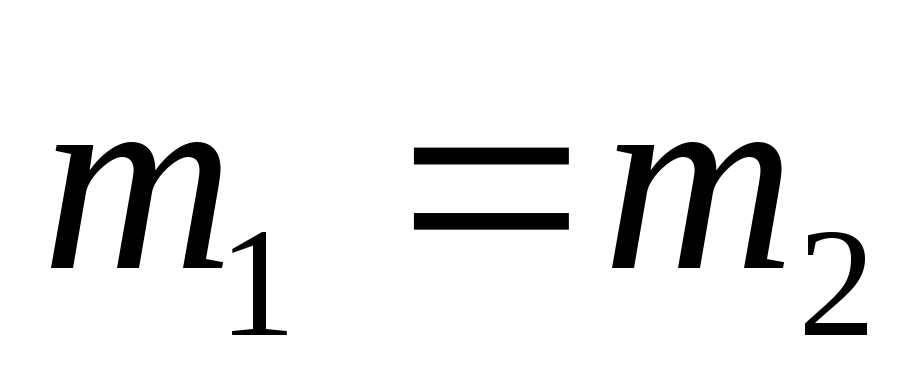или, учитывая,
что масса есть произведение скорости,
сечения потока
и плотности, получаем
.
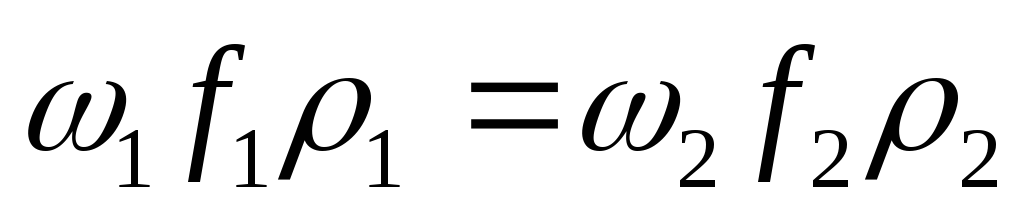При
условии постоянства плотности (
)
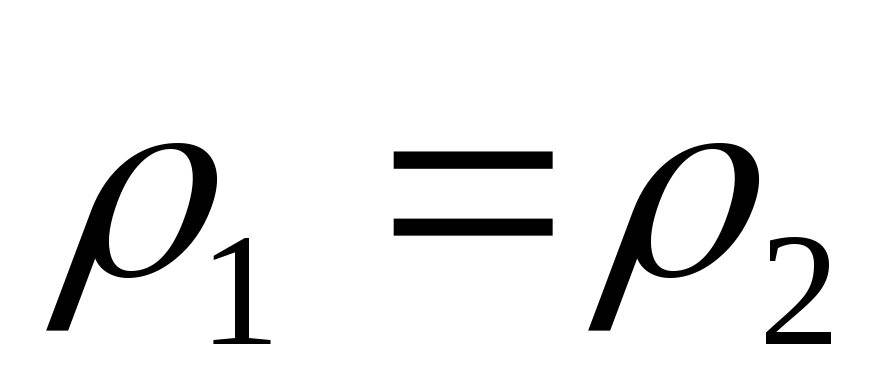последнее
выражение принимает вид
.
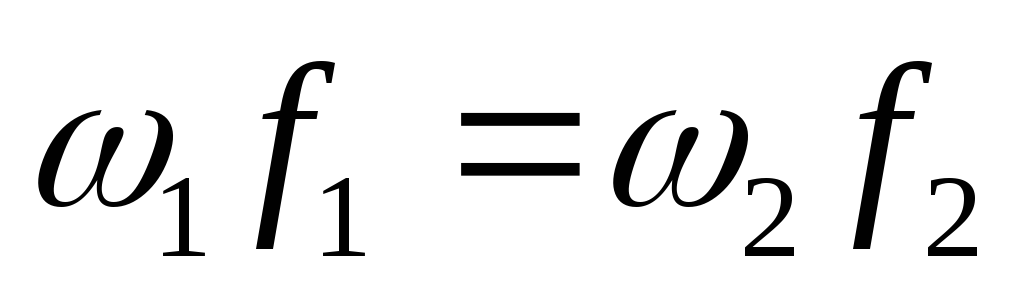(15)
Если
в качестве скорости принимать среднюю
скорость потока, то выражение (15) применимо
для практических расчетов при течении
в трубах и каналах, причем средняя
скорость
потока определяется как частное от
деления секундного
объема среды, проходящего через данное
сечение,
на величину площади сечения, т. е.
.
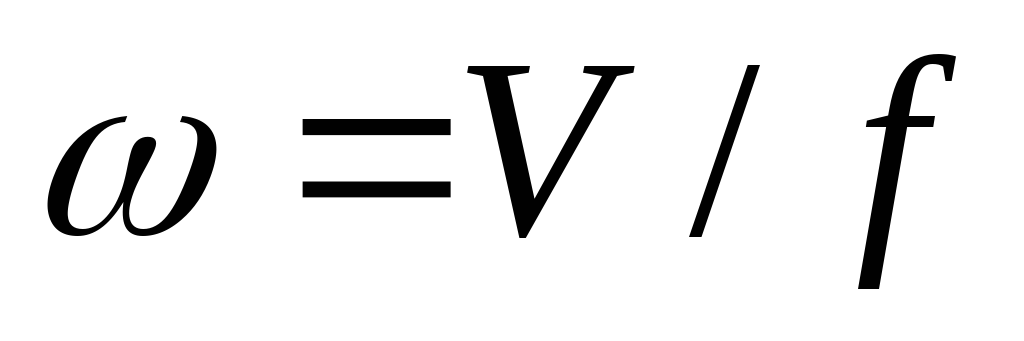Уравнение
импульсов Эйлера.
Уравнение
импульсов (количества
движения) Эйлера имеет важное значение
для некоторых
практических расчетов. Это уравнение
применимо
к какому-то воображаемому контуру,
выделенному в общем
потоке газа, через боковую поверхность
которого ни
движения, ни массообмена не происходит.
В
подобном контуре под действием внешних
сил (в потоке газа
– под действием давления) происходит
изменение количества
движения газа. Если изменение импульсов
проходящего газа и
изменение внешних сил отнести к единице
времени, то теорема импульсов Эйлера
может быть сформулирована
следующим образом: «Изменение импульса
всех
сил, приложенных к газу, проходящему
через выделенный
контур, равно результирующей внешних
сил, действующих
на данный контур».
Записывается это
уравнение так:
.
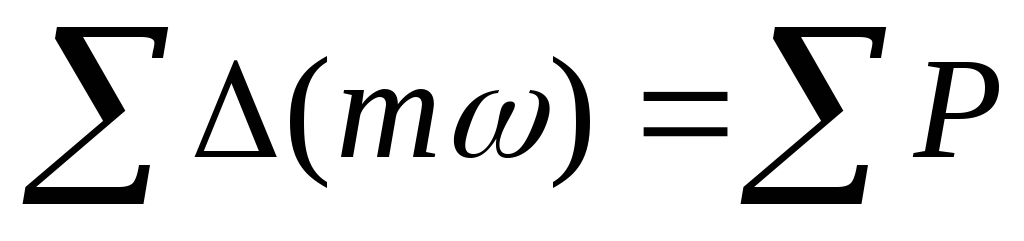(16)
Применение
уравнения импульсов будет проиллюстрировано
ниже при рассмотрении струйных аппаратов.
Наиболее
важные случаи применения уравнения
Бернулли.
Истечение газов
через отверстия и насадки
Истечение
газов через отверстия и насадки
наблюдается
при работе горелок, форсунок, при
выбивании газа через отверстия
в стенах печи и в других случаях. Установим
связь
между количеством вытекающего газа и
размерами отверстия
и давлением, под которым происходит
истечение.
Для простоты возьмем истечение
несжимаемого газа, температура
которого в процессе истечения практически
не изменяется.
Отверстия с
острыми краями.
.
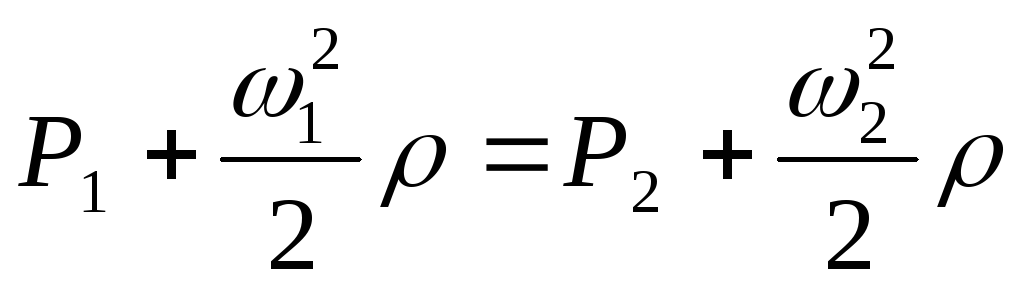Вследствие большого
размера сосуда можно принять
.
.
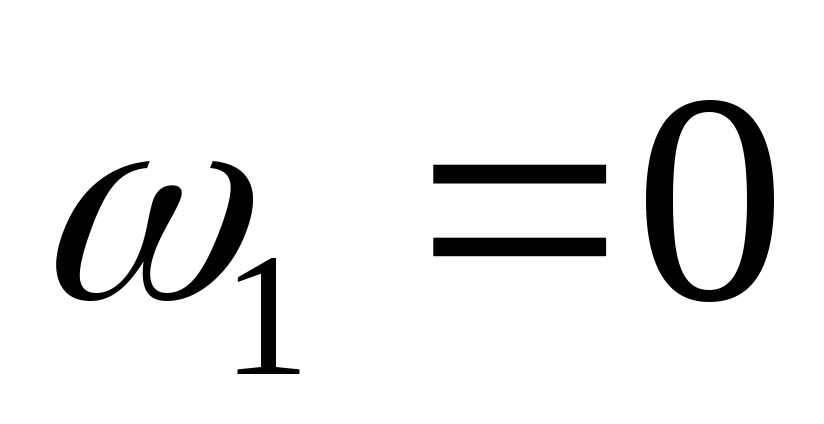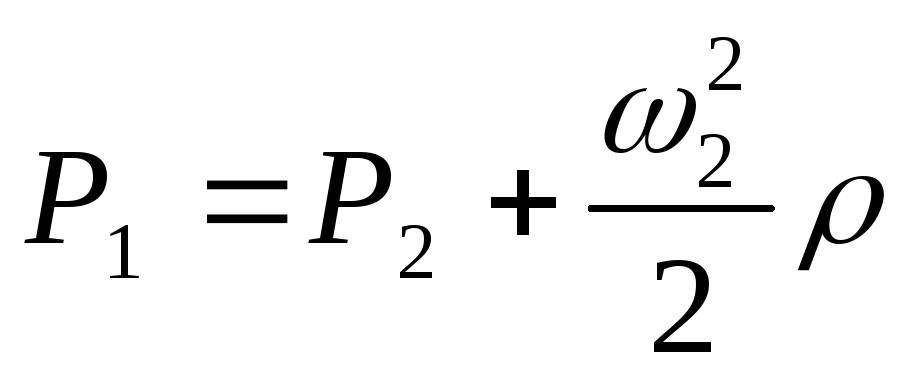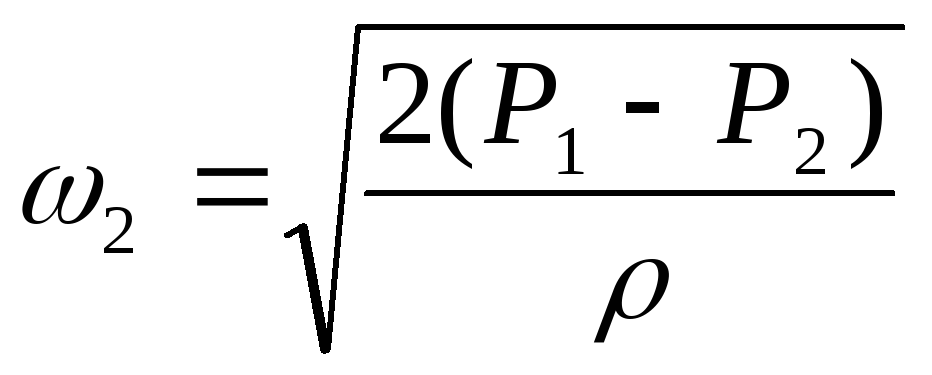.м/с.
(17)
.
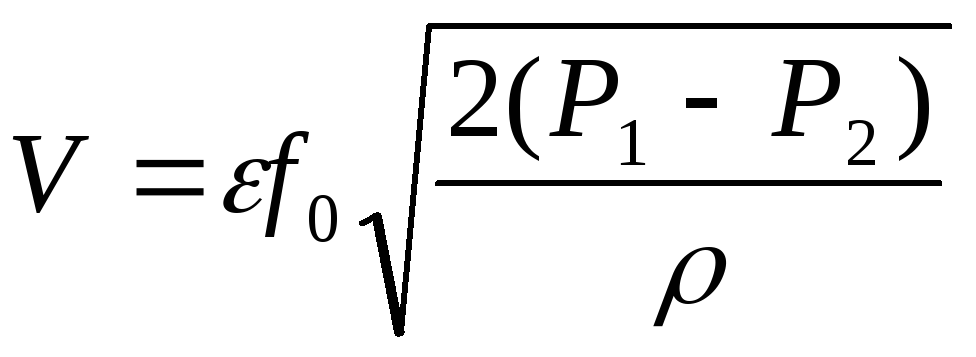(18)
С учетом
гидродинамических потерь при истечении
через отверстие выражение (18) принимает
вид (м 3 /с)
.
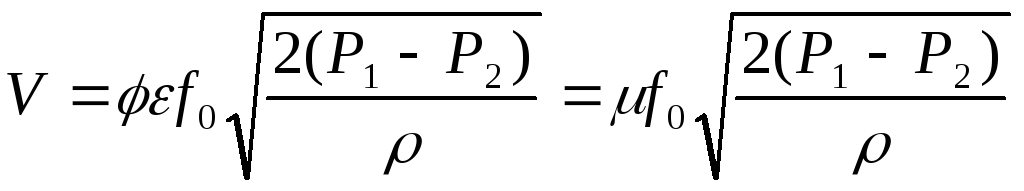Смысл коэффициентов
и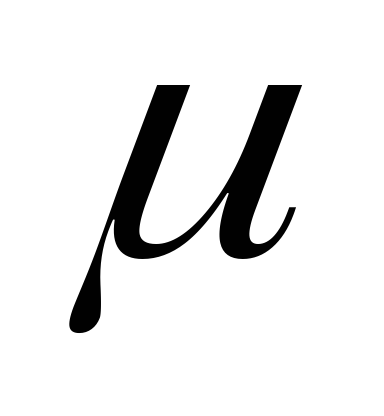
ясен из следующего примера.
Истечение из
отверстия в стенке печи (рис. 9) – весьма
распространенный на практике случай.
Рассмотрим подобный случай истечения
(с учетом потерь) из отверстия сечением
,
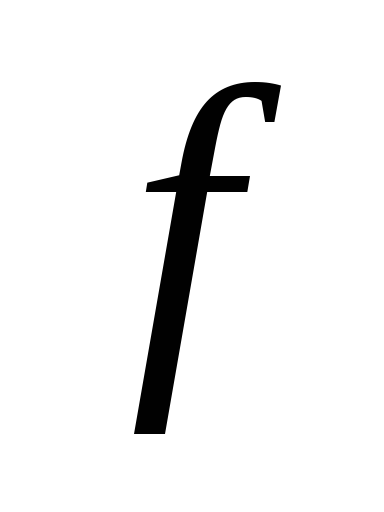расположенного на участкеH
от уровня пода печи. Напишем уравнение
Бернулли для сечения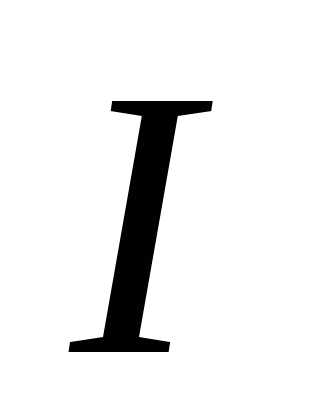и
точкиA
в сечении
:
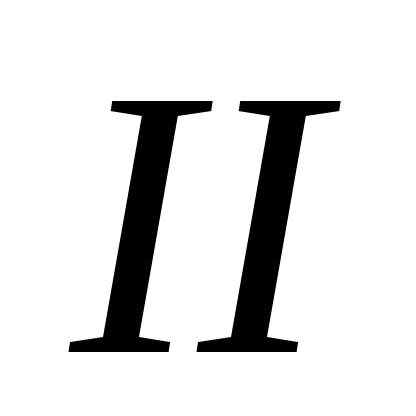Скорость движения
газов в отверстии
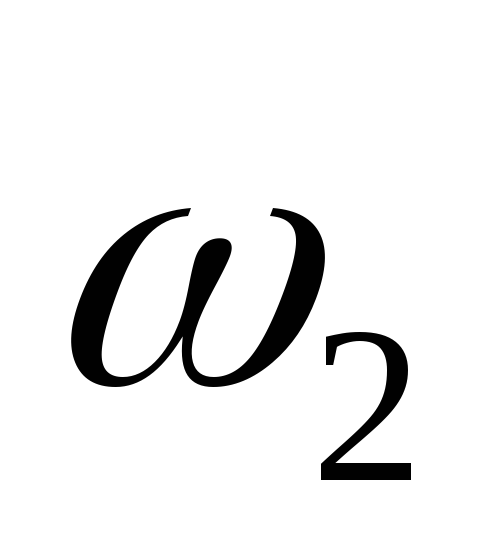много больше скорости
;
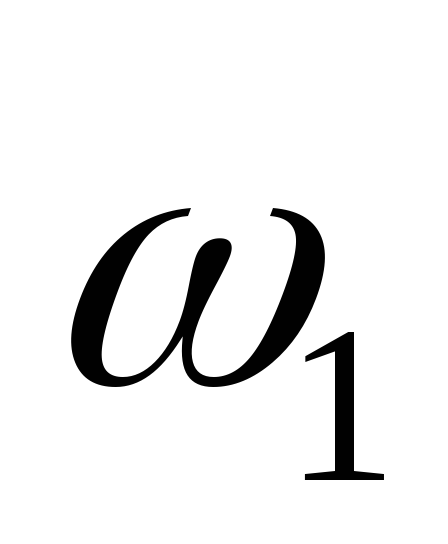исходя из
,
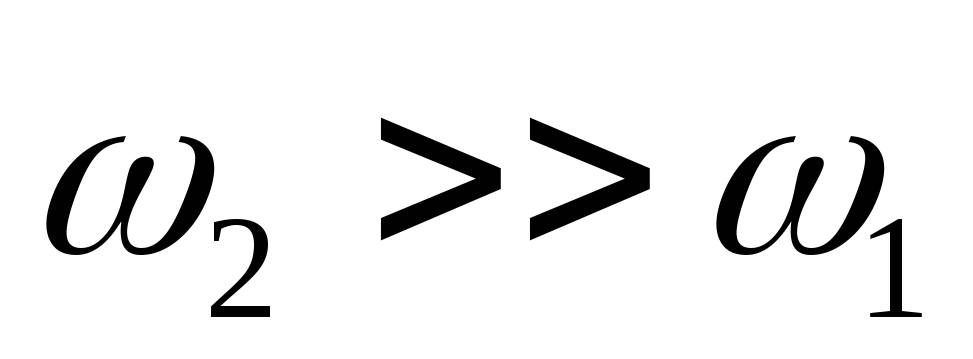принимаем
.
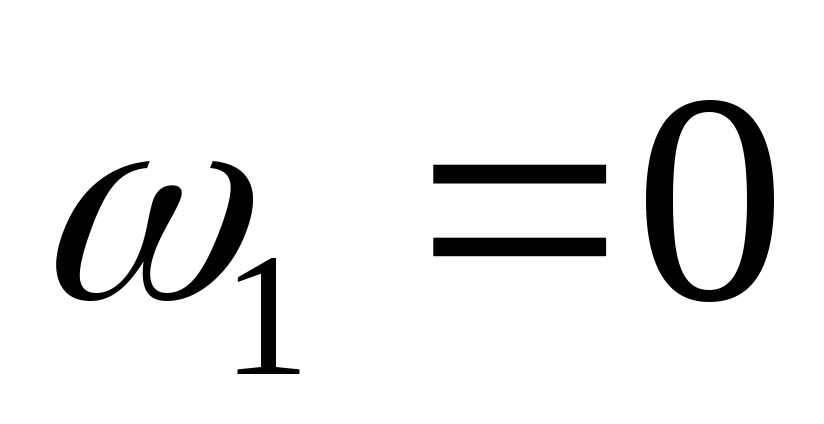Как следует из
изложенного выше, потери на местные
сопротивления могут быть определены
как
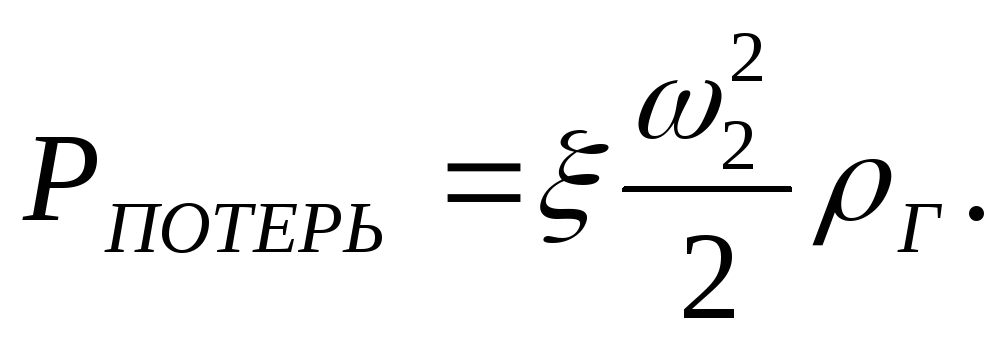
Так как печь
сообщается с атмосферой на уровне пода,
то пьезометрическое давление газа
внутри печи и давление воздуха снаружи
равны между собой и равны
.
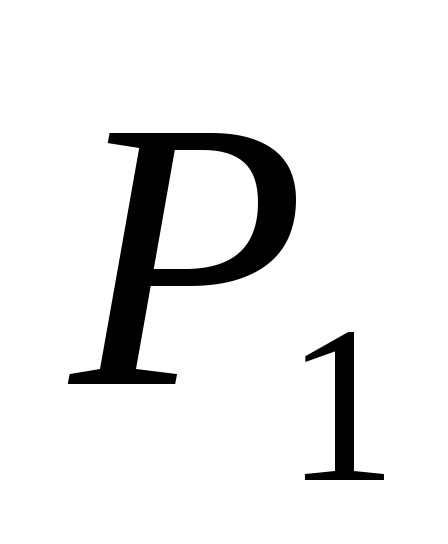Давление
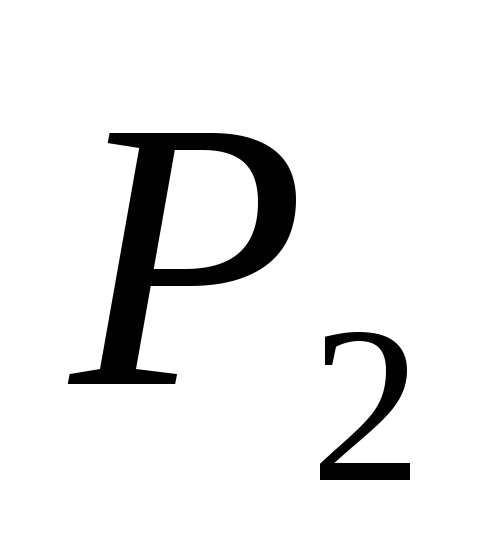в точкеА
соответствует атмосферному
давлению на высотеН
от уровня
сечения
,
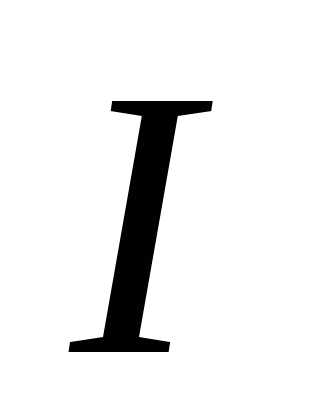т.е.
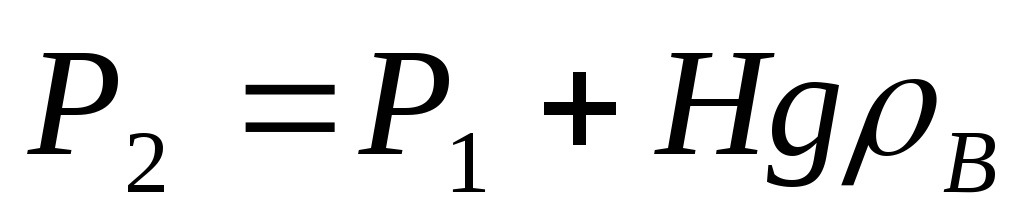и
.
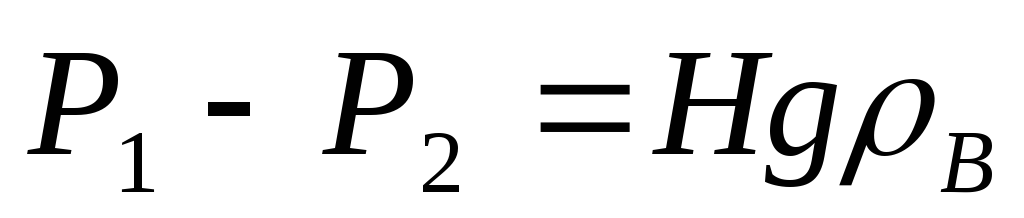С использованием
этих зависимостей уравнение Бернулли
принимает вид
.
.
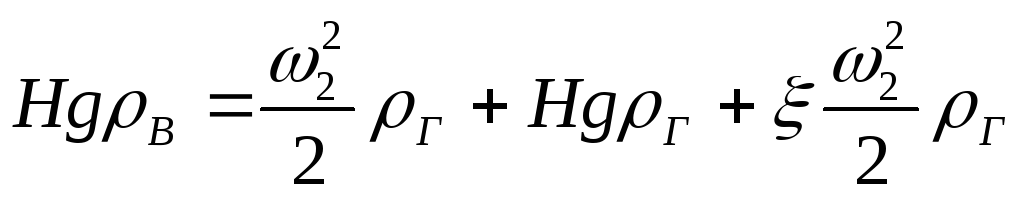
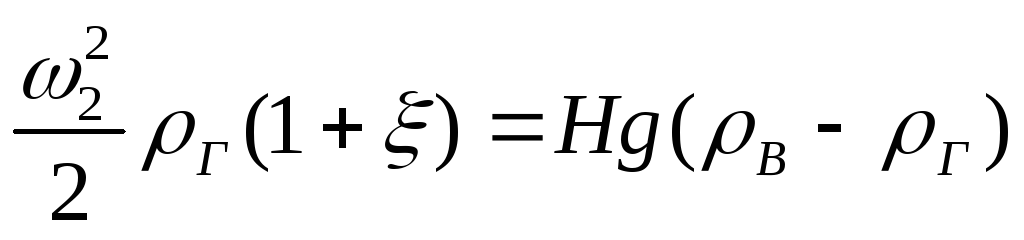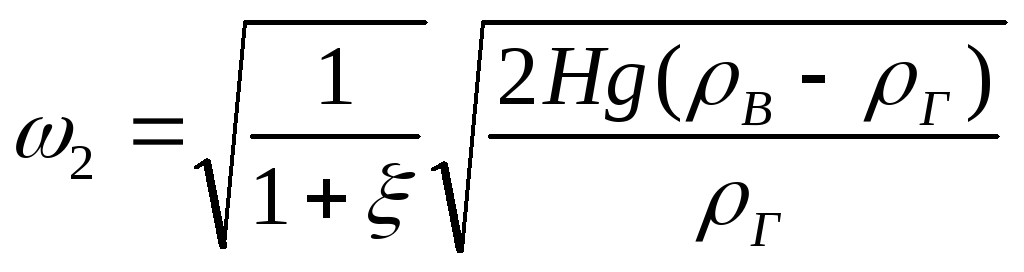(19)
Величина
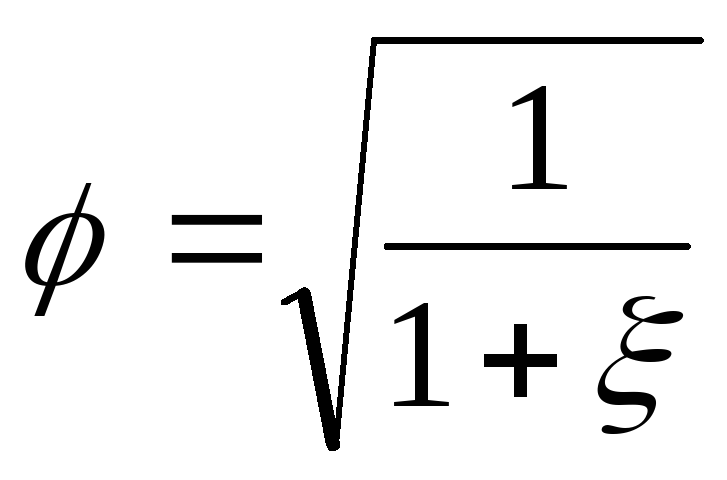учитывает
гидравлическое сопротивление отверстия,
через которое происходит истечение.
Количество истекающей из рассматриваемого
течения среды (м 3 /с)
,
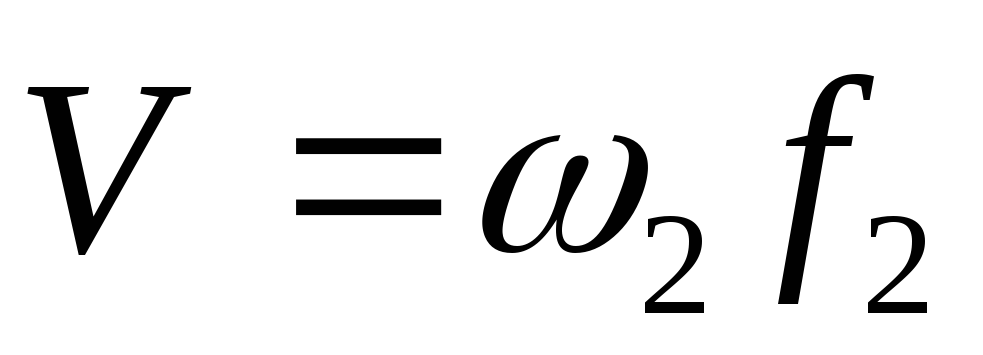где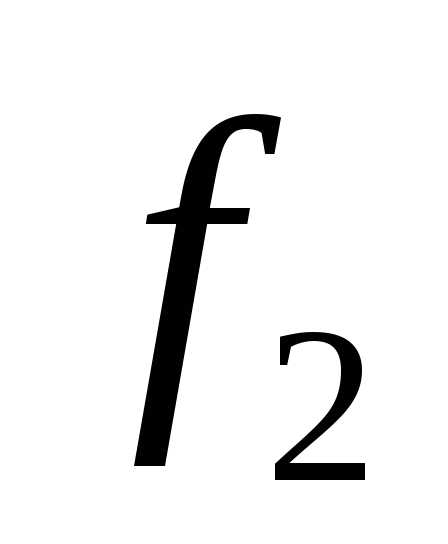
– сечение струи, м 2 .
Но если использовать
понятие коэффициента сжатия струи
,
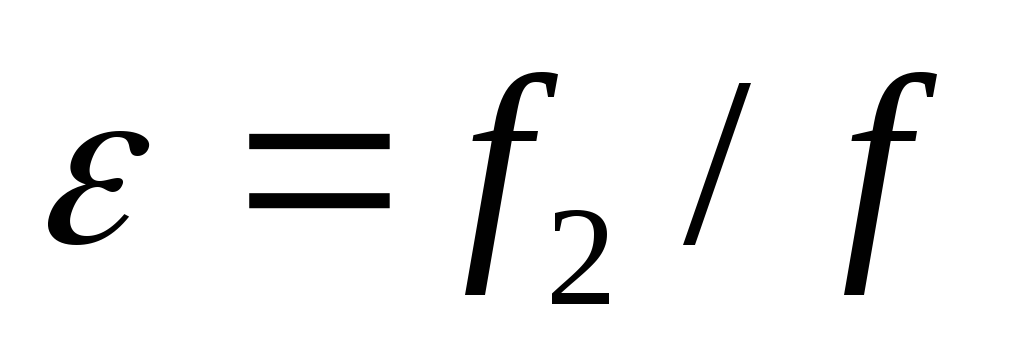то
.
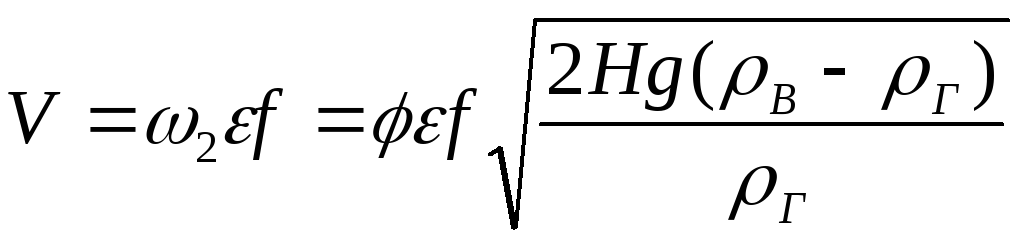Произведение
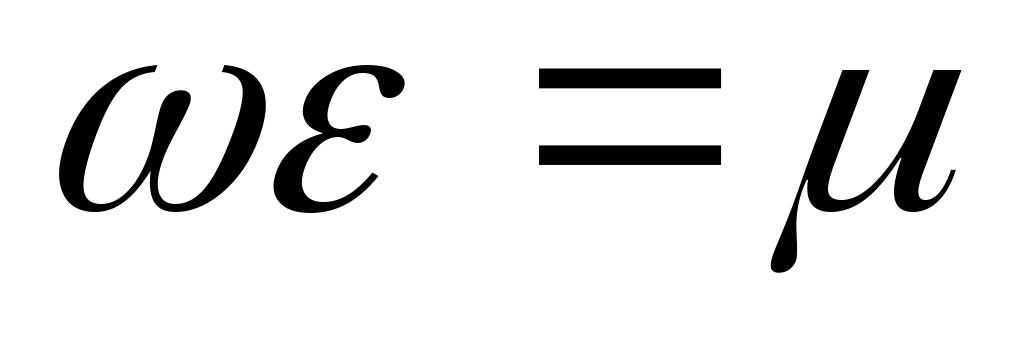называют
коэффициентом расхода.
Истечение через
насадки.
Насадкой называют
короткий патрубок, присоединенный к
отверстию в тонкой стенке. Длина насадки
обычно составляет 3 – 4 его диаметров.
Количество газа, протекающее через
насадку, при прочих равных условиях
зависит от формы входных кромок и формы
самой насадки. Рассмотрим насадки трех
видов, представленные на рис. 10. Пользуясь
уравнением (19) получим для них
следующие расчетные
формулы:
для насадки с
острыми кромками:
;
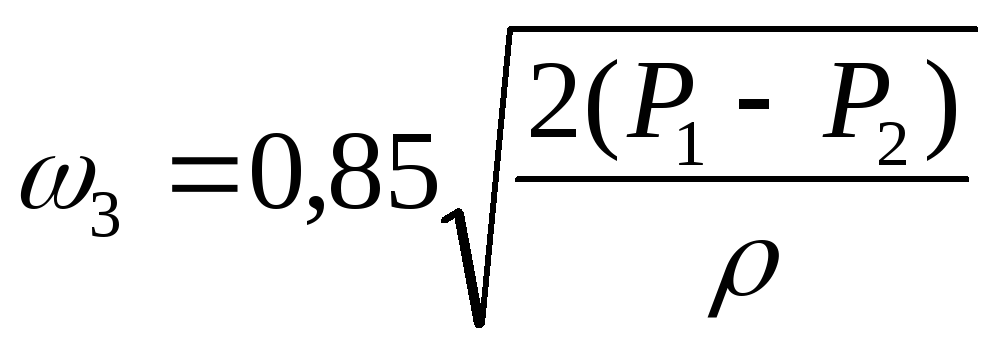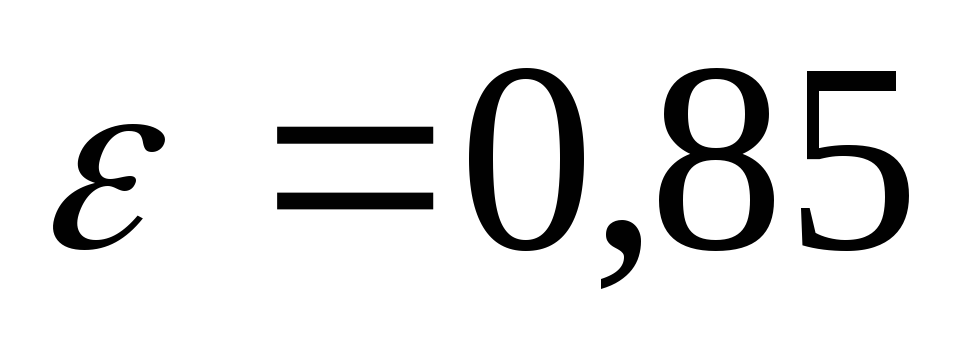(20)
.
(21)
Для насадок с
закругленными кромками и диффузора:
.
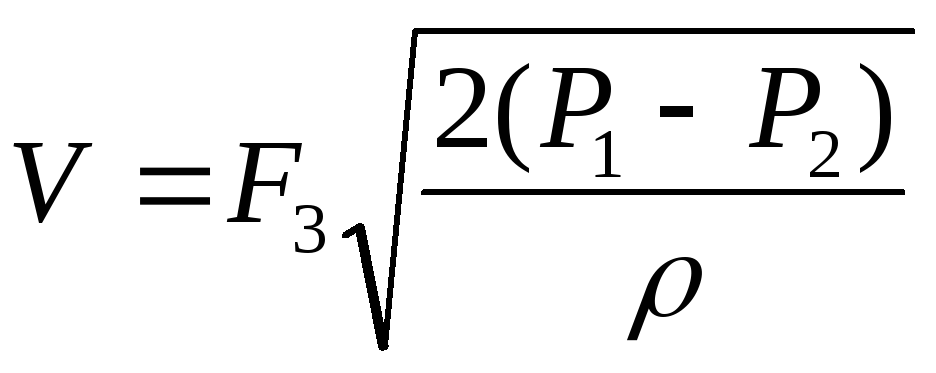(22)
Для этих насадок
в сечении
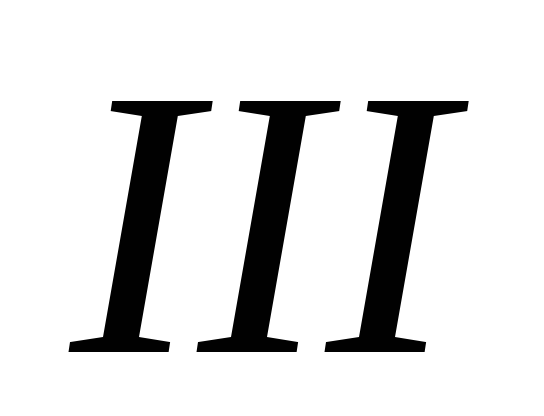сечения
струи и отверстия равны друг другу и
поэтому здесь
.
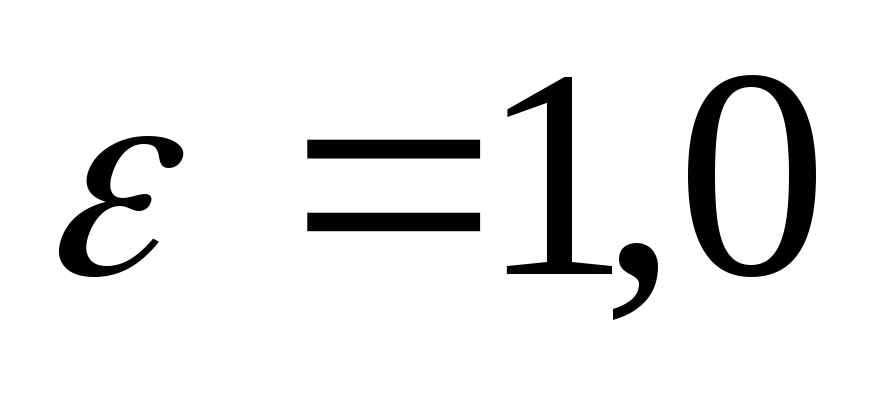Сравнение выражений (20), (21) и (22) показывает,
что наибольший расход при одинаковом
значении
и при одинаковом минимальном сечении
насадок получается при истечения газа
через диффузор, так как площадь выходного
сечения у диффузора
больше, чем у насадок других типов. Угол
конусности диффузора не должен превышать
6 – 7º во избежание отрыва потока от
стенок диффузора.
Дымовая
труба.
Дымовая труба
служит для удаления продуктов сгорания
из печи. Необходимое разрежение создается
в дымовой трубе благодаря стремлению
горячих газов подняться, обусловленному
разностью плотностей холодного наружного
воздуха и горячих газов.
Найдем зависимость
разряжения, создаваемого трубой, от
высоты трубы H
и
температуры газов. На рис. 11 представлена
схема дымовой трубы. За уровень отсчета
принимаем сечение
.
Напишем уравнение Бернулли в избыточных
давлениях для сеченийи
:
Труба в сечении
сообщается с атмосферой, поэтому
.
Из приведенного выше уравнения следует,
что пьезометрическое давление в основании
трубы
Ввиду незначительных
скоростей движения газов в трубе величины
потерь, выражаемые в правой части
приведенного выше уравнения тремя
последними членами, значительно меньше
абсолютной величины потери, выражаемой
первым членом. Следовательно,
пьезометрическое давление в основании
трубы будет отрицательным, т.е. там будет
разряжение. Умножив правую и левую части
последовательно на минус единицу,
получаем
Потери давления
в трубе
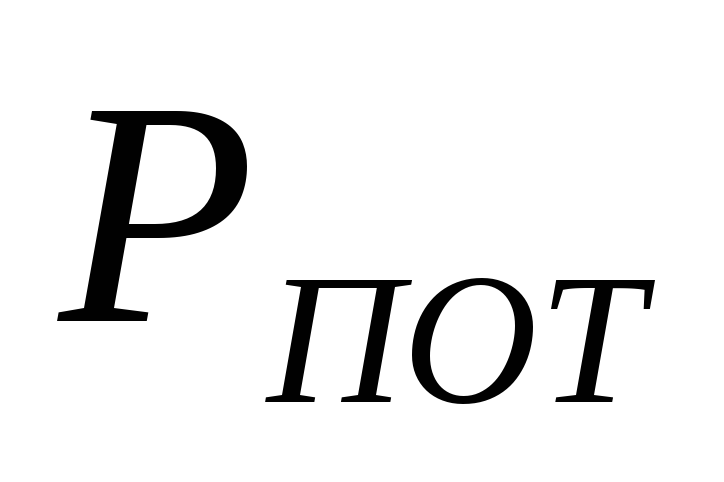складываются из потерь на трение
и потерь, возникающих при выводе газов
из трубы в атмосферу и равных
.
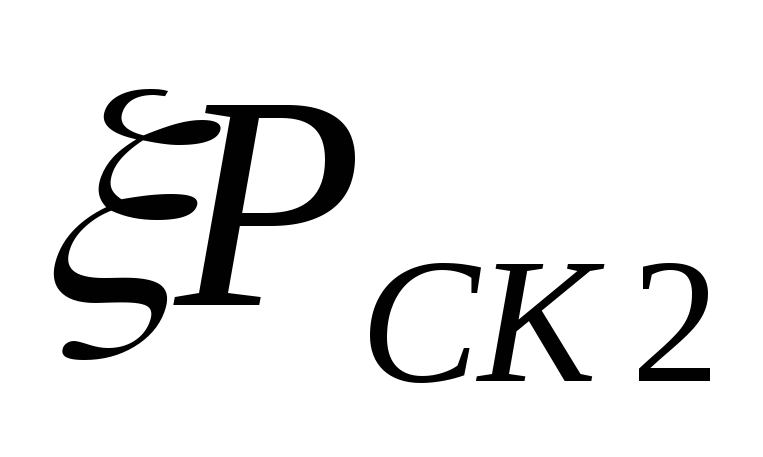Учитывая, что коэффициент местного
сопротивления на выходе из трубы равен
единице (
),
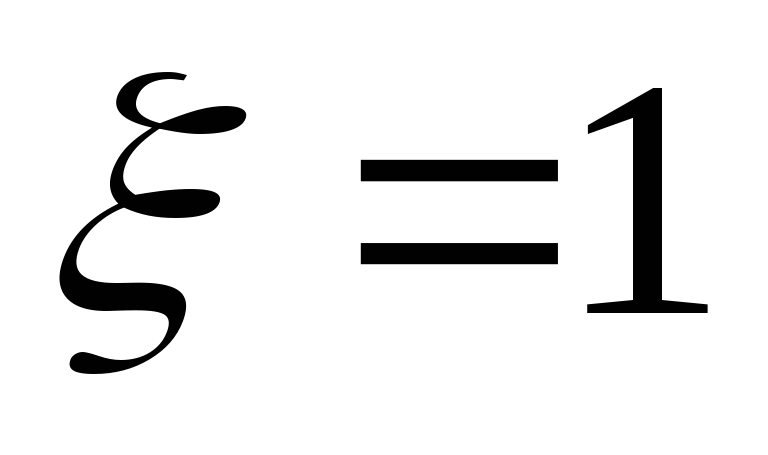можно написать, что
.
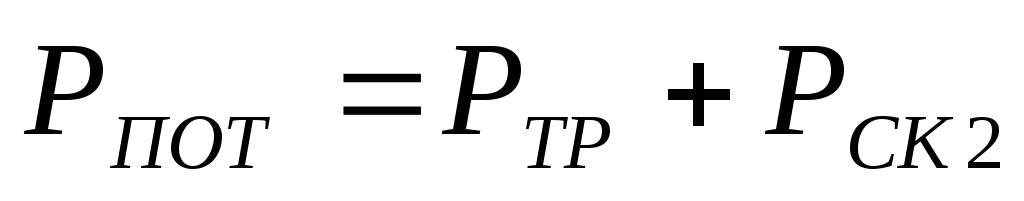Вследствие этого
уравнение (23):
Для того чтобы
получить окончательное выражение для
,
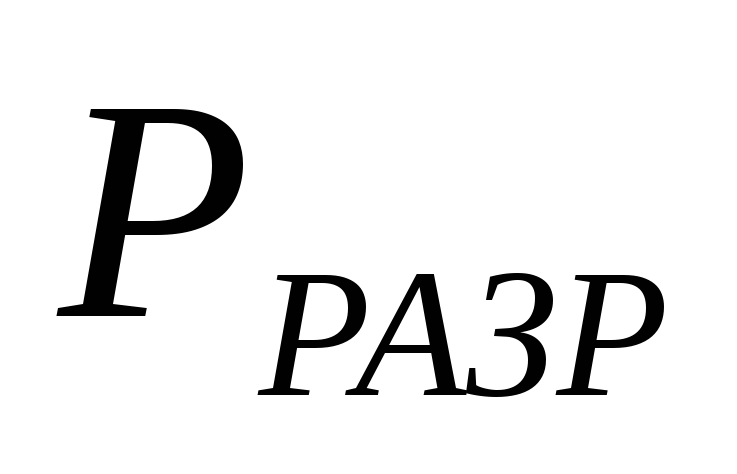в уравнение (24) необходимо подставить
все входящие в него величины. Температура
газов по высоте дымовой трубы и её
сечение существенно изменяются, поэтому
принимаемые в расчете плотность и
скорость движения газов в дымовой трубе
определяются по средней температуре
по высоте трубы. Величина геометрического
давления
,
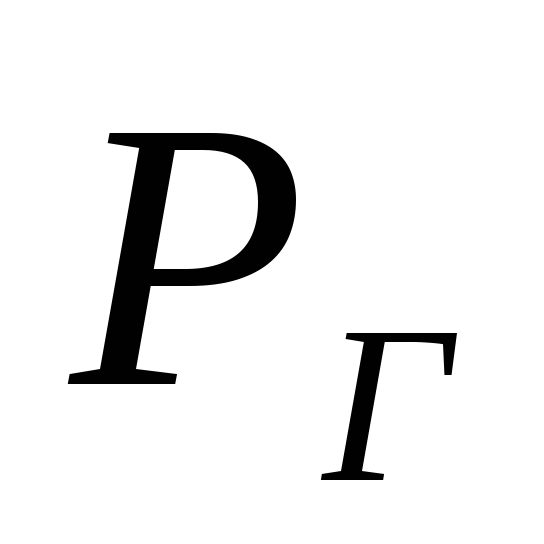входящего в уравнение (24), выражается
уравнением (3). Динамические давления
будут соответственно равны
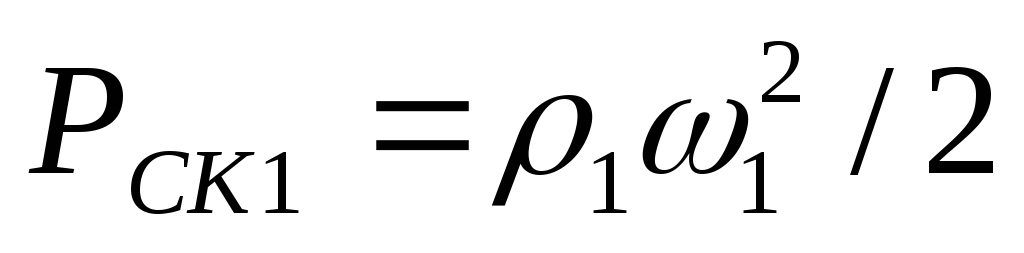и
.
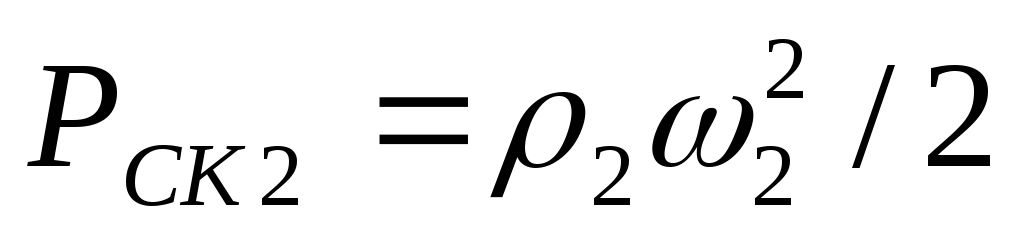Потери давления
на трение находят по уравнению
.
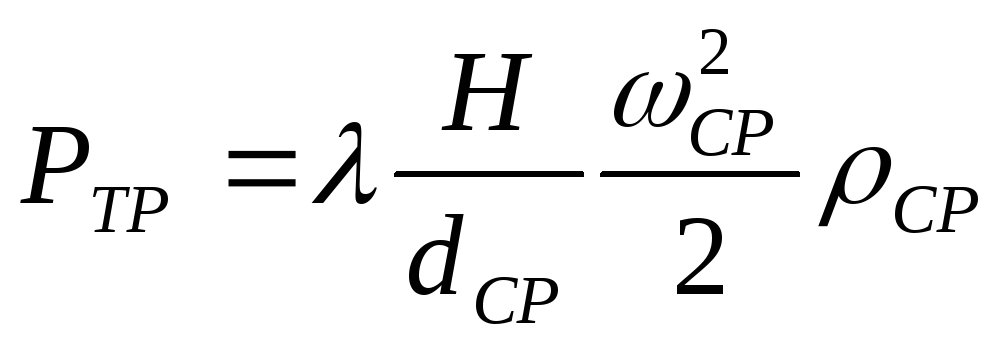Подставив в
уравнение (24) значения
,
,
,
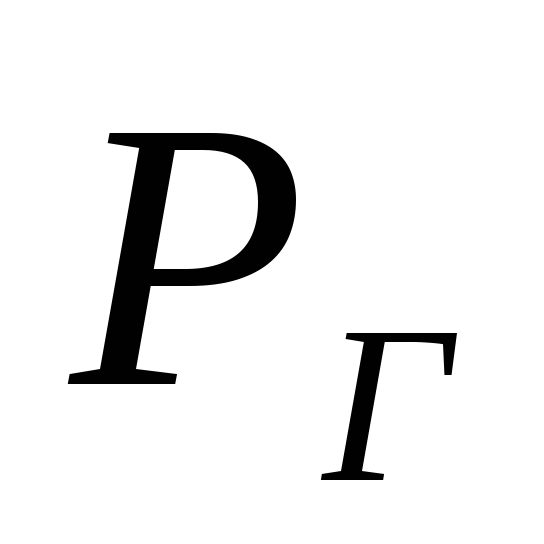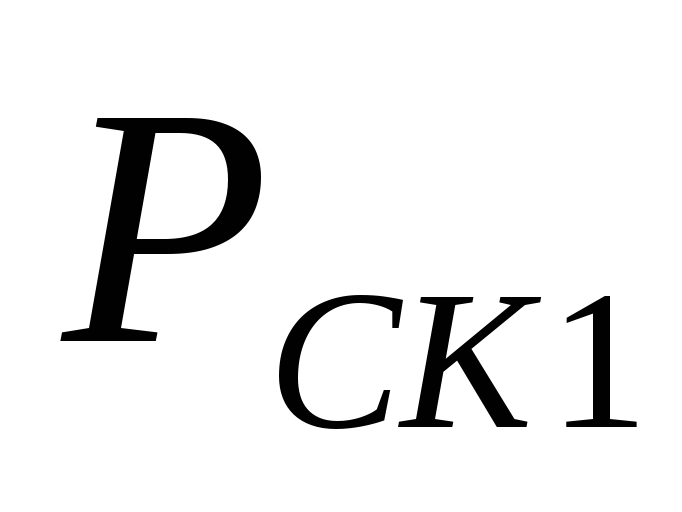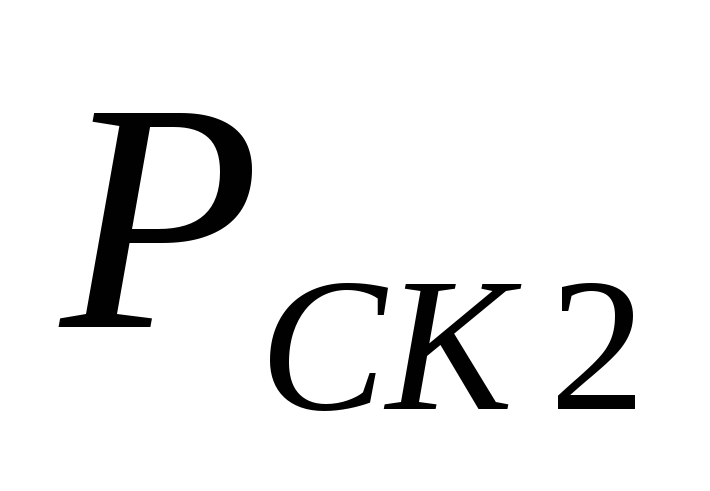и выразив их через скорости и плотности
при нормальных условиях (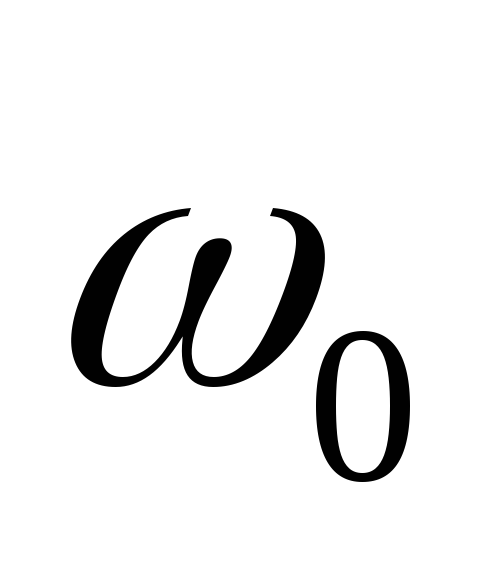и)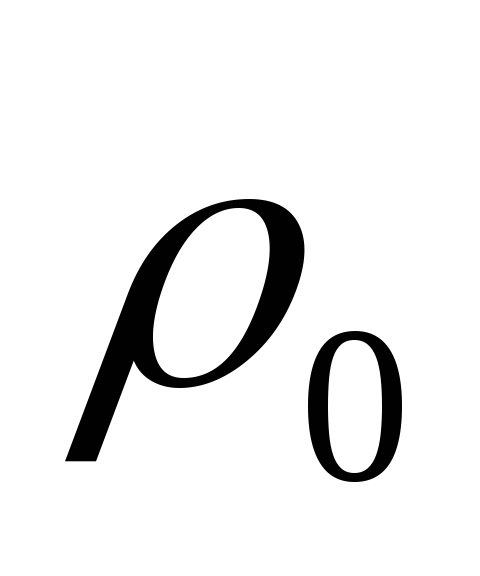
по указанным выше выражениям, окончательно
получаем (Па)
,
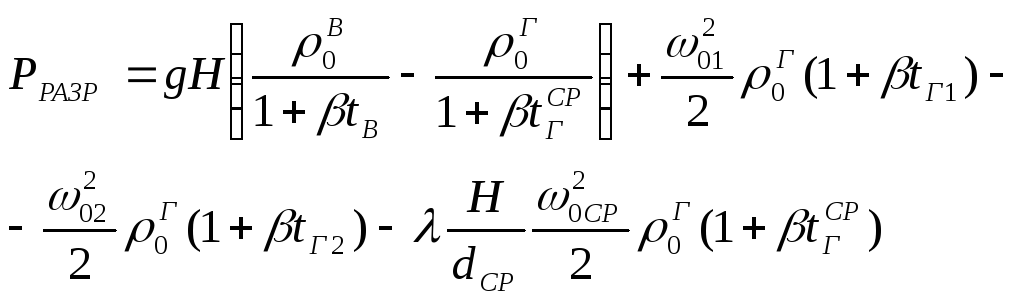(25)
где
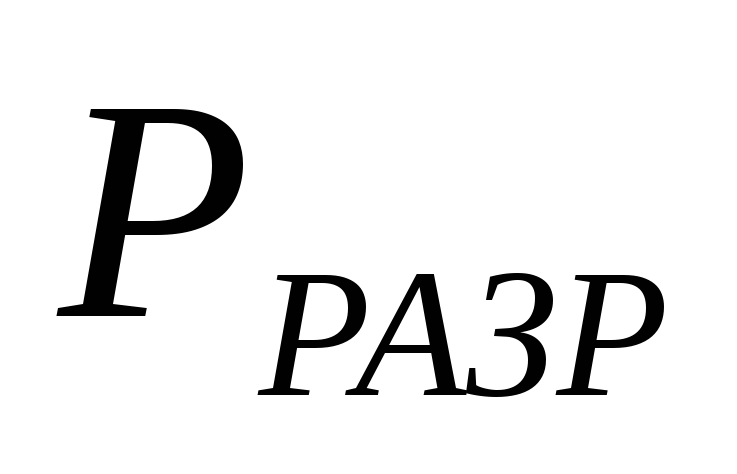– действительное разрежение трубы в
основании дымовой трубы (сечение),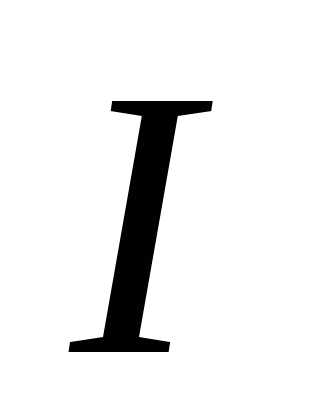
Па;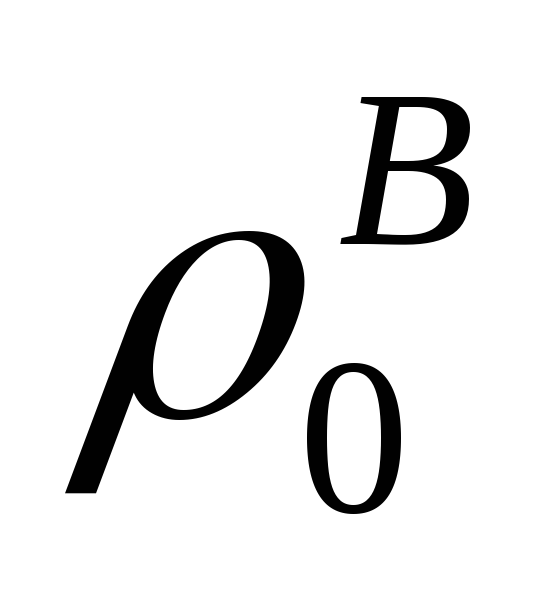
и
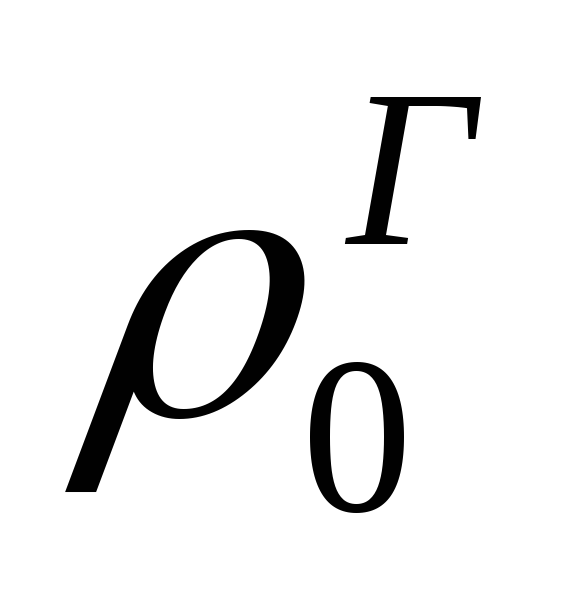– плотность соответственно воздуха и
газов при нормальных условиях, кг/м 3 ;
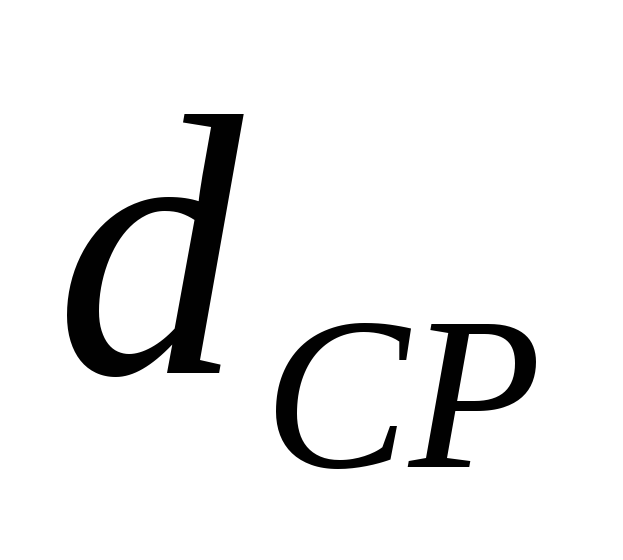– средний по высоте диаметр трубы, м;
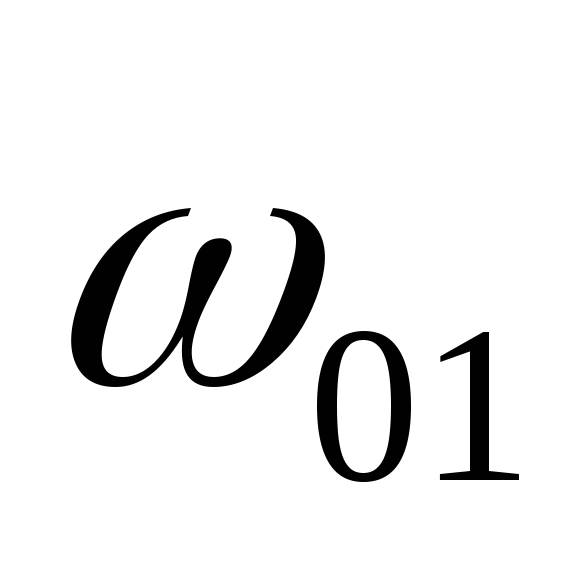и
–
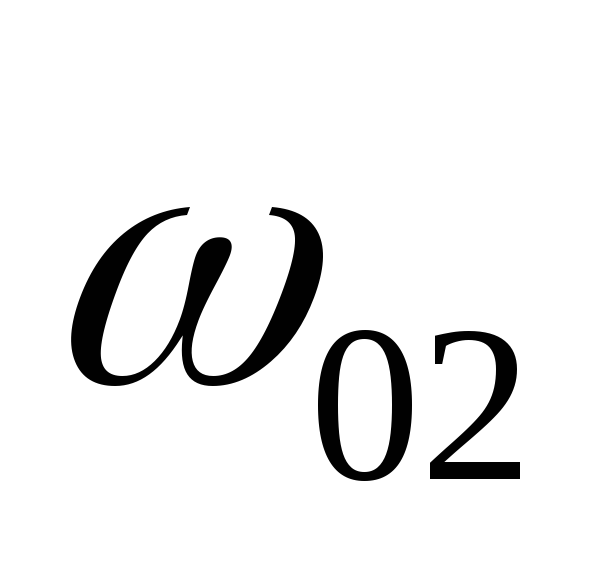скорость газов в сечениях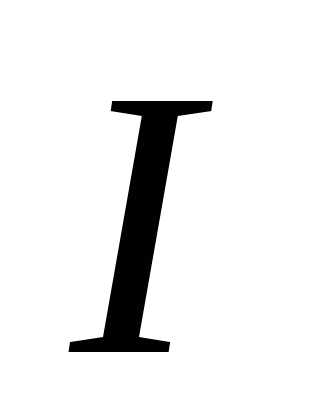(в основании трубы) и
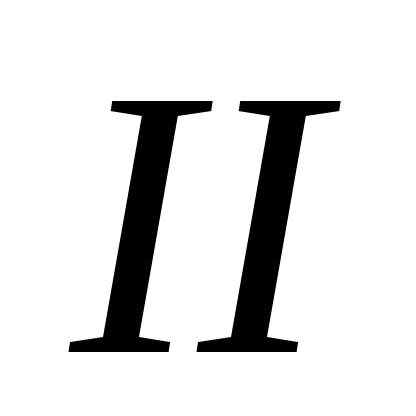(в устье трубы) при 0ºС, м/с;
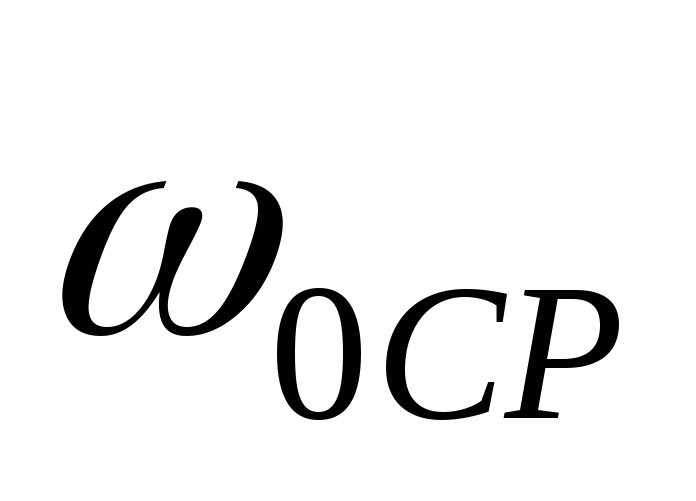– средняя скорость газов по высоте трубы
при 0ºС, м/с;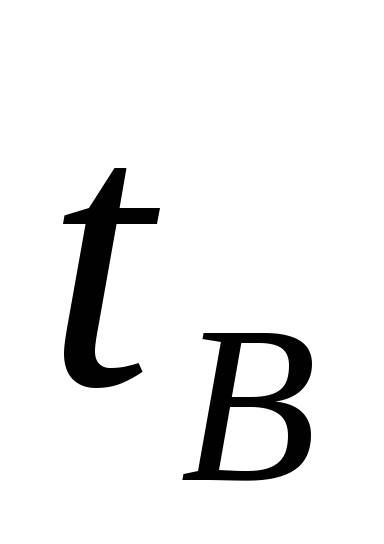
– температура окружающего воздуха, ºС;
–
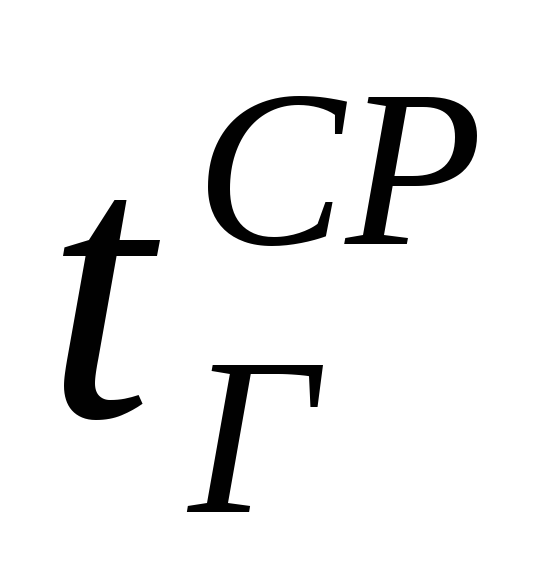средняя температура газов по высоте
трубы, ºС;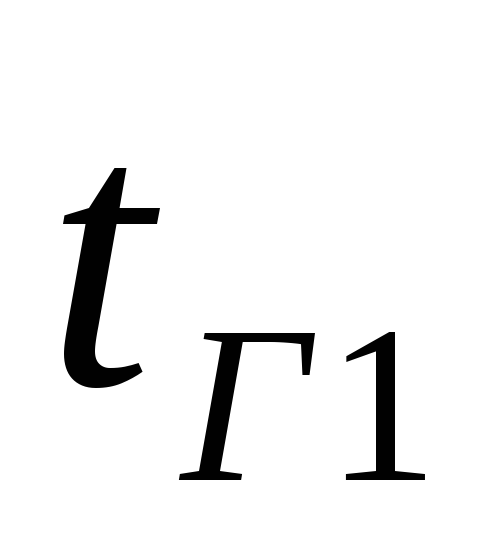
и
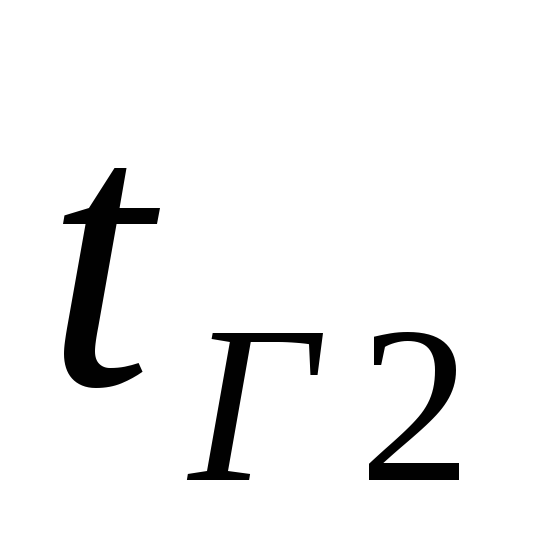– температура газов в сечениях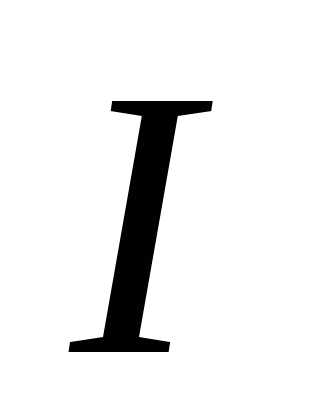и
,
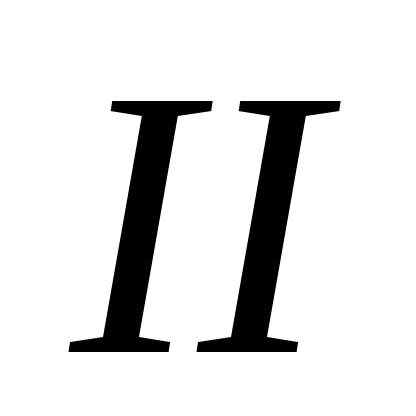ºС.
Если учесть, что
,
,
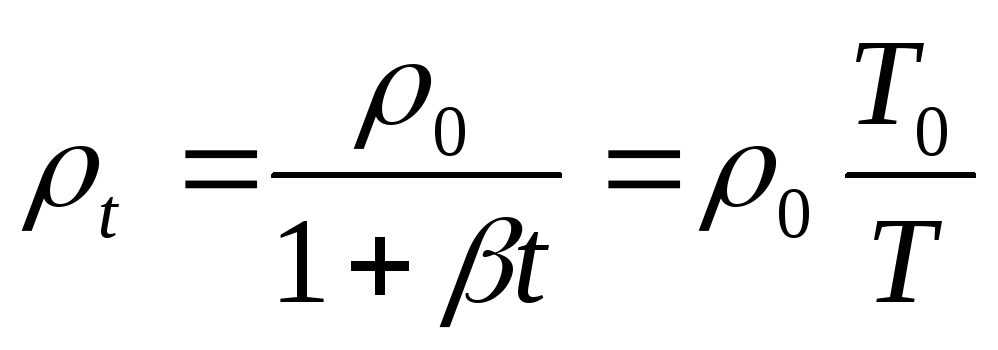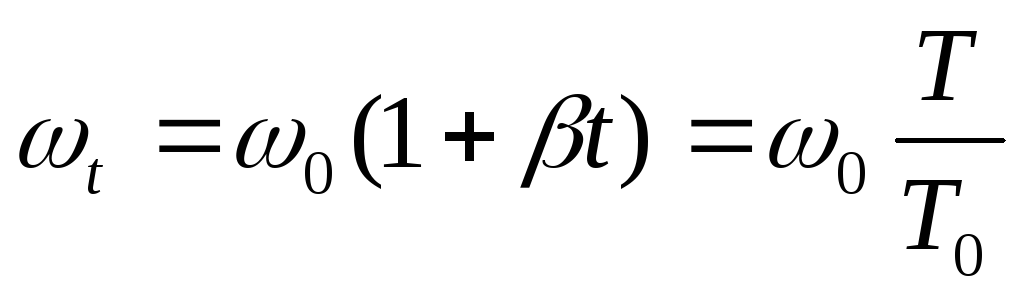где
,
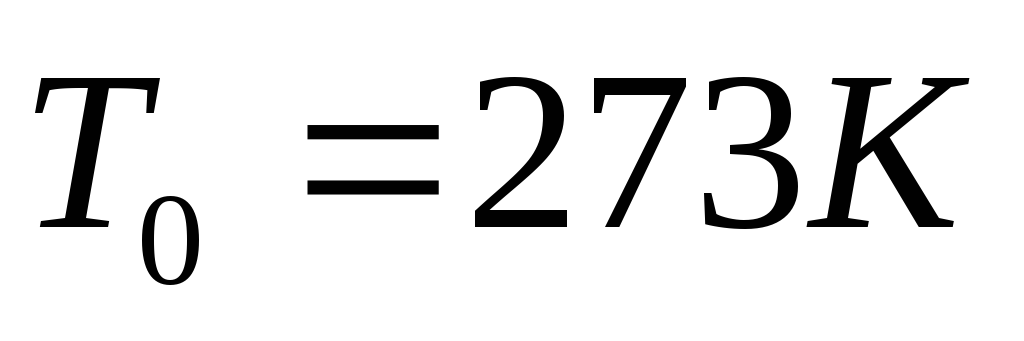то выражение (25) может быть переписано
следующим образо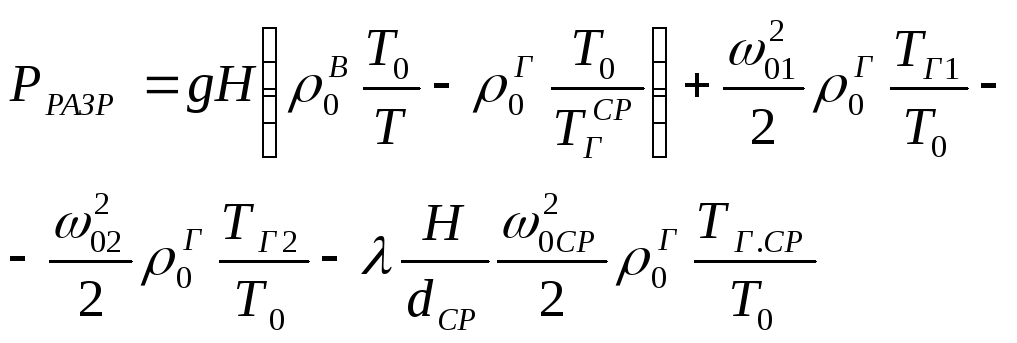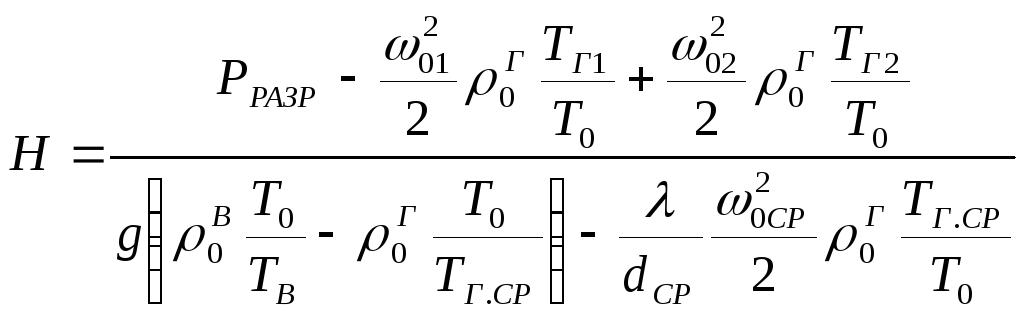м:
.
м.
(26)
В расчетах разряжение
в основании дымовой трубы принимают
обычно с запасом, равным
.
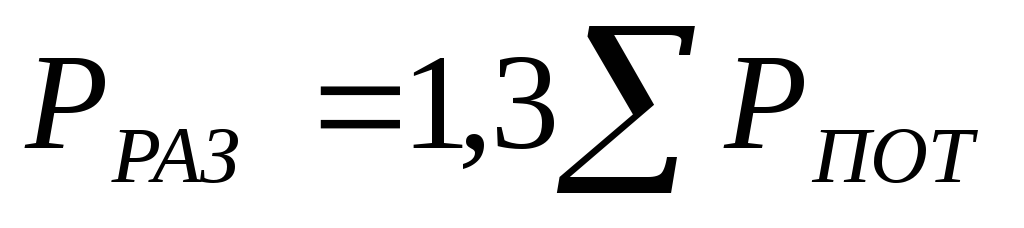Величина
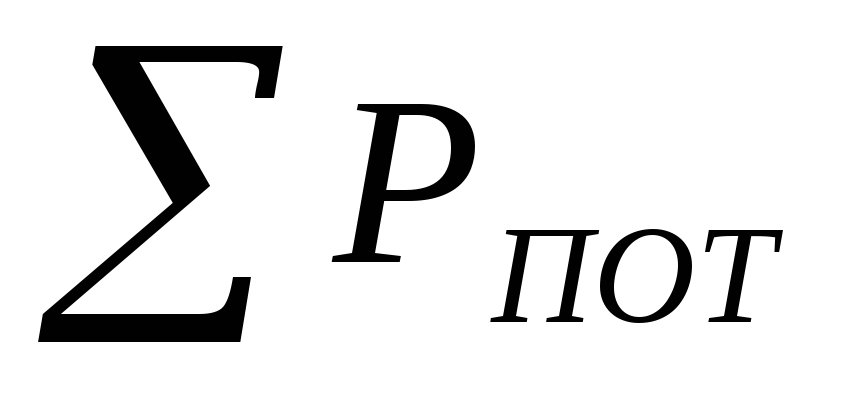представляет собой суммарные потери
давления на пути движения газов от печи
до основания дымовой трубы..
При расчете дымовой
трубы внутренний диаметр в устье ее
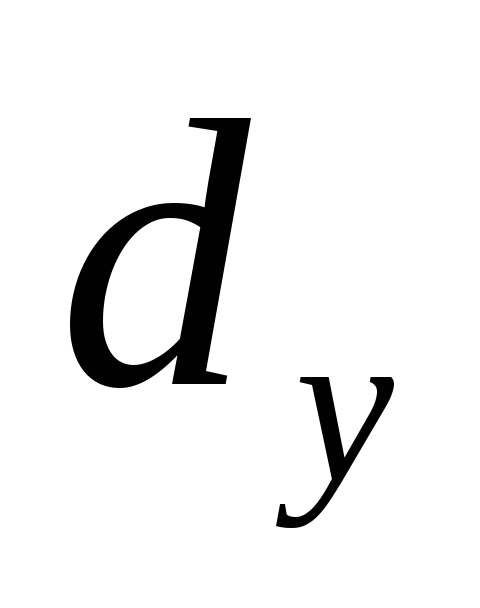(на
выходе) принимают, исходя из скорости
газов, равной 3 – 10 м/с (при скорости
выхода газов, меньшей 3 м/с, при ветре
может происходить их задувание в трубу).
Кирпичные и железобетонные дымовые
трубы для большей устойчивости делают
более широкими в основании. При расчетах
внутренний диаметр в основании трубы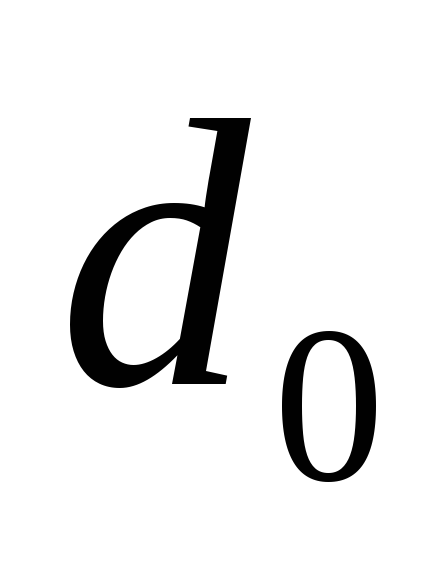
принимают в 1,5 раза больше внутреннего
диаметра устья трубы,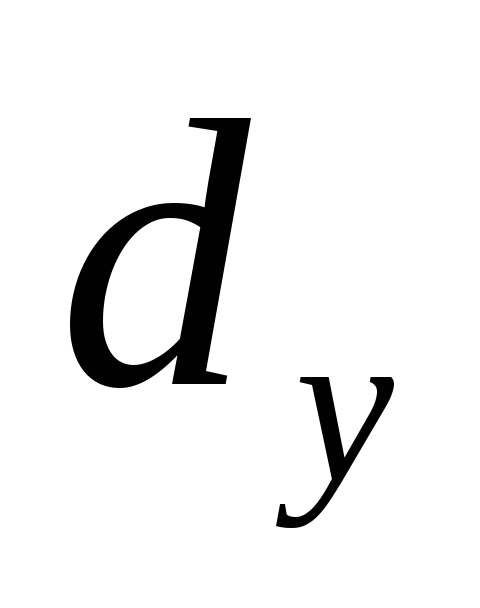
т.е.
.
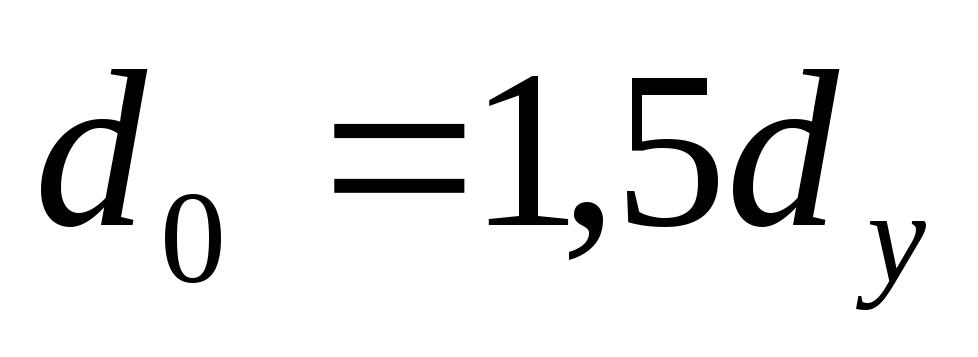По условиям
выполнения кладки
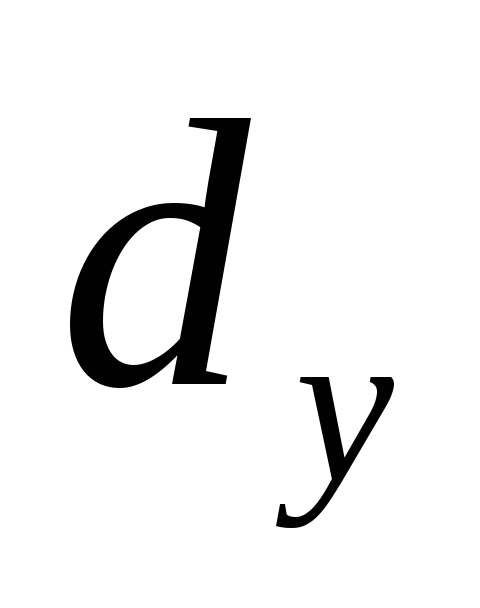для кирпичных труб не должен быть меньше
0,8 м.
Падение температуры
газов на 1 м высоты трубы принимается
для кирпичных и железобетонных 1,0 –
1,5ºС, а для металлических 3 – 4 ºС.
Ориентировочно высота трубы может быть
определена по уравнению (26) без трёх
последних его членов. Подсчитав сумму
потерь всех видов на пути движения
газов от печи до основания дымовой
трубы, по уравнению (26) находят расчетную
высоту трубы
.
Независимо от расчета высота дымовой
трубы по санитарным нормам должна быть
не менее 16 м и в 2 раза выше самого высокого
здания, находящегося в радиусе 100 м
вокруг трубы.
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются весьма малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства практических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости. При движении газа таких допущений делать нельзя. Поскольку изучение общих решений уравнений газодинамики не является предметом настоящего курса, рассмотрим лишь частные задачи, встречающиеся в практике работы специалистов горных отраслей промышленности. К числу таких первоочередных задач относится изучение движения газов, включая воздух по газопроводам (воздуховодам).
Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных потерь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наиболее простой случай газопровода (воздуховода) собранного из труб одинакового диаметра (простой газопровод S = const
) при установившемся движении газа. Тогда в соответствии с уравнением неразрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной= const.
При этом объёмный расход газа будет меняться от одного сечения газопровода к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется.
Тогда скорость движения газа также будет меняться вдоль длины газопровода:
При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движение газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т =
const
и= const.
При таких условиях будет постоянным для всего потока и число Рейнольдса, и как следствие будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
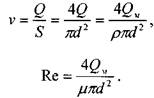
Отметим, что в последнем выражении все величины, входящие в правую часть равенства являются величинами постоянными, отсюда: Re = const
и /I = const.
По этой причине для определения величины потерь напора и расхода газа можно воспользоваться обычным уравнением Бернулли.
Основные уравнения газового потока
- Если движение газа по каналу стабильно, то одинаковое количество газа в единицу времени протекает по каждому участку канала. В этом случае (рис. 10.1), при определенном расходе газа в каждом участке канала расход газа равен(10.1). Где O-2-й массовый расход газа. Рх, РГ-площадь поперечного сечения канала. w и r-это скорости потока соответствующих поперечных сечений. Определенный объем одного и того же поперечного сечения; формула (10.1) называется уравнением неразрывности или непрерывности, поскольку постоянство массового расхода всех участков канала в каждый момент времени устанавливает условия неразрывности струи.
В рассматриваемом процессе первый закон термодинамики. Форма газа урав-кг газа через канал является = Фунт / + 4-С—(- (3% Си、 (10.2), где же буква «Л». Основное количество тепла, подаваемого или отводимого к газу в целевом участке движения. L / — изменение внутренней энергии газа в соответствующем сечении. го /. ’- Работа газа против внешних сил; С-приращение кинетической энергии газа при движении газа в выбранной области. С ^ а ^ — элемент Сила против работы тары 10.1 Этот компонент в олове; газ можно проигнорировать. Работа газа по противодействию внешним силам движущегося газа — это работа, которая тратится на прессование. Рассмотрим поток газа в канале рис.
За пределами пограничного слоя градиент скорости, нормальный к направлению потока, обычно настолько мал, что вязкостью можно пренебречь.
Людмила Фирмаль
В 1-мерном измерении stream. In в разделах/-/и 11-11 различают газы определенной массы. Поток, поступающий в секцию 1-1, действует как поршень, отталкивая газ, заполняющий канал. сила pP действует на массу газа, выделенную в левом канале, а сила (p + Lp) (P4-LR) действует справа. Учитывая признаки работы, признанные в термодинамике, работа движения является Л ’=(П 4-С / П)(П 4-ЛХ) (Н + Ла») — ППУ>-(10 3） Если вы уменьшите небольшое количество 2 или более и отбросите его, это будет выглядеть так: Л ’ — rRLchi 4-Рих / Р 4-shRLr, (10.4） L ’= pL (Pu>) 4-PsLr.
Где N-уравнение неразрывности ТЧ = ТС. Расход потока постоянн и в непрерывной среде Если мы связываем работу против внешних сил с 1 кг газа、 L ’=(1 (ri) = Рио + ойр. (U. Seven） Количество cir, масса экстрагируемого вещества Это за гранью несжимаемости. 2-й член pc1i представляет собой основную работу, выполняемую движущимся телом продукта газа в результате деформации под действием равномерно распределенного давления. При замене работы на внешние силы в уравнениях первого закона термодинамики записывается около 1 кг газа 1е = c1u + c1G + =(1и + С1 (ПУ) 4- = я(п + Пи)+.(10.8） Потому что, как известно,+ ri = I — Си+ .
- Эта формула показывает, что тепло, подводимое к движущемуся газу, расходуется в двух направлениях: увеличение энтальпии газа и увеличение внешней кинетической энергии. То есть скорость потока газа увеличивается. Формула (10.9) является основой течения газа или пара, она эффективна как для обратимых течений без действия сил трения, так и для необратимых течений с трением.
Для потока, в котором присутствует сила трения, необходимо добавить 2 члена к формуле (10.9).1 учитывает работу, затраченную на преодоление силы трения — / тр, еще 1 представляет собой приращение теплоты газового потока за счет трения-поскольку работа над силой трения проходит полностью, в тепле эти 2 элемента имеют одинаковый размер, а так как знаки различны, то они исчезают друг от друга. Поэтому наличие сил трения не может нарушить общий энергетический баланс.
Это явление, весьма важное для гидродинамики и теории теплообмена, было впервые установлено Людвигам Прандтлем в 1904 г.
Людмила Фирмаль
В изолированных потоках газа, если тепло не передается при движении газа ПО КАНАЛУ (1 / = 0）、 Из уравнения (10.10) следует, что в изолированном стационарном потоке газа через канал сумма удельной энтальпии и удельной кинетической энергии остается постоянной. Выражение (10.9), как и в (10.10), справедливо как для обратимых, так и для необратимых flows. It следует отметить, что эти формулы эффективны только в том случае, если газ на ходу выполняет работу расширения и не производит полезной (технической) работы (например, вращение рабочего класса турбины).
Приводимый в движение потоком газа. Первый закон термодинамики (10.8). Вам нужно записать В форме че = ух + ^(Р’) + ^ МС,+ — ^ г — = а + г(ТЭН+ -^ -, (10.11） Здесь/ т» — техническая работа*. Если техническая работа осуществляется потоком, то работа деформации при расширении отдается внешнему потребителю, но в канале она воспринимается соседними элементами, изменяя его кинетическую энергию. Из сравнения формулы (10.11) и формулы первого закона термодинамики (4.9) получается интегральная форма, записанная о выделенных элементах деформированного, но не смещенного потока. ’тек = С П’ ^ + P1V!-.
Смотрите также:
- Решение задач по теплотехнике
