Как найти поток мощности

А
ТАКЖЕ ПОТЕРЬ МОЩНОСТИ В СЕТИ

Расчет установившихся
режимов сложных электроэнер-
гетических
систем методом узловых напряжений
состоит из
двух частей: определения
напряжений узлов; определения
токов,
потоков и потерь мощности в ветвях.

Напряжения узлов
определяются в результате решения

системы уравнений узловых напряжений
(§
9.5- -9.8).
После
того как напряжения всех узлов
найдены, можно легко оп-

Рис.
9.4. Расчет
токов, потоков и потерь мощности в линии:

а–
токи; б-
потоки мощности; в- потоки мощности при
учете активной прово-
димости на землю

ределить
для каждой ветви ток по закону Ома, а
также по-
токи и потери мощности в
соответствии с приведенными
ниже
выражениями.

Определение
токов и потоков мощности в линии при
из-
вестных
напряжениях на ее концах.
Ток (фазный) в про-
дольной
части .линии
(рис.
9.4, а) по
закону Ома равен

(9.100)

где
,–
линейные
напряжения узлов k,
и
j;

,-
сопротивление
ветви kj;
–
взаимная

проводимость¹
узлов kj.

Ток
(рис.
9.4, а),
текущий от узла k,
в линию kj,
по
первому
закону Кирхгофа равен

(9.101)

где
-фазный
емкостный ток в начале линии kj;

–
половина
емкостной
проводимости на землю ли-
нии
kj;

.

Ток
,
текущий из линии kj
к узлу
j,
равен

(9.102)

Мощность трех фаз
в начале продольной части линии kj,

т.
е.
текущая по продольной части линии от
узла k
к узлу
j

(рис.
9.4,6), равна

(9.103)

Мощность в конце
продольной части линии kj,
т. е. под-
текающая
по продольной части линии от узла k
к узлу
j

(рис.
9.4, б),
равна

(9.104)

Потери мощности
в продольной части линии kj
(в со-
противлении
)
равны разности потоков мощности в
на-
чале
и в конце линии, т. е.

(9.105)

В последнем
выражении учтено, что произведение
ком-
плексно-сопряженных
чисел равно квадрату их модуля.

Мощность, текущую
от узла k
в линию kj
(рис.
9.4, б),

можно
получить из
(9.101):

(9.106)

Мощность, текущая
к узлу
j
из линии kj,
в соответствии
с
(9.102) равна

(9.107)

Потери мощности
в линииkj
включают как потери
в
продольной части линии
,
так и реактивную мощность,
генерируемую
в начале и в конце линии. Потери

мож-
но
определить как разность потоков мощности,
текущих от
узла
k
в линию
kj
и из линии kj
к узлу
j:

(9.108)

Если просуммировать
эти выражения по всем ветвям
сложной
системы, то получим выражение для
суммарных
потерь
мощности электрической системы.

В тех случаях,
когда в схеме замещения линии учиты-
вается
и активная проводимость на землю (рис.
9.4, в),

в
выражениях
(9.101), (9.102), (9.106)-
(9.108)
следует

+j
заменить на комплексные проводимости
на землю

.

Активные и реактивные
составляющие потоков мощно-
сти в
продольной части линии (рис.
9.4, б) можно
опреде-
лить по выражениям
(9.103), (9.104).
Например, из
(9.103)
следует

(9.109)

(9.110)

где
,
–
активная
и реактивная мощности в начале
продольной
части линии kj,

,
–
активная
и реактив-
ная составляющие тока в
линии kj;
,

– активная
и ре-
активная составляющие напряжения
узла k.

Составляющие тока
в линии kj
можно определить сле-
дующим образом:

(9.111)

(9.112)

где
,

– активная
и реактивная составляющие взаим-
ной
проводимости между узлами k
и j
(равна проводимости
ветви kj
с обратным знаком).

Потери мощности
в активном и индуктивном сопротив-
лениях
линии, т.е.
в ее продольной части, равны разности

потоков мощности в начале и в конце
продольной части ли-
нии (рис.
9.4,6).
Суммарные потери мощности в продоль-
ной
части электрической сети можно определить,
просумми-
ровав
потери мощности в продольной части всех
линий, т. е.

по
следующему выражению:

(9.113)

где суммирование
ведется по всем ветвям сети.

Суммарные потери
мощности в сети
,
т. е. в ее про-
дольной
и поперечной частях, получаются в
результате до-
бавления
к
(9.113)
реактивной мощности, генерируемой
в
емкостных проводимостях линий.

Часто используется
выражение потерь мощности в виде

квадратичной
формы от узловых напряжений. Потери
мощ-
ности
равны разности между мощностями
генераторов и на-
грузок
в узлах. Если для генерирующего узла
мощность
и
ток принимаются со знаком плюс, а для
нагрузочного-

со знаком
минус, то потери мощности в сети с n+1
узлами
определяются
так:

(9.114)

Подчеркнем, что

–
это
суммарные потери в про-
дольной
и поперечной частях сети.

В матричном виде
(9.114) можно
записать следующим
образом:

(9.115)

где
–
вектор-строка
сопряженных узловых токов раз-
мерности
(п+1);

–
вектор-столбец
комплексных узло-
вых
напряжений размерности (п+1);
индекс «т» означает
транспонирование
матрицы.

Уравнение узловых
напряжений с учетом правил дейст-
вий
с матрицами можно записать в следующем
виде:

(9.116)

Если подставить
(9.116) в
(9.115), потери
мощности
можно вычислить по следующей
формуле:

(9.117)

где

–
полная
комплексная матрица узловых проводи-
мостей
размерности (п+1).

Выражение в правой
части
(9.117)
называется квадра-
тичной формой от
напряжений. Если обозначим

то из
(9.108) получим
следующие выражения для потерь
активной
и реактивной мощностей:

(9.118)

(9.119)

В
(9.118), (9.119)
опущен индекс транспонирования
у
матриц
ив силу их симметричности. В
(9.118),
(9.119)
потери определяются как квадратичные
формы от
активных и реактивных
составляющих напряжений узлов.
Если
использовать полную матрицу собственных
и вза-
имных сопротивлении
узлов

размерности(п+1),
то из
(9.115)
получим аналогично
(9.117)
выражение потерь в ви-
де квадратичной
формы от токов в узлах:

(9.120)

Выразив в
(9.120) токи
в узлах через мощности в узлах

;
.

получим следующее
выражение потерь мощности в сети:

(9.121)

где

–
вектор-строка
комплексных узловых мощностей
размерности
(п+1);

–
вектор-столбец
сопряженных уз-
ловых мощностей
размерности (п+1);

–
диагональные
матрицы размерности (п+1),
k-е
элементы
которых равны соответственно
и.

Пример
9,11. Для
схемы на рис.
9.2 вычислим
токи, потоки и поте-
ри мощности по
линиям при исходных данных, приведенных
в примере
9.7,
и напряжениях узлов, определенных в
примере
9.10.

Модули, кВ,
и фазы, град, напряжений узлов:

115;

=
115,415;
=
109,721;
=0;

=
0,1352;
=-
2,
1553.

Активные и реактивные
составляющие напряжений, кВ, равны

=
115;
=
115,4146;

=
109,6434;

=0;

=
0,2723;
=-4,1264.

Взаимные проводимости
узлов, 1/Ом:

=-0,02;

=-0,04;

=-0,0133;

=-0,0267;

=-0,0138;

=-0,0345.

Примем направления
токов и потоков мощности, как указано
на рис.
9.2. Вычислим
токи по линиям, кА,
используя формулы
(9.111) и
(9.112):

=
0,1047;

=-0,0509;

=
0.1336;

=-0,0799.

Определим потоки
мощности, МВт и Мвар,
по формулам типа
(9.109)
и
(9.110). За
положительное направление потоков
мощности
,

принято направление от узлаk
к
j.
Полученный в результате
вычисления
по
(9.109) или
(9.110) знак
илипоказывает, сов-
падает ли фактическое
направление потоков мощности с принятым:

Определим по
(9.104) потери
активной и реактивной мощностей
в
каждой ветви и суммарные потери, МВт и
Мвар:

Пример
9.12. Для
схемы на рис.
9.2 вычислить
потери мощности по
формулам
(9.118) и
(9.119).

1.
Вычислим собственные проводимости
узлов,
1/Ом:

2.
Составим
матрицы:

3.
Векторы

и

имеют следующий вид:

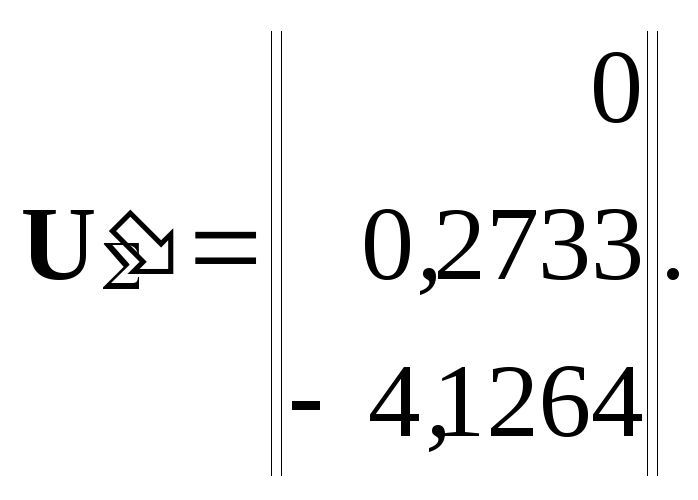
4.
Определим потери активной мощности:

5.
Вычислим потери реактивной мощности:

Потери активной и
реактивной мощностей совпадают с
результатом
примера
9.11.

В энергетика, то исследование потока мощности, или исследование потока нагрузки, это численный анализ потока электроэнергии во взаимосвязанной системе. В исследовании потока мощности обычно используются упрощенные обозначения, такие как однолинейная схема и единичная система, и фокусируется на различных аспектах Мощность переменного тока параметры, такие как напряжения, углы напряжения, активная мощность и реактивная мощность. Он анализирует энергосистемы в нормальном установившемся режиме.

Исследования потоков мощности или нагрузки важны для планирования будущего расширения энергосистем, а также для определения наилучшей работы существующих систем. Основная информация, полученная при исследовании потока мощности, – это величина и фазовый угол напряжения на каждом автобус, а также реальную и реактивную мощность, протекающую по каждой линии.

Коммерческие энергосистемы обычно слишком сложны, чтобы их можно было решить вручную. Спец. Назначение сетевые анализаторы были построены между 1929 и началом 1960-х годов для создания лабораторных физических моделей энергосистем. Крупномасштабные цифровые компьютеры заменили аналоговые методы численными решениями.

В дополнение к исследованию потока мощности компьютерные программы выполняют связанные вычисления, такие как короткое замыкание анализ неисправностей, исследования устойчивости (переходные и установившиеся), обязательство установки и экономическая отправка.^[1] В частности, некоторые программы используют линейное программирование найти оптимальный поток мощности, условия, которые дают самую низкую стоимость за киловатт-час доставлен.

Исследование потока нагрузки особенно важно для системы с несколькими центрами нагрузки, такой как нефтеперерабатывающий комплекс. Исследование потока мощности – это анализ способности системы адекватно питать подключенную нагрузку. Общие системные потери, а также потери отдельных линий также сведены в таблицу. Положения ответвлений трансформатора выбираются для обеспечения правильного напряжения в критических местах, например, в центрах управления двигателями. Выполнение исследования потока нагрузки в существующей системе дает представление и рекомендации относительно работы системы и оптимизации настроек управления для получения максимальной производительности при минимизации эксплуатационных расходов. Результатом такого анализа являются активная мощность, реактивная мощность, величина и фазовый угол. Кроме того, вычисления потока мощности имеют решающее значение для оптимальная работа групп энергоблоков.

С точки зрения подхода к неопределенностям исследование потока нагрузки можно разделить на детерминированный поток нагрузки и связанный с неопределенностью поток нагрузки. Детерминированное исследование потока нагрузки не принимает во внимание неопределенности, возникающие как от выработки электроэнергии, так и от поведения нагрузки. Чтобы принять во внимание неопределенности, было использовано несколько подходов, таких как вероятностный, возможностный, теория информационного разрыва, робастная оптимизация и интервальный анализ.^[2]

В Инициатива по моделированию открытой энергии продвигает Открытый исходный код модели потока-нагрузки и другие типы моделей энергосистем.

Модель

An модель потока мощности переменного тока модель, используемая в электротехнике для анализа электрические сети. Он обеспечивает нелинейная система который описывает поток энергии через каждую линию передачи. Проблема является нелинейной, потому что поток мощности в импеданс нагрузки является функцией квадрата приложенных напряжений. Из-за нелинейности во многих случаях анализ большой сети с помощью модели потока мощности переменного тока невозможен, и вместо этого используется линейная (но менее точная) модель потока мощности постоянного тока.

Обычно анализ трехфазной системы упрощается, если предположить сбалансированную нагрузку всех трех фаз. Предполагается установившийся режим работы без переходных изменений потока мощности или напряжения из-за изменений нагрузки или генерации. Системная частота также считается постоянной. Дальнейшее упрощение – использование единичная система для представления всех напряжений, потоков мощности и импедансов, масштабируя фактические значения целевой системы до некоторой удобной базы. Система однолинейная схема является основой для построения математической модели генераторов, нагрузок, шин и линий передачи системы, а также их электрических сопротивлений и номиналов.

Постановка задачи потока мощности

Цель исследования потока мощности – получить полную информацию об угле и величине напряжений для каждой шины в энергосистеме для заданных условий нагрузки и реальной мощности и напряжения генератора.^[3] Как только эта информация известна, можно аналитически определить поток активной и реактивной мощности в каждой ветви, а также выходную реактивную мощность генератора. Из-за нелинейного характера этой проблемы численные методы используются для получения решения, которое находится в пределах допустимого отклонения.

Решение проблемы потока мощности начинается с определения известных и неизвестных переменных в системе. Известные и неизвестные переменные зависят от типа шины. Шина без подключенных к ней генераторов называется шиной нагрузки. За одним исключением, шина, к которой подключен хотя бы один генератор, называется шиной генератора. Исключение составляет одна произвольно выбранная шина с генератором. Этот автобус упоминается как слабый автобус.

В задаче потока мощности предполагается, что реальная мощность п_D и реактивная мощность Q_D на каждой шине нагрузки известны. По этой причине грузовые автобусы также известны как автобусы PQ. Для генераторных автобусов предполагается, что реальная генерируемая мощность п_г и величина напряжения |V| известен. Для Slack Bus предполагается, что величина напряжения |V| и фаза напряжения Θ известны. Следовательно, для каждой шины нагрузки и величина напряжения, и угол неизвестны и должны быть решены; для каждой шины генератора необходимо определить угол напряжения; для Slack Bus нет переменных, которые необходимо решить. В системе с N автобусы и р генераторы, тогда есть неизвестные.

Чтобы решить неизвестные, должно быть уравнения, которые не вводят никаких новых неизвестных переменных. Возможные уравнения для использования – это уравнения баланса мощности, которые можно записать для активной и реактивной мощности для каждой шины. Уравнение баланса реальной мощности выглядит следующим образом:

где чистая активная мощность, подаваемая на шину я, реальная часть элемента в матрица пропускной способности шины Y_{Автобус} соответствующий ряд и столбец мнимая часть элемента в Y_{Автобус} соответствующий ряд и столбец и разница в угле напряжения между и Автобусы (). Уравнение баланса реактивной мощности:

где чистая реактивная мощность, подаваемая на шину я.

Включенные уравнения представляют собой уравнения баланса реальной и реактивной мощности для каждой шины нагрузки и уравнение баланса реальной мощности для каждой шины генератора. Для шины генератора записывается только уравнение баланса реальной мощности, поскольку вводимая чистая реактивная мощность предполагается неизвестной, и поэтому включение уравнения баланса реактивной мощности приведет к появлению дополнительной неизвестной переменной. По тем же причинам для Slack Bus не написано никаких уравнений.

Во многих системах передачи полное сопротивление линий электропередачи является чисто индуктивным, то есть фазовые углы импеданса линий электропередачи обычно относительно велики, близки к 90 градусам. Таким образом, существует сильная связь между реальной мощностью и углом напряжения, а также между реактивной мощностью и величиной напряжения, в то время как связь между реальной мощностью и величиной напряжения, а также реактивной мощностью и углом напряжения является слабой. В результате реальная мощность обычно передается от шины с более высоким углом напряжения к шине с меньшим углом напряжения, а реактивная мощность обычно передается от шины с более высокой величиной напряжения на шину с более низкой величиной напряжения. Однако это приближение не выполняется, когда фазовый угол импеданса линии питания относительно мал.^[4]

Метод решения Ньютона – Рафсона

Существует несколько различных методов решения полученной нелинейной системы уравнений. Самый популярный из них известен как метод Ньютона – Рафсона. Этот метод начинается с первоначальных предположений всех неизвестных переменных (величины и углов напряжения на шинах нагрузки и углов напряжения на шинах генератора). Далее Серия Тейлор записывается с игнорированием членов более высокого порядка для каждого из уравнений баланса мощности, включенных в систему уравнений. В результате получается линейная система уравнений, которая может быть выражена как:

где и называются уравнениями рассогласования:

и матрица частных производных, известная как Якобиан:.

Линеаризованная система уравнений решается для определения следующего предположения (м + 1) величины напряжения и углов на основе:

Процесс продолжается до тех пор, пока не будет выполнено условие остановки. Обычным условием остановки является прекращение, если норма из уравнений рассогласования ниже указанного допуска.

Примерный план решения проблемы потока мощности:

1. Сделайте первоначальное предположение обо всех неизвестных величинах и углах напряжения. Обычно используется «плоский пуск», при котором все углы напряжения установлены на ноль, а все величины напряжения установлены на 1,0 о.е.
2. Решите уравнения баланса мощности, используя самые последние значения угла и величины напряжения.
3. Выполните линеаризацию системы вокруг самых последних значений угла и величины напряжения.
4. Найдите изменение угла и величины напряжения
5. Обновите величину напряжения и углы
6. Проверьте условия остановки, если они выполнены, то прекратите, иначе перейдите к шагу 2.

Другие методы потока мощности

• Метод Гаусса – Зейделя: Это самый ранний разработанный метод. Он показывает более медленную скорость сходимости по сравнению с другими итерационными методами, но использует очень мало памяти и не требует решения матричной системы.
• Метод быстрой развязки нагрузки и потока представляет собой разновидность Ньютона-Рафсона, которая использует приблизительное разделение активных и реактивных потоков в электрических сетях с хорошим поведением и дополнительно фиксирует значение Якобиан во время итерации, чтобы избежать дорогостоящих разложений матриц. Также называется «NR с фиксированным наклоном и развязкой». В рамках алгоритма матрица Якоби инвертируется только один раз, и есть три предположения. Во-первых, проводимость между автобусами равна нулю. Во-вторых, величина напряжения на шине – одна на единицу. В-третьих, синус фаз между шинами равен нулю. Быстрый независимый поток нагрузки может вернуть ответ в течение нескольких секунд, тогда как метод Ньютона-Рафсона занимает гораздо больше времени. Это полезно для управления электросетями в реальном времени.^[5]
• Метод голоморфного вложения нагрузочного потока: Недавно разработанный метод, основанный на передовых методах комплексного анализа. Он является прямым и гарантирует расчет правильной (оперативной) ветви из множества решений, присутствующих в уравнениях потока мощности.

Поток мощности постоянного тока

Поток нагрузки постоянного тока дает оценку потоков мощности в линиях в энергосистемах переменного тока. Поток нагрузки постоянного тока смотрит только на активная мощность течет и пренебрегает Реактивная сила потоки. Этот метод является неитерационным и абсолютно сходящимся, но менее точным, чем решения AC Load Flow. Постоянный ток нагрузки используется везде, где требуются повторяющиеся и быстрые оценки расхода нагрузки.^[6]

использованная литература

6-я лекция.

23.03.12

6. КИНЕМАТИКА И ДИНАМИКА РЕАЛЬНОЙ ЖИДКОСТИ-2

6.1 Уравнение Бернулли для потока реальной (вязкой) жидкости.

6.2 Мощность потока.

6.3 Коэффициент Кориолиса.

6.4 Гидравлические потери (общие сведения).

6.5 Местные потери.

6.6. Потери энергии на трение по длине  

Рекомендуемые материалы

6.7.Примеры использования уравнения Бернулли в технике

6.1.Уравнение Бернулли для потока реальной (вязкой) жидкости.

При выводе уравнения Бернулли для потока реальной (вяз­кой) жидкости  необходимо учесть: неравномерность распределения  скоростей по сечению и потери энергии. Эти  явления  соответствуют вязкой жидкости.

При движении жидкости из-за влияния вязкости  происхо­дит торможение потока.  Наибольшие значения ско­рость достигает в центральной части потока, по мере приближения к стенке она уменьшается почти до нуля. Пример распределения скоростей показан на рис. 6.1.

Из-за неравномерного распределения скоростей происходит скольжение  или сдвиг одних слоев по другим и между слоями возникают касательные напряжения или напряжения трения. Движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием.

При движении реальной жидкости на преодоление сопротивлений, связанных с вязкостью,  требуются затраты энергии, поэтому удельная  энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а уменьшается вдоль потока.

При выводе уравнения Бернулли для потока вязкой жидкости вместо неравномерного распределения скоростей рассматриваются средние скорости и средние значения удельной энергии жидкости в данном сечении. Измерение скорости в различных точках сечения потока  выполнить сложно, измерение средней скорости потока выполнить проще и они могут быть сделаны с большей точностью.

Для потока вязкой жидкости делается допущение: принимается, что в пределах рассматриваемых поперечных сечений потока,  справедлив основной закон гидростатики  и  гидростатический  напор есть величина одинаковая для всех точек данного сечения.

6.2. Мощность потока

Мощностью потока  называется полная энергия, которую проносит поток через данное сечение в единицу времени.

Мощностью называется отношение работы, выполненной за определенный промежуток времни к длительности этого промежутка. Например, для гидроцилиндра

где давление p = ρgh, , работа А =pghS*L,  массовый расход δQ_m = ρW/t =  ρ(L*S) /t

Выразим работу, как произведение силы  или произведение давления р на площадь S гидроцилиндра на ход – L, который поршень проходит под действием этой силы. Это выражение мощности гидравлического потока подведенного к гидроцилиндру.

Элементарные струйки, составляющие поток обладают различной энергией.  

Мощность элементарной струйки это произведение полной удельной энергии струйки жидкости в виде третьей формы уравнения Бернулли в данной точке

gН= gz + p/(ρ) + (V²/2),         (6.1)

на элементарный массовый расход струйки

δQ_m = ρ(V*δS /δt),

 где V – скорость в сечении δS струйки .

Это произведение  позволяет выразить мощность струйки:

δN = gH*δQ_m = (gz + p/ρ + v²/2)*ρ* v*δS = P*δQ                (6.2)

Мощность всего потока найдем, как интеграл от предыдущего выражения по площади S:

                                  (6.3)

Учитывая, допущение о том, что гидростатический напор для всех элементарных струек в сечении  потока есть величина постоянная, получим мощность потока:

                           (6.4)

6.3 Коэффициент Кориолиса

Для  определения полной удельной мощности потока разделим  мощность потока на  средний массовый расход:   Q_m =  ρQ = , где Q=Vср*S.

     (6.5)

Умножив и разделив последний член на V , получим, переходя к напорам (третья степень в знаменателе получается умножением на скорость в составе расхода)

                     (6.6)

где α – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей и равный

                             (6.7)

Умножив числитель и знаменатель на ρ/2, получим:   коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечения, но при равномерном распределении скоростей, поскольку интеграл от dm =  ρ*VdS – масса потока в данном сечении:

Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно Н_ср1 и Н_ср2. Тогда

Н _ср1 = Н_ср2 + Σh_п,

где  Σh_п  – суммарная потеря полного напора на участке между рассматриваемыми сечениями.

Это уравнение Бернулли для потока вязкой жидкости:

              (6.8)

От уравнения для элементарной струйки идеальной жидкости это уравнение отличается четвертым членом – потерей полного напора, и коэффициентами Кориолиса, учитывающим неравномерность распределения скоростей. Скорости, входящие в это уравнение, являются средними скоростями в первом и тором  сечениях потока.

Это уравнение Бернулли применимо не только для жидкостей, но для газов при условии, что скорость их движения значительно меньше скорости звука.

Графически это уравнение представляется  диаграммой подобно уравнению Бернулли для идеальной жидкости с учетом потерь напора. Потери напора вдоль потока возрастают.

Уравнение Бернулли для струйки идеальной жидкости  – это  закон сохранения механической энергии.

Уравнение Бернулли для потока реальной жидкости – уравнение баланса энергии  с учетом потерь.

Энергия, теряемая жидкостью на рассматриваемом участке течения   превращается в тепловую форму энергии.

Хотя удельная теплоемкость жидкостей велика и  тепловая энергия непрерывно рассеивается, повышение температуры рабочей жидкости в гидросистемах бывает значительным. Процесс преобразования механической энергии в тепловую необратим, обратное превращение тепловой энергии в механическую здесь невозможно.

Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины, называется гидравлическим уклоном.

6.4 Гидравлические потери .

Гидравлические потери удельной энергии, выраженные напором или давлением,  зависят от формы и размеров трубопровода, скорости течения и вязкости жидкости.

При турбулентном режиме движения жидкости гидравлические потери пропорциональны скоростям во второй степени, в единицах длины

   h _п = ζ V² _ср /(2g),              (6.9)

где ζ – безразмерный коэффициент местного сопротивления; V – средняя скорость потока (обычно – в сечении трубопровода перед местным сопротивлением или после него). В единицах давления

p_п = ρgh_п = ζρ V² _ср /2.       (6.10)

Безразмерный  коэффициент потерь ζ – дзета называется  коэффициентом  сопротивления и равен  отношению величины потерянного напора к скоростному напору.

Гидравлические потери разделяют на местные потери и потери на трение по длине.

Значение ζ  вообще зависит от формы местного сопротивле­ния, шероховатости его стенок, условий входа и выхода из него жидкости и основного критерия динамического подобия напор­ных потоков – числа Рейнольдса.

Число Рейнольдса обычно относят к сечению трубопровода, в котором находится местное сопротивление

.

где V и Q – средняя скорость потока и расход в трубе; D – диа­метр трубы; ν- кинематическая вязкость жидкости.

Для большинства местных сопротивлений в трубопроводах при числах Рейнольдса Re > 10⁵ имеет место турбулентная автомодельность – потери напора пропорциональны скорости во вто­рой степени и коэффициент сопротивления не зависит от Re (квадратичнаνя зона сопротивления).

В тех местных сопротивлениях, где основной является вихре­вая потеря напора (например, резкое изменение сечения трубопровода, диафрагмы и др.), автомодельность устанавливается при значительно меньших числах Рейнольдса Re≥10⁴.

Число Рейнольса определяет режим течения жидкости. При его значении меньше Re≤2300 режим течения жидкости называется ламинарным, от слова ламина – слой или слоистым.

Ламинарным движением жидкости называется режим ее течения  упорядоченным слоями без ее перемешивания.

Струи жидкости, находящиеся на разном удалении от оси движутся с различными скоростями. Наибольшую скорость имеет осевая струйка, при стенках скорость равна нулю.

Увеличение скорости понижает устойчивость ламинарного течения и нарушает его режим. На устойчивость ламинарного режима оказывают влияние вязкость жидкости, плотность, скорость движения частиц, а также диаметр трубопровода.

При увеличении скорости струйки разрываются, разрыву предшествует образование волнообразных колебаний. При усилении колебаний струйка полностью перемешивается с окружающей жидкостью. Движение частиц производит впечатление беспорядочных вихрей. При числах Рейнольса больше Re>2300 режим течения жидкости становится турбулентным.

Турбулентным движением жидкости называется режим ее течения  неупорядоченным слоями с их перемешиванием.

6.5.Местные потери

Местные потери  энергии вызваны изменениями формы и размера трубопровода, вызывающими деформацию потока. Жидкости, протекая через местные сопротивления, изменяет скорость и образует вихри. После отрыва потока от стенок вихри образуют области, в которых частицы жидкости движутся в основном по замкнутым траекториям.

Примеры местных сопротивлений приведены на рис. 6.3. Здесь же показаны отрывы потока и вихреобразование.

Каждое местное сопротивление характеризуется значением коэффициента сопротивления  ζ,  которое приближенно можно считать постоянным для данной формы местного сопротивления.

6.6. Потери энергии на трение по длине

Эти потери возникают в прямых трубах постоянного сечения и  при равномерной скорости течения, возрастают пропорционально длине трубы (рис.6.4).

Потери энергии на трение по длине связаны с  внутренним трением в жидкости, эти потери можно определять по формуле  для гидравлических потерь, т. е.

h _тр = ζ _тр v²/(2g).

Поскольку длины труб разные, коэффициент потерь на трение ζтр  связывают  с относительной длиной трубы   l/d.

Коэффициент потерь на трение участка круглой трубы с длиной равной ее диаметру

l = d обзначают буквой  λ –лямбда, если длина трубы  l  не равна диаметру d,  коэффициент потерь будет в l/d  раз больше:

ζ _тр = λ* l/d  .

Формула для определения потерь на трение по длине называется формулой  Вейсбаха – Дарси.

  (6.11)

или в единицах давления

 (6.11′)

Коэффициент   λ, входящий в формулы для определения потерь по длине  называется  “коэффициентом потерь на трение по длине”, или “коэффициентом Дарси”.

Физический смысл коэффициента λ.  При равномерном движении в трубе длиной l и диаметром d, имеет место равновесие сил, действующих на объем: сил давления и силы трения. Это равновесие выражается равенством

πd²p_тр/4 – πdlτ₀ = 0,

где τ₀ — напряжение трения на стенке трубы.

Так как          , то                 λ=   ,

λ есть величина, пропорциональная отношению напряжения от силы трения на стенке трубы к динамическому давлению, определяемому по средней скорости.

6.6. Применение уравнения Бернулли в технике

6.6.1.  Расходомер Вентури – устройство, устанавливаемое  в трубопроводах и выполняющее сужение потока — дросселирование (рис.6.5).

Расходомер состоит из двух участков — плавно сужающегося сопла и постепенно расширяющегося диффузора. Скорость потока в суженном месте возрастает, а давление падает. Возникает перепад давлений, который измеряется двумя пьезометрами и дифференциальным U-образным манометром.

В сечении 1-1 перед сужением скорость потока равна V₁, давление Р₁, площадь сечения S₁ , а в cечении 2-2: V₂, P₂ ,S₂ , разность показаний пьезометров, присоединенных к сечениям ΔН.

Запишем для сечений 1-1 и 2-2 потока уравнение Бернулли и уравнение расхода, считая распределение скоростей равномерным.

где hм — потеря напора между сечениями 1-1 и 2-2.

Объемный расход

где С — величина постоянная для данного расходомера.

Зная величину С, можно найти расход в трубопроводе по формуле. Коэффициент  С можно определить теоретически, но лучше найти его экспериментально при тарировании расходомера.

Вместо пьезометров для измерения перепада давлений в расходомере можно применить дифференциальный манометр, заполненный ртутью. Над ртутью в трубках находится жидкость с плотностью ρ, поэтому можно записать для уровня 0-0, уравнение статики

Р₁+ρgΔh= Р₂+ρ_ртgΔh,  (Р₁– Р₂ ) = ρ_ртgΔh – ρgΔh,   (Р₁– Р₂ ) =ΔНρg, откуда  

6.6.2. Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешивания его с потоком воздуха (рис. 6.6). Поток воздуха  засасываемого в  двигатель, сужается  в том месте, где установлен распылитель бензина (трубка диаметром d). Скорость воздуха этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному  давлению бензин подсасывается  в поток воздуха.

Найдем соотношение между массовыми расходами бензина Q_б и воздуха Q_в при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) и жиклера ζж (сопротивлением бензотрубки пренебрегаем).

Записав уравнение Бернулли для потока воздуха (сечение 1-1 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z₁= z₂‚  и  α= 1):

откуда

Учитывая, что массовые расходы

получим

Таким образом, обеспечивается постоянство соотношения расходов бензина и воздуха.

Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рис.6.6), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В.

 Вследствие увеличения скорости потока в струе на выходе из насадка и по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в  атмосферу), следовательно в камере В давление обычно меньше атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.

Трубка полного напора ( трубка Пито) служит для измерения скорости в трубе (рис. 1.34). Если установить в этом потоке трубку, повернутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту равную скоростному напору.

“3. Освещение” – тут тоже много полезного для Вас.

 Объясняется это тем, что скорость v частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив  разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. На этом же принципе основано измерение скорости полета самолета. На рис.6.7 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью звука скоростей полета.

Запишем уравнение Бернулли для струйки , которая набегает на трубку вдоль  ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где v =0), получаем

Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р₂ ≈ р₀ , следовательно,  из предыдущего имеем

4. 
Расчет установившегося режима
электрической сети

При расчете параметров режима электрической сети рассматривают
два случая: расчет проводят “по данным конца”, если задано напряжение на шинах
наиболее удаленного потребителя; расчет проводится методом последовательных
приближений, если известно напряжение на шинах источника (расчет “по данным
начала”). В том и другом случаях расчет ведут последовательно для каждого
участка сети. Формулы принимаются в соответствии с работой [4].

В рассматриваемой задаче известной величиной является
напряжение в базисном узле, следовательно, расчет проводится “по данным
начала”. Начиная расчет, проанализируем полученную расчетную схему сети (рис. 7). Рассматриваемая схема содержит 10 узлов, включая базисный,
и 10 ветвей, состоящих из активных и индуктивных сопротивлений. Причем участки
между узлами 1,2,3,4 образуют замкнутую электрическую сеть, а остальные
представляют собой ответвления от нее.

Если сеть содержит
замкнутый контур, схема её рассчитывается как кольцевая. Все подстанции,
получающие питание по ответвлениям от кольцевой схемы, должны быть заменены эквивалентной
нагрузкой в соответствующем узле кольца, которую определяют суммированием
собственной нагрузки узла с нагрузками и потерями мощности на ответвлении.
Таким образом, вначале необходимо рассчитать магистральные участки, а затем
кольцевую сеть. Расчет “по данным начала” проводится в два этапа.

4.1. 
Расчет
потоков мощности в электрической сети

В
первом приближении (на первом этапе) напряжения во всех узловых точках приравнивают
номинальному напряжению сети и находят распределение мощности по участкам сети.
Расчет ведется от конца (наиболее удаленные потребители) к началу линии
(базисный узел). Добавляя к потоку мощности у приемного конца каждого участка
потери мощности на нем, определяют значение мощности у его питающего конца. В
узловых пунктах производят сложение значений мощности собственной нагрузки и
потоков мощности отходящих ветвей. Расчет продолжается до определения полной
мощности, поступающей в сеть из пункта питания.

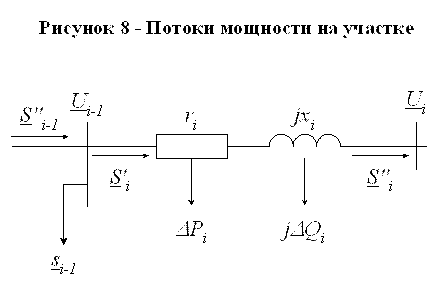Обозначения,
принятые в дальнейшем расчете, показаны на рисунке 8.

Рассчитаем
распределение мощности на магистральных ответвлениях.

Участок 10 (узлы 9 – 10)

Поток мощности в конце
участка:

Потери мощности на участке:

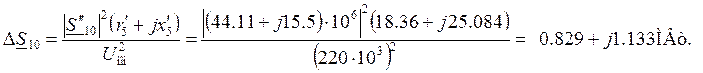
Поток мощности в начале
участка:

Участок 9 (узлы 3 – 9)

Поток мощности в конце
участка:

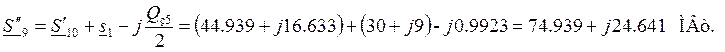
Потери мощности на участке:

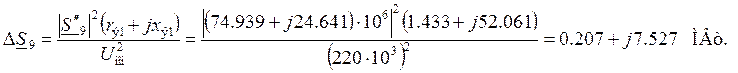
Поток мощности в начале
участка:

Участок 8 (узлы 6 – 7)

Поток мощности в конце
участка:

Потери мощности на участке:

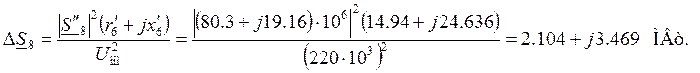
Поток мощности в начале
участка:

Участок 7 (узлы 5 – 6)

Поток мощности в конце
участка:

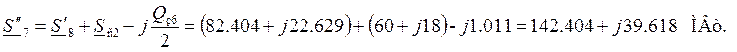
Потери мощности на участке:

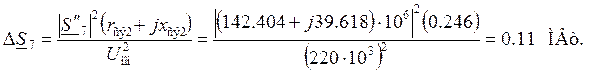
Поток мощности в начале
участка:

Участок 6 (узлы 5 – 8)

Поток мощности в конце
участка:

Потери мощности на участке:

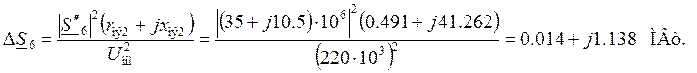
Поток мощности в начале
участка:

Участок 5 (узлы 4 – 5)

Поток мощности в конце
участка:

Потери мощности на участке:

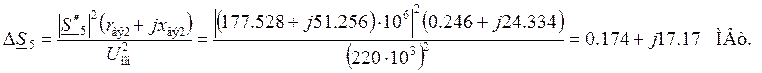
Поток мощности в начале
участка:

            Рассчитав потоки мощности
на магистральных ответвлениях, можем найти эквивалентные нагрузки на
подстанциях №1 и №2 по балансу мощности для узлов сети 3 ,4:

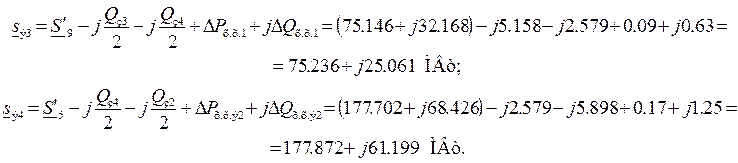
Теперь рассчитаем кольцевую
схему сети, разрезая её по балансирующему узлу 1 (рисунок.9).

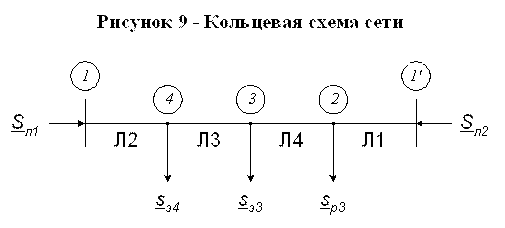            Вначале находим
распределение потоков мощности в сети без учета потерь в зависимости от
нагрузок и полных комплексных сопротивлений ветвей сети, входящих в кольцо.
Потоки мощности, поступающие в сеть с двух сторон, находим по формулам:

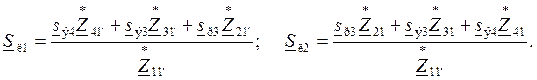
            Запишем полные комплексные сопротивления
ветвей:

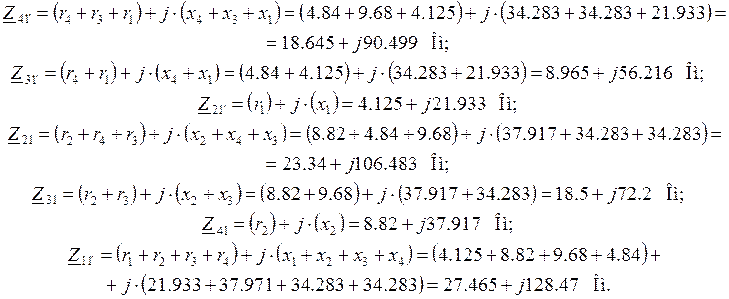
            Таким
образом,

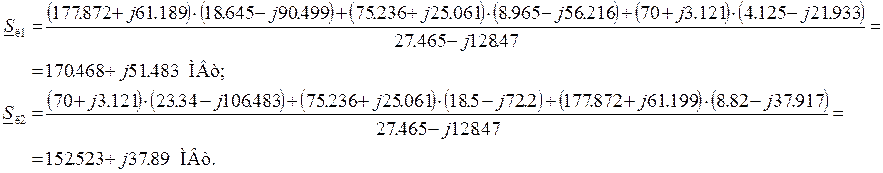
            Произведем проверку:

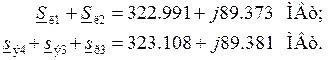
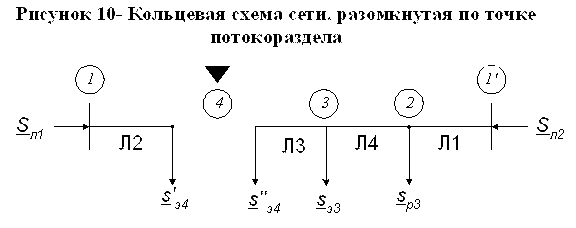            Очевидно, точка 4 является точкой потокораздела, поэтому разбиваем
кольцевую сеть на две магистральные ветви (рисунок 10) и определяем частичные потоки
мощности, поступающие в четвертый узел с двух сторон:

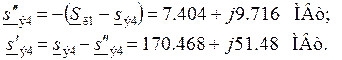
Теперь
рассчитаем потоки мощности с учетом потерь в ветвях.

Участок 3 (узлы 3 – 4)

Поток мощности в конце
участка:

Потери мощности на участке:

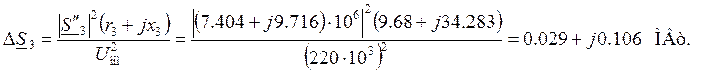
Поток мощности в начале
участка:

Участок 4 (узлы 4 – 1)

Поток мощности в конце
участка:

Потери мощности на участке:

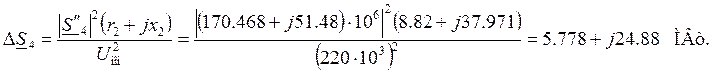
Поток мощности в начале
участка:

Участок 2 (узлы 3 – 2)

Поток мощности в конце
участка:

Потери мощности на участке:

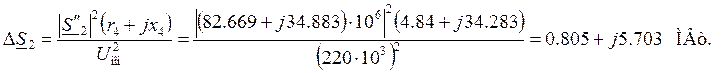
Поток мощности в начале
участка:

Участок 1 (узлы 2 – 1′)

Поток мощности в конце
участка:

Потери мощности на участке:

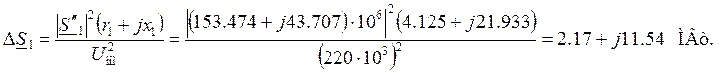
Поток мощности в начале
участка:

            Таким образом,
заканчивая первый этап расчета, мы находим мощность, поступающую в сеть из
балансирующего узла:

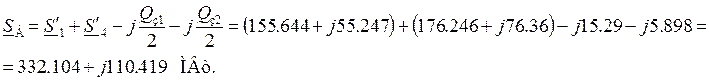
4.2. 
Расчет
напряжений на подстанциях

Во втором
приближении (на втором этапе) по напряжению базисного узла

---

Подборка по базе: курсовая работа Экономический расчет зарплаты работников и рента, 6 ЛАБ СЕТИ.docx, Локальные и глобальные компьютерные сети.pptx, Копия Расчет подъемного механизма (методика).doc, Экономический расчет Сидоленко электромашин.docx, курсач расчетная часть 2.docx, 2.1. Гидравлический расчет.docx, Пример расчета эвольвентного зац.pdf, «Аэродинамический расчет котельных установок» 19.doc, Данные и расчеты.docx

---

№4. РАСЧЕТ ЗАМКНУТОЙ СЕТИ

4. РАСПРЕДЕЛЕНИЕ ПОТОКОВ МОЩНОСТИ И НАПРЯЖЕНИЙ
В ПРОСТЫХ ЗАМКНУТЫХ СЕТЯХ

Ранее рассматривались разомкнутые сети. Ниже будут рассматриваться замкнутые сети. Напомним, что в разомк­нутых сетях все узлы получают питание только по одной
ветви.

В простых замкнутых сетях есть узлы, питающиеся по двум ветвям, но нет узлов, получающих питание более чем по двум ветвям, отсутствуют узлы, с которыми соединены три и более ветви (рис. 3.14, а, б). Простые замкнутые сети содержат только один контур.

Рис. 3.13. Примеры простых разом-
кнутых сетей:

а — неразветвленной; б — разветвлен-
ной

Рис. 3.14. Примеры простых замкнутых сетей:

а — треугольник; б — линия с двусторонним питанием; в — сложнозамкнутая сеть

Характерным частным видом простой замкнутой сети является кольцевая сеть (рис. 3.14, а). Она содержит один замкнутый контур. В качестве источников питания могут служить или электростанции, или шины подстанций, в свою очередь связанные сетью с электростанциями системы.
Кольцевая сеть на рис. 3.14, а может быть представлена в виде линии с двухсторонним питанием (рис. 3.14, б). Действительно, если источник питания в узле 1 мысленно раз­делить на два и представить в виде узлов 1 и 4, то из коль­цевой сети на рис. 3.14, а получим линию с двухсторонним питанием на рис. 3.14,б.

В сложной замкнутой сети есть узел, с которым соеди­нены три ветви или более (рис 3.14, в). Сложная замкну­тая сеть содержит два и более контуров.

К достоинствам замкнутых сетей следует отнести по­вышенную надежность электроснабжения потребителей, меньшие потери мощности, к недостаткам — сложность эксплуатации, удорожание за счет дополнительных линий. Расчеты замкнутых сетей сложнее, чем разомкнутых.

Распределение потоков мощности в простой замкнутой сети без учета потерь мощности. Представим простейшую замкнутую сеть в виде линии с двухсторонним питанием
( рис. 3.15, а) и рассмотрим различные случаи.

Рис. 3.15. Распределение потоков мощности в линии с двухсторонним питанием без учета потерь мощности:

а—схема замещения линии с четырьмя узлами; б—иллюстрация второго закона Кирхгофа; в—линия с п узлами; г,д—распределение Р и в однородной линии; е—линия с четырьмя узлами при ; ж, з—эквивалентное представление линии на рис, е; и—схема кольцевой сети 110 кВ
Заданы одинаковые напряжения по концам линии . Известны мощности нагрузки , , сопротивления участков линии , где k. — узел начала участка линии; j — узел конца.

Принимаем следующие допущения:

а) пренебрегаем потерями мощности при опреде­лении потоков ;

б) предполагаем, что ток участка определяется по но­минальному напряжению:

;

в) используем расчетные мощности нагрузок под­станции.

При равенстве напряжений источников питания на ос­новании второго закона Кирхгофа можно записать (рис. 3.15,б)

.

Если заменим в последнем выражении все комплексные величины на сопряженные, то получим следующее урав­нение:

. (3.70)

Так как потери мощности не учитываются, первый за­кон Кирхгофа для узлов 2 и 3 можно записать так:

; (3.71)

. (3.72)

Подставив значения мощностей (3.71) и (3.72) в урав­нение (3.70), получим уравнение с одним неизвестным:

.

Отсюда находим значение потока мощности :

, (3.73)

где

.

Аналогично можно вывести формулу для определения потока мощности :

, (3.74)

где .

Значение потока мощности можно легко найти на основании первого закона Кирхгофа из (3.71).

Кольцевая сеть (рис. 3.15, и) напряжением …… кВ свя­зывает электростанцию 1 с понижающими подстанциями 2, 3, имеющими расчетные нагрузки , МВА и , МВА. Марки проводов, длины линий указаны. Выбрать сечения проводов и подсчитать их со­противления и проводимости, зарядную мощность. Напряжение на шинах электростанции, …..кВ. Определить мощность, которая поступает с шин электростанции. Расчет проведем с учетом потерь мощности.

РЕШЕНИЕ. Составим схему замещения сети в виде линии с двухсторонним питанием, разрезая кольцо в узле 1 (рис. 3.15,а). Определим по выраже­ниям (3.73) и (3.74) приближенное потокораспределение в кольце с целью выявления точки потокораздела:

МВА;

МВА.

Проверим правильность определения потоков мощности на головных линиях кольца по условию :

Значения и определены верно. Находим поток мощности в линии 23 по первому закону Кирхгофа для узла 2:

МВА.

Узел 3 — точка потокораздела активной и реактивной мощности.
Мощность, поступающая с шин электростанции и определенная без уче­та потерь мощности, равна

МВА.

При одинаковом сечении проводов вдоль всей линии

(3.80)

где , , — длины участков линии между узлами со­ответственно k и п, 1 и k, 1 и n.

В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке
между точками потокораздела:

; .

Расчет с учетом потерь мощности. Рассмотрим линию
с двухсторонним питанием, к которой преобразуется прос­тая замкнутая сеть (рис. 3.16, а). Мощности , ,

Рис. 3.16. Распределение потоков мощности в замкнутой сети с учетом потерь мощности:

а—исходная сеть; б—представление исходной сети в виде двух линий; в—услов­ные обозначения для расчета потоков в линиях с учетом потерь мощности; г—на­правления потоков в случае несовпадения точек потокораздела активной и реак­тивной мощностей; д—разделение сети при несовпадающих точках потокораздела
определим сначала без учета потерь по выражениям (3.73), (3.74), (3,71). Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который от­мечен залитым треугольником. «Разрежем» линию в узле 3 (рис. 3.16, б) и рассчитаем потоки мощности в линиях 13 и 43‘, как это делалось для разомкнутых сетей.

На участке 23 потери активной мощности

;

потери реактивной мощности

,

потери полной мощности

.

Находим значение потока мощности в начале участка 23 (рис, 3.16,в):

.

Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей (1-й этап в § 3.6).

Может оказаться, что 1-й этап расчета кольцевой сети выявит две точки потокораздела: одну — для активной, а другую — для реактивной мощности. Такой случай ил­люстрируется на рис. 3.16, г, где узел 2—точка потоко­раздела для активной, а узел 3 — для реактивной мощ­ности.

В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке между точками потокораздела:

; .

Если теперь принять, что в точке 2 включена нагрузка

,

а в точке 3 — нагрузка

.

где , , , определяются по (3.73), (3.74), а , —по (3.71), то при дальнейшем расчете можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис. 3.16, д.

«Разрежем» линию с двухсторонним питанием в узле 3 потокораздела, как на рис. 3.16,б. Нагрузки в узлах 3 и 3‘ равны МВА , МВА . Рассчитаем потоки мощности в линиях 23, 12 (рис. 3.16, в).

Мощность в конце линии 23 МВА. Потери мощности в линии 23

МВА.

Мощность в конце линии 12

МВА.

Потери мощности в линии 12

МВА.

Мощность в начале линии 12 .

МВА.

Рассчитаем потоки мощности в линии 43 (рис. 3.16,е). Мощность в конце линии 43 МВА. Потери мощности в ли­нии 43

МВА.

Мощность в начале линии 43

МВА.

Мощность, потребляемая с шин электростанции,

МВА.
№4. ЗАДАНИЕ. РЕШЕНИЕ.

1) Для подстанции №2 : – определить активную мощность, а затем реактивную мощность через tgφ или .

2) «Разрежем» линию с двухсторонним питанием в узле А.

3) Определим по выраже­нию (3.80) приближенное потокораспределение в кольце с целью выявления точки потокораздела:

,МВА;

,МВА.

Проверим правильность определения потоков мощности на головных линиях кольца по условию :

значения и определены верно, если условие выполняется.

4) Находим поток мощности в линии 23 по первому закону Кирхгофа для узла 2:

МВА.
5) Находим поток мощности в линии 43 по первому закону Кирхгофа для узла 4:

МВА.

Узлы 2 или 3 — точка потокораздела активной и реактивной мощности.
6) Определим токи по участкам:

7)Определим сечение по экономической плотности тока:

и так для всех участков.

8) Выбираем по справочнику провода (по коронированию), данные провода записываем по участкам, определяем
Участок А-2 и так для всех участков.

9) Определяем параметры линии по участкам
Участок А-2 и так для всех участков.

10) Произведем расчёт мощностей в режиме максимальных нагрузок
Участок 3-1

Участок А-1

Участок А-3

11) Определение напряжения на шинах подстанции на высокой стороне.

Напряжение в ЦП: Umax=232кВ.

Пример 1. Мощности нагрузок на стороне ВН трансформаторов =280 МВА, =320 МВА, =380 МВА, линий длиной 200, 160, 235 км. Соs φ=0,91. Напряжение в ЦП 545 кВ.

Пример 2. Мощности нагрузок на стороне ВН трансформаторов =70 МВА, =100 МВА, =90 МВА, линий длиной 60, 50, 80 км. Соs φ=0,92. Напряжение в ЦП 239 кВ.

Пример 3. Мощности нагрузок на стороне ВН трансформаторов =75 МВА, =70 МВА, =65 МВА, линий длиной 49, 78, 60 км. Соs φ=0,93. Напряжение в ЦП 242 кВ.

Пример 4. Мощности нагрузок на стороне ВН трансформаторов =32 МВА, =18 МВА, =20 МВА, линий длиной 14, 26, 20 км. Соs φ=0,94. Напряжение в ЦП 119 кВ.

Пример 5. Мощности нагрузок на стороне ВН трансформаторов =28 МВА, =24 МВА, =21 МВА, линий длиной 15, 22, 10 км. Соs φ=0,95. Напряжение в ЦП 118 кВ.

Пример 6. Мощности нагрузок на стороне ВН трансформаторов =20 МВА, =26 МВА, =10 МВА, линий длиной 30,18,22 км. Соs φ=0,96. Напряжение в ЦП 117 кВ.

Пример 7. Мощности нагрузок на стороне ВН трансформаторов =70 МВА, =62 МВА, =96 МВА, линий длиной 45, 75, 60 км. Соs φ=0,89. Напряжение в ЦП 229 кВ.

Пример 8. Мощности нагрузок на стороне ВН трансформаторов =84 МВА, =74 МВА, =86 МВА, линий длиной 90, 60, 50 км. Соs φ=0,79. Напряжение в ЦП 239 кВ.

Пример 9. Мощности нагрузок на стороне ВН трансформаторов =120 МВА, =70 МВА, =88 МВА, линий длиной 85, 57, 74 км. Соs φ=0,88. Напряжение в ЦП 238 кВ.

Пример 10. Мощности нагрузок на стороне ВН трансформаторов =96 МВА, =209 МВА, =160 МВА, линий длиной 120, 95, 100 км. Соs φ=0,87. Напряжение в ЦП 351 кВ.

Пример 11. Мощности нагрузок на стороне ВН трансформаторов =182 МВА, =148 МВА, =226 МВА, линий длиной 105, 85, 120 км. Соs φ=0,86. Напряжение в ЦП 350 кВ.

Пример 12. Мощности нагрузок на стороне ВН трансформаторов =16, =22, =20 МВА, линий длиной 20 км, 15км, 12км. Соs φ=0,85. Напряжение в ЦП 121 кВ.

Пример13. Мощности нагрузок на стороне ВН трансформаторов =138МВА, =179 МВА, =106 МВА, линий длиной 100 км,80км, 75км. Соs φ=0,90. Напряжение в ЦП 348 кВ.

Пример 14. Мощности нагрузок на стороне ВН трансформаторов =182 МВА, =219 МВА, =316 МВА, линий длиной 100,180, 200 км. Соs φ=0,84. Напряжение в ЦП 550 кВ.

Пример 15. Мощности нагрузок на стороне ВН трансформаторов =232 МВА, =319 МВА, =416 МВА, линий длиной 240, 125, 190 км. Соs φ=0,83. Напряжение в ЦП 540 кВ.

Пример 16. Мощности нагрузок на стороне ВН трансформаторов =332 МВА, =419 МВА, =266 МВА, линий длиной 100, 165, 125 км. Соs φ=0,82. Напряжение в ЦП 543 кВ.

Пример 17. Мощности нагрузок на стороне ВН трансформаторов =54 МВА, =80 МВА, =70 МВА, линий длиной 50, 60, 85км. Соs φ=0,81. Напряжение в ЦП 233 кВ.

Пример 18. Мощности нагрузок на стороне ВН трансформаторов =100 МВА, =90 МВА, =72 МВА, линий длиной 55, 70, 90 км. Соs φ=0,8. Напряжение в ЦП 240 кВ.

Пример 19. Мощности нагрузок на стороне ВН трансформаторов =16 МВА, =24 МВА, =19 МВА, линий длиной 14, 21, 22 км. Соs φ=0,94. Напряжение в ЦП 120 кВ.

Пример 20. Мощности нагрузок на стороне ВН трансформаторов =360 МВА, =315 МВА, =420 МВА, линий длиной 235, 155, 200 км. Соs φ=0,91. Напряжение в ЦП 537 кВ.

Пример 21. Мощности нагрузок на стороне ВН трансформаторов =105 МВА, =135 МВА, =215 МВА, линий длиной 90, 88, 75 км. Соs φ=0,98. Напряжение в ЦП 348 кВ.