From Wikipedia, the free encyclopedia
| Heat flux | |
|---|---|

Heat flux |
|
|
Common symbols |
 |
| SI unit | W/m2 |
|
Other units |
Btu/(h⋅ft2) |
| In SI base units | kg⋅s−3 |
| Dimension |  |
In physics and engineering, heat flux or thermal flux, sometimes also referred to as heat flux density[1], heat-flow density or heat flow rate intensity, is a flow of energy per unit area per unit time. Its SI units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small.
Heat flux is often denoted 
Fourier’s law[edit]
For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier’s law.
Fourier’s law in one dimension[edit]
where 
Multi-dimensional extension[edit]
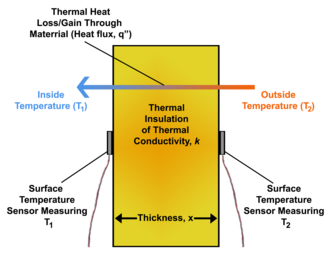
Diagram depicting heat flux through a thermal insulation material with thermal conductivity, k, and thickness, x. Heat flux can be determined using two surface temperature measurements on either side of the material using temperature sensors if k and x of the material are also known.

Diagram depicting heat flux through a thermal insulation material with thermal conductivity, k, and thickness, x. Heat flux can be directly measured using a single heat flux sensor located on either surface or embedded within the material. Using this method, knowing the values of k and x of the material are not required.
The multi-dimensional case is similar, the heat flux goes “down” and hence the temperature gradient has the negative sign:
where 
Measurement[edit]
The measurement of heat flux can be performed in a few different manners. A commonly known, but often impractical, method is performed by measuring a temperature difference over a piece of material with known thermal conductivity. This method is analogous to a standard way to measure an electric current, where one measures the voltage drop over a known resistor. Usually this method is difficult to perform since the thermal resistance of the material being tested is often not known. Accurate values for the material’s thickness and thermal conductivity would be required in order to determine thermal resistance. Using the thermal resistance, along with temperature measurements on either side of the material, heat flux can then be indirectly calculated.
A second method of measuring heat flux is by using a heat flux sensor, or heat flux transducer, to directly measure the amount of heat being transferred to/from the surface that the heat flux sensor is mounted to. The most common type of heat flux sensor is a differential temperature thermopile which operates on essentially the same principle as the first measurement method that was mentioned except it has the advantage in that the thermal resistance/conductivity does not need to be a known parameter. These parameters do not have to be known since the heat flux sensor enables an in-situ measurement of the existing heat flux by using the Seebeck effect. However, differential thermopile heat flux sensors have to be calibrated in order to relate their output signals [μV] to heat flux values [W/(m2⋅K)]. Once the heat flux sensor is calibrated it can then be used to directly measure heat flux without requiring the rarely known value of thermal resistance or thermal conductivity.
Science and engineering[edit]
One of the tools in a scientist’s or engineer’s toolbox is the energy balance. Such a balance can be set up for any physical system, from chemical reactors to living organisms, and generally takes the following form
where the three 
Now, if the only way the system exchanges energy with its surroundings is through heat transfer, the heat rate can be used to calculate the energy balance, since
where we have integrated the heat flux 

In real-world applications one cannot know the exact heat flux at every point on the surface, but approximation schemes can be used to calculate the integral, for example Monte Carlo integration.
See also[edit]
- Radiant flux
- Latent heat flux
- Rate of heat flow
- Insolation
- Heat flux sensor
- Relativistic heat conduction
Notes[edit]
- ^ The word “flux” is used in most physical disciplines to refer to the flow of a quantity (mass, heat, momentum, etc.) across a surface per unit time per unit area, with the primary exception being in electromagnetism, where it refer to the integral of a vector quantity through a surface. Refer to the Flux article for more detail.
Как определить тепловой поток
Тепловой поток — это количество тепловой энергии, которое передается через изотермическую поверхность за единицу времени. Основной характеристикой этого понятия является плотность.
Инструкция
Теплота является суммарной кинетической энергией молекул тела, переход которой от одних молекул к другим или от одного тела к другому может осуществляться посредством трех типов передачи: теплопроводностью, конвекцией и тепловым излучением.
При теплопроводности тепловая энергия переходит от более нагретых частей тела к более холодным. Интенсивность ее передачи зависит от градиента температур, а именно от отношения разности температур, а также площади поперечного сечения и коэффициента теплопроводности. В таком случае формула для определения теплового потока q выглядит так:q = -kS(∆T/∆x), где:k – коэффициент теплопроводности материала;S – площадь поперечного сечения.
Эта формула называется законом теплопроводности Фурье, а знак минус в формуле указывает направление вектора теплового потока, который противоположен градиенту температуры. Согласно этому закону, понижению теплового потока можно добиться, уменьшив один из его составляющих. Например, можно воспользоваться материалом с другим коэффициентом теплопроводности, меньшим поперечным сечением или разностью температур.
Конвективный тепловой поток осуществляется в газообразных и жидких веществах. В этом случае говорят о передаче тепловой энергии от нагревателя к среде, которая зависит от совокупности факторов: размера и формы нагревающего элемента, скорости движения молекул, плотности и вязкости среды и пр. В этом случае применима формула Ньютона:q = hS(Tэ – Tср), где:h – коэффициент конвективного переноса, отражающий свойства нагреваемой среды;S – площадь поверхности нагревательного элемента;Tэ – температура нагревательного элемента;Tср – температура окружающей среды.
Тепловое излучение – метод передачи тепла, который являются разновидностью электромагнитного излучения. Величина теплового потока при такой теплопередаче подчиняется закону Стефана-Больцмана:q = σS(Ти^4 – Тср^4), где:σ – постоянная Стефана-Больцмана;S – площадь поверхности излучателя;Tи – температура излучателя;Тср – температура окружающей среды, поглощающей излучение.
Источники:
- расчет тепловых потоков
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 декабря 2022 года; проверки требуют 6 правок.
Теплопередача — физический процесс передачи тепловой энергии от более горячего тела к менее горячему, либо непосредственно (при контакте), либо через посредника (проводника) или разделяющую перегородку (тела или среды) из какого-либо материала. Когда физические тела одной системы находятся при разной температуре, то происходит передача тепловой энергии, или теплопередача от одного тела к другому до наступления термодинамического равновесия. Самопроизвольная передача тепла всегда происходит от более горячего тела к менее горячему, что является следствием второго закона термодинамики, и этот процесс является необратимым.
Виды теплопередачи[править | править код]
Всего существует три простых (элементарных) механизма передачи тепла:
- теплопроводность,
- конвекция,
- тепловое излучение.
Существуют также различные виды переноса тепла, которые являются сочетанием элементарных видов. Основные из них:
- теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела),
- теплопередача (теплообмен от горячей среды [жидкость, газ или твёрдое тело] к холодной через разделяющую их стенку),
- конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией),
- термомагнитная конвекция.
Внутренние источники теплоты — понятие теории теплопередачи, которое описывает процесс производства (реже поглощения) тепловой энергии внутри материальных тел без какого-либо подвода или переноса тепловой энергии извне. К внутренним источникам теплоты относятся:
- тепловыделение при работе электрического тока,
- тепловыделение при ядерных реакциях,
- тепловыделение при химических реакциях.

Моделирование конвекции в мантии Земли. Цвета варьируются от красного и зелёного для высокой температуры до синего для низкой температуры. Горячий, и менее плотный нижний пограничный слой поставляет горячее вещество вверх в виде струй, а холодное вещество движется вниз.
Адвекция[править | править код]
Адвекция происходит путём передачи вещества и энергии, включая тепловую, перемещая посредством физического переноса горячего или холодного объёма из одного места в другое.[1] В качестве примеров можно указать заполнение бутылки горячей водой и передвижение айсберга посредством океанских течений. Практический пример — теплогидравлика, которую можно описать простой формулой:
где
Теплопроводность[править | править код]
В микроскопическом масштабе теплопроводность происходит, когда горячие, быстро движущиеся или колеблющиеся атомы и молекулы взаимодействуют с соседними атомами и молекулами, передавая часть своей кинетической энергии этим частицам. Другими словами, тепло передаётся за счёт теплопроводности, когда соседние атомы движутся друг относительно друга или когда электроны перемещаются от одного атома к другому. Теплопроводность представляется наиболее важным средством передачи тепла внутри твёрдого тела или между твёрдыми объектами, находящимися в тепловом контакте. Жидкости, особенно газы, обладают меньшей теплопроводностью. Контактная теплопроводность — это исследование теплопроводности между соприкасающимися твердыми телами.[2] Процесс передачи тепла из одного объёма в другой без макроскопического движения частиц называется теплопроводностью. Например, когда вы кладете руку на холодный стакан с водой — тепло передается от теплой кожи к холодному стеклу, но если рука находится на расстоянии нескольких сантиметров от стекла, то теплопроводность будет незначительной, поскольку воздух плохо проводит тепло. Стационарная теплопроводность — это идеализированная модель теплопроводности, которая возникает при постоянной разности температур, то есть когда возникающая через некоторое время пространственное распределение температур в теплопроводящем объекте не изменяется (см Закон Фурье).[3] В установившемся режиме теплопроводности количество тепла, поступающего в тело, равно количеству выходящего тепла, поскольку, в этом режиме, изменение температуры (мера тепловой энергии) равно нулю. Примером стационарной теплопроводности является поток тепла через стены теплого дома в холодный день — внутри дома поддерживается высокая температура, а снаружи температура остаётся низкой, поэтому передача тепла в единицу времени остается постоянной, определяемой теплоизоляцией стены, а пространственное распределение температуры в стенах будет примерно постоянным во времени.
Нестационарная теплопроводность описывается уравнением теплопроводности и возникает, когда температура внутри объекта изменяется как функция времени. Анализ нестационарных систем более сложен, и аналитические решения уравнения теплопроводности получены только для идеализированных модельных систем. В практических приложениях обычно используются численных методы, методы аппроксимации или эмпирические исследования.[2]
Конвекция[править | править код]
Конвективная теплопередача, или просто конвекция, — это процесс передачи тепла от одного объёма к другому за счёт движения жидкостей и газов, процесс, который по сути является передачей тепла посредством массообмена.
Движение массы жидкости улучшает теплопередачу во многих физических ситуациях, таких как теплообмен между твёрдой поверхностью и жидкостью.[4]
Конвекция обычно доминирует в процессе теплопередачи в жидкостях и газах. Хотя иногда её называют третьим методом теплопередачи, конвекция обычно используется для описания комбинированных эффектов теплопроводности внутри текучей среды (диффузия) и теплопередачи за счёт объёмного потока текучей среды.[5]
Процесс переноса тепла с потоком жидкости известен как адвекция, но чистая адвекция — это термин, который обычно ассоциируется только с переносом массы в жидкости, например адвекцией гальки в реке. В случае теплопередачи в жидкости, перенос посредством адвекции в жидкости всегда сопровождается переносом тепла посредством диффузии (также известной как теплопроводность), процесс конвекции понимается как сумма переноса тепла посредством адвекции и диффузии/теплопроводности.
Свободная или естественная конвекция возникает, когда объёмные движения жидкости (потоки и течения) вызываются силами плавучести, которые возникают в результате изменения плотности зависящей от температуры жидкости. Вынужденная конвекция возникает, когда потоки в жидкости индуцируются внешними средствами, такими как вентиляторы, мешалки и насосы.[6]
Тепловое излучение[править | править код]

Раскалённый железный предмет, передающий тепло в окружающую среду посредством теплового излучения
Тепловое излучение передаётся через вакуум или любую прозрачную среду (твёрдую, жидкую или газообразную). Такая передача энергии с помощью фотонов электромагнитных волн, подчиняющаяся тем же законам.[7]
Тепловое излучение — это энергия, излучаемая веществом в виде электромагнитных волн из-за наличия тепловой энергии во всем веществе при температуре выше абсолютного нуля. Тепловое излучение распространяется без материи в вакууме.[8]
Тепловое излучение существует благодаря беспорядочным движениям атомов и молекул в веществе. Поскольку эти атомы и молекулы состоят из заряженных частиц (протонов и электронов), их движение приводит к испусканию электромагнитного излучения, которое уносит энергию от поверхности.
Уравнение Стефана — Больцмана, которое описывает скорость передачи лучистой энергии, для объекта в вакууме записывается следующим образом:
Для переноса излучения между двумя телами уравнение выглядит следующим образом:
где
Излучение обычно важно только для очень горячих объектов или для объектов с большой разницей температур или для тел в вакууме.
Излучение солнца или солнечное излучение можно использовать для получения тепла и энергии.[10] В отличие от теплопроводности и конвективных форм теплопередачи, тепловое излучение, приходит в узком углу, то есть исходящее от источника, намного меньшего, чем расстояние до него, и может быть сконцентрировано в небольшом пятне с помощью отражающих зеркал, которые используются для концентрации солнечной энергии, или выжигательной линзой.[11] Например, солнечный свет, отражённый от зеркал, используется в солнечной электростанции PS10, которая днём может нагреть воду до 285 °C (545 °F).
Достижимая температура на цели ограничена температурой горячего источника излучения. (Закон T 4 позволяет обратному потоку излучения нагревать источник). Горячее солнце (на своей поверхности имеет температуру примерно 4000 К) позволяет достичь примерно 3000 К (или 3000 ° C) на маленьком зонде в фокусе большого вогнутого концентрирующего зеркала в солнечной печи Мон-Луи во Франции.[12]
Коэффициент теплопередачи[править | править код]
Коэффициент теплопередачи показывает, какое количество теплоты переходит в единицу времени от более нагретого к менее нагретому теплоносителю через 1 м2 теплообменной поверхности при разности температур между теплоносителями 1 К. Обычно выражается в Вт/(м2·К), в справочниках также может приводиться величина потока за один час. В строительстве получила распространение обратная величина — «коэффициент термического сопротивления».
Основное уравнение теплопередачи[править | править код]
Основное уравнение теплопередачи: количество теплоты, переданное от более нагретого тела к менее нагретому, пропорционально поверхности теплообмена, среднему температурному напору и времени:
где
- K — коэффициент теплопередачи[⇨] вдоль поверхности теплообмена,
- F — поверхность теплообмена,
- Δtср — среднелогарифмический температурный напор (средняя разность температур между теплоносителями),
- τ — время.
Примечания[править | править код]
- ↑ Mass transfer. Thermal-FluidsPedia. Thermal Fluids Central. Дата обращения: 9 марта 2021. Архивировано 12 апреля 2021 года.
- ↑ 1 2 Abbott, J.M. Introduction to Chemical Engineering Thermodynamics / J.M. Abbott, H.C. Smith, M.M. Van Ness. — 7th. — Boston, Montreal : McGraw-Hill, 2005. — ISBN 0-07-310445-0.
- ↑ Heat conduction. Thermal-FluidsPedia. Thermal Fluids Central. Дата обращения: 9 марта 2021. Архивировано 12 апреля 2021 года.
- ↑ Çengel, Yunus. Heat Transfer: A practical approach. — 2nd. — Boston : McGraw-Hill, 2003. — ISBN 978-0-07-245893-0. Архивная копия от 26 мая 2021 на Wayback Machine
- ↑ Convective heat transfer. Thermal-FluidsPedia. Thermal Fluids Central. Дата обращения: 9 марта 2021. Архивировано 31 октября 2018 года.
- ↑ Convection — Heat Transfer. Engineers Edge. Дата обращения: 20 апреля 2009. Архивировано 18 ноября 2018 года.
- ↑ Transport Processes and Separation Principles. — Prentice Hall, 2003. — ISBN 0-13-101367-X.
- ↑ Radiation. Thermal-FluidsPedia. Thermal Fluids Central. Дата обращения: 9 марта 2021. Архивировано 14 марта 2021 года.
- ↑ Thermal Radiation Heat Transfer. — Taylor and Francis.
- ↑ Mojiri, A (2013). “Spectral beam splitting for efficient conversion of solar energy—A review”. Renewable and Sustainable Energy Reviews. 28: 654—663. DOI:10.1016/j.rser.2013.08.026.
- ↑ Taylor, Robert A. (March 2011). “Applicability of nanofluids in high flux solar collectors”. Journal of Renewable and Sustainable Energy. 3 (2): 023104. DOI:10.1063/1.3571565. Архивировано из оригинала 2021-04-19. Дата обращения 2021-03-09.
- ↑ Megan Crouse: This Gigantic Solar Furnace Can Melt Steel Архивная копия от 25 июля 2019 на Wayback Machine manufacturing.net, 28 July 2016, retrieved 14 April 2019.
Литература[править | править код]
- Григорьев Б. А., Цветков Ф. Ф. Тепломассообмен: Учеб. пособие — 2-е изд. — М: МЭИ, 2005.
- Исаченко В. П. и др. Теплопередача: Учебник для вузов. 3-е изд., перераб. и доп. — М.: Энергия, 1975.
- Галин Н. М., Кириллов П. Л. Тепломассообмен. — М.:Энергоатомиздат, 1987.
- Карташов Э. М. Аналитические методы в теплопроводности твердых тел. — М.: Высш. шк., 1989.
- Крупнов Б. А., Шарафадинов Н. С. Руководство по проектированию систем отопления, вентиляции и кондиционирования воздуха. 2008
- Котляр Я. М., Совершенный В. Д., Стриженов Д. С. Методы и задачи тепломассообмена. — М.: Машиностроение, 1987. — 320 с.
- Лыков А. В., Михайлов Ю. А. Теория переноса энергии и вещества. — Минск, АН БССР, 1959. — 330 с.
Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 12. Электростатические аналогии
Поток тепла. Точечный источник вблизи бесконечной плоской границы
Ранее мы уже обсуждали (гл. 3, § 4) поток тепла. Вообразите кусок какого-то материала, необязательно однородного (в разных местах может быть разное вещество), в котором температура меняется от точки к точке. Как следствие этих температурных изменений возникает поток тепла, который можно обозначить вектором h. Он представляет собой количество тепловой энергии, которое проходит в единицу времени через единичную площадку, перпендикулярную потоку. Дивергенция h есть скорость ухода тепла из данного места в расчете на единицу объема:
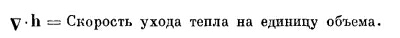
(Мы могли, конечно, записать уравнение в интегральном виде, как мы поступали в электродинамике с законом Гаусса, тогда оно выражало бы тот факт, что поток через поверхность равен скорости изменения тепловой энергии внутри материала. Мы не будем больше переводить уравнения из дифференциальной формы в интегральную и обратно, это делается точно так же, как в электростатике.)
Скорость, с которой тепло поглощается или рождается в разных местах, конечно, зависит от условий задачи. Предположим, например, что источник тепла находится внутри материала (возможно, радиоактивный источник или сопротивление, через которое пропускают ток). Обозначим через s тепловую энергию, производимую этим источником в единице объема за 1 сек. Кроме того, могут возникнуть потери (или, наоборот, дополнительное рождение) тепловой энергии за счет перехода в другие виды внутренней энергии в данном объеме. Если и — внутренняя энергия в единице объема, то —du/dt будет тоже играть роль «источника» тепловой энергии. Итак, имеем

Мы не собираемся здесь обсуждать полное уравнение, величины в котором изменяются со временем, потому что мы проводим аналогию с электростатикой, где ничто не зависит от времени. Мы рассмотрим только задачи с постоянным потоком тепла, в которых постоянные источники создают состояние равновесия. В таких случаях

Нужно иметь, конечно, еще одно уравнение, которое описывает, как поток течет в разных местах. Во многих веществах поток тепла примерно пропорционален скорости изменения температуры с положением: чем больше разность температур, тем больше поток тепла. Мы знаем, что вектор потока тепла пропорционален градиенту температуры. Константа пропорциональности К, зависящая от свойств материала, называется коэффициентом теплопроводности

Если свойства материала меняются от точки к точке, то К=К (х, у, z) и есть функция положения. [Уравнение (12.7) не столь фундаментально, как (12.5), выражающее сохранение тепловой энергии, потому что оно зависит от характерных свойств вещества.] Подставляя теперь уравнение (12.7) в (12.6), получаем

что в точности совпадает по форме с (12.4). Задачи с постоянным потоком тепла и задачи электростатики одинаковы. Вектор потока тепла h соответствует Е, а температура Т соответствует φ. Мы уже отмечали, что точечный тепловой источник создает поле температур, меняющееся, как 1/r, и поток тепла, меняющийся, как 1/r2. Это есть не более чем простой перенос утверждений электростатики, что точечный заряд дает потенциал, меняющийся, как 1/r, и электрическое поле, меняющееся, как 1/r2. Вообще мы можем решать статистические тепловые задачи с той же степенью легкости, как и задачи электростатики.
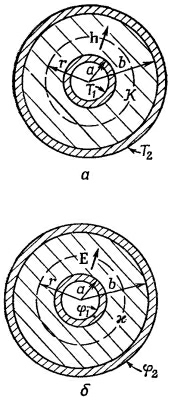 Рассмотрим простой пример. Пусть имеется цилиндр с радиусом а при температуре Т1, поддерживающейся за счет генерации тепла в цилиндре. (Это может быть, скажем, проволока, по которой течет ток, или трубка с конденсацией пара внутри цилиндра.) Цилиндр покрыт концентрической обшивкой из изолирующего материала с теплопроводностью К. Пусть внешний радиус изоляции равен b, а в наружном пространстве поддерживается температура Т2 (фиг. 12.1, а). Нам нужно определить скорость потери тепла проволокой или паропроводом (все равно чем), проходящим по центру цилиндра. Пусть полное количество тепла, теряемого на длине трубы L, равно G, его-то мы и хотим найти.
Рассмотрим простой пример. Пусть имеется цилиндр с радиусом а при температуре Т1, поддерживающейся за счет генерации тепла в цилиндре. (Это может быть, скажем, проволока, по которой течет ток, или трубка с конденсацией пара внутри цилиндра.) Цилиндр покрыт концентрической обшивкой из изолирующего материала с теплопроводностью К. Пусть внешний радиус изоляции равен b, а в наружном пространстве поддерживается температура Т2 (фиг. 12.1, а). Нам нужно определить скорость потери тепла проволокой или паропроводом (все равно чем), проходящим по центру цилиндра. Пусть полное количество тепла, теряемого на длине трубы L, равно G, его-то мы и хотим найти.
Как надо решать такую задачу? У нас есть дифференциальные уравнения, но поскольку они такие же, как в электростатике, то математическое решение их нам уже известно. Аналогичная задача электростатики относится к проводнику радиусом а при потенциале φ1 отделенном от другого проводника радиусом b при потенциале φ2, с концентрическим слоем диэлектрика между ними (фиг. 12.1, б). Далее, поскольку поток тепла h соответствует электрическому полю Е, то наша искомая величина G соответствует потоку электрического поля от единичной длины (другими словами, электрическому заряду на единице длины, деленному на ε0). Мы решали электростатическую задачу с помощью закона Гаусса. Нашу задачу о потоке тепла будем решать таким же способом.
Из симметрии задачи мы видим, что h зависит только от расстояния до центра. Поэтому мы окружим трубку гауссовой поверхностью — цилиндром длиной L и радиусом r. С помощью закона Гаусса мы выводим, что поток тепла h, умноженный на площадь поверхности 2πrL, должен быть равен полному количеству тепла, рождаемому внутри, т. е. тому, что мы назвали G:
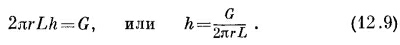
Поток тепла пропорционален градиенту температуры
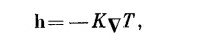
или в данном случае величина h равна
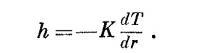
Вместе с (12.9) это дает

Интегрируя от r=a до r=b, получаем
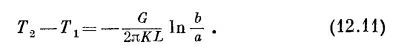
Разрешая относительно G, находим
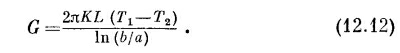
Этот результат в точности соответствует формуле для заряда цилиндрического конденсатора:
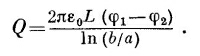
Задачи одинаковые и имеют одинаковые решения. Зная электростатику, мы тем самым знаем, сколько тепла теряет изолированная труба.
Рассмотрим еще один пример. Пусть мы хотим узнать поток тепла в окрестности точечного источника, расположенного неглубоко под поверхностью земли или же вблизи поверхности большого металлического предмета. В качестве локализованного источника тепла может быть и атомная бомба, которая взорвалась под землей и представляет собой мощный источник тепла, или же небольшой источник радиоактивности внутри железного блока — возможностей очень много.
Рассмотрим идеализированную задачу о точечном источнике тепла, мощность которого G, на расстоянии а под поверхностью бесконечной однородной среды с коэффициентом теплопроводности К. Теплопроводностью воздуха над поверхностью среды мы пренебрежем. Мы хотим определить распределение температуры на поверхности среды. Насколько горячо будет прямо над источником и в разных местах на поверхности?
Как же решить эту задачу? Она похожа на задачу по электростатике, в которой имеются два материала с разной диэлектрической проницаемостью х по обе стороны от разделяющей их границы. Здесь что-то есть! Возможно, это похоже на точечный заряд вблизи границы между диэлектриком и проводником или что-нибудь вроде этого. Посмотрим, что происходит вблизи границы. Физическое условие состоит в том, что нормальная составляющая h на поверхности равна нулю, поскольку мы предположили, что потока из блока нет. Мы должны задать вопрос: в какой электростатической задаче возникает условие, что нормальная компонента электрического поля Е (представляющая собой аналог h) равна нулю у поверхности? Нет такой!
Это один из тех случаев, к которым следует относиться с осторожностью. По физическим причинам могут быть определенные ограничения тех математических условий, которые возникают в каком-либо случае. Поэтому если мы проанализировали дифференциальное уравнение только для некоторых ограниченных примеров, то вполне можем упустить ряд решений, возникающих в других физических условиях. Например, нет материала, обладающего диэлектрической проницаемостью, равной нулю, а теплопроводность вакуума равна нулю. Поэтому нет электростатического аналога идеального теплоизолятора. Мы можем, однако, попытаться использовать те же методы. Попробуем вообразить, что произошло бы, если бы диэлектрическая проницаемость была равна нулю. (Разумеется, в реальных условиях диэлектрическая проницаемость никогда не обращается в нуль. Но может представиться случай, когда вещество имеет очень большую диэлектрическую проницаемость, так что диэлектрической проницаемостью воздуха вне среды можно пренебречь.)
Как же найти электрическое поле, у которого нет составляющей, перпендикулярной к поверхности? Иначе говоря, такое поле, которое всюду касательно к поверхности? Вы заметите, что эта задача обратна задаче о точечном заряде вблизи проводящей плоскости. Там нам нужно было поле, перпендикулярное к поверхности, потому что проводник всюду находился при одном и том же значении потенциала.
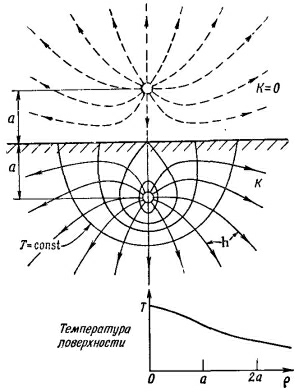 В задаче об электрическом поле мы придумали решение, вообразив за проводящей плоскостью точечный заряд. Можно воспользоваться снова этой же идеей. Попытаемся выбрать такое «изображение» источника, которое автоматически обращало бы в нуль нормальную компоненту поля вблизи поверхности. Решение показано на фиг. 12.2. Электрическое изображение источника с тем же знаком и той же величины, находящееся на расстоянии а над поверхностью, дает поле, горизонтальное повсюду у поверхности. Нормальные компоненты от обоих источников взаимно уничтожаются.
В задаче об электрическом поле мы придумали решение, вообразив за проводящей плоскостью точечный заряд. Можно воспользоваться снова этой же идеей. Попытаемся выбрать такое «изображение» источника, которое автоматически обращало бы в нуль нормальную компоненту поля вблизи поверхности. Решение показано на фиг. 12.2. Электрическое изображение источника с тем же знаком и той же величины, находящееся на расстоянии а над поверхностью, дает поле, горизонтальное повсюду у поверхности. Нормальные компоненты от обоих источников взаимно уничтожаются.
Итак, наша задача о потоке тепла решена. Температура во всем пространстве одинакова по непосредственной аналогии с потенциалом от двух одинаковых точечных зарядов. Температура Т на расстоянии r от одного точечного источника G в бесконечной среде равна

(Это, конечно, полностью аналогично φ= q/4πε0r.) Температура точечного источника и, кроме того, его изображения равна
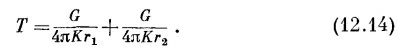
Эта формула дает нам температуру всюду внутри блока. Несколько изотермических поверхностей приведено на фиг. 12.2. Показаны также линии h, которые можно получить из выражения h = – КvТ.
В самом начале мы интересовались распределением температуры на поверхности. Для точки на поверхности, находящейся на расстоянии ρ от оси, r1 = r2 = √ρ2 + а2, следовательно,
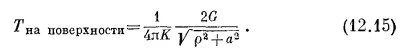
Эта функция также изображена на фиг. 12.2. Естественно, что температура прямо над источником выше, чем вдали от него. Такого рода задачи часто приходится решать геофизикам. Теперь мы видим, что это те же самые задачи, которые мы решали в электричестве.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
Начальной
стадией проектирования любой системы
теплоснабжения является определение
тепловых потоков и их требуемых
параметров. При этом существенным
моментом становится такое определение
расходов тепла, при котором сумма
расходов всеми потребителями системы
достигает максимального значения.
Отпуск суммарного максимального
теплового потока из тепловых сетей, с
учетом несовпадения максимумов у
отдельных потребителей и видов
потребления тепла при проектировании,
должен обеспечиваться надлежащим
выбором основного и вспомогательного
оборудования источников тепла, а также
соответствующих диаметров труб на
отдельных участках тепловых сетей.
Правильный расчет теплового потока
может оказать влияние и на величину
капитальных затрат, и на эксплуатационные
расходы.
Максимальные
тепловые потоки на отопление, вентиляцию,
горячее водоснабжение, технологические
процессы промышленных предприятий
принимаются при проектировании тепловых
сетей по соответствующим проектам. При
отсутствии проектов допускается
определять тепловые потоки по
рекомендациям СНиП 2.04.07-86. «Тепловые
сети».
Тепловые
потоки при отсутствии проектов отопления,
вентиляции и горячего водоснабжения
зданий и сооружений определяются:
–
для предприятий – по укрупненным
ведомственным нормам, утвержденным в
установленном порядке, либо по проектам
аналогичных предприятий;
–
для жилых районов городов и других
населенных пунктов – по формулам.
Максимальный
тепловой поток, на отопление жилых и
общественных зданий, Вт:
![]()
,
(3.1)
где
![]()
– укрупненный показатель максимального
теплового потока на отопление жилых
зданий на 1 м2
общей площади, Вт/м (табл. П.2.1);
![]()
– общая
площадь жилых зданий, м2;
![]()
– коэффициент,
учитывающий тепловой поток на отопление
общественных зданий,
= 0,25.
Общую
площадь жилых зданий
,
м2,
определяют,
исходя из жилой площади
![]()
,
квартала и безразмерного планировочного
коэффициента квартиры
![]()
,
который принимается равным 0,7:
![]()
.
(3.2)
Жилую
площадь квартала
,
м2,
можно найти двумя способами:
-
По
плотности жилого фонда

,
м2/га,
и площади квартала в гектарах:
![]()
.
(3.3)
-
Исходя
из плотности населения

,
чел/га и нормы жилой площади на человека

,
м/чел.
Количество
жителей
![]()
,
чел., и жилая площадь квартала:
![]()
,
(3.4)
![]()
.
(3.5)
Плотность
жилого фонда
,
м2/га,
принимают в зависимости от этажности
застройки (табл. П.2.1):
а)
максимальный
тепловой поток, Вт, на вентиляцию
общественных зданий –
![]()
,
(3.6)
где
![]()
– коэффициент, учитывающий тепловой
поток на вентиляцию общественных
зданий,
=
0,6;
– коэффициент,
учитывающий тепловой поток на отопление
общественных зданий,
= 0,25;
б)
средний тепловой поток, Вт, на горячее
водоснабжение жилых и общественных
зданий:
![]()
(3.7)
или
![]()
,
(3.8)
где
![]()
– укрупненный показатель среднего
теплового потока на горячее водоснабжение
на одного человека (табл. П.2.3.)
– число
жителей в квартале;
в)
максимальный тепловой поток, Вт, на
горячее водоснабжение жилых и общественных
зданий:
![]()
.
(3.9)
Число жителей в
квартале определяют двумя способами:
1.
Задаются нормой жилой площади на
человека
,
т.е.
= 9 м2
или
= 12м2,
тогда –
![]()
.
(3.10)
2.
Количество жителей, приходящихся на 1
га территории квартала (табл. П.2.1),
умножают на площадь квартала.
Определяя
расчетный расход теплоты для района
города, учитывают, что при транспортировке
теплоносителя происходят потери теплоты
в окружающую среду, которые принимаются
равными 5 % тепловой нагрузки. Поэтому
суммарные расходы тепла на отопление,
вентиляцию и горячее водоснабжение
умножают на коэффи-
циент 1,05.
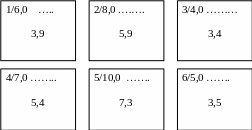
Рис.
3.3. План
района города:
Числитель
дроби – номер квартала; знаменатель –
площадь, га;
…-
этажность застройки; число в центре –
тепловая нагрузка квартала
ПРИМЕР
3.1. Определить
расчетные расходы теплоты на отопление,
вентиляцию и горячее водоснабжение
района города, включающего шесть
кварталов (рис. 3.3). Расчетная температура
наружного воздуха
to=
-25 oC.
Решение.
Расчет
теплопотребления сводим в табл. 3.1. В
графы 1, 2, 3 таблицы заносим соответственно
номер, этажность и площадь квартала в
гектарах. Плотность жилого фонда Р,
м/га,
(графа 4) находим по табл. П.3.1 в зависимости
от этажности застройки. Тогда жилая
площадь зданий квартала № 1 (графа 5):
Fж
= P.Fкв.
= 3200.6
= 19200 м2.
Приняв
безразмерный планировочный коэффициент
квартиры
К
=
0,7, находим общую площадь жилых зданий
квартала № 1
(графа 6):
А
= 19200/0,7 =
27428,6 м2.
Количество
жителей в квартале № 1 (графа 7) определяем,
принимая норму жилой площади на
одного человека
fж
= 9 м2:
m
= 19200/9 = 2133
чел.
Принимая
по табл. П.2.2., укрупненный показатель
максимального теплового потока на
отопление жилых зданий
qо
= 81 Вт/м2,
по
формуле
(3.1)
находим расчетный расход теплоты на
отопление жилых и общественных
зданий квартала № 1 (графа 8):
Qomax
=
81.27428,6.(1
+ 0,25) = 2777145,7 = 2777,1 кВт.
Максимальный
тепловой поток на вентиляцию общественных
зданий квартала № 1 (графа 9) определяем
по формуле (3.6):
Qvmax
=
0,25.0,6.81.27428,6
= 333257,5 = 333,2 кВт.
Принимая
норму расхода воды на горячее водоснабжение
в сутки на 1 человека а
=
105 л/сут, по табл. П.2.3. находим укрупненный
показатель среднего теплового потока
на горячее водоснабжение:
qh
= 376
Вт/чел.
Средний
тепловой поток на горячее водоснабжение
жилых и общественных зданий квартала
№ 1 (графа 10):
Qhm
= 376.2133
= 802008 = 802 кВт.
Суммарное
теплопотребление квартала № 1 (графа
11) складывается из расходов теплоты на
отопление, вентиляцию и горячее
водоснабжение.
Расчет
теплопотребления для остальных кварталов
производят аналогично. Расчет
теплопотребления в кварталах приведен
в
табл. 3.1.
Таблица
3.1
Расчет
теплопотребления в кварталах
|
№ квартала |
Этажность |
Площадь Fкв.,га |
Площадь |
Жилая Fж.,м2 |
Общая А,м2 |
Число
жителей
m |
Расходы |
|||
|
Qomax |
Qvmax |
Qhm |
ΣQ |
|||||||
|
1 |
5 |
6 |
3200 |
19200 |
27428,6 |
2133 |
2777,1 |
333,2 |
802,0 |
3912,3 |
|
2 |
7 |
8 |
3600 |
28800 |
41142,8 |
3200 |
4165,7 |
499,9 |
1203,2 |
5868,8 |
|
3 |
9 |
4 |
4200 |
16800 |
24000,0 |
1867 |
2430,0 |
291,6 |
702,0 |
3423,6 |
|
4 |
8 |
7 |
3800 |
26600 |
38000,0 |
2956 |
3847,5 |
461,7 |
1111,4 |
5420,6 |
|
5 |
7 |
10 |
3600 |
36000 |
51428,6 |
4000 |
5207,1 |
624,8 |
1504,0 |
7335,9 |
|
6 |
6 |
5 |
3400 |
17000 |
24285,7 |
1889 |
2458,9 |
295,1 |
710,3 |
3464,3 |
|
Итого: |
20886,3 |
2505,3 |
6032,9 |
29425,5 |
||||||
|
С в размере 5 % от Q |
21930,6 |
2631,6 |
6334,5 |
30896,7 |
Годовые
расходы теплоты на отопление, вентиляцию
и горячее водоснабжение определяют по
формулам:
![]()
,
(3.11)
![]()
,
(3.12)
![]()
,
(3.13)
где
![]()
– средние тепловые потоки на отопление
и вентиляцию за отопительный период.
Вт, рассчитываются по формулам:
![]()
,
(3.14)
![]()
,
(3.15)
где
![]()
– средняя температура наружного воздуха
за отопительный период, оС;
![]()
– средний
тепловой поток на горячее водоснабжение
в неотапливаемый период, Вт.
![]()
,
(3.16)
где
![]()
– температура горячей воды в системе
горячего водоснабжения потребителей,
оС;
![]()
– температура
холодной воды в отопительный период,
принимается равной 5
оС;
![]()
– температура
холодной воды в
неотапливаемый
период, принимается равной 15 оС;
![]()
– коэффициент,
учитывающий изменение среднего расхода
горячей воды летом по сравнению с зимним
периодом, для жилищно-коммунального
сектора
= 0,8, для курортных и южных городов
= 1,5;
8400
– количество
часов работы системы горячего
водоснабжения в году.
ПРИМЕР
3.2.
Построить графики часовых расходов
теплоты на отопление, вентиляцию и
горячее водоснабжение в зависимости
от температуры наружного воздуха.
Расчетные расходы теплоты:
на
отопление
Qomax
=
200 МВт, вентиляцию Qvmax
= 20
МВт, горячее водоснабжение
Qhm
=
50 МВт. Климатологические данные принять
для г. Воронежа. (рис. 3.4).

Рис.
3.4. График
годового расхода теплоты
Решение.
По
данным СНиП 23-01-99, находим для г. Воронежа
расчетную температуру наружного воздуха
для проектирования отопления, принимаемую
равной средней температуре наиболее
холодной пятидневки обеспеченностью
0,92 согласно СНиП 23-01-99
to
= -25 0С.
Графики
часовых расходов теплоты строим в
координатах
(Q–
tн
) (рис.
3.4, правая часть).
При to
= -25 0С:
Qomax
= 200 МВт;
Qvmax
=
20
МВт;
Qhm
=
0 МВт.
При
tн
=
8 0С
по формулам (3.7, 3.8):
Qо+8
= 200.(18
– 8)/(18 + 25) = 46,5 МВт;
Qv
= 20.(18
– 8)/(18 + 25) = 7,1 МВт.
Отложив
на графике значения Qо
и
Qv
при различных tн
и соединив их прямой, получим графики
Qо=f
(tн),
Qv=
f
(tн),
(см.
рис. 3.4).
Расход
теплоты на горячее водоснабжение не
зависит от tн,
поэтому его график представляет прямую,
параллельную оси абсцисс – прямая Qhm.
График
суммарного часового расхода теплоты
на отопление, вентиляцию и горячее
водоснабжение строим путем сложения
соответствующих ординат при tн
=
8 0С
и to
= -25 0С
(линия Σ Q).
ПРИМЕР
3.3.
Построить график годового расхода
теплоты по продолжительности стояния
температур наружного воздуха для жилого
района города. График суммарного
часового расхода теплоты и климатологические
данные взять из примера 3.2.
Решение.
По
СНиП 23-01-99 находим продолжительность
отопительного периода для г. Воронежа
п0
=
203 сут = 4872 час, продолжительность стояния
температур наружного воздуха в часах
с интервалом 5 °С в течение отопительного
периода. Данные сводим в табл. 3.2.
Таблица
3.2
Продолжительность
стояния температур наружного воздуха
|
Продолжитель-
ность
п, |
Температура |
|||||||
|
-30-25 |
-25-20 |
-20-15 |
-15-10 |
-10-5 |
-5-0 |
0-+5 |
+5-+8 |
|
|
n |
19 |
51 |
158 |
395 |
696 |
1375 |
1542 |
636 |
|
Σ |
19 |
70 |
228 |
623 |
1319 |
2694 |
4236 |
4872 |
График
годовой тепловой нагрузки строим на
основании графика суммарных часовых
расходов теплоты, располагая его справа,
а в левой части, в координатах (Q–n)
–
график годового расхода теплоты (см.
рис. 3.4).
Для
построения графика годовой тепловой
нагрузки из точек на оси абсцисс графика
часового расхода теплоты, соответствующих
температурам +8, 0, -5, -10, -15, -20, -25 °С,
восстанавливаем перпендикуляры до
пересечения с линией суммарного расхода
теплоты ΣQ.
Из
полученных
точек проводим горизонтальные прямые
до пересечения с перпендикулярами,
восстановленными к оси абсцисс из
точек, соответствующих продолжительности
стояния температур наружного воздуха.
Соединив
найденные точки, получим искомый график
годового расхода теплоты за отопительный
период.
В
летний период (диапазон продолжительности
стояния
tн
от 4872 до 8400 час) тепловые нагрузки на
отопление и вентиляцию отсутствуют,
нагрузка на горячее водоснабжение
согласно формуле (3.16) составит:
QShm=50.0,8.(55-15)/(55-5)=32
МВт.
Поскольку
QShm
в летний период не зависит от tн,
проводим горизонтальную прямую до
пересечения с ординатой, соответствующей
общему расчетному числу часов работы
тепловой сети в году
n
=
8400 час.
Площадь,
ограниченная осями координат (Q–n)
– и полученной
кривой расхода теплоты, представляет
собой годовой расход теплоты в районе
города.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #








