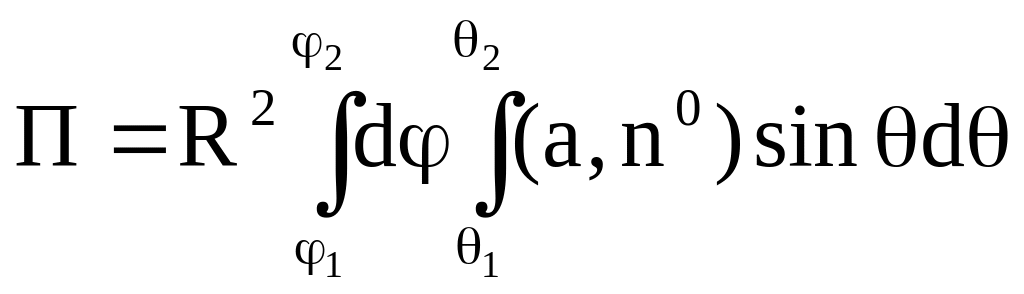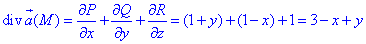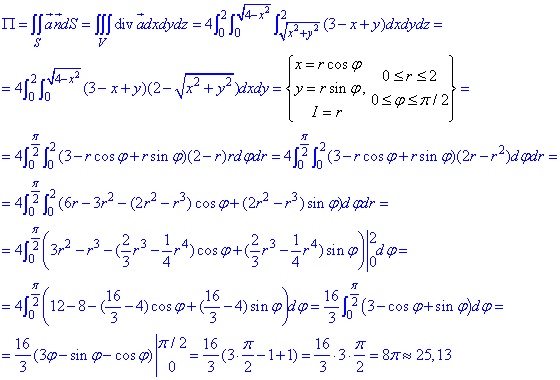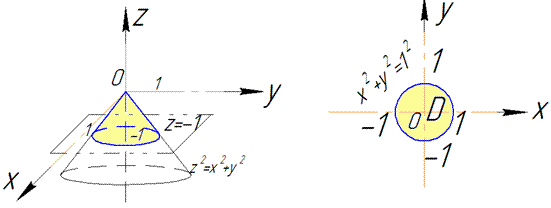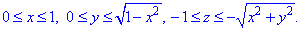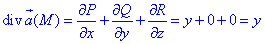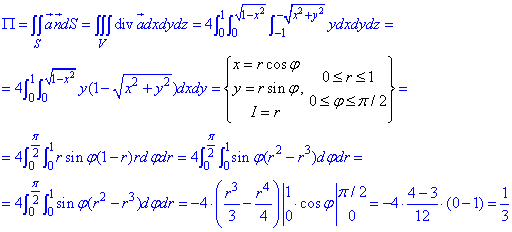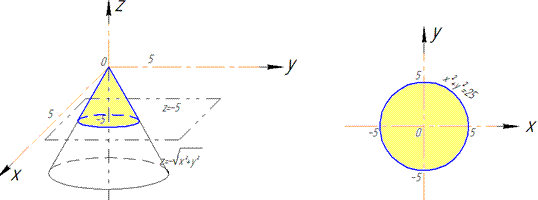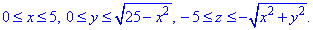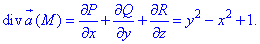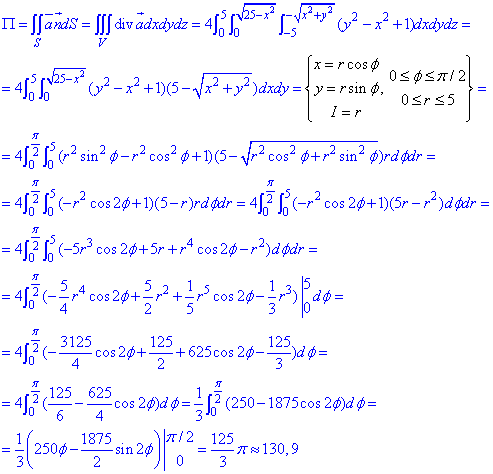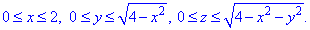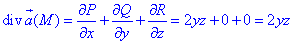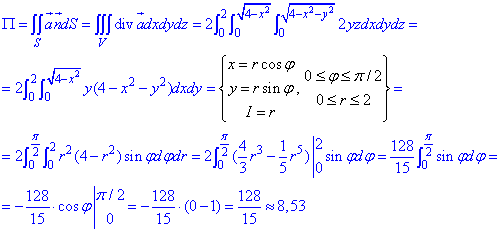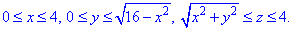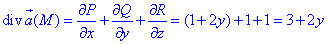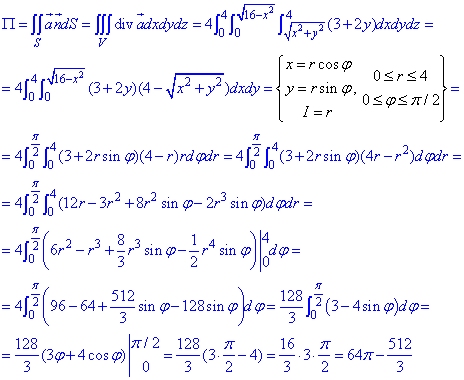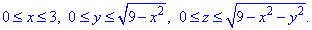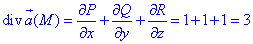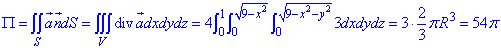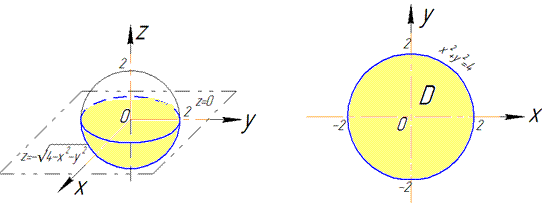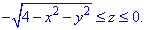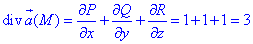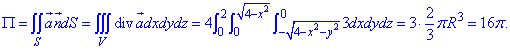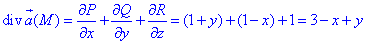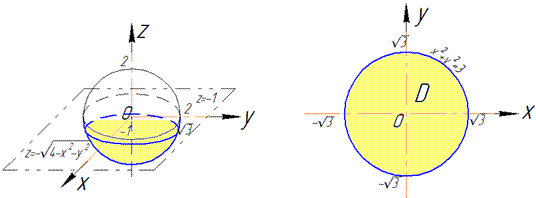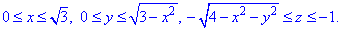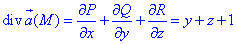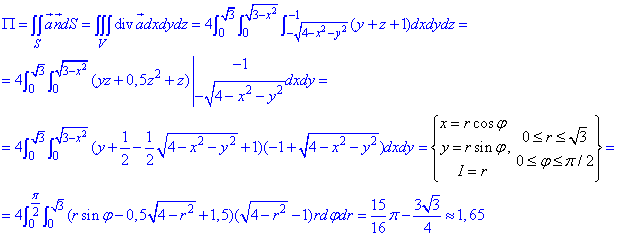Как найти поток векторного поля через плоскость

2.1.1. Вычисление методом проектирования на одну

из координатных
плоскостей

Пусть поверхность

задана уравнением

.

Единичный вектор
нормали

,
но, как известно,

.
Следовательно,

.

Знак в правой части
берется так, чтобы получить нормальный
вектор

именно к выбранной стороне поверхности.

Если поверхность
задана уравнением

,
то

.

Знак «+» соответствует
выбору верхней стороны поверхности,
нормаль к которой образует острый угол
с осью

и, следовательно, направляющий косинус
положителен.

Известно также,
что

и

.

Пусть поверхность

взаимно однозначно проектируется на
плоскость

в область

,
тогда вычисление потока векторного
поля через поверхность

сводится к вычислению двойного интеграла

по области

:

.
(2.2)

Аналогично, если
поверхность

взаимно однозначно проектируется на
плоскость

или

,
то поток вычисляется по формулам

;

.

Пример 2.1. Найти
поток векторного поля

через поверхность конуса

и плоскость

.

Решение. Обозначим
потоки векторного поля:

через

боковую
поверхность конуса

и

через плоскость

.

Тогда
весь поток П=П₁
+П₂ =

.

Вычислим

.
Уравнение

:

.

Проекция вектора

на ось

отрицательна.

;

.

Из выражения для
(2.2.) найдем

.

.

Вычислим

.
Уравнения поверхности

:

,

,

(На поверхности

),

.

Следовательно,

.

Пример 2.2. Найти
поток векторного поля

через верхнюю сторону треугольника с
вершинами в точках

,

,

.

Решение. Уравнение
плоскости

составим как уравнение

плоскости,
проходящей через три точки

.
Следовательно,

,

.

.

Пример 2.3. Вычислить
поток векторного поля

через внешнюю
сторону однополостного гиперболоида

,ограниченного плоскостями

.

Решение. Данная
поверхность проектируется взаимно
однозначно на плоскость

в область

,
ограниченную окружностями

и

.

Находим внешнюю
нормаль

:


.

Т
.к.

образует с осью

тупой угол

(рис.2.4),
то берем знак минус и, значит,

.

Находим скалярное
произведение


.

Применяя формулу

,

получим

Рис.2.4

.

Переходя к полярным
координатам

,
,
будем иметь

2.1.2. Вычисление потока методом проектирования

на все
три координатные плоскости

Пусть поверхность

взаимно однозначно проектируется на
все три координатные плоскости:

Тогда поток
векторного поля

равен

(2.3.)

где знак перед
каждым из двойных интегралом берется
соответственно таким, каков знак

,

,

на поверхности

.

Пример 2.3. Найти
поток векторного поля

через треугольник, получаемый при
пересечении плоскости

с координатными плоскостями (выбор
указан на рис. 2.5).

Р
ешение.
Найдем

.
P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z

(выразили
из уравнения плоскости)

.

По
формуле (2.3) получим

Рис. 2.5

.

При вычислении
потока векторного поля через боковую
поверхность кругового цилиндра или
через сферу удобно пользоваться
соответственно цилиндрическими или
сферическими координатами.

Пример 2.4. Найти
поток векторного поля

через часть
сферической поверхности

,
расположенную в первом октанте.

Решение. Найдем
вектор- градиент

,

тогда единичный
вектор

;

.

По условию задачи
поверхность находится в первом октанте,
т.е.

,

,
элемент площади в сферических координатах
равен

.
Следовательно, поток через часть сферы
вычисляется по формуле

.

2.1.3. Вычисление
потока методом введения

криволинейных
координат на поверхности

В некоторых случаях
при вычислении потока векторного поля
через данную поверхность
S
возможно выбрать на самой поверхности
простую систему координат, в которой
удобно вычислять поток, не применяя
проектирования на координатные плоскости.

Рассмотрим частные
случаи.

Случай 1). Пусть
поверхность S
является частью кругового цилиндра

,
ограниченного поверхностями

и

.

Полагая

,
будем иметь для данной поверхности

,

, а для элемента
площади dS
получаем следующее выражение (рис.
2.6.):

.

Тогда поток
векторного поля a

через
внешнюю сторону поверхности S

вычисляется по
формуле

,
(2.4)

где

Рис. 2.6

Пример 2.5. Вычислить
поток радиуса-вектора

через боковую
поверхность кругового цилиндра

,
ограниченного снизу плоскостью

,
а сверху – плоскостью

.

Р
ешение.
В данном случае (рис. 2.7) имеем

.

Переходя
к координатам на цилиндре

,
будем иметь

,

Согласно
формуле (2.4) поток вектора r

будет
равен

Но
так как на цилиндре

Рис.
2.7

то

и,
следовательно,

Случай 2). Пусть
поверхность S является
частью сферы

,
ограниченной коническими поверхностями,
уравнения которых в сферических
координатах имеют вид

и
полуплоскостями

.

Положим для точек
данной сферы

г
де

.

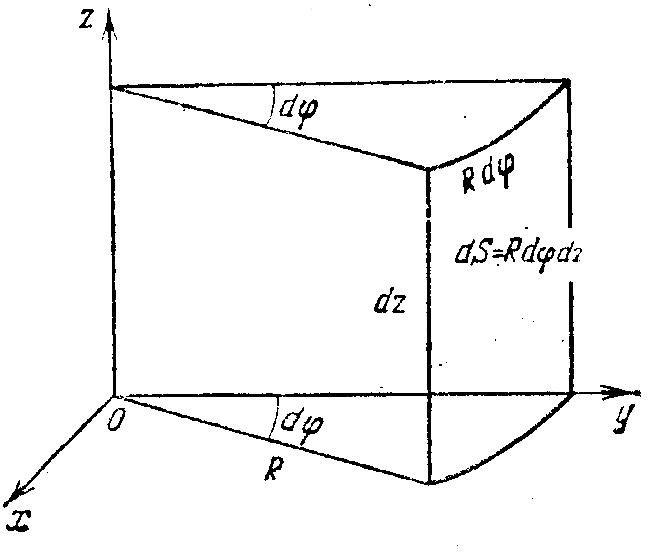
Тогда для элемента
площади dS
полу- чим (рис. 2.7)

.

В этом случае поток
векторного поля а
через внешнюю часть S
сферы вычисляется по формуле

, ( 2.5)

Рис. 2.8
где

Пример 2.6. Найти
поток вектора

через
часть поверхности сферы

,
расположенную в первом октанте, в
область, где

.

Решение. В данном
случае имеем

,

,

Введем
на сфере

координаты

и

так, что

Тогда
будет иметь

и,
применяя формулу (2.5), получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Формула Остроградського-Гаусса имеет широкое приложение в математике, физике, химии.
Дальше будут приведенные ответы к примерам по интегрированию, которые предусматривают нахождение потока векторного поля через дивергенцию.
В большинстве заданий вычисления двойных интегралов предусматривает замену переменных, а точнее – переход к полярной системе координат. Это упрощает подынтегральные выражения, однако ведет к пересчету пределов интегрирование.
На словах это легко понять, однако на практике необходимо анализировать приведенные примеры на формулу Остроградського-Гаусса и много решать самостоятельно, чтобы разобраться в теме.

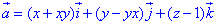
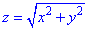
Пример 7.1 Найти поток векторного поля через часть поверхности S:
, что отсекается плоскостью P:
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 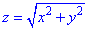– коническая поверхность с вершиной в точке (0;0;0), которая вытянута вдоль оси Oz.
z=2 – плоскость параллельная к плоскости Oxy. (шапка).
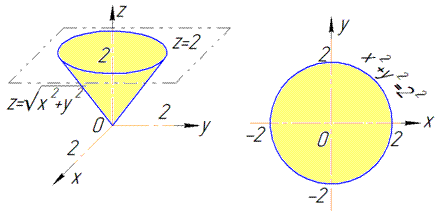
Приведены поверхность и плоскость изобразим в пространстве

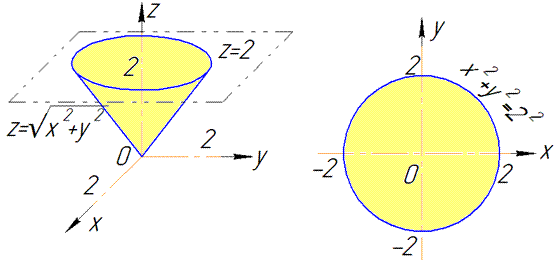
В сечении с конусом получим круг радиуса R=2.
Как видим из рисунка, четверть области V задается следующими пределами:

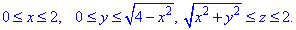
Здесь учли четность всех функций, поєтому результат интегрирования умножим на 4.
Вычислим дивергенцию векторного поля :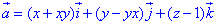

где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
Последние функции берем из a.
Найдем поток векторного поля за формулой Остроградського-Гаусса:

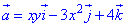
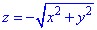
Пример 7.3 Найти поток векторного поля через часть поверхности S:

, что отсекается плоскостью P:
z=-1 (нормаль внешня к замкнутой поверхности, образованной данным сечением).
Решение: 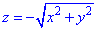– коническая поверхность (нижняя часть) с вершиной в начале координат (0;0;0), которая вытянута вдоль оси Oz.
z=-1 – плоскость параллельная к Oxy.

В сечении с конусом получим круг радиуса R=1.
Как видим из рисунка четверть области V задается следующими пределами:

Здесь учли четность всех функций, поэтому результат интегрирования будем умножать на 4.
Находим дивергенцию векторного поля :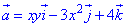

где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x², R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем тройной интеграл:

Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.

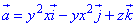
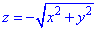
Пример 7.4 Вычислить поток векторного поля через часть поверхности S: , что вырезается плоскостью P:
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 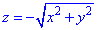– задает коническую поверхность с вершиной в точке(0;0;0), которая вытянута вдоль оси Oz.
z=-5 – плоскость параллельная к плоскости Oxy.

В сечении с конусом получим круг радиуса R=1.
Из рисунка следует что четверть области V задается следующими пределами:

Здесь учитываем четность функций, поэтому результат будем множить на 4.
Находим дивергенцию векторного поля :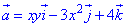

где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x², R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем поток поля :

Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.

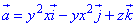
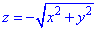
Пример 7.5 Вычислить поток векторного поля через часть поверхности S:
, что вырезается плоскостью P:
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 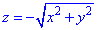– задает коническую поверхность с вершиной (0;0;0), которая вытянута вдоль оси Oz.
z=-5 – плоскость, какая параллельная к плоскости Oxy.

В сечении с конусом получим круг радиуса R=5.
Как видим из рисунка четверть области V задается следующими пределами:
Принимая во внимание четность всех функций, можем сузить область интегрирования, а результат умножить на 4.
Дивергенция векторного поля 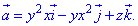равна

где P=P(x;y;z)=y²x, Q=Q(x;y;z)=-yx², R=R(x;y;z)=z.
Поток поля находим переходом к двойному интегралу по формуле:

Опять имеем замену переменных под интегралом. Этот прием является незаменимым при нахождении интегралов по поверхностям вращения – подынтегральные функции и пределы упрощаются, отпадает потребность бороться с корнями и выискивать экзотические формулы интегралов из справочников.

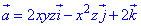
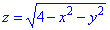
Пример 7.7 Найти поток векторного поля через часть поверхности S:
, что отсекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Сведем поверхность 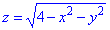к каноническому виду z²=4-x²-y², x²+y²+z²=2²– сфера (верхняя половина) с центром в (0;0;0) и радиусом R=2.
z=0 – плоскость параллельная к плоскости Oxy.

В сечении со сферой получим круг с центром в (0;0;0) и радиусом R=2.
Из рисунку видим четверть области V задается следующими пределами:

Здесь учли четность всех функций поэтому результат будем множить на 2.
Вычисляем дивергенцию :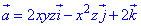

где P=P(x;y;z)=2xyz, Q=Q(x;y;z)=-x²z, R=R(x;y;z)=2.
Поток векторного поля определяем через формулу Остроградського-Гаусса:

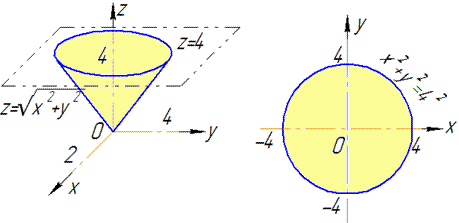
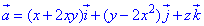
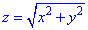
Пример 7.8 Найти поток векторного поля через часть поверхности S:
, что вырезается плоскостью P:
z=4 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 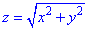описывает коническую поверхность с вершиной в начале координат (0;0;0), вытянутую вдоль оси Oz.
Сечение z=4 – плоскость параллельная к плоскости Oxy.

В сечении с конусом получим круг радиуса R=4.
Как видим из рисунка, четверть области V задается следующими пределами:

Четность всех функций позволяет искать интеграл на меньшей поверхности, затем результат нужно будет умножить на 4.
Дивергенцию векторного поля 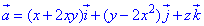определяем по формуле:

где P=P(x;y;z)=x+2xy, Q=Q(x;y;z)=y-2x², R=R(x;y;z)=z.
Интегрированием вычисли поток векторного поля :

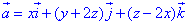
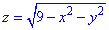
Пример 7.14 Определить поток векторного поля через часть поверхности S:
, что отсекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 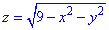– описывает верхнюю часть полусферы с центром в (0;0;0) и радиусом R=3.
В сечении с плоскостью z=0 получим круг радиуса R=3.

Четверть области V задается следующими пределами:

Принятие во внимание четности функций позволяет записать пределы лишь в четверти области, потому поток необходимо умножить на 4.
Посчитаем дивергенцию поля :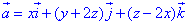

где P=P(x;y;z)=x, Q=Q(x;y;z)=y+2z, R=R(x;y;z)=z-2x.
Применяем формулу Остроградського-Гаусса для определения потока векторного поля :

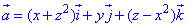
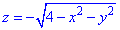
Пример 7.15 Найти поток векторного поля через часть поверхности S:
, что пересекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Поверхность 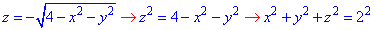– сфера (нижняя часть) с центром в начале декартовой СК (0;0;0) и радиусом R=2.

В сечении плоскости z=0 со сферой получим круг радиуса R=2.
Четверть области V задается следующими пределами:
и
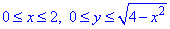
Результат интегрирования необходимо умножить на 4, поскольку учитываем четность функций.
Вычислим дивергенцию векторного поля :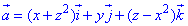

где функции P=P(x;y;z)=x+z², Q=Q(x;y;z)=-y, R=R(x;y;z)=z-x².
Интегрированием находим поток векторного поля :

Он равен P=16pi.

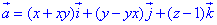
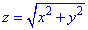
Пример 7.16 Найти поток векторного поля через часть поверхности S:
, что отсекается плоскостью P:
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Корневая зависимость 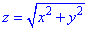– задает коническую поверхность с вершиной в точке (0;0;0), которая вытянута вдоль оси Oz.
z=2 – плоскость параллельная к плоскости Oxy.
В сечении с конусом получим круг радиусом R=2.

Четверть области V задается следующими пределами: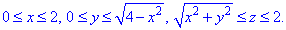

Четность функций учтена, поэтому результирующий интеграл нужно умножить на четверку.
Вычислим дивергенцию векторного поля :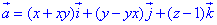

где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
За формулой Остроградського-Гаусса вычисляем поток векторного поля :
Алгоритм вычисления двойных интегралов из примера в пример не изменяется.
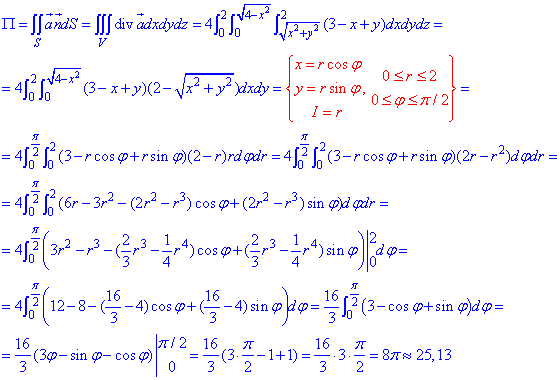
Переход к полярной системе координат при интегрировании Вы должны хорошо знать, такой прием позволяет упростить широкий класс интегралов, а дальнейшие вычисления свести к простым интегралам от показательных  и тригонометрических функций. В отдельных случаях Вам придется применять формулы понижение степеней для перехода от квадратов синусов и косинусов к их первым степеням.

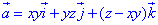
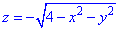
Пример 7.24 Вычислить поток векторного поля через часть поверхности S:
, что отсекается плоскостью P:
z=-1 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
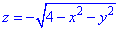
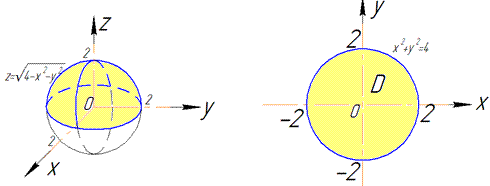
Решение: Превращаем уравнение поверхности к каноническому виду
z^2=4-x^2-y^2, x^2+y^2+z^2=2^2 – сфера (нижняя часть) с центром в начале координат (0;0;0) и радиусом R=2.
z=-1 – плоскость параллельная к плоскости Oxy.

В сечении со сферой получим круг радиусом корень из трех
Четверть области V задается следующими пределами:

В силу четности функций, выписываем пределы лишь на 1/4 поверхности сферы.
Дивергенция векторного поля 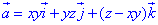через частичные производные равна:

где функции P=P(x;y;z)=xy, Q=Q(x;y;z)=yz, R=R(x;y;z)=z-xy.
Поток векторного поля определяем из двойного интеграла:

На этом ознакомление с примерами на вычисление потока векторного поля не завершается, больше готовых ответов Вы найдете на соседних страницах.

Поток вектора через незамкнутую поверхность. Теорема Гаусса—Остроградского

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Укажем некоторые способы вычисления потока вектора через незамкнутые поверхности. 1. . Пусть поверхность 5 однозначно проектируется на область Dxy плоскости хОу. В этом случае поверхность S можно задать уравнением вида Орт п° нормали к поверхности S находится по формуле Если в формуле (1) берется знак« то угол 7 между осью Oz и нормалью острый; если же знак то угол 7 — тупой.

Так как элемент площади этой поверхности равен то вычисление потока П через выбранную сторону поверхности 5 сводится к вычи-слениюдвойного интеграла по формуле Символ Поток вектора через незамкнутую поверхность метод проектирования на одну из координатных плоскостей Метод проектирования на все координатные плоскости Метод введения криволинейных координат на поверхности Поток вектора через замкнутую поверхность.

Теорема Гаусса—Остроградского означает, что при вычислении в подынтегральной функции надо вместо z всюду поставить f(x> у). Пример 1. Найти поток вектора через часть поверхности параболоида z = s2 + y2, отсеченной плоскостью z = 2. По отношению к области, ограниченной параболоидом, берется внешняя нормаль (рис. 15). Данная поверхность проектируется на круг плоскости хОу с центром в начале координат радиуса .

Находим орт п° нормали к параболоиду: Согласно условию задачи вектор п° образует с осью Oz тупой угол 7, поэтому перед дробью следует взять знак минус. Таким образом, Находим скалярное произведение , значит, Согласно формуле (3) Вводя полярные координаты где получаем Если поверхность 5 проектируется однозначно на область плоскости yOz, то ее можно задать уравнением х = г). В этом случае имеем Наконец, если поверхность S проектируется однозначно на область Dxz плоскости xOzy то ее можно задать уравнением и тогда Знак « + » перед дробью в формуле (10) означает, чтоугол /3 между осью Оу и вектором нормали п° — острый, а знак «-», что угол /3 — тупой.

Замечание. Для нахождения потока вектора через поверхность 5, заданную уравнением г = /(х,у), методом проектирования на координатную плоскость хОу, не обязательно находить орт п° нормали, а можно брать вектор Тогда формула (2) для вычисления потока П примет вид: Аналогичные формулы получаются для потоков через поверхности, задэнные уравнениями Пример 2. Вычислить поток вектора а = хг через внешнюю сторону параболоида ограниченного плоскостью.

Имеем Так как угол 7 — острый, следует выбрать знак « + ». Отсюда Искомый поток вычисляется так: Переходя к полярным координатам , получим Метод проектирования на все координатные плоскости. Пусть поверхность S однозначно проектируется на все три координатные плоскости. Обозначим через Dzy, Dxz, Dyz проекции 5 на плоскости хОу, xOz, yOz соответственно. В этом случае уравнение F у, z) = 0 поверхности S однозначно разрешимо относительно каждого из аргументов, т. е.

Возможно вам будут полезны данные страницы:

Тогда погок вектора к через поверхность S, единичный вектор нормали к которой равен можно записать так: Известно, что причем знак в каждой из формул (14) выбирается таким, каков знак на поверхности S. Подставляя соотношения (12) и (14) в формулу (13), получаем, что Пример 3. Вычислить поток векторного поля через треугольник, ограниченный плоскостями 4 Имеем так что Значит, перед всеми интегралами в формуле (15) следует взять знак « + ».

Полагая получим Вычислим первый интеграл в правой части формулы (16). Область Dvz —треугольник ВОС в плоскости yOz, уравнение стороны . Имеем Аналогично получим . Значит, искомый поток равен 3. Метод введения криволинейных координат на поверхности. Если поверхность 5 является частью кругового цилиндра или сферы, при вычислении потока удобно, не применяя проектирования на координатные плоскости, ввести на поверхности криволинейные координаты. А.

Поверхность 5 является частью кругового цилиндра ограниченного поверхностями будем иметь Элемент площади поверхности выражается так: и поток вектора а через внешнюю сторону поверхности 5 вычисляется по формуле: где 4. Найти поток вектора через внешнюю сторону поверхности цилиндра ограниченной плоскостями Так как то скалярное произведение (а, п°) на цилиндре равно: Тогда по формуле (18) получим В.

Поверхность 5 является частью сфсры офаничснной коническими поверхностями, уравнения которых в сферических координатах имеют вид и полуплоскостями.

Точки данной сферы описываются соотношениями где Поэтому элемент площади В этом случае поток векторного поля а через внешнюю часть поверхности 5 вычисляется по формуле где Пример 5. Найти поток вектора через внешнюю часть сферы Положим Тогда скалярное произведение выразится так: По формуле (21) получим.

Замечание:

Здесь мы воспользовались формулой Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского Теорема 4.

Если в некоторой области G пространства R3 координаты вектора непрерывны и имеют непрерывные частные производные , то поток вектора а через любую замкнутую кусочно-гладкую поверхность S, лежащую в области G, равен тройному интегралу от дх ду dz по области V, ограниченной поверхностью S: Здесь — орт внешней нормали к поверхности, а символ означает поток через замкнутую поверхность 5. Эта формула называется формулой Гаусса—Остроградского.

Рассмотрим сначала векгор а, имеющий только одну компоненту а = R(x, у, z)k, и предположим, что гладкая поверхность 5 пересекается каждой прямой, параллельной оси Oz, не более чем в двух точках. Тогда поверхность 5 разбивается на две части 5| и 52, однозначно проектирующиеся на некоторую область D плоскости хОу (рис.21). Внешняя нормаль к поверхности 52 образует острый угол 7 с осью Oz, а внешняя нормаль к поверхности 51 образует тупой угол с осью Oz.

Поэтому cos так что на 52 имеем 7. В силу аддитивности потока имеем Пусть da — элемент площади на поверхности S. Тогда

элемент площади области D. Сведем интегралы по поверхности к двойным интегралам по области D плоскости хОу, на которую проектируются поверхности Si и S2. Пусть S2 описывается уравнением — уравнением z = z(x>y). Тогда Так как приращение непрерывно дифференцируемой фунмции можно представить как интеграл от ее производной то для функции R(x, у, z) будем иметь.

Пользуясь этим, получаем из формулы (3) Поток вектора через незамкнутую поверхность метод проектирования на одну из координатных плоскостей Метод проектирования на все координатные плоскости Метод введения криволинейных координат на поверхности Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского Если поверхность S содержит часть цилиндрической поверхности с образующими, параллельными оси Oz (рис. 22), то на этой части поверхности (Як, п°) = 0 и интеграл / da по ней равен нулю.

Поэтому формула (4) остается

справедливой и для поверхностей, содержащих указанные цилиндрические части. Формула (4) переносится и на случай, когда поверхность S пересекается вертикальной прямой более, чем в двух точках (рис. 23). Разрежем область V на части, поверхность каждой из которых пересекается вертикальной прямой не более чем в двух точках, и обозначим через Sp поверхность разреза.

Пусть S и S2 — те части поверхности 5, на которые она разбивается разрезом 5Р, a V и Vj — соответствующие части области V, ограниченные поверхностями . Здесь Sp означает, что вектор нормали к разрезу Sp направлен вверх (образует с осью Oz острый угол), a Sp — что этот вектор нормали направлен вниз (образует с осью Oz тупой угол). Имеем: Складывая полученные равенства и пользуясь аддитивностью потока и тройною интеграла, получим (интегралы по разрезу взаимно уничтожаются).

Рассмотрим, наконец, вектор Для каждой компоненты Лк мы можем написать формулу, аналогичную формуле (4) (все компоненты равноправны). Получим Складывая эти равенства и пользуясь линейностью потока и тройного интеграла, получаем формулу Гаусса—Остро градского Пример 1. Вычислить поток век-гора через замкнутую поверхность по определению, 2) по формуле Остроградского. 4 1)

Поток вектора а равен сумме на поверхности Si), на поверхности S2 К так как Перейдем на цилиндре к криволинейным координатам Тогда 2) По формуле Гаусса—Остроградского имеем Пример 2. Вычислить поток радиус-вектора через сферу радиуса R с центром 8 начале координат: 1) по определению; 2) по формуле Остроградского. Так как для сферы и поэтому 2) Сначала находим Отсюда Пример 3.

Вычислить поток вектора через замкнугую поверхность S, заданную условиями: 1) по определению; 2) по формуле Острогрздя ого (рис.25). Имеем Значит, Поэтому Итак, Имеем Поэтому Переходя к цилиндрическим координатам и замечая,на поверхности 5, имеем Замечание . При вычислении потока через незамкнутую поверхность часто бывает удобно подходящим образом дополнить седо замкнутой и воспользоваться формулой Гаусса—Ос гроградского.

Пример 4:

Вычислить поток вектора Заданная поверхность S есть конус с осыо Оу (рис.26). Замкнем этот конус куском £ плоскости у – I. Тогда, обозначая через П| искомый поток, а через Н2 поток по поверхности будем иметь где V — объем конуса, ограниченного поверхностями S Поток вектора через незамкнутую поверхность метод проектирования на одну из координатных плоскостей Метод проектирования на все координатные плоскости Метод введения криволинейных координат на поверхности Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского Так как на поверхности Е выполняется равенство у = 1. Следовательно, ITj

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Поток векторного поля: теория и примеры

Понятие потока векторного поля и его вычисление как поверхностного интеграла

Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.

Пусть в некоторой области пространства задано векторное поле

и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора – непрерывные функции координат x, y, z точки M.

Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл

.

Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода

.

.

поток векторного поля можно вычислить и как поверхностный интеграл второго рода

.

Направление и интенсивность потока векторного поля

Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.

Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля – это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.

Если поток векторного поля – поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k – коэффициент теплопроводности, а u(M) – температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .

Вычисление потока векторного поля: примеры

Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy – треугольник AOB .

Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:

.

Длина вектора нормали:

.

Единичный вектор нормали:

.

Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .

Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:

Выразим переменную “зет”:

Продолжаем вычислять интеграл и, таким образом, поток векторного поля:

Получили ответ: поток векторного поля равен 64.

2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем

.

Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:

Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:

Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:

Осталось только сложить все три интеграла:

.

Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.

Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.

1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:

.

Длина этого вектора:

,

единичный вектор нормали (орт):

.

Скалярное произведение векторного поля и единичного нормального вектора:

Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода

.

Выразим “зет” и продифференцируем то, что уже можно продифференцировать:

2) Представим поток векторного поля в виде поверхностного интеграла второго рода:

.

Первый и второй интегралы берём со знаком “минус”, так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.

Вычисляем первый интеграл:

Вычисляем второй интеграл:

Вычисляем третий интеграл:

Складываем три интеграла и получаем тот же самый результат:

.

Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .

Поток векторного поля представим в виде поверхностного интеграла второго рода:

Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:

Вычисляем второй интеграл:

В сумме получаем искомый поток векторного поля:

.

Поток вектора через поверхность

Эта тема будет полезна для понимания теоремы Гаусса .

Коротко. Основная информация

Нормалью к поверхности называется вектор единичной длины n ⃗ vec n ⃗ , перпендикулярный поверхности.

Для плоской поверхности вектор нормали в каждой точке одинаков.

Если поверхность не плоская, то нормаль определяется для каждой точки поверхности путем выделения настолько малого элемента поверхности △ S triangle S △ S , окружающего эту точку, что его можно приближенно считать плоским.

Для замкнутых выпуклых поверхностей принято брать в качестве нормали вектор, обращенный наружу области, ограниченной поверхностью.

Понятие потока вектора (векторного поля) через поверхность используется в различных разделах физики. В частности, говорят о потоке вектора напряженности E ⃗ text< >vec E ⃗ или о потоке вектора магнитной индукции B ⃗ vec B ⃗ .

Наглядное представление об этом понятии дает такой пример.
Рассмотрим проволочную плоскую рамку, погруженную в поток воды. Количество протекающей через рамку воды зависит от площади рамки, скорости потока и ориентации рамки относительно потока (если плоскость рамки перпендикулярна потоку, количество воды максимально для данной точки, если плоскость сонаправлена с потоком воды, вода через рамку не протекает).

[spoiler title=”источники:”]

http://function-x.ru/fields_stream.html

http://lampa.io/p/%D0%BF%D0%BE%D1%82%D0%BE%D0%BA-%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B0-%D1%87%D0%B5%D1%80%D0%B5%D0%B7-%D0%BF%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D1%8C-00000000580fa49d7f243c0e1921bf05

[/spoiler]