![]() – масса вещества, переносимого через
– масса вещества, переносимого через
площадь
![]() ,
,
перпендикулярную движению частиц, в
единицу времени.
2. Плотность потока вещества – масса вещества, переносимого через единицу площади, перпендикулярной движению частиц, за единицу времени.
Молекулы жидкости перескакивают из
одного равновесного состояния в другое.
В одном из равновесных состояний поместим
площадку
![]() и определим, какое число молекул пройдет
и определим, какое число молекул пройдет
через неё из двух ближайших равновесных
состояний![]() и
и![]() .
.

Отложим слева и справа от
![]() расстояния
расстояния![]() (длина свободного пробега молекулы) и
(длина свободного пробега молекулы) и
построим параллепипеды![]() и
и![]() ,
,
площадью![]() и
и
толщиной![]() .
.
Объёмы параллепипедов
![]() .
.
Для упрощения будем считать, что
молекулы движутся с одинаковыми средними
скоростями![]() ,
,
где![]() –
–
время свободного пробега (перескока).
Пусть число молекул в единице объёма
(концентрация) в первом объёме
![]() ,
,
во втором![]() .
.
Тогда общее число молекул в первом
объёме![]() ,
,
во втором –![]() .
.
Молекулы движутся хаотично по всем
трем направлениям:
![]() .
.
Из них![]() движется в направлении оси
движется в направлении оси![]() ,
,![]() –
–![]() ,
,![]() –
–![]() .
.
Причем в направлении![]() ,
,
например, половина из этой![]() движется влево, половина – вправо. Поэтому
движется влево, половина – вправо. Поэтому
вдоль оси![]() от первого параллепипеда к площадке
от первого параллепипеда к площадке![]() движется
движется![]() молекул, а от второго –
молекул, а от второго –![]() .
.
Т.о. за время![]() через площадку
через площадку![]() проходит число молекул
проходит число молекул
![]() .
.
Пусть масса одной молекулы
![]() ,
,
тогда за время![]() через
через
площадку
![]() переносится масса вещества
переносится масса вещества
![]() .
.
Время пролета молекулами площадки
![]() параллепипедов
параллепипедов![]() и
и![]() (через центральную оно будет таким же)
(через центральную оно будет таким же)
![]() .
.
Поток вещества через площадку
определится как
![]() .
.
Можно показать, что
![]() ,
,
где
![]() градиент концентраций. Поток вещества
градиент концентраций. Поток вещества
тогда запишем как
![]()
Через единицу площади переносится
поток вещества (плотность потока)
![]() .
.
Введем массовую концентрацию
![]() .
.
Тогда
![]() – градиент массовой концентрации.
– градиент массовой концентрации.
Обозначим
![]() и назовем её коэффициентом диффузии, а
и назовем её коэффициентом диффузии, а
также учтем, что суммарная плотность
потока направлена в сторону уменьшения
концентрации, и укажем это напрвавлние
знаком “-“. Получим уравнение Фика:
![]() .
.
![]() .
.
Физический смысл коэффициента диффузии:
он численно равен массе вещества,
переносимого через единичную площадку
за 1 секунду при градиенте концентраций
равном 1.
![]() ,
,
если
![]() ,
,
![]() ,
,
если
![]()
Лекция 7.
Транспорт веществ через мембрану.
Являясь открытой термодинамической
сиситемой, клетка постоянно осуществляет
обмен веществом с окружающей средой.
Такой обмен возможен благодаря способности
клеток пропускать различные вещества
через свою оболочку. Эта способность
клеток называется проницаемостью.
Перемещение веществ в клетку или из
неё в окружающую среду может осуществляться
многими способами. В зависимости от
того, что является источником энергии
для переноса вещестыва, что является
силой перемещения, все виды переноса
веществ можно разделить на пассивный
и активный транспорт.
Пассивный транспорт веществ.
Пассивный транспорт всегда осуществляется
за счет энергии, сконцентрированной в
каком-либо градиенте. Энергия метаболических
процессов клеток (энергия гидролиза
АТФ) на этот процесс непосредственно
не переносится. Пассивный транспорт
всегда идет от более высокого
энергетического уровня к более низкому.
Основными градиентами, присущими
живым организмам, являются градиенты
концентрационные, электрические,
осмотические, градиенты гидростатического
давления.
В соответствии с этими градиентами
имеются следующие виды пассивного
транспорта веществ в клетках и тканях:
диффузия, осмос, электроосмос, аномальный
осмос, фильтрация.
Основным механизмом пассивного
транспорта является диффузия-
самопроизвольный процесс проникновения
вещества из области большей концентрации
в область ментшей концентрации в
результате теплового хаотического
движения.
Перенос незаряженных частиц (атомов и
молекул) через мембрану
Очевидно, что при переносе незаряженных
частиц единственным градиентом является
градиент концентраций. Следовательно,
механизм переноса молекул и атомов
через мембрану – диффузия, а сам транспорт
описывется уравнением Фика:
![]()
Концентрационный градиент клеточной
мембраны определить трудно, поэтому
лучше использовать более простое
уравнение, предложенное Коллендором и
Берлундом и которое легко вывести из
уравнения Фика.
![]() –
–
концентрация вещес тва
тва
в клетке;
![]() –
–
концентрация этого же вещества снаружи
клетки;
![]() –
–
концентрация этого же вещества внутри
клетки на границе клетка – мембрана;
![]() –
–
концентрация этого же вещества внутри
клетки на границе окружающая среда-мембрана.
![]() >
>
![]() .
.
Следовательно, перенос идет из клетки
в окружающую среду. Для мембраны
![]() .
.
Измерить
![]() и
и![]() трудно,
трудно,
но зато экспериментально можно измерить![]() и
и![]() .
.
Кроме того, считают, что
![]()
![]() –
–
коэффициент распределения частиц между
мембраной и окружающей средой.
Следовательно,
![]()
Тогда
![]() .
.
Обозначим
![]() – проницаемость мембраны, получим
– проницаемость мембраны, получим
![]()
– это и есть уравнение Коллендора-Берлунда.
Перенос заряженных частиц (ионов) через
мембрану
Проникновение заряженных частиц через
мембрану (а это ионы), через мембрану
зависит не только от концентрационного
градиента, но и от градиента электрического
потенциала. Плотность потока вещества
при этом следует рассчитывать как сумму
двух слагаемых:
![]()
Здесь
![]() – плотность потока вещества, обусловленная
– плотность потока вещества, обусловленная
градиентом концентраций.![]() – плотность потока вещества, обусловленная
– плотность потока вещества, обусловленная
градиентом электрического потенциала.
Откуда возникает на мембране
электрический градиент, т.е. разность
потенциалов? Согласно полиэлектролитной
теории основой цитоплазмы является
комплексный полиэлектролитный гель
сетчатой структуры с фиксированными
на ней отрицательными зарядами, который
способен избирательно накаплиаить ионы
![]() .
.
В результате, на наружней поверхности
мембраны скапливается положительный
заряд и положительный потенциал, а на
внутренней – отрицательный потенциал
(позже мы покажем это доказательно).Поэтому вокруг мембраны возникает
электричкское поле напряженностью
![]() .
.
Это поле убывет по силе при удалении от
мембраны. Между напряженностью поля и
градиентом потенциала имеется связь:![]() .
.
Это электрическое поле действует на
ионы с силой
![]() ,
,
ускоряя или замедляя их (![]() заряд всех ионов).
заряд всех ионов).
Возьмем 1 моль ионов, в котором содержится
![]() ионов. Чтобы найти поток ионов, выделим
ионов. Чтобы найти поток ионов, выделим
обеъм электролита в виде прямоугольного
параллепипеда с ребом![]() (
(![]() – скорость движения ионов) и площадью
– скорость движения ионов) и площадью
основания![]() .
.
Пусть за время![]() ,
,
все ионы, находящиеся в этом объёме,
пройдут через площадку![]() .
.
Будем считать, что концентрация ионов
равна![]() ,
,
следовательно масса 1 моля ионов
определится как
![]() ,
,
а поток ионов как
![]() .
.
Плотность потока ионов тогда будет
![]() .
.
Скорость
![]() направленного движения ионов
направленного движения ионов
пропорциональна действующей силе![]() ,
,
где![]() – сила, действующая на 1 ион,
– сила, действующая на 1 ион,![]() заряд иона.
заряд иона.
![]() ,
,
где
![]() – подвижность ионов.
– подвижность ионов.
![]() ,
,
где
![]() –
–
зарядовое число иона,![]() – заряд электрона. Тогда
– заряд электрона. Тогда
![]() .
.
Здесь![]() -числоФарадея
-числоФарадея
(заряд 1 моля ионов). Следовательно,
![]() ,
,
а
![]() .
.
Это уравнение называется уравнением
Нернста-Планка.
Совокупность концентрационного и
электрического градиентов называется
градиентом электрохимического потенциала.
Виды диффузии.
1. Простая диффузия – диффузия, при
которой молекулы
диффундирующего вещества движутся
без образования комплекса с другими
молекулами. В живой клетке такая диффузия
обеспечивает прохождение кислорода,
лекарственных веществ и ядов через
мембрану. Механизм такой диффузии
простой: в жидкой фазе молекулы
фосфолипидов могут образовывать полости
(кинки), в которые способны внедряться
молекулы перечисленных веществ. Эти
кинки движутся поперек мембраны и
переносят диффундирующее вещество.
Простая диффузия протекает медленно и
не может в достаточном количестве
обеспечить клетку питательными
веществами. Но природа обеспечила другие
виды диффузии.
Диффузия через каналы.

Наличие каналов увеличивает проницаемость
мембран.
Облегченная диффузия.

Вещество А самостоятельно слабо
диффундирует через мембрану. Но скорость
диффузии значительно возрастает, когда
молекула А+ этого вещества
образует комплекс с некоторым
вспомогательным веществом Х, которое
растворено в липиде. Этот комплекс
диффундирует в мембрану, достигает её
противоположной стороны, здесь молекула
А освобождается и выходит в клетку, а
молекула Х освободившись, диффундирует
обратно к наружней стороне мембраны,
где снова вступает во взаимодействие
с другой молекулой А и процесс повторяется.
Переносчики Х могут быть фиксированными
и образовывать пору:
Молекула А+ захватывается
ближайшей  молекулой
молекулой
Х и переходит внутри мембраны от одной
молекулы Х к другой по эстафете, достигает
противоположной стороны мембраны, где
выходит в клетку.
Размеры поры не должны превышать
размеров молекулы А.
Молекулы переносчики называются
ионофорами.
Обменная диффузия.
Вспомогательное вещество Х образует
комплекс с
с
молекулой проникающего вещества А+,
комплекс диффундирует через мембрану.
На другой стороне мембраны молекула
А+, освободившись,уходит
в клетку, а ионофор берёт из клетки
другую молекулу А++ и
переносит её в окружающую среду. В
результате концентрация вещества А по
обе стороны мембраны не меняется,
следовательно, этот вид диффузии,
фактически не принимает участия в обмене
веществ.
Все рассмотренные виды диффузии
описываются уравнением Фика, если
переносится молекулы или атомы, и
уравнением Нернста-Планка, если
переносятся ионы.
5.Осмос –движение молекул воды
(растворителя) через полупроницаемую
мембрану из области большей концентрации
растворённого вещества в область меньшей
концентрации растворенного вещества.
Т.е. это тоже диффузия, но диффузия
растворителя.
Сила, которая вызывает это движение
растворителя, называется осмотическим
давлением.
Плотность потока вещества определяется
как
![]() .
.
Здесь
![]() –
–
коэффициент проницаемости;![]() и
и![]() – осмотическое давление по одну и другую
– осмотическое давление по одну и другую
сторону мембраны, соответственно.
6. Фильтрация –движение молекул
воды (растворителя) через полупроницаемую
мембрану из области большей концентрации
растворённого вещества в область меньшей
концентрации растворенного вещества
при наличии гидростатического давления
(давления, обусловленного столбом
жидкости).
формулу
Явления фильтрации и осмоса имеют
особое значение в процессе обмена водой
между кровью и тканью.
Активный транспорт.
Пассивный транспорт веществ всегда
стремится выровнять неравномерность
в распределении вещества между клеткой
и средой. Но клеточное содержимое резко
отличается по своему составу от окружающей
клетку среды. В клетке в большом количестве
находятися ионы
![]() ,
,
недиффундирующие ионы белков, фосфолипидов,
анионы аминокислот и др, содержание
которых в жидкости, окружающей клетку,
незначительно. Другие вещества, наоборот,
в значительно более высоких концентрациях
содержатся в окружающей клетку жидкости,
например,![]() .
.
В результате такого неравномерного
распределения концентраций ионов между
клеткой и окружающей средой пассивный
перенос не может полностью обеспечить
равномерное распределение концентраций.
Поэтому в организме одновременно с
пассивным транспортом происходит
активный транспорт.
Активный транспорт обеспечивает
перенос молекул и ионов из области
меньших концентраций и электрических
потенциалов в область больших концентраций
и электрических потенциалов.
Для осуществления такого транспорта
клетка совершает работу против градиентов
концентраций и потенциалов.
Если через клетку переносится
незаряженная частица (атом или молекула),
то эта работа равна
![]() ,
,
где
![]() –
–
количество молей вещества, перенесенного
через мембрану из области меньших
концентраций![]() в область больших концентраций
в область больших концентраций![]() ;
;![]() – универсальная газовая постоянная,
– универсальная газовая постоянная,![]() – абсолютная температура.
– абсолютная температура.
Если переносится ион через электрически
заряженную мембрану, то эта работа равна
![]() ,
,
где
![]() – валентность ионов,
– валентность ионов,![]() – число Фарадея (заряд 1 моля ионов),
– число Фарадея (заряд 1 моля ионов),![]() разность потенциало между поверхностыми
разность потенциало между поверхностыми
мембраны.![]() зависит от знака заряда ионов.
зависит от знака заряда ионов.
Чтобы совершить эту работу, клетке
нужна энергия. Эту энергию клетка
получает пригидролизе фермента
![]() (адезинтрифосфатоза).
(адезинтрифосфатоза).
Особое внимание следует обратить на
активный транспорт ионов
![]() и
и![]() ,
,
калий – натриевый насос, т.к. именно эти
ионы играют большую роль при генерации
биоэлектрических потенциалов и проведении
возбуждения.
Переход
![]() из клетки зависит от концентрации
из клетки зависит от концентрации![]() во внешней среде, а переход
во внешней среде, а переход![]() в клетку, в свою очередь, эависит от
в клетку, в свою очередь, эависит от
концентрации![]() в цитоплазме.
в цитоплазме.
Предполагают, что перенос
![]() и
и![]() осуществляется специальным переносчиком
осуществляется специальным переносчиком
белковой или белково-липидной природы.
Рассмотрим перенос
![]() из окружающей среды в клетку. Он начинается
из окружающей среды в клетку. Он начинается
на внутренней поверхности мембраны и
происходит в три стадии.

Киназная. Переносчик на внутренней
стороне мембраны захватывет из цитоплазмы
ион
![]() :
:
![]()
Комплекс
![]() переносится на наружнюю поверхность
переносится на наружнюю поверхность
мембраны за счет гидролиза![]() .
.
Ионообменная. На наружней поверхности
мембраны ионы
![]() обмениваются на ионы
обмениваются на ионы![]()
![]()
Комплекс
![]() снова движется к внутренней стороне
снова движется к внутренней стороне
мембраны.
3. Фосфатозная. Эта фаза заканчивает
цикл на внутренней поверхности мембраны
дефосфолированием переносчика и
освобождением ионов
![]()
![]()
Лекция 8
Электромагнитные явления в биологических
системах.
Природа биопотенциалов и способы их
описания.
Все процессы жизнедеятельности организмов
сопровождаются появлением в клетках и
тканях электродвижущих сил. Электрические
явления играют большую роль в важнейших
физиологических процессах: возбуждение
клеток и проведение возбуждения по
клеткам.
В возникновении биопотенциалов решающую
роль играет разность потенциалов,
обусловленная несимметричным
распределением ионов. К таким разностям
потенциалов относятся диффузионные,
мембранные и фазовые.
1. Диффузионные потенциалывозникают
на границе раздела двух жидких сред в
результате различной подвижности ионов.
Рассмотрим пример: Имеется раствор
серной кислоты, разделенный пористой
перегородкой. Пусть концентрация![]() в левой части больше, чем в прав
в левой части больше, чем в прав ой.
ой.
Ионы![]() и
и![]() будут диффундировать из левой части в
будут диффундировать из левой части в
правую часть сосуда с разной скоростью
по градиенту концентрации. Скорость
диффузии определяется подвижностью
ионов. Подвижность ионов![]() больше подвижности ионов
больше подвижности ионов![]() :
:![]() Следовательно, ионы
Следовательно, ионы![]() будут намного опережать ионы
будут намного опережать ионы![]() .
.
По обе стороны перегородки установятся
потенциалы: слева “-“ справа “+”.
Возникает диффузионная разность
потенциалов. Эта разность потенциалов
будет замедлять “быстрые“ ионы и
ускорять “медленные“, т.е. возникающее
электрическое поле направлено против
сил диффузии. Диффузионная разность
потенциалов максимален в тот момент,
когда скорости диффузии становятся
равными:
![]() .
.
Здесь
![]() – ;подвижность катионов;
– ;подвижность катионов;![]() – подвижность анионов;
– подвижность анионов;![]() – универсальная газовая постоянная;
– универсальная газовая постоянная;![]() – абсолютная температура;
– абсолютная температура;![]() -валент-ность ионов;
-валент-ность ионов;![]() –
–
число Фарадея;![]() – активная концентрация в области откуда
– активная концентрация в области откуда
идет диффузия;![]() – активная концентрация в области куда
– активная концентрация в области куда
идет диффузия.
2. Мембранный потенциал. В рассматриваемом
примере пористую перегородку заменим
полупроницаемой мембраной, пропускающую
только катионы – положительно заряженные
ионы (это может быть мембрана с большой
концентрацией фиксированных отрицательных
ионов).
В этом случае подвижность ионов при
переходе через мембрану не является
определяющим фактором – в правую часть
переходят только положительно заряженные
ионы водорода. Через некоторое время
диффузия ионов
![]() прекратится, т.к. они испытывают притяжение
прекратится, т.к. они испытывают притяжение
со стороны оставшихся в левой части
ионов![]() .
.
Поэтому установится равновесие , в
результате чего возникает двойной
электрический слой: слева заряды “-“,
справа заряды “+”, между сторонами
мембраны возникнет разность потенциалов,
называемая мембранным потенциалом,
величина которого есть
![]() уравнение Нернста.
уравнение Нернста.
3. Фазовый потенциал возникает на
границе раздела двух несмешивающихся
фаз (например, раствор электролита в
воде и какое-нибудь масло) в результате
различной растворимости анионов и
катионов в неводной фазе. Если, например,
катионы растворимы в неводной фазе, то
они активнее перейдут в нее и зарядят
ее положительно относительно водной
фазы. Наблюдается фазовый потенциал
при механическом повреждении мембраны.
Равенство Доннана.
При выводе уравнений, описывающих
распределение ионов между клеткой и
окружающей средой, выполняется условие
электронейтральности, равенство
суммарной концентрации анионов ( в
основном
![]() и ионов макромолекул
и ионов макромолекул![]() )
)
катионов![]()
как внутри клетки
![]() ,
,
так и снаружи клетки
![]() .
.
Здесь
![]()
![]() —
—
число отрицательных зарядов на каждой
белковой молекуле.
В межклеточной жидкости содержание
катионов значительно выше, чем ионов
макромолекул
![]() .
.
Поэтому
 – равенство Доннана
– равенство Доннана
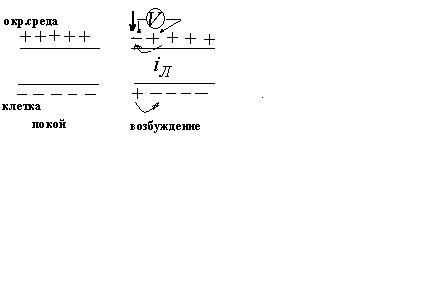
Потенциал покоя
Экспериментально установлено, что
цитоплазма в состоянии покоя имеет
отрицательный потенциал, а окружающая
среда- положительный.
Действительно, в первом приближении
В клетке
![]() в 20-40 раз.
в 20-40 раз.
Снаружи
![]() в 10 раз.
в 10 раз.
Это неравномерное распределение
концентраций обусловлено
![]() насосом, при котором при переносе
насосом, при котором при переносе![]() переносится
переносится![]() .
.
Кроме того, в клетке имеются анионы
макромолекул![]() (белков, аминокислот, и др.).
(белков, аминокислот, и др.).
Ионы
![]() внутри клетки не связаны с другими
внутри клетки не связаны с другими
ионами и могут диффундировать туда, где
их мало, т.е. в окружающую среду. Т.е. в
состоянии покоя клетка проницаема
только для ионов![]() .
.
Анионы не могут проникать через мембрану
и остаются на внутренней поверхности
мембраны. Т.о. мембрана снаружи зарядится
положительно, а внутри – отрицательно.
Между внутренней и внешней поверхностями
мембраны возникает разность потенциалов
мембранной природы. Эта разность
потенциалов между клеткой и окружающей
средой, измеренная в состоянии
физиологического покоя, называется
потенциалом покоя.
Если принять, в первом приближении, что
потенциал покоя определяется только
диффузией ионов
![]() ,
,
то величина потенциала покоя определяется
как
 уравнение
уравнение
Нернста.
![]() – активная концентрация ионов
– активная концентрация ионов![]() внутри клетки,
внутри клетки,
![]() – активная концентрация ионов
– активная концентрация ионов![]() снаружи.
снаружи.
Если
![]() =
=![]() ,
,
то![]() клетка мертва.
клетка мертва.
Но
![]() ,
,
поэтому![]() .
.
Например, для аксона гигантского кальмара![]()
![]() ,
,
а это подтверждает, что в основе
возникновения потенциала действия
лежит перенос ионов.
В реальности в состоянии покоя мембрана
проницаема не только для ионов
![]() ,
,
но и для ионов![]() и
и![]() .
.
Например, для аксона гигантского кальмара
экспериментально установлено, что![]() .
.
Основной вклад в потенциал покоя вносят
ионы![]() и
и![]() .
.
Ионов![]() переносится очень мало. Поэтому на
переносится очень мало. Поэтому на внешней
внешней
поверхности сосредоточивается
положительный заряд, а на внутренней –
отрицательный. Потенциал покоя
определяется тремя диффузионными
потоками и вычисляется (с учетом равенства
Доннана) по формуле
 .
.
Кроме простой диффузии ионов
![]() и
и![]() может
может
идти обменная диффузия, но, как мы
отмечали, потоки их равны и обменная
диффузия не влияет на мембранный
потенциал.
Потенциал действия.
Все клетки возбудимых тканей (нервная,
мышечная, железистая) под действием
различных раздражителей достаточной
силы способны переходить в возбужденное
состояние. Обязательным признаком
возбуждения является изменение
электрического состояния мембраны.
Опыт показывает, что возбужденный
участок становится электроотри-цательным
по отношению к невозбужденному участку.
Следовательно, на возбужденном участке
происходит перераспределение ионов.
При возбуждении  это
это
перераспределение кратковременно и
концентрации восстанавливаются после
снятия возбуждения, а разность потенциалов
становится равной исходной, т.е. потенциалу
покоя. Для аксона кальмара обнаружена
такая зависимость изменения потенциала
при возбуждении от времени

![]() – потенциал покоя;
– потенциал покоя;![]() мембранный потенциал при возбуждении;
мембранный потенциал при возбуждении;
![]()
![]() – общее изменение разности потенциалов.
– общее изменение разности потенциалов.
Общее изменение разности потенциалов
между клеткой и окружающей средой,
происходящее при пороговом и сверхпороговом
возбуждении клетки, называется потенциалом
действия.
Механизм возникновения потенциала
действия. В
1938 году Круэл и Картис показали, что
сопротивление аксона кальмара в состоянии
покоя 1000 Ом/см2,
а при возбуждении 25 Ом/см2,
т.е. уменьшается в 40 раз. При этом
сопротивление цитоплазмы не изменяется.
Следовательно, уменьшение сопротивления
мембраны обусловлено только её
проницаемости для ионов, т.к. именно они
являются переносчиками электричества
в мембранах и клетках.
Хаджкин, Хаксли и Катц показали, что при
возбуждении про-ницаемость мембраны
увеличивается только для ионов
![]() ,
,
причем в 500 раз. Это приводит к увеличению
диффузии ионов![]() из
из
окружающей среды в клетку (по
концентрационному градиенту), что
приводит к изменению потенциала мембраны.
В первые моменты возбуждения интенсивность
потока ионов![]() из клетки остается такой же, как и до
из клетки остается такой же, как и до
возбуждения.
Поэтому поток ионов
![]() вызывает
вызывает
исчезновение избыточного отрицательного
потенциала на внутренней поверхности
мембраны. Эта фаза называется деполяризацией
и длится короткое время. Затем начинается
другая фаза – реполяризация., заключающаяся
в следующем. Диффузия ионов![]() внутрь клетки нарушает равновесие
внутрь клетки нарушает равновесие
концентраций в клетке. В связи с этим
повышается проницаемость мембраны для
ионов![]() ,
,
начинается диффузия ионов![]() из клетки в окружающую среду. Поток
из клетки в окружающую среду. Поток
ионов![]() из клетки приводит к уменьшению
из клетки приводит к уменьшению
проницаемости для ионов![]() .
.
В результате происходит реполяризация
мембраны и восстановление потенциала
покоя. Проницаемость мембраны для ионов![]() и
и![]() падает до исходной величины. Фаза
падает до исходной величины. Фаза
реполяризации длится дольше фазы
деполяризации, поэтому и кривая более
пологая.
В некоторых случаях регистрируется так
называемый следовой потенциал, как на
данном рисунке. Он вызван тем, что после
окончания возбуждения проницаемость
мембраны для ионов
![]() и
и![]() остпется повышенной.
остпется повышенной.
Т.о. формирование потенциала действия
обусловлено двумя потоками через
мембрану: поток
![]() внутрь клетки приводит к перезарядке
внутрь клетки приводит к перезарядке
мембраны, а противоположный поток![]() обусловливает восстановление потенциала.
обусловливает восстановление потенциала.
Потоки эти приблизительно равны по
величине, но сдвинуты по времени.
Благодаря этому сдвигу во времени и
возможно появление потенциала действия.
Распространение потенциала действия.
(проведение возбуждения по нервным
волокнам).
Потенциал действия, возникнув в одном
участке нервной клетки, распространяется
по всей её поверхности.
В результате возбуждения между
возбужденным и невозбужденным участками
возникает разность потенциалов. Эта
разность потенциалов создает электрический
ток, называемый локальным током (от
невозбужденного участка к возбужденному).
Локальный ток оказывает на соседний
невозбужденный участок такое же действие
как и исходный возбудитель и увеличивает
проница-емость мембраны для ионов
![]() .
.
В результате и в этом участке снижкется
потенциал покоя и возникает потенциал
действия.
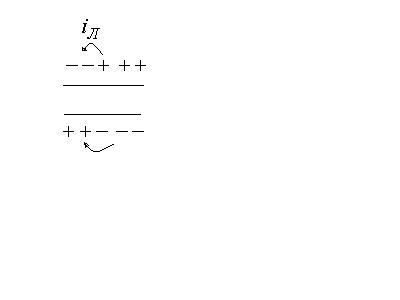
В участке, который был ранее возбужден,
происходят восстановительные процессы
реполяризации.
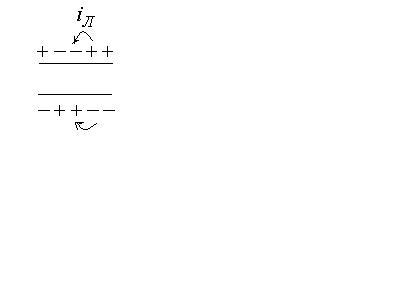
Э тот
тот
процесс повторяется многократно и
обусловливает распространение импульсов
по всей длине клетки в обоих направлениях.
Разность потенциалов между возбужденным
и невозбужденным участками изменяется
как
Волна возбуждения под влиянием локальных
токов распространяется по нервному
волокну без затухания. Это обусловлено
тем, что локальные токи только деполяризуют
мембрану, а потенциал действия в каждом
участке мембраны поддерживается
независимыми потоками, перпендикулярно
направлению распространения возбуждения,
т.е. источником энергии такой
электромагнитной волны является сама
среда.
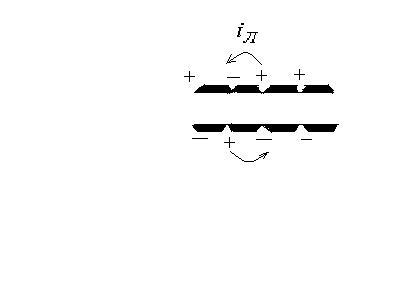
Если в нервных волокнах нет миелиновых
оболочек, то возбуждение в них
распространяется так, как мы рассмотрели.
Если же имеются миелиновые оболочки
(миелин – жироподобное вещество
– диэлектрик), то локальные токи
распространяются между участками, на
которых оболочки прерываются– между
перехватами Ранвье, т.к. миелин является
изолятором:

Лекция 8
Электромагнитные явления в биологических
системах
Природа биопотенциалов и способы их
описания
Все процессы жизнедеятельности организмов
сопровождаются появлением в клетках и
тканях электродвижущих сил. Электрические
явления играют большую роль в важнейших
физиологических процессах: возбуждение
клеток и проведение возбуждения по
клеткам.
В возникновении биопотенциалов решающую
роль играет разность потенциалов,
обусловленная несимметричным
распределением ионов. К таким разностям
потенциалов относятся диффузионные,
мембранные и фазовые.
1. Диффузионные потенциалывозникают
на границе раз-
дела двух жидких сред в результате
различной подвижности ионов. Рассмотрим
пример: имеется раствор серной кислоты,
разделенный пористой перегородкой.
Пусть концентрация
![]() в левой части больше, чем в правой. Ионы
в левой части больше, чем в правой. Ионы![]() и
и![]() будут диффундироватьи
будут диффундироватьи з
з
левой части в правую часть сосуда с
разной скоростью по градиенту концентрации.
Скорость диффузии определяется
подвижностью ионов. Подвижность ионов![]() больше подвижности ионов
больше подвижности ионов![]() :
:![]() Следовательно, ионы
Следовательно, ионы![]() будут намного опережать ионы
будут намного опережать ионы![]() .
.
По обе стороны перегородки установятся
потенциалы: слева “-“ справа “+”.
Возникает диффузионная разность
потенциалов. Эта разность потенциалов
будет замедлять “быстрые“ ионы и
ускорять “медленные“, т.е. возникающее
электрическое поле направлено против
сил диффузии. Диффузионная разность
потенциалов максимален в тот момент,
когда скорости диффузии становятся
равными:
![]() .
.
Здесь
![]() – ;подвижность катионов;
– ;подвижность катионов;![]() – подвижность анионов;
– подвижность анионов;![]() – универсальная газовая постоянная;
– универсальная газовая постоянная;![]() – абсолютная температура;
– абсолютная температура;![]() -валентность ионов;
-валентность ионов;![]() –
–
число Фарадея;![]() – активная концентрация в области откуда
– активная концентрация в области откуда
идет диффузия;![]() – активная концентрация в области куда
– активная концентрация в области куда
идет диффузия.
2. Мембранный потенциал. В рассматриваемом
примере пористую перегородку заменим
полупроницаемой мембраной, пропускающую
только катионы – положительно заряженные
ионы (это может быть мембрана с большой
концентрацией фиксированных отрицательных
ионов).

В этом случае подвижность ионов при
переходе через мембрану не является
определяющим фактором – в правую часть
переходят только положительно заряженные
ионы водорода. Через некоторое время
диффузия ионов
![]() прекратится, т.к. они испытывают притяжение
прекратится, т.к. они испытывают притяжение
со стороны оставшихся в левой части
ионов![]() .
.
Поэтому установится равновесие , в
результате чего возникает двойной
электрический слой: слева заряды “-“,
справа заряды “+”, между сторонами
мембраны возникнет разность потенциалов,
называемая мембранным потенциалом,
величина которого есть
![]() уравнение Нернста.
уравнение Нернста.
3. Фазовый потенциал возникает на
границе раздела двух несмешивающихся
фаз (например, раствор электролита в
воде и какое-нибудь масло) в результате
различной растворимости анионов и
катионов в неводной фазе. Если, например,
катионы растворимы в неводной фазе, то
они активнее перейдут в нее и зарядят
ее положительно относительно водной
фазы. Наблюдается фазовый потенциал
при механическом повреждении мембраны.
Равенство Доннана.
При выводе уравнений, описывающих
распределение ионов между клеткой и
окружающей средой, выполняется условие
электронейтральности, равенство
суммарной концентрации анионов ( в
основном
![]() и ионов макромолекул
и ионов макромолекул![]() )
)
катионов![]()
как внутри клетки
![]() ,
,
так и снаружи клетки
![]() .
.
Здесь
![]()
![]() –число отрицательных зарядов на каждой
–число отрицательных зарядов на каждой
белковой молекуле.
В межклеточной жидкости содержание
катионов значительно выше, чем ионов
макромолекул
![]() .
.
Поэтому
 – равенство Доннана
– равенство Доннана
Потенциал покоя
Экспериментально установлено, что
цитоплазма в состоянии покоя имеет
отрицательный потенциал, а окружающая
среда- положительный.
Действительно, в первом приближении

В клетке
![]() в 20-40 раз.
в 20-40 раз.
Снаружи
![]() в 10 раз.
в 10 раз.
Это неравномерное распределение
концентраций обусловлено
![]() насосом, при котором при переносе
насосом, при котором при переносе![]() переносится
переносится![]() .
.
Кроме того, в клетке имеются анионы
макромолекул![]() (белков, аминокислот, и др.).
(белков, аминокислот, и др.).
Ионы
![]() внутри клетки не связаны с другими
внутри клетки не связаны с другими
ионами и могут диффундировать туда, где
их мало, т.е. в окружающую среду. Т.е. в
состоянии покоя клетка проницаема
только для ионов![]() .
.
Анионы не могут проникать через мембрану
и остаются на внутренней поверхности
мембраны. Т.о. мембрана снаружи зарядится
положительно, а внутри – отрицательно.
Между внутренней и внешней поверхностями
мембраны возникает разность потенциалов
мембранной природы. Эта разность
потенциалов между клеткой и окружающей
средой, измеренная в состоянии
физиологического покоя, называется
потенциалом покоя.

Если принять, в первом приближении, что
потенциал покоя определяется только
диффузией ионов
![]() ,
,
то величина потенциала покоя определяется
как
 уравнение
уравнение
Нернста.
![]() – активная концентрация ионов
– активная концентрация ионов![]() внутри клетки,
внутри клетки,
![]() – активная концентрация ионов
– активная концентрация ионов![]() снаружи.
снаружи.
Если
![]() =
=![]() ,
,
то![]() клетка мертва.
клетка мертва.
Но
![]() ,
,
поэтому![]() .
.
Например, для аксона гигантского кальмара![]()
![]() ,
,
а это подтверждает, что в основе
возникновения потенциала действия
лежит перенос ионов.
В реальности в состоянии покоя мембрана
проницаема не только для ионов
![]() ,
,
но и для ионов![]() и
и![]() .
.
Например, для аксона гигантского кальмара
экспериментально установлено, что![]() .
.
Основной вклад в потенциал покоя вносят
ионы![]() и
и![]() .
.
Ионов![]() переносится очень мало. Поэтому на
переносится очень мало. Поэтому на
внешней поверхности
сосредоточивается положительный заряд, а на внутренней – отрицательный.
а на внутренней – отрицательный.
Потенциал покоя определяется тремя
диффузионными потоками и вычисляется
(с учетом равенства Доннана) по формуле
 .
.
Кроме простой диффузии ионов
![]() и
и![]() может
может
идти обменная диффузия, но, как мы
отмечали, потоки их равны и обменная
диффузия не влияет на мембранный
потенциал.
Потенциал действия.
Все клетки возбудимых тканей (нервная,
мышечная, железистая) под действием
различных раздражителей достаточной
силы способны переходить в возбужденное
состояние. Обязательным признаком
возбуждения является изменение
электрического состояния мембраны.
Опыт показывает, что возбужденный
участок становится 
электроотрицательным по отношению к
невозбужденному участку. Следовательно,
на возбужденном участке происходит
перераспределение ионов. При возбуждении
это перераспределение кратковременно
и концентрации восстанавливаются после
снятия возбуждения, а разность потенциалов
становится равной исходной, т.е. потенциалу
покоя. Для аксона кальмара обнаружена
такая зависимость изменения потенциала
при возбуждении от времени

![]() – потенциал покоя;
– потенциал покоя;![]() мембранный потенциал при возбуждении;
мембранный потенциал при возбуждении;
![]()
![]() – общее изменение разности потенциалов.
– общее изменение разности потенциалов.
Общее изменение разности потенциалов
между клеткой и окружающей средой,
происходящее при пороговом и сверхпороговом
возбуждении клетки, называется потенциалом
действия.
Механизм возникновения потенциала
действия. В 1938 году Круэл и Картис
показали, что сопротивление аксона
кальмара в состоянии покоя 1000 Ом/см2,
а при возбуждении 25 Ом/см2, т.е.
уменьшается в 40 раз. При этом сопротивление
цитоплазмы не изменяется. Следовательно,
уменьшение сопротивления мембраны
обусловлено только её проницаемости
для ионов, т.к. именно они являются
переносчиками электричества в мембранах
и клетках.
Хаджкин, Хаксли и Катц показали, что при
возбуждении проницаемость мембраны
увеличивается только для ионов
![]() ,
,
причем в 500 раз. Это приводит к увеличению
диффузии ионов![]() из
из
окружающей среды в клетку (по
концентрационному градиенту), что
приводит к изменению потенциала мембраны.
В первые моменты возбуждения интенсивность
потока ионов![]()

из клетки остается
такой же, как и до возбуждения. Поэтому
поток ионов
![]() вызывает
вызывает
исчезновение избыточного отрицательного
потенциала на внутренней поверхности
мембраны. Эта фаза называется деполяризацией
и длится короткое время. Затем начинается
другая фаза – реполяризация., заключающаяся
в следующем. Диффузия ионов![]() внутрь клетки нарушает равновесие
внутрь клетки нарушает равновесие
концентраций в клетке. В связи с этим
повышается проницаемость мембраны для
ионов![]() ,
,
начинается диффузия ионов![]() из клетки в окру-жающую среду. Поток
из клетки в окру-жающую среду. Поток
ионов![]() из клетки приводит к уменьшению
из клетки приводит к уменьшению
проницаемости для ионов![]() .
.
В результате происходит реполяризация
мембраны и восстановление потенциала
покоя. Проницаемость мембраны для ионов![]() и
и![]() падает до исходной величины. Фаза
падает до исходной величины. Фаза
реполяризации длится дольше фазы
деполяризации, поэтому и кривая более
пологая.
В некоторых случаях
регистрируется так называемый следовой
потенциал, как на данном рисунке. Он
вызван тем, что после окончания возбуждения
проницаемость мембраны для ионов
![]() и
и![]() остпется повышенной.
остпется повышенной.
Т.о. формирование
потенциала действия обусловлено двумя
потоками через мембрану: поток
![]() внутрь клетки приводит к перезарядке
внутрь клетки приводит к перезарядке
мембраны, а противоположный поток![]() обусловливает восстановление потенциала.
обусловливает восстановление потенциала.
Потоки эти приблизительно равны по
величине, но сдвинуты по времени.
Благодаря этому сдвигу во времени и
возможно появление потенциала действия.
Распространение
потенциала действия.
(проведение
возбуждения по нервным волокнам).
Потенциал действия,
возникнув в одном участке нервной
клетки, распространяется по всей её
поверхности.
В результате
возбуждения между возбужденным и
невозбужденным участками возникает
разность потенциалов. Эта разность
потенциалов создает электрический ток,
называемый локальным током (от
невозбужденного участка к возбужденному).
Локальный ток оказывает на соседний
невозбужденный участок такое же действие
как и исходный возбудитель и увеличивает
проница-емость мембраны для ионов
![]() .
.
В результате и в этом участке снижкется
потенциал покоя и возникает потенциал
действия.

В участке, который
был ранее возбужден, происходят
восстановительные процессы реполяризации.

Этот процесс
повторяется многократно и обусловливает
распространение импульсов по всей длине
клетки в обоих направлениях. Разность
потенциалов между возбужденным и
невозбужденным участками изменяется
как

Волна возбуждения
под влиянием локальных токов
распространяется по нервному волокну
без затухания. Это обусловлено тем, что
локальные токи только деполяризуют
мембрану, а потенциал действия в каждом
участке мембраны поддерживается
независимыми потоками, перпендикулярно
направлению распространения возбуждения,
те. Источником энергии такой электромагнитной
волны является сама среда.
Если в нервных
волокнах нет миелиновых оболочек, то
возбуждение в них распространяется
так, как мы рассмотрели.
Если же имеются
миелиновые оболочки (миелин –
жироподобное
вещество
– диэлектрик),
то локальные токи распространяются
между участками, на которых оболочки
прерываются –
между
перехватами Ранвье, т.к. миелин является
изолятором:
Лекция 9
Биофизические принципы исследования
Электрических полей в организме.
Нервные волокна, мышцы, и, следовательно,
клетки, по которым распространяется
раздражение, можно моделировать как
электрический диполь. Действительно:

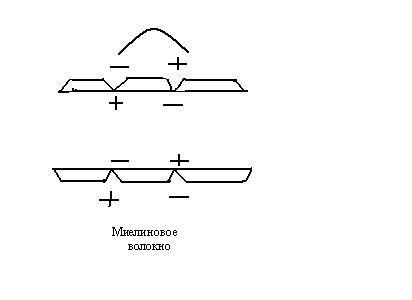
Электрический диполь
Электрический диполь- система двух
точечных зарядов, равных по величине и
противоположных по знаку и находящихся
на некотором расстоянии друг от друга.

Основные характеристики диполя:
Плечо диполя
![]() –
–
вектор по величине равный расстоянию
между зарядами и направленный от
отрицательного заряда к положительному.
Электрический дипольный момент диполя
![]() .
.
Вектор
![]() приложен к центру диполя и направлен
приложен к центру диполя и направлен
от отрицательного заряда к положительному.
![]() .
.
Вокруг диполя образуется электрическое
поле, основными характеристиками
которого являются напряженность (силовая
характеристика) и потенциал и разность
потенциалов (энергетические характеристики).
Напряженность электрического поля
диполя.
По определению напряженность электрического
поля определяется как сила, действующая
со стороны поля на единичный пробный
заряд
![]() :
:
![]() .
.![]()
Пробным зарядом называется точечный
положительный заряд, электрическое
поле которого не искажает исследуемое
электрическое поле.
По закону Кулона
![]() в вакууме и
в вакууме и![]() в среде.
в среде.
Если заряд
![]() – одиночный заряд, создающий поле, а
– одиночный заряд, создающий поле, а![]() ,
,
которым мы исследуем поле заряда![]() ,
,
то![]() ,
,
а![]() .
.
Графически электрическое поле изображается
с помощью силовых линий – линий,
касательные к которым совпадают с
вектором
![]() .
.
Для поля одиночного заряда электрическое
поле изображается так:

Если поле образуется несколькими
зарядами, то напряженность в каждой
точке общего поля определяется по
принципу суперпозиции, который для
поля образованного двумя зарядами
диполя записывается как
![]() .
.
В скалярном виде напряженность находится
так:
а) на оси диполя в точку, в которой
рассчитывается напряженность вносится
пробный заряд и определяется направления
векторов
![]() и
и![]() ,
,
которые направлены в одну сторону, затем
складываем их по правилу сложения
однонаправленных коллениарных векторов
![]()

б )
)
в произвольной точке В, на лежащей на
оси диполя:
![]()
С помощью силовых линий электрическое
поле диполя изображается

Потенциал. Разность потенциалов.
Напоминаю, что это энергетические
характеристики электрического поля.
Потенциал электрического поля в любой
его точке определяется как
![]() .
.![]()
и равен потенциальной энергии единичного
заряда, внесенного в данную точку поля.
Если заряд
![]() переместить в поле из точки 1 в точку
переместить в поле из точки 1 в точку
2, то между этими точками возникает
разность потенциалов
![]() .
.
Смысл разности потенциалов: это работа
электрического поля по перемещению
заряда из одной точки в другую.
Потенциал поля также можно интерпретировать
через работую Если т.2 находится в
бесконечности, где поля нет (![]() ),
),
то![]() – это работа поля по перемещению заряда
– это работа поля по перемещению заряда
из данной точки в бесконечность. Потенциал
поля, созданного одиночным зарядом
рассчитывается как![]() .
.
Поверхности, в каждой точке которой
потенциалы поля одинаковы, называются
эквипотенциальными поверхностями. В
поле диполя потенциальные поверхности
распределены следующим образом:
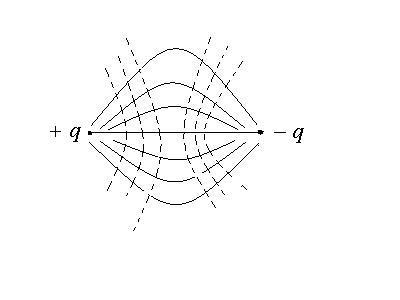
Потенциал поля, образованного несколькими
зарядами, рассчитывается по принципу
суперпозиции:
![]() .
.
а) Расчет потенциала в т. А, расположенной
не на оси диполя:


![]() найдем из треугольника (
найдем из треугольника (![]() ).
).
Очевидно,![]() .
.
Поэтому![]() и
и![]() .
.
![]() .
.
б) Между точками А и В, равноотстоящими
от диполя на расстоянии
![]()
(![]() )
)
разность потенциалов определяется как
(примем без доказательства, которое Вы
найдете в учебнике Ремизова)

 .
.
в) Можно показать, что если диполь
находится в центре равностороннего
треугольника, то разность потенциалов
между вершинами треугольника соотносятся
как проекции вектора
![]() на стороны этого треугольника (
на стороны этого треугольника (![]() ).
).

Диполь в электрическом поле.
а) В однородном поле напряженности
![]() .
.
![]()

На каждый заряд диполя действует сила,
соответственно
![]() .
.
Модули этих сил равны,
![]() ,
,
но направлены эти силы в противоположные
стороны, и, следовательно, создают
вращающий момент пары сил
![]() ,
,
а это выражение есть векторное произведение
![]() .
.
Т.о. в однородном электрическом поле на
диполь действует момент сил, который
стремится установить диполь вдоль
силовых линий поля. Величина этого
момента зависит как от
![]() – характеристики диполя, так и от
– характеристики диполя, так и от![]() – характеристики поля, а также от
– характеристики поля, а также от
ориентации диполя.
б) В неоднородном поле.

Если диполь расположен на силовой линии,
то на его заряды действуют неравные
силы:
![]() .
.
Здесь
![]() – напряженность поля в окрестности
– напряженность поля в окрестности
положительного заряда,![]() – напряженность поля в окрестности
– напряженность поля в окрестности
отрицательного заряда. По густоте
силовых линий видим, что![]() ,
,
т.к поде неоднородно.
Равнодействующая сил, действующих на
диполь, есть
![]()
На протяженности диполя мерой
неоднородности поля служит величина
![]() – среднее изменение напряженности,
– среднее изменение напряженности,
приходящееся на единицу длины диполя.
![]() –
–
мера неоднородности поля вдоль
соответствующего направления поля.
Откуда![]() .
.
Следовательно,
![]() ,
,
т.е.
![]() зависит от величины
зависит от величины![]() – характеристики диполя, так и от градиента
– характеристики диполя, так и от градиента![]() – характеристики поля. Под действием
– характеристики поля. Под действием
силы![]() диполь втягивается в область большей
диполь втягивается в область большей
напряженности поля.
Если диполь находится не на силовой
линии, то он и вращается, и втягивается
в область больших значений напряженности
поля.
Токовый диполь. Эквивалентный
электрический генератор.
Рассмотренный нами диполь может
сохраняться сколь угодно долго только
в вакууме или идеальном диэлектрике.
Однако нас диполь интересует в применении
к объяснению электрических явлений в
организме – электропроводящей среде.
В такой среде диполь не сохраняется,
т.к. свободные заряды среды, притягиваясь
к противоположно заряженным полюсам
диполя, либо экранируют его, либо
нейтрализуют.
Т.к. электрическое поле, образующееся
в организме, не исчезает в процессе
жизнедеятельности, то необходима иная
модель диполя. Можно представить его
как электрический генератор с э.д.с.
![]() .
.
Если использовать его в цепи, то для
этой цепи закон Ома записывается как![]() ,
,

то сила тока зависит, от внешнего
сопротивления цепи
![]() .
.
Создавая модель диполя как источника
электрического поля, мы должны исключить
внешнее сопротивление. Примем![]() ,
,
к клеммам источника диполь, или, иначе,
клеммы источника будем рассматривать
как полюса диполя, который в электропроводящей
среде будет сохраняться до тех пор, пока
функционирует источник тока.

Отрицательный полюс назовем истоком
тока, положительный – стоком тока.
Такую модель диполя называют токовым
диполем.
Для токового диполя
![]() ,
,
следовательно, сила тока не зависит от
сопротивления среды, в которой он
находится
![]() .
.
Дипольный момент токового диполя
![]() ,
,
где
![]() – плечо диполя, по модулю этот вектор
– плечо диполя, по модулю этот вектор
равен расстоянии. Между стоком и истоком
тока.
Потенциал поля токового диполя аналогичен
потенциалу электростатического диполя,
но электрические свойства среды в
формуле заменяются на её электропроводящие
свойства
![]()
![]() ,
,
![]() удельная электропроводность среды.
удельная электропроводность среды.
Суперпозиция токовых диполей называется
эквивалентным электрическим генератором.
Электрокардиография
Итак, при функционировании органов и
тканей, а также клеток в организме
возникает электрическое поле, элементарным
источником которого является диполь.
Мы показали, что характеристики этого
поля можно рассчитать, а это значит, что
их можно измерить.
Метод регистрации разности потенциалов
называют электрографией. В принципе он
прост: достаточно двух электродов,
накладываемых на пациента, гальванометра
и усилителя. В зависимости от того, на
каких органах регистрируется разность
потенциалов электрографию классифицируют
на ЭКГ – регистрация разности потенциалов
при сокращении сердца; ЭЭГ –
электроэнцефалография- регистрируется
активность мозга; ЭМГ- регисрация
активности мышц.
Мы рассмотрим электрокардиографию как
наиболее распространенный метод.
За цикл работы сердца возбуждение
распространяется по различным отделам
его нервно-мышечного аппарата с
определенной последовательностью,
поэтому мгновенные значения результирующей
разности потенциалов за цикл работы
изменяется как по величине, так и по
расположению точек, между которыми они
имеют наибольшее значение. Из этих
значений наибольшей является разность
потенциалов между основанием и верхушкой
сердца в направ лении
лении
электрической оси![]() .
.
:

Кривая зависимости разности потенциалов
от времени за время одного кардиоцикла
называется электрокардиограммой
В основу электрокардиографии положена
теория Эйнтховена:
1. сердце моделируется как источник
разности потенциалов в виде токового
диполя (эквивалентный электрический
генератор);
2. диполь находится в однородной
электропроводящей среде;
3. дипольный момент
![]() сердца образуется суперпозицией
сердца образуется суперпозицией
дипольных моментов элементарных токовых
диполе, которые во множестве имеются в
возбужденном миакарде сердца
![]()
и называется интегральным дипольным
вектором сердца (интеградьным дипольным
моментом сердца)
Проекции эквипотенциальных поверхностей
диполя на фронтальную поверхность тела
показаны на рисунке штриховыми линиями;
дипольный момент сердца располагается
во фронтальной плоскости тела;
5. точку приложения дипольного момента
сердца можно считать постоянной – это
нервный узел межпредсердной перегородки.
6. Связь между интегральным дипольным
моментом и разностью
потенциалов определяется исходя из
наших прежних рассмотрений:
![]() .
.
При таком расположении вектора
![]() ,
,
как показано на нашем рисунке, разность
потенциалов наибольшая в направлении
электрической оси между верхушкой и
основанием сердца. На ЭКГ она соответствует
зубцу![]() .
.
Метод отведений Эйнтховена
Эйнтховен предложил при проведении
электрокардиографии измерять разность
потенциалов между каждыми двумя вершинами
равностороннего треугольника, построенного
симметрично относительно тела человека,
а центр теугольника совпадает с точкой
интегрального электрического вектора
сердца. Вершины этого треугольника
лежат на левом предплечье (ЛР), правом
предплечье (ПР) и левой ноге (ЛН). На
каждые две точки накладываются по
электроду, и между ними измеряется
разность потенциалов. Каждые две точки
наложения электродов называются
стандартными отведениями.
Отведения:
I– ЛР-ПР;
II– ЛН-ПР;
III- ЛН-ЛР.
Разности потенциалов между каждыми
двумя точками пропорциональны проекциям
дипольного момента на линию, соединяющую
соответствующие точки:

Вектор-электрокардиография.
Точку приложения вектора
![]() можно считать постоянной (точка,
можно считать постоянной (точка,
совпадающая с нервным узлом межпредсердной
перегородки), а конец вектора![]() за цикл работы описывает сложную
за цикл работы описывает сложную
пространственную кривую. С помощью
осциллографа, используя его усилители,
можно наблюдать проекции этой
пространственной кривой на фронтальную,
горизонтальную и сагиттальную плоскости,
совмещенные с телом обследуемого.

В плоскости при этом наблюдаются петли
![]() ,
,
образованные сложением взаимноперпендикулярных
колебаний мгновенных значений ЭКГ в
двух каких-либо отведениях (фигуры
Лиссажу)
Этот метод называется вектор-электрокардтографией,
а полученная кривая вектор-
электрокардиограммой (ВЭКГ).
Вектор-электрокардиограмма – кривая,
показывающая геометрическое место
точек, соответствующих положению конца
вектора
![]() за время одного цикла.
за время одного цикла.
Блок-схема осциллографа.
Электрокардиограмма регистрируется
на приборе, называемом электрокардиографом.
Он содержит следующие основные блоки:

Лекция 10
ЭЛЕКТРОДИНАМИКА
Электрические колебания.
Процессы, происходящие в идеальном
колебательном контуре.
Электромагнитные колебания–колебания величин заряда, силы тока,
напряжения, эдс индукции.
Электромагнитные колебания создаются
в закрытом колебательном контуре,
который представляет собой электрическую
цепь, содержащую катушку индуктивности
и конденсатор.
М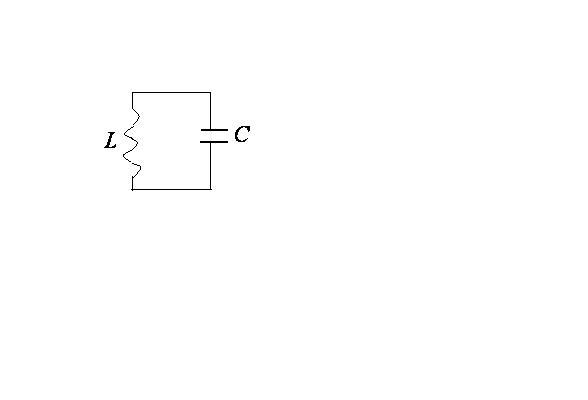 ы
ы
начнем с изучения свободных (собственных)
колебаний, т.е. колебаний, которые
совершаются без внешнего воздействия
за счет первоначально накопленной
энергии.
Рассмотрим идеальный колебательный
контур, т.е. контур, в котором активное
сопротивление
![]() (сопротивление проводов катушки) равно
(сопротивление проводов катушки) равно
нулю.

Если переведем ключ в положение 1 , то
конденсатор зарядится от источника
тока так, что на его пластинах накопится
максимальный заряд
![]() (на одной пластине +, на другой-).Перебросим ключ в положение 2 и? будем
(на одной пластине +, на другой-).Перебросим ключ в положение 2 и? будем
считать, что с этого момента времени
![]() рассматриваем процессы, происходящие
рассматриваем процессы, происходящие
в контуре.
Пассивный транспорт веществ через мембрану. Уравнение Теорелла. Уравнение Фика
Все виды переноса веществ через мембрану можно разделить на пассивный и активный транспорт. Пассивный транспорт веществ это вид транспорта, который осуществляется без затрат энергии. Имеются следующие видыпассивного транспортавеществ в клетках и тканях: диффузия, осмос, электроосмос и аномальный осмос, фильтрация.
Пусть Ф – потоквещества, с – его концентрация, m – электрохимический потенциал, u – подвижность, D – диффузия, и u=D/RT. Тогда взаимосвязь между перечисленными величинами может быть найдена с помощью уравнения Теорелла:
Ф = – с u dm/dx (1)
Согласно уравнению Теорелла поток вещества Ф равен произведению концентрации носителя на подвижность и на градиент его электрохимического потенциала. Знак “минус” указывает на то, что поток направлен в сторону убывания m..
Основным механизмом пассивного транспорта веществ, обусловленным наличием концентрационного градиента, является диффузия. Диффузия—это самопроизвольный процесс проникновения вещества из области большей в область меньшей его концентрации в результате теплового хаотического движения молекул.Математическое описание процесса диффузии дал Фик. Согласно закону Фика, скорость диффузии dm/dt прямо пропорциональна градиенту концентрации dC/dx, и площади S, через которую осуществляется диффузия:
Ф = dm/dt = – DS dC/dx (2)
Где Ф – это поток вещества, численно равный количеству вещества диффундирующему через данную площадь в единицу времени. Плотность потока j = Ф/S – это количество вещества диффундирующего через единицу площади в единицу времени. Под скоростью диффузии понимают количество вещества (в молях или других единицах), диффундирующего в единицу времени через данную площадь. Градиент концентрации—это изменение концентрации С вещества, приходящееся на единицу длины, в направлении диффузии. Знак минус в правой части уравнения (2) показывает, что диффузия происходит из области_большей концентрации, в область_меньшей концентрации вещества. Коэффициент пропорциональности Dв уравнении (2) называется коэффициентом диффузии. Его физический смысл легко выяснять, если S и dC/dx приравнять к единице. Коэффициент диффузии численно равен количеству вещества, диффундирующего в единицу времени через единицу площади при градиенте концентрации, равном единице. Коэффициент диффузии зависит, от природы вещества и от температуры. Он характеризует способность вещества к диффузии.
Так как концентрационный градиент клеточной мембраны определить трудно, то для описания диффузии веществ через клеточные мембраны пользуются более простым уравнением:
dm/dt = – PS (C1 – C2) (3), где Р = D/ d
где C1 и C2 — концентрации вещества по разные стороны мембраны; Р — коэффициент проницаемости, аналогичный коэффициенту диффузии, d – толщина мембраны. В отличие от коэффициента диффузии, который зависит только от природы вещества и температуры, Р зависит еще и от свойств мембраны и от ее функционального состояния.
Простая и облегченная диффузия.
Диффузия—это самопроизвольный процесс проникновения вещества из области большей в область меньшей его концентрации в результате теплового хаотического движения молекул.
Различают несколько типов пассивного переноса веществ (диффузии):
1. простая диффузия.
2. перенос через поры.
3. транспорт с помощью переносчиков (подвижных и эстафетной передачи).
Простая диффузия выражается соотношением (уравнение Фика):
J = (dm/dt) / S = -D (dС/dx) , где j -плотность потока вещества, (dС/dx) – градиент концентрации, D – коэффициент диффузии. Это уравнение даёт возможность рассчитать количество вещества (m) попавшее в клетку за определённое время (t) и через известную площадь (S): m = j t S.
Последние два вида диффузии относят к облегченной, т.к. количество вещества переносимое при таком виде транспорта существенно больше.
Если молекулыдиффундирующего вещества движутся без образования комплекса с другими молекулами, то такая диффузия называется простой.
Облегченная диффузиясостоит в том, что вещество слабо диффундирующее через мембрану, транспортируется через нее с помощью подвижных или фиксированных в мембране переносчиков. Разновидностью облегченной диффузии является обменная диффузия, которая состоит в том, что вспомогательное вещество образует соединение с диффундирующим веществом и перемещается к другой поверхности мембраны. На другой поверхности мембраны молекула проникающего вещества освобождается и на ее место присоединяется другая молекула такого же вещества. Например, установлено, что натрий эритроцитов благодаря обменной диффузии быстро обменивается на натрий плазмы.
Электродиффузия. Уравнение Нернста – Планка.
Поскольку в диффузии участвуют не только нейтральные вещества, но и ионы разной полярности, Нернст и Планк предложили формулу:
Ф = -uRT (dc/dx) – cuz F (dj/dx)
где: u = D/RT (называется подвижностью молекул)
R – универсальная газовая постоянная;
T – абсолютная температура;
с – концентрация вещества;
F – число Фарадея;
(dc/dx), (dj/dx) – градиент концентрации и градиент потенциала (то же, что электрическая напряжённость).
Это уравнение выведено из уравнения Теорелла: Ф = -cu (dm/dx), где m – электрохимический потенциал.
Пассивный перенос веществ через мембрану
Пассивный транспорт– это перенос вещества из мест с большим значением электрохимического потенциала к местам с его меньшим значением.
Пассивный транспорт идет с уменьшением энергии Гиббса, и поэтому этот процесс может идти самопроизвольно без затраты энергии.
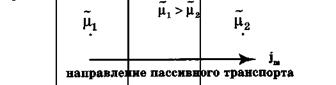
Рис.Схема пассивного транспорта
Плотность потока вещества jm при пассивном транспорте подчиняется уравнению Теорелла:
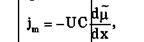
где U – подвижность частиц, С – концентрация. Знак минус показывает, что перенос происходит в сторону убывания μ.
Для разбавленных растворов при μ = const плотность потока вещества выражается уравнением Нернста-Планка:
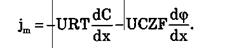
где U – подвижность частиц.
Итак, могут быть две причины переноса вещества при пассивном транспорте: градиент концентрации dC / dxи градиент электрического потенциала dφ / dx.Знаки минусов перед градиентами показывают, что градиент концентрации вызывает перенос вещества от мест с большей концентрацией к местам с его меньшей концентрацией; а градиент электрического потенциала вызывает перенос положительных зарядов от мест с большим к местам с меньшим потенциалом.
В случае неэлектролитов (Z = 0) или отсутствия электрического поля (dφ/dx =0) получаем уравнение:
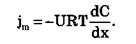
Согласно соотношению Эйнштейна коэффициент диффузии D=URT. В результате получаем уравнение, описывающее простую диффузию – закон Фика:
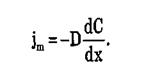
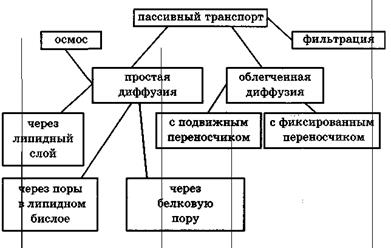
Рис.Классификация видов пассивного транспорта
Диффузия — самопроизвольное перемещение вещества из мест с большей концентрацией в места с меньшей концентра вещества вследствие хаотического теплового движения.
Диффузия вещества через липидный бислой вызывается градиентом концентрации в мембране.
Коэффициент проницаемости мембраны зависит от свойств мембраны и переносимых веществ.
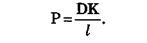
Величина К носит название коэффициента распределения, который показывает соотношение концентрации вещества вне мембраны и внутри ее. Коэффициент проницаемости тем больше, чем больше коэффициент диффузии (чем меньше вязкость мембраны), чем тоньше мембрана (чем меньше l) и чем лучше вещество растворяется в мембране (чем больше К).
Хорошо растворимы в фосфолипидной фазе мембраны неполярные вещества, например органические жирные кислоты, эфиры. Этим вещества хорошо проникают через липидную фазу мембраны.
Плохо проходят через липидный бислой полярные, водорастворимые вещества: соли, основания, сахара, аминокислоты, спирты.
В биологических мембранах был обнаружен еще один вид диффузии – облегченная диффузия. Облегченная диффузия происходит при участии молекул переносчиков. Например, валиномицин – переносчик ионов калия. Молекула валиномицина имеет форму манжетки, устланной внутри полярными группами, а снаружи – неполярными.
Молекулы валиномицина, оказавшиеся у поверхности мембраны, могут захватывать из окружающего раствора ионы калия. Диффундируя в мембране, молекулы переносят калий через мембрану, и некоторые из них отдают ионы в раствор по другую сторону мембраны. Таким образом, происходит перенос иона калия через мембрану валиномицином.
Облегченная диффузия, таким образом, происходит от мест с большей концентрацией переносимого вещества к местам с меньшей концентрацией. По-видимому, облегченной диффузией объясняется также перенос через биологические мембраны аминокислот, сахаров и других биологически важных веществ.
Отличия облегченной диффузии от простой:
· перенос вещества с участием переносчика происходит значительно быстрее;
· облегченная диффузия обладает свойством насыщения: при увеличении концентрации с одной стороны мембраны плотность потока вещества возрастает лишь до некоторого предела, когда все молекулы переносчика уже заняты;
· при облегченной диффузии наблюдается конкуренция переносимых веществ в тех случаях, когда переносчиком переносятся разные вещества; при этом одни вещества переносятся лучше, чем другие, и добавление одних веществ затрудняет транспорт других; так, из сахаров глюкоза переносится лучше, чем фруктоза, фруктоза лучше, чем ксилоза, а ксилоза лучше, чем арабиноза, и т.д.;
· есть вещества, блокирующие облегченную диффузию – они образуют прочный комплекс с молекулами переносчика, например, флоридзин подавляет транспорт сахаров через биомембрану.
Фильтрацией называется движение раствора через поры в мембране под действием градиента давления P. Скорость переноса при фильтрации подчиняется закону Пуазейля:
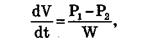
гда dV/dt – объемная скорость переноса раствора, w – гидравлическое сопротивление/
Явление фильтрации играет важную роль в процессах переноса воды через стенки кровеносных сосудов.
Осмос– преимущественное движение молекул воды через полупроницаемые мембраны (непроницаемые для растворенного вещества и проницаемые для воды) из мест с меньшей концентрацией растворенного вещества в места с большей концентрацией. Осмос – по сути дела, простая диффузия воды из мест с ее большей концентрацией в места с меньшей концентрацией воды. Осмос играет большую роль во многих биологических явлениях. Явление осмоса обусловливает гемолиз эритроцитов в гипотонических растворах.
Дата добавления: 2016-02-02 ; просмотров: 2763 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Мембранный транспорт. Лекция 7 Ж (1). Физические процессы в биологических мембранах
| Название | Физические процессы в биологических мембранах |
| Анкор | Мембранный транспорт |
| Дата | 08.11.2021 |
| Размер | 0.7 Mb. |
| Формат файла | |
| Имя файла | Лекция 7 Ж (1).doc |
| Тип | Лекция #266686 |
| страница | 2 из 2 |
Как известно , на мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле. Оно ока зывает влияние на диффузию заряженных частиц (ионов и элект ронов). Между напряженностью поля Е и градиентом потенциала d / dx существует известное соотношение (см. § 12.1):
(11.22)
Заряд иона равен Ze. На один ион действует сила ; сила, действующая на 1 моль ионов, равна
(11.23)
Скорость направленного движения ионов пропорциональна дей ствующей силе [см. (11.4), (11.5)]:
(11.24)
Чтобы найти поток вещества (ионов), выделим объем электролита (рис. 11.12) в виде прямоугольного параллелепипеда с ребром, численно равным скорости ионов. Все ионы, находящиеся в параллелепипе де, за 1 с пройдут через площадку S . Это и будет поток Ф. Число молей этих ионов можно найти, умножая объем параллелепипеда ( S ) на молярную концентрацию ионов с:
Плотность потока вещества найдем, используя формулы (11.24) и (11.25):
(11.26)
В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т.е. градиентом концентра ции [см. (11.11)], и воздействием электрического поля [см. (11.26)]:
(11.27)
Это уравнение Нернста — Планка. Используя выражение для подвижности (11.12), преобразуем уравнение (11.27) к виду
(11.28)
Это другая форма записи уравнения Нернста—Планка.
Используем уравнение Нернста—Планка для установления за висимости плотности диффузионного потока от концентрации ионов и от напряженности электрического поля. Предположим, система находится в стационарном состоянии, т. е. плотность потока J постоянна. Электрическое поле в мембране примем за од нородное, следовательно, напряженность поля одинакова, а по тенциал линейно изменяется с расстоянием. Это позволит счи тать, что где м — разность потенциалов на мембране. Упростим запись слагаемого в уравнении (11.28):
(11.29)
— вспомогательная величина (безразмерный потенциал). С учет ом (11.29) получим уравнение Нернста—Планка в виде:
(11.30)
Разделим переменные и проинтегрируем уравнение:
(11.31)
Потенцируя (11.31), получаем
(11.32)
Преобразуем формулу (11.32), учитывая выражения (11.19) и (11.20):
(11.33)
Вообще говоря, формула (11.33) справедлива как для положи тельных ( Z > 0, > 0), так и для отрицательных ( Z 0, ионов. Однако для отрицательных ионов целесообразно видоизме нить это выражение, подставив в него отрицательное значение безразмерного потенциала:
Разделим числитель и знаменатель этого выражения на е – :
(11.34)
При использовании этой формулы необходимо помнить, что отри цательные значения Z и уже учтены в самой формуле, т. е. — положительная величина.
Уравнения (11.33) и (11.34) устанавливают связь плотности стационарного потока ионов с тремя величинами: 1) проницаемо стью мембран для данного иона, которая характеризует взаимо действие мембранных структур с ионом; 2) электрическим полем; 3) молярной концентрацией ионов в водном растворе, окружаю щем мембрану (ciи c0).
Проанализируем частные случаи уравнения (11.33):
а) = 0, что означает либо Z = 0 (нейтральные частицы), либо отсутствие электрического поля в мембране ( м = 0), либо и то, и другое:
Найдем пределы отдельных сомножителей.
Эту неопределенность можно раскрыть по пра вилу Лопиталя:
Отсюда получаем, как и следовало ожидать, уравнение (11.21):
б) одинаковая молярная концентрация ионов по разные сторо ны от мембраны ( c i = с 0 = с ) при наличии электрического поля:
Это соответствует электропроводимости в электролите (см. § 12.9). Для нейтральных частиц ( Z = 0 и = 0) J = 0;
в) если мембрана непроницаема для частиц (Р = 0), то, естест венно, плотность потока равна нулю.
11.5. Разновидности пассивного переноса молекул и ионов через мембраны
Явления переноса (см.§ 11.3 и §11.4) относятся к пассивному транспорту: диффузия молекул и ионов в направлении их мень шей концентрации, перемещение ионов в соответствии с направле нием силы, действующей на них со стороны электрического поля. Пассивный транспорт не связан с затратой химической энергии. Наиболее общая классификации видов пассивного транспорта веществ через мембрану включает в себя простую диффузию, диф фузию через поры и диффузию с переносчиком.
Простая диффузия через липидный бислой подчиняется урав нению Фика для молекул (11.21) или, в более общем случае для нейтральных и заряженных частиц, — уравнению Нернста— Планка (11.28). В живой клетке такая диффузия обеспечивает прохождение кислорода и углекислого газа (см. рис. 11.13, а). Ряд жирорастворимых лекарственных веществ и ядов также про никает через липидный бислой по схеме, изображенной на рисун ке. Как уже отмечалось в § 11.1, определенная конфигурация ли пидов способствует диффузии поперек мембраны благодаря пере мещению «кинков».
Однако подобная простая диффузия протекает достаточно мед ленно и не может снабдить клетку в нужном количестве питатель ными веществами. Поэтому есть иные механизмы пассивного пе реноса веществ через мембрану, к ним относятся диффузия через канал (пору) и диффузия в комплексе с переносчиком. Два по следних варианта называют иногда облегченной диффузией (рис. 11.13, б, в).
Порой или каналом называют участок мембраны, включаю щий липидные или белковые молекулы и образующий в мембране проход (см. рис. 11.13, б). Этот канал допускает проникновение через мембрану не только малых молекул, например, молекул во ды, кислорода, но и более крупных ионов. Диффузия через поры также описывается диффузионными уравнениями, однако нали чие пор увеличивает коэффициент проницаемости Р. Каналы могут проявлять селективность (избирательность) по отношению к разным ионам, это проявится и в различии проницаемости для разных ионов.
Еще одно «облегчение» диффузии — перенос ионов специаль ными молекулами-переносчиками (см. рис. 11.13, в). При этом пе реносчик может быть подвижным либо неподвижным. Так, антибиотик валиномицин при связывании с ионом калия образует рас творимый в липидах комплекс и проходит через мембрану. Молекулы другого антибиотика, грамицидина, образуют времен ную цепочку поперек мембраны и «по эстафете» передают перено симое через мембрану вещество (ионы натрия) от одной молекулы переносчика к другой. За способность переносить ионы через мембраны валиномицин, грамицидин и другие переносчики получили название ионофоров.
Следует отметить, что диффузия комплекса переносчика и иона также описывается общим уравнением диффузии, посколь ку облегченная диффузия происходит от мест с большей концент рацией диффундирующего вещества к местам с меньшей концент рацией. Вывод о том, что имеет место облегченная диффузия, по зволяют сделать некоторые особенности, отличающие ее от простой.
Во-первых, перенос вещества с помощью переносчика любого типа идет с существенно большими скоростями, по сравнению с простой диффузией. Во-вторых, для облегченной диффузии ха рактерно «насыщение», когда с увеличением концентрации дан ного вещества с одной стороны мембраны плотность его потока становится больше только до определенного предела, зависящего от количества молекул переносчика. Наконец, при облегченной диффузии возможна конкуренция близких по структуре веществ за связывание с молекулой переносчика.
11.6. Активный транспорт. Опыт Уссинга
Наряду с пассивным транспортом в мембранах клетки проис ходит перенос молекул в область большей концентрации, а ионов — против силы, действующей на них со стороны электрического по ля. Такая разновидность переноса поручила название активного транспорта. Если пассивный транспорт может происходить в любых полупроницаемых мембранах, как биологических, так и искусственных, то активный транспорт присущ только биологи ческим мембранам. Благодаря активному транспорту сохраняет ся пространственная неоднородность в клетке (отличие внутри клеточной среды от внеклеточного пространства), создаются и поддерживаются градиенты концентраций, электрических потен циалов и т. д. Активный перенос веществ через мембрану осу ществляется за счет энергии гидролиза молекул (АТФ).
С уществование активного транспорта через биологические мембраны впервые было показано датским ученым Уссингом в опытах с переносом ионов натрия через кожу лягушки, которая имеет более сложную структуру, чем одиночная мембрана. Кожу лягушки можно представить как два последовательно располо женных барьера (1 и 2 на рис. 11.14). Наружный барьер 1 (мемб рана) отличается тем, что он избирательно проницаем для ионов натрия, но не калия. В то же время внутренняя мембрана 2 более проницаема для калия, чем для натрия. Экспериментальная ка мера Уссинга, изображенная на рис. 11.14, разделена на две части кожей лягушки. На рисунке кожа лягушки располагается между наружным и внутренним раствором: снаружи и изнутри камеры заполнены раствором Рингера, содержащим ионы натрия, калия, кальция и хлора.
В результате пассивного транспорта ионы натрия диффундиру ют из наружного раствора в кожу. При этом цитоплазма заряжа ется положительно относительно этого раствора. Ионы калия, проходя из цитоплазмы во внутренний раствор, заряжают ее от рицательно. Таким образом, на коже лягушки между внутренним и внешним барьерами возникает разность потенциалов. В уста новке имеется блок компенсации напряжения, позволяющий ус тановить разность потенциалов на коже, равную нулю. Это можно контролировать вольтметром. Концентрацию ионов с наружной и внутренней сторон поддерживают одинаковой. Если бы при этих условиях перенос ионов определялся только пассивным транспортом, потоки частиц в обе стороны были бы одинаковыми, а суммарный поток через мембрану был бы равен нулю.
Однако с помощью амперметра был зарегистрирован ток в це пи, проходящий через кожу лягушки. Это свидетельствует о том, что через кожу лягушки происходит односторонний перенос заря женных частиц. Методом меченых атомов было показано, что имеет место движение ионов натрия от наружного раствора к внутреннему. Таким образом, результаты опыта Уссинга показа ли, что перенос ионов натрия через кожу лягушки не подчиняет ся законам пассивного транспорта. В этом случае имеет место активный перенос ионов.
Согласно современным представлениям, в биологических мембранах имеются ионные насосы — специальные системы интег ральных белков (транспортные АТФазы). Известны четыре вида ионных насосов, три из которых обеспечивают перенос ионов Na + , К + , Ca 2+ и Н + через мембраны за счет энергии гидролиза АТФ. Ме ханизм переноса протонов при работе дыхательной цепи митохондрий изучен менее всего.
Натрий-калиевый насос работает при условии сопряжения переноса ионов калия и натрия. Это означает, что если во внеш ней среде нет ионов калия, не будет активного переноса ионов натрия из клетки, и наоборот. Другими словами, ионы натрия активируют натрий-калиевый насос на внутренней поверхности клеточной мембраны, а ионы калия — на внешней.
Натрий-калиевый насос переносит из клетки во внешнюю сре ду три иона натрия в обмен на перенос двух ионов калия внутрь клетки. Один акт переноса требует затраты энергии одной молекулы АТФ. При этом создается и поддерживается разность потенциалов на мембране, причем внутренняя часть клетки имеет отрицательный заряд.
Надо отметить, что существует также активный перенос сахаров, аминокислот, нуклеотидов, но кинетика этих процессов не достаточно хорошо изучена. Интересно, что до сих пор нет досто верных сведений об активном транспорте анионов, хотя они игра ют важную роль в жизнедеятельности клеток (в особенности ионы хлора). По-видимому, анионы попадают в клетку путем пассивно го переноса.
[spoiler title=”источники:”]
http://helpiks.org/6-74696.html
http://topuch.ru/fizicheskie-processi-v-biologicheskih-membranah-v2/index2.html
[/spoiler]
Перенос молекул (атомов) через мембраны. Уравнение Фика
Важной характеристикой мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Вероятность такого проникновения зависит как от направления перемещения частиц (в клетку или из клетки), так и от разновидности молекул и ионов.
Эти вопросы относятся к явлениям переноса. Таким термином называют самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.
Рассмотрим наиболее существенные для биологических мембран явления: перенос вещества (диффузию) и перенос заряда (электропроводность).
Как синоним переноса частиц в биофизике используется термин «транспорт частиц».
Основное уравнение диффузии имеет вид
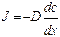 , (1)
, (1)
где J -плотность потока частиц, 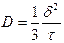 – коэффициент диффузии, τ – среднее время оседлой жизни молекулы (среднее время перескока), δ – среднее расстояние между молекулами, c=m∙n – массовая концентрация, m – масса молекулы, n – концентрация молекул. Знак «-» показывает, что суммарная плотность потока частиц при диффузии направлена в сторону уменьшения их концентрации (увеличения градиента концентрации).
– коэффициент диффузии, τ – среднее время оседлой жизни молекулы (среднее время перескока), δ – среднее расстояние между молекулами, c=m∙n – массовая концентрация, m – масса молекулы, n – концентрация молекул. Знак «-» показывает, что суммарная плотность потока частиц при диффузии направлена в сторону уменьшения их концентрации (увеличения градиента концентрации).
(1) называется уравнением Фика.
Уравнение Фика описывает диффузию в однородной среде. Модифицируем его для случая диффузии через мембрану. Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества. Например, если в сосуд, в котором поверх воды налито масло, бросить соль, то ее концентрации в этих средах будут различны.
Пусть концентрация частиц, диффундирующих через мембрану, изменяется в мембране линейно (рис.11).
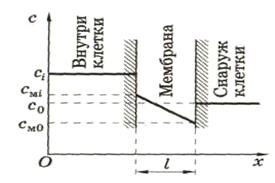
Рис.11. Распределение концентрации частиц, проходящих через мембрану
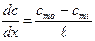
где 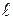 – толщина мембраны, сi – концентрация частиц внутри клетки, с0 – снаружи клетки, сmi – концентрация частиц в мембране у ее внутренней поверхности, cmo – концентрация частиц в мембране у ее внешней поверхности.
– толщина мембраны, сi – концентрация частиц внутри клетки, с0 – снаружи клетки, сmi – концентрация частиц в мембране у ее внутренней поверхности, cmo – концентрация частиц в мембране у ее внешней поверхности.
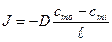
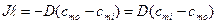 .
.
Практически легче определять концентрации частиц не внутри мембраны (cmi и cmo), а вне мембраны: в клетке (сi) и снаружи клетки (co). Предположим, что
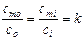
где k -коэффициент распределения частиц между мембраной и окружающей средой. Тогда cmo = kco, cmi = kci , и имеем
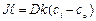 .
.
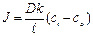
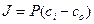 , (2)
, (2)
где 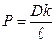 – коэффициент проницаемости
– коэффициент проницаемости 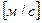 , характеризующий способность мембраны пропускать те или иные вещества.
, характеризующий способность мембраны пропускать те или иные вещества.
Перенос заряженных частиц. Электродиффузное уравнение Нернста-Планка
На мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле, которое влияет на диффузию заряженных частиц (ионов и электронов).
Плотность потока заряда дается выражением
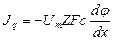 , (3)
, (3)
где φ – потенциал поля, F=eNA -постоянная Фарадея, Z – валентность, Um – подвижность диффундирующих частиц для одного моля.
В общем случае перенос ионов зависит от неравномерности их распределения и воздействия электрического поля. Суммарная плотность потока частиц определяется электродиффузным уравнением Нернста-Планка
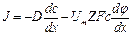 . (4)
. (4)
Для нейтральных частиц (Z=0) уравнение Нернста-Планка переходит в уравнение Фика.
ПАССИВНЫЙ ПЕРЕНОС. ПРОСТАЯ И ОБЛЕГЧЁННАЯ ДИФФУЗИЯ
В зависимости от того, что является движущей силой перемещения, все виды переноса можно разделить на пассивные и активные. Пассивный транспорт веществ осуществляется за счет энергии, сконцентрированной в каком-либо градиенте и не связан с затратой химической энергии гидролиза АТФ. Наиболее значимыми для биологических систем являются градиенты концентрации – dc/dx, электрического потенциала – dφ/dx и гидростатического давления – dр/dx.
Выделяют следующие виды пассивного переноса через биологические мембраны: простая диффузия, диффузия через поры, облегченная диффузия, осмос и фильтрация:
а) Простая диффузия – это самопроизвольное перемещение вещества из мест с большей концентрацией в места с меньшей концентрацией вследствие хаотического теплового движения частиц. Рассмотрим в качестве примера диффузию из клетки незаряженных частиц определённого вида через биологическую мембрану толщиной l. Запишем уравнение Фика через концентрацию вещества данного вида в растворе. Не трудно видеть, что для раствора масса растворённого вещества в единице объёма и есть его массовая концентрация (кг/м 3 ). Теперь плотность потока вещества через поверхность мембраны в направлении нормали к ней, в соответствии с (10), запишется:
 , (1)
, (1)
где D – коэффициент диффузии, Δc/Δx – градиент массовой концентрации
вдоль направления переноса. Будем считать, что концентрация частиц, диффундирующих через мембрану, изменяется в мембране по линейному закону от значения сi,м до значения со,м (рис.1). Тогда градиент концентрации можно выразить соотношением: 
 . (2)
. (2)
Измерить концентрации со,м и сi,м в приграничных слоях мембраны практически невозможно. Поэтому воспользуемся соотношением:
 , (3)
, (3)
где со и сi концентрации данного вещества в межклеточной жидкости и цитоплазме, соответственно. С учётом того, что сi,м = k сi , a со,м = k со , получим:
 . (4)
. (4)
С учётом (4) уравнение диффузии частиц через мембрану примет вид:
 – уравнение Коллендера. (5)
– уравнение Коллендера. (5)
Величина Р = Dk / l называетсякоэффициентом проницаемости.
Проницаемость характеризует способность биологических мембран пропускать или не пропускать молекулы, атомы и ионы. Изучение проницаемости играет важную роль для медицины и, особенно, для фармакологии и токсикологии. Для лечения необходимо знать проникающую способность фармакологических средств и ядов через мембрану в норме и при патологии.
В живой клетке такая диффузия обеспечивает прохождение кислорода и углекислого газа, а также ряда лекарственных веществ и ядов.
 б) Диффузия через липидные и белковые поры или каналы (рис.6). Такой механизм проникновения сквозь мембрану характерен для молекул нерастворимых в липидах веществ и водорастворимых гидратированных ионов. Этот вид переноса допускает проникновение через мембрану не только малых молекул, например, молекул воды, но и более крупных частиц. Значение проницаемости при этом определяется размерами молекул: с ростом размеров молекул их проницаемость уменьшается. Каналы могут проявлять селективность или избирательность по отношению к разным ионам, это проявляется в разной величине проницаемости для разных ионов.
б) Диффузия через липидные и белковые поры или каналы (рис.6). Такой механизм проникновения сквозь мембрану характерен для молекул нерастворимых в липидах веществ и водорастворимых гидратированных ионов. Этот вид переноса допускает проникновение через мембрану не только малых молекул, например, молекул воды, но и более крупных частиц. Значение проницаемости при этом определяется размерами молекул: с ростом размеров молекул их проницаемость уменьшается. Каналы могут проявлять селективность или избирательность по отношению к разным ионам, это проявляется в разной величине проницаемости для разных ионов.
Диффузия через поры также описывается уравнением Фика. Наличие пор увеличивает значение коэффициента проницаемости Р.
в) Облегченная диффузияпроисходит при участии молекул-переносчиков. Было обнаружено, что скорость проникновения в клетку глюкозы, глицерина, аминокислот не имеет линейной зависимости от разности концентраций. Для определенных концентраций скорость проникновения вещества через мембрану намного больше, чем следует ожидать для простой диффузии. При увеличении разности концентраций скорость диффузии возрастает в меньшей степени, чем это следует из уравнения Коллендера (5).  В данном случае наблюдается облегченная диффузия. Её механизм состоит в том, что вещество A, которое самостоятельно плохо проникает через мембрану, способно образовать комплекс с молекулами X вспомогательного вещества (рис.7), которое хорошо растворяется в липидах. Молекулы вещества Х, оказавшись у поверхности мембраны, образуют с молекулами А комплекс AX, который способен растворяться в липидах. Оказавшись в результате диффузии по другую сторону мембраны, некоторые из комплексов отщеплют молекулы A. Молекула X возвращается к наружной поверхности мембраны и может образовать новой комплекс с молекулой А. Разумеется транспорт вещества А таким способом происходит в одну и другую сторону. Поэтому результирующий перенос возникнет только при условии, что концентрация А по одну и другую стороны мембраны разная. Таким способом, например, антибиотик валиномицин переносить через мембраны ионы калия.
В данном случае наблюдается облегченная диффузия. Её механизм состоит в том, что вещество A, которое самостоятельно плохо проникает через мембрану, способно образовать комплекс с молекулами X вспомогательного вещества (рис.7), которое хорошо растворяется в липидах. Молекулы вещества Х, оказавшись у поверхности мембраны, образуют с молекулами А комплекс AX, который способен растворяться в липидах. Оказавшись в результате диффузии по другую сторону мембраны, некоторые из комплексов отщеплют молекулы A. Молекула X возвращается к наружной поверхности мембраны и может образовать новой комплекс с молекулой А. Разумеется транспорт вещества А таким способом происходит в одну и другую сторону. Поэтому результирующий перенос возникнет только при условии, что концентрация А по одну и другую стороны мембраны разная. Таким способом, например, антибиотик валиномицин переносить через мембраны ионы калия.
Соединения, обладающие способностью избирательно увеличивать скорость переноса ионов через мембрану получили название ионофоров.
Если концентрация молекул А в среде такова, что все молекулы вещества-переносчика задействованы, то дальнейшее повышении концентрации вещества А не будет больше вызывать рост скорости диффузии. Это означает, что облегчённая диффузия обладает свойством насыщения.
При облегчённой диффузии наблюдается конкуренция переносимых веществ в тех случаях, когда переносчиком выступает одно и тоже соединение. Например, глюкоза переносится лучше, чем фруктоза; фруктоза лучше, чем ксилоза; ксилоза, лучше, чем арабиноза и т.д.
Известны также соединения, способные избирательно блокировать облегчённую диффузию ионов через мембрану. Они образуют прочные комплексы с молекулами переносчиками. Например яд рыбы фугу тетродотоксин блокирует транспорт натрия, флоридзин подавляет транспорт сахаров и т.д.
 Разновидностью облегчённой диффузии является транспорт с помощью неподвижных переносчиков. Молекулы X образуют фиксированные цепочки поперек мембраны, например, выстилать изнутри пору (рис.8). Молекулы переносимого вещества А передаются от одной молекулы переносчика к другой, как по эстафете. При этом предполагается, что пространство в поре недостаточно велико для прохождения через нее частиц А, если только они не способны к специфическому взаимодействию с переносчиком Х.
Разновидностью облегчённой диффузии является транспорт с помощью неподвижных переносчиков. Молекулы X образуют фиксированные цепочки поперек мембраны, например, выстилать изнутри пору (рис.8). Молекулы переносимого вещества А передаются от одной молекулы переносчика к другой, как по эстафете. При этом предполагается, что пространство в поре недостаточно велико для прохождения через нее частиц А, если только они не способны к специфическому взаимодействию с переносчиком Х.
Диффузия является основным видом пассивного транспорта веществ через мембрану клетки. Все остальные виды пассивного переноса связаны в основном с транспортом воды.
г) Осмос – диффузия растворителя через полупроницаемую мембрану, разделяющую два раствора с разной концентрацией.Сила, которая вызывает это движение растворителя, называется осмотическим давлением. Рассмотрим это явление на примере водных растворов. Осмос возникает вследствие теплового движения молекул воды и растворённого вещества. Некоторые молекулы воды, векторы скорости которых параллельны каналам мембраны, проникают через неё. В то же время для растворённого вещества А мембрана непроницаема. По этой причине поток воды из раствора, где концентрация А ниже будет больше (в этом растворе выше концентрация воды). Процесс приводит к возрастанию гидростатического (водяного) давления в растворе с большей концентрацией А. Это избыточное давление вызывает фильтрацию воды в обратном направлении. В некоторый момент наступает состояние динамического равновесия. Давление соответствующее этому состоянию называется осмотическим давлением. Величина осмотического давления определяется уравнением Ван-Гоффа:
где с – концентрация растворённого вещества; Т – термодинамическая температура; R – газовая постоянная; i – изотонический коэффициент, показывает во сколько раз из-за диссоциации молекул возросло число частиц в растворе. Скорость осмотического переноса воды через мембрану определяется соотношением:
 , (7)
, (7)
где Ро – коэффициент проницаемости, S – площадь мембраны, (р1 – р2) – разность осмотических давлений по одну и другую стороны мембраны.
д) Фильтрацией называется движение жидкости через поры в мембране под действием градиента гидростатического давления. Объёмная скорость переноса жидкости при этом подчиняется закону Пуазейля:
 , (8)
, (8)
где r – радиус поры; l – длина канальца поры; (р1-р2) – разность давлений на концах канальца поры; η – коэффициент вязкости переносимой жидкости;  – модуль градиента давления вдоль поры;
– модуль градиента давления вдоль поры;  – гидравлическое сопротивление. Это явление наблюдается при переносе воды через стенки кровеносных сосудов (капилляров). Явление фильтрации играет важную роль во многих физиологических процессах. Так, например, образование первичной мочи в почечных нефронах происходит в результате фильтрации плазмы крови под действием давления крови. При некоторых патологиях фильтрация усиливается, что приводит к отёкам.
– гидравлическое сопротивление. Это явление наблюдается при переносе воды через стенки кровеносных сосудов (капилляров). Явление фильтрации играет важную роль во многих физиологических процессах. Так, например, образование первичной мочи в почечных нефронах происходит в результате фильтрации плазмы крови под действием давления крови. При некоторых патологиях фильтрация усиливается, что приводит к отёкам.
Перенос молекул (атомов) через мембраны.Уравнение Фика
Важным элементом функционирования мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Существенно, что вероятность такого проникновения частиц зависит как от направления их перемещения, например в клетку или из клетки, так и от разновидности молекул и ионов.
Эти вопросы рассматриваются в разделе физики, относящемся — к явлениям переноса. Таким термином называют необратимые F, процессы, в результате которых в физической системе происходит пространственное перемещение (перенос) массы, импульса, энергии, заряда или какой-либо другой физической величины.
К явлениям переноса относят диффузию (перенос массы вещества), вязкость (перенос импульса), теплопроводность (перенос энергии), электропроводность (перенос электрического заряда). Здесь и в следующих параграфах рассматриваются наиболее существенные для биологических мембран явления: перенос вещества и перенос заряда. Как синоним переноса частиц в биофизике широкое распространение получил также термин транспорт частиц.
Выведем основное уравнение диффузии (уравнение Фика), рассматривая процесс переноса в жидкостях.
Пусть через некоторую площадку S (рис. 11.10) во всех направлениях перемещаются молекулы жидкости. Учитывая теорию : молекулярного строения жидкости (см. § 7.6), можно сказать, что молекулы пересекают площадку, перескакивая из одного положения равновесия в другое.
 На расстояниях, равных среднему перемещению 5 молекул (среднее расстояние между молекулами жидкости), вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины l (l 1 /6 Sln1 молекул, а противоположно оси ОХ от второго параллелепипеда перескакивает 1 /6 Sln2 молекул.
На расстояниях, равных среднему перемещению 5 молекул (среднее расстояние между молекулами жидкости), вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины l (l 1 /6 Sln1 молекул, а противоположно оси ОХ от второго параллелепипеда перескакивает 1 /6 Sln2 молекул.

Время Δt «пролета» этими молекулами площадки S может быть найдено следующим образом. Предположим, что все молекулы из выделенных объемов движутся с одинаковыми средними скоростями . Тогда молекулы в объеме 1 или 2, дошедшие до площадки S, пересекают ее в течение промежутка времени
Подставляя в (11.1)выражение для средней скорости ύ из (7.20), получаем

где т — среднее время «оседлой жизни» молекулы, оно может рассматриваться как среднее время перескока. «Баланс» переноса молекул через площадку S за промежуток времени Δt равен

Умножая (11.3)на массу тотдельной молекулы и деля на Δt, находим массовый поток сквозь площадку S:

т. е. масса вещества, которая за 1 с переносится через площадку S. Изменение концентрации п2 — п1 молекул можно представить как произведение dn/dxна расстояние 2δ между выделенными объемами:

В уравнении (11.4) заменим Δt согласно (11.2)и (п2 — п1) согласно (11.5):
Отношение потока к площади S, через которую он переноситься, называется плотностью потока:


Произведение массы молекулы на их концентрацию есть плотность вещества (парциальная плотность):
Это есть уравнение диффузии (уравнение Фика), которое обычно записывают в виде:

Знак «-» показывает, что суммарная плотность потока вещества при диффузии направлена в сторону уменьшения плотности (в сторону, противоположную градиенту плотности), D — коэффициент диффузии, применительно к рассмотренному примеру диффузии в жидкости он равен
Как видно из (11.10),единица измерения коэффициента диффузии [м 2 /с].
Уравнение диффузии можно записать не только для плотности
массового потока кг/(м 2 *с), но и для плотности потока частиц 1/(м 2 *с) и плотности потока вещества моль/(м 2 *с), при этом в уравнении (11.9) вместо градиента плотности следует использовать соответственно градиент концентрации  или градиент молярной концентрации
или градиент молярной концентрации 

А. Эйнштейн показал, что коэффициент диффузии пропорционален температуре:

И поэтому вместо (11.11) имеем

В формуле (11.12) и далее ит — подвижность диффундирующих молекул (частиц), выраженная для моля. Вообще говоря, подвижностью диффундирующей частицы (молекулы, атома, иона, электрона) и называют коэффициент пропорциональности между скоростью v частицы и силой f, двигающей частицу, в том случае, когда на частицу не действуют другие силы (например, трение или соударение с другими частицами) и она перемещается равномерно:

Как видно из (11.14), единица подвижности 1 м/(с • Н). Величины um и u связаны через постоянную Авогадро:

Преобразуем уравнение (11.9) применительно к биологической мембране. Будем считать, что концентрация частиц, диффундирующих через мембрану, изменяется в мембране по линейному закону (рис. 11.11). Молярные концентрации частиц внутри и вне клетки соответственно равны ci и с0. Молярная концентрация этих же частиц в мембране изменяется от внутренней к наружной ее части соответственно от сmi до см0. Учитывая линейное изменение концентрации молекул, запишем

где I — толщина мембраны, тогда вместо (11.11) имеем


Практически доступнее определить молярные концентрации частиц не внутри мембраны (cMi и см0), а вне мембраны: в клетке (сi) и снаружи клетки (с0). Считают, что отношение граничных значенийконцентраций в мембране равно отношению концентраций в прилегающих к мембране слоях: см0/сMi = co/ci, откуда

где k — коэффициент распределения вещества (частиц) между мембраной и окружающей средой (обычно водная фаза). Из (11.18) следует
Подставляя (11.19) в (11.17), имеем
Пусть

где Р — коэффициент проницаемости. В результате получаем уравнение для плотности потока вещества при диффузии через биологическую мембрану:

Уравнение Нернста—Планка. Перенос ионов через мембраны
Как известно, на мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле. Оно оказывает влияние на диффузию заряженных частиц (ионов и электронов). Между напряженностью поля Е и градиентом потенциала dφ/dx существует известное соотношение (см. § 12.1):

Заряд иона равен Ze. На один ион действует сила f=Ze(dφ/dx); сила, действующая на 1 моль ионов, равна
где F — постоянная Фарадея, F = eNA.

 Скорость направленного движения ионов пропорциональна действующей силе [см. (11.4), (11.5)]:
Скорость направленного движения ионов пропорциональна действующей силе [см. (11.4), (11.5)]:
Чтобы найти поток вещества (ионов), выделим объем электролита (рис. 11.12) в виде прямоугольного параллелепипеда с ребром, численно равным скорости ионов. Все ионы, находящиеся в параллелепипеде, за 1 с пройдут через площадку S. Это и будет поток Ф. Число молей этих ионов

можно найти, умножая объем параллелепипеда (vS) на молярную концентрацию ионов с:

Плотность потока вещества найдем, используя формулы (11.24) и (11.25):

В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т. е. градиентом концентрации [см. (11.11)], и воздействием электрического поля [см. (11.26)]:
Это уравнение Нернста—Планка. Используя выражение для подвижности (11.12), преобразуем уравнение (11.27) к виду

Это другая форма записи уравнения Нернста—Планка
Используем уравнение Нернста—Планка для установления зависимости плотности диффузионного потока от концентрации ионов и от напряженности электрического поля. Предположим, система находится в стационарном состоянии, т. е. плотность потока Jпостоянна. Электрическое поле в мембране примем за однородное, следовательно, напряженность поля одинакова, а потенциал линейно изменяется с расстоянием. Это позволит считать, что  , где φм — разность потенциалов на мембране.
, где φм — разность потенциалов на мембране.
Упростим запись слагаемого в уравнении (11.28):
где
— — —

вспомогательная величина (безразмерный потенциал). С учетом (11.29) получим уравнение Нернста—Планка в виде

Разделим переменные и проинтегрируем уравнение:

Потенцируя (11.31), получаем

откуда

Преобразуем формулу (11.32), учитывая выражения (11.19) и (11.20):

Вообще говоря, формула (11.33) справедлива как для положительных (Z > 0, у > 0), так и для отрицательных
При использовании этой формулы необходимо помнить, что отрицательные значения Z и ψ уже учтены в самой формуле, т. е. ψ— положительная величина.
Уравнения (11.33) и (11.34) устанавливают связь плотности стационарного потока ионов с тремя величинами: 1) проницаемостью мембран для данного иона, которая характеризует взаимодействие мембранных структур с ионом; 2) электрическим полем; 3) молярной концентрацией ионов в водном растворе, окружающем мембрану <сi и с0).
Проанализируем частные случаи уравнения (11.33):

а) ψ = 0, что означает либо Z = 0 (нейтральные частицы), либо отсутствие электрического поля в мембране (φм = 0), либо и то, и другое:
Найдем пределы отдельных сомножителей.
1.  Эту неопределенность можно раскрыть по правилу Лопиталя:
Эту неопределенность можно раскрыть по правилу Лопиталя:

2.Отсюда получаем, как и следовало ожидать, уравнение (11.21):

б) одинаковая молярная концентрация ионов по разные стороны от мембраны (ci = с0 = с) при наличии электрического поля:

Это соответствует электропроводимости в электролите (см. § 12.9). Для нейтральных частиц (Z = 0 и ψ=0) J = 0;
в) если мембрана непроницаема для частиц (Р = 0), то, естественно, плотность потока равна нулю.
источники:
http://poisk-ru.ru/s11482t3.html
http://megaobuchalka.ru/1/16502.html
