Магнитное поле в соленоиде и тороиде
Соленоидом называется катушка с
большим числом витков. Рассмотрим
соленоид длиной
![]() ,
,
имеющей N витков. По
соленоиду течет ток .
Предположим, что у соленоида:
![]() d,
d,
где d – диаметр витков
(бесконечно длинный соленоид).
В

нутри соленоида магнитное поле
однородно, а вне соленоида – неоднородное
и очень слабое (рисунок 15). Можно считать,
что в бесконечно длинном соленоиде все
поле сосредоточено внутри его, а полем
вне соленоида можно пренебречь.
Рисунок 15. Магнитное поле соленоида
Выберем замкнутый прямоугольный контур
АВСДА, охватывающий N
витков. Тогда циркуляция:![]() .
.
Н
![]()
![]()
а участках АВ, СД и СВ контур
перпендикулярен линиям магнитной
индукции и индукция
![]()
= 0; На участке ДА циркуляция индукции
![]()
равна
![]()
(контур совпадает с линией магнитной
индукцией):
![]()
отсюда магнитная индукция и напряженность
поля внутри соленоида:
Тороид
– кольцевая катушка.
М

агнитная индукция внутри обмотки
тороида (в вакууме):
![]() ,
,
где
![]() –
–
число витков. Магнитное поле вне тороида
отсутствует.
Рисунок 16. Тороид
r
Контрольные вопросы
-
Изложите закон Ампера. Как определить
направление силы Ампера? -
Приведите формулу для определения силы
взаимодействия двух параллельных
токов. -
Чему равна магнитная индукция, создаваемая
движущимся электрическим зарядом? -
Дайте определение силы Лоренца. Как
определить модуль и направление силы
Лоренца? -
Как вычисляется циркуляция вектора

по произвольному замкнутому контуру
и что она показывает? -
Что такое соленоид и чему равна магнитная
индукция внутри соленоида? -
Что такое тороид и чему равна магнитная
индукция внутри тороида?
Поток вектора магнитной индукции. Теорема Гаусса для вектора .
П

оток вектора магнитной индукции
(магнитным потоком) через
площадку
![]()
называется скалярная физическая
величина, равная:
![]()
![]()
– проекция вектора
![]()
на направление нормали к площадке
![]()
(рисунок 17), – угол
между векторами
![]()
и
![]() .
.
![]()
Поток вектора
![]()
через произвольную поверхность
![]() :
:
![]() .
.
Размерность потока:
Рисунок 17. Проекция вектора
![]()
на нормаль
![]() (вебер)=
(вебер)=
1 Тл×м2
Д
![]()
ля однородного поля и плоской
поверхности, расположенной перпендикулярно
вектору![]() :
:
![]()
и
Теорема Гаусса: поток вектора магнитной
индукции
![]()
через любую замкнутую поверхность равен
0.
![]()
Отсюда следует, что магнитных зарядов
не существует, вследствие чего линии
магнитной индукции не имеют ни начала,
ни конца и всегда замкнуты.
Для одного витка соленоида:
![]()
Полный поток, сцепленный со всеми
витками соленоида, называется
потокосцеплением:
![]()
, где
![]() и
и
![]() –
–
длина,
площадь сечения и
число витков соленоида соответственно.
Работа по перемещению проводника и контура с током в магнитном поле
По закону Ампера
![]() .
.
Элементарная работа (рисунок 18):
![]()

Рисунок 18. Работа по перемещению
проводника с током в магнитном поле
Работа по перемещению проводника
с постоянным током
![]()
в магнитном поле равна произведению
силы тока на величину магнитного потока,
пересеченного движущимся проводником.
![]()
Работа по перемещению замкнутого
контура с током в магнитном поле равна
произведению силы тока в контуре на
изменение магнитного потока, сцепленного
с контуром. Формула справедлива для
контура любой формы в произвольном
магнитном поле.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
14.04.2015225.76 Кб14ЛР.pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 мая 2016 года; проверки требуют 5 правок.
| Потокосцепление | |
|---|---|
 |
|
| Единицы измерения | |
| СИ | Вебер |
| СГС | Максвелл |
Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, который пронизывает замкнутый проводящий контур (как бы «сцепляется» с ним). Обозначается буквой 
Термин используется, в основном, в электротехнике применительно к дискретным элементам цепи — катушкам индуктивности, а также является одним из основных параметров, описывающих обмотки электрических машин и электромеханическое преобразование энергии в них.
Определение[править | править код]
Потокосцеплением называется суммарный магнитный поток
через поверхность (более строго, риманову поверхность), натянутую на замкнутый контур. От конфигурации натянутой поверхности такой поток не зависит.
Магнитное поле, а значит, и магнитный поток, могут создаваться током в самом этом контуре или током в другом контуре. Соответственно, различаются потокосцепление самоиндукции (потокосцепление элемента цепи обусловлено электрическим током в этом же элементе) и потокосцепление взаимной индукции (потокосцепление одного элемента электрической цепи обусловлено электрическим током в другом элементе).
Понятие «потокосцепление» (в отличие от «магнитный поток») не применяется к фрагментам поверхности.
Основной случай[править | править код]
Чаще всего рассматривается потокосцепление в катушке с током в ситуации, когда магнитный поток в катушке создается ею самой; этот поток сцепляется со всеми витками.
Потокосцепление в таком случае численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как
,
где 
В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитные потоки витков одинаковы. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:
,
где 


Если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:
,
где 
Величина потокосцепления, помимо магнитного потока, имеет связь с током I в индуктивности, определяющуюся выражением:
,
где 
Принцип непрерывности[править | править код]
Запас энергии магнитного поля в катушке индуктивности не может измениться скачком. Это выражает принцип непрерывности во времени. Невозможность скачкообразного изменения потокосцепления индуктивности объясняется, в свою очередь, тем, что в противном случае на индуктивности появилось бы бесконечно большое напряжение, что противоречит опыту.
Принцип непрерывности также означает, что ток в индуктивности не может измениться скачком (см. переходные процессы в электрических цепях): 
См. также[править | править код]
- Магнитный поток
- Индуктивность
- Катушка индуктивности
Литература[править | править код]
- Иродов И.Е. Электромагнетизм. Основные законы. 2010. 319 с. — ISBN 978-5-9963-0281-9
Магнитный поток в замкнутой цепи обусловлен движущимся током в катушке, намотанной по всей ее длине. Давайте посмотрим на магнитный поток в соленоиде.
Магнитный поток следует продольному пути по длине соленоида и постоянен в любой точке области. Магнитный поток в соленоиде зависит от величины и направления тока в катушке и плотности витков катушки.
Магнитный поток постоянен во внутренней области соленоида и пренебрежимо мал вне его. В этой статье давайте подробно обсудим магнитный поток, его плотность и связь.
Что такое магнитный поток в соленоиде?
Поток – это воображаемые линии, проходящие через площадь проводника. Кратко обсудим магнитный поток в соленоиде.
Магнитный поток в соленоиде равен сумме напряженности магнитного поля в соленоиде, умноженной на общую площадь соленоида. Линии магнитного потока проходят от сердечника соленоида к окружающей области замкнутыми круговыми петлями.
Линии магнитного потока всегда параллельны и никогда не перекрываются и не пересекают другую линию или петлю магнитного потока. По мере увеличения расстояния между центральной осью соленоида и точкой рассмотрения в окружающей его области увеличивается и расстояние между двумя параллельными контурами.
Что такое плотность магнитного потока в соленоиде?
Сила магнитного поля зависит от плотности магнитного потока. Остановимся подробнее на плотности магнитного потока в соленоиде.
Плотность магнитного потока в соленоиде – это отношение магнитного потока, проникающего через площадь. Это число линий потока, проходящих через единицу объема. Плотность магнитного потока эквивалентна магнитному полю соленоида.
Плотность магнитного потока может определять силу поля. Чем выше плотность, тем сильнее поле. Магнитный поток целесообразно воздействовать на частицу в области магнитного поля.
Как найти магнитный поток соленоида?
Магнитный поток через соленоид также зависит от угла с нормалью площади поперечного сечения. Давайте посмотрим, как найти магнитный поток в соленоиде.
Магнитный поток соленоида рассчитывается по формуле,Ф=м0NIA. Где n – общее число витков катушки на единицу длины соленоида, м0 — проницаемость свободного пространства, I — ток в соленоиде, A — его площадь.
Магнитный поток представляет собой произведение магнитного поля в соленоиде на его площадь, определяемое формулой Φ=BA, где B — магнитное поле, а A — площадь соленоида.
Как рассчитать плотность магнитного потока соленоида?
Плотность магнитного потока увеличивается с увеличением числа витков на единицу длины соленоида. Давайте посмотрим, как рассчитать плотность магнитного потока соленоида.
Плотность магнитного потока соленоида рассчитывается по формуле d =m0nI, где d — плотность магнитного поля в соленоиде. Это выражение показывает, что плотность магнитного потока не зависит от магнитного поля в соленоиде.
Плотность магнитного потока соленоида представляет собой отношение полного магнитного потока в соленоиде к общей площади поперечного сечения соленоида, а формула для него дается как d = φ/A, где φ — это магнитный поток.
Как рассчитать потокосцепление с соленоидом?
Связь магнитного потока представляет собой восходящий магнитный поток, поскольку он пересекает различные поверхности в поле. Давайте посмотрим, как рассчитать магнитную потокосцепление в соленоиде.
Магнитный потокосцепление является произведением магнитного потока и числа витков катушки вокруг соленоида и рассчитывается по формуле катушка, A — площадь, B — плотность магнитного потока.
Численность катушки вокруг соленоида определяется как n = N/L. Следовательно, мы можем записать N как N = nL. Используя это выражение, мы можем найти магнитную потокосцепление как φL=nLAB. Магнитная потокосцепление – это часть исходящего потока, захваченная из стока.
Магнитный поток внутри соленоида равен нулю?
Магнитный поток является равнодействующей магнитного поля в регионе. Посмотрим, равен ли нулю магнитный поток внутри соленоида.
Магнитный поток внутри соленоида отличен от нуля, потому что магнитное поле не равно нулю и однородно внутри соленоида из-за высокой плотности магнитного потока в этой области. Магнитный поток является произведением магнитного поля и площади; магнитный поток не может быть равен нулю внутри соленоида.
Магнитное поле вне соленоида примерно равно нулю. Объем области внутри соленоида намного меньше, чем вне соленоида. Линии магнитного поля проходят параллельно по длине соленоида.
Чему равен магнитный поток внутри и снаружи соленоида длиной 30 см и радиусом 10 см, имеющего 300 витков катушки с током 5 А?
Данный: Длина соленоида L = 30 см = 0.3 м.
Число витков катушки N = 300 витков.
Сила тока в катушке I = 5 А.
Радиус соленоида r = 10 см = 0.1 м.
Плотность витков на единицу длины соленоида рассчитывается как
n = N/L = 300/0.3 м = 1000 витков/м
Площадь поперечного сечения соленоида внутри составляет,
А = πr2 = π × (0.1 м)2 = π × 0.01 м2 = 0.031 м2
Магнитное поле внутри соленоида рассчитывается по формуле
В = м0nI
Здесь, м0– проницаемость свободного пространства, заданная как 4π × 10-7 Тм/А.
Подставляя значения в это выражение, мы имеем,
В = 4π × 10-7 Тм/А × 1000 витков/м × 5 А = 62.9 × 10-4 Т = 6.29 × 10-3 Т ≈ 6.3 мТл
Магнитное поле внутри соленоида оказалось равным 6.3 мТл.
Магнитный поток внутри соленоида рассчитывается по формуле
Ф = АВ
Подставляя значения в эту формулу, получаем,
Ф = 0.031 м2 × 6.3 мТл = 0.2 мВб.
Следовательно, магнитный поток внутри соленоида равен 0.2 мВб.
Магнитное поле вне соленоида B = 0. Следовательно, магнитный поток вне соленоида равен
Ф = АВ = А × 0 = 0
Следовательно, магнитный поток вне соленоида равен нулю.
Заключение
Из этой статьи мы можем сделать вывод, что магнитный поток является произведением магнитного поля и площади поперечного сечения. Он максимален внутри соленоида и равен нулю снаружи. Магнитный поток представляет собой продольные линии внутри соленоида и течет в противоположном направлении снаружи, образуя замкнутые петли.
M_Transducer:
Программа расчета магнитоэлектрического преобразователя
1. Введение
Магнитоэлектрический преобразователь –
преобразователь механического движения постоянного магнита относительно обмотки
в электрический сигнал. Может либо выполнять функцию датчика скорости, либо
использоваться в качестве электрогенератора. Основная задача – по заданным
геометрическим и физическим параметрам системы необходимо рассчитать
электродвижущую силу (ЭДС) на выходе.
2. Конструкция преобразователя
Магнитоэлектрический
преобразователь состоит из закрепленного на неподвижном основании
дифференциального соленоида и соосно с ним расположенного подвижного кольцевого
(или цилиндрического) постоянного магнита. Дифференциальный соленоид
представляет собой два одинаковых расположенных соосно на некотором расстоянии и
последовательно включенных цилиндрических соленоида со встречным направлением
намотки. Магнит, как правило, размещается таким образом, что в исходном
положении его центр совпадает с центром дифференциального соленоида, но, вообще
говоря, центры магнита и дифференциального соленоида могут и не совпадать.
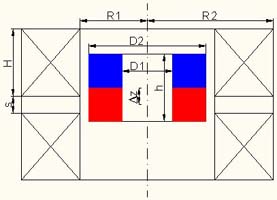
Рис. 2.1. Схема
магнитоэлектрического преобразователя.
Постоянный магнит
представляет собой кольцо (или цилиндр) внешним диаметром D2 высотой
h с отверстием диаметром D1 (или без отверстия).
Дифференциальный соленоид состоит из двух одинаковых цилиндрических соленоидов с
радиусом отверстия R1 внешним радиусом R2 высотой H, намотанных проводом
диаметром D с фактором упаковки l
и разделенных прокладкой толщиной s. Расстояние между центрами
дифференциального соленоида и магнита
Dz (Delta z).
Дифференциальный соленоид закреплен неподвижно. Осевая скорость магнита в
заданной точке v.
3. Расчет индукции магнитного поля постоянного кольцевого
(цилиндрического) магнита
Цилиндрический
постоянный магнит с аксиальным направлением намагниченности можно
рассматривать как однослойный соленоид с бесконечно тонкой обмоткой,
геометрически соответствующей боковой поверхности магнита, по которой течет
намагничивающий ток I.
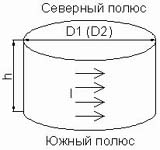
Рис. 3.1.
Представление цилиндрического постоянного магнита эквивалентным соленоидом.
Условием
эквивалентности магнита и соленоида является равенство их магнитных моментов.
Магнитный момент магнита P может быть найден по
формуле:
P = M V =
M S
h, где M – намагниченность магнита,
V – его объем,
S – площадь сечения,
h – высота.
Магнитный момент
эквивалентного соленоида:
P = j h
S, где
j = I/h – линейная
плотность намагничивающего тока.
Тогда:
j =
M
Для материалов с
прямоугольной петлей гистерезиса (феррит бария, феррит стронция,
неодим-железо-бор, самарий-кобальт и т. п.):
M ≈
Br/m0,
где Br – остаточная индукция,
m0 = 4p
∙ 10-7 Гн/м – магнитная постоянная. Таким образом, линейную
плотность намагничивающего тока можно выразить приближенной формулой:
j = Br/m0
Кольцевой
постоянный магнит с аксиальным направлением намагниченности может быть
представлен как два однослойных цилиндрических соленоида с бесконечно тонкой
обмоткой, вложенных друг в друга. Соленоид диаметром D2
и высотой h соответствует внешней боковой поверхности
магнита, а соленоид диаметром D1 и высотой
h – внутренней поверхности отверстия. Намагничивающие
токи в соленоидах равны по величине и противоположны по направлению.
Величину и направление
вектора магнитной индукции
dB
в произвольной точке магнитного поля, создаваемого в вакууме (или воздухе)
элементом проводника длиной
dl
с током
I,
можно найти с помощью закона Био – Савара – Лапласа [6]:
![]()
где
dl
– вектор элемента проводника, численно равный
dl
и проведенный в направлении тока,
r
– радиус-вектор, проведенный из этого элемента проводника в рассматриваемую
точку поля,
r
=
mod(r).
Этот принцип положен в основу программы A_Magnet
[1].
4. Расчет потокосцепления соленоида с
магнитом и электродвижущей силы
Электродвижущая сила (ЭДС) E соленоида в соответствии с законом электромагнитной
индукции Фарадея [6] может быть найдена по формуле:
![]()
где
Y – потокосцепление
соленоида с магнитным полем, t – время.
Формулу (4.1) можно записать в виде:
![]()
где z0 = H/2 + s/2 +
Dz – расстояние между
центрами магнита и соленоида, v – скорость движения
магнита.
Дифференциальный соленоид состоит из двух
одинаковых соленоидов. При последовательном электрическом и встречном магнитном
включении соленоидов общая ЭДС равна сумме ЭДС каждого из соленоидов. Для одного
соленоида z0 = H/2 + s/2 + Dz,
для другого z0 = H/2 + s/2 – Dz.
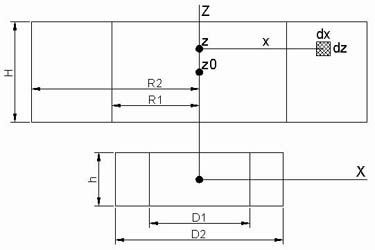
Рис. 4.1. К расчету потокосцепления магнита
и соленоида.
Для расчета потокосцепления соленоид можно
разбить на элементы прямоугольного сечения со сторонами dx ∙ dz (рис. 4.1),
найти потокосцепление d2
Y каждого такого элемента,
а затем проинтегрировать по сечению обмотки.
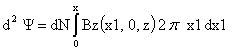
где Bz (x1, 0, z) –
аксиальная (осевая) составляющая магнитной индукции поля магнита,
dN – число витков обмоточного провода в элементе dx ∙
dz, выражаемое через фактор упаковки
l и диаметр обмоточного
провода D следующим образом:
![]()
Тогда:
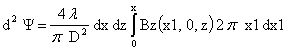
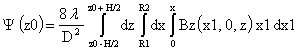
С учетом этого ЭДС может быть выражена таким
образом:
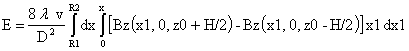
Тогда ЭДС EDIF
дифференциального соленоида:
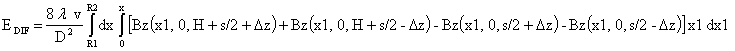
5. Расчет активного сопротивления и
индуктивности дифференциального соленоида
Дифференциальный
соленоид состоит из двух одинаковых цилиндрических соленоидов (рис. 5.1), каждый
из которых может быть охарактеризован следующими параметрами:
R1 – внутренний радиус соленоида, м
R2 – внешний радиус соленоида, м
H – высота соленоида, м
D – диаметр обмоточного провода без изоляции (для проводов прямоугольного
сечения производится пересчет по формуле D=(4S/p)1/2,
где S – площадь поперечного сечения провода, м2),
м
Lambda =
l – фактор упаковки
(отношение площади, занятой проводом в поперечном сечении соленоида без учета
изоляции, к площади поперечного сечения соленоида) [12].
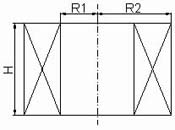
Рис. 5.1.
Цилиндрический соленоид
Расчет активного сопротивления и индуктивности
дифференциального соленоида может быть сделан с использованием решений,
заложенных в программу Coil [2], и методики расчета индуктивности системы из
двух соосных цилиндрических соленоидов [9].
6. Программа Magnetoelectric
Transducer версия 1.0
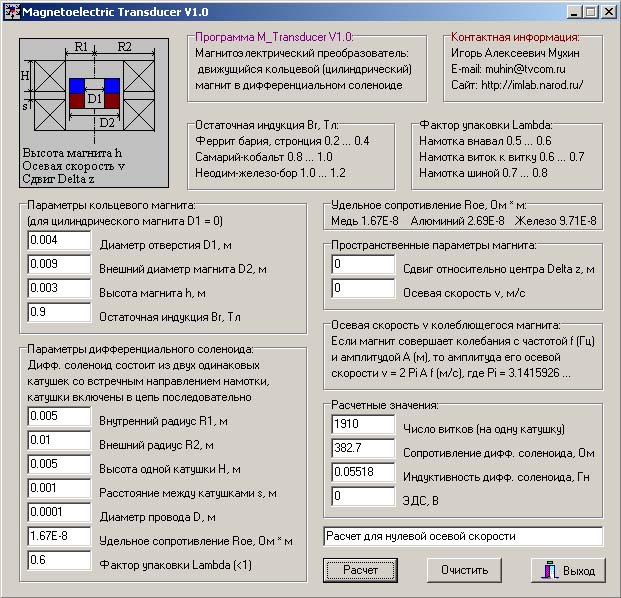
Рис. 6.1. Внешний вид окна программы
Magnetoelectric Transducer (версия 1.0).
Входные данные:
D1
– диаметр отверстия в постоянном магните, м
D2 –
внешний диаметр постоянного магнита, м
h – высота
постоянного магнита, м
Br –
остаточная индукция материала постоянного магнита, Тл
R1 – радиус отверстия в катушках дифференциального соленоида, м
R2 – внешний радиус катушек дифференциального соленоида, м
H – высота каждой из катушек дифференциального соленоида,
м
s –
расстояние между катушками дифференциального соленоида, м
D – диаметр обмоточного провода без изоляции (для проводов прямоугольного
сечения производится пересчет по формуле D=(4S/p)1/2,
где S – площадь поперечного сечения провода, м2),
м
re (Roe)
– удельное электрическое сопротивление материала обмоточного провода, Ом ∙ м
l (Lambda)
– фактор упаковки (отношение площади, занятой проводом в поперечном сечении
соленоида без учета изоляции, к площади поперечного сечения соленоида)
Dz
(Delta z) – сдвиг центра магнита относительно центра
дифференциального соленоида, м
v –
скорость движения магнита в осевом направлении, м/с
Если магнит
совершает гармонические колебания в заданной точке (определяется параметром
Delta z) с частотой f и амплитудой A, то амплитудное значение скорости в данной
точке v определяется по формуле: v
= 2 p A
f. При подстановке амплитудного значения скорости в программу можно
произвести расчет амплитуды ЭДС для случая гармонических колебаний магнита.
Выходные данные:
Число витков одной катушки дифференциального
соленоида
Активное сопротивление дифференциального соленоида (катушки соединены
последовательно, условия нормальные), Ом
Индуктивность дифференциального соленоида (катушки соединены последовательно,
направление намотки встречное), Гн
ЭДС на выходе дифференциального соленоида, В (амплитуда ЭДС для случая
гармонических колебаний при использовании амплитудного значения скорости
магнита)
Расчеты
производятся в системе СИ. Результаты выводятся на экран монитора.
После запуска
программы можно вводить входные данные и производить расчет нажатием кнопки
“Расчет”. Входные данные (D1, D2,
h, Br, R1,
R2, H, s,
D, Roe,
Lambda, Delta z и v)
необходимо вводить, учитывая принятый в операционной системе (ОС) формат
разделителя для десятичной дроби – точка или запятая, например, 0.005 или 0,005,
либо установите в ОС точку в качестве разделителя. Для удельного сопротивления
используется формат X.XXEY,
где латинская буква E обозначает основание 10, а Y –
степень (например, 1.67E-8 = 1.67 ∙ 10-8 = 0.0000000167).
Для очистки окон
с выходными данными следует нажать кнопку “Очистить”.
Для того, чтобы закрыть программу, следует нажать кнопку “Выход”.
7. Демонстрационная версия программы M_Transducer:
Версия 1.0 демо:
M_Transducer10d.rar (~81 Кбайт)
Демонстрационная версия программы позволяет рассчитывать
параметры магнитоэлектрического преобразователя только для нулевой скорости
движения магнита (v = 0). Время одного расчета может
составлять до нескольких десятков секунд при использовании компьютера с
процессором Pentium-I 200 МГц или аналогичным. Программа может работать с
операционными системами (ОС) Windows 3.1, Windows 95, 98 и XP (с другими ОС
семейства Windows не проверялась).
Файл M_Transducer10d.rar
необходимо распаковать в заранее созданную папку. Упаковка производилась с
помощью WinRAR 3.60.
Результат распаковки: M_Transducer10d.exe –
исполняемый файл программы. После запуска программы можно вводить входные данные
в системе СИ и производить расчет нажатием соответствующей кнопки. Проверить
правильность расчетов можно по внешнему виду окна программы, приведенному на
рис. 6.1.
Скопированные файлы могут быть проверены на отсутствие
вирусного кода в режиме on-line [11].
По вопросу получения полной версии программы обращайтесь к
автору (см. раздел Контактная информация).
Ссылки:
- A_Magnet: Программа-калькулятор индукции
магнитного поля кольцевого (цилиндрического) магнита методом эквивалентного
соленоида - Coil: Программа для расчета параметров и
магнитного поля цилиндрического соленоида - Выгодский М. Я. Справочник по
высшей математике. – М.: Издательство
“Наука“, гл. ред. физ.-мат. лит., 1977.
– 872 с.; ил. - Гофман Ю. В.
Законы, формулы, задачи физики. Справочник. – К., “Наук. думка”, 1977. – 576
с. - Двайт Г. Б.
Таблицы интегралов и другие математические формулы. – М.: Наука. Главная
редакция физико-математической литературы, 1983. – 176 с. - Законы и уравнения магнитного поля
- Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей:
Справочная книга. – 3-е изд., перераб. и доп. Л.: Энергоатомиздат. Ленингр.
отд-ние, 1986. – 488 с.: ил. - Корн Г., Корн Т. Справочник по
математике для научных работников и инженеров. –
М.: Издательство “Наука“, гл. ред. физ.-мат. лит., 1968 г.
– 720 с.;
ил. - Методика расчета индуктивности системы из двух
соосных цилиндрических соленоидов - Постоянные магниты: Справочник / Альтман А. Б., Герберг
А. Н., Гладышев П. А. и др.; Под ред. Ю. М. Пятина. – 2-е изд., перераб. и
доп. – М.: Энергия, 1980. – 488 с., ил. - Проверка файлов пользователя на наличие вирусного кода в режиме
on-line - Расчет фактора
упаковки при намотке соленоидов - Яворский Б. М., Детлаф А. А.
Справочник по физике / Для инженеров и студентов вузов. – 7 изд., испр. –
М.: Издательство “Наука”, Гл. ред. физ.-мат лит., 1978. – 944 с.; ил.
Словарь
терминов:
- Активное сопротивление – часть полного
сопротивления, связанная с тепловыделением. - Дифференциальный соленоид – соленоид, состоящий из
двух одинаковых соленоидов, расположенных соосно вблизи друг от друга и
включенных встречно. - Индуктивность
– величина, численно равная потоку самоиндукции контура при токе единичной
силы. - Магнитная индукция – вектор, численно
равный пределу отношения силы, действующей со стороны магнитного поля на
элемент проводника с электрическим током, к произведению тока и длины
элемента проводника, если длина этого элемента стремится к нулю, а элемент
так расположен в поле, что этот предел имеет наибольшее значение, и
направленный перпендикулярно к направлению элемента проводника и к
направлению силы, действующей на этот элемент со стороны магнитного поля,
причем из его конца вращение по кратчайшему расстоянию от направления силы к
направлению тока в элементе проводника должно быть видно происходящим против
часовой стрелки. - Магнитное поле – разновидность
электромагнитного поля, создаваемая движущимися электрическими зарядами или
токами и оказывающая силовое воздействие на движущиеся электрические заряды
или токи. - Магнитоэлектрический преобразователь –
преобразователь механического движения постоянного магнита относительно
обмотки в электрический сигнал. - Намагниченность – магнитный момент
единицы объема.
Операционная система (англ. operating system) – базовый набор
программ, обеспечивающий работу компьютера и его взаимодействие с
пользователем.- Остаточная индукция – величина магнитной
индукции, сохраняющейся в образце после уменьшения напряженности внешнего
поля до нуля. - Постоянный магнит – объект, создающий
магнитное поле за счет собственных внутренних элементарных электрических
токов, текущих без использования внешнего источника энергии в составляющем
объект материале. - Цилиндрический соленоид – соленоид в виде цилиндра
с центральным цилиндрическим отверстием (если таковое имеется).
30.03.2012
Альтернативные источники
энергии
Компьютеры и
Интернет
Магнитные поля
Механотронные системы
Перспективные
разработки
Электроника и
технология
Главная страница
![]()
Содержание:
- Электромагнитная индукция
- Потокосцепление и индуктивность
- Явление электромагнитной индукции
- ЭДС индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки
- Опыты Фарадея
- Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений
- Величина ЭДС индукции
- Вихревое электрическое поле и его связь с магнитным полем
- Вихревые токи
- Роль магнитных полей в явлениях, происходящих на Солнце и в космосе
- Явление самоиндукции ЭДС самоиндукции
- Энергия магнитного поля
Электромагнитная индукция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Электромагнитная индукция
Электромагнитная индукция – это явление возникновения тока в замкнутом проводнике при прохождении через него магнитного потока, изменяющегося со временем.
Потокосцепление и индуктивность
Была приведена формула (22.10), которую можно использовать для вычисления работы при повороте контура с током во внешнем магнитном поле. Выясним теперь, как подсчитать работу при повороте соленоида во внешнем магнитном поле, если он имеет  витков.
витков.
Поскольку работа при повороте одного витка равна  а в рассматриваемом случае магнитный поток пронизывает
а в рассматриваемом случае магнитный поток пронизывает  витков, то работа при повороте соленоида выразится формулой
витков, то работа при повороте соленоида выразится формулой

Если обозначить произведение  через
через  (греч. «пси»), то для работы получим формулу
(греч. «пси»), то для работы получим формулу
 или
или  (23.1)
(23.1)
Величину  характеризующую связь («сцепление») магнитного потока с замкнутой цепью, сквозь которую он проходит, называют потокосцеплением. Если магнитный поток Ф пронизывает катушку с числом витков
характеризующую связь («сцепление») магнитного потока с замкнутой цепью, сквозь которую он проходит, называют потокосцеплением. Если магнитный поток Ф пронизывает катушку с числом витков  то потокосцепление равно произведению числа витков на магнитный поток:
то потокосцепление равно произведению числа витков на магнитный поток:
 (23.2)
(23.2)
(Покажите, что единицей потокосцепления в СИ является вебер; §22.12.)
Теперь представим себе любую замкнутую цепь, по которой течет ток I. Этот ток создает свое собственное магнитное поле вокруг цепи. Пусть сквозь поверхность, охваченную проводниками замкнутой цепи, проходит собственный поток Ф. Если эта цепь представляет собой один плоский контур, то  равно Ф. Если же проводники цепи образуют катушку с
равно Ф. Если же проводники цепи образуют катушку с  витками, то
витками, то  Таким образом, собственное потокосцепление цепи зависит от ее конфигурации, т. е. от расположения проводников в пространстве.
Таким образом, собственное потокосцепление цепи зависит от ее конфигурации, т. е. от расположения проводников в пространстве.
Опыт показал, что когда в замкнутой цепи нет ферромагнетиков, то собственное потокосцепление этой цепи изменяется прямо пропорционально силе тока I в ней:
 (23.3)
(23.3)
Коэффициент пропорциональности L остается постоянным только при неизменной конфигурации проводов замкнутой цепи и неизменной окружающей среде. Коэффициент L, характеризующий зависимость собственного потокосцепления замкнутой цепи от ее формы и от окружающей среды, называется индуктивностью цепи.
Выведем единицу индуктивности L в СИ:

За единицу индуктивности в СИ принимают генри (Гн). Генри называют индуктивность такой цепи, в которой возникает потокосцепление в 1 Вб при токе в 1 А.
Вспомним, что единица магнитной проницаемости в СИ имеет наименование  (§22.8) или
(§22.8) или  (§22.14). Так как
(§22.14). Так как  (§22.12), то
(§22.12), то  Обычно используют последнее наименование — генри на метр.
Обычно используют последнее наименование — генри на метр.
В качестве примера определим индуктивность соленоида Lcoл. Из (23.3) имеем

Так как Фсол определяется соотношением (22.15), то
 (23.4)
(23.4)
Таким образом, индуктивность соленоида определяется средой, размерами и числом витков соленоида.
Явление электромагнитной индукции
Было установлено, что электрический ток и его магнитное поле всегда существуют одновременно. Фарадей, зная о тесной связи между током и магнитным полем, был уверен, что с помощью магнитного поля можно создать в замкнутом проводнике электрический ток. Он провел многочисленные опыты и доказал это, открыв в 1831 г. явление электромагнитной индукции.
Возникновение в замкнутом проводнике электрического тока, обусловленное изменением магнитного поля, называют явлением электромагнитной индукции. Полученный таким способом ток называют индукционным (наведенным), а создающую его э. д. с. называют э. д. с. индукции.
Всесторонние исследования явления электромагнитной индукции показали, что с помощью этого явления можно получить электрический ток практически любой мощности, что позволяет широко использовать электрическую энергию в промышленности. В настоящее время почти вся электрическая энергия, используемая на производстве, получается с помощью индукционных генераторов, принцип работы которых основан на явлении электромагнитной индукции. Поэтому Фарадей по праву считается одним из основателей электротехники.
Рассмотрим подробнее явление электромагнитной индукции.
ЭДС индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки
Пусть в однородном магнитном поле с индукцией В находится прямолинейный металлический проводник длиной l (рис. 23.1). Если этот проводник привести в движение со скоростью  так, чтобы угол
так, чтобы угол  между векторами В и
между векторами В и  составлял 90°, то вместе с проводником будут направленно двигаться и его собственные электроны. Так как их движение происходит в магнитном поле, то на них должна действовать сила Лоренца.
составлял 90°, то вместе с проводником будут направленно двигаться и его собственные электроны. Так как их движение происходит в магнитном поле, то на них должна действовать сила Лоренца.

Рис. 23.1.
С помощью правила левой руки можно установить, что свободные электроны будут смещаться к концу провода А. Напряжение U, которое при этом возникает между концами провода A и В, создаст в нем электрическую силу  которая уравновесит силу Лоренца
которая уравновесит силу Лоренца  Итак, смещение электронов к концу А прекратится при
Итак, смещение электронов к концу А прекратится при  Поскольку
Поскольку  a
a  имеем
имеем  откуда
откуда

Так как напряжение на полюсах при разомкнутой цепи равно э. д. с., то э. д. с. индукции, возникающая в проводнике при его движении в магнитном поле, выражается формулой
 (23.5)
(23.5)
Заметим, что сторонними силами, создающими э. д. с., здесь являются магнитные силы, действующие на свободные электроны в проводнике. Если этот проводник включить в цепь, то в ней возникнет индукционный ток; это можно установить по показанию гальванометра G.
Направление индукционного тока, возникающего в прямолинейном проводнике при его движении в магнитном поле, определяется по правилу правой руки (рис. 23.2): если правую руку расположить вдоль проводника так, чтобы линии магнитной индукции входили в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике.

Рис. 23.2.
Опыты Фарадея
Рассмотрим опыты Фарадея, с помощью которых он открыл явление электромагнитной индукции.
1. Возьмем соленоид, соединенный с гальванометром (рис. 23.3), и будем вдвигать в него постоянный магнит. Оказывается, что при движении магнита стрелка гальванометра отклоняется. Если же магнит останавливается, то стрелка гальванометра возвращается в нулевое положение. То же самое получается при выдвижении магнита из соленоида или при надевании соленоида на неподвижный магнит. Такие опыты показывают, что индукционный ток возникает в соленоиде только при относительном’ перемещении соленоида и магнита.

Рис. 23.3.
2. Будем опускать в соленоид В катушку с током А (рис. 23.4). Оказывается, что и в этом случае в соленоиде В возникает индукционный ток только при относительном перемещении соленоида В и катушки А.

Рис. 23.4.
3. Вставим катушку А в соленоид В и закрепим их неподвижно (рис. 23.5). При этом тока в соленоиде нет. Но в моменты замыкания или размыкания цепи катушки А в соленоиде В появляется индукционный ток. То же самое получается в моменты усиления или ослабления тока в катушке А с помощью изменения сопротивления R.

Рис. 23.5.
В дальнейшем цепь катушки А, соединенную с источником электрической энергии, будем называть первичной, а цепь соленоида В, в которой возникает индукционный ток, — вторичной. Эти же названия будем применять и к самим катушкам.
4. Включим первичную катушку в сеть переменного тока, а вторичную катушку соединим с лампой накаливания (рис. 23.6). Оказывается, лампа непрерывно горит, пока в первичной катушке течет переменный ток.

Рис. 23.6.
Нетрудно заметить, что общим для всех описанных опытов является изменение магнитного поля в соленоиде, которое и создает в нем индукционный ток.
Выясним теперь, всякое ли изменение магнитного поля вокруг замкнутого контура наводит в нем индукционный ток. Возьмем плоский контур в виде рамки, соединенной с гальванометром. Поместим рядом с рамкой магнит так, чтобы его линии индукции не проходили внутри рамки, а находились в ее плоскости (рис. 23.7, а).

Рис. 23.7.
Оказывается, что при перемещении рамки или магнита вдоль плоскости рисунка .стрелка гальванометра не отклоняется. Если же рамку поворачивать вокруг оси 00′ (рис. 23.7, б), то в ней возникает индукционный ток.
На основании описанных опытов можно сделать следующий вывод: индукционный ток (и э. д. с. индукции) в замкнутом контуре появляется только в том случае, когда изменяется магнитный поток, который проходит через площадь, охваченную контуром.
Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений
Индукционный ток создает собственное магнитное поле. Связь между направлением индукционного тока в контуре и индуцирующим магнитным полем была установлена Ленцем.
В опыте, изображенном, на рис. 23.3, индукционный ток в соленоиде создает магнитное поле, полюсы которого указаны в отверстии соленоида. Проследив взаимодействие между магнитными полюсами соленоида и магнита во всех четырех случаях, приведенных на рисунке, и сравнив его с направлением движения магнита, можно видеть, что взаимодействие между полюсами всегда препятствует движению магнита. Ленцу удалось обобщить эту закономерность на все случаи электромагнитной индукций. Найденную им связь называют законом (правилом) Ленца для электромагнитной индукции: э. д. с. индукции создает в замкнутом контуре такой индукционный ток, который своим магнитным полем препятствует причине, вызывающей появление этой э. д. с.
Используя закон Ленца для определения направления индукционного тока, следует поступать следующим образом:
1) найти причину, создающую индукционный ток;
2) считая, что индукционный, ток противодействует этой причине, найти направление его магнитного поля;
3) определить направление индукционного тока по направлению его магнитного поля.
Приведем пример. Причиной, вызывающей появление индукционного тока во вторичной катушке при размыкании цепи первичной катушки (рис. 23.5), является исчезновение поля первичной катушки. Мешая этому исчезновению, индукционный ток во_вторичной катушке должен создавать магнитное поле такого же направления, как у поля первичной катушки. Следовательно, направление индукционного тока во вторичной катушке будет совпадать с направлением тока, который протекал в первичной катушке до размыкания. (Покажите, что при замыкании цепи первичной катушки во вторичной возникает ток обратного направления.)
Из закона Ленца можно установить, что энергия индукционного тока в проводнике получается за счет той энергии, которая затрачивается на преодоление противодействия магнитного поля индукционного тока. Например, если разомкнуть цепь катушки, изображенной на рис. 23.3, и подсчитать работу, нужную для того, чтобы вставить в нее и вынуть магнит определенное число раз, а затем повторить этот опыт при замкнутой цепи, то во втором случае работа будет заметно больше, чем в первом. Это объясняется тем, что в первом случае собственного магнитного поля вокруг катушки нет, так как в ней нет тока, а во втором случае поле есть. Лишняя работа во втором случае идет на преодоление противодействия этого поля и равна энергии индукционного тока в катушке. Нетрудно видеть, что с помощью явления электромагнитной индукции можно превращать механическую энергию в электрическую, а также передавать электрическую энергию из одной цепи в другую.
Когда индукционный ток возникает вследствие какого-либо механического движения, то электрическая энергия получается за счет механической. Такое превращение энергии происходит в индукционных генераторах, установленных на электростанциях. Когда же индукционный ток возникает при отсутствии механического движения, то электрическая энергия переходит из одной цепи в другую. Такая передача энергии происходит в трансформаторах (§ 26.5).
Явлением электромагнитной индукции объясняют диамагнитный эффект. Когда вещество попадает в магнитное поле, на каждый движущийся по орбите электрон начинает действовать сила Лоренца, которая увеличивает или уменьшает (в зависимости от направления вращения электрона) центростремительную силу, действующую на электрон. Это приводит к изменению орбиты и частоты обращения электрона, что равносильно уменьшению или увеличению кругового тока, соответствующего движению электрона по орбите, причем получается, что круговые токи электронов усиливаются, если их магнитные поля направлены против внешнего поля, и уменьшаются, если они направлены по полю.
Таким образом, если в отсутствие внешнего поля круговые токи электронов в молекуле диамагнетика уравновешивают друг друга и молекула не имеет магнитного момента, то во внешнем поле это равновесие нарушается и возникает результирующий магнитный момент молекулы, направленный против внешнего поля. Этот результат, вообще говоря, прямо следует и из закона Ленца: изменение круговых токов в молекуле является индукционным током, и его магнитное поле должно быть направлено против вызвавшего его внешнего поля.
Диамагнитный эффект возникает во всех веществах, но если молекулы вещества имеют собственные магнитные моменты, которые ориентируются по направлению внешнего магнитного поля и усиливают его, то диамагнитный эффект перекрывается более сильным парамагнитным эффектом и вещество оказывается парамагнетиком.
Сильный диамагнитный эффект наблюдается при сверхпроводимости. Когда сверхпроводник попадает в магнитное поле, в нем, как и в обычном проводнике, наводятся индукционные токи, но, в отличие от молекулярных индукционных токов, их образуют свободные электроны. В сверхпроводнике эти индукционные токи не встречают сопротивления и циркулируют, пока существует внешнее магнитное поле, противодействуя его проникновению внутрь сверхпроводника. Сверхпроводники, как и все диамагнетики, выталкиваются из магнитного поля.
Величина ЭДС индукции
При выполнении опытов Фарадея можно видеть, что стрелка гальванометра отклоняется тем дальше, чем быстрее вдвигается в соленоид магнит или катушка с током (§ 23.4). То же самое получится, если усилить магнитное поле первичной катушки, увеличив в ней ток. Подробное изучение этого явления показало, что э. д. с. индукции, возникающая в какой-либо цепи, прямо пропорциональна скорости изменения потокосцепления магнитного поля с этой цепью:
 (23.6)
(23.6)
Отметим, что когда цепь состоит из одного витка, т. е. является простым контуром, то формула (23.6) принимает вид
 (23.6а)
(23.6а)
В этих формулах  — время, за которое происходит изменение потокосцепления на
— время, за которое происходит изменение потокосцепления на Если
Если  очень мало, то формулы (23.6) дают мгновенное значение э. д. с. индукции. Если же
очень мало, то формулы (23.6) дают мгновенное значение э. д. с. индукции. Если же  велико, то при подсчете по этим формулам получается среднее значение э. д. с. индукции.
велико, то при подсчете по этим формулам получается среднее значение э. д. с. индукции.
Знак минус в формулах показывает, что, когда потокосцепление уменьшается ( отрицательно), э. д. с. создает индукционный ток, увеличивающий потокосцепление, и наоборот. Таким образом, знак минус показывает, что в соответствии с законом Ленца э. д. с. индукции должна препятствовать причине, вызывающей ее появление.
отрицательно), э. д. с. создает индукционный ток, увеличивающий потокосцепление, и наоборот. Таким образом, знак минус показывает, что в соответствии с законом Ленца э. д. с. индукции должна препятствовать причине, вызывающей ее появление.
Из формулы (23.6а) видно, что единицу магнитного потока в СИ можно назвать вольт-секундой, так как

Вихревое электрическое поле и его связь с магнитным полем
Появление э. д. с. индукции в прямолинейном проводнике, движущемся в магнитном поле, было объяснено действием силы Лоренца на подвижные носители зарядов. Однако объяснить таким способом появление э. д. с. индукции во вторичной цепи при неподвижной относительно нее первичной цепи (четвертый опыт в § 23.4) оказалось невозможным, поскольку магнитное поле не действует на покоящиеся заряды.
Вспомним, что на покоящиеся заряды действует электрическое поле. Не оно ли создает индукционный ток во вторичной цепи? Если это так, то откуда это электрическое поле берется? Объяснить это можно тем, что переменное магнитное поле может создавать электрическое поле, которое уже и возбуждает в замкнутом проводнике индукционный ток.
Такое объяснение явления электромагнитной индукции впервые дал Д. Максвелл. Развивая эту идею, он создал теорию электромагнитного поля, которая была подтверждена многими опытами. По теории Максвелла в пространстве, в котором изменяется магнитное поле, обязательно возникает электрическое поле с замкнутыми линиями напряженности, независимо от присутствия вещества.
На рис. 23.8 прямые линии изображают изменяющееся магнитное поле с индукцией В, возрастающей (а) и убывающей (б), а замкнутые линии — возникшее электрическое поле, напряженность которого Е. Если в этом пространстве окажется проводник, то в нем возникнет индукционный ток. Например, при выдвижении магнита из катушки на рис. 23.3, г возникает электрическое поле, изображенное на рис. 23.8, б, которое и создает ток в соленоиде. (Объясните, как возникает ток в других случаях, показанных на рис. 23.3.)

Рис. 23.8.
На рис. 23.8 видно, что линии электрического и магнитного полей расположены во взаимно перпендикулярных плоскостях. Исследования показали, что вектор напряженности (индукции) магнитного поля в каждой точке пространства перпендикулярен вектору напряженности созданного им электрического поля. Именно поэтому наибольшая э. д. с. индукции в прямолинейном проводнике возникает тогда, когда он движется перпендикулярно к линиям индукции магнитного поля.
Вихревые токи
Возьмем катушку с выступающим сердечником из мягкого ферромагнетика и положим на его конец металлический предмет. Если катушку включить в сеть переменного тока, то предмет быстро и сильно нагревается.
Заменим предмет алюминиевым кольцом К, надетым на сердечник (рис. 23.9), и снова включим катушку в сеть. Если кольцо держать, то оно сильно нагревается, а если не держать, то при включении катушки в сеть оно соскакивает с сердечника. Описанные явления объясняются тем, что изменяющееся магнитное поле вокруг сердечника создает электрическое поле, поэтому в теле и в кольце возникают сильные индукционные токи, так как сопротивление тела и кольца очень маленькое. Эти токи и нагревают их. Соскакивает кольцо потому, что индукционный ток в кольце направлен противоположно току в катушке, а такие токи отталкиваются друг от друга.

Рис. 23.9.
Индукционные токи, которые возникают в сплошных металлических телах, находящихся в переменном магнитном поле, и замыкаются внутри этих тел, называют вихревыми токами или токами Фуко (в честь французского ученого Ж. Фуко, который их исследовал).
Якорь электродвигателя и сердечник трансформатора по условиям
своей работы находятся в переменном магнитном поле, поэтому в них должны циркулировать вихревые токи. Энергия, затраченная на создание вихревых токов, превращается во внутреннюю энергию якоря и сердечника, т. е. идет на их нагревание (кроме потерь энергии на нагревание вихревыми токами, в них возникают еще и потери, обусловленные гистерезисом). Для ослабления вредного действия вихревых токов тела, которые должны находиться в переменном магнитном поле, делают из отдельных листов, изолированных друг от друга (рис. 23.10).

Рис. 23.10.
Заметим, что ферриты имеют очень большое удельное сопротивление, поэтому вихревые токи в них практически не возникают, и это значительно уменьшает потери энергии в них. Поскольку потери энергии, вызванные гистерезисом, в ферритах тоже очень малы, их применение заметно повышает к. п. д. приборов, например трансформаторов.
Если вихревой ток вызывается движением тела в магнитном поле, то согласно закону Ленца этот ток должен тормозить движение тела. Тормозящее действие вихревых токов можно проиллюстрировать с помощью следующего опыта.
Если медную пластинку Р (рис. 23.11) заставить колебаться при выключенном токе в электромагните М, а затем при включенном токе в нем, то будет видно, что во втором случае колебания прекращаются почти мгновенно. Внешне кажется, что в этом случае пластинка как бы вязнет в густой жидкости. Тормозящее действие вихревых токов используется в измерительных приборах для успокоения колебаний стрелки измерительного механизма.

Рис. 23.11.
В современной технике нагревание вихревыми токами используется для закалки деталей и для изготовления сплавов в индукционных печах.
Роль магнитных полей в явлениях, происходящих на Солнце и в космосе
Изучение Солнца показало, что оно имеет магнитное поле, напряженность которого примерно в два раза выше, чем у поля Земли. Многие явления, происходящие в атмосфере Солнца (образование темных пятен, факелов и др.), тесно связаны с возникновением и развитием в отдельных областях сильных местных магнитных полей. Эти области получили название активных.
Как отмечалось выше, в слое, лежащем под фотосферой, происходит интенсивное перемешивание газа — конвекция. Исследования показали, что в области пятна всегда существует сильное магнитное поле, напряженность которого в тысячу раз больше, чем в других, невозмущенных областях. Это поле отклоняет заряженные частицы плазмы и препятствует образованию конвекционных потоков. В этой области подъем горячего газа из глубины прекращается, и газ в пятне сильно охлаждается.
В области факела магнитное ноле далеко не такое сильное, чтобы остановить вертикальные конвекционные потоки плазмы. Однако оно подавляет беспорядочные движения плазмы в потоке и уменьшает внутреннее трение. Таким образом, создается устойчивый восходящий поток горячего газа — факел.
Многие явления, наблюдаемые в атмосфере Солнца, связаны с изменяющимися магнитными полями. Как было показано выше, при движении заряженной частицы в постоянном магнитном поле изменяется только направление скорости ее движения. Оказывается, что изменяющееся во времени магнитное поле, пронизывающее плазму, изменяет не только направление, но и величину скорости заряженных частиц и может создавать направленное движение плазмы. Так иногда образуются мощные потоки плазмы, которые выбрасывают огромные массы газа в корону и образуют протуберанцы — гигантские облака газа, простирающиеся далеко в корону (рис. 6.4).
Сильное магнитное поле, изменяющееся при развитии группы пятен, оказывает давление на плазму, и в хромосфере над областью пятен иногда происходит резкое сжатие плазмы, вызывающее сильное повышение температуры газа. В этой зоне хромосферы наблюдается внезапное резкое усиление свечения газа, называемое хромосферной вспышкой.
Изменяющееся магнитное поле выбрасывает в космическое пространство потоки частиц плазмы, движущихся со скоростью около 1000 км/с, которые называют корпускулярными потоками. Некоторые частицы разгоняются до огромных скоростей (сравнимых со скоростью света), образуя солнечные космические лучи.
Многолетние наблюдения показали, что число и общая площадь пятен периодически изменяются, достигая максимума в среднем через каждые 11 лет. В это время увеличивается число факелов, количество протуберанцев, чаще, чем обычно, наблюдаются вспышки, в десятки раз возрастает интенсивность корпускулярного излучения. Все эти явления объединяются под общим названием — солнечная активность.
Потоки выброшенных Солнцем заряженных частиц, долетая до Земли, отклоняются ее магнитным полем и в свою очередь воздействуют на магнитное поле Земли. В периоды максимума солнечной активности наблюдаются сильные возмущения магнитного поля Земли — магнитные бури, вызывающие беспорядочные колебания стрелки компаса. Часть заряженных частиц проникает в магнитное поле Земли и, двигаясь по спиралям вдоль силовых линий, оказывается как бы в ловушке. Скапливаясь в кольцевых зонах вокруг Земли, заряженные частицы образуют радиационные пояса, обнаруженные с помощью спутников. В области полюсов космические частицы легко проникают в атмосферу, вызывая полярные сияния.
Магнитные поля существуют и в межзвездном пространстве. Они в десятки тысяч раз слабее земного магнитного поля, но обладают огромной протяженностью и поэтому оказывают большое влияние на характер движения заряженных частиц в межзвездном пространстве.
Явление самоиндукции ЭДС самоиндукции
Вспомним, что собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания и размыкания цепи, а также при изменении в ней силы тока. Это означает, что в указанные моменты в такой цепи должна возникать э. д. с. индукции. Возникновение э. д. с. индукции в цепи, которое вызвано изменением магнитного поля тока, текущего в этой же цепи, называют явлением самоиндукции, а появляющуюся электродвижущую силу — э. д. с. самоиндукции.
Выясним подробнее, что происходит при замыкании цепи. Пусть имеется разомкнутая цепь (рис. 23.12), состоящая из источника электрической энергии Б и последовательно соединенных ключа К, лампочки М и катушки с сердечником из ферромагнетика S. При замыкании цепи лампочка загорается с некоторым запозданием. Это объясняется возникновением в катушке значительной э. д. с. самоиндукции, которая согласно закону Ленца мешает быстрому нарастанию тока в цепи (см. рис. 23.13; I0 — сила постоянного тока в цепи).

Рис. 23.12.

Рис. 23.13.
Заметим, что энергия источника, затраченная на преодоление противодействия э. д. с. самоиндукции, накапливается в магнитном поле этой цепи, главным образом внутри катушки с сердечником S. (Почему?) Когда сила тока в цепи становится постоянной, то и энергия магнитного поля цепи не изменяется. Энергия магнитного поля цепи зависит не только от силы тока, но и от вида цепи, т. е. от ее индуктивности L. В сильных электромагнитах магнитная энергия особенно велика.
Для наблюдения явления самоиндукции при размыкании составляют цепь, показанную на рис. 23.14. При размыкании этой цепи ключом К остается замкнутой цепь катушки S и лампочки М. Так как ток в катушке начинает быстро спадать (рис. 23.15), то в ней создается э. д. с. самоиндукции, которая замедляет спад тока. При этом катушка на короткое время становится источником энергии, который создает ток в лампочке М. В момент размыкания цепи ток в лампе спадает до нуля и, изменив направление, скачком увеличивается до такой величины, которая может быть значительно больше, чем сила тока в лампе до размыкания. Поэтому лампа в момент размыкания может ярко вспыхнуть и даже перегореть.

Рис. 23.14.

Рис. 23.15.
Явление самоиндукции создает искру в том месте, где происходит размыкание цепи. Если в цепи имеются мощные электромагниты, в которых запасена большая магнитная энергия, то искра может перейти в дуговой разряд и испортить выключатель. Для размыкания таких цепей на электростанциях пользуются масляными выключателями и применяются другие меры предосторожности.
Выведем формулу для вычисления э. д. с. самоиндукции. Так как всякая э. д. с. индукции может быть найдена по формуле (23.6)  а
а  то
то  откуда
откуда
 (23.7)
(23.7)
Э. д. с. самоиндукции в цепи пряно пропорциональна скорости изменения силы тока в этой цепи.
Энергия магнитного поля
В предыдущем параграфе говорилось, что энергия магнитного поля цепи зависит от силы тока в ней и от ее формы. Уточним эту зависимость. Вспомним, что энергия магнитного поля цепи  равна работе, которая затрачивается на преодоление э. д. с. самоиндукции, возникающей при замыкании цепи. Если среднее значение э. д. с. самоиндукции при этом равно
равна работе, которая затрачивается на преодоление э. д. с. самоиндукции, возникающей при замыкании цепи. Если среднее значение э. д. с. самоиндукции при этом равно  а по цепи за время нарастания тока в ней
а по цепи за время нарастания тока в ней  прошел заряд q, то работа по преодолению э. д. с. самоиндукции равна
прошел заряд q, то работа по преодолению э. д. с. самоиндукции равна  Тогда
Тогда

Знак минус означает, что заряды при этом движутся против э. д. с. самоиндукции. Так как — то
то

Поскольку ток в цепи возрастает от 0 до  получаем, что
получаем, что  a
a  есть средняя сила тока за время его нарастания. Приняв среднюю силу тока за
есть средняя сила тока за время его нарастания. Приняв среднюю силу тока за  и подставляя значения
и подставляя значения  и
и  в приведенное выше соотношение, найдем формулу для вычисления энергии магнитного поля цепи, в которой идет.ток
в приведенное выше соотношение, найдем формулу для вычисления энергии магнитного поля цепи, в которой идет.ток 
 (23.8)
(23.8)
Энергия магнитного поля цепи прямо пропорциональна квадрату величины тока в ней и зависит от ее индуктивности L. Поскольку индуктивность соленоида с сердечником из ферромагнетика особенно велика, большая магнитная энергия получается в цепи, содержащей электромагниты.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома

