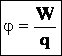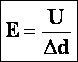№
37. Связь между напряженностью и разностью потенциалов электрического поля.
Напряженность
электрического поля – величина, численно равная силе, действующей на заряд.
Потенциал φ – величина, численно равная
потенциальной энергии заряда.
Каждой точке
электрического поля соответствуют определенные значения потенциала и напряженности.
Найдем связь напряженности электрического поля с потенциалом.
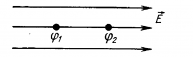
Пусть заряд q перемещается
в направлении вектора напряженности однородного электрического поля ![]() из точки 1 в точку 2,
из точки 1 в точку 2,
находящуюся на расстоянии ![]() от точки 1 (рис.93, стр. 119).
от точки 1 (рис.93, стр. 119).
Электрическое поле совершает работу: A=qEΔd

Эту работу согласно формуле можно выразить через
разность потенциалов в точках 1 и 2: A=qU
Приравнивая выражения для работы, найдем модуль
вектора напряженности поля:
qEΔd=qU
E= ![]() =
= ![]()
Где U –
разность потенциалов между точками 1 и 2, которые
связаны вектором перемещения ![]() , совпадающим по направлению с вектором напряженности
, совпадающим по направлению с вектором напряженности ![]() .
.
Формула E= ![]()
показывает: чем меньше меняется потенциал на
расстоянии ![]() , тем меньше напряженность электростатического
, тем меньше напряженность электростатического
поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
Так как при
перемещении положительного заряда в направлении вектора напряженности ![]() электростатическое поле совершает
электростатическое поле совершает
положительную работу ![]() , то потенциал
, то потенциал ![]() больше потенциала
больше потенциала ![]() .
.
Следовательно, напряженность
электрического поля направлена в сторону убывания потенциала.
Любое
электростатическое поле в достаточно малой области пространства можно считать
однородным. Поэтому формула E= ![]() справедлива
справедлива
для произвольного электростатического поля, если только расстояние ![]() настолько мало, что изменением
настолько мало, что изменением
напряженности поля на этом расстоянии можно пренебречь.
Единица напряженности
электрического поля. Единицу напряженности электрического поля в СИ
устанавливают, используя последнюю формулу . Напряженность
электрического поля численно равна единице, если разность потенциалов между
двумя точками на расстоянии 1 м в однородном поле равна 1
В. Наименование этой единицы – вольт на метр (В/м).
Напряженность можно
также выражать в ньютонах на кулон. Действительно,
![]()
Эквипотенциальные поверхности.
Потенциал
электростатического поля представляет собой функцию, меняющуюся от точки к
точке. Однако, во всяком реальном случае можно выделить совокупность точек,
потенциалы которых одинаковы.
Геометрическое
место точек постоянного потенциала называется поверхностью равногопотенциала
или эквипотенциальной поверхностью.
Возьмем
равномерно заряженную бесконечную плоскость. Поле, создаваемое та
кой
плоскостью однородно, а линии напряженности нормальны к плоскости.
Отсюда
следует, что работа перемещения заряда из некоторой точки В1
в любую другую точку В2,
находящуюся на таком же расстоянии от заряженной поверхности, что и точка В1равна
нулю. Действительно, при перемещении некоторого заряда q по прямой В1
В2 сила, действующая на заряд со стороны поля, будет все время
перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но
эта работа может быть представлена, с другой стороны, в виде:
A
= q(φ1– φ2)= 0
где
φ1 и φ2 – соответственно
потенциалы точек В1 и В2. Отсюда, так как
А
= 0, то φ1= φ2, т.е., потенциалы
точек, равноудаленных от заряженной
плоскости,
одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные
поверхности) являются плоскостями, параллельными заряженной плоскости. Если
плоскость заряжена положительно, то значение потенциала убывает по мере
удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала
расположены симметрично по обе стороны от заряженной плоскости.
Эквипотенциальные
поверхности поля точечного заряда это сферы с радиусом
r,
центр которых находится в центре точечного заряда, т.е. φ=![]() .
.
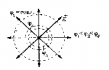
На
рисунке 95 вектор напряженности E перпендикулярен эквипотенциальным
поверхностям.
Покажем,
что вектор напряженности перпендикулярен эквипотенциальной поверхности.
Рассмотрим работу по перемещению заряда по поверхности равного потенциала
на малом участке пути ∆d. При этом, работа электрической
силы F=qE на данном пути будет:
A=F∆dcos
α= qE∆dcos
α, где α – угол между направлением силы f
и
перемещением ∆d. С другой стороны, эта работа может
быть выражена как произведение величины перемещающегося заряда на разность
потенциалов в начальном и конечном положениях заряда, т.е. A
= q(φ1– φ2)
Так
как перемещение идет по эквипотенциальной поверхности, то разность потенциалов (φ1–
φ2)=0 и qE∆dcos
α=0, или cosα= 0,
значит α = 900 т.е.
угол
между направлением силы F и
перемещением ∆d равен 900.
Но F и Е совпадают, поэтому угол
между E и ∆d, α=900, т.е.
направление вектора напряженности электростатического поля всегда
перпендикулярно к эквипотенциальной поверхности.
Значит, если провести поверхность,
перпендикулярную в каждой ее точке силовым линиям, то при перемещении заряда
вдоль этой поверхности работа не совершается. А это означает, что все точки
поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Поверхности равного потенциала называют эквипотенциальными.
Эквипотенциальные
поверхности однородного
поля представляют собой плоскости (рис.94, стр. 120), а поля точечного
заряда – концентрические сферы (рис. 95, стр. 120).


Подобно силовым линиям, эквипотенциальные
поверхности качественно характеризуют распределение поля в пространстве. Вектор напряженности перпендикулярен
эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
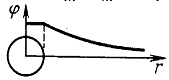
Эквипотенциальные
поверхности строятся обычно так, что разность потенциалов между двумя соседними
поверхностями постоянна. Поэтому согласно формуле расстояния между соседними
эквипотенциальными поверхностями увеличиваются по мере удаления от точечного
заряда, так как напряженность поля уменьшается.
Эквипотенциальные
поверхности однородного поля расположены на равных расстояниях друг от друга.
Эквипотенциальной является
поверхность любого проводника в электростатическом поле. Ведь силовые
линии перпендикулярны поверхности проводника. Причем не только поверхность, но
и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля
внутри проводника равна нулю, значит, равна нулю и разность потенциалов между
любыми точками проводника.
Модуль напряженности электростатического поля
численно равен разности потенциалов между двумя близкими точками в этом поле,
деленной на расстояние между этими точками.
В однородном электрическом
поле напряженностью Е = 2*105 В/м
переместили заряд q = –20 нКл в направлении
силовой линии поля на расстояние d = 10 см. Найти работу
поля А, изменение потенциальной
энергии поля ΔWп и напряжение (разность
потенциалов) U между начальной и конечной
точками перемещения.
Домашнее
задание
§ 45-46,
вопросы.

Поверхность – равный потенциал
Cтраница 2
Поверхностями равного потенциала являются плоскости, проходящие через начало координат, а линиями тока – окружности.
[16]
Следы поверхностей равного потенциала в плоскости чертежа называют линиями равного потенциала. Линии равного потенциала пересекаются с линиями напряженности поля всюду под прямым углом.
[17]
Следы поверхности равного потенциала на плоскости чертежа называют линиями равного потенциала. Очевидно, линии равного потенциала пересекаются с линиями напряженности поля всюду под прямым углом.
[18]
Проведем поверхности равного потенциала, соответствующие определенным значениям р, отличающимся одно от другого на бесконечно малое количество. Если мы возьмем элемент 6s, нормальный к какой-нибудь поверхности р const, то получим, что скорость в любой точке рассматриваемой поверхности обратно пропорциональна взаимному расстоянию в области этой точки двух соседних поверхностей равного потенциала. Поэтому, если какая-нибудь поверхность равного потенциала пересекает самое себя, то скорость жидкости для линии пересечения равна нулю. Пересечение же двух различных поверхностей равного потенциала указывает на бесконечно большую скорость.
[19]
Следовательно, поверхности равного потенциала образуют связку плоскостей, а проекции их на плоскость ху-пучок прямых, проходящих через начало координат.
[20]
Следовательно, поверхности равного потенциала образуют связку плоскостей, а проекции их на плоскость ху – пучок прямых, проходящих через начало координат.
[21]
При перемещении по поверхности равного потенциала ( эквипотенциальная поверхность) изменения скорости электрона не происходит.
[22]
Пересекающиеся круги представляют поверхности равного потенциала и поверхности равной электронной плотности. Остальная часть атома аргона вне шестнадцати элементов объема вносит очень мало в аффект индукции.
[24]
Если условиться строить поверхности равного потенциала со значениями, отличающимися друг от друга на одну и ту же величину Аф, то семейство эквипотенциальных поверхностей будет наглядно характеризовать свойства поля: чем ближе друг к другу поверхности, тем больше модуль напряженности поля. При этом вектор напряженности направлен по нормали в сторону убывания потенциала.
[25]
При потенциальном движении поверхности равного потенциала являются живыми сечениями. Векторы скорости движения частиц нормальны к поверхностям равного потенциала.
[26]
Построить следы пяти поверхностей равных потенциалов в поле цилиндрического конденсатора с радиусами г – I см и R6 см, выбранных так, чтобы разность потенциалов между соседними поверхностями была одинакова.
[27]
Для такой линии поверхностями равного потенциала, как известно, являются поверхности концентрических цилиндров. Силовые же линии поля будут направлены по радиусам.
[28]
В этом случае поверхностями равного потенциала являются гиперболические цилиндры, и поэтому за потенциал следует принять мнимую часть ( i) комплексного потенциала.
[29]
Мы видим, что поверхности равного потенциала играют по отношению к электрическим силам ту же роль, какую горизонтальные поверхности уровня играют по отношению к силе тяжести.
[30]
Страницы:
1
2
3
4
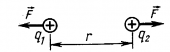
закону Кулона взаимодействия между точечными зарядами
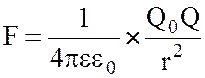 , где Q0 – заряд, образующий
, где Q0 – заряд, образующий
поле, Кл; r – расстояние между зарядами Q0 и Q, м; ![]() – диэлектрическая проницаемость среды;
– диэлектрическая проницаемость среды; ![]() = 8,85*
= 8,85*
10-12 Ф/м – диэлектрическая постоянная вакуума.
Напряженность
поля, созданная точечным зарядом
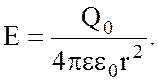
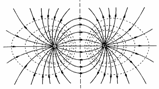
Линия,
касательная к которой в каждой точке совпадает по направлению с напряженностью
электростатического поля, называется силовой линией, причем их густота
характеризует численное значение напряженности (рис. 1).
Графическое изображение полей с помощью силовых линий
представлено на рис. 20.1, где а – поле положительного точечного заряда; б
– поле отрицательного точечного заряда; в – поле двух разноименных точечных зарядов
Рис. 1
Энергетической
характеристикой поля является потенциал
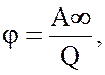
где ![]() – потенциал данной точки поля, В;
– потенциал данной точки поля, В; ![]() – работа, Дж.
– работа, Дж.
Потенциал
поля численно равен работе, совершаемой силами поля при перемещении единичного
положительного заряда их данной точки поля в бесконечность.
Работа
по перемещению единичного положительного заряда из одной точки поля в другую
равна разности потенциалов этих точек
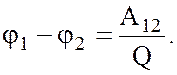
Работа
по перемещению заряда Q между точками, потенциалы которых
![]() и
и ![]()
![]()
Потенциал
поля точечного заряда Q0 на расстоянии r
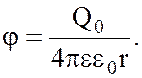
Электростатическое
поле является консервативным. Работа по перемещению заряда в электрическом
поле не зависит от траектории, а определяется лишь положением начальной и
конечной точек перемещения.
Каждой
точке поля соответствует свой потенциал, который является функцией расстояния.
Однако, можно выделить такую совокупность точек, для которых потенциал
одинаков.
Геометрическое
место точек равного потенциала называется эквипотенциальной поверхностью.
Силовые
линии везде перпендикулярны к поверхности равного потенциала (рис. 2).
Между
напряженностью поля и потенциалом существует соотношение  .
.
Напряженность
поля численно равна изменению потенциала на единицу длины, отсчитанной в
перпендикулярном к поверхности потенциала направлении. Знак (-) говорит о том,
что напряженность направлена в сторону убывания потенциала.
Графическое
изображение полей с помощью сечений эквипотенциальных поверхностей и силовых
линий показано на рис. 2., где а – поле положительного точечного заряда; б – поле
отрицательного точечного заряда; в – поле двух разноименных зарядов; ![]() …. – потенциалы поверхностей
…. – потенциалы поверхностей
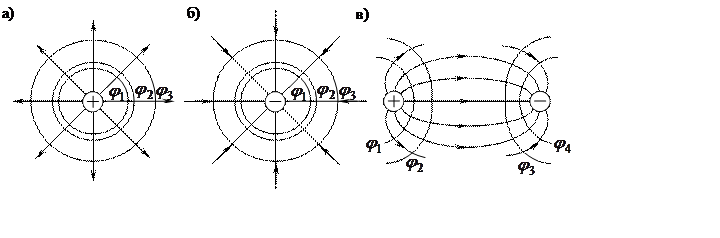 |
Рис. 2
Величина ![]() показывает
показывает
быстроту изменения потенциала в направлении, перпендикулярном к
эквипотенциальной поверхности и называется градиентом потенциала, ![]() , где qrad j – градиент
, где qrad j – градиент
потенциала, В/м.
Градиент
потенциала направлен противоположно вектору напряженности поля (см. рис. 2).
Ортогональность
силовых линий и поверхностей равного потенциала существенно облегчает как
экспериментальное, так и теоретическое исследование электростатического поля.
По найденным значениям вектора напряженности можно построить поверхности
равного потенциала и наоборот: найденное положение поверхностей равного
потенциала позволяет построить силовые линии поля.
Экспериментально
измерения потенциалов оказываются проще, чем измерения напряженности поля, так
как большинство приборов, пригодных для изучения полей, измеряют разность
потенциалов. Поэтому в данной работе экспериментально изучается распределение
потенциалов в поле.
Силовые
линии строятся как ортогональные кривые к экспериментально найденным
поверхностям равного потенциала.
2 ОПИСАНИЕ УСТАНОВКИ
И МЕТОДА ИЗМЕРЕНИЙ
В
данном эксперименте постоянные электростатические поля моделируются с помощью
постоянного тока, который пропускают через
Теория поля: Методические указания к выполнению семестрового задания (с вариантами заданий)
Страницы работы
Содержание работы
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
для студентов металлургических специальностей
к выполнению семестрового задания по теме «Теория поля»
с вариантами заданий
Рекомендовано на заседании кафедры высшей математики
Протокол № 4 от 14.02.2002 г.
Утверждено на заседании
Протокол № 8 от 22.04.2002 г.
1 Скалярное поле
Функция U=U(p)=U(x,y,z) называется скалярной, если она характеризуется только числовым значением. Если в каждой точке некоторой области задана скалярная функция U, то говорят, что в этой области задано скалярное поле. Примером скалярного поля может служить поле температур неравномерно нагретого тела, поле плотностей распределения электрических зарядов в изолированном наэлектризованном теле, поле потенциалов электрического поля и т.д.
Скалярное поле может совпадать со всем пространством, если функция U определена в любой точке, или являться некоторой его частью, если функция U определена только в этой части пространства.
Скалярное поле называется стационарным, если функция U=U(p) не зависит от времени t, и называется нестационарным, если такая зависимость функции U от t существует.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U принимает постоянное значение, т.е.
U (x,y,z) = C.
В курсе физики при рассмотрении поля потенциала поверхности уровня называют обычно эквипотенциальными поверхностями (т.е. поверхностями равного потенциала).
Если скалярное поле плоское, т.е. U = U(x,y), то поверхности уровня будут линиями уровня
Уравнение поверхности уровня, проходящей через данную точку M0 (x0,y0,z0) записывается так:
1) Найти линии уровня скалярного поля U = xy
Линии уровня удовлетворяют уравнению:
xy = C или ,
т.е. линиями уровня будет семейство гипербол в 1-й и 3-ей четвертях при C>0 или во 2-й и 4-й четверти при C 1 2 3 4 5 6
Типовой расчёт. «Теория поля»
Задача 1. Дано векторное поле 
1. Проверить, что это поле является потенциальным.
2. Найти потенциал поля 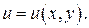
3. Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
4. Составить уравнение векторных линий поля  и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
5. Вычислить линейный интеграл  .
.
| Вар. | Векторное поле | Точка A | Точка B |
 |
 |
 |
|
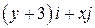 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
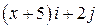 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
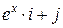 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
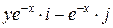 |
 |
 |
|
 |
 |
 |
|
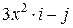 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
Задача 2. Дано векторное поле  .
.
1. Найти дивергенцию векторного поля 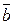 , исследовать расположение источников и стоков векторных линий поля.
, исследовать расположение источников и стоков векторных линий поля.
2. Найти поток векторного поля 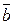 через замкнутую поверхность
через замкнутую поверхность  .
.
3. Найти ротор векторного поля 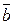 .
.
4. Вычислить циркуляцию поля 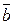 вдоль замкнутой линии
вдоль замкнутой линии  двумя способами: а) преобразовав линейный интеграл в определенный с использованием уравнений линии
двумя способами: а) преобразовав линейный интеграл в определенный с использованием уравнений линии  ; б) преобразовав линейный интеграл в поверхностный с помощью теоремы Стокса.
; б) преобразовав линейный интеграл в поверхностный с помощью теоремы Стокса.
5. Выяснить, как изменится циркуляция поля 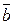 вдоль контура
вдоль контура  , если изменить расположение контура в данном поле. Найти наибольшее значение циркуляции для данного контура.
, если изменить расположение контура в данном поле. Найти наибольшее значение циркуляции для данного контура.
| Вар. | Поле 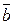 : :  – поверхность, ограничивающая тело Т. – поверхность, ограничивающая тело Т.  – замкнутая линия – замкнутая линия |
   . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами  |
|
   . .  состоит из дуги окружности состоит из дуги окружности   и двух отрезков прямых и двух отрезков прямых  и и  , ,  |
|
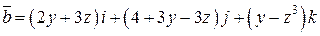   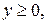  . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
     . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   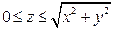 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами  |
|
    . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 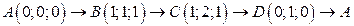 |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   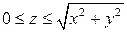 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами  |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
  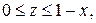 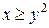 . .  состоит из дуги эллипса состоит из дуги эллипса   и его диаметра и его диаметра  : :  |
|
  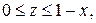   . .  -эллипс -эллипс 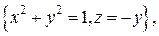 обходимый в направлении обходимый в направлении  |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 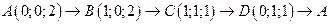 |
|
   . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
    . .  состоит из дуги окружности состоит из дуги окружности   и ее диаметра и ее диаметра  : :  |
|
  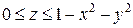 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 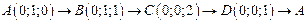 |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
    . .  -контур ромба с вершинами -контур ромба с вершинами  |
|
    . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 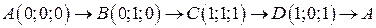 |
|
  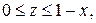   . .  состоит из дуги эллипса состоит из дуги эллипса  : :  и его диаметра и его диаметра  , ,  |
|
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   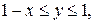  . .  состоит из дуги окружности состоит из дуги окружности   и ее диаметра и ее диаметра  : :  |
|
   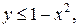  . .  – контур ромба с вершинами – контур ромба с вершинами 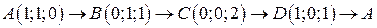 |
|
    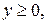  . .  -контур треугольника с вершинами -контур треугольника с вершинами  |
|
   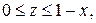   – состоит из дуги окружности – состоит из дуги окружности   и двух отрезков прямых и двух отрезков прямых  и и  : :  |
|
   . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 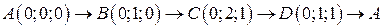 |
|
    . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами  |
Список литературы.
1.Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2, изд.13. – М.:Наука,1985.560 с.
2.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.- М.:Наука,1989.464 с.
3. Кудрявцев Л.Д.Курс математического анализа Т.1,2. -М.: Высшая школа,1981.614с.;470 с.
4. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. Учебник для вузов. Под ред. В.С. Зарубина, А.П. Крищенко. Серия «Математика в техническом университете». Вып. VII.- М.:МГТУ,2001.492 с.
5. Осипова М.З. Теория поля. Учебное пособие по выполнению контрольного задания. – М.:МВТУ,1978.
Оглавление.
1. Скалярные и векторные поля. 4
2. Поверхности и линии уровня. 5
3. Производная по направлению скалярного поля. 7
4. Градиент скалярного поля. 9
5. Векторные линии векторного поля. 12
6. Криволинейный интеграл векторного поля. 15
7. Потенциальное векторное поле. 20
8. Поток векторного поля. 28
9. Дивергенция векторного поля. Соленоидальное векторное поле. 32
10. Ротор (вихрь) векторного поля. Формула Стокса. 37
Дано векторное поле Проверить что это поле является потенциальным
Дано векторное поле .
Проверить, что это поле является потенциальным.
Найти потенциал поля .
Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
Составить уравнение векторных линий поля и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
Вычислить линейный интеграл , , .
Проверим, что данное поле является потенциальным.
Найдем ротор данного поля:
,
.
.
.
.
Отсюда следует, что данное поле является потенциальным.
Найдем потенциал поля .
Найдем потенциал данного поля с помощью криволинейного интеграла:
Найдем уравнение линий равного потенциала и изобразим линии равного потенциала на чертеже.
Линии равного потенциала определяются уравнением:
или ,
.
Изобразим линии равного потенциала на чертеже при нескольких значениях константы ():
Составим уравнение векторных линий поля и изобразим векторные линии на том же чертеже, указав стрелками направление векторных линий.
Векторные линии данного поля определяются дифференциальным уравнением:
.
.
.
Изобразим векторные линии поля на том же чертеже при нескольких значениях константы (), указав стрелками направление векторных линий:
Вычислим линейный интеграл , , .
Поскольку данное поле является потенциальным, то данный интеграл не зависит от пути интегрирования, а определяется разницей значений потенциала в точке и точке :
Исследование электрических полей (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |

Министерство образования Российской Федерации.
Омский Государственный Технический Университет.
Кафедра «Электрической техники»
Исследование электрических полей
Методические указания к лабораторным работам по курсу
Министерство образования Российской Федерации.
Омский Государственный Технический Университет.
Исследование электрических полей.
Методические указания к лабораторным работам.
Омск 2003
Введение
Данное методическое указание предназначено для помощи студентам при выполнении лабораторных работ по курсу ТОЭ «Исследование электростатических полей». Выполнение работ предусмотрено с использованием персонального компьютера, что позволяет не только рассчитать параметры поля, но и наглядно увидеть графическое представление картины поля, получаемое в ходе лабораторных расчетов.
Курс лабораторных работ рассчитан на выполнение четырех работ по математическому моделированию электрических полей :
– исследование электрического поля двухпроводной линии передачи;
– исследование электрического поля параллельных несоосных цилиндров;
– исследование плоскопараллельного электрического поля между электродами заданной геометрии;
– исследование электрического поля у края плоского конденсатора.
Каждая лабораторная работа содержит несколько обязательных разделов:
2. Краткая теория;
3. Рабочее задание;
4. Домашнее задание;
5. Вопросы к защите.
В первом разделе содержатся задачи, которые должны быть решены студентом в ходе лабораторной работы. В краткой теории изложены основные теоретические положения, используемые для составления и решения конкретной задачи. Раздел рабочее задание содержит указания для выполнения той части работы, в которой используется персональный компьютер. Домашнее задание предлагается студенту для закрепления теоретической базы, а также для расширения знаний по данным вопросам. Выполнение пятого раздела позволяет студенту подготовиться к защите теоретической части лабораторной работы.
Лабораторная работа 1
Исследование электрического поля двухпроводной линии передачи
Цель работы. Математическое моделирование электрического поля двухпроводной линии. Расчет основных величин, характеризующих поле и линию. Исследование влияния расстояния между проводами, радиуса провода на характеристики электрического поля и параметры линии.
Расчетная схема двухпроводной линии передачи приведена на рис.1.

Электрическое поле двухпроводной линии является плоскопараллельным, так как основные величины, характеризующие поле (вектор напряженности электрического поля  и электрический потенциал
и электрический потенциал  в любой точке поля) являются функциями только двух пространственных координат ( х и у ) при условии, что провода линии передачи ориентированы параллельно оси z. Это обстоятельство значительно облегчает задачу расчета электрического поля двухпроводной линии. Для построения картины поля и определения его основных характеристик воспользуемся функцией комплексного переменного.
в любой точке поля) являются функциями только двух пространственных координат ( х и у ) при условии, что провода линии передачи ориентированы параллельно оси z. Это обстоятельство значительно облегчает задачу расчета электрического поля двухпроводной линии. Для построения картины поля и определения его основных характеристик воспользуемся функцией комплексного переменного.
Будем рассматривать плоскость, в которой расположены линии напряженности электрического поля, как плоскость комплексного переменного  , где
, где  и
и  соответственно действительная и мнимая части переменного
соответственно действительная и мнимая части переменного  .
.
Функция

 (1)
(1)
– есть функция комплексного переменного. Запись (1) означает, что каждому значению чисел  и
и  соответствуют вполне определенные числа
соответствуют вполне определенные числа  и
и  . При этом
. При этом  и
и  – есть функции двух действительных переменных. Функции комплексного переменного так же, как функции действительного переменного могут быть однозначными и многозначными. Однозначной называют функцию, для которой каждому значению независимого комплексного переменного
– есть функции двух действительных переменных. Функции комплексного переменного так же, как функции действительного переменного могут быть однозначными и многозначными. Однозначной называют функцию, для которой каждому значению независимого комплексного переменного  соответствует только одно значение
соответствует только одно значение  . Напротив, если одним и тем же значениям
. Напротив, если одним и тем же значениям  соответствует несколько различных значений
соответствует несколько различных значений  , то такая функция называется многозначной. Для исследования поля используются только однозначные функции комплексного переменного. Необходимым и достаточным условием непрерывности функции комплексного переменного является непрерывность ее действительной и мнимой частей. При этом сумма, разность, произведение и частное непрерывных функций комплексного переменного также непрерывны. Определение дифференцируемости функции по комплексному переменному аналогично соответствующему определению дифференцируемости по действительному переменному, а именно,
, то такая функция называется многозначной. Для исследования поля используются только однозначные функции комплексного переменного. Необходимым и достаточным условием непрерывности функции комплексного переменного является непрерывность ее действительной и мнимой частей. При этом сумма, разность, произведение и частное непрерывных функций комплексного переменного также непрерывны. Определение дифференцируемости функции по комплексному переменному аналогично соответствующему определению дифференцируемости по действительному переменному, а именно,

 ,
,  (2)
(2)
Поскольку по определению производные для дифференцируемой функции не зависят от пути, по которому производится приближение к точке, то должно выполняться равенство
 ,
,  (3)
(3)
Эти уравнения называют условиями Коши – Римана. Если продифференцировать первое уравнение в выражении (3) по  , а второе уравнение по
, а второе уравнение по  , то
, то
 ,
,  (4)
(4)
 (5)
(5)
Аналогичным образом, дифференцируя в выражении (3) первое уравнение по  , а второе уравнение по
, а второе уравнение по  , после суммирования получим
, после суммирования получим
 . (6)
. (6)
Уравнения (5) и (6) представляют собой уравнения Лапласа для функций  и
и  .
.
Аналитические функции  и
и  можно использовать в расчетах плоских электрических и магнитных полей. При этом расчет поля с использованием функции комплексного переменного заключается в отыскании или подборе такой функции, которая удовлетворяла бы заданным граничным условиям поставленной задачи.
можно использовать в расчетах плоских электрических и магнитных полей. При этом расчет поля с использованием функции комплексного переменного заключается в отыскании или подборе такой функции, которая удовлетворяла бы заданным граничным условиям поставленной задачи.
Будем считать, что функция  является потенциальной функцией электрического поля двухпроводной линии. Напряженность такого поля определится из условия
является потенциальной функцией электрического поля двухпроводной линии. Напряженность такого поля определится из условия
 (7)
(7)
Тогда для расчета напряженности электрического поля  имеем:
имеем:

 ,
,  и
и  .
.
С учетом условия Коши – Римана из соотношений (3) следует
 ,
,  ,
,  . (8)
. (8)
Уравнение силовой линии поля в декартовых координатах имеет вид
 (9)
(9)
после подстановки в него составляющих напряженности электрического поля согласно ( 8 ) получим:



 (10) Равенство ( 10 ) показывает, что приращение функции
(10) Равенство ( 10 ) показывает, что приращение функции  вдоль силовой линии поля отсутствует, следовательно уравнение
вдоль силовой линии поля отсутствует, следовательно уравнение  следует рассматривать как уравнение силовой линии поля. Так как функция
следует рассматривать как уравнение силовой линии поля. Так как функция  неизменна вдоль любой линии поля, то между двумя соседними линиями значение функции также неизменно. Это свойство функции
неизменна вдоль любой линии поля, то между двумя соседними линиями значение функции также неизменно. Это свойство функции  аналогично свойству потока вектора напряженности электрического поля, поэтому ее можно рассматривать как поток вектора
аналогично свойству потока вектора напряженности электрического поля, поэтому ее можно рассматривать как поток вектора  . Используя условия Коши – Римана, легко показать, что функции
. Используя условия Коши – Римана, легко показать, что функции  и
и  оказываются взаимно ортогональными, образуя в плоскости чертежа прямоугольную сетку. При этом совершенно безразлично, какую из частей функции комплексного переменного
оказываются взаимно ортогональными, образуя в плоскости чертежа прямоугольную сетку. При этом совершенно безразлично, какую из частей функции комплексного переменного  или
или  следует считать потенциалом, а какую потоком вектора, поскольку обе они удовлетворяют уравнению Лапласа (5), (6).
следует считать потенциалом, а какую потоком вектора, поскольку обе они удовлетворяют уравнению Лапласа (5), (6).
 ,
,  (11)
(11)
где А – действительная постоянная.
Принимая во внимание, что  ,
, 
 – аргумент переменной, находим:
– аргумент переменной, находим:
 (12)
(12)
Из выражения (12) видно, что действительная и мнимая части функции комплек-сного переменного есть
 и
и  . (13)
. (13)
Линии равного электрического потенциала и линии функции потока в этом случае определяются следующими условиями  и
и  . По структуре линии
. По структуре линии  и
и  представляют собой концентрические окружности с радиуса-ми, проведенными из центра
представляют собой концентрические окружности с радиуса-ми, проведенными из центра  Точно такую же структуру имеет электрическое поле уединенного провода, имеющего линейную плотность заряда
Точно такую же структуру имеет электрическое поле уединенного провода, имеющего линейную плотность заряда  .
.
Воспользовавшись теоремой Гаусса нетрудно найти постоянную
 , (14)
, (14)
где  Ф/м – диэлектрическая постоянная воздуха (вакуума) ,
Ф/м – диэлектрическая постоянная воздуха (вакуума) ,  – отно-сительная диэлектрическая проницаемость среды.
– отно-сительная диэлектрическая проницаемость среды.
Подставляя в (12) постоянную  , находим комплексный потенциал поля линейного заряда с полюсами в центре координатных осей.
, находим комплексный потенциал поля линейного заряда с полюсами в центре координатных осей.
Напряженность электрического поля при этом будет
 . (15)
. (15)
Если две из эквипотенциальных поверхностей такого поля заменить тонкими про-водящими поверхностями с потенциалами  и
и  , то структура поля от этого не изменится. Однако за счет изменившихся граничных условий
, то структура поля от этого не изменится. Однако за счет изменившихся граничных условий
при 
 ,
,
при 
 ,
,
постоянная  комплексного потенциала изменится
комплексного потенциала изменится
 . (17)
. (17)
Подставляя ее выражение в уравнение (11), можно определить комплексный потен-циал поля коаксиального кабеля
 . (18)
. (18)
Для поля двух линейных зарядов  , имеющих координаты
, имеющих координаты  ;
;  , комплексный потенциал поля
, комплексный потенциал поля
 , (19)
, (19)
где  – постоянная.
– постоянная.
Обозначая расстояния от точки  до местоположения линейных зарядов через
до местоположения линейных зарядов через  и
и  , в полярных координатах выразим
, в полярных координатах выразим  и
и  , где
, где  и
и  – есть углы с осью Х ( рис.1 ).
– есть углы с осью Х ( рис.1 ).
 . (20)
. (20)
 ;
;  . (21)
. (21)
Линии равного электрического потенциала определяются условием  , а линии функции потока – соответственно
, а линии функции потока – соответственно  . Первое условие представляет собой уравнение окружности, а второе – уравнение дуги окружности, для которой хордой является отрезок прямой, соединяющий линейные заряды.
. Первое условие представляет собой уравнение окружности, а второе – уравнение дуги окружности, для которой хордой является отрезок прямой, соединяющий линейные заряды.
Уравнение линии равного потенциала удобнее записывать в декартовых координа-тах

 . (22)
. (22)
Полученное уравнение – есть уравнение окружности с радиусом  и координатами центра
и координатами центра
 и
и  .
.
Координата  в уравнении (22) получается положительной для
в уравнении (22) получается положительной для  , то есть для полупространства с отрицательной заряженной осью. Окружности равного потен-циала оказываются при этом справа от оси
, то есть для полупространства с отрицательной заряженной осью. Окружности равного потен-циала оказываются при этом справа от оси  ( рис.2 ).
( рис.2 ).
Если принять в выражении (21)  , то получим
, то получим  при
при  , то есть линией нулевого потенциала является ось ординат. Чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным необходимо соблюдать условие:
, то есть линией нулевого потенциала является ось ординат. Чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным необходимо соблюдать условие:
 , (23)
, (23)
то есть числа  при возрастании
при возрастании  должны изменяться в геометрической прогрес-сии
должны изменяться в геометрической прогрес-сии
 . (24)
. (24)

Приняв в выражении функции потока  , получим
, получим  при
при  , то есть начальной линией напряженности поля при
, то есть начальной линией напряженности поля при  являются участки абсцисс, уходящие от проводов в бесконечность.
являются участки абсцисс, уходящие от проводов в бесконечность.
Рис.2 Построение линии равного электрического потенциала.
Уравнение любой линии напряженности электрического поля имеет вид:
 или
или  (25)
(25)
и, следовательно, является уравнением дуги окружности, пересекающейся с линей-ными проводами, что видно непосредственно по рис. 3.

Рис.3 Построение линии напряженности электрического поля.
Действительно,  QMP, под которым виден отрезок QP из точек
QMP, под которым виден отрезок QP из точек  , лежащих на линии напряженности поля, равен углу
, лежащих на линии напряженности поля, равен углу  и остается постоянным по величине.
и остается постоянным по величине.
Координаты центра окружности
 , (26)
, (26)
 .
.
Чтобы подразделить поле на трубки равного потока, следует считать разность  одинаковой для двух любых соседних линий. Для этого необходимо при переходе от любой линии напряженности поля к соседней изменять угол
одинаковой для двух любых соседних линий. Для этого необходимо при переходе от любой линии напряженности поля к соседней изменять угол  на постоянную величину
на постоянную величину .
.
Провода реальной двухпроводной линии передачи имеют конечные сечения. Пусть  и R – это координата центра и радиус окружности равного потенциала, совпадающей с окружностью сечения провода.
и R – это координата центра и радиус окружности равного потенциала, совпадающей с окружностью сечения провода.
 и
и  (27)
(27)
нетрудно убедится, что  . Отсюда находим положение электрических осей по заданному расстоянию
. Отсюда находим положение электрических осей по заданному расстоянию  между геометрическими осями и радиусу сечений проводов, как
между геометрическими осями и радиусу сечений проводов, как
 . (28)
. (28)
При этом поле внутри металлических проводов будет отсутствовать, а поле в диэ-лектрике с учетом замены реальных проводов электрически заряженными осями останется без изменения, так как удовлетворяется граничное условие – постоянство потенциала на поверхности провода.
На рис.5 построена картина электрического поля двухпроводной линии пере-дачи, причем принято  и
и  . Из картины поля видно, что напря-женность поля принимает максимальное значение в точках
. Из картины поля видно, что напря-женность поля принимает максимальное значение в точках  и
и  . Около этих точек диэлектрик находится в наиболее напряженном состоянии, и при повышении напряжения между проводами нарушение электрической прочности диэлектрика начинается именно в этих точках.
. Около этих точек диэлектрик находится в наиболее напряженном состоянии, и при повышении напряжения между проводами нарушение электрической прочности диэлектрика начинается именно в этих точках.
Согласно выражению (15) напряженность электрического поля в точке  будет:
будет:
 . (29)
. (29)
Если принять во внимание притяжение зарядов разного знака, то очевидно, что распределение плотности электрического заряда  по поверхности прово-дов, даже в случае их круглого сечения, также будет неравномерным.
по поверхности прово-дов, даже в случае их круглого сечения, также будет неравномерным.
Напряжение между проводами линии с учетом выражения (21) будет:
 . (30)
. (30)
Емкость двухпроводной линии передачи не зависит от заряда ( =
= 
 , где
, где  – длина линии ), а является функцией геометрических размеров проводов, их взаимного расположения и диэлектрической проницаемости среды
– длина линии ), а является функцией геометрических размеров проводов, их взаимного расположения и диэлектрической проницаемости среды  :
:
 . (31)
. (31)
1. Открыть окно программы по расчету электрического поля параллельных несоосных цилиндров, запускающий файл программы mkp. exe (рис.4).
Внимание! Программа содержит встроенную помощь и информацию о прог-рамме, которые можно получить нажатием на расположенные в вернем левом углу окна кнопки «Помощь» и «О программе».
Произвести ввод данных по коду (по указанию преподавателя) нажатием на кнопки «Ввод данных» и после завершения ввода кода «Ok».
2. Нажать на кнопку «Решение» и войти в диалоговое окно построения картины электрического поля двухпроводной линии передачи (рис. 5).
Заполнить табл. 1 значениями расчетных параметров K,  ,
,  , R для опреде-ления эквипотенциальных линий электрического поля в соответствии с исход-ными данными, используя соотношения (22), (24), (27), (28).
, R для опреде-ления эквипотенциальных линий электрического поля в соответствии с исход-ными данными, используя соотношения (22), (24), (27), (28).
[spoiler title=”источники:”]
http://lektsii.org/5-41051.html
http://pandia.ru/text/79/133/66118.php
[/spoiler]
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
– следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |