В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.
- Нахождение радиуса сферы/шара
- Формулы площади и объема сферы/шара
Нахождение радиуса сферы/шара
Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).
Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:
1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса
![]()
Высота (h) конуса – это отрезок BE на рисунках выше.
Формулы площади и объема сферы/шара
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
![]()

Примечание: π округленно равняется 3,14.
1) Конус в шаре выглядит, примерно как на рисунке. Чтобы найти радиус шара R1, нужно определить, как соотносятся друг с другом R и H.
Рассмотрим треугольник АВD. Он прямоугольный, и состоит из радиуса R, высоты H и образующей L конуса.
Найдем угол а:
L^2 = R^2 + H^2
cos a = H / L
Рассмотрим красный треугольник АВО – он равнобедренный, и состоит из двух радиусов R1 шара и образующей L конуса.
Найдем R1 по теореме косинусов:
R1^2 = R1^2 + L^2 – 2*R1*L*cos a
2*R1*L*cos a = L^2
R1 = L / 2cos a = L / (2H/L) = L^2 / (2H) = (R^2 + H^2) / (2H)
Поверхность шара
S = 4*Pi*R1^2 = 4Pi * (R^2 + H^2)^2 / (2H)^2 = Pi * (R^2 + H^2)^2 / H^2 
2) С призмой сложнее, сразу не сообразишь. Единственное, что могу подсказать – общие формулы.
Объем призмы: V = S(осн) *H
Основание правильной треугольной призмы – равносторонний треугольник, поэтому
S(осн) = a^2 * V(3)/4
По условию H = 2a
V = a^3 * V(3)/2
Объем шара V = 4Pi / 3 * R^3 = Pi/6 * D^3
Теперь надо как-то выразить радиус или диаметр шара из известных данных о призме.

ТЕЛА ВРАЩЕНИЯ
РЕШЕНИЕ ЗАДАЧ
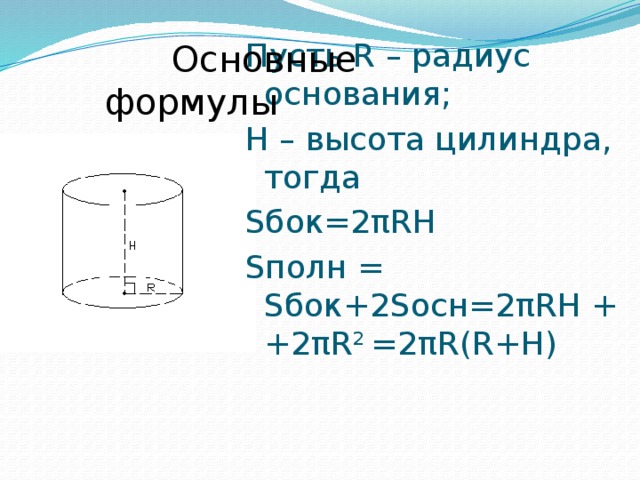
Основные формулы
Пусть R – радиус основания;
H – высота цилиндра, тогда
Sбок=2πRH
Sполн = Sбок+2Sосн=2πRH + +2πR 2 =2πR(R+H)
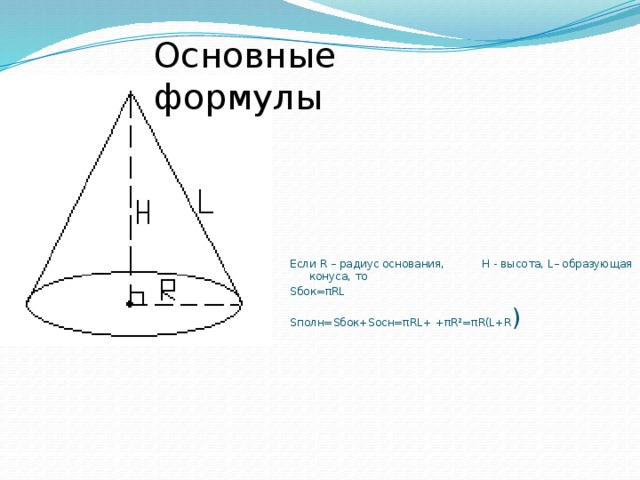
Основные формулы
Если R – радиус основания, H – высота, L– образующая конуса, то
Sбок=πRL
Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R )

Усеченный прямой конус
h – высота усеченного конуса ; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая
Формулы:
Основные формулы
R – радиус шара
Sсферы=4πR²
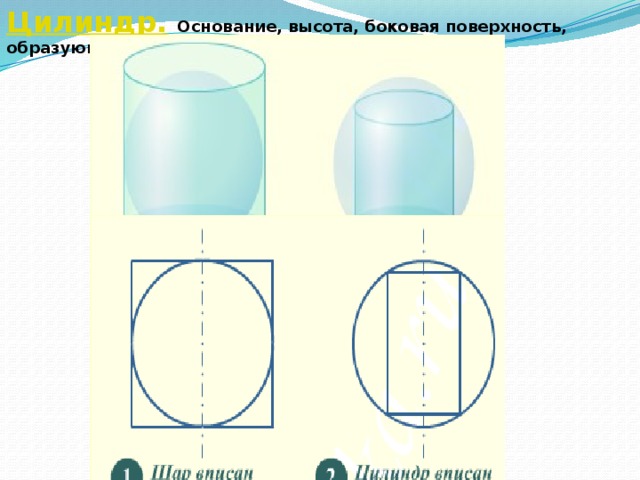
Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
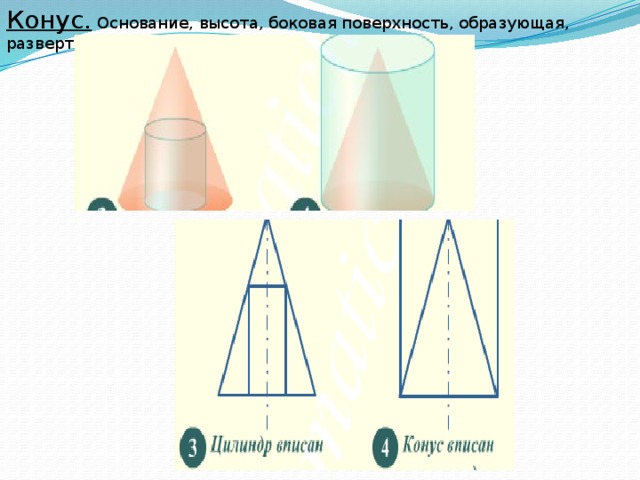
Конус. Основание, высота, боковая поверхность, образующая, развертка
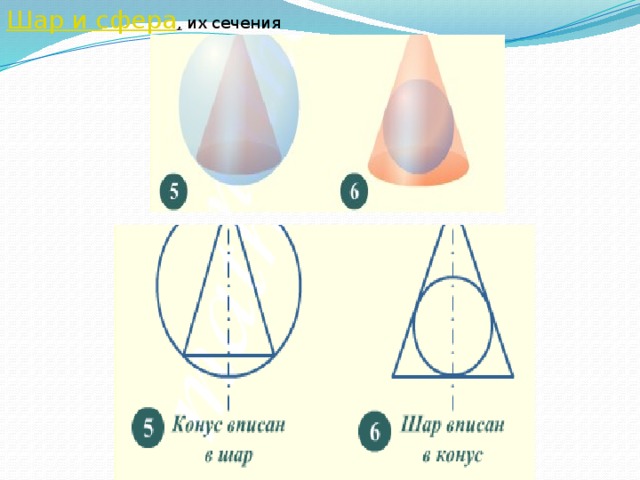
Шар и сфера , их сечения

Задача 1.
Шар вписан в цилиндр. Площадь поверхности шара равна 111.
Найдите площадь полной поверхности цилиндра.

Решение.
Площадь полной поверхности цилиндра находим по формуле S ц = 2 πrh + 2 πr 2 .
Из рисунка (1) для плоского
сечения видно, что радиус
основания цилиндра ( r ) равен
радиусу вписанного шара ( R ),
а его высота ( h ) равна диаметру
шара (удвоенному радиусу).
Поэтому S ц = 2 πR ·2 R + 2 πR 2 = 6 πR 2 . Величину πR 2 найдем из формулы поверхности шара S ш = 4 πR 2 . Следовательно, πR 2 = S ш / 4 = 111/4. Окончательно находим S ц = 6·111 / 4 = 333/2 = 166,5.
Ответ: 166,5

Задача 2
В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.
Дополним чертеж осевого сечения радиусом шара и расставим буквы для обозначения отрезков. Площадь поверхности шара S ш = 4 πR 2 = 100π. Отсюда R 2 = 25 и R = 5. В треугольнике OAB : OA = x – половина искомой высоты цилиндра; AB = 4 – радиус основания цилиндра; OB = 5 – радиус шара. По теореме Пифагора: x 2 + 4 2 = 5 2 ,
x 2 = 25 − 16 = 9; x = 3. h = 6.
Ответ: 6

Задача 3
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.
 l 2 = h 2 + r 2 По условию задачи h = r , следовательно l 2 = r 2 + r 2 ; l 2 = 2 r 2 ; l = √2· r . Площадь боковой поверхности цилиндра S ц = 2 πrh = 2 πr 2 . Площадь боковой поверхности конуса S к = πrl = πr ·√2· r = √2 πr 2 ; т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно S к = 3√2 / √2 = 3/ Ответ: 3 A C B ” width=”640″
l 2 = h 2 + r 2 По условию задачи h = r , следовательно l 2 = r 2 + r 2 ; l 2 = 2 r 2 ; l = √2· r . Площадь боковой поверхности цилиндра S ц = 2 πrh = 2 πr 2 . Площадь боковой поверхности конуса S к = πrl = πr ·√2· r = √2 πr 2 ; т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно S к = 3√2 / √2 = 3/ Ответ: 3 A C B ” width=”640″
Воспользуемся чертежом осевого сечения, расставим буквы для обозначения отрезков: AC = h – высота конуса и цилиндра, CB = r – радиус оснований конуса и цилиндра, AB = l – образующая цилиндра.
Из треугольника ABC по теореме Пифагора: AB 2 = AC 2 + CB 2 == l 2 = h 2 + r 2 По условию задачи h = r , следовательно l 2 = r 2 + r 2 ; l 2 = 2 r 2 ; l = √2· r . Площадь боковой поверхности цилиндра
S ц = 2 πrh = 2 πr 2 . Площадь боковой поверхности конуса S к = πrl = πr ·√2· r = √2 πr 2 ;
т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно S к = 3√2 / √2 = 3/ Ответ: 3
A
C
B

Задача 4
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2. Найдите радиус сферы.

Так как по условию задачи центр сферы находится в центре основания конуса, то основание конуса, в свою очередь, является диаметральным сечением сферы. Т.о. на плоском чертеже отрезок AB является диаметром окружности, и ∠ ACB = 90° как вписанный угол, опирающийся на её диаметр.
Пусть l = 7√2 – образующая конуса, R – радиус сферы. Тогда в прямоугольном треугольнике ABC AC = BC = l – катеты, AB = 2 R – гипотенуза. По теореме Пифагора AB 2 = AC 2 + BC 2 ; (2 R ) 2 = l 2 + l 2 ; 4 R 2 = l 2 + l 2 = 2 l 2 ; 4 R 2 = 2(7√2_) 2 ; 4 R 2 = 2·49·2 = 4·49; R 2 = 49; R = 7.
Ответ: 7

Задача 5
Найти площадь поверхности шара, описанного около конуса, у которого радиус основания 2/√π, а высота 1/√π.
Пусть R – радиус сферы. Поскольку СD – диаметр окружности осевого сечения, то СH + HD = 2 R . Воспользуемся свойством пересекающихся хорд окружности, чтобы найти длину отрезка HD = x .
DH·HС = AH·HC; x · 1/√π = 2/√π · 2/√π; Преобразуя, получим х = 4/√π. 2 R = 1/√π + 4/√π = 5/√π; R = 5/2√π. Площадь сферы S = 4π R 2 = 4π·25/4π = 25.
Ответ: 25

Задача 5
В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности этого конуса к поверхности шара.
Пусть образующая конуса ( AC = BC ) равна a . Тогда по условию задачи диаметр конуса ( AB ) тоже равен a . То есть, треугольник ABC – равносторонний.
Чтобы найти радиус шара ( R ), используем формулу, связывающую длину стороны равностороннего треугольника и радиус описанной около него окружности.

Радиус основания конуса r = a /2 (половина диаметра).
Площадь полной поверхности конуса S к = π r ( r + l ) = π· a /2·( a /2 + a ) = 3π a 2 /4.
Площадь поверхности шара S ш = 4π R 2 = 4π· a 2 ·(√3/3) 2 = 4π a 2 /3.
Их отношение
S к / S ш = 3π a 2 /4/4π a 2 /3 = 9/16 = 0,5625.
Ответ: 0,5625

ЗАДАНИЕ НА ДОМ
№ 616
Задачи ЕГЭ (распечатка)
11.096 _Определить поверхность шара, описанного около конуса
| 26.11.2013, 03:13 | |
Определить поверхность шара, описанного около конуса, у которого радиус основания равен R, а высота равна h.
|
|
Категория: Задачи стереометрии | Добавил: alexlat |
|
| Просмотров: 626 | Загрузок: 0
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]
Статистика
куба равен 3.Найдите площадь поверхности куба… 3)В шар площадь поверхности которого равна 100n, вписан цилиндр.Найдите высоту цилиндра, если радиус его основания равен 4… 4)В шар вписан конус… Найдите высоту конуса, еслирадиус шара равен 5, а радиус основания конуса равен 4
катя
08.02.17
Учеба и наука / Математика
1 ответ
