Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 января 2023 года; проверки требуют 3 правки.
Монета, лежащая на поверхности воды благодаря силе поверхностного натяжения
Когезия формирует водяные капли, поверхностное натяжение делает их почти сферическими, а адгезия держит их на поверхности другого вещества
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1].
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности

Но более правильно дать определение поверхностному натяжению, как энергии в джоулях на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
В 1983 году было доказано теоретически и подтверждено данными из справочников[2], что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии[3][4]).
В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения как части внутренней энергии при решении другой физической задачи был опубликован В. Вайскопфом в США[5].
Поверхностное натяжение возникает на границе газообразных, жидких и твёрдых тел. Обычно под термином «поверхностное натяжение» имеется в виду поверхностное натяжение жидких тел на границе жидкость — газ. В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.
Прибор для измерения поверхностного натяжения называется тензиометр.
Проявления[править | править код]
Водомерка на поверхности воды.
Так как увеличение площади поверхности раздела жидкость — газ требует совершения работы, жидкость «стремится» уменьшить площадь своей поверхности:
- в невесомости порция жидкости принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма). То же самое происходит с каплей жидкости, помещаемой внутрь другой, несмешивающейся жидкости с первой жидкостью той же плотности (опыт Плато).
- ламинарная струя воды образует цилиндр, который затем разбивается на шаровидные капли из-за неустойчивости Рэлея — Плато.
- небольшие предметы со средней плотностью большей плотности жидкости способны «плавать» на поверхности жидкости, так как их вес оказывается уравновешенным силой поверхностного натяжения.
- некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
- На многих поверхностях, именуемых несмачиваемыми (гидрофобными), вода (или другая жидкость) собирается в капли.
- Поплавок Ван Дер Месбрюгге – поплавок, имеющий кольцо. Если нажать на поплавок, то он будет удерживаться в нажатом состоянии благодаря силам поверхностного натяжения, они действуют на кольцо, и в свою очередь уравновешивают гидростатические силы, стремящиеся вытолкнуть поплавок из воды.
Теория[править | править код]
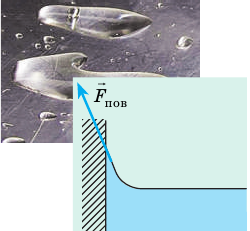
Пояснение возникновения силы поверхностного натяжения. Молекулы на границе раздела испытывают силы, стремящиеся втянуть их в жидкость, так как со стороны газа на них не действуют силы притяжения.
Площадь поверхности[править | править код]
Поверхность жидкости обладает свободной энергией:
- где
— коэффициент поверхностного натяжения,
— полная площадь поверхности жидкости[6].
Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля стремится принять форму шара, однако при более сложных начальных условиях задача о форме поверхности жидкости становится математически исключительно сложной.
Формула Лапласа[править | править код]
Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется образование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления поверхностного натяжения плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и задаётся формулой Лапласа:
Здесь 
Для случая поверхности кругового цилиндра радиуса 
Так как 
Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.
Зависимость от температуры[править | править код]
С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена Лорандом Этвёшом, так называемое правило Этвёша. В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правило Этвёша[7].
Способы определения[править | править код]
Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами. В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения.
Например, для раствора мыла после перемешивания поверхностное натяжение 58 мДж/м², а после отстаивания — 35 мДж/м². То есть поверхностное натяжение меняется.
До установления равновесного оно будет динамическое.
Статические методы:
- Метод измерения высоты поднятия мениска в капилляре.
- Метод Вильгельми.
- Метод лежачей капли.
- Метод определения по форме висячей капли.
- Метод вращающейся капли.
Динамические методы:
- Метод дю Нуи (метод отрыва кольца).
- Сталагмометрический, или метод счета капель.
- Метод максимального давления пузырька.
- Метод осциллирующей струи.
- Метод стоячих волн.
- Метод бегущих волн.
Методы[править | править код]
Полностью стандартизованные методы измерений описываются в соответствующих ASTM, ГОСТ и т. д.
Метод вращающейся капли[править | править код]
Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости[8]. Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения. Он широко применяется для микроэмульсий, измерения эффективности поверхностно-активных веществ (ПАВ) в нефтедобыче, а также для определения адсорбционных свойств.
Метод Дю Нуи (метод отрыва кольца)[править | править код]
Метод является классическим. Сущность метода вытекает из названия. Кольцо из платиновой проволоки плоскость которого параллельна поверхности жидкости медленно поднимают из жидкости, смачивающей его, усилие в момент отрыва кольца от поверхности и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения поверхностного натяжения ПАВ, трансформаторных масел и т. д.
Метод капиллярных волн[править | править код]
При возмущении жидкости колеблющейся пластиной, лежащей на её поверхности, по поверхности жидкости распространяются капиллярные волны. Если осветить кювету с жидкостью импульсным источником света (стробоскопом) с частотой вспышек равной частоте колебания пластины возмущения, то будет наблюдаться зрительно неподвижная волновая картина. По измеренной длине волны можно рассчитать величину поверхностного натяжения по формуле:
- где
— поверхностное натяжение;
— плотность жидкости;
— длина волны;
— частота колебания пластины;
— ускорение свободного падения.
Поверхностное натяжение некоторых жидкостей на границе с воздухом[править | править код]
| Вещество | Температура °C | Поверхностное натяжение(10−3 Н/м) |
|---|---|---|
| Хлорид натрия 6 M водный раствор | 20 | 82,55 |
| Хлорид натрия | 801 | 115 |
| Глицерин | 30 | 64,7 |
| Олово | 400 | 518 |
| Азотная кислота 70 % | 20 | 59,4 |
| Анилин | 20 | 42,9 |
| Ацетон | 20 | 23,7 |
| Бензол | 20 | 29,0 |
| Вода | 20 | 72,86 |
| Глицерин | 20 | 59,4 |
| Нефть | 20 | 26 |
| Ртуть | 20 | 486,5 |
| Серная кислота 85 % | 20 | 57,4 |
| Спирт этиловый | 20 | 22,8 |
| Уксусная кислота | 20 | 27,8 |
| Эфир этиловый | 20 | 16,9 |
| Раствор мыла | 20 | 43 |
Проявления[править | править код]
-
Мыльный пузырь
-
Маргаритка
-
На фотографии виден эффект, получивший название «слёзы вина»
-
Капля воды на листе
-
Вода набегает на сухую поверхность асфальта
| Видео, демонстрирующее передвижение водомерки по поверхности воды за счёт поверхностного натяжения. |
См. также[править | править код]
- Тензиометр
- Формула Жюрена
Ссылки[править | править код]
- [www.xumuk.ru/colloidchem/19.html Методы определения поверхностного натяжения]
- Видео о физической природе поверхностного натяжения жидкости как части внутренней энергии Архивная копия от 20 декабря 2020 на Wayback Machine (рус.)
Примечания[править | править код]
- ↑ Сумм Б. Д. Основы коллоидной химии
- ↑ (Cтатья: Журнал физической химии. 1983, № 10, с. 2528—2530). Дата обращения: 16 февраля 2014. Архивировано 21 февраля 2014 года.
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч. Физическая природа поверхностного натяжения жидкости // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия) 2011. Выпуск 1. с.3-8. Дата обращения: 16 февраля 2014. Архивировано из оригинала 22 февраля 2014 года.
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч., Майоров Е. Е. Влияние температуры на поверхностное натяжения // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия). 2012. Выпуск 1. с.24-28. Дата обращения: 16 февраля 2014. Архивировано из оригинала 22 февраля 2014 года.
- ↑ Weisskopf V. F. American Journal of Physics 53 (1985) 19-20.; V. F. Weisskopf, American Journal of Physics 53 (1985) 618—619.
- ↑ Обратите внимание, что плёнка, вроде стенки мыльного пузыря, имеет две стороны, так что площадь поверхности жидкости в два раза больше площади плёнки.
- ↑ Журнал «Вестник Санкт-Петербургского университета», 2012, вып. 1, с. 24—28
- ↑ Тензиометр SITE100. Дата обращения: 19 ноября 2008. Архивировано 3 апреля 2009 года.
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов
|
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
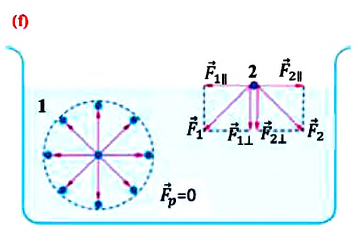
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения – это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 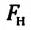
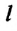
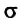
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения – численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
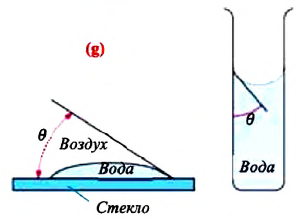
Мениск – это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 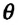
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде – смачивающая жидкость (g).
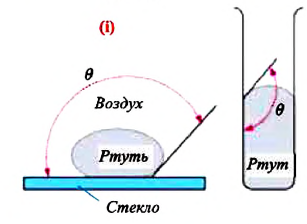
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек – капилляров.
Капилляр – это узкая трубка (канал) диаметром меньше 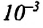
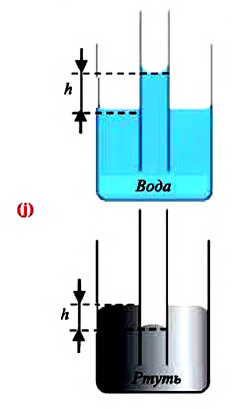
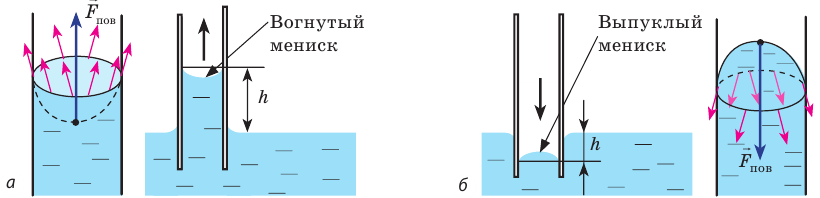
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 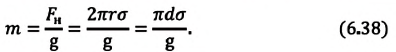 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в Где |
| Давление жидкости, поднимающейся в капилляре | 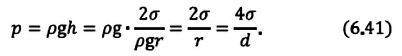 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
Каковы особенности поверхностного слоя жидкости
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
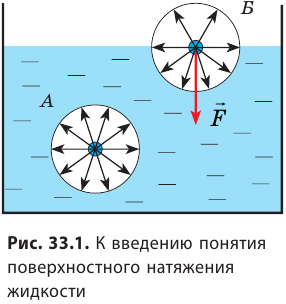
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
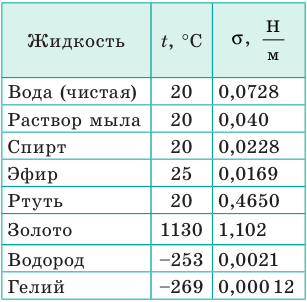
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (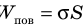
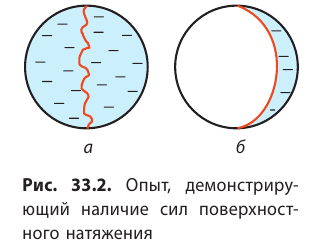
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
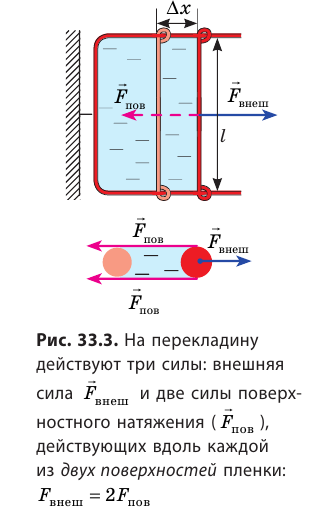
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 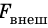
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 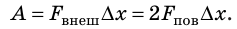
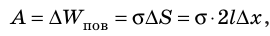
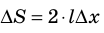
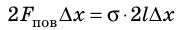
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения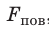
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (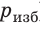
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (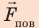
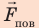
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 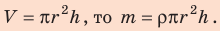
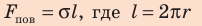
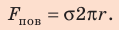
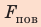

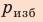
где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
- Высота подъема жидкости в капилляре прямо пропорциональна поверхностному натяжению жидкости и обратно пропорциональна плотности жидкости и радиусу капилляра:
.
- Лапласово давление (избыточное давление) под сферической поверхностью жидкости прямо пропорционально поверхностному натяжению жидкости и обратно пропорционально радиусу кривизны мениска:
.
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
Наличие
у жидкости свободной поверхности
обусловливает существование особых
явлений, называемых поверхностными.
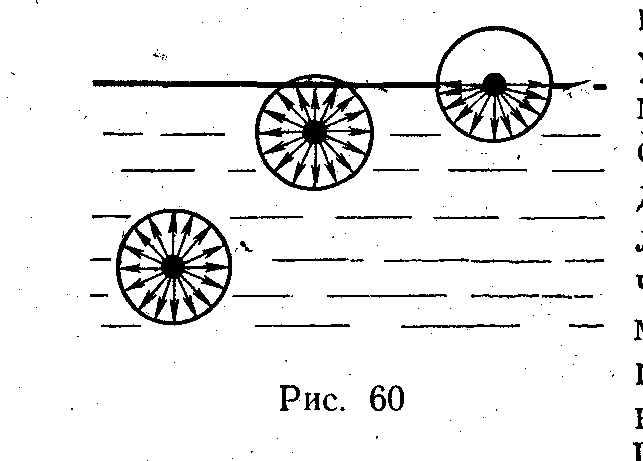
Они возникают в связи с тем, что молекулы
в толще жидкости и на ее поверхности
находятся в неодинаковых условиях. В
толще жидкости каждая молекула испытывает
притяжение со стороны всех соседних
молекул, находящихся в пределах ее сферы
молекулярного действия. В этом случае
силы притяжения, действующие на
молекулу
со всех сторон, взаимно компенсируются
и поэтому их равнодействующая в среднем
равна нулю (рис. 4.7.1).
Рис.4.7.1.
Иначе
обстоит дело с молекулами, находящимися
от поверхности жидкости на расстояниях
меньших, чем радиус молекулярного
действия. У таких молекул сфера
молекулярного действия лишь частично
находится внутри жидкости. В той части
сферы молекулярного действия, которая
выступает из жидкости, будет значительно
меньше молекул, чем в остальной ее части,
так как плотность пара или газа, с которым
граничит жидкость, меньше плотности
жидкости. Силы притяжения со стороны
соседних молекул в этом случае уже не
будут взаимно скомпенсированными и их
равнодействующая в среднем отлична от
нуля и направлена внутрь жидкости (см.
рис. 4.7.1). Таким образом, вблизи поверхности
жидкости в слое толщиной меньшей, чем
радиус молекулярного действия, на каждую
молекулу жидкости со стороны других ее
молекул действуют силы притяжения,
равнодействующая которых направлена
внутрь жидкости.
Для
того, чтобы молекула переместилась из
глубины жидкости в поверхностный слой,
она должна совершить работу против сил,
действующих в поверхностном слое.
Итак,
в поверхностном слое жидкости молекулы
обладают дополнительной потенциальной
энергией. Этот избыток энергии молекул
жидкости, находящихся в поверхностном
слое, по сравнению с их энергией внутри
остального объема жидкости, называют
поверхностной энергией.
Очевидно,
что поверхностная энергия пропорциональна
площади поверхности S:
(4.7.4)
Коэффициент
пропорциональности α зависит не только
от природы и состояния жидкости, но и
от природы и состояния той среды, с
которой соприкасается данная поверхность
жидкости. Его называют поверхностным
натяжением.
Отметим,
что только в случае, когда жидкость
граничит со своим паром, говорят просто
о поверхностном натяжении жидкости.
Предположим,
что увеличение поверхности жидкости
происходит адиабатически. Тогда по
первому закону термодинамики работа,
совершаемая над жидкостью, должна быть
равна изменению внутренней энергии
жидкости, т. е.
.
Это изменение внутренней энергии
жидкости будет происходить не только
за счет приращения ее поверхностной
энергии, но и за счет охлаждения жидкости.
Увеличение
площади поверхности жидкости связано
с уменьшением кинетической энергии
молекул, переходящих в поверхностный
слой. Поскольку при тепловом движении
молекулы все время обмениваются энергией
друг с другом, то это приводит к уменьшению
средней кинетической энергии жидкости
в целом, т. е жидкость охлаждается.
Наоборот, при уменьшении поверхности
жидкости (например, при слиянии капель)
поверхностная энергия уменьшается и
жидкость нагревается. Чтобы внутренняя
энергия жидкости изменялась только за
счет увеличения поверхностной энергии,
процесс увеличения поверхности жидкости
должен происходить изотермически. Ту
часть внутренней энергии, которая может
быть превращена в работу при изотермическом
процессе, в термодинамике называют
свободной энергией.
Таким
образом, работа, затрачиваемая при
изотермическом процессе создания
поверхности жидкости, по существу идет
на увеличение свободной энергии ее
поверхности. Значит, дополнительная
потенциальная энергия поверхности
жидкости является свободной энергией
поверхности жидкости. Поэтому поверхностное
натяжение можно определить как работу,
затрачиваемую на изотермическое
образование 1 м2
поверхности жидкости:
(4.7.5)
В
состоянии устойчивого равновесия
жидкость стремится иметь минимальное
значение свободной поверхностной
энергии и принимает форму, при которой
ее поверхность минимальна. Именно с
этим и связана сферическая форма мелких
капель и пузырьков. В состоянии невесомости
такую же сферическую форму принимает
и любая масса жидкости. В земных условиях
форма крупных капель заметно отличается
от сферической потому, что они сплющиваются
под действием сил тяжести. Действием
сил тяжести объясняют и те, что в земных
условиях жидкости принимают форму
сосуда, в который они налиты, т. е. жидкости
стремятся принять такую форму, при
которой их центр масс будет иметь
наименьшее положение.
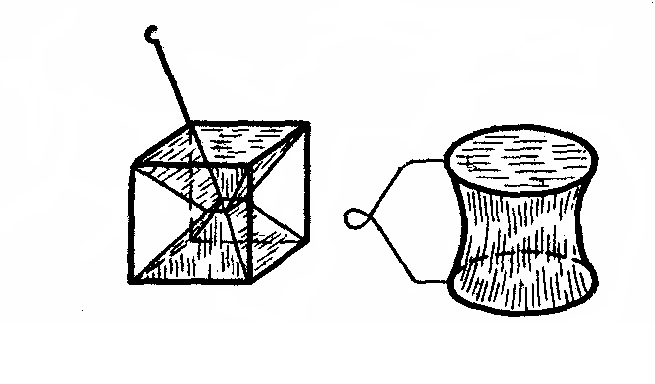
Стремлением
свободной энергии поверхности жидкости
к минимуму объясняется и своеобразие
форм мыльных пленок, возникающих на
проволочных каркасах (рис. 4.7.2).
Рис.
4.7.2.
Конечно,
термин «пленка» нельзя понимать в
буквальном смысле этого слова. Между
обычной упругой пленкой и поверхностным
слоем жидкости, который часто называют
жидкой пленкой, существует лишь некоторое
чисто внешнее сходство. Оно проявляется
в том, что жидкость, стремясь сократить
свою поверхность, ведет себя так, как
если бы она была заключена в упруго
растянутую пленку, стремящуюся сжаться.
Однако, в отличие от резиновой, жидкая
пленка не обладает упругостью. При
увеличении поверхности жидкости
расстояние между молекулами в поверхностно
слое не изменяется (что происходит за
счет перехода молекул из толщи жидкости
в поверхностный слой).
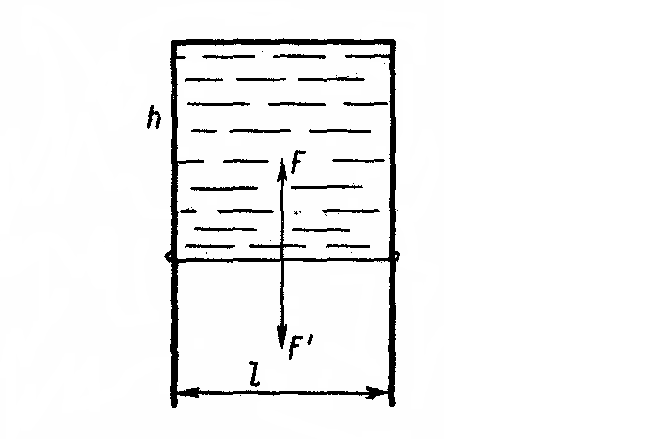
Рассмотрим
такой опыт. Опустим в мыльный раствор
проволочную рамку, одна сторона которой,
имеющая длину
,
может перемещаться (рис. 4.7.3.).
Рис.
4.7.3.
Если
вынуть рамку из раствора, то на ней
останется тонкий слой жидкости — мыльная
пленка. Поскольку жидкость стремится
сократить свою поверхность, то подвижная
сторона рамки начнет перемещаться. Чтоб
удержать ее на месте, к ней нужно приложить
некоторую силу F.
Очевидно, что мыльная пленка действует
на подвижную сторону рамки с такой же
по значению силой F,
но имеющей противоположное направление,
т. е. F
= –F’.
Изменяя положение перекладины (перемещая
ее вверх или вниз по рамке), нетрудно
убедиться в том, что значение силы F
не изменяется. Если же подобный опыт
повторить с другими рамками, имеющими
разную длину подвижной перекладины, то
можно установить, что сила F
возрастает пропорционально длине
перекладины.
Значение
силы F
можно, как известно из механики, найти,
если
взять
производную от энергии (в данном случае
от поверхностной энергии) по координате
вдоль направления действия силы:
Так
как на проволочной рамке мыльная пленка
имеет две стороны, площадь поверхности
мыльной пленки
и тогда
Знак
минус указывает на то, что сила F
направлена внутрь поверхности пленки.
Очевидно,
для односторонней поверхности жидкости
эта сила будет меньше, т.е.
(4.7.6)
Таким
образом, на любую линию, ограничивающую
поверхность жидкости или ее какую-либо
часть ее, действуют силы, направленные
перпендикулярно этой линии по касательной
к поверхности жидкости.
Эти
силы называют силами поверхностного
натяжения.
Из
формулы (4.7.6) следует, что сила, отнесенная
к единице длины линии, ограничивающей
поверхность жидкости, равна поверхностному
натяжению.
Итак,
единицу поверхностного натяжения можно
определить как по формуле (4.7.4), так и по
формуле (4.7.6). В первом случае оно
выражается в единицах энергии на единицу
площади, а во втором – силы на единицу
длины:
Поверхностное
натяжение зависит от температуры. для
сравнительно небольших интервалов
температуры оно обычно убывает по
линейному закону ростом температуры.
Это объясняют тем, что с повышением
температуры уменьшается различие в
плотности жидкости и ее насыщенного
пара. В критической точке, когда плотность
жидкости и пара одинакова, поверхностное
натяжение жидкости равно нулю.
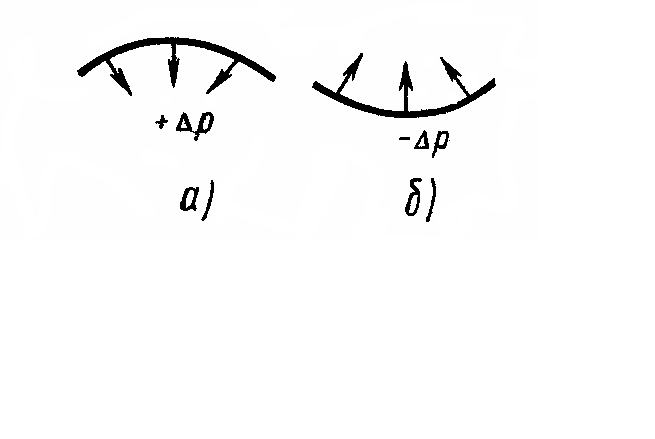
Силы
поверхностного натяжения, когда
поверхность жидкости не плоская, создают
дополнительное давление к тому, которое
испытывает жидкость с плоской поверхностью.
При выпуклой поверхности жидкости это
дополнительное давление положительно
(рис. 4.7.4, а), а при вогнутой отрицательно
(рис. 4.7.4, б).
Рис.
4.7.4.
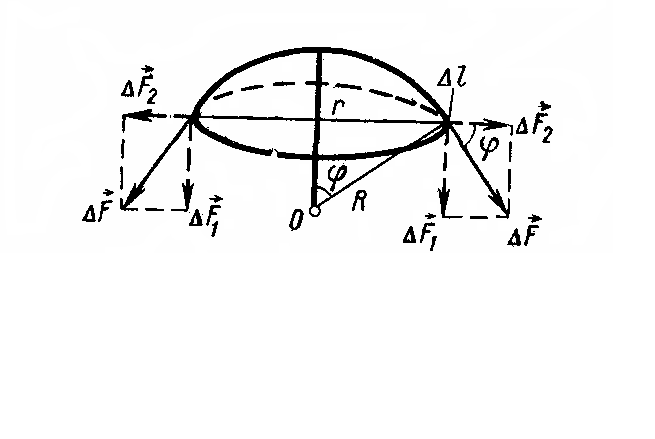
Вычислим
дополнительное давление для сферической
поверхности жидкости радиусом R.
Для этого рассечем мысленно жидкость
плоскостью и выделим шаровой сегмент,
ограниченный от остальной поверхности
жидкости окружностью радиусом
(рис. 4.7.5).
Рис.
4.7.5.
На
каждый элемент длины
этой окружности в направлении, касательном
к поверхности сегмента, действует сила
поверхностного натяжения
Разложим
силу
на две составляющие, одна из которых
лежит в плоскости сечения, а другая
направлена перпендикулярно к ней. Эти
составляющие силы будут соответственно
равны
и
Очевидно,
геометрическая сумма составляющих
для всего периметра окружности,
ограничивающей рассматриваемый сегмент,
будет равна нулю. Составляющие
в сумме дадут равнодействующую,
направленную по нормали к плоскости
сечения и равную
Равнодействующая
сил поверхностного натяжения будет
прижимать рассматриваемый сегмент к
остальной части жидкости по всей
разделяющей их поверхности
.
Значит, дополнительное давление внутри
жидкости, создаваемое силами поверхностного
натяжения и обусловленное кривизной
ее поверхности, равно
(4.7.7)
Отметим,
что поскольку в формулу не входит r,
то, как и следовало ожидать, дополнительное
давление
не зависит от того, в каком месте
поверхности Жидкости выделен шаровой
сегмент.
Для
вогнутой поверхности ее центр кривизны
О лежит вне жидкости. Повторяя для этого
случая весь предыдущий вывод, нетрудно
найти, что
(4.7.8)
т.
е. под вогнутой поверхностью давление
внутри жидкости меньше, чем в случае
плоской поверхности на Δр.
Если радиусу R
кривизны поверхности приписывать знак
плюс, когда он лежит внутри жидкости
(выпуклая поверхность) и знак минус,
когда он лежит вне жидкости (вогнутая
поверхность), то формулы (4.7.7) и (4.7.8) можно
объединить в одну:
(4.7.9)
В
общем случае, когда поверхность жидкости
отличается от сферической, кривизну
поверхности характеризуют средней
кривизной, которая может иметь разное
значение для различных точек поверхности.
Среднюю кривизну поверхности в данной
точке определяют через кривизну
нормальных сечений, т. е. через кривизну
линий пересечения поверхности с взаимно
перпендикулярными плоскостями,
проходящими через нормаль к поверхности
в рассматриваемой точке. При этом под
кривизной кривой понимают величину,
обратную ее – радиусу кривизны. Например,
для сферы любое нормальное сечение
представляет собой окружность радиусом
R,
а величина Н = 1/R
будет ее кривизной. Полусумма обратных
радиусов кривизны нормальных сечений
и характеризует среднюю кривизну
поверхности в данной точке:
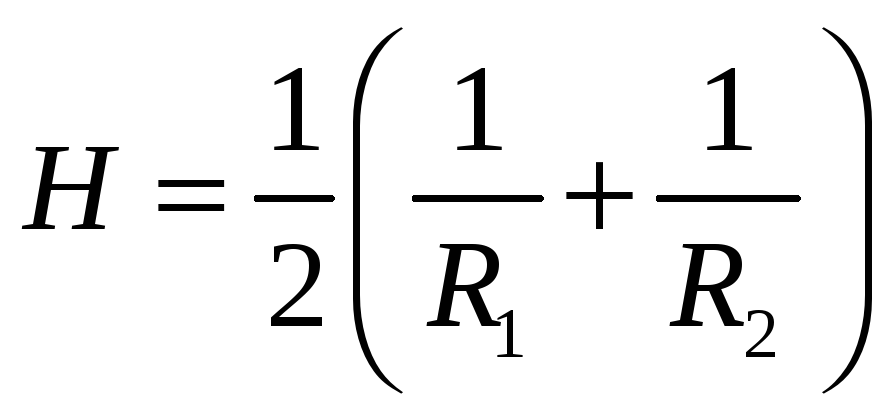
Лаплас
доказал, что формула (4.7.10) справедлива
для поверхности
любой
формы, если ее записать в форме
,
(4.7.11)
где
Н —
средняя кривизна поверхности в той
точке, под которой
определяется
дополнительное давление Δр.
Эта
формула получила название формулы
Лапласа.
Иначе ее можно
записать
в виде
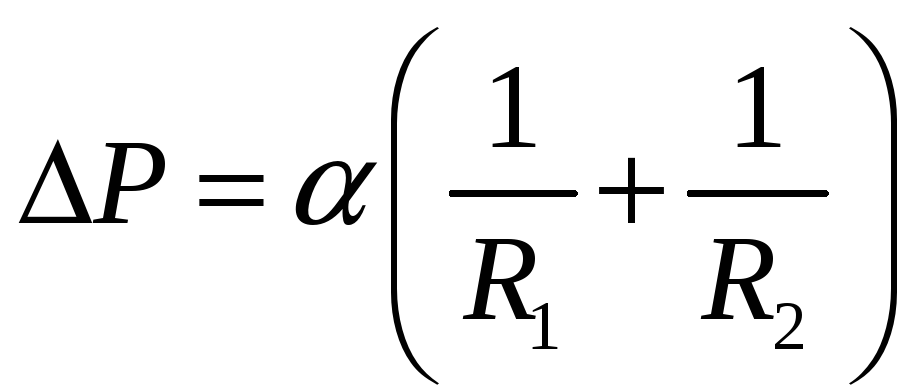
для
плоской поверхности R1
и R2
,
а следовательно и дополнительное
давление Δр,
часто называемое лапласовским, будет
равно нулю.
Свойства
поверхности жидкости могут существенно
изменяться при скоплении на ней
посторонних веществ. Процесс
концентрирования веществ из газа или
раствора, происходящий на поверхности
жидкости, называют адсорбцией. Изменение
свойств поверхности жидкости особенно
заметно в тех случаях, когда силы
взаимодействия между молекулами
адсорбируемого вещества значительно
отличаются от сил взаимодействия между
молекулами самой жидкости.
Если
молекулы постороннего вещества
взаимодействуют между собой более
сильно, чем с молекулами жидкости, то
жидкость вытесняет их в поверхностный
слой. Естественно, что они плохо
растворяются и их концентрация на
поверхности жидкости оказывается
больше, чем в объеме жидкости. Такие
вещества называют поверхностно-активными.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Surface tension is the ability of fluid surfaces to contract into the smallest possible surface area. Have you ever found that even after filling a glass full of water, you can only add a few more drops before it spills? Have you ever lost a thermometer and watched how the mercury reacts as it falls? All of which are caused by the surface tension of the surface. Its isolated surface behaves like a strong rubber membrane due to the suppressive force in the fluid molecules. As a result, the individual surface of the fluid is still in a state of stress and tends to have the smallest field. Thus, Surface Tension refers to the tension on the fluid’s individual surface.
Let’s discuss more surface tension in detail in this article.
Surface Tension Definition
Surface tension is described as the phenomenon that occurs when the surface of a liquid comes into contact with another phase (it can be a liquid as well). Liquids appear to have the smallest possible surface area. The liquid’s surface looks like an elastic sheet.
Imagine a line XY (as shown in the figure below) on the independent surface of the fluid in the equilibrium, then at every point on this line, the same force acts in its exact opposite direction. Every point stretched with the same force in both directions.
Thus, in the equilibrium, a force acting on any other per unit length of an imaginary line on an independent surface of the fluid, which is perpendicular to the line and in the direction of the tangent line of the surface, is called Surface Tension.
Surface tension is denoted by σ or T symbol.
Cohesion and Surface Tension
Surface Tension at liquid molecules is generated by the cohesion force among the atoms of the liquid. The cohesion force is the attractive force between two particles of Solid and Liquid. Cohension force is the force required to hold the solid and liquid particles together.
Surface Tension is the property of the substance because of the cohesion forces. The surface tension resists the change in the structure of the surface.
Surface Tension at Molecular Level
Due to the Cohesion force the water molecule tends to stick together. The water molecule at the bottom layer has various molecules above them to stick but the molecule at the top layer does not have various other molecules to cling together. Thus, they attach to each other with a larger force and resist any change in their structure.
The molecule inside the body of the liquid experiences the forces from all directions and thus, the net force cancels out each other, whereas the particle at the top layer experiences a strong inward force resulting in the surface tension of the water. Because of this water has one of the highest surface tension among liquids.
Formula for Surface Tension
Mathematically, the surface tension is defined as the force (F) acting on the surface and the length (l) of the surface, so is given as:
T = F / l
Also, the ratio of the work done (W) and the change in the area of the surface (A) is termed surface tension.
T = W / A
Unit of Surface Tension
Surface tension is the ratio of the dragging force to the length and thus its SI unit is N/m as force is measured in N and length is measured in m. In the CGS system, its unit is Dyne/cm.
Dimension of Surface Tension
The dimension formula of Force is [MLT-2] whereas the dimension of length is [L] thus, the dimensional formula of Surface Tension is [M L0 T-2].
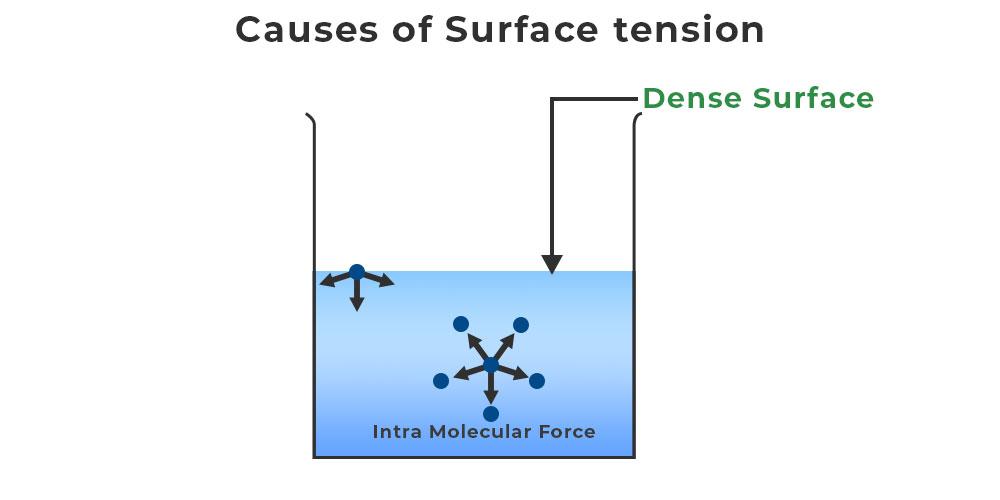
What is the Causes of Surface Tension?
The effect known as surface tension is caused by the cohesive forces between liquid molecules. Since the molecules at the surface lack like molecules in both directions, they cohere more closely to those specifically aligned with them on the surface. This creates a surface “film” that makes moving an object across the surface more difficult than moving it while fully submerged.
Assume a jar is filled with water; the water molecules can be found in two positions in this jar: First, beneath the water, and second, on the surface of the water. Since there are no molecules above these molecules, the molecules at the water’s surface are unbalanced. As a result, only the molecules below will be attracted. As a result, a thin crust will form on the liquid’s upper surface. Because of this thick layer, a form of stress is generated, which is known as Surface Tension. These phenomena can also be explained in terms of energy.
How to Calculate Surface Tension?
The surface Tension of any substance can easily be calculated using the surface tension formula as discussed above in the article. Let’s take an example to understand the calculation of Surface Tension in detail.
Example: Find the surface tension of the liquid with a dragging force of 12 N when the length at which the force acts is 4 m.
Solution:
Given,
F = 12 N
L = 4 mAccording to the Surface Tension formula, T = F/L
T = 12/4
T = 3 N/m
Methods of Measurement
Various methods which are used to measure the surface tension of any liquid are,
- Capillary Rise Method
- Bubble Pressure Method
- Spinning Drop Method
- Du Noüy–Padday Method
- Du Noüy Ring Method
- Stalagmometric Method
- Sessile Drop Method
Other than these there are various other methods that are used for measuring the surface tension of the liquids.
What is Surface Energy?
Surface energy measures the breakdown of intermolecular bonds caused by the formation of a surface. Surface-free energy and interfacial-free energy are other names for it. Surface energy is defined as the work done per unit area by the force that forms the new surface.
The image given below shows the surface of the water molecules.
When the free surface area of a liquid is increased, effort must be done against the force of surface tension. This work is stored as potential energy on the liquid surface. This increased potential energy per unit area of the free surface of the liquid is referred to as surface energy.
Mathematically, the surface energy is defined as:
Surface energy = Surface tension × Change in the surface area
or
ES = T × ΔA
where T denotes surface tension and ΔA denotes an increase in surface area.
Therefore, the SI unit of surface energy is Nm-2 and the dimensional formula is [MT– 2].
What is Angle of Contact?
The angle of contact is defined as the angle subtended between the tangents drawn at the liquid surface and the solid surface within the liquid at the point of contact, or it is defined as the angle subtended between the tangents drawn at the liquid surface and the solid surface within the liquid at the angle of contact (θ).
The angle of contact depends on the following factors:
- The nature of the liquid, the solid with which it comes into contact.
- The medium that exists above the free surface of the liquid.
- As the temperature of the liquid rises, so does the angle of contact.
- When soluble impurities are added to a liquid, the angle of contact drops.
Examples of Surface Tension
Various examples which are explained with the help of Surface tension are,
Walking on Water
Various insects can easily walk on the surface of the water because the force of their weight is not enough to penetrate the surface of the water.
Floating Needle
A needle made of steel can easily be made to float on the surface of the water even though it is many times denser than water because of the surface tension of the water.
Spherical Shape of Water Droplets
Small droplets of fluid are spherical due to surface tension. The molecules of water tend to stick together due to intramolecular force, and the energy of molecules that are located on the surface of droplets contains higher energy and try to push the other molecule to the centre of the droplet. Due to this the drop makes the shape that contains the least surface area and the spherical shape is best for the least surface area, that’s why The droplets of water and raindrops are spherical.
Fire Polishing of Glass
The method of polishing glass or thermoplastic with the help of fire or flame is called Fire Polishing. When we heat a glass material in flames, the glass surface starts melting. But due to surface tension, it starts to become soft and smooth which makes the glass very flat and smooth. This method is most applicable to flat external surfaces. Flame polishing is frequently in acrylic plastic fabrication because of its high speed compared to abrasive methods. In this application, an oxyhydrogen torch is typically used, one reason being that the flame chemistry is unlikely to contaminate the plastic.
Soaps and Detergents
Soaps and Detergents can easily clean clothes because they lower the surface tension of the water and thus allowing it to easily soak the grease and soil particles and then remove them.
Rise of Liquids in Capillary Tubes
A tube whose radius is very short and uniform is called a capillary tube. When an open capillary is dipped in water. The water rises to some height in the capillary tube.
Factors affecting Surface Tension
Various factors which affect the Surface Tension of any liquid are,
- If the solute is highly soluble in the fluid, the surface tension of the fluid would increase. And if the solute is less soluble in the fluid, then the surface tension of the fluid would decrease.
- If there are dust particles or any lubricant present on the surface of the fluid, the surface tension of the fluid decreases.
- Increasing the temperature reduces the surface tension of the fluid. And decreasing the temperature increases the surface tension.
Solved Example on Surface Tension
Example 1: Find the surface tension of the liquid with a dragging force of 20 N when the length at which the force acts is 5 m.
Solution:
Given,
F = 20 N
L = 5 mAccording to the Surface Tension formula, T = F/L
T = 20/5
T = 5 N/m
Thus, the surface tension of the liquid is 5 N/m
Example 2: Find the dragging force on the 2 m surface of the liquid if the surface tension is 10 N/m
Solution:
Given,
T = 10 N/m
L = 2 mAccording to the Surface Tension formula, T = F/L
10 = F / 2
F = 10 × 2
F = 20 N
Thus, the dragging force is 20 N.
Example 3: Find the surface tension of the liquid with a dragging force of 26 N when the length at which the force acts is 2 m.
Solution:
Given,
F = 26 N
L = 2 mAccording to the Surface Tension formula, T = F/L
T = 26/2
T = 13 N/m
Thus, the surface tension of the liquid is 13 N/m
Example 4: Find the dragging force on the 3 m surface of the liquid if the surface tension is 9 N/m
Solution:
Given,
T = 9 N/m
L = 3 mAccording to the Surface Tension formula, T = F/L
9 = F / 3
F = 9 × 3
= 27 N
Thus, the dragging force is 27 N.
Related Articles
- Surface Energy
- Viscosity
- Bernoulli’s Principle
FAQs on Surface Tension
Question 1: What is Surface Tension?
Answer:
The attraction caused by the particles of any liquid at their surface that tends to resist the change is called as Surface Tension. It is the force applied on the surface of liquid per unit of its length.
Question 2: What is the Unit of Surface Tension?
Answer:
The SI unit of Surface Tension is N/m whereas in CGS system it is measured in dyn/cm
Question 3: When the temperature is increased what happens to the surface tension of the water?
Answer:
The increase in the temperature decreases the surface tension of the water as increasing the temperature increases the kinetic energy of the molecules and thus the intermolecular attraction decreases.
Question 4: What is the origin of Surface Tension?
Answer:
The effect known as surface tension is caused by the cohesive forces between liquid molecules. Since the molecules at the surface lack like molecules in both directions, they cohere more closely to those specifically aligned with them on the surface. This creates a surface “film” that makes moving an object across the surface more difficult than moving it while fully submerged.
Question 5: Why soap is helpful in cleaning clothes?
Answer:
Soap reduces the surface tension of water. So water penetrates into small areas of clothing and removes stains. So soap is helpful for washing clothes.
Что такое поверхностное натяжение жидкости
Поверхностное натяжение — характеристика поверхности раздела двух фаз, которые находятся в равновесии. Характеристика определяется работой образования единицы площади этой поверхности раздела.
Выражается произведением:
(mathcal F=sigmamathcal l), Н
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(sigma) — коэффициент поверхностного натяжения, Н/м
(mathcal l) — длина, м
Направление силы: по касательной к поверхности.
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения ((sigma)) — сила, которая действует на единицу длины линии, ограничивающей поверхность жидкости (Н/м).
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью (S) при постоянной температуре.
(sigma=frac{{mathcal F}_{пов}}{mathcal l} )
(sigma=frac{{mathcal F}_{пов}}{mathcal S})
(mathcal S) — площадь поверхности жидкости
Зависит от:
- Рода жидкости и ее свойств.
- Температуры (чем больше температура, тем меньше натяжение).
- Наличия ПАВ (поверхностно-активных веществ. Например, мыло).
- Присутствия каких-либо примесей.
- Свойств газа, контактирующего с жидкостью.
Чем вызвано поверхностное натяжение
Причина возникновения явления поверхностного напряжения: молекулы, которые составляют верхний слой жидкости. Они создают взаимодействие между собой, возникает натяжение.
Жидкости стремятся принять форму, которая требует минимальной площади поверхности.
Силы поверхностного натяжения
Силы поверхностного натяжения работают вдоль поверхности жидкости перпендикулярно контуру. Сокращают ее площадь. Это похоже на пленку, которая стягивает объем. На сам объем силы не оказывают влияние.
Примеры в окружающей среде
- движение водомерки по воде (ее лапки покрыты воскообразным веществом);
- капля росы, дождя, из пипетки;
- цилиндрическая форма струи воды;
- мыльный пузырь.
Расчет поверхностного натяжения в задачах
Задача 1
Дано
Имеется пипетка с диаметром отверстия (d=2) мм. В ходе опыта выяснилось, что (40) капель имеют массу равную (1,9) г. Вычислите коэффициент поверхностного натяжения.
Решение
Найдем массу одной капли и длину окружности.
(mathcal m=frac{{mathcal m}_{общ}}{mathcal n}\)
(mathcal l=mathrmpimathcal d\)
Напишем условие равновесия капли из пипетки.
({mathcal m}_0mathcal g=mathcal F\)
Подставим формулы.
(frac{mathcal m}{mathcal n}mathcal g=sigmamathrmpimathcal d\)
Выразим коэффициент поверхностного натяжения.
(sigma=frac{mathcal{mg}}{mathcal nmathrmpimathcal d}=frac{1,9ast10^{-3}ast10}{40ast3,14ast2ast10^{-3}}=75,6ast10^{-3};Н/м\)
Ответ: (75,6ast10^{-3};Н/м\)
Задача 2
Дано
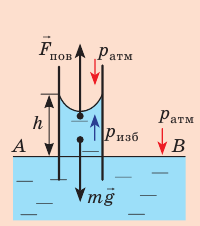
Сосуд со ртутью имеет отверстие диаметром 70 мкм. Возможно ли без измерения определить максимальную высоту слоя ртути, при которой она не будет вытекать через отверстие?
Решение
Ртуть начнет вытекать тогда, когда произойдет увеличение силы ее давления относительно силы поверхностного натяжения.
(mathcal{pS}=mathcal F\rhomathcal{ghS}=sigmamathcal l\)
Выразим высоту.
(mathcal k=frac{sigmamathcal l}{rhomathcal{gS}}=frac{sigmamathrmpimathcal d}{rhomathcal g{displaystylefrac{mathrmpimathcal d^2}4}}=frac{4sigma}{rhomathcal{gd}}=frac{4ast472ast10^{-3}}{13600ast9,8ast70ast10^{-6}}=0,2;м\\)
Ответ: (0,2) м
Задача 3
Дано
Есть игла длиной (3,5) см и массой (0,3) г. Сможем ли мы произвести следующее действие: положить иголку на поверхность воды. Или же она утонет? Какие силы действуют на иголку?
Решение
На иглу действует сила тяжести. Если мы найдем ее и сравним с силой поверхностного натяжения, то узнаем ответ.
({mathcal F}_{тяж}=mathcal{mg}=0,3ast10^{-3}ast9,8=2,9ast10^{-3};Н\\\\)
({mathcal F}_{пн}=sigmamathcal l=73ast10^{-3}ast3,5ast10^{-2}=2,5ast10^{-3};Н\\\\\\\\)
Сравниваем силы и видим, что значение силы тяжести больше величины поверхностного натяжения.
Ответ: Игла утонет.
Задача 4
Почему возникают сложности с тем, чтобы снять мокрые перчатки с рук?
Ответ: Молекулы воды взаимодействуют с молекулами перчатки. По этой причине мы чувствуем сопротивление при стягивании перчаток с рук.
Задача 5
Дано
Есть капиллярная трубка ((R=0,5) мм). В ней столб жидкости высотой 11 мм. Определите плотность жидкости, если (sigma=22;мН/м.\\\\)
Решение
Воспользуемся формулой для капилляра.
(rho=frac{2sigmacosleft(alpharight)}{mathcal{hrg}}\\\\)
(alpha-угол;смачивания;жидкостью;стенки;капилляра.;Возьмем;за;90^circ\\\\)
(rho=frac{2,22ast10^{-3}ast1}{11ast10^{-3}ast0,5ast10^{-3}ast10}=800;кг/м^3\\\\)
Ответ: (800 кг/м^3\\\\)
Задача 6
Дано
Алюминиевое кольцо массой 7 г и радиусом 7,8 см соприкасается с мыльным раствором. Какую силу нужно приложить, чтобы оторвать кольцо от жидкости? Раствор имеет комнатную температуру.
Решение
Помимо натяжения на кольцо действует внешняя сила и сила тяжести.
Важно то, что кольцо соприкасается жидкости двумя сторонами. Умножаем на 2.
({mathcal F}_{пн}=2sigmamathcal l\mathcal l=2mathrm{πR}\{mathcal F}_{mathrm{пн}}=4mathrm{πσR}\\\\)
(mathcal F=mg+4mathrm{πσR}\mathcal F=7ast10^{-3}ast9,8+4mathrmpiast4ast10^{-2}ast7,8ast10^{-2}=0,11;mathrm Н\\\)
Ответ: 11 Н






















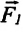


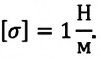
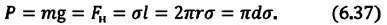
 — радиус капилляра,
— радиус капилляра, 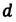 — диаметр капилляра.
— диаметр капилляра.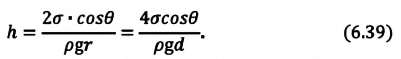
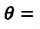
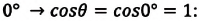

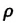 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
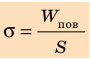
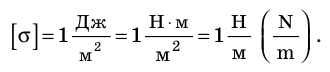
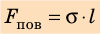
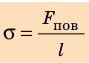



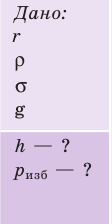
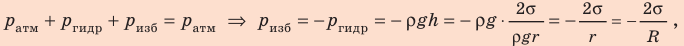
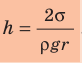 .
.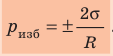 .
.

.png)

