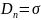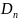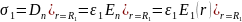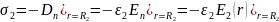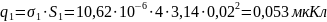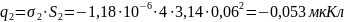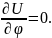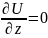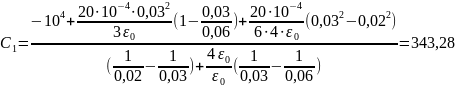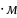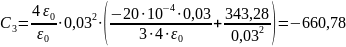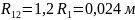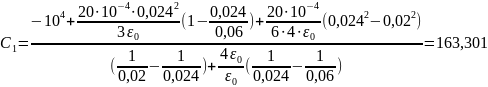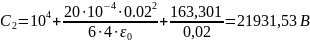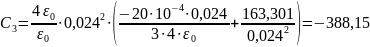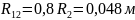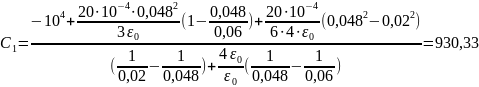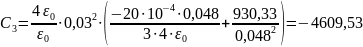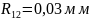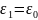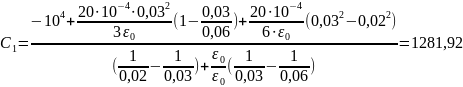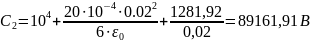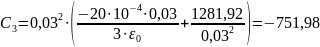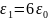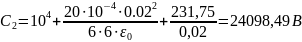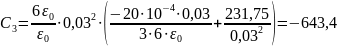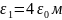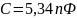Как найти поверхностную плотность заряда конденсатора

Как найти поверхностную плотность заряда на пластинах конденсатора

Решение:

Напряженность поля двух пластин

(1)

Связь диэлектрической проницаемости и диэлектрической

(2)

Выразим напряженность через напряжение и расстояние

(3)

Отсюда поверхностная плотность свободных зарядов с диэлектриком

Связь между поляризованностью и напряженностью электрического поля

Поляризованность равна поверхностной плотности связанных зарядов

Ответ: а)

б)

в)

г)

(у Волькенштейн В.С. ответ для χ дан в Гауссовой системе

Источник

Электрическое поле в конденсаторе: что, как, типы, когда, почему и подробные факты

Конденсатор представляет собой устройство, которое накапливает электрический заряд в виде разности потенциалов между двумя пластинами и электрического поля в конденсаторе при приложении источника напряжения.

Разность потенциалов создается переносом электронов от положительной клеммы к отрицательной клемме конденсатора и созданием электрического поля в конденсаторе. Эта разность зарядов хранит электрическую энергию в виде потенциала заряда и пропорциональна плотности заряда на каждой пластине.

Электрическое поле в формуле конденсатора

Подобно положительным и отрицательным зарядам, пластина конденсатора также ведет себя как акцепторная и донорная пластина, когда источник проходит через пластины конденсатора. Положительный вывод конденсатора будет отдавать электрон, и эти свободные электроны будут приняты отрицательным выводом конденсатора.

Из-за подвижности свободных зарядов внутри конденсатора будет введен электрический поток и полное электрическое поле в конденсаторе будет

Плотность заряда каждой пластины конденсатора называется поверхностной плотностью, которая определяется как заряд, присутствующий на поверхности пластины на единицу площади, и выражается как σ =В/О.

Следовательно,

Это уравнение дает электрическое поле, создаваемое между двумя пластинами конденсатора.

Электрическое поле внутри конденсатора

Конденсатор состоит из двух обкладок с разной плотностью заряда. электрический поток проходит через обе поверхности каждой пластины, следовательно, площадь = 2A.

Рассмотрим две пластины, имеющие положительную плотность поверхностного заряда и отрицательную плотность поверхностного заряда, разделенные расстоянием d. Пусть А — площадь пластин. Линия электрического потока проходит от положительно заряженной пластины к пластине с большинством отрицательных носителей, как показано на рисунке ниже.

Пусть P будет любой точкой посередине двух заряженных пластин конденсатора.

Применяя закон Гаусса,

Электрическое поле, создаваемое одной заряженной пластиной конденсатора, равно

Мы знаем, что σ = Q/A

Используя это в приведенном выше уравнении

Следовательно, результирующее электрическое поле в любой точке между пластинами конденсатора будет складываться.

Подставляя значение для σ, мы получаем

Это полное электрическое поле внутри конденсатора из-за двух параллельных пластин.

Какое электрическое поле создает плоский конденсатор с площадью поверхности 0.3 м? 2 и несущий заряд 1.8С?

Данный: д=1.8°С

У нас есть

= 0.68 х 10 12 В / м

Электрическое поле, создаваемое параллельным конденсатором с зарядом 1.8 Кл, составляет 0.68 х 10 12 В / м.

Электрическое поле вне конденсатора

Теперь, если точка P лежит вне конденсатора, то электрическое поле в точке P из-за пластины, имеющей положительно заряженную поверхностную плотность, равно

Принимая во внимание, что электрическое поле в точке P из-за отрицательного заряда пластины поверхностной плотности конденсатора равно

Следовательно, суммарное электрическое поле, создаваемое обеими пластинами конденсатора, равно

Э=Э₁+E₂

В любой точке вне конденсатора электрическое поле всегда равно нулю. Потому что при подаче электрического тока через конденсатор один вывод конденсатора будет иметь положительную поверхностную плотность заряда, а другой — отрицательную.

Электрическое поле в конденсаторе с диэлектриком

Теперь мы знать, что в присутствии вакуума, электрическое поле внутри конденсатора равно E=σ/ε₀ , разность потенциалов между двумя пластинами равна V=Ed, где d — расстояние, разделяющее две пластины, и, следовательно, емкость в этом случае равна

С= Q/V = ε₀Объявление

Теперь, если мы поместим диэлектрик между двумя пластинами конденсатора с поляризацией, занимающий все пространство между двумя пластинами, поверхностные плотности заряда двух пластин равны +σ_p и –σ_n. Таким образом, суммарная плотность поверхностного заряда обеих пластин равна

Следовательно, электрическое поле через конденсатор равно

Таким образом, разность потенциалов становится

Для линейных диэлектриков

Итак,

Где k является диэлектрической проницаемостью и больше 1, т.е. k>1.

Следовательно, разность потенциалов теперь становится

Вставка значения поверхностной плотности заряда

Следовательно, емкость конденсатора равна

ε₀k — диэлектрическая проницаемость среды и обозначается как ε

Поэтому уравнение теперь становится

Чему равны электрическое поле и разность потенциалов конденсатора в присутствии диэлектрической среды с проницаемостью 6×10? -12 C 2 N -1 m -2 шириной 3 см при плотности поверхностного заряда 6 Кл/м 2 и -5.8 Кл/м 2 ?

Данный: σ_p=6 Кл/м 2

ε₀= 6 x 10 -12 C 2 N -1 m -2

Электрическое поле конденсатора равно

Электрическое поле конденсатора равно 3.3 х 10 10 В/м, поэтому разность потенциалов между обкладками конденсатора равна

= 3.3 х 10 10 х 0.03

Разность потенциалов между двумя пластинами конденсатора составляет 0.1 х 10 10 V.

Последовательный конденсатор электрического поля

При последовательном соединении конденсаторов разность потенциалов между обкладками складывается. Если у нас есть два конденсатора C₁ и C₂ соединены последовательно, а разность потенциалов на пластинах равна V₁ и V₂ соответственно, тогда чистая разность потенциалов становится

Используя это в приведенном выше уравнении, мы получаем

Решение этого дальше

Разность потенциалов также равна V=Ed

Следовательно, электрическое поле из-за последовательно соединенных конденсаторов можно рассчитать как

Е= В/д

Если есть n конденсаторов, соединенных последовательно, то электрическое поле на n конденсаторах будет равно

Электрическое поле в цилиндрическом конденсаторе

Цилиндрический конденсатор состоит из двух цилиндрических пластин. Внутренний цилиндр имеет положительную плотность поверхностного заряда +σ радиуса «r», а внешний цилиндр имеет отрицательную плотность поверхностного заряда –σ радиуса «R».

Электрический поток проходит от поверхности внутреннего цилиндра к внешнему цилиндру, как показано на рисунке выше. На рис. (б) показано поперечное сечение цилиндрического конденсатора. Пусть ds — поверхность Гаусса в середине двух заряженных цилиндров.

Электрическое поле внутри внутреннего цилиндра равно нулю, так как через эту область нет электрического потока, а также снаружи цилиндра радиуса R также равно нулю. Электрический поток течет между двумя цилиндрами на расстоянии s от центра.

Электрический поток через гауссову поверхность ds определяется выражением

Следовательно,

Это уравнение дает электрическое поле, создаваемое цилиндрическим конденсатором.

Чему равно электрическое поле в точке, удаленной на 0.6 см от центра цилиндрического конденсатора высотой 2 см, имеющего внешний радиус 0.8 см и внутренний радиус 0.35 см, несущего заряд 5 Кл?

Данный: г = 0.35 см = 0.0035 м

Р = 0.8 см = 0.08 м

S = 0.6 см = 0.06 м

У нас есть,

= 74.62 х 10 12 В / м

Электрическое поле конденсатора на расстоянии 0.6 см от центра цилиндрического конденсатора равно 74.62 х 10 12 В / м.

Напряженность электрического поля в конденсаторе

Напряженность электрического поля вне области заряженного конденсатора всегда равна нулю, так как носители заряда присутствуют на поверхности конденсатора.

Во внутренней области конденсатора напряженность электрического поля равна отношению плотности поверхностных носителей заряда, а проницаемость среды в этой области одинакова во всех точках внутри конденсатора.

Где σ — поверхностная плотность заряда носителей заряда, присутствующих на пластине конденсатора, а

ε₀ проницаемость среды

Кроме того, электрическое поле можно рассчитать, измерив разность потенциалов между двумя пластинами и найдя расстояние между пластинами как

Где V — разность потенциалов между обкладками конденсатора и

d — расстояние между двумя пластинами

Электрическое поле в сферическом конденсаторе

Подобно цилиндрическому конденсатору, сферический конденсатор также состоит из двух сфер, имеющих противоположные носители заряда на поверхности каждой сферы.

Рассмотрим сферу радиуса ‘R₂‘ с плотностью поверхностного заряда как +σ и другой сферой радиуса ‘R₁‘ плотности поверхностного заряда –σ, покрывающего малую сферическую оболочку.

Электрический поток течет от сферы, состоящей из положительной поверхностной плотности заряда, к внешней сфере. Рассмотрим гауссову поверхность «ds» в середине двух сферических поверхностей на расстоянии «r» от центра сфер. Пусть заряд равен q на поверхности Гаусса. Применяя закон Гаусса

S — площадь поверхности, равная 4πr 2 , следовательно, мы получаем

Электрическое поле в сферическом конденсаторе равно

Разность потенциалов между двумя заряженными сферами равна

Мы нашли электрическое поле сферического конденсатора, поэтому подставим его в это уравнение.

Следовательно, емкость сферического конденсатора равна

Подставив значение разности потенциалов, получим

Это уравнение дает емкость сферического конденсатора.

Часто задаваемые вопросы

Чему равно электрическое поле заряженного шара радиусом 3 см, несущего заряд 4 Кл?

Данный: г=3 см=0.03 м

Электрическое поле внутри сферы E=0.

Площадь поверхности шара равна

Следовательно, поверхностная плотность заряда шара равна

Поэтому электрическое поле заряженного шара равно

= 45.2 х 10 12 В / м

Игровой автомат электрическое поле на поверхности и в точке вне сферы 45.2 х 10 12 В / м.

Чему равно электрическое поле сферического конденсатора на расстоянии 4 см от центра, имеющего внутренний радиус 3 см и внешнюю сферу 5 см, несущую заряд 2 мКл?

Данный: R₁=3 см=0.03 м

Электрическое поле на гауссовой поверхности на расстоянии 0.04 м от центра сферического конденсатора равно

= 11.23 х 10 6 В / м

Емкость сферического конденсатора равна

Привет, я Акшита Мапари. Я сделал M.Sc. по физике. Я работал над такими проектами, как Численное моделирование ветра и волн во время циклона, Физика игрушек и механизированных острых ощущений в парке развлечений на основе классической механики. Я прошел курс по Arduino и выполнил несколько мини-проектов на Arduino UNO. Мне всегда нравится исследовать новые области в области науки. Лично я считаю, что обучение проходит с большим энтузиазмом, если учиться с творчеством. Кроме того, я люблю читать, путешествовать, играть на гитаре, определять горные породы и пласты, фотографировать и играть в шахматы. Свяжись со мной в LinkedIn — linkedin.com/in/akshita-mapari-b38a68122

Последние посты

NaOH — сильное неорганическое основание с молекулярной массой 40 г/моль. Давайте обсудим больше NaOH в следующей статье. NaOH является основанием щелочного металла, поэтому природа основания очень сильная. Это ион.

MgSO4 широко используется в качестве реагента в удобрениях для уменьшения дефицита магния в почве. Подробнее о характеристиках сульфата магния поговорим ниже. MgSO4 выглядит как белые кристаллы.

О НАС

Мы являемся группой профессионалов отрасли из различных областей образования, таких как наука, инженерия, английская литература, и создаем универсальное образовательное решение, основанное на знаниях.

Источник

0 Пользователей и 1 Гость просматривают эту тему.

---

---

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Для определения
поверхностной плотности заряда
воспользуемся одним из граничных
условий:

,
где

–
нормальная к поверхности электрода
часть электрического смещения.

Учитывая симметрию
поля относительно оси конденсатора
получаем, что на внутреннем электроде
поверхностная плотность заряда
определяется выражением:
(1)

Подставляя числа,
получим:

Аналогично получим
поверхностную плотность заряда на
внешнем электроде, с учётом знака

,
так как вектор

направлен к внешнему электроду:

(2)

Подставляя значения,
получим:

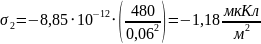
Найдем заряды
электродов и суммарный заряд конденсатора

(3)

(4)

Суммарный заряд
конденсатора равен сумме зарядов на
обкладках конденсатора:

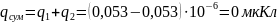
Ёмкость определяется
следующим образом:

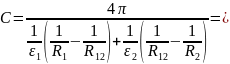
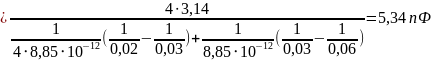
Часть 2. Расчёт электрического поля в пространстве между электродами сферического конденсатора с объёмным зарядом.

2.1. Расчёт потенциала и напряжённости поля в конденсаторе.

Дано:

					, кВ	ρ, 10—4 Кл/м3
0,02	0,06	0,03			10	20

Решение:

Область расчёта
электрического поля конденсатора
представляет собой пространство между
его электродами и состоит из двух
подобластей: 1 – внутренний слой
диэлектрика и 2 – внешний слой. Согласно
условию задачи, во внутреннем слое
диэлектрика присутствует объёмный
заряд, и распределение потенциала
находится с помощью уравнения Пуассона.
Принимая во внимание условие, что поле
конденсатора изменяется вдоль координаты,
перпендикулярной поверхности электродов
(координаты r) выбираем сферическую
систему координат для записи уравнения:

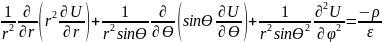
Учитывая симметрию
поля относительно оси конденсатора,
принимаем E_φ=0
и, следовательно,

Кроме того, поле сферического конденсатора
является плоскопараллельным (картина
поля во всех плоскостях, перпендикулярных
оси конденсатора, одинакова), и,
следовательно, E_z=0
и

.
Таким образом, уравнение Пуассона
принимает вид:

Для внешнего слоя
распределение потенциала находится с
помощью уравнения Лапласа, так как там
нет объёмного заряда. И оно принимает
вид:

Рассмотрим
зависимость потенциала от радиуса
сферы.

Вследствие наличия
между обкладками двухслойного диэлектрика
необходимо рассмотреть два случая.
Однако, так как во внутреннем слое
присутствует объёмный заряд, то
зависимости будут различными.

При

≤ r
≤
:

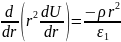
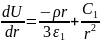
При

≤
r
≤

после двукратного интегрирования
уравнения Лапласа по переменной r
получаем функцию:

При этом, используя
формулу

находим распределение
напряжённости электрического поля:

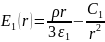
Для
определения постоянных интегрирования

воспользуемся
граничными условиями:

1.
При r=

потенциал
равен U=
,
тогда:

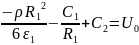
2.
При r=

потенциал равен U=
,
тогда:

3.
При r=

на границе раздела двух диэлектриков
нормальные составляющие вектора
электрического смещения равны, тогда:
D_1n=D_2n→

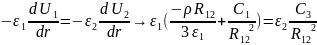
4.
При r=

на границе раздела двух диэлектриков
потенциалы

и

равны, тогда:

;

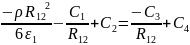
Запишем систему
уравнений для нахождения постоянных:

(1)

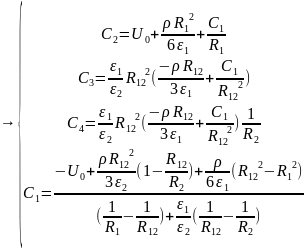
Подставим численные
значения:

В

;

;

В
;

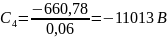
Таким образом,
выражения распределения
потенциала и напряжённости
электростатического поля между
электродами сферического конденсатора
будет иметь вид:

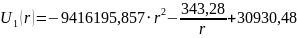
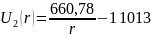
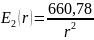
Для определения
поверхностной плотности заряда на
электродах, воспользуемся формулами
(1) и (2), которые представлены в пп1.3:

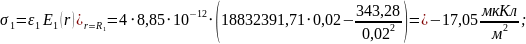
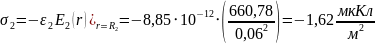
Для определения
заряда на электродах, воспользуемся
формулами (3) и (4), которые представлены
в пп1.3:

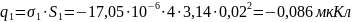
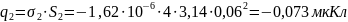
Для нахождения
объемного заряда, распределенного во
внутреннем слое диэлектрика, найдем
объем данной области:

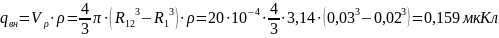
Суммарный
заряд конденсатора равен сумме зарядов
на обкладках конденсатора и заряда,
распределенного во внутреннем слое
диэлектрика:

Максимальное
по модулю значение напряженности поля
конденсатора достигается при

:
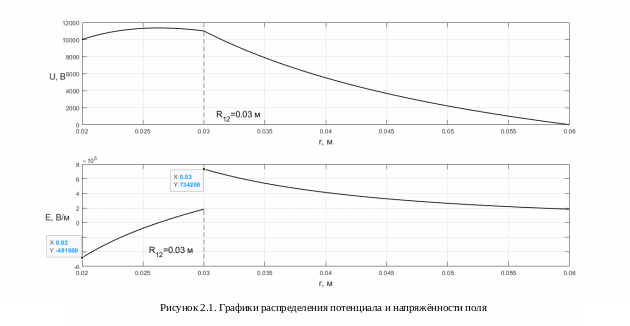
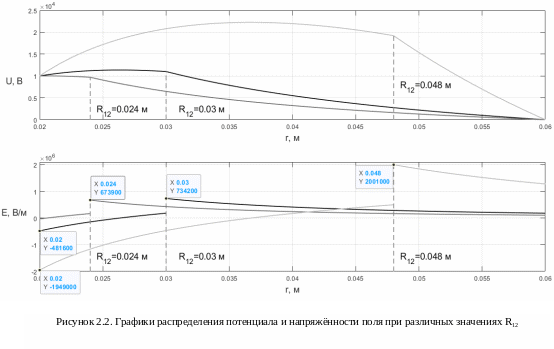
|E_max|=734200 В/м.

2.2. Расчёт потенциала и напряжённости
при изменённом значении радиуса границы
раздела R₁₂ (R₁₂ =
1,2R₁ и R₁₂ = 0,8 R₂).

Используем
выражениями для постоянных интегрирования
из п. 2.1
и подставим

:

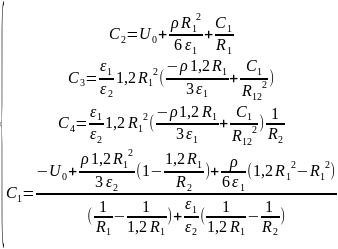
Подставим численные
значения:

В
;

;

В
;

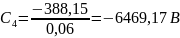
Таким
образом, выражения распределения
потенциала и напряжённости
электростатического поля между
электродами сферического конденсатора
будет иметь вид:

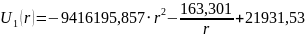
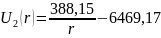
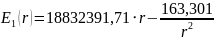
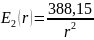
Для определения
поверхностной плотности заряда на
электродах, воспользуемся формулами
(1) и (2):

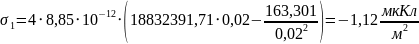
Для определения
заряда на электродах, воспользуемся
формулами (3) и (4), которые представлены
в пп1.3:

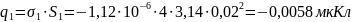
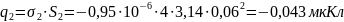
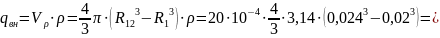
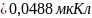
Суммарный заряд
конденсатора:

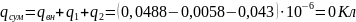
Аналогично
при

:

Подставим численные
значения:

В

;

;

В
;

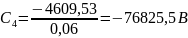
Таким
образом, выражения распределения
потенциала и напряжённости
электростатического поля между
электродами сферического конденсатора
будет иметь вид:

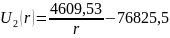
Для определения
поверхностной плотности заряда на
электродах, воспользуемся формулами
(1) и (2):

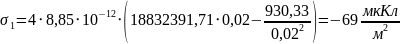
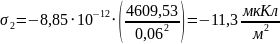
Для определения
заряда на электродах, воспользуемся
формулами (3) и (4), которые представлены
в пп1.3:

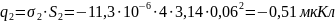
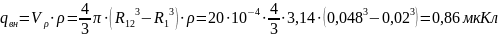
Суммарный заряд
конденсатора:

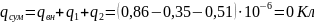
При

максимальное по модулю значение
напряженности поля конденсатора
достигается при

:
|E_max|=673900В/м.

При

аксимальное
по модулю значение напряженности поля
конденсатора достигается при

:
|E_max|=734200 В/м.

При

максимальное по модулю значение
напряженности поля конденсатора
достигается при

:
|E_max|=2001000 В/м.

2.3. Расчёт потенциала и напряжённости
при изменённом значении диэлектрической
проницаемости внутреннего слоя изоляции
ε₁ (ε₁ = ε₀ и
ε₁ = 6ε₀).

Используем
выражениями для постоянных интегрирования
из п. 2.1
и подставим

:

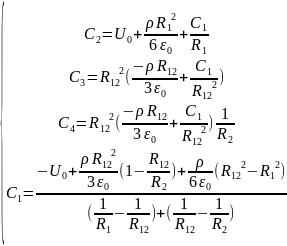
Подставим численные
значения:

В

;

;

В
;

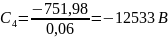
Таким
образом, выражения распределения
потенциала и напряжённости
электростатического поля между
электродами сферического
конденсатора будет иметь вид:

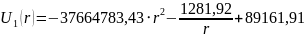
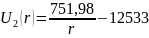
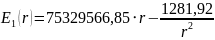
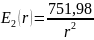
Для определения
поверхностной плотности заряда на
электродах, воспользуемся формулами
(1) и (2):

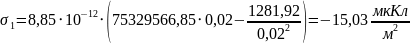
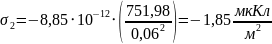
Для определения
заряда на электродах, воспользуемся
формулами (3) и (4), которые представлены
в пп1.3:

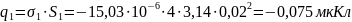
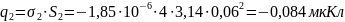
Суммарный заряд
конденсатора:

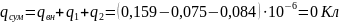
Аналогично
при

:

Подставим численные
значения:

В

;

;

В
;

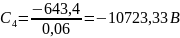
Таким образом,
выражения распределения
потенциала и напряжённости
электростатического поля между
электродами сферического конденсатора
будет иметь вид:

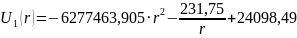
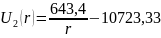
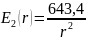
Для определения
поверхностной плотности заряда на
электродах, воспользуемся формулами
(1) и (2):

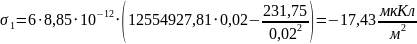
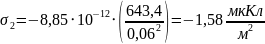
Для определения
заряда на электродах, воспользуемся
формулами (3) и (4), которые представлены
в пп1.3:

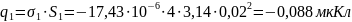
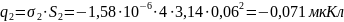
Суммарный заряд
конденсатора:

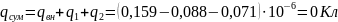
Рисунок
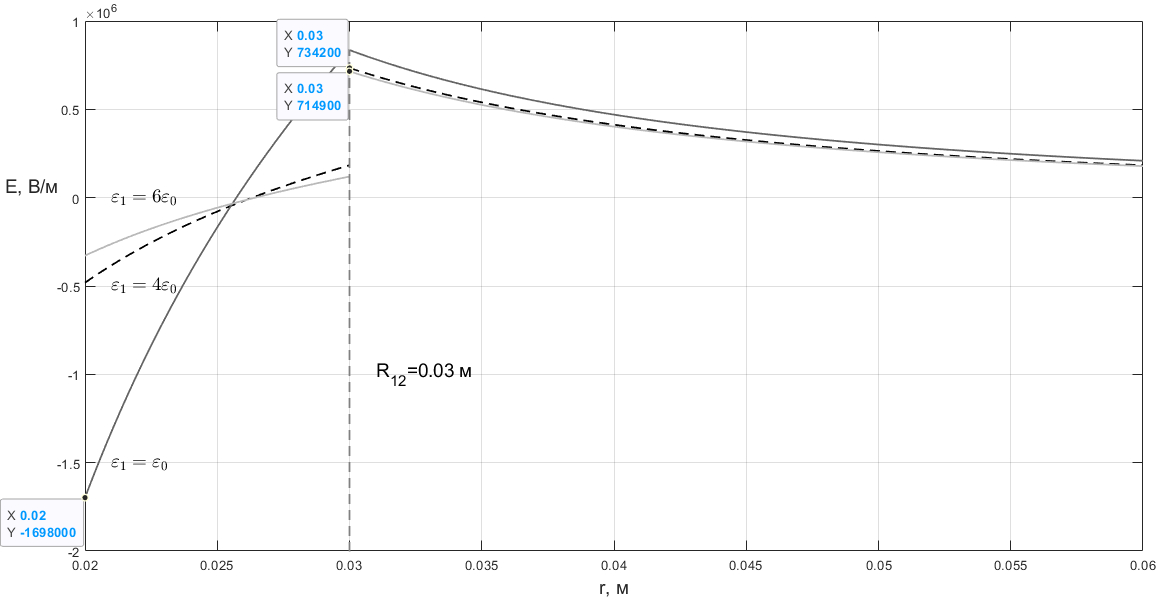
2.4. Графики
распределения напряженности поля при
различных значениях ε₁

При

максимальное по модулю значение
напряженности поля конденсатора
достигается при

:
|E_max|=1698000 В/м.

При

аксимальное
по модулю значение напряженности поля
конденсатора достигается при

:
|E_max|=734200 В/м.

При

максимальное по модулю значение
напряженности поля конденсатора
достигается при

:
|E_max|=714900 В/м.

1. Выводы

В сферическом
конденсаторе с двухслойной изоляцией
с различной диэлектрической проницаемостью
слоёв и без объёмного заряда, потенциал
и напряженность убывают (рисунок 1.1).
Были рассчитаны поверхностные плотности
заряда на электродах, заряды электродов,
суммарный заряд конденсатора и определена
его ёмкость (
).

При внесении
объёмного заряда во внутренний слой
изоляции, форма кривых потенциала и
напряжённости изменилась (рисунок
2.1). На
участке

≤ r
≤

потенциал возрастает, а на

≤ r
≤

убывает. Модуль
напряженности на первом участке сначала
убывает, затем возрастает. А после скачка
напряженность убывает. Также рассчитанные
поверхностные плотности заряда на
электродах одного знака, заряды
электродов одного знака, суммарный
заряд конденсатора с учетом объёмного
заряда равен нулю.
Максимальный модуль напряжённости
электрического поля увеличился.

Были построены
графики распределения потенциала и
напряжённости при различных значениях
радиуса границы раздела R₁₂
(рисунок 2.2). Чем больше R₁₂,
тем при большем r
напряжённость поля меняет своё
направление. Также, чем меньше R₁₂,
тем меньше максимальный модуль
напряжённости. Кривые имеют большую
крутизну при большем R₁₂.

Были построены
графики распределения потенциала и
напряжённости при различных значениях
диэлектрической проницаемости внутреннего
слоя изоляции ε₁
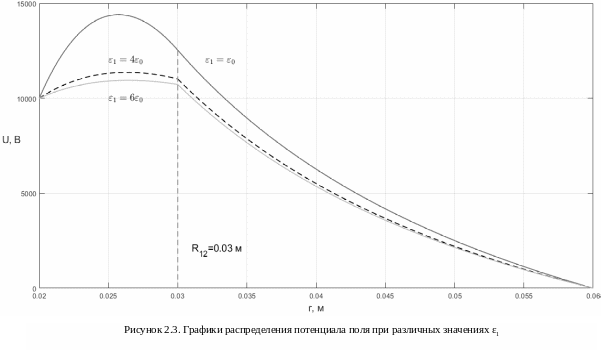
(рисунок 2.3, рисунок 2.4). При ε₁ = ε₀
нет разрыва на графике напряжённости.
Чем меньше значение ε₁,
тем больше крутизна U(r)
и E(r).
При меньшем значении ε₁
максимальный модуль напряжённости
больше.

Соседние файлы в папке Курсач от Кочетковой

• #
• #
• #

  22.04.2021448.86 Кб18РАСЧЁТ СФЕРЫ.xmcd

• #

  22.04.2021422.17 Кб16РАСЧЁТ ЦИЛИНДРА.xmcd