Электрическое поле. ЗАДАЧИ с решениями
Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.
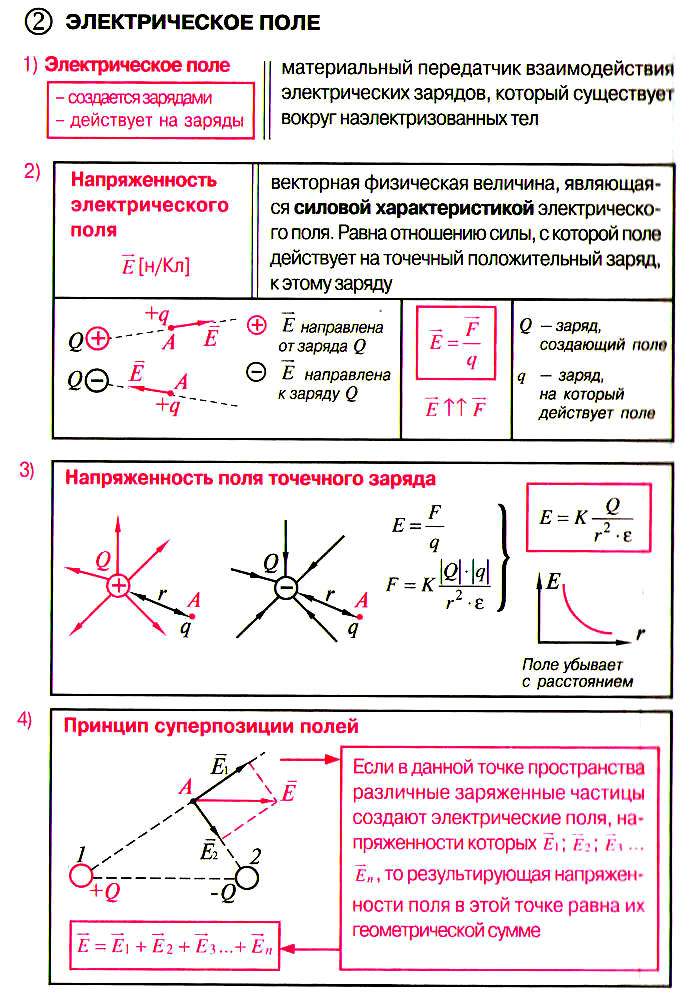

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10–19 Кл, его масса me = 9,1 • 10–31 кг.

Задача № 2.
Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 104 Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка? 
Смотреть решение и ответ

Задача № 3.
Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р1 с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р2. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх. 
Смотреть решение и ответ

Задача № 4.
На каком расстоянии г2 от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε2 = 81 (вода) такая же, как на расстоянии r1 = 9 см от этого заряда в воздухе?
Смотреть решение и ответ

Задача № 5.
Электрон влетает в однородное электрическое поле со скоростью v0, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона Wк через время t ? Напряженность поля Е. Масса электрона те и его заряд е известны. 
Задача № 6.
Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды Fсоnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона me, его заряд е.
Задача № 7.
К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10–10 Кл. Плотность вещества шарика р = 2 • 103 кг/м3. Натяжение нити Fн = 4,9 • 10–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости? 
Задача № 8.
Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см2. Найти напряженность Е1 электрического поля на расстоянии r1 = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r0 = 0 до r1 = 10 см. Среда — воздух. 
Задача № 9.
Заряды q1 = 20 нКл и q2 = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е1, созданного этими зарядами в точке 1, расположенной на расстоянии r1 = 4 см от заряда q1 и напряженность Е2 в точке 2, расположенной на расстоянии г2 = 2 см от заряда q2 (рис. 2-15). Среда — вакуум. 
Задача № 10.
Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r1 от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r2 от заряда q находится такая точка, если эти заряды разноименные?
Задача № 11.
На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м2. Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r1 = 4 см от центра шара, и г2 = 3 см от заряда q. Среда — воздух.
Задача № 12.
В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.
(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».
Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Подготовка к олимпиаде. Применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел
Опубликовано ср, 08/14/2019 – 10:50 пользователем fizportal.ru
Применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел
Рассмотрим применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел простой формы: плоскости, сферы, шара, нити, цилиндра
1. Поле равномерно заряженной бесконечной плоскости
Когда заряд распределен по какой-либо поверхности, то для расчета полей удобно ввести поверхностную плотность заряда $sigma$. Выделим на плоской поверхности маленький участок площадью $Delta S$. Пусть заряд этого участка равен $Delta q$. Поверхностной плотностью заряда называют отношение заряда $Delta q$ к площади поверхности, по которой он распределен
$sigma = frac{Delta q}{Delta S}$.
Эта плотность может непрерывно изменяться вдоль поверхности. Конечно, электрический заряд имеет дискретную (прерывную) структуру, так как сосредоточен в элементарных частицах. Но если на поверхности площадью $Delta S$ содержится огромное число элементарных зарядов, то дискретную структуру заряда можно не принимать во внимание. Мы ведь пользуемся понятием плотности, считая, что масса непрерывно распределена в пространстве. А на самом деле все тела состоят из дискретных образований – атомов.
В случае равномерного распределения заряда $q$ по поверхности площадью $S$ поверхностная плотность заряда постоянна и равна $sigma = frac{q}{S} = const$.
Задача 1. Найдите напряженность электрического поля, создаваемого равномерно заряженной бесконечной плоскостью. Поверхностная плотность заряда $sigma$.
Решение
Для использования этой теоремы для определения напряженности поля, необходимо рассмотреть симметрию поля, которая, очевидно связана с симметрией зарядов. Распределение зарядов не изменится, если плоскость сместить на любой вектор $vec{a}$, лежащий в самой плоскости. Поэтому при таком смещении не изменится и напряженность поля (рис.).

Следовательно, напряженность поля может зависеть только от расстояния до плоскости $h$. Любая прямая, перпендикулярная плоскости является осью симметрии, то есть при повороте плоскости на любой угол относительно любой оси, перпендикулярной плоскости, распределение зарядов не изменяется – следовательно, и вектор напряженности при таком повороте не изменится, поэтому этот вектор должен быть перпендикулярен плоскости. Наконец, заряженная плоскость является плоскостью симметрии для поля. Поэтому в симметричных точках векторы напряженности также симметричны. Выявленные свойства симметрии электрического поля позволяют выбрать поверхность, для которой можно выразить поток вектора напряженности в простой форме. Итак, в качестве такой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны плоскости, а основания площадью $S$ параллельны ей и находятся на равных расстояниях от плоскости.
Прежде всего, заметим, что поток вектора напряженности через боковую поверхность цилиндра равен нулю, так как во всех точках боковой поверхности векторы напряженности $vec{E}$ и нормали $vec{n}$ взаимно перпендикулярны (поэтому $cosalpha = 0$) (рис.).

Поток через верхнее основание цилиндра может быть записан в виде
$Ф_1 = E_1 cdot S$,
так модуль напряженности поля на основании цилиндра постоянен, а по направлению совпадает с вектором нормали. Такое же значение имеет поток через нижнее основание.
Таким образом, суммарный поток вектора напряженности электрического поля через поверхность цилиндра равен
$Ф = E_1 cdot S + E_2 cdot S = 2E cdot S$.
С другой стороны, по теореме Гаусса
$Ф = frac{q}{varepsilon_0}$,
где $q$ – заряд, заключенный внутри поверхности цилиндра:
$q = sigma cdot S$.
Следовательно, $E = frac{sigma}{2varepsilon_0}$.
Главная составляющая успеха – анализ симметрии поля, позволивший разумно выбрать поверхность, для использования теоремы Гаусса. Также обратите внимание, что напряженность данного поля одинакова во всех точках, следовательно, это поля является однородным. Подчеркнем, независимость напряженности поля от расстояния до плоскости $h$ никак не следует из симметрии поля, это результат нашего расчета.
Примечание.
Для плоскости, заряженной отрицательно, результат будет таким же, лишь направление вектора $vec{E}$ изменится на противоположное.
2. Поле равномерно заряженной сферы
Задача 2. Найдите напряженность электрического поля, создаваемого равномерно заряженной сферой радиуса $R$. Суммарный заряд сферы $q$.
Решение
Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление – радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис.).

Пусть радиус сферы $r$ больше радиуса оболочки $r > R$. Тогда во всех точках этой сферы вектор напряженности направлен вдоль нормали к поверхности, а его модуль постоянен. Поэтому поток вектора напряженности $vec{E}$ через сферу равен произведению модуля напряженности на площадь сферы
$Ф = E cdot S = E cdot 4pi r^2$.
По теореме Гаусса это поток равен $Ф = frac{q}{varepsilon_0}$. Следовательно,
$E cdot 4pi r^2 = frac{q}{varepsilon_0}$, $E = frac{1}{4pi varepsilon_0}frac{q}{r^2}$.
Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы.
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис.)

также выражается формулой
$Ф = E cdot 4pi r^2$.
Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.
Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса $R$, имеет вид:
$E(r) = 0$, при $r < R$;
$E(r) = frac{kq}{r^2}$, при $r > R$.
Примечание.
1) Очевидно, что для сферы, заряженной отрицательно, формулы остаются справедливыми, только векторы напряженности будут направлены в противоположные стороны (к центру сферы).
2) Если вместо заряда q задана поверхностная плотность заряда $sigma$, то заряд будет равен $q = sigma S = sigma cdot 4pi R^2$, а напряженность
$E = frac{1}{4pi varepsilon_0}frac{1}{r^2}sigma 4pi R^2 = frac{sigma R^2}{epsilon_0 r^2}$.
3. Поле равномерно заряженного шара
Для характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда $Delta q$ к объему $Delta V$, в котором он распределен:
$rho = frac{Delta q}{Delta V}$.
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд $q$ равномерно распределен по объему $V$, то объемная плотность заряда постоянна и равна:
$rho = frac{q}{V} = const$.
Задача 3. Вычислить напряженность электрического поля, создаваемого равномерно заряженным шаром радиуса $R$. Объемная плотность заряда $rho$.
Решение
Поле, создаваемое таким шаром, будет центрально-симметричным. Легко понять, что вне шара для поля получится такой же результат, что и для поля вне сферы (см. задачу 2),
$E = frac{1}{4pi varepsilon_0}frac{q}{r^2}$.
Полный заряд шара
$q = rho V = rho frac{4}{3}pi R^3$.
Тогда
$E = frac{1}{4pi varepsilon_0}frac{q}{r^2} = frac{1}{4pi varepsilon_0}frac{4pi R^3 rho}{3r^2} = frac{rho R^3}{3varepsilon_0 r^2}$
(при условии, что $r > R$).
Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом $r < R$ (рис.).

Поток вектора напряженности поля через поверхность этой сферы
$Ф = E cdot 4pi r^2$.
С другой стороны, по теореме Гаусса
$Ф = frac{q^/}{varepsilon_0}$,
где $q^/ = rho frac{4}{3}pi r^3$
– заряд, заключенный в сфере радиуса $r$. Следовательно,
$E cdot 4pi r^2 = frac{q^/}{varepsilon_0}, E = frac{1}{4pi varepsilon_0}frac{q^/}{r^2} = frac{1}{4pi varepsilon_0}frac{1}{r^2}rho frac{4}{3}pi r^3 = frac{rho cdot r}{3varepsilon_0}$.
Таким образом, внутри равномерно заряженного шара напряженность поля растет линейно с расстоянием от его центра.
Функция, описывающая напряженность поля равномерно заряженного шара радиуса $R$, имеет вид:
$E(r) = frac{rho}{3varepsilon_0}r$, при $r leq R$,
$E(r) = frac{rho R^3}{3varepsilon_0}frac{1}{r^2}$, при $r > R$.
Примечание.
Если вместо объемной плотности заряда $rho$ задан заряд $q$, то объемной плотности заряда будет равна
$rho = frac{q}{V} = frac{q}{frac{4}{3}pi R^3}$,
а напряженность
$E(r) = frac{r}{3varepsilon_0}frac{q}{frac{4}{3}pi R^3} = frac{q}{4pi varepsilon_0 R^3}cdot r = kfrac{q}{R^3}cdot r$, при $r leq R$,
$E(r) = frac{R^3}{3varepsilon_0}frac{1}{r^2}frac{q}{frac{4}{3}pi R^3} = frac{q}{4pi varepsilon_0}cdot frac{1}{r^2} = kfrac{q}{r^2}$, при $r > R$,
4. Поле равномерно заряженной нити
Для характеристики распределения заряда по длине используется понятие линейная плотности заряда. Линейной плотностью заряда называется отношение заряда $Delta q$ к длине $Delta l$, в которой он распределен:
$tau = frac{Delta q}{Delta l}$.
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд $q$ равномерно распределен по длине $l$, то линейная плотность заряда постоянна и равна:
$tau = frac{q}{l} = const$.
Задача 4. Найдите напряженность электрического поля, создаваемого в вакууме бесконечно длинной заряженной нитью с линейной плотностью заряда t.
Решение
Проще всего решить задачу с помощью теоремы Гаусса. Вычислим поток напряженности через цилиндр, ось которого совпадает с заряженной нитью (рис.).

Радиус цилиндра $r$, а его высота $l$.
Из соображений симметрии очевидно, что линии напряженности $vec{E}$ перпендикулярны боковой поверхности цилиндра. Поэтому поток напряженности через боковую поверхность цилиндра равен
$Ф = ES = Ecdot 2pi rl$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
С другой стороны, по теореме Гаусса
$Ф = frac{q}{varepsilon_0}$,
где $q = tau cdot l$ – заряд, заключенный внутри цилиндра. Следовательно,
$E cdot 2pi rl = frac{ltau}{varepsilon_0}$,
$E = frac{tau}{2pi varepsilon_0 r} = frac{2kcdot tau}{r}$.
5. Поле равномерно заряженного бесконечного цилиндра
Задача 5. Бесконечно длинный круговой цилиндр радиусом $R$ равномерно заряжен по объему с плотностью $rho$. Найти напряженность электростатического поля в точке, удаленной на расстояние $r$ от оси цилиндра.
Решение
Используя симметрию распределения заряда и теорему Гаусса, найдем напряженность электрического поля внутри и вне цилиндра. В качестве поверхности, через которую будем определять поток вектора $vec{E}$, выберем цилиндр радиусом $r$ и высотой $h$, имеющий ту же ось симметрии, что и заданный цилиндр (рис.).

Во всех точках боковой поверхности цилиндра вектор $vec{E}$ совпадает с внешней нормалью к этой поверхности и имеет одинаковую величину. Поток вектора $vec{E}$ через боковую поверхность цилиндра
$Ф = E_1 cdot S = E_1 cdot 2pi rh$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
Из теоремы Гаусса следует, что
$Ф = frac{q}{varepsilon_0}$,
где $q = rho V = rho pi r^2h$ – заряд, заключенный внутри цилиндра.
Следовательно,
$E_1 cdot 2pi rh = frac{rho pi r^2h}{varepsilon_0}$, и $E_1 = frac{rho r}{2varepsilon_0}$.
Чтобы найти $E_2$ для $r > R$, окружим заданный цилиндр цилиндрической поверхностью радиусом $r > R$ и высотой $h$, ось симметрии которой совпадает с осью цилиндра (см. рис.).
Во всех точках боковой поверхности цилиндра вектор $vec{E}$ совпадает с внешней нормалью к этой поверхности и имеет одинаковую величину. Поток вектора $vec{E}$ через боковую поверхность цилиндра
$Ф = E_2 cdot S = E_2 cdot 2pi rh$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
Из теоремы Гаусса следует, что
$Ф = frac{q}{varepsilon_0}$,
где $q = rho V = rho pi R^2h$ – заряд, заключенный внутри цилиндра. Следовательно,
$E_2 cdot 2pi rh = frac{rho pi R^2h}{varepsilon_0}$, и $E_2 = frac{rho R^2}{2varepsilon_0 r}$.
6. Дополнительные задачи
Задача 6. Докажите, что система свободных зарядов не может находиться в состоянии устойчивого равновесия. (Теорема Иршноу.)
Решение
Предположим противное, то есть какой-либо из зарядов, для определенности положительный, находится в состоянии устойчивого равновесия. По определению устойчивого равновесия, при выведении заряда из этого положения в любом направлении на сколь угодно малую величину, возникает сила, направленная к положению равновесия.
Окружим заряд, замкнутой поверхностью, например, сферой, так, чтобы внутрь ее не попадали другие заряды (рис.).

Очевидно, что для устойчивости необходимо, чтобы поле, создаваемое всеми прочими зарядами кроме рассматриваемого, на поверхности сферы было направлено к положению равновесия (только в этом случае возникает сила, возвращающая заряд в положение равновесия). Отсюда находим, что поток вектора $vec{E}$ через замкнутую поверхность отрицателен.
Но это противоречит теореме Гаусса, согласно которой данный поток, создаваемый зарядами вне сферы, равен нулю. Таким образом, теорема доказана.
Задача 7. С какой силой расталкиваются равномерно заряженные грани куба? Поверхностная плотность заряда $sigma$, длина ребра куба $l$.
Решение
Для определенности рассмотрим силу, действующую на верхнюю грань куба. Разобьем эту грань на малые площадки $Delta S_i$ и представим силу, действующую на грань, как сумму $vec{F_i}$ сил, действующих на каждую площадку $Delta S_i$:
$vec{F} = sum vec{F_i}$.
Обозначим через $vec{E_i}$ напряженность электрического поля, создаваемого в области нахождения площадки $Delta S_i$ зарядами всех граней, кроме самой верхней грани (рис.).

Тогда сила
$vec{F_i} = q^/ cdot vec{E_i} = sigma cdot Delta S_i cdot vec{E_i}$,
ее проекция на нормаль к грани $vec{n}$ равна
$F_{in} = sigma cdot Delta S_i cdot E_i^/ cdot cosalpha_i$,
а суммарная сила, действующая на верхнюю грань вдоль нормали $vec{n}$:
$F_n = sum F_{in} = sigma cdot sum{E_i^/ Delta S_i cdot cosalpha_i} = sigma cdot Ф^/$, (1)
где $sum{E_i^/ Delta S_i cdot cosalpha_i} = Ф^/$ – поток вектора $vec{E}$ через верхнюю грань куба, создаваемый зарядами всех других граней.
В качестве замкнутой поверхности для применения теоремы Гаусса выберем куб, размеры которого на бесконечно малую величину превышают размеры рассматриваемого куба, то есть их грани практически совпадают. Тогда поток через верхнюю грань куба внешнего куба равен
$Ф = Ф^/ + Ф^{//}$,
где
$Ф^{//} = E^{//} cdot S_1 = frac{sigma}{2varepsilon_0} cdot S_1 = frac{sigma}{2varepsilon_0} cdot l^2$
поток, создаваемый заряженной верхней гранью куба.
Тогда
$Ф = Ф^/ + frac{sigma}{2varepsilon_0} cdot l^2$, (2)
Воспользуемся теоремой Гаусса для всего куба
$Ф_0 = 6Ф = frac{q}{varepsilon_0}$,
где $q = sigma cdot 6l^2$ – заряд куба.
Тогда
$6Ф = frac{6l^2 cdot sigma}{varepsilon_0}$. (3)
Выразим $Ф^/$ из (2), а $Ф$ из (3)
$Ф^/ = Ф – frac{sigma}{2varepsilon_0} cdot l^2 = frac{sigma}{varepsilon_0} cdot l^2 – frac{sigma}{2varepsilon_0} cdot l^2 = frac{sigma}{2varepsilon_0} cdot l^2$.
Учитывая уравнение (1), окончательно находим:
$F_n = frac{sigma^2 cdot l^2}{2varepsilon_0}$.
Задача 8. Грани куба с ребром $a$ однородно заряжены с поверхностной плотностью $sigma$. В центр куба помещен заряд $Q$. С какой силой этот заряд взаимодействует с каждой из граней?
Решение
По теореме Гаусса вычислим $Ф$ – поток вектора напряженности, создаваемой зарядом $Q$, через поверхность куба. Он равен $frac{Q}{varepsilon_0}$. С другой стороны
$Ф = 6 cdot displaystylesum_{Delta S} frac{Q}{r^2} cdot Delta S cdot cosalpha$.
В этом выражении $Delta S$ – площадь малого элемента поверхности куба, $r$ – длина вектора, соединяющего заряд $Q$ с этим элементом, $alpha$ – угол, который составляет этот вектор с нормалью к элементу $Delta S$. Суммирование идет по одной из граней куба. Заметим, что сила $F$, действующая на грань куба, задается выражением:
$F = sigma cdot displaystylesum_{Delta S} frac{Q}{r^2} cdot Delta S cdot cosalpha$
Следовательно,
$F = sigma cdot frac{Ф}{6} = frac{sigma Q}{6varepsilon_0}$.
Тип 20 № 1648 

i
Металлическому шару радиусом 3 см сообщили заряд 16 нКл. Найти поверхностную плотность заряда и напряженность поля в точках, удаленных от центра шара на 2 и 4 см.
Спрятать решение
Решение.
Поверхностная плотность заряда равна
Напряженность поля на расстоянии 2 см равна 0, так как напряженность поля на расстоянии 4 см равна
Ответ: 1,4 мкКл/м2; 0; 90 кВ/м.
Источник: Рымкевич А. П. Сборник задач по физике для 9−11 классов, М.: «Просвещение», 1990 (№ 713)
Рассмотрим общий случай произвольной
поверхности, окружающей n
зарядов. В соответствии с принципом
суперпозиции напряженность Е поля,
создаваемого всеми зарядами, равна
сумме напряженностей Ei
полей, создаваемых каждым зарядом в
отдельности:
![]()
![]()
Согласно каждый из интегралов, стоящий
под знаком суммы, равен Qi
/0.
![]()
Формула выражает теорему Гаусса для
электростатического поля в вакууме:
поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на 0..
В общем случае электрические заряды
могут быть «размазаны» с некоторой
объемной плотностью =dQ/dV,
различной в разных местах пространства.
![]()
Используя формулу , теорему Гаусса
![]()
Поле равномерно заряженной бесконечной
плоскости.
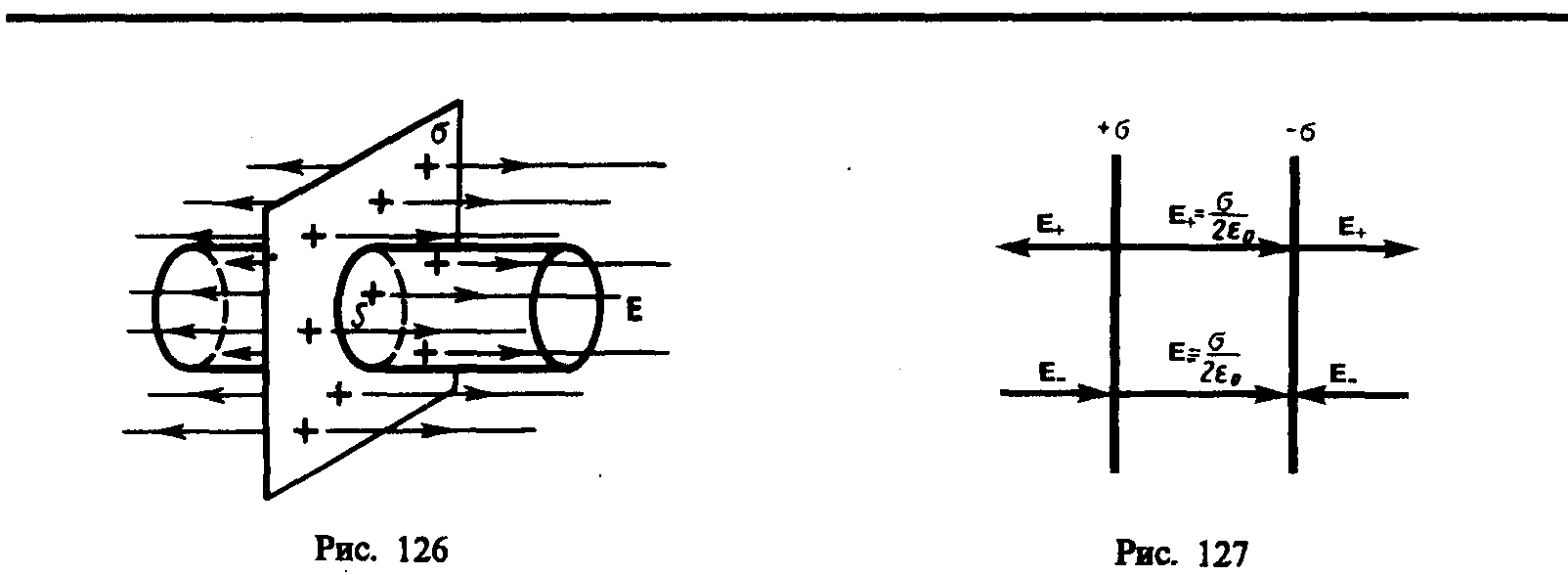
Бесконечная плоскость заряжена с
постоянной поверхностной плотностью
+ (=dQ/dS
— заряд, приходящийся на единицу
поверхности). Линии напряженности
перпендикулярны рассматриваемой
плоскости и направлены от нее в обе
стороны. В качестве замкнутой поверхности
мысленно построим цилиндр, основания
которого параллельны заряженной
плоскости, а ось перпендикулярна ей.
Так как образующие цилиндра параллельны
линиям напряженности (соs=0),
то поток вектора напряженности сквозь
боковую поверхность цилиндра равен
нулю, а полный поток сквозь цилиндр
равен сумме потоков сквозь его
основания (площади оснований равны и
для основания Еn
совпадает с Е), т. е. равен 2ES.
Заряд, заключенный внутри построенной
цилиндрической поверхности, равен S.
Согласно теореме Гаусса 2ES=S/0,
откуда
![]()
Из формулы (82.1) вытекает, что Е не
зависит от длины цилиндра, т. е.
напряженность поля на любых расстояниях
одинакова по модулю, иными словами, поле
равномерно заряженной плоскости
однородно.
6) Расчёт электрического поля сферы заряженной по поверхности.
Сфера радиусом R. Пусть заряд +q равномерно
распределён по сферической поверхности
радиуса R. Распределение заряда по
поверхности характеризуется поверхностной
плотностью заряда. Поверхностной
плотностью заряда называют отношение
заряда к площади поверхности, по которой
он распределён. ![]()
.
В СИ ![]()
.

Определим напряжённость поля:
а) вне сферической поверхности,
а) Возьмём точку А вне сферы расстоянии
r>R. Проведём через неё мысленно
сферическую поверхность S радиуса r,
имеющую общий центр с заряженной
сферической поверхностью. Из соображения
симметрии очевидно, что силовые линии
являются радиальными прямыми
перпендикулярными к поверхности S и
равномерно пронизывают эту поверхность,
т.е. напряжённость по всех точках этой
поверхности постоянна по величине.
Применим теорему Остроградского-Гаусса
к этой сферической поверхности S радиуса
r. Поэтому полный поток через сферу равен
Ф = EdS=E*4 п2. С другой
стороны
![]()
.
Приравниваем:
![]()
.
Отсюда: ![]()
при
r>R.
Таким образом: напряжённость, создаваемая
равномерно заряженной сферической
поверхностью, вне её такая же, как если
бы весь заряд находился в её центре

б) внутри сферической поверхности.
Найдём напряжённость поля в точках,
лежащих внутри заряженной сферической
поверхности. Возьмём точку В отстоящую
от центра сферы на расстоянии ![]()
<R,
и проведём через эту точку сферическую
поверхность имеющую общий центр с
заряженной сферической поверхностью.
Из соображения симметрии ясно, что
напряжённость ![]()
должна
быть численно одинакова на всей выбранной
поверхности сферы S и нормальна к ней.
Применяя теорему Остроградского-Гаусса
к сферической поверхности S на основании
формулы: N=E? S, S=4p*r2*т.к.
заряд внутри сферы S q = 0, то![]()
.
Тогда
![]()
,
E = 0 при r<R. Следовательно, напряжённость
электрического поля во всех точках
внутри равномерно заряженной сферической
поверхности равна нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти поверхностную плотность заряда формула

Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.
Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность  во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность  будетодинакова по величине и противоположна по направлению.
будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
 |
|
| Рис. 2.11 | Рис. 2.12 |
Применим теорему Остроградского-Гаусса. Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.к .  Дляоснования цилиндра
Дляоснования цилиндра 
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд  . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
откуда видно, что напряженность поля плоскости S равна:
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 
Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей  .
.
Вне плоскостей напряженность поля 


Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
Механические силы, действующие между заряженными телами, называют пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
где S – площадь обкладок конденсатора. Т.к.  , то
, то
Это формула для расчета пондермоторной силы.
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью  , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров  для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
Следовательно, поток вектора  через рассматриваемую поверхность, равен
через рассматриваемую поверхность, равен 
При  на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
Если 
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

Если уменьшать радиус цилиндра R (при  ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.
Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
Внутри меньшего и вне большего цилиндров поле будет отсутствовать  (рис. 2.16) .
(рис. 2.16) .

В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Поле заряженного пустотелого шара
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным,  – в любой точке проходит через центр шара.
– в любой точке проходит через центр шара.  ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
Если  то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
Внутри сферы, при  поле будет равно нулю, т.к. там нет зарядов:
поле будет равно нулю, т.к. там нет зарядов: 


Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:
Но внутри шара при  сферическая поверхность будет содержать в себе заряд, равный
сферическая поверхность будет содержать в себе заряд, равный

где ρ – объемная плотность заряда, равная:  ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем:
Таким образом, внутри шара 
Источник
