Как и для криволинейных интегралов, существуют два рода поверхностных интегралов.
Поверхностный интеграл первого рода[править | править код]
Определение[править | править код]
Пусть 








Тогда число 

Предел 




Параметрическая форма[править | править код]
Пусть на поверхности 
заданных в ограниченной замкнутой области 





где:
Свойства[править | править код]
Из определения поверхностного интеграла первого рода следует независимость этого интеграла от выбора ориентации векторного поля единичных нормалей к поверхности или, как говорят, от выбора стороны поверхности. Пусть функции 


- Линейность:
для любых вещественных чисел
.
- Аддитивность:
при условии, что
и
не имеют общих внутренних точек.
- Монотонность:
- Теорема о среднем для непрерывной функции
и замкнутой ограниченной поверхности
:
, где
, а
— площадь области
.
Поверхностный интеграл второго рода[править | править код]
Определение[править | править код]
Рассмотрим двустороннюю поверхность 
Для определенности предположим сначала, что поверхность задана явным уравнением 



Пусть теперь в точках данной поверхности 







Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
распространённым на выбранную сторону поверхности 
(здесь 

Если вместо плоскости 


или
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
где 


Связь между поверхностными интегралами второго и первого рода[править | править код]
где 


Свойства[править | править код]
- Линейность:
.
- Аддитивность:
.
- При изменении ориентации поверхности поверхностный интеграл меняет знак.
См. также[править | править код]
- Криволинейный интеграл
- Поток векторного поля
- Первообразная
- Методы интегрирования
- Теорема Стокса
Литература[править | править код]
- Фихтенгольц, Г. М. Глава 17. Поверхностные интегралы // [Курс дифференциального и интегрального исчисления]. — Т. 3.
- Ильин, В. А., Позняк, Э. Г. Глава 5. Поверхностные интегралы // Основы математического анализа. — Т. 2. — (Курс высшей математики и математической физики).
Ссылки[править | править код]
- Мир математических уравнений Архивная копия от 21 ноября 2019 на Wayback Machine.
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.

Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
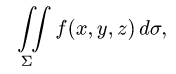
где  — часть поверхности, описываемая уравнением F(x,y,z) = 0
— часть поверхности, описываемая уравнением F(x,y,z) = 0
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием  на координатную плоскость XOY по формуле
на координатную плоскость XOY по формуле
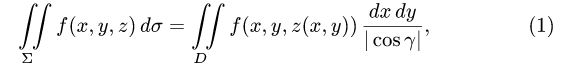
где D — проекция  на плоскость XOY,
на плоскость XOY, 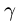 — угол между нормалью
— угол между нормалью
к поверхности  и осью OZ; z(x, у) определяем из уравнения поверхности F(x, у, z) = 0.
и осью OZ; z(x, у) определяем из уравнения поверхности F(x, у, z) = 0.
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем  на другую координатную плоскость или используем криволинейные координаты (можно
на другую координатную плоскость или используем криволинейные координаты (можно
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 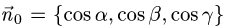 к поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
к поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
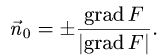
2.Проекцию D поверхности  на плоскость XOY находим, исключая z из условий, определяющих
на плоскость XOY находим, исключая z из условий, определяющих  .
.
3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Записываем ответ.
Пример:
Вычислить поверхностный интеграл
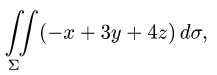
где  — часть плоскости
— часть плоскости
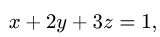
расположенная в первом октанте (т.е. 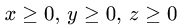 ).
).
Решение:
1.Единичные нормальные векторы 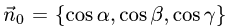 к по-
к по-
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
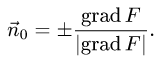
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
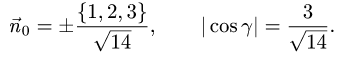
2.Поверхность  определяется условиями
определяется условиями
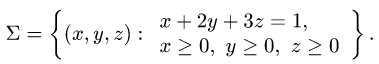
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих  :
:
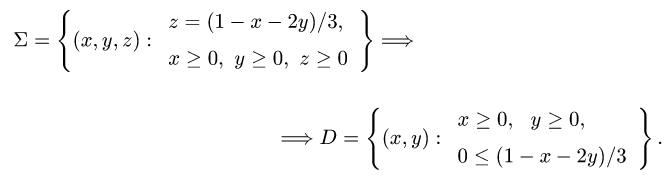
Отсюда
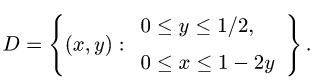
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
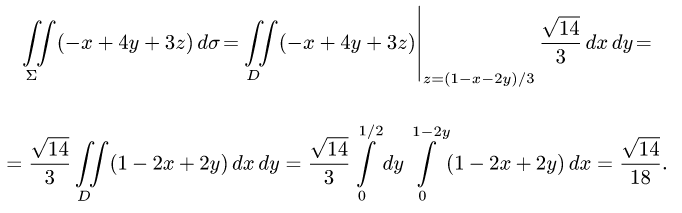
Ответ. 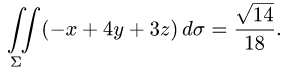
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
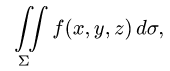
где  — часть поверхности
— часть поверхности 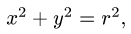 вырезаемая плоскостями
вырезаемая плоскостями
z = 0 и z = h.
План решения.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
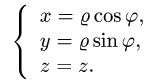
В этих координатах поверхность задается условиями
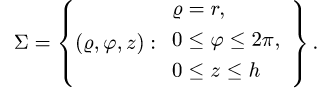
2.Так как
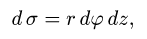
то
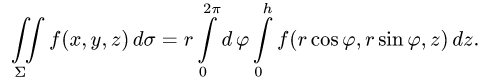
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
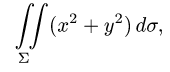
где  — часть поверхности
— часть поверхности 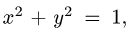 вырезаемая плоскостями
вырезаемая плоскостями
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
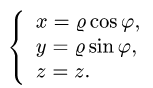
В этих координатах поверхность задается условиями
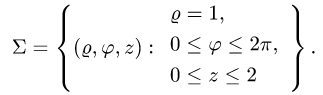
2.Так как 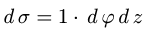 и
и 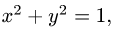 то имеем
то имеем
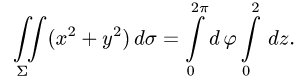
3.Вычисляем повторный интеграл:
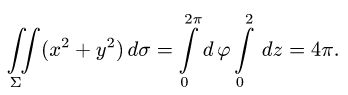
Ответ. 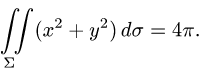
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
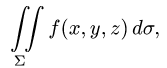
где 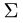 — верхняя полусфера
— верхняя полусфера
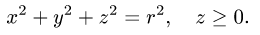
План решения.
1.Вводим на заданной поверхности (сфере) криволинейные координаты
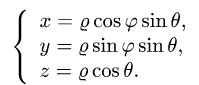
В этих координатах поверхность задается условиями
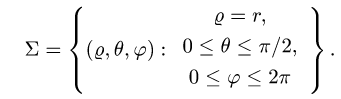
2.Так как 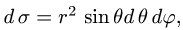 имеем
имеем
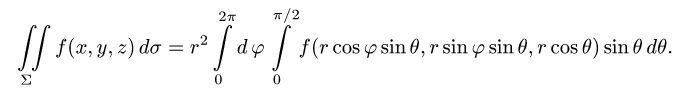
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
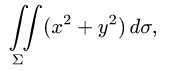
где 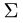 — верхняя полусфера
— верхняя полусфера
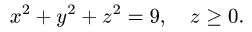
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
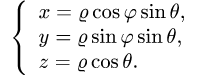
В этих координатах поверхность задается условиями
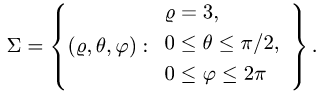
2.Так как 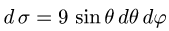 и
и 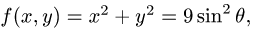 имеем
имеем
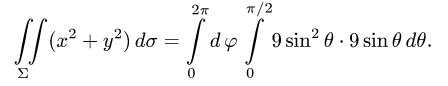
3.Вычисляем повторный интеграл:
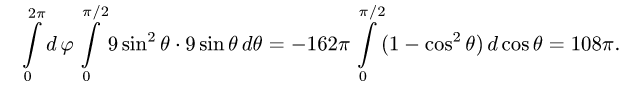
Ответ.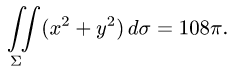
Определение и свойства поверхностных интегралов





Смотрите также:
Решение задач по математическому анализу
Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 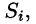 площади которых обозначим через ДSi (см. рис. 246), а диаметры — через
площади которых обозначим через ДSi (см. рис. 246), а диаметры — через 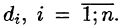 В каждой части
В каждой части 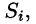 возьмем произвольную точку
возьмем произвольную точку 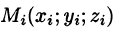 и составим сумму
и составим сумму

Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 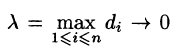 интегральная сумма (57.1) имеет пре-дел, то он называется поверхностным интегралом I рода от функции f(x;y;z) по поверхности S и обозначается
интегральная сумма (57.1) имеет пре-дел, то он называется поверхностным интегралом I рода от функции f(x;y;z) по поверхности S и обозначается 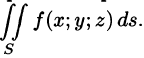
Таким образом, по определению,
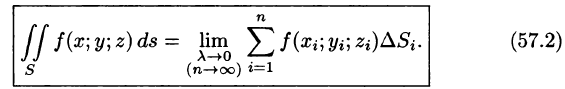
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
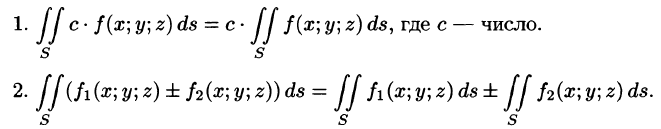
3. Если поверхность S разбить на части 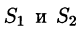 такие, что
такие, что 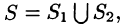 а пересечение
а пересечение 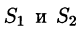 состоит лишь из границы, их разделяющей, то
состоит лишь из границы, их разделяющей, то
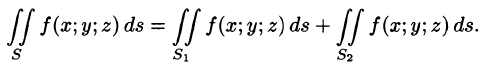
4.Если на поверхности S выполнено неравенство
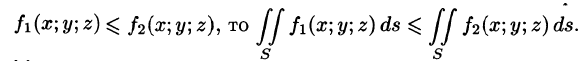
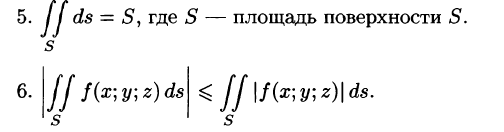
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка  такая, что
такая, что
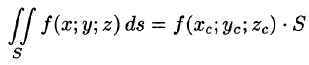
(теорема о среднем значении).
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем поверхность S на части 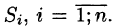 Обозначим через
Обозначим через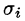 проекцию
проекцию 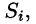 на плоскость Оху. При этом область D окажется разбитой на п частей
на плоскость Оху. При этом область D окажется разбитой на п частей 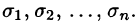 Возьмем в произвольную точку
Возьмем в произвольную точку 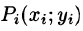 и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку
и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку 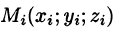 на поверхности
на поверхности  . Проведем в точке М, касательную плоскость и рассмотрим ту ее часть
. Проведем в точке М, касательную плоскость и рассмотрим ту ее часть 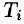 , которая на плоскость Оху проектируется в область
, которая на плоскость Оху проектируется в область 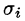 (см. рис. 247). Площади элементарных частей
(см. рис. 247). Площади элементарных частей 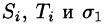 обозначим как
обозначим как 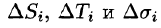 соответственно. Будем приближенно считать, что
соответственно. Будем приближенно считать, что

Обозначив через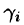 , острый угол между осью Oz и нормалью п, к поверхности в точке
, острый угол между осью Oz и нормалью п, к поверхности в точке 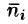 получаем:
получаем:
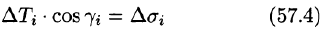
(область 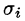 есть проекция
есть проекция 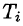 на плоскость Оху).
на плоскость Оху).
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 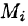 есть
есть
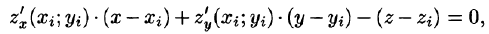
где 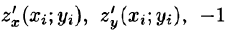 — координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами
— координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами 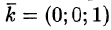 и
и
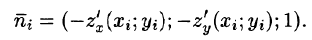
Следовательно,
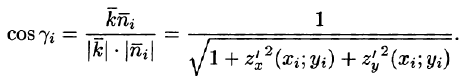
Равенство (57.4) принимает вид
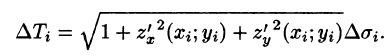
В правой части формулы (57.2) заменим  (учитывая (57.3)) на полученное выражение для
(учитывая (57.3)) на полученное выражение для 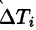 , a
, a 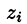 заменим на
заменим на 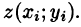 Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра
Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра  (а следовательно, и
(а следовательно, и 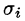 ), получаем формулу
), получаем формулу
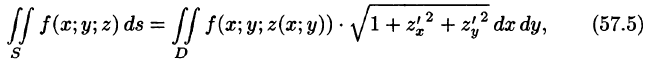
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
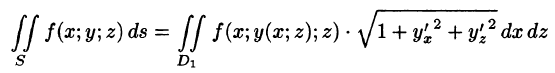
и
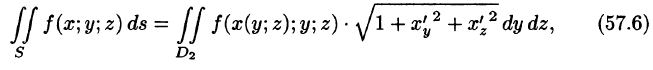
где 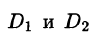 — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
— проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
Пример:
Вычислить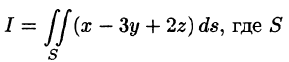 — часть плоскости
— часть плоскости 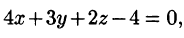 расположенной в I октанте (см. рис. 248).
расположенной в I октанте (см. рис. 248).
Решение:
Запишем уравнение плоскости в виде 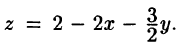
Находим 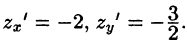 По формуле (57.5) имеем:
По формуле (57.5) имеем:
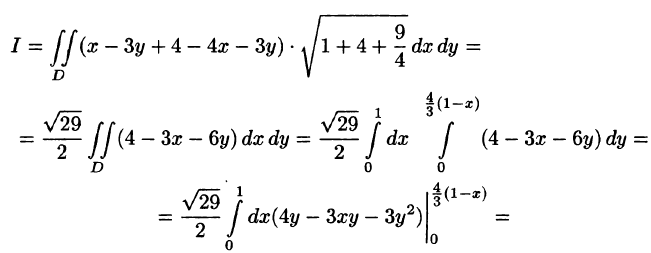
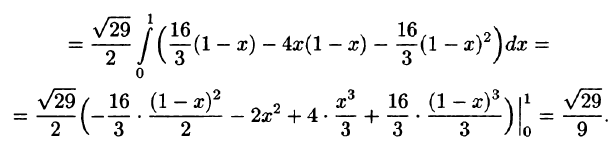
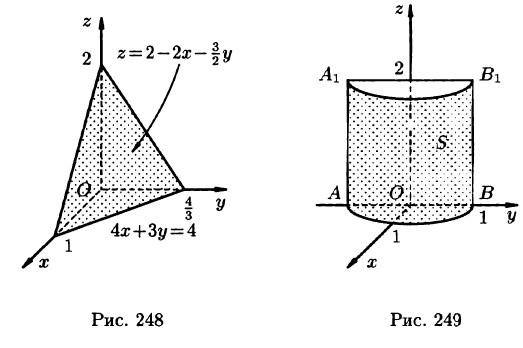
Пример:
Вычислить
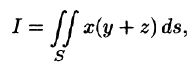
где S — часть цилиндрической поверхности 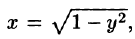 отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
Решение:
Воспользуемся формулой (57.6). Поскольку
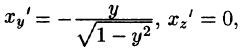
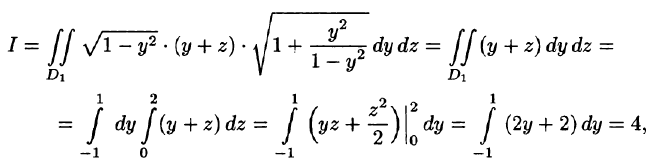
то где 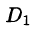 — прямоугольник
— прямоугольник 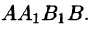
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
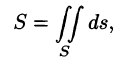
или
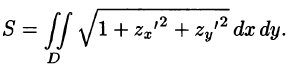
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы  Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 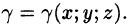 Для нахождения массы поверхности:
Для нахождения массы поверхности:
- Разбиваем поверхность S на п частей
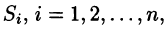 площадь которой обозначим
площадь которой обозначим 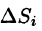 .
. - Берем произвольную точку
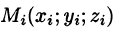 в каждой области
в каждой области  . Предполагаем, что в пределах области
. Предполагаем, что в пределах области 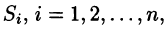 плотность постоянна и равна значению ее в точке
плотность постоянна и равна значению ее в точке 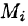 .
. - Масса
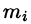 области
области мало отличается от массы
мало отличается от массы 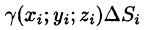 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью
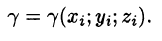
4. Суммируя 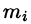 по всей области, получаем:
по всей области, получаем: 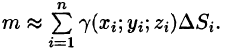
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей  , т. е.
, т. е.
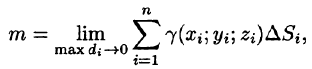
т. е.
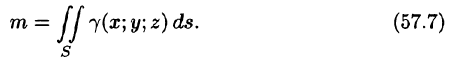
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
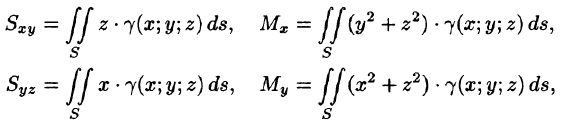
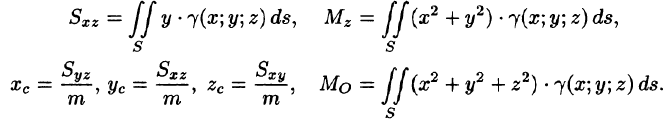
Пример:
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 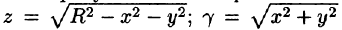 — поверхностная плотность полусферы.
— поверхностная плотность полусферы.
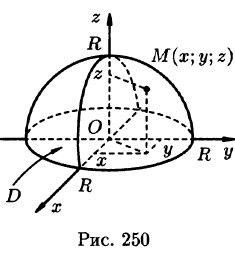
По формуле (57.7) находим:
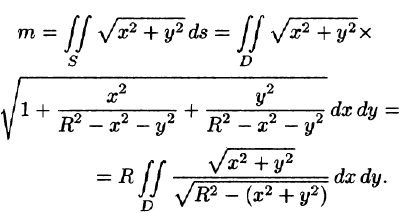
Переходим к полярным координатам:
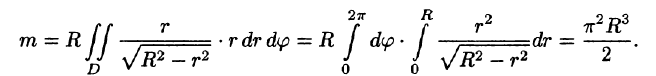
внутренний интеграл вычислен с помощью подстановки r= Rsint:
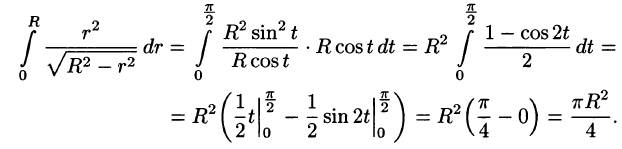
Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 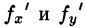 — функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).
— функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).
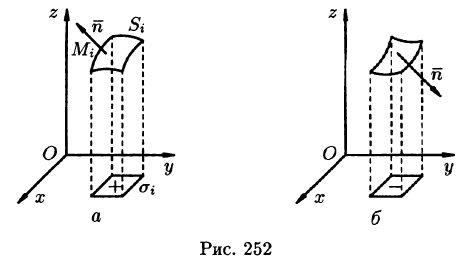
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части  , где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции
, где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е.
берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е.  со знаком «минус», если выбрана нижняя сторона поверхности (или
со знаком «минус», если выбрана нижняя сторона поверхности (или  ) (см. рис. 252, б). В этом случае интегральная сумма имеет вид
) (см. рис. 252, б). В этом случае интегральная сумма имеет вид

где  — площадь проекции
— площадь проекции  на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
Предел интегральной суммы (58.1) при  если он существует и не зависит от способа разбиения поверхности S на части
если он существует и не зависит от способа разбиения поверхности S на части  и от выбора точек
и от выбора точек 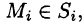 называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается
называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается
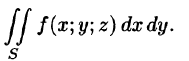
Итак
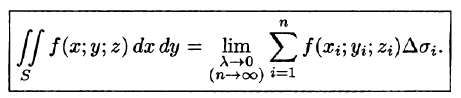
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
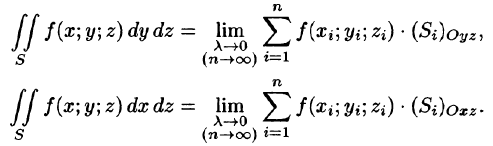
Общим видом поверхностного интеграла II рода служит интеграл
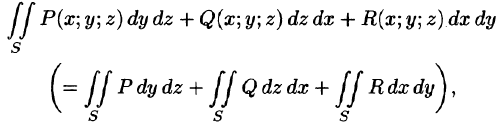
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 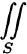 , по внутренней
, по внутренней 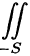 .
.
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям 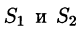 (аддитивное свойство), если
(аддитивное свойство), если 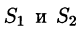 пересекаются лишь по границе, их разделяющей.
пересекаются лишь по границе, их разделяющей. - Если
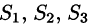 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
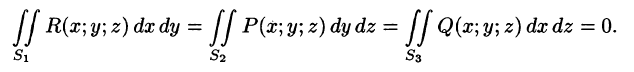
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 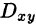 ) — проекции поверхности S на плоскость Оху.
) — проекции поверхности S на плоскость Оху.
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда 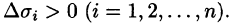
Так как 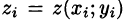 , то интегральная сумма (58.1) может быть записана в виде
, то интегральная сумма (58.1) может быть записана в виде
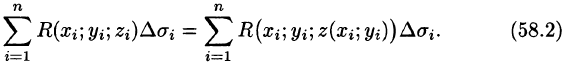
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 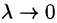 , получаем формулу
, получаем формулу
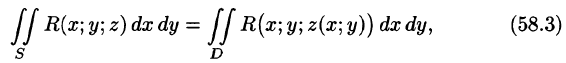
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
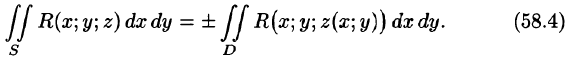
Аналогично
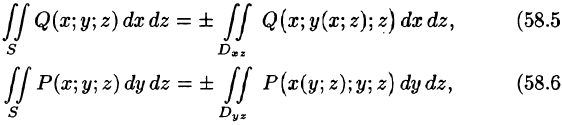
где 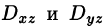 — проекции поверхности S на плоскости Oxz и Oyz соответственно (замкнутые области).
— проекции поверхности S на плоскости Oxz и Oyz соответственно (замкнутые области).
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
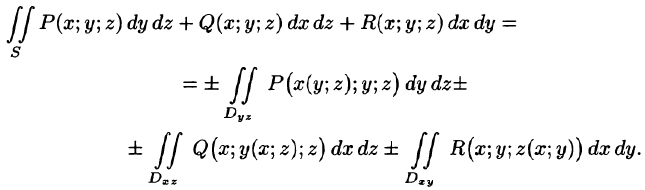
Замечание:
Можно показать справедливость равенств
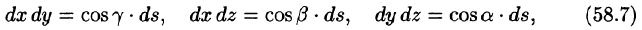
— элемент площади поверхности 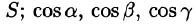 — направляющие косинусы нормали n к выбранной стороне поверхности S.
— направляющие косинусы нормали n к выбранной стороне поверхности S.
Поверхностные интегралы I и II рода связаны соотношением
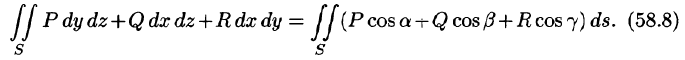
Пример:
Вычислить
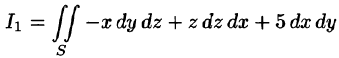
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора  = (2; —3; 1) плоскости:
= (2; —3; 1) плоскости:
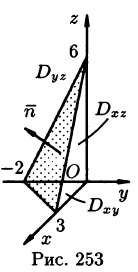
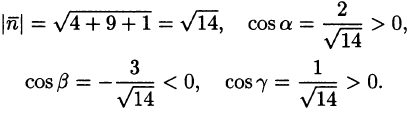
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
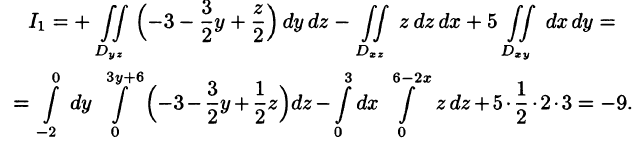
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
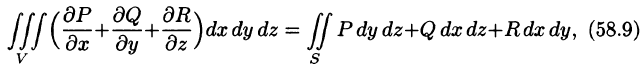
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
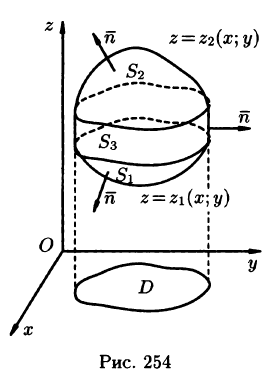
Пусть область V ограничена снизу поверхностью  , уравнение которой
, уравнение которой 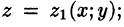 сверху — поверхностью
сверху — поверхностью 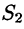 , уравнение которой
, уравнение которой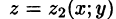 (функции
(функции 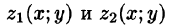 непрерывны в замкнутой области D — проекции V на плоскость
непрерывны в замкнутой области D — проекции V на плоскость 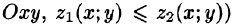 , сбоку — цилиндрической поверхностью
, сбоку — цилиндрической поверхностью 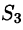 , образующие которой параллельны оси Oz (см. рис. 254).
, образующие которой параллельны оси Oz (см. рис. 254).
Рассмотрим тройной интеграл
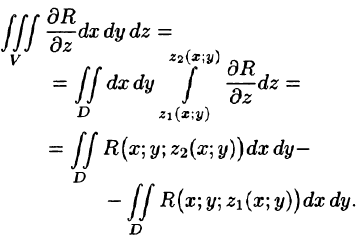
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 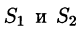 соответственно (см. (58.3)). Получаем:
соответственно (см. (58.3)). Получаем:
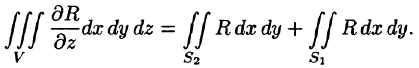
Добавляя равный нулю интеграл 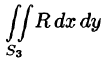 по внешней стороне
по внешней стороне 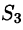 (см. свойство 5 п. 58.1), получим:
(см. свойство 5 п. 58.1), получим:
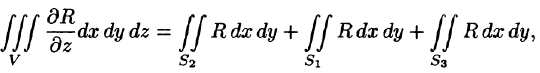
или
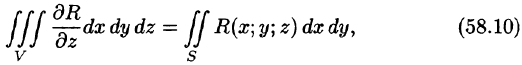
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
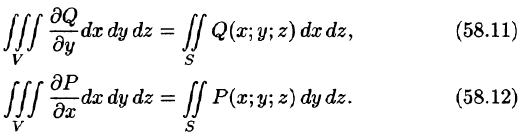
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример:
Вычислить
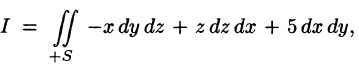
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
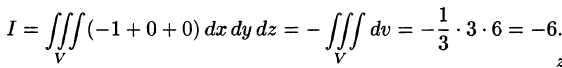
Заметим, что интеграл 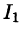 (см. пример 58.1) можно вычислить иначе:
(см. пример 58.1) можно вычислить иначе:
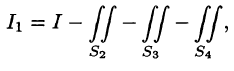
где поверхности 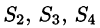 есть соответственно треугольники ОАС, АОВ, СОВ (см. рис. 255). Имеем:
есть соответственно треугольники ОАС, АОВ, СОВ (см. рис. 255). Имеем:
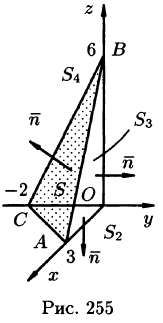
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
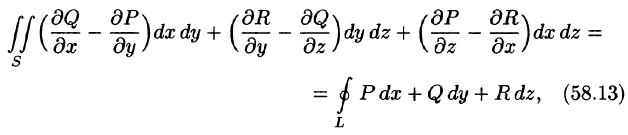
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции  непрерывны в замкнутой области D (проекции поверхности S на плоскость Оху),
непрерывны в замкнутой области D (проекции поверхности S на плоскость Оху),  — граница области D (см. рис. 256).
— граница области D (см. рис. 256).
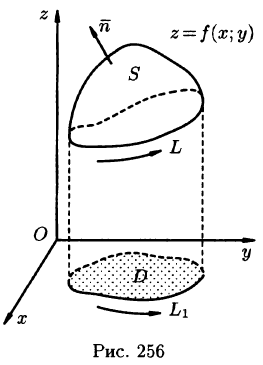
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида 
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на  . Интегральные суммы для криволинейных интегралов II рода по контурам
. Интегральные суммы для криволинейных интегралов II рода по контурам 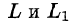 совпадают. Поэтому
совпадают. Поэтому
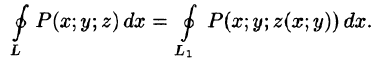
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
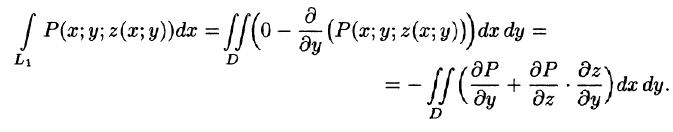
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
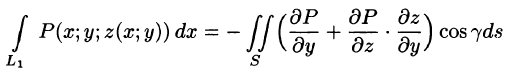
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е.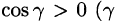 — острый угол между нормалью
— острый угол между нормалью 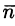 к поверхности S и осью Oz), то нормаль
к поверхности S и осью Oz), то нормаль 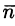 имеет проекции
имеет проекции 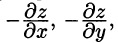 1. Направляющие косинусы пропорциональны соответствующим проекциям:
1. Направляющие косинусы пропорциональны соответствующим проекциям:
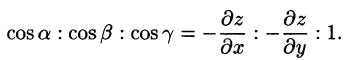
Отсюда 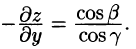 Тогда
Тогда
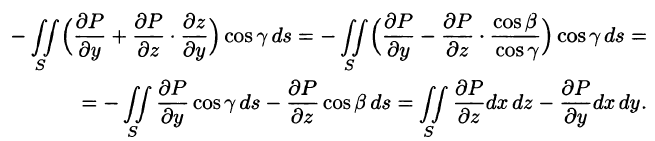
Следовательно,
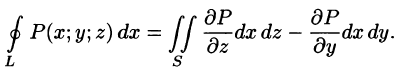
Аналогично получаются при соответствующих условиях еще два равенства:
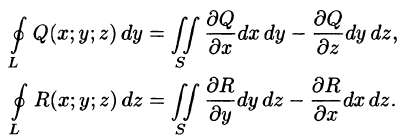
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
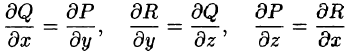
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
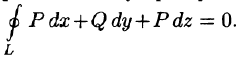
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
Пример:
Вычислить 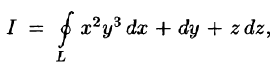 где контур L — окружность
где контур L — окружность 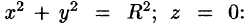 а) непосредственно,
а) непосредственно,
б) используя формулу Стокса, взяв в качестве поверхности полусферу 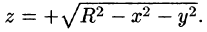
Решение: Поверхность интегрирования изображена на рисунке 257.
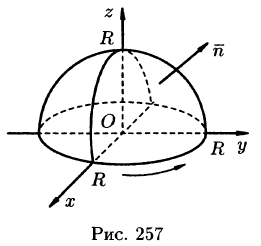
а) Запишем уравнение окружности в параметрической форме:
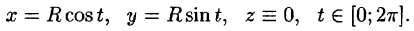
По формуле (56.7) имеем:
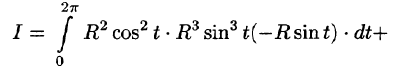
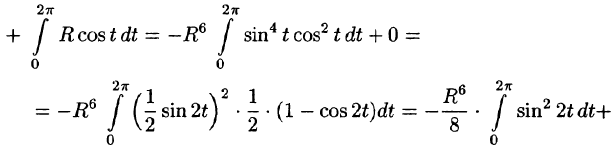
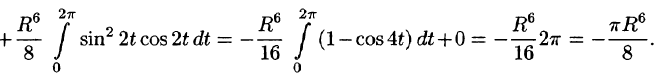
б) По формуле Стокса (58.13) находим:
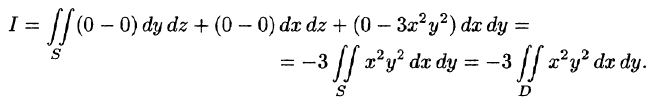
Переходя к полярным координатам, получаем:
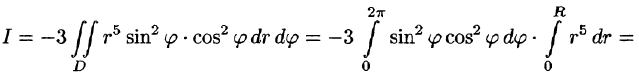
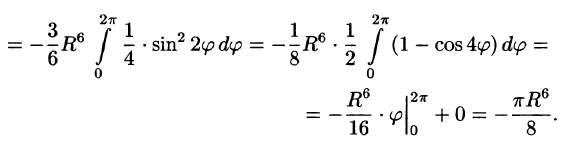
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью 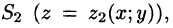 снизу — поверхностью
снизу — поверхностью 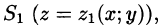 сбоку — цилиндрической поверхностью
сбоку — цилиндрической поверхностью 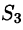 , образующие которой параллельны оси Oz:
, образующие которой параллельны оси Oz:
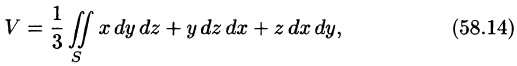
где 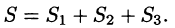
Действительно, положив в формуле Остроградского-Гаусса (58.9) 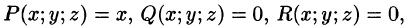 находим:
находим:
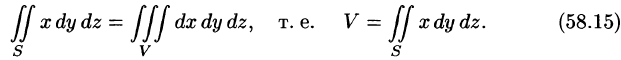
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:

Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу

выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат


4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Рассмотрим интегралы от функций, заданных на поверхностях, так называемые поверхностные интегралы.Теория поверхностных интегралов во многом аналогична теории криволинейных интегралов. Различают поверхностные интегралы первого и
второго рода.
4.1. Поверхностные интегралы первого типа. Пусть функция f (x, y, z)
определена на кусочно-гладкой поверхности S , ограниченной кусочногладким контуром (рис. 4.1). Разобьем
|
поверхность |
S кривыми на n |
частей |
|
|
Рис. 4.1 |
S1, S2…, Sn , |
площади которых |
равны |
соответственно ∆s1, ∆s2…, ∆sn . Взяв в пределах каждой части Si ,i =1, n произвольную точку M i (xi , yi , zi ) , вычислим значение функции в ней и составим следующую сумму:
|
n |
|||||
|
σn = ∑ f (xi , yi, zi )∆si |
|||||
|
i=1 |
для функции f (x, y, z) по |
||||
|
которая называется интегральной |
суммой |
||||
|
поверхности S. |
|||||
|
Конечный предел I этой |
суммы |
при стремлении |
к нулю |
||
|
наибольшего λ из диаметров всех частичных поверхностей S i |
i = |
, |
|||
|
1, n |
если он существует и не зависит ни от способа разбиения поверхности на частичные, ни от выбора точек, то он называется поверхностным интегралом первого типа (по площади поверхности) от функции
|
f (x, y, z) по поверхности S и обозначается символом |
∫∫ f (x, y, z)ds. |
|
|
Значит, по определению |
S |
|
|
n |
= ∫∫ f (x, y, z)ds. |
|
|
I = lim ∑ f (xi , yi, zi )∆si |
(4.1) |
|
|
λ→0 i =1 |
S |
Поверхностный интеграл первого типа представляет собой обобщение двойного интеграла, поэтому условия существования двойного интеграла и его свойства легко переносятся на поверхностный интеграл первого типа.
Вычисление поверхностных интегралов первого типа сводится к вычислению двойных интегралов: исходя из уравнения поверхности S,
35
подынтегральное выраражение преобразуется к двум переменным, областью изменения которых будет проекция поверхности S на соответствующую этим переменным координатную плоскость.
Пусть поверхность S задана уравнением z = z(x, y) и z(x, y) непрерывна вместе со своими частными производными z′x , z′y в замкнутой области Sxy , являющейся проекцией поверхности S на координатную плоскость xOy, тогда
|
∫∫ f (x, y, z)ds = ∫∫ f (x, y, z(x, y)) 1+(z′x )2 +(z′y )dxdy . |
(4.2) |
|
|
S |
S xy |
Эта формула выражает поверхностный интеграл первого типа через двойной интеграл по проекции поверхности S на координатную плоскостьxOy.
Аналогично вычисляются поверхностные интегралы первого типа по поверхности S через двойные интегралы по ее проекциям на
|
координатные плоскости xOz и yOz соответственно: |
|||
|
∫∫ f (x, y, z)ds = ∫∫ f (x, y(x, z), z) |
1+( y′x )2 +( y′z )dxdz , |
(4.3) |
|
|
S |
S xz |
||
|
∫∫ f ( x, y,z )ds = ∫∫ f ( x( y,z ), y,z ) |
1 +( x′y )2 +( x′z )dydz . |
(4.4) |
|
|
S |
S yz |
С помощью поверхностных интегралов первого типа можно вычислить площадь поверхности, а также массу, статические моменты, моменты инерции и координаты центра масс для материальных поверхностей с известной поверхностной плотностью распределения масс.
Пример 4.1. Вычислить
∫∫ 1 + 4x2 + 4 y 2 ds , где S – часть парабо-
1 + 4x2 + 4 y 2 ds , где S – часть парабо-
S
лоида вращения z =1 − x2 − y 2 , отсеченного плоскостью z = 0 .
Решение. Спроектируем поверхность
Рис. 4.2
S на плоскость xOy.
Проекция Sxy – есть круг, ограниченный окружностью x2 + y2 =1 (рис.
4.2). Заданный поверхностный интеграл будем вычислять по формуле (4.2), для чего найдем z′x = −2x, z′y = −2 y.Тогда, совершая в двойном
36

|
интеграле |
переход |
к полярным |
координатам, |
так как |
Sxy есть круг, |
||||||
|
получим |
|||||||||||
|
∫∫ |
1+4x2 + 4 y2 ds = ∫∫ |
1+4x2 + 4 y2 |
1+4x2 + 4 y2 dxdy = |
||||||||
|
S |
S xy |
||||||||||
|
= ∫∫(1+ 4x2 + 4 y2 )dxdy = |
|||||||||||
|
S xy |
|||||||||||
|
2π |
1 |
2π |
ρ |
2 |
1 |
3 |
2π |
||||
|
= ∫ dϕ∫(1 + 4ρ2 )ρdρ = ∫ |
( |
+ ρ4 ) |
dϕ = |
∫dϕ. |
|||||||
|
2 |
|||||||||||
|
0 |
0 |
0 |
2 |
0 |
0 |
||||||
#
4.2. Двусторонние поверхности. Поверхность S называется
двусторонней, если обход по любому замкнутому контуру, лежащему на поверхности S и не пересекающему ее границ, при возвращении в исходную точку не меняет направление нормали к поверхности. В противном случае поверхность называется односторонней. Примеры двусторонних поверхностей: плоскость, сфера и любая поверхность, заданная уравнениемz = z(x, y), гдеz = z(x, y), z′x (x, y) , z′y (x, y) – непрерывны в некоторой области G. Примером односторонней поверхности является лист Мёбиуса.
4.3. Поверхностный интеграл второго типа. Пусть S – гладкая поверхность, заданная уравнением z = z(x, y) и функция f (x, y, z)
определена в точках поверхности S.
Выберем одну из сторон поверхности, то есть одно из двух возможных направлений нормали в точках поверхности (этим мы сориентировали поверхность). Если нормали составляют острые углы с
осью Oz , то будем говорить о верхней стороне поверхности ( о положительном направлении нормали), а если нормали составляют – тупые углы с осью Oz , то говорим о нижней стороне поверхности ( об отрицательном направлении нормали).
Разобьем поверхность S произвольным образом на n частей S1, S2…, Sn , и через (Sxy )i обозначим проекцию i-ой части поверхности
на плоскость xOy. В пределах каждой частичной поверхности Si ,i =1, n выберем произвольную точку M i (xi , yi , zi ) , вычислим значение функции
в ней и составим сумму
n
σn = ∑ f (xi , yi , zi )∆si , i =1
где ∆si – площадь(Sxy )i , взятая со знаком плюс, если выбрана верхняя сторона поверхности S и со знаком минус, если выбрана нижняя сторона
37
поверхности S. Эта сумма σn называется интегральной суммой для функции f (x, y, z) .
Конечный предел I интегральной суммы, при стремлении к нулю наибольшего λ из всех диаметров проекций (Sxy )i , если он существует и
не зависит ни от способа разбиения поверхности S, ни от выбора точек
M i (xi , yi , zi ) , то этот предел называется поверхностным интегралом второго типа от функции f (x, y, z) по выбранной стороне поверхности по переменным x и y и обозначается ∫∫ f (x, y, z)dxdy . Таким образом, по
S
определению
|
n |
||
|
I = lim ∑ f (xi , yi , zi )∆si = ∫∫ f (x, y, z)dxdy . |
(4.5) |
|
|
λ→0 i =1 |
S |
|
|
Функция f (x, y, z) |
называется в этом случае интегрируемой по |
поверхности S по переменным x и y .
Аналогично можно определить поверхностные интегралы второго типа по выбранной стороне поверхности S по переменным y и z, по переменным x и z:
|
∫∫ f (x, y, z)dydz , |
∫∫ f (x, y, z)dxdz . |
|
S |
S |
Пусть P(x, y, z),Q(x, y, z), R(x, y, z) функции, интегрируемые по
поверхности S по переменным y и z, x и z, x и y соответственно. Сумма интегралов
|
∫∫P(x, y, z)dydz, |
∫∫Q(x, y, z)dxdz, |
∫∫R(x, y, z)dxdy |
|
|
S |
S |
S |
|
|
называется общим интегралом второго типа и обозначается |
|||
|
∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy . |
(4.6) |
||
|
S |
Так как поверхность S считаем двусторонней и интеграл распространяется на определенную ее сторону, то при изменении стороны поверхности интегрирования поверхностный интеграл второго типа меняет знак на противоположный – в этом его отличие от поверхностного интеграла первого типа.
Вычисление поверхностных интегралов второго типа сводится к вычислению двойных интегралов.
Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность S задана уравнениемz = z(x, y), где z(x, y) непрерывна в
замкнутой области Sxy – проекции поверхности S на плоскость xOy; функция f (x, y, z) непрерывна на S. Тогда справедлива формула
38

|
∫∫ f (x, y, z)dxdy = ∫∫ f (x, y, z(x, y))dxdy , |
(4.7) |
|||
|
S |
S xy |
|||
|
выражающая поверхностный интеграл второго типа по переменным x и |
y |
|||
|
через двойной. Если выбрать нижнюю сторону поверхности S, то перед |
||||
|
интегралом в правой части появится знак минус. |
||||
|
Аналогично справедливы формулы |
||||
|
∫∫ f (x, y, z)dydz = ∫∫ f (x( y, z), y, z)dydz , |
(4.8) |
|||
|
S |
S yz |
|||
|
∫∫ f (x, y, z)dxdz = ∫∫ f (x, y(x, z), z)dxdz , |
(4.9) |
|||
|
S |
S xz |
|||
|
где поверхность S |
задана |
соответственно уравнениями |
x = x( y, z) |
и |
|
y = y(x, z) а Syz |
и Sxz – |
проекции поверхности S соответствено |
на |
плоскости yOz и xOz .
Для вычисления интеграла общего вида (4.6) используются формулы (4.7)–(4.9), если поверхность S однозначно проектируется на все
координатные плоскости. В более сложных случаях поверхность S разбивают на части, обладающие указанными свойствами, а общий интеграл представляют в виде интегралов по этим частям.
Пример 4.2.Вычислить
∫∫( y2 + z2 )dxdy , где S верхняя сторона
|
S |
||||||||||
|
поверхности z = |
1 − x2 |
, отсекаемая плос- |
||||||||
|
костями y = 0, y =1. |
||||||||||
|
Решение. Уравнением x2 + z2 =1 – |
||||||||||
|
задается круговой цилиндр с образующей, |
||||||||||
|
параллельной оси Oy , а плоскости y = 0 и |
||||||||||
|
y =1 |
параллельны |
координатной |
||||||||
|
плоскости xOz (рис. |
4.3). |
Проекцией |
||||||||
|
Рис. 4.3 |
поверхности S на плоскость xOy является |
|||||||||
|
прямоугольник Sxy , определяемый неравенствами −1 ≤ x ≤1, |
0 ≤ y ≤1. |
|||||||||
|
Тогда по формуле (4.7) имеем |
1 |
1 |
||||||||
|
∫∫( y2 + z2 )dxdy = ∫∫( y2 +(1− x2 ))dxdy = ∫dx∫( y2 − x2 +1)dy = |
||||||||||
|
S |
S xy |
−1 |
0 |
|||||||
|
1 |
y |
3 |
+(1− x2 ) y) |
1 |
||||||
|
= ∫dx( |
= |
|||||||||
|
−1 |
3 |
0 |
||||||||
39
|
1 |
4 |
− x2 )dx |
4x |
x |
3 |
1 |
4 |
1 |
4 |
1 |
||||||||||||||||||||
|
= ∫( |
= ( |
− |
) |
= |
− |
+ |
− |
= 2. |
||||||||||||||||||||||
|
3 |
3 |
|||||||||||||||||||||||||||||
|
−1 |
3 |
3 |
−1 |
3 |
3 |
3 |
||||||||||||||||||||||||
|
# |
||||||||||||||||||||||||||||||
|
Пример 4.3. Вычислить |
||||||||||||||||||||||||||||||
|
∫∫xdydz + ydxdz + zdxdy, где S – верхняя |
||||||||||||||||||||||||||||||
|
S |
||||||||||||||||||||||||||||||
|
сторона части плоскости x + z −1 = 0 |
||||||||||||||||||||||||||||||
|
отсеченная плоскостями y = 0, y = 4 и |
||||||||||||||||||||||||||||||
|
расположенная в первом октанте (рис. 4.4). |
||||||||||||||||||||||||||||||
|
Решение. Проекция поверхности S на |
||||||||||||||||||||||||||||||
|
плоскость xOy есть прямоугольник Sxy , |
||||||||||||||||||||||||||||||
|
определяемый неравенствами 0 ≤ x ≤1, |
Рис. 4.4 |
|||||||||||||||||||||||||||||
|
0 ≤ y ≤ 4 . Проекция поверхности S на |
||||||||||||||||||||||||||||||
|
плоскость yOz есть прямоугольник |
S yz , определяемый неравенствами |
|||||||||||||||||||||||||||||
|
0 ≤ z ≤1, 0 ≤ y ≤ 4 . Так как плоскость S перпендикулярна плоскости |
||||||||||||||||||||||||||||||
|
xOz , то ∫∫ydxdz = 0. Тогда по формулам (4.7) и (4.9) имеем |
||||||||||||||||||||||||||||||
|
S |
∫∫xdydz + ydxdz + zdxdy = ∫∫(1 − z)dydz + |
|||||||||||||||||||||||||||||
|
S |
S yz |
|||||||||||||||||||||||||||||
|
4 |
1 |
4 |
1 |
|||||||||||||||||||||||||||
|
+ ∫∫(1 − x)dxdy = ∫dy∫(1− z)dz + ∫dy∫(1 − x)dx = |
||||||||||||||||||||||||||||||
|
S xy |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||
|
4 |
(1 |
− z) |
2 |
1 4 |
(1− x) |
2 |
1 |
4 |
1 |
|||||||||||||||||||||
|
=2∫ |
dy = 4. |
|||||||||||||||||||||||||||||
|
= ∫dy − |
2 |
+ ∫dy − |
2 |
2 |
||||||||||||||||||||||||||
|
0 |
0 0 |
0 |
0 |
|||||||||||||||||||||||||||
#
4.4. Формула Остроградского. Формула Остроградского устанавливает связь между поверхностным интегралом по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью.
Пусть V–правильная замкнутая область, ограниченная поверхностью S, и пусть функции P(x, y, z),Q(x, y, z), R(x, y, z)
непрерывны вместе со своими частными производными первого порядка в данной области. Тогда имеет место следующая формула:
|
∫∫∫( |
∂P |
+ |
∂Q |
+ |
∂R)dxdydz = ∫∫Pdydz +Qdxdz + Rdxdy, (4.10) |
|
|
V |
∂x |
∂y |
∂z |
S |
||
40

называемая формулой Остроградского1.
С помощью формулы Остроградского удобно вычислять поверхностные интегралы по замкнутым поверхностям.
Пример 4.4. С помощью формулы Остроградского вычислить
|
∫∫xdydz + ydxdz + zdxdy , |
где S |
– |
внешняя |
||||||||||||||||||||||||
|
S |
|||||||||||||||||||||||||||
|
сторона пирамиды, |
ограниченной |
плоскостями |
|||||||||||||||||||||||||
|
x + y + z =1, |
x = 0, y = 0, |
z = 0(рис. 4.5). |
|||||||||||||||||||||||||
|
Решение. |
Согласно |
формуле |
|||||||||||||||||||||||||
|
Остроградского: |
|||||||||||||||||||||||||||
|
P(x, y, z) = x, Q(x, y, z) = y, R(x, y, z) = z. |
|||||||||||||||||||||||||||
|
Тогда: ∂P + |
∂Q + |
∂R |
=1 +1 +1 = 3, и находим |
Рис. 4.5. |
|||||||||||||||||||||||
|
∂x |
∂y |
∂z |
|||||||||||||||||||||||||
|
1 |
1−x |
1−x−y |
|||||||||||||||||||||||||
|
∫∫xdydz + ydxdz + zdxdy = 3∫∫∫dxdydz = 3∫dx ∫dy |
∫dz = |
||||||||||||||||||||||||||
|
S |
V |
0 |
0 |
0 |
|||||||||||||||||||||||
|
1 |
1−x |
1−x−y |
1 |
1−x |
|||||||||||||||||||||||
|
= 3∫dx ∫dy ∫dz = 3∫dx ∫(1 − x − y)dy = |
|||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
|||||||||||||||||||||||
|
1 |
y2 |
1−x |
|||||||||||||||||||||||||
|
3∫dx( y − xy − |
) |
= |
|||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||
|
0 |
0 |
||||||||||||||||||||||||||
|
1 |
1 |
||||||||||||||||||||||||||
|
x |
2 |
−2x +1 |
3 |
1 |
3 (x −1) |
3 |
1 |
||||||||||||||||||||
|
= 3∫(1− x − x + x2 − |
)dx = |
∫(x −1)2 dx = |
= |
. |
|||||||||||||||||||||||
|
2 |
2 |
3 |
2 |
||||||||||||||||||||||||
|
0 |
2 |
0 |
0 |
||||||||||||||||||||||||
#
Замечание 4.1. Связь между поверхностными интегралами первого и второго типов аналогична связи криволинейных интегралов:
∫∫ f (x, y, z)dxdy = ∫∫ f (x, y, z) cosαds ,
S S
∫∫ f (x, y, z)dydz = ∫∫ f (x, y, z) cos βds ,
S S
∫∫ f (x, y, z)dxdz = ∫∫ f (x, y, z) cosγ ds ,
S S
где cosα , cos β , cosγ – направляющие косинусы нормали, отвечающей
|
выбранной стороне поверхности. |
# |
1 Аргументы функций P, Q, R для сокращения записи опускаем.
41

4.5. Формула Стокса. Формула Стокса устанавливает связь между поверхностными и криволинейными интегралами.
|
Пусть поверхность S задана уравнением |
z = z(x, y) , |
где z(x, y), |
|||||||||||||||||||||
|
z′x (x, y) , z′y (x, y) |
непрерывные в области Sxy – проекции поверхности S |
||||||||||||||||||||||
|
на плоскость xOy ; L |
– контур, |
ограничивающий |
поверхность |
S; l – |
|||||||||||||||||||
|
проекция пространственной линии L на плоскость |
xOy , |
являющаяся |
|||||||||||||||||||||
|
конуром, ограничивающим область D. Выберем верхнюю сторону |
|||||||||||||||||||||||
|
поверхности S. Если функции P(x, y, z),Q(x, y, z), R(x, y, z) |
непрерывны |
||||||||||||||||||||||
|
вместе со своими частными производными первого порядка на |
|||||||||||||||||||||||
|
поверхности S, то имеет место следующая формула: |
|||||||||||||||||||||||
|
∫Pdx +Qdy + Rdz = |
|||||||||||||||||||||||
|
L |
|||||||||||||||||||||||
|
= ∫∫ |
(∂Q |
− |
∂P)dxdy +( |
∂R |
− |
∂Q)dydz +(∂P |
− |
∂R)dxdz |
(4.11) |
||||||||||||||
|
S |
∂x |
∂y |
∂y |
∂z |
∂z |
∂x |
|||||||||||||||||
|
(L – обходится в положительном направлении), |
называемая формулой |
||||||||||||||||||||||
|
Стокса. |
|||||||||||||||||||||||
|
Если в качестве поверхности S взять область D на плоскости xOy |
|||||||||||||||||||||||
|
( z = 0 ), то из (4.11) получится формула Грина |
∂Q |
∂P)dxdy . |
|||||||||||||||||||||
|
∫P(x, y)dx +Q(x, y)dy = ∫∫( |
− |
||||||||||||||||||||||
|
L |
D |
∂x |
∂y |
||||||||||||||||||||
|
Таким образом, формула Грина есть частный случай формулы Стокса. |
|||||||||||||||||||||||
|
Заметим, что поверхностный интеграл второго типа в формуле |
|||||||||||||||||||||||
|
Стокса (4.11) может быть заменен поверхностным интегралом первого |
|||||||||||||||||||||||
|
типа. Тогда эта формула примет вид |
|||||||||||||||||||||||
|
∫Pdx +Qdy + Rdz = |
|||||||||||||||||||||||
|
∂Q |
∂P |
L |
∂R |
∂Q |
∂P |
∂R |
|||||||||||||||||
|
= ∫∫ |
− |
) cosα +( |
− |
) cos β +( |
− |
) cosγ |
|||||||||||||||||
|
( |
∂x |
∂y |
∂y |
∂z |
∂z |
∂x |
ds , |
||||||||||||||||
|
S |
|||||||||||||||||||||||
|
где cosα, cos β, cosγ , |
означают |
направляющие |
косинусы |
нормали, |
|||||||||||||||||||
|
отвечающей выбранной стороне поверхности. |
|||||||||||||||||||||||
|
Пример |
4.5. |
С |
помощью формулы |
Стокса |
вычислить |
||||||||||||||||||
|
∫x2 y3dx + dy + zdz, |
где |
L |
окружность, |
заданная уравнениями |
|||||||||||||||||||
|
L |
|||||||||||||||||||||||
|
x2 + y 2 +1, z = 0. |
Поверхностью S служит верхняя сторона полусферы |
||||||||||||||||||||||
|
x2 + y 2 + z 2 =1, |
z > 0 (L обходится в положительном направлении). |
42
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поверхностный интеграл I
рода
Краткая теория
Пусть
– гладкая
поверхность,
– непрерывная
функция на поверхности
. Разобьем произвольным образом поверхность
на
поверхностей,
площади которых
. На каждой поверхности
возьмем
произвольную точку
.
Обозначим
диаметр
поверхности
, а
– наибольший из
диаметров всех поверхностей
данного
разбиения. Тогда предел последовательности интегральных сумм
при
и
, то есть при неограниченном увеличении частичных
поверхностей, когда все частичные поверхности стягиваются в точку, называется
поверхностным интегралом по площади поверхности или поверхностным интегралом I рода:
Основные свойства поверхностных интегралов I рода
1. Поверхностный интеграл не зависит
от выбора стороны поверхности интегрирования, то есть:
где
и
– стороны
поверхности
2. Если поверхность
разбита на
непересекающиеся части
и
то
3. Если
и
– непрерывные
функции
и
– постоянные
числа, то
Вычисление поверхностного интеграла I рода
Если
поверхность
задана уравнением
, однозначно проецируется
на какую-либо координатную плоскость, например плоскость
, и область
является проекцией поверхности
на плоскость
, то поверхностный интеграл
I рода можно вычислить по формуле:
Площадь поверхности
определяют по
формуле:
Примеры решения задач
Задача 1
Вычислить
поверхностный интеграл 1-го рода по поверхности
, где
-часть плоскости
, отсеченная координатными
плоскостями
Решение
Поверхностный
интеграл можно вычислить по формуле:
Проекция
на
плоскости:
Искомый поверхностный
интеграл:
Ответ:
Задача 2
Вычислить
поверхностные интегралы первого рода по поверхности
:
где
– часть поверхности
, отсеченная плоскостью
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сведем
поверхностный интеграл к двойному:
– проекция поверхности
на плоскость
– проекция
Перейдем
к полярным координатам:
Ответ:
Задача 3
С помощью
поверхностного интеграла первого рода
Вычислить
расход
жидкости с полем скоростей.
, протекающей за единицу
времени через часть
плоскости
, лежащую в первом октанте.
Единичная нормаль
направлена вне начала координат.
Решение
Сделаем рисунок плоскости:
Единичная нормаль к плоскости имеет
компоненты
Поверхностный интеграл можно
выразить через двойной интеграл:
где уравнение поверхности
записано в
явном виде:
Область
является
проекцией
на плоскость
и ограничена
линиями:
Внося в двойной интеграл заданные
функции, находим:
Последний запишется через повторный
интеграл:
Ответ:














