Магнитное поле, подобно полю электрическому может быть макроскопическим и микроскопическим. Микроскопическое поле возникает в результате движения элементарных зарядов в веществе. Макроскопическое поле — результат усреднения микроскопических полей по бесконечно малым объемам пространства. Вращения электронов и ядер атомов по отношению к создаваемому ими магнитному полю эквивалентны токам, которые текут в атомах вещества. Средняя плотность такого тока в веществе равна нулю, переноса электрического заряда на макроскопические расстояния не происходит.
В ненамагниченных магнетиках молекулярные токи распределены хаотично, их магнитные поля в среднем взаимно компенсируют друг друга. Намагниченный магнетик можно характеризовать упорядоченным характером молекулярных токов, благодаря чему результирующее магнитное поле вещества не равно нулю.
В тех магнетиках, которые являются проводниками (например, металлы) различают токи проводимости (плотность тока проводимости $overrightarrow{j_{pr}}$), которые относят к упорядоченному движению заряда в макроскопическом понимании (например, движению свободных электронов в металле) и молекулярные токи ($overrightarrow{j_m}$), тогда микроскопическую плотность тока ($overrightarrow{j_{mik}}$) в среде вычисляют как:
[overrightarrow{j_{mik}}=overrightarrow{j_m}+overrightarrow{j_{pr}} left(1right).]
Часто предполагают, что отличие токов проводимости от молекулярных токов в том, что молекулярные токи замыкаются внутри микроскопически малых объектов пространства. Подобное разделение токов на два типа упрощает вывод макро уравнений поля из посылок электронной теории.
Молекулярные токи и индукция магнитного поля
Для того, чтобы вычислить индукцию макроскопического поля молекулярные токи заменяют макроскопическими токами, которые непрерывно изменяются в пространстве. Такие токи имеют название токов намагничивания. Дальше эти плотность этих токов будем обозначать $overrightarrow{j_m}$. Плотность токов проводимости будем обозначать $overrightarrow{j}$. Так получаем, что магнитное поле порождается токами проводимости и токами намагничивания. Если известны эти токи, то можно вычислять индукцию поля $overrightarrow{B},$ используя формулы для вакуума. В таком случае теорема о циркуляции вектора индукции магнитного поля будет иметь вид:
[ointlimits_L{overrightarrow{B}overrightarrow{dl}}={mu }_0left(I+I_mright)left(2right)]
или в дифференциальной форме:
[rotoverrightarrow{B}={mu }_0left(overrightarrow{j}+{overrightarrow{j}}_mright)left(3right),]
где I — ток проводимости, $I_m$ — ток намагничивания, полные токи, которые пронизывают контур L.
Итак, возникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, которые приводят к возникновению магнитных моментов, назвали молекулярными токами. Однако не следует воспринимать этот термин буквально. Молекулярные токи, строго говоря, могут течь только внутри молекулы. При определении намагниченности и других параметров имеют в виду усредненные величины. Магнитные моменты представляют размазанными по объему вещества, а молекулярные токи текущими по всему объему.
Намагниченность
Для характеристики состояния намагниченного состояния магнетика используют вектор намагниченности $(overrightarrow{J})$.
Намагниченностью ($overrightarrow{J}$) называют физическую величину, которая равна:
[overrightarrow{J}=frac{1}{triangle V}sumlimits_{triangle V}{{overrightarrow{p}}_{mi}(4)},]
где $triangle V$ — элементарный объем, $overrightarrow{p_{mi}}$ — магнитные моменты молекул, суммирование осуществляется по всем молекулам в объеме $triangle V$. Из формулы (4) имеем, что:
[p_m=overrightarrow{J}dVleft(5right).]
Связь намагниченности с молекулярными токами
Рассмотрим бесконечно маленький замкнутый контур L, который ограничивает элемент площади $triangle S$ (рис.1). Вычислим циркуляцию намагниченности ($overrightarrow{J}$) по контуру:
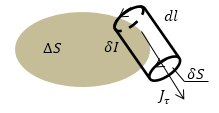
Рис. 1
[intlimits_L{overrightarrow{J}overrightarrow{dl}=intlimits_L{J_{tau }dl}left(6right),}]
где $J_{tau }$- тангенциальная составляющая вектора намагниченности вдоль контура L. Эта составляющая возникает за счет токов, которые текут по замкнутым контурам вокруг линии, вдоль которой проводится интегрирование. Умножим и разделим правую часть выражения (6) на величину $delta S$ (площадь которую обтекает ток в плоскости, которая перпендикулярная линии интегрирования), проведем преобразования в том числе используя выражение (5):
[intlimits_L{J_{tau }dl}=intlimits_L{J_фfrac{dldelta S}{delta S}}=intlimits_L{J_{tau }frac{dV}{delta S}}=intlimits_L{frac{dp_m}{delta S}}left(7right).]
В соответствии с определением магнитного момента ($p_m=ISto {dp}_m=delta Idelta S, $)$ где delta I сила тока, который обтекает площадку delta S,$ причем$ delta I$ пересекает $triangle S$ по нармали. Получаем из (7):
[intlimits_L{frac{dp_m}{delta S}}=intlimits_L{frac{delta I delta S}{дS}}=intlimits_L{delta I}=triangle I_nleft(8right),]
где $triangle I_n$- нормальная составляющая силы тока, которая пересекает площадку $triangle S.$ В результате мы получили:
[intlimits_L{overrightarrow{J}overrightarrow{dl}=triangle I_nleft(9right).}]
Из выражения (9) легко получить:
[overrightarrow{j_m}=rotoverrightarrow{J}left(10right).]
Формула (10) — выражение для объемной плотности молекулярных токов, которые являются причиной намагниченности $overrightarrow{J}$.
Молекулярные токи могут течь и по поверхности раздела меду магнетиками или между магнетиком и вакуумом. Тогда поверхностная плотность молекулярного тока ($i_{m.p}=frac{triangle I_{m.pov}}{l}$) равна:
[overrightarrow{i_{m.p}}=overrightarrow{n}times left(overrightarrow{J_2}-overrightarrow{J_1}right)left(11right),]
где $overrightarrow{n}$ — единичные вектор нормали к поверхности раздела, направленные во вторую среду.
Пусть вещество находится в однородном магнитном поле с индукцией B.
Рассмотрим мысленно внутри тела произвольную поверхность S, ограниченную контуром L (рис.90). Магнитные моменты молекулярных токов ориентированы по вектору магнитной индукции и через поверхность S течет суммарный молекулярный ток.
Полный молекулярный ток через эту поверхность будет определяться только теми токами, которые охватывают контур L, поскольку токи, не охватывающие этот контур, либо не пересекают поверхность совсем, либо пересекают ее дважды в противоположных направлениях.


РИС.90 РИС.91
Чтобы рассчитать полный молекулярный ток через всю поверхность, найдем — какой суммарный ток дают молекулярные токи, охватывающие элемент контура ![]() (рис.91). Этот элемент охватывают только те токи, центры которых лежат внутри изображенного на рисунке косоугольного цилиндра. Суммарный ток будет определяться величиной тока одной молекулы на число молекул, центры которых попадают внутрь цилиндра.
(рис.91). Этот элемент охватывают только те токи, центры которых лежат внутри изображенного на рисунке косоугольного цилиндра. Суммарный ток будет определяться величиной тока одной молекулы на число молекул, центры которых попадают внутрь цилиндра.
Пусть ![]() — концентрация молекул или число молекулярных токов в единице объема, s – площадь обтекаемая молекулярным током, i – величина тока молекулы.
— концентрация молекул или число молекулярных токов в единице объема, s – площадь обтекаемая молекулярным током, i – величина тока молекулы.
![]()
Тогда, суммируя по всем элементам контура L, получим:
 — полный молекулярный ток через поверхность S равен циркуляции вектора намагничивания по контуру L, ограничивающему эту поверхность.
— полный молекулярный ток через поверхность S равен циркуляции вектора намагничивания по контуру L, ограничивающему эту поверхность.
Если ввести объемную плотность токов намагничивания
![]() , то
, то ![]() .
.
Используя теорему Стокса, получим: ![]() .
.
Физический смысл этого выражения в том, что поле вектора намагничивания вихревое, линии замыкаются вокруг вектора объемной плотности тока.
Если ![]() , т. е. вещество однородно, то
, т. е. вещество однородно, то ![]() — молекулярные токи компенсируют друг друга.
— молекулярные токи компенсируют друг друга.
Объемные молекулярные токи возникают в неоднородном веществе, а также в неоднородном магнитном поле.
Рассмотрим картину молекулярных токов вблизи поверхности однородного изотропного тела, находящегося в однородном магнитном поле (рис.92).



РИС.92 РИС.93 РИС.94
В тонком приповерхностном слое толщиной порядка радиуса отдельного молекулярного тока все молекулярные токи текут одном направлении, образуя поверхностный ток с линейной поверхностной плотностью ![]() (рис.92).
(рис.92).
Найдем связь вектора намагничивания с поверхностной плотностью тока намагничивания, выделив внутри тела малый объем в виде цилиндра с образующими, составляющими угол ![]() с вектором магнитной индукции и основаниями перпендикулярными направлению поля (рис.93).
с вектором магнитной индукции и основаниями перпендикулярными направлению поля (рис.93).
Рассчитаем магнитный момент этого малого объема, исходя из двух позиций. Во-первых, если вещество однородное и изотропное, то: ![]() .
.
Во вторых, если учесть поверхностный ток намагничивания, то: ![]() .
.
Сравнив эти выражения, получим: ![]() — линейная плотность поверхностного тока намагничивания вдоль произвольного направления равна проекции вектора намагничивания на это направление.
— линейная плотность поверхностного тока намагничивания вдоль произвольного направления равна проекции вектора намагничивания на это направление.
В отличие от объемных токов поверхностные токи всегда возникают при намагничивании тел.
На рис.94 картина поверхностных молекулярных токов в случае однородно намагниченного шара. Линейная плотность поверхностного тока максимальна на «экваторе» так как
![]() и убывает до нуля при приближении к полюсам.
и убывает до нуля при приближении к полюсам.
Молекулярные токи в физике, теория и онлайн калькуляторы
Молекулярные токи
Определение молекулярных токов
Определение
Молекулярными токами называют токи, которые существуют в пределах одного атома (молекулы), вызваны они движением электронов в
атомах (молекулах, ионах).
Молекулярные токи еще называют микротоками в противовес макротокам, которые связывают с движением заряженных тел. Молекулярные токи существуют во всех веществах. О существовании молекулярных токов говорил еще А. Ампер.
Молекулярные токи являются причиной намагничивания веществ (магнетиков) во внешнем магнитном поле. Если магнетик не намагничен, то молекулярные токи располагаются в нем хаотично, при этом суммарное действие их равно нулю. При внесении магнетика в магнитное поле расположение молекулярных токов становится частично или полностью упорядоченным. Так, магнетик можно представлять как систему мелких ориентированных токов. Каждый молекулярный ток в магнетике имеет определенный магнитный момент (${overline{p}}_m$), при внесении магнетика в магнитное поле, вещество в целом приобретает магнитный момент, который равен векторной сумме моментов молекулярных токов.
Суммарный магнитный момент молекулярных токов, которые заключены в единице объема вещества, называют вектором намагниченности ($overline{J}$):
[overline{J}=frac{1}{Delta V}sumlimits^N_{i=1}{{overline{p}}_{mi} left(1right).}]
${overline{p}}_{mi}$ – магнитный момент отдельной молекулы (атома); N – число молекул в объеме $Delta V$.
Природа молекулярных токов
Все атомы состоят из положительного ядра, в котором сосредотачивается почти вся масса атома и некоторого числа электронов. Суммарный отрицательный заряд электронов в атоме равен положительному заряду ядра, атом в нормальном состоянии электрически нейтрален.
Электроны в атоме непрерывно движутся. При объяснении многих явлений считают, что орбиты движения электронов вокруг ядра представляют собой окружности (или в крайнем случае эллипсы). Каждый электрон в атоме перемещается по собственной орбите, разные орбиты электронов находятся в разных плоскостях.
Электроны, вращающиеся по орбитам, образуют замкнутые токи, поэтому и предполагают, что именно они являются молекулярными токами.
Гиромагнитное отношение
Электроны имеют не только заряд, но и массу. Поэтому каждый электрон, движущийся по орбите, обладает не только магнитным моментом, как любой замкнутый ток, но и имеет определенный механический момент.
Магнитный момент электрона ($p_m$) на орбите и его момент импульса ($L$) связаны:
[frac{p_m}{L}=-frac{q_e}{2m}left(2right),]
где $q_e$ – заряд электрона; $m$ – масса электрона. Отношение $frac{p_m}{L}$ называют гиромагнитным отношением. Формула (1) справедлива для круговых и эллиптических орбит электронов. Направления векторов магнитного и механического моментов электрона при движении его по орбите направлены в противоположные стороны.
Теорема Лармора
Если на электрон, движущийся по своей орбите, действует магнитное поле, то он получит дополнительное равномерное вращение (явление прецессии), при котором вектор $overline{L}$ будет описывать конус вокруг направления вектора магнитной индукции ($overline{B}$) c некоторой угловой скоростью $overline{omega }$. Электрон – отрицательно заряженная частица, вектор угловой скорости $overline{omega }$ будет направлен параллельно $overline{B}$, величина угловой скорости $omega $ равна:
[omega =frac{q_eB}{2m}left(3right).]
Скорость прецессии не зависит от угла между векторами $overline{L}$ и $overline{B}$.
Описанный выше результат действия магнитного поля на движение электрона по его орбите является содержанием теоремы Лармора, которая говорит:
Действие магнитного поля на электрон состоит в том, что на первоначальное движение частицы накладывается равномерное вращение вокруг направления внешнего магнитного поля.
Так как атом имеет в своем составе совокупность электронов, следовательно, обладает магнитным и механическим моментами. Во внешнем магнитном поле атомы сначала прецессируют, а за тем под воздействием соударений, ориентируются в направлении поля, из-за чего вещество намагничивается.
Примеры задач с решением
Пример 1
Задание. Какова частота прецессии Лармора для орбиты электрона в атоме, если магнитное поле
Земли составляет $B=5cdot {10}^{-5}Тл?$
Решение. Так как масса и заряд электрона нам известны и равны они: $q_e=1,6cdot {10}^{-19}Кл;; m=9,1cdot {10}^{-31}кг,$ то найдем угловую скорость, с которой осуществляется прецессия электрона на его орбите как:
[omega =frac{q_eB}{2m}left(1.1right).]
Проведем вычисления:
[omega =frac{1,6cdot {10}^{-19}cdot 5cdot {10}^{-5}}{2cdot 9,1cdot {10}^{-31}}approx 4,4cdot {10}^6left(frac{1}{с}right).]
Ответ. $omega =4,4cdot {10}^6frac{1}{с}$
Пример 2
Рассмотрим изотропный магнетик. Намагниченность ($overline{J}$) в точке магнетика появляется при действии магнитного поля и определяется $overline{B}. $При слабых магнитных полях:
[overline{J}sim overline{B} left(2.1right).]
В изотропном магнетике $overline{J}||overline{B}$, кроме того имеем:
[overline{J}={mathbf chi }overline{H}left(2.2right),]
где $chi $ – магнитная восприимчивость вещества.
Объемная плотность молекулярного тока (${overline{j}}_{mol}$) пропорциональна объёмной плотности стороннего тока ($overline{j}$):
[{overline{j}}_{mol}=chi overline{j}left(2.3right).]
При отсутствии объемных сторонних токов остаются при намагничивании только поверхностные молекулярные токи.
Рассмотрим бесконечный цилиндрический провод круглого сечения (рис.1). По проводу течет ток, плотность которого $overline{j}$.
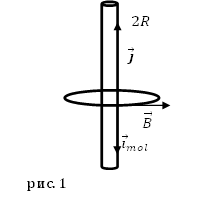
Тогда молекулярный ток в объеме цилиндра имеет плотность:
[{overline{j}}_{mol}=chi overline{j}=left(mu -1right)overline{j}left(2.4right),]
где $mu $ – магнитная проницаемость вещества.
Напряженность магнитного поля тока равна:
[left{ begin{array}{c}
H=frac{I}{2pi r} при r > R \
H=frac{Ir}{2pi R^2} при r < R end{array}
right.left(2.5right).
]
Величина намагниченности:
[left{ begin{array}{c}
J=frac{left(mu -1right)Ir}{2pi R^2} \
J=0 при r>R end{array}
right.при r < Rleft(2.6right).
]
Линии магнитной индукции – концентрические окружности, $overline{J}$ и $overline{H}$ параллельны $overline{B}$.
Величина поверхностного молекулярного тока равна:
[i_{mol}=left(mu -1right)frac{I}{2pi R}left(2.7right).]
Полный молекулярный ток равен нулю.
Читать дальше: постулаты Бора.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как
мы уже выяснили, намагничивание вещества
обусловлено преимущественной ориентацией
и индуцированием (гиромагнитный эффект)
магнитных моментов отдельных молекул
в одном направлении. Это же можно сказать
и об элементарных
круговых токах, связанных с каждой
молекулой (ее
магнитным моментом). Эти токи называют
молекулярными
токами.
Такое поведение молекулярных токов
приводит к появлению макроскопических
токов I′,
называемых токами намагничивания. Они
могут быть как объемными (внутри
вещества), так и поверхностными. Обычные
токи, текущие по проводникам, связаны
с перемещением в веществе носителей
тока (зарядов), их называют токами
проводимости.
Что
бы понять, как возникают токи намагничивания,
представим себе сначала цилиндр из
однородного
магнетика
(магнитные свойства постоянны во всем
объеме вещества),
намагниченность J
которого однородна и направлена вдоль
его оси (цилиндра). В таком случае,
молекулярные токи в намагниченном
магнетике ориентированы в плоскости
перпендикулярной J
и, соответственно оси цилиндра. На рис.17
показана часть цилиндра с его сечением
перпендикулярным оси цилиндра. В сечении
нанесены молекулярные круговые токи.
Все они одинаковы как по величине
кругового тока (отражаем одинаковой
жирностью круговых Рис.17
линий
тока), так и по радиусу, что отражает
однородность намагниченности магнетика.
Из рисунка видно, что у соседних молекул
токи в местах их соприкосновения текут
в противоположном направлении и
макроскопически взаимно компенсируют
друг друга. Нескомпесированными остаются
только те токи, которые выходят на
боковую поверхность цилиндра. Эти токи
и образуют макроскопический поверхностный
ток намагничивания I′,
циркулирующий по боковой поверхности
цилиндра. Ток I′
возбуждает такое же макроскопическое
магнитное поле, что и молекулярные токи
вместе взятые.
Теперь
пусть магнетик неоднородный, например,
только в направлении оси X
и вектор его намагниченности направлен
параллельно оси Z.
Тогда, как показано на рис.18, молекулярные
токи в намагниченном магнетике
ориентированы в плоскости XY,
перпендикулярной, соответственно,
вектору J.
Указанная неоднородность магнетика
отражена возрастающей в направлении
оси X
силой молекулярных токов, соответствующей
толщине их линий. Направление и сила
молекулярных токов указывает на то, что
вектор J
направлен за плоскость рисунка и растет
по модулю с увеличением координаты X.
Из рис.18 видно, что в точках касания
молекулярных токов компоненты токов
параллельные оси X
полностью компенсируют друг друга, а
параллельных оси Y
нет и, следовательно, внутри неоднородного
магнетика возникает макроскопический
объемный ток намагничивания I′,
в данном случае, текущий в направлении
оси Y.
Соответственно говорят о линейной j′
(А/м2)
и поверхностной i′
(А/м) плотностях тока намагничивания.
Рис. 18
6.4.3. О расчете поля b в магнетике.
Можно
утверждать, что вклад от намагниченного
магнетика в поле B
равен вкладу, который был создан тем
же распределением токов намагничивания
I′
в вакууме. То есть в соответствии с
законом Био-Савара это поле B′
и, соответственно, результирующее поле
B
будет определяться выражением (6.23):
B
= B0
+ B′.
Напомним,
что B0
– поле, создаваемое сторонними токами,
например, токами проводимости.
Однако,
неприятность в том, что распределением
токов намагничивания I′
и, соответственно поля B′,
зависит не только от свойств и конфигурации
магнетика, но и от искомого поля B.
Поэтому задача о нахождении поля B
в магнетике в общем случае непосредственно
решена быть не может. Поэтому, так же
как и для P,
устанавливаем связь между током
намагничения I′
и определенным свойством поля вектора
J,
а именно его циркуляцией.
6.4.4.
Циркуляция вектора
J.
Оказывается,
что для стационарного случая циркуляция
намагниченности J
по произвольному замкнутому контуру Г
равна алгебраической сумме токов
намагничивания I′,
охватываемых контуром Г:
 =I′,
=I′,
(6.31)
Г
где
I′
=

, причем интегрирование
проводится по произвольной поверхности,
натянутой на контур Г.
Докажем
эту теорему. Для этого вычислим
алгебраическую сумму молекулярных
токов, охватываемых контуром Г.
Натянем
на контур Г
произвольную поверхность S.
Из рис.19 видно, что внутри контура большая
часть молекулярных токов, которые
пересекают поверхность S
дважды – входят и выходят, пересекая
последнюю, следовательно, вклад от них
в результирующий искомый ток равен
нулю. Другая часть токов овивает контур
Г,
пересекая поверхность S
только один раз. Эти молекулярные токи
и создают макроскопический ток
намагничивания I′,
пронизывающий поверхность S.
Определим его. Рис.19.
Пусть
для простоты магнетик однородный.
Тогда можно положить, что каждый
молекулярный ток и площадь им охватываемая
равны Iм
и Sм
, соответственно. Теперь рассмотрим
малый элемент длиной
dl
контура Г,
который показан на рис.20. Положим, что
вектор намагниченности J
в месте нахождения элемента dl
направлен под углом α
к элементу dl,
направление которого (на рисунке –
слева на право) определяется, выбранным
направлением обхода по контуру Г.
Напомним, что Рис.20.
площади
Sм
молекулярных токов перпендикулярны J.
Из рисунка видно, что элемент dl
контура Г
овивают те молекулярные токи, центры
которых попадают внутрь косого цилиндра
с объемом ∆V
=
Sмcosα
dl.
Все эти молекулярные токи пересекают
поверхность
S
только один раз. Их вклад в ток
намагничивания dI′
= Iмn∆V
, где n
концентрация молекул. Подставляя сюда
выражение для ∆V,
получим dI′
=
IмSмn
cosα
dl
= Jcosα
dl
= Jdl
(в этой записи учли, что IмSм
=
pm
– модуль
магнитного момента отдельного
молекулярного тока, а IмSмn
= J
– модуль магнитного момента единицы
объема вещества). Проинтегрировав
полученное выражение dI′
=
Jdl
по всему контуру Г,
получим выражение (6.31). Таким образом,
теорема доказана.
Необходимо
отметить, что в случае неоднородного
магнетика ток намагничивания пронизываю
всю поверхность
S
(смотри для сравнения рисунки рис.20 и
рис.18), а не только у ее границы, прилегающей
к контуру Г.
Именно поэтому этот ток и можно (нужно)
представить как I′
=
 , где интегрирование ведется по всей
, где интегрирование ведется по всей
поверхностиS,
ограниченной контуром Г.
Дифференциальная
форма записи уравнения (6.31)
имеет вид:
rotJ
= j′
или
[ J]
J]
= j′
, (6.32)
т.е.
ротор вектора J
равен плотности тока намагничивания в
той же точке пространства.
Заметим,
поле J
– вектора намагниченности магнетика
определяется всеми токами, как токами
I′
, так и токами проводимости
I
(сторонними
токами).
(Но!
в
некоторых случаях – определенная
симметрия, J
может определяться только I′.)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
(![]() – радиус-вектор, проведенный от элемента тока в точку наблюдения 4)? находится из закона Био-Савара, который в системе единиц измерений СИ имеет вид:
– радиус-вектор, проведенный от элемента тока в точку наблюдения 4)? находится из закона Био-Савара, который в системе единиц измерений СИ имеет вид:
![]() ,
, ![]() – численный коэффициент, появляющийся в системе СИ.
– численный коэффициент, появляющийся в системе СИ.
С ила
ила ![]() , действующая на элемент с током
, действующая на элемент с током ![]() в магнитном поле напряженности
в магнитном поле напряженности ![]() при отсутствии среды
при отсутствии среды ![]() , определяются из формулы Ампера:
, определяются из формулы Ампера: ![]() в системе СИ.
в системе СИ.
Используя эти формулы, найдем силу взаимодействия элементов тока. Рассмотрим два элемента тока ![]() и
и ![]() , находящиеся на расстоянии
, находящиеся на расстоянии ![]() друг от друга. (рис.12)? Поле создаваемое первым элементом тока в месте нахождения второго, по закону Био-Савара, равно
друг от друга. (рис.12)? Поле создаваемое первым элементом тока в месте нахождения второго, по закону Био-Савара, равно ![]() , а сила
, а сила ![]() , испытываемая вторым элементом со стороны первого, находится по формуле Ампера и равна
, испытываемая вторым элементом со стороны первого, находится по формуле Ампера и равна  .
.
Аналогично можно найти и силу, испытываемую первым элементом по стороны второго: ![]() , где
, где ![]() .
.
При полевом описании используют инварианты поля (т.е. величины, зависящие только от свойств поля): поток, циркуляцию их дифференциальные аналоги (дивергенция, ротор).
С помощью математических операций было установлено:
1. Поток напряженности магнитного поля ![]() через любую замкнутую поверхность равен нулю, т.е.
через любую замкнутую поверхность равен нулю, т.е. ![]()
2. Циркуляция вектора напряженности магнитного поля по любому замкнутому контуру L, пропорциональна алгебраической сумме сил токов, пересекающих поверхность S, ограниченную этим контуром, т.е. ![]()
![]() .
.
-
Дивергенция вектора напряженности магнитного поля
 равна нулю:
равна нулю:  .
. -
Ротор напряженности магнитного поля равен плотности тока проводимости:
![]()
Ротор и дивергенция как математические величины, содержащие производные, задаются в областях, удовлетворяющим определенным условиям, в частности, ими нельзя пользоваться на поверхностях разрыва вектора и поэтому важно постановить граничные условия. Используя математические операции можно показать, что нормальные составляющие вектора напряженности магнитного поля на границе двух сред не изменяются, т.е. если ![]() – нормальная составляющая напряженности магнитного поля во второй среде,
– нормальная составляющая напряженности магнитного поля во второй среде, ![]() – нормальная составляющая напряженности магнитного поля в первой среде, то
– нормальная составляющая напряженности магнитного поля в первой среде, то ![]() –
–![]() =0. Это условие записывают, используя символ
=0. Это условие записывают, используя символ ![]() ,
,
т.е. ![]()
![]() –
– ![]() =0.
=0.
Ч то касается тангенциальных составляющих вектора
то касается тангенциальных составляющих вектора ![]() ,
, ![]() и
и ![]() , то для них граничное условие имеет вид
, то для них граничное условие имеет вид ![]() , где – есть перпендикулярная к
, где – есть перпендикулярная к ![]() слагающая плотности поверхностного тока (рис. 13). Под N нужно понимать единичный вектор, касательный к поверхности и перпендикулярный к касательному же к поверхности вектору
слагающая плотности поверхностного тока (рис. 13). Под N нужно понимать единичный вектор, касательный к поверхности и перпендикулярный к касательному же к поверхности вектору ![]() . Под плотностью
. Под плотностью ![]() поверхностных токов понимают количество электричества, протекающего в единицу времени через единицу длины отрезка, расположенного на поверхности, по которой течет ток, и перпендикулярного направлению тока. Если
поверхностных токов понимают количество электричества, протекающего в единицу времени через единицу длины отрезка, расположенного на поверхности, по которой течет ток, и перпендикулярного направлению тока. Если ![]() отлично от нуля, то сила протекающего через заштрихованную площадку
отлично от нуля, то сила протекающего через заштрихованную площадку ![]() в пределе
в пределе ![]() будет равна
будет равна ![]() , где
, где ![]() – есть перпендикулярная к
– есть перпендикулярная к ![]() слагающая плотности поверхностного тока. Это условие обычно записывают, используя символ
слагающая плотности поверхностного тока. Это условие обычно записывают, используя символ ![]() :
: ![]() .
.
Здесь введен индекс ![]() вместо
вместо ![]() , чтобы сохранить за
, чтобы сохранить за ![]() значение нормали
значение нормали
к поверхности раздела (![]() направленно из среды 1 в среду 2). Под
направленно из среды 1 в среду 2). Под ![]() надо понимать единичный вектор, касательный к поверхности и перпендикулярный к касательному же вектору
надо понимать единичный вектор, касательный к поверхности и перпендикулярный к касательному же вектору ![]() . Из рассмотрения рис. 13, в котором, соответственно избранному нами направлению отхода заштрихованной площадки
. Из рассмотрения рис. 13, в котором, соответственно избранному нами направлению отхода заштрихованной площадки ![]() , вектор
, вектор ![]() должен быть направлен перпендикулярно плоскости “на нас”, (единичные векторы
должен быть направлен перпендикулярно плоскости “на нас”, (единичные векторы ![]() ,
,![]() ,
,![]() связаны соотношением
связаны соотношением ![]() ).
).
М агнитное поле постоянных токов, как и поле электрическое, можно представить графически с помощью силовых линий магнитного поля. По определению магнитной силовой линией называется линия, направление касательных к которой в каждой точке поля совпадает с направлением вектора
агнитное поле постоянных токов, как и поле электрическое, можно представить графически с помощью силовых линий магнитного поля. По определению магнитной силовой линией называется линия, направление касательных к которой в каждой точке поля совпадает с направлением вектора ![]() в той же точке. Дифференциальное уравнение магнитной силовой линии:
в той же точке. Дифференциальное уравнение магнитной силовой линии:
![]()
Магнитные силовые линии проводят обычно с таким расчетом, чтобы в любом участке поля число линий, пересекающих перпендикулярно к ним площадку единичной поверхности, было пропорционально напряженности поля на этой площадке. Из анализа математических выражений, полученных для магнитного поля следует, что силовые линия магнитного поля должны быть линиями замкнутыми или идти из бесконечности в бесконечность (рис. 14).
2.5.3.Магнитное поле молекулярных токов. (Магнитное поле в непроводящей среде)
Так как молекулярные токи существуют в строго ограниченных областях (например, в объеме молекулы), то в макроскопических объемах их прямое измерение невозможно. Поэтому нужна удобная количественная характеристика магнитных свойств среды, связанная с молекулярными токами. Такой мерой является магнитный момент, создаваемый молекулярными токами. Другими словами, мерой намагниченности магнетика является вектор намагниченности ![]() , равный магнитному моменту молекулярных токов, приходящемуся на единицу объема магнетика, т.е.
, равный магнитному моменту молекулярных токов, приходящемуся на единицу объема магнетика, т.е. ![]() . Этот вектор (по аналогии с вектором электрической поляризации) называют также магнитной поляризацией.
. Этот вектор (по аналогии с вектором электрической поляризации) называют также магнитной поляризацией.
В учебнике Д.В. Белова «Электромагнетизм и волновая оптика» дан вывод формулы, связывающий величину молекулярных токов У с вектором намагниченности ![]() (стр. 73). Сама формула имеет вид
(стр. 73). Сама формула имеет вид ![]()
![]() , т.е. полный молекулярный ток через поверхность S равен циркуляции вектора намагниченности по контуру L, ограничивающему эту поверхность. Так как по определению ток равен потоку вектора плотности тока через поверхность S, то
, т.е. полный молекулярный ток через поверхность S равен циркуляции вектора намагниченности по контуру L, ограничивающему эту поверхность. Так как по определению ток равен потоку вектора плотности тока через поверхность S, то ![]() . Используя математическую формулу теории поля
. Используя математическую формулу теории поля ![]() , можно получить связь плотности молекулярных токов и вектора намагниченности:
, можно получить связь плотности молекулярных токов и вектора намагниченности: ![]() .
.
В однородно намагниченных средах (![]() ) плотность молекулярных токов равна нулю. На границе намагниченных магнетиков и вакуума имеются поверхностные молекулярные токи, так как в вакууме
) плотность молекулярных токов равна нулю. На границе намагниченных магнетиков и вакуума имеются поверхностные молекулярные токи, так как в вакууме ![]() . Существует общая формула, которая связывает величину поверхностного молекулярного тока
. Существует общая формула, которая связывает величину поверхностного молекулярного тока ![]() с вектором намагниченности на границе двух сред. Она имеет вид
с вектором намагниченности на границе двух сред. Она имеет вид ![]() , где
, где ![]() и
и ![]() значения вектора
значения вектора ![]() по обеим сторонам поверхности разрыва, а
по обеим сторонам поверхности разрыва, а ![]() – нормаль к этой поверхности, направленная от 1 к 2.
– нормаль к этой поверхности, направленная от 1 к 2.
Это выражение записывают, используя символ ![]() , т.е.
, т.е. ![]() =
=![]() . Согласно этой формуле, на границе магнетика и вакуума плотность поверхностного молекулярного тока
. Согласно этой формуле, на границе магнетика и вакуума плотность поверхностного молекулярного тока ![]() .
.
В качестве примера рассмотрим цилиндрический магнит, однородно намагниченный по всему объему параллельно своей оси. Внутри магнита плотность молекулярных токов равно нулю. На основаниях цилиндра поверхностных токов также не будет, так как нормаль к этим основаниям параллельна ![]() .
.
Н ормаль к боковой поверхности цилиндра перпендикулярна к
ормаль к боковой поверхности цилиндра перпендикулярна к ![]() , и поэтому плотность поверхностных молекулярных токов на боковой поверхности цилиндра будет отлична от нуля и равна
, и поэтому плотность поверхностных молекулярных токов на боковой поверхности цилиндра будет отлична от нуля и равна ![]() .
.
Качественное объяснение происхождения поверхности токов на границе магнетика и вакуума может быть дано с помощью рис. 15.
На рис. 15 схематично изображен поперечный разрез магнита. Совокупность молекулярных токов внутри магнита может быть представлена как совокупность токов одинаковой силы, обтекающих каждую ячейку (молекулу) магнита в одинаковом направлении, например, против часовой стрелки. Внутри магнита токи смежных молекул взаимно компенсируются, на поверхности же магнита они складываются в круговой ток, обтекающий магнит по поверхности.
2.5.4.Магнитное поле в проводящей среде
В любой микроскопической области проводящего магнетика могут существовать токи проводимостью с плотностью ![]() и молекулярные токи с плотностью
и молекулярные токи с плотностью ![]() и т.о. плотность общего микроскопического тока.
и т.о. плотность общего микроскопического тока.
![]() =
= ![]() +
+![]()
Эти токи создают в микроскопической области магнитное поле напряженностью ![]() , для которого справедливы уравнения:
, для которого справедливы уравнения: ![]()
![]()
Чтобы получить уравнение для макроскопической области, надо усреднить параметры по макроскопическому объему.
Усреднение приводит к выражениям:
![]()
![]() =
=![]() +
+![]()
Среднее значение токов проводимости равно плотности макроскопического тока проводимости ![]() , т.е.
, т.е. ![]() ,
,
а среднее значение молекулярного тока ![]() .
.
Таким образом, ![]() или
или ![]()
В электростатике напряженность макроскопического электрического поля
по определению равна средней напряженности <Е микро> микроскопического поля; Казалось бы, и в случае магнитостатики надо поступить аналогично, т.е. определить напряженность макроскопического магнитного поля как среднюю напряженность поля микроскопического.
Однако исторически сложилось по другому. Напряженность магнитного поля ![]() в магнитной среде в системе СИ определили как
в магнитной среде в системе СИ определили как ![]() , а среднее значение напряженности микроскопического поля назвали вектором магнитной индукции и обозначили
, а среднее значение напряженности микроскопического поля назвали вектором магнитной индукции и обозначили ![]() . В новых обозначениях уравнения приняли вид:
. В новых обозначениях уравнения приняли вид:
