Прежде, чем приступить к рассмотрению новой темы вспомним, что
каждой точке прямой ставится в соответствие некоторая точка окружности.
Также вспомним, что центральный угол, опирающийся на дугу, длина
которой равна радиусу окружности, называется углом в один радиан.
Вспомним формулу перехода от радианной меры к градусной рад
и формулу перехода от градусной меры к радианной
рад.
А теперь на координатной плоскости рассмотрим окружность
единичного радиуса с центром в начале координат. Такую окружность называют
единичной окружностью.
Введём понятие поворота точки единичной окружности вокруг начала
координат на угол рад, где
– это любое действительное число. Отметим точку
. Эта точка расположена на окружности.
Пусть . Представим, что точка, двигаясь по единичной окружности от точки
против часовой стрелки, прошла путь длиной
. Конечную точку пути обозначим
.
В таком случае будем говорить, что точка получена из точки
путём поворота на угол
рад вокруг начала координат.
Теперь пусть . В этом случае поворот на угол
рад будем совершать по часовой стрелке. Точка пройдёт путь длиной
модуль . Конечную точку пути обозначим
.
Если же , то точка остаётся на месте.
Давайте рассмотрим некоторые примеры поворотов точки на некоторый угол.
Итак, при повороте точки на угол
рад мы совершаем движение против часовой стрелки и получаем точку
.
А при повороте точки на угол
рад мы двигаемся по часовой стрелке и получаем точку
.
При повороте точки на угол
рад мы осуществим поворот против часовой стрелки на
рад трижды и окажемся в точке
.
При повороте точки на угол
рад мы осуществим поворот по часовой стрелке на
рад трижды и окажемся в точке
.
При повороте точки на угол
рад мы осуществим поворот по часовой стрелке и окажемся в точке
.
При повороте точки на угол
рад мы осуществим поворот против часовой стрелки и снова окажемся
в точке .
Ранее в курсе геометрии вы рассматривали углы от до
. Теперь, используя поворот точки единичной окружности вокруг
начала координат, можно рассматривать углы, которые больше , а также отрицательные углы.
А задавать угол поворота надо в градусах или радианах? Угол
поворота можно задавать и в градусах, и в радианах. Так, например, поворот
точки на угол
означает то же, что и поворот на
. А поворот на
– это поворот на
.
Далее приведена таблица поворотов на наиболее часто встречающиеся
углы, выраженные в радианной и градусной мере:
Обратите внимание, что при повороте на , то есть на
, точка возвращается в своё первоначальное положение.
А где окажется точка при повороте на ? При повороте на
, то есть на
, точка также вернётся в своё первоначальное положение.
Давайте рассмотрим пример поворота на угол, который больше . Например, на угол
. Представим
. Получается, что при повороте на этот угол точка
совершает три полных оборота против часовой стрелки и ещё
проходит путь .
Теперь рассмотрим пример поворота на угол , то есть на угол меньший
. Представим
. В этом случае точка совершает три полных оборота по часовой
стрелке и ещё проходит путь в этом же направлении.
Получается, что при повороте точки на угол
получаем ту же точку, что и при повороте на угол
, а при повороте точки
на угол
получаем ту же точку, что и при повороте на угол
.
Вообще, если угол можно представить как
, где
– целое число, то при повороте на угол
получаем ту же самую точку, что и при повороте на угол
.
Таким образом, можем сделать вывод, что каждому
действительному числу соответствует единственная точка единичной окружности, получаемая
поворотом точки на угол
рад.
Однако одной и той же точке единичной окружности соответствует бесконечное множество
действительных чисел , где
– целое число, задающих поворот точки
в точку
.
Найдём координаты точки, полученной поворотом точки на угол
. Представим
. Тогда при повороте точки на угол
мы получим ту же самую точку, что и при повороте на угол
, то есть точку с координатами
.
Найдём координаты точки, полученной поворотом точки на угол
. Представим
. Тогда при повороте на
мы получаем ту же самую точку, что и при повороте на
, то есть точку с координатами
.
И найдём координаты точки, полученной поворотом точки на угол
.
Для этого выполним поворот точки против часовой стрелки на угол , то есть на
, и получим точку
. Опустим из неё перпендикуляр
на ось
и рассмотрим прямоугольный треугольник
. Так как координаты точки
численно равны длинам катетов этого треугольника, то нам остаётся
найти длины и
.
Гипотенузой этого треугольника является отрезок . Причём
, так как это радиус нашей единичной окружности. Угол
равен
, так как мы осуществляли поворот на
, то есть на
.
А мы ведь знаем из геометрии, что катет прямоугольного треугольника,
лежащий против угла в , равен половине гипотенузы. Значит, катет
.
Теперь вспомним теорему Пифагора: в прямоугольном треугольнике
квадрат длины гипотенузы равен сумме квадратов длин катетов (). Запишем её для нашего треугольника:
. Выразим неизвестный нам катет
:
. Подставим значения
и
:
. Выполним вычисления и в результате получим
.
Таким образом, можем записать, что точка имеет абсциссу, равную длине катета
, то есть
, и ординату, равную длине катета
, то есть
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найти
координаты точки, полученной поворотом точки на угол а)
; б)
; в)
.
Решение.
И решим ещё одно задание. Найдите
число , где
, и натуральное число
, такие, чтобы выполнялось равенство
, если а)
; б)
.
Решение.
Вечный думатель
Мыслитель
(9020)
14 лет назад
Поворачиваем точку A(1;0). Если на положительный угол, то ПРОТИВ часовой стрелки, если на отрицательный – то ПО часовой стрелке. Точки, в которые про этом попадаем, обозначены соответственно B, C, D и E. В скобках около них указаны их координаты.
Максим
Мыслитель
(6828)
14 лет назад
Всё очень просто. Координаты точки определяются по формуле:
x=r*cos(альфа)
y=r*sin(альфа) ,
где альфа – угол поворота против часовой стрелки, r – радиус, который в данном случае равен 1. Это следует просто из определения косинуса и синуса.
а) (соs(-3pi/2); sin(-3pi/2))=(0;1)
б) (соs(-13pi/2); sin(-13pi/2))=(0;1)
в) (соs(pi/3); sin(pi/3))=(1/2; (корень из 3)/2)
г)) (соs(-pi/4); sin(-pi/4))=( (корень из 2)/2; -(корень из 2)/2)
Поворот – это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.
Синтаксис
Координаты – строка, содержащая координаты в виде x:y (где x – абсцисса координаты, y – ордината координаты), разделенные хотя бы одним пробелом
Точка вращения – точка, относительно которой будет осуществляться поворот, всех заданных координат.
Поворот в градусах – поворот фигуры на заданный угол. Если число положительное – то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке.
Примеры
Пример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7)
Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3
Поворот осей координат
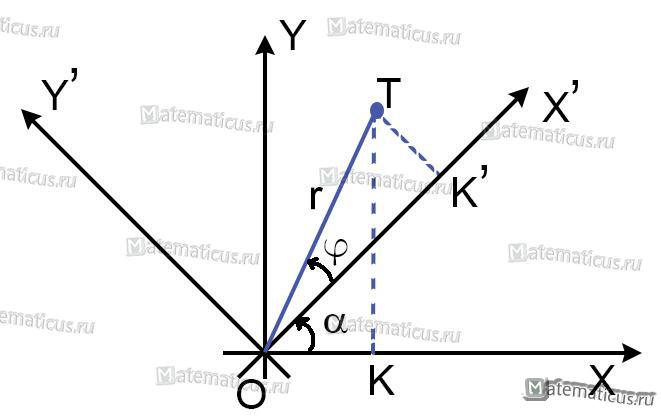
Чтобы найти поворот осей, зададим две системы координат, согласно рисунку
Пусть точка T в новой полярной системе координат имеет полярный радиус r и полярный угол φ. В старой полярной системе координат полярный угол точки T будет равен α+φ, а полярный радиус r будет как в новой системе координат.
Тогда уравнения примут вид:
x = r cos(α+φ)
y = r sin(α+φ)
Применяя тригонометрические тождества суммы двух углов для синуса и косинуса , получим выражения:
x = r (cosα cosφ — sinα sinφ) = r (cosφ) cosα — (r sinφ) sinα
y = r (sinα cosφ — cosα sinφ) = r (cosφ) sinα — (r sinφ) cosα
X = r cosφ и Y = r sinφ
Получим уравнения поворота осей координат
x = X cosα — Y sinα
y = X sinα — Y cosα
Если обозначим следующим образом
x = OK , y = KT — старые координаты точки T
x´= OK´, y´ = KT´ — новые координаты точки T
α — угол поворота осей
тогда ф ормулы поворота осей координат примут вид:
Пример
До поворота осей на угол -30 0 точка L имела абсциссу x=2 и ординату y=0
Требуется найти координаты точки L после поворота осей.
Решение
Подставляя в формулу, находим новые координаты осей x´, y´
Компьютерная Графика
Двумерный алгоритм преобразование в новые координаты
Поворот.
Пусть необходимо повернуть точку P(x, y) вокруг начала координат O на угол (фи) . Изображение новой точки на рис. 2.2. обозначим через P’(x’, y’). Всегда существуют четыре числа a, b, c, d, такие, что новые координаты могут быть вычислены по значениям старых координат x и y из следующей системы уравнений:
(2.1)
Для получения значений a, b, c, d рассмотрим вначале точку (x, y) = (1, 0). Полагая x =1 и y =0 в уравнении (2.1), получим
Но в этом простом случае, как это видно из рис. 2.3(а), значения x’ и y’ равны соответственно Cos (фи) и Sin (фи). Тогда будем иметь:
Аналогичным образом из рис. 2.3(б) следует
Тогда вместо системы уравнений (2.1) можем записать
(2.2)
Система уравнений (2.2) описывает поворот вокруг точки O – начала системы координат. Но часто это не то, что нам нужно. Если требуется выполнить поворот относительно заданной точки, то в этих уравнениях можно заменить: x – на (x-xo) , y – на (y-yo), x’ – на (x`-xo) и y’ – на (y`-yo) (сдвигаем систему координат) .
Система уравнений, которая описывает поворот точки вокруг любой точки:
(2.3)
Система уравнений (2.3) неудобна для реализации на PC. Применяем матричную запись.
[spoiler title=”источники:”]
http://codenet.ru/progr/cg/lec_1_2.php
[/spoiler]
Инфоурок
›
Алгебра
›Другие методич. материалы›Методический материал по математике на тему ” Поворот точки вокруг начала координат”
Методический материал по математике на тему ” Поворот точки вокруг начала координат”
Скачать материал
Скачать материал


- Сейчас обучается 20 человек из 16 регионов


- Сейчас обучается 28 человек из 15 регионов




Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 251 903 материала в базе
- Выберите категорию:
-
Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
Тема
§ 22. Поворот точки вокруг начала координат
Больше материалов по этой теме
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Скачать материал
-
06.11.2017
3160
-
DOCX
200 кбайт -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Головина Ирина Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 10 месяцев
- Подписчики: 0
- Всего просмотров: 43382
-
Всего материалов:
47
Алгебра и начала математического анализа, 10 класс
Урок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг – часть плоскости, ограниченной окружностью – то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)
Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, 

Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна 
Длина полуокружности равна 


Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.


Длину дуги l окружности радиуса R (рис.4)
можно вычислять по формуле
А площадь S кругового сектора радиуса R и дугой 
находят по формуле: 

Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки. (рис.2)
- Пусть
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
- Пусть
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол 
угол 
(рис.6)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найти градусную меру угла, равного 
Решение: Используя формулу (1),
находим 
Так как 


Ответ: 
Пример 2. Найти радианную меру угла, равного 60
Решение:
Вычисляем по формуле (2): 

При обозначении мер угла, наименование «рад» опускают.
Ответ: 

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера 
Решение: Используя формулу (3),
получим: 
Ответ: 
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла 
Решение:
По формуле (4) вычисляем
Ответ: 45 
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный 
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как 
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны 
На окружности можно найти координаты любой точки.
Ответ:

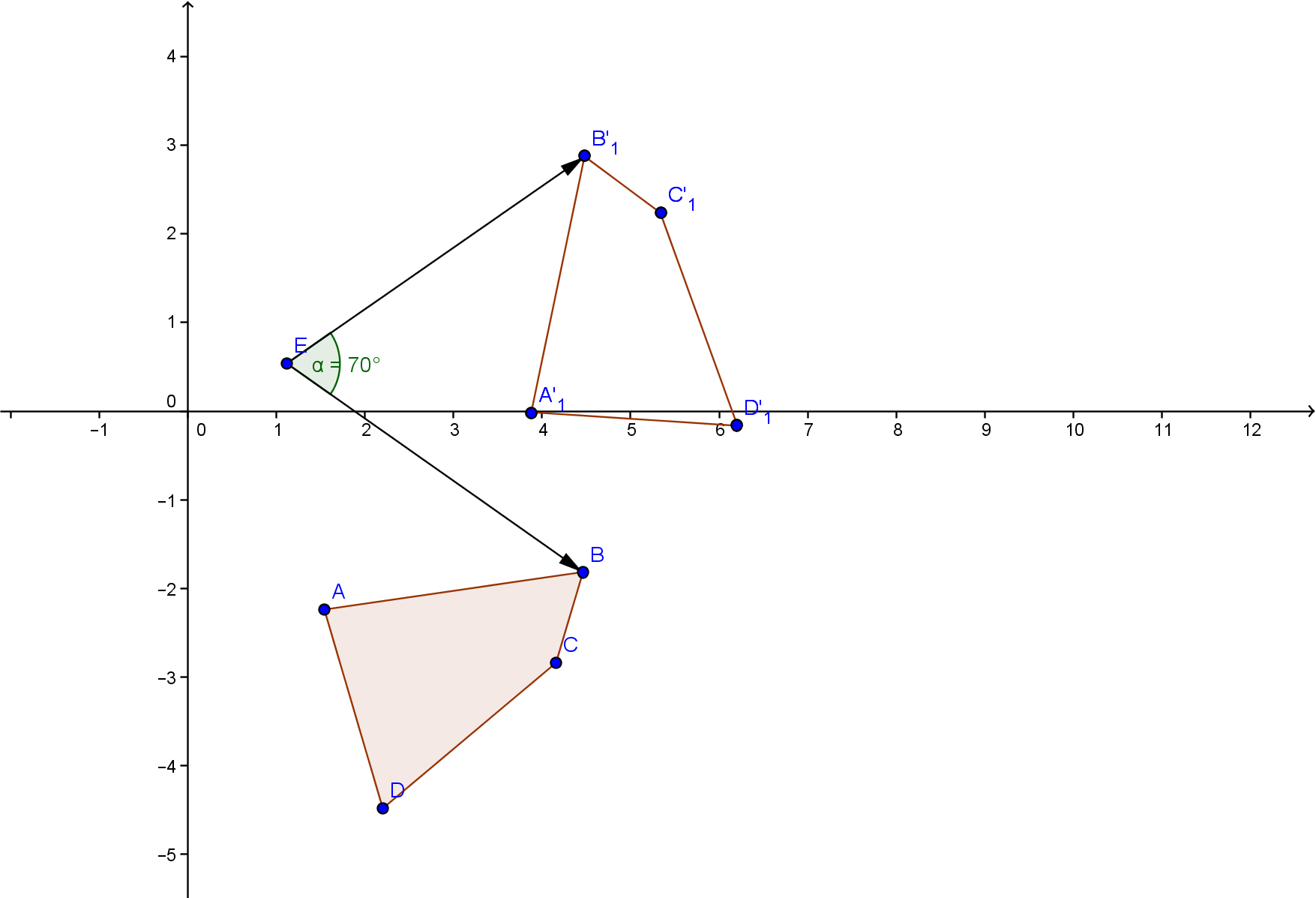









 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 
 точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.



