Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 ноября 2014 года; проверки требуют 8 правок.
К функции нескольких переменных 
можно применить предел по одной из переменных 
при фиксированных значениях остальных переменных. Повторный предел — результат выполнения такой операции по каждой переменной.
В то время как предел функции вычисляется при одновременном стремлении всех аргументов к их пределам, повторный предел получается в результате ряда последовательных предельных переходов по каждому аргументу в отдельности.
Определение[править | править код]
Рассмотрим функцию двух переменных 
, определённую в некоторой проколотой окрестности точки 
. Для каждого фиксированного значения переменной 
рассмотрим предел:
Будем считать, что 
существует и определена для каждого значения . В результате получим функцию одной переменной. Теперь рассмотрим предел :
Если этот предел существует, то говорят, что 
есть повторный предел функции в точке .
Аналогично мы можем сначала фиксировать переменную 
и брать предел по переменной . В этом случае мы также получим повторный предел, но, вообще говоря, другой:
Это определение можно распространить и на функции нескольких переменных 
.
Равенство повторных пределов[править | править код]
Пусть функция 
определена в проколотой окрестности точки 
.
Если существует (конечный или нет) двойной предел
и если при любом из проколотой окрестности точки 
существует конечный предел по
то существует повторный предел
и равен двойному.
См. также[править | править код]
- Предел функции
Литература[править | править код]
- Ильин, В. А., Позняк, Э. Г. Глава 14. Функции нескольких переменных // Основы математического анализа. — 4. — М.: ФИЗМАТЛИТ, 2002. — Т. 1. — 648 с. — (Курс высшей математики и математической физики). — 5000 экз. — ISBN 5-9221-0536-1.
- Фихтенгольц, Г.М. Глава 5. Функции нескольких переменных // Курс дифференциального и интегрального исчисления. Том 1. — М., 1962. — Т. 1. — 608 с. — (Курс дифференциального и интегрального исчисления в 3 томах).
Для
функций нескольких переменных наряду
с обычным понятием предела функции (при
одновременном стремлении всех аргументов
к их пределам) вводится понятие повторного
предела, получаемого в результате ряда
последовательных предельных переходов
по каждому аргументу в отдельности в
том или ином порядке. (Обычный предел
функции n
переменных называется n-кратным:
двойным, тройным и т.д.)
Рассмотрим
случай функции двух переменных. Пусть
функция определена в области G.
Пусть область G
такова, что х
может принимать (независимо от у)
любые значения в некотором множестве
Х,
для которого х0
– предельная точка, а переменная у
(независимо
от х)
изменяется на множестве Y.
Тогда G
можно символически обозначить G
=XY.
При фиксированном значении переменной
у
функция f(x;y)
становится функцией одной переменной
х.
Если при фиксированном yY
существует
,
то, вообще говоря, этот предел зависит
от наперед зафиксированного у:
.
Теперь можно рассматривать
.
Пусть он существует и равен А:
=А.
Тогда говорят, что в точке (х0;у0)
существует повторный предел функции
f(x;y)
. (1)
При
этом
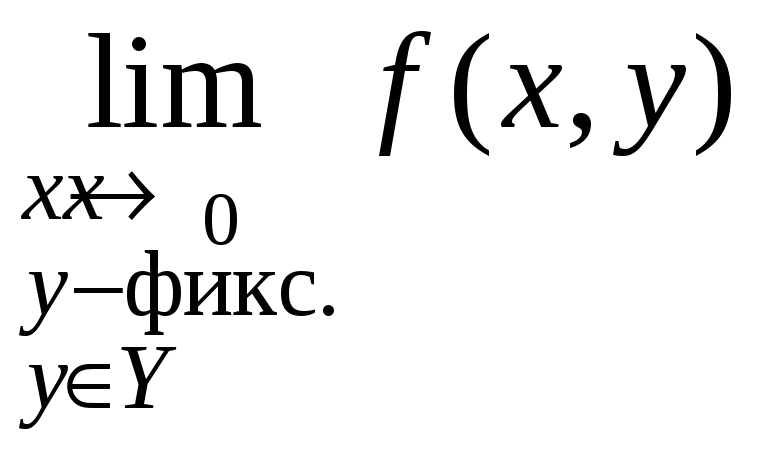
называется внутренним пределом в
повторном пределе (1).
Другой
повторный предел
(2)
получится,
если предельные переходы произвести в
обратном порядке. В (2) внутренний предел
–
.
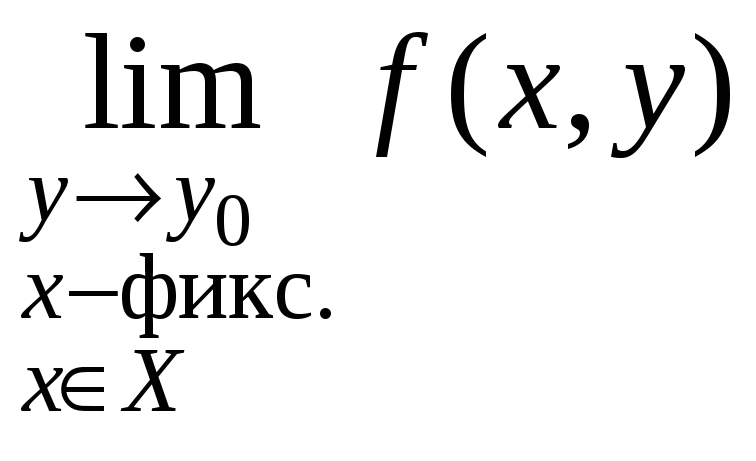Повторные
пределы (1) и (2) вовсе не обязательно
равны.
Пример
4. Вычислить
повторные пределы функции
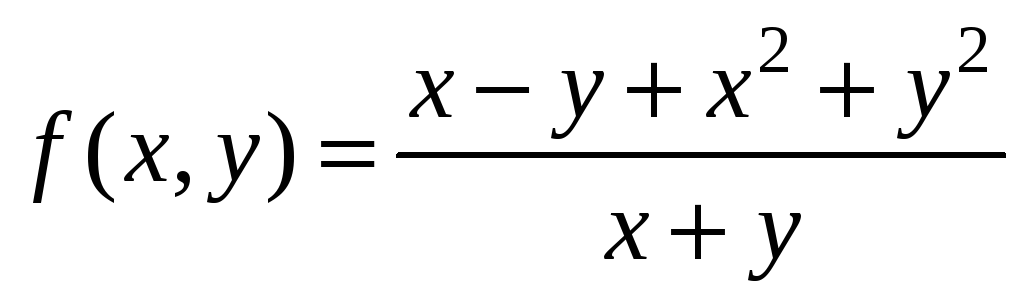
в точке О(0;0).
О(0;0)D(f
),
является
предельной точкой
D(f
).
,
.
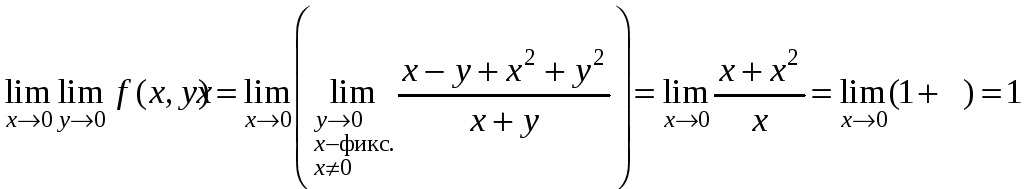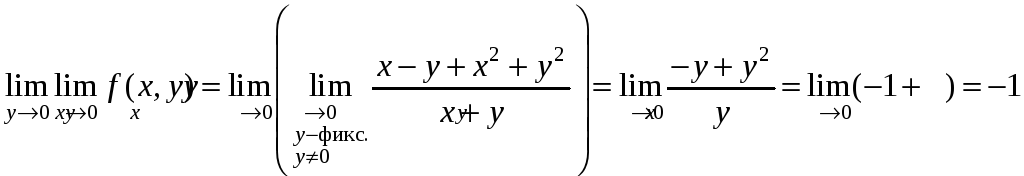Может
случиться, что один из повторных пределов
существует, а другой – нет.
Пример
5.
Вычислить повторные пределы функции
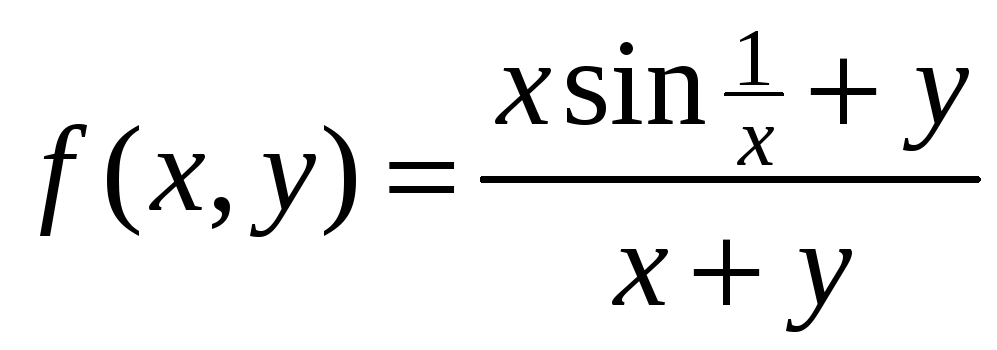
в О(0;0).
–
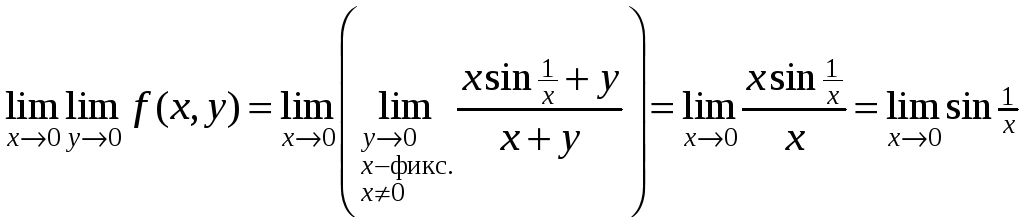
не существует,
.
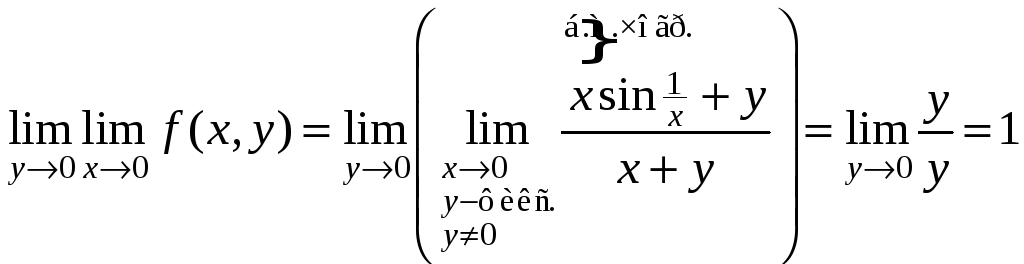Всякая
перестановка двух предельных переходов
по разным переменным должна быть
обоснована. Одно из таких обоснований
дает следующая теорема. Она также
устанавливает связь между двойными и
повторными пределами. Вообще говоря,
из существования двойного предела не
следует существование повторных
пределов, и из существования повторных
не следует существование двойного.
Теорема.
Пусть в точке (х0;у0)
существует (конечный или бесконечный)
двойной предел
,
а также yY
существует внутренний предел
.
Тогда существует повторный предел
.
Аналогично, если 
,
и хХ
существует внутренний предел
,
то существует
повторный предел
=А.
Если
и оба внутренних предела, то существуют
и оба повторных предела, и
.
Замечание.
Обратное утверждение неверно. Если
существуют и равны оба повторных предела,
то двойной не обязательно существует.
Пример
6.
.
,
,
,
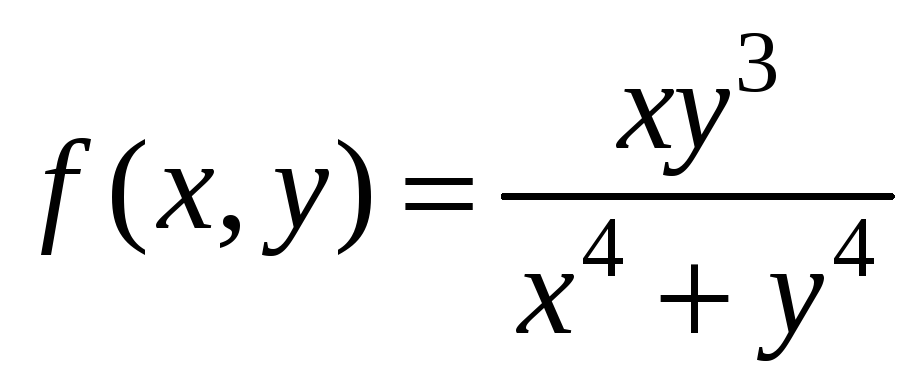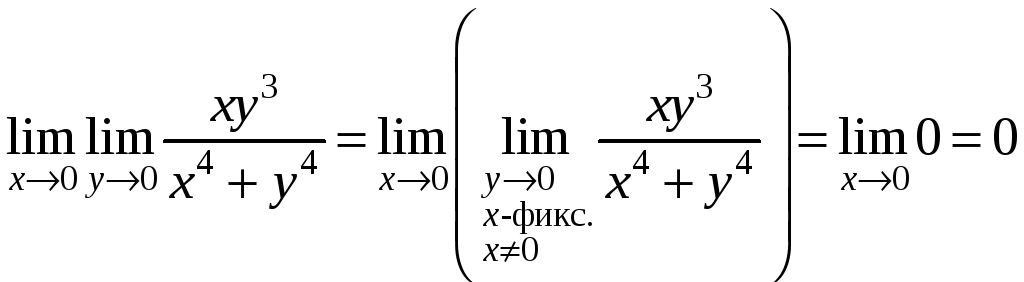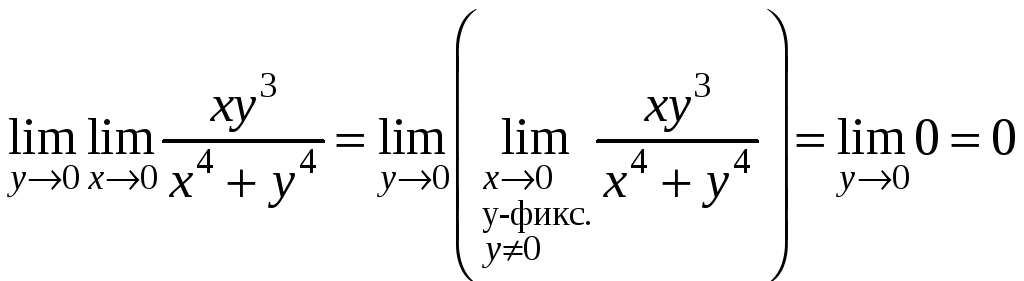но
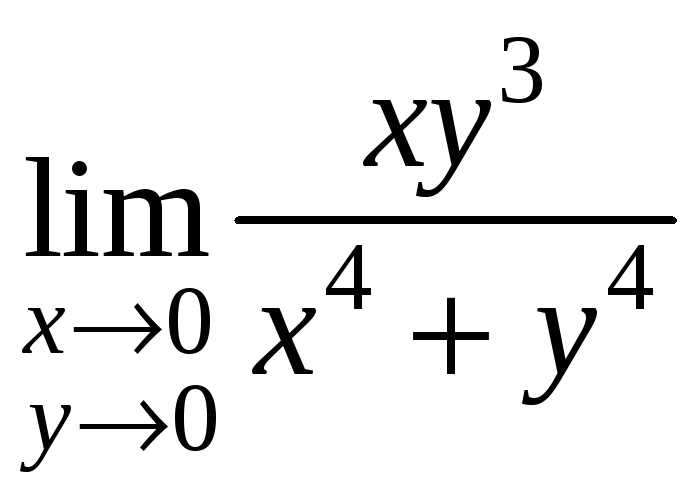
не существует (см. пример 2).
3. Непрерывность функции n переменных
Определение
1. Функция
z=f(x,y)
называется непрерывной
в точке
M0(x0;y0),
если она определена в некоторой
окрестности этой точки, и предел функции
равен значению функции в этой точке:
. (1)
Аналогично
определяется непрерывность в точке
функции n
переменных.
Обозначим
х=х0+х,
у=у0+у.
Тогда (1) можно переписать с. о.:
или
.
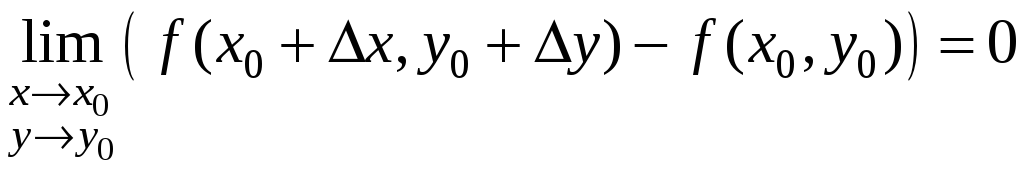Величина
называется полным
приращением функции
z=f(x,y)
в точке
(x0;y0).
Т. о., получаем эквивалентное определение
непрерывности функции в точке.
Определение
2. Функция
z=f(x,y)
называется непрерывной
в точке
M0(x0;y0),
если бесконечно малым приращениям
аргументов х
и у
соответствует бесконечно малое полное
приращение функции:
.
Если
переменную у0
оставить постоянной, а переменной х0
придать некоторое приращение х,
то функция z=f(x,y)
получит приращение
,
которое называется частным
приращением функции z
в точке (х0,
у0)
по
переменной х.
Аналогично, если переменная х0
остается постоянной, а у0
получает приращение у,
то
– частное
приращение функции z
в точке (х0,у0)
по
переменной у.
Для функций
нескольких переменных вводится понятие
непрерывности по каждой из независимых
переменных.
Определение.
Частным
приращением функции
u=f(x1,x2,…xn)
в точке
по переменной
xj
называется величина
.
Определение.
Функция u=f(x1,x2,…,xn)
называется непрерывной
в точке М0
по переменной
xj
,
если
.
Пример
7. Доказать,
что функция
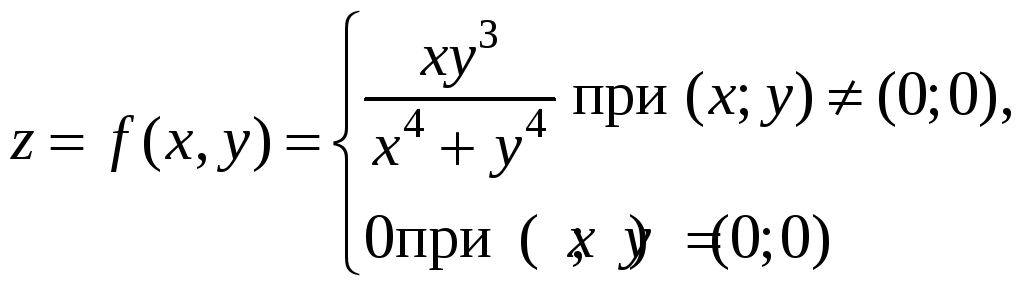
непрерывна
в точке О(0;0) по каждой переменной х
и у,
но не является непрерывной по совокупности
переменных.
Частное
приращение функции по переменной х
в точке О(0;0):
.
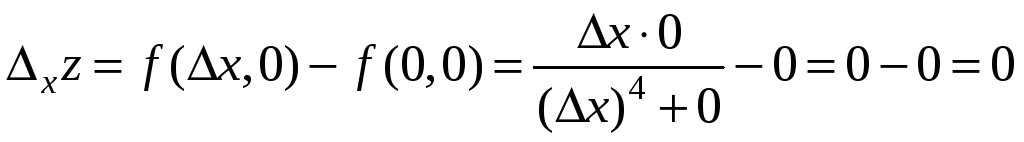
Следовательно,
функция непрерывна в т. О(0;0) по переменной
х.
Частное
приращение функции по переменной у
в точке О(0;0):
.
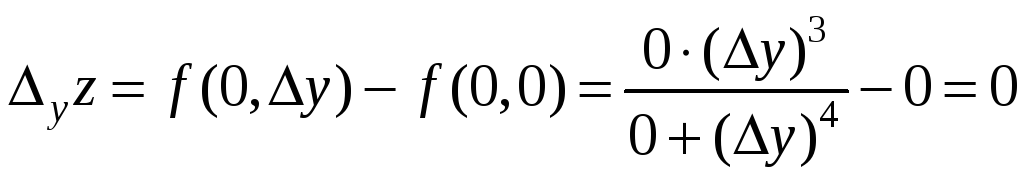
Следовательно,
функция непрерывна в т. О(0;0) по переменной
у.
Но
функция не является непрерывной в
т.О(0;0) по совокупности переменных, т.к.
предел функции в этой точке не существует
(см. пример 2 из п.2).
Определение.
Функция называется непрерывной
на множестве,
если она непрерывна в каждой точке этого
множества.
Определение.
Точка M0(x0;y0),
в которой не выполняется условие
непрерывности, называется точкой
разрыва функции
z=f(x;y).
Это может быть,
например, в следующих случаях:
-
z=f(x;y)
определена во всех точках некоторой
окрестности точки М0,
кроме самой точки М0; -
функция
определена во всех точках V(М0),
но
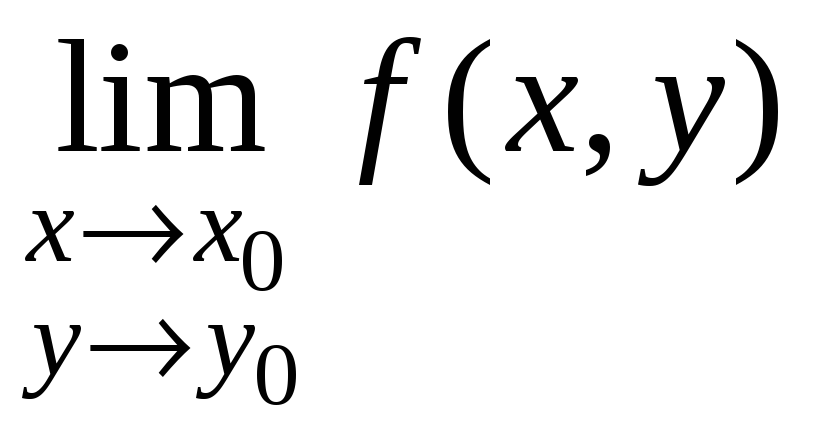
не существует; -
функция
определена во всех точках V(М0),
и существует
,
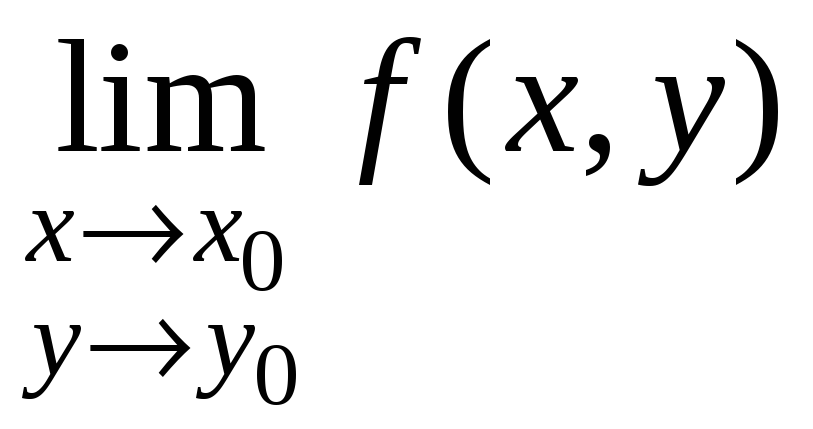но
.
,
.
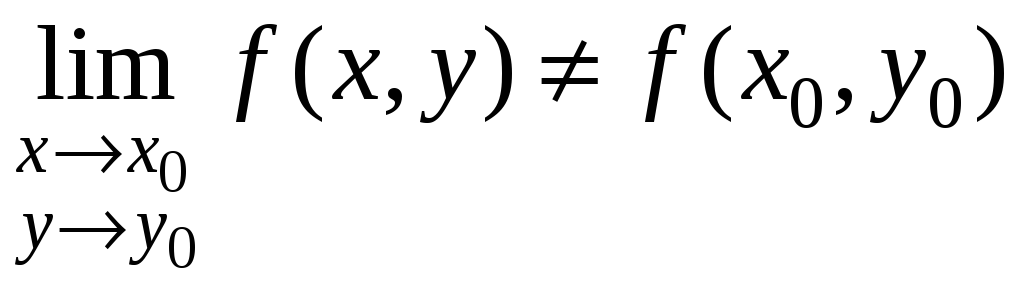Пример
2. Найти точки
разрыва функции
.
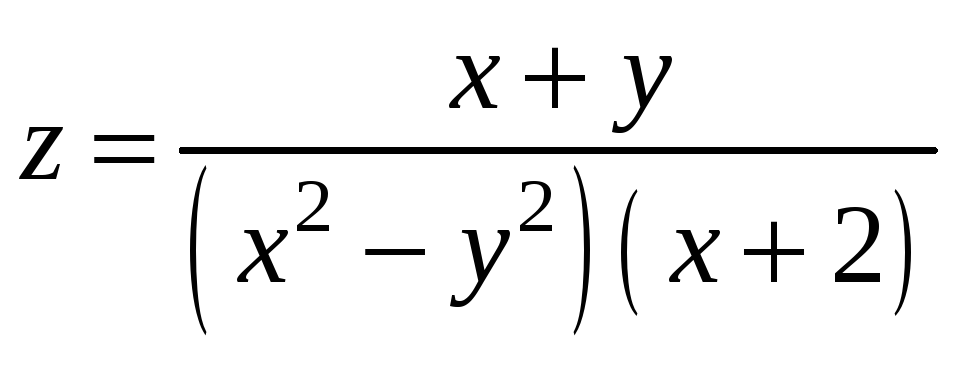Функция
может иметь разрыв лишь в точках, где
=0
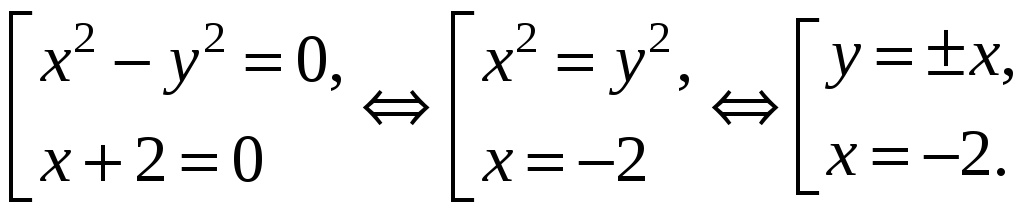
Итак,
данная функция имеет разрыв на прямых
у=х,
у=-х,
х=2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Предел функции в точке.
Начать изучение
-
Предел по множеству.
Начать изучение
-
Повторные пределы. Бесконечные пределы.
Начать изучение
Предел функции в точке.
Напомним, что окрестностью (O(x^0)) точки (x^0) в метрическом пространстве (X) называется любое множество, для которого точка (x^0) является внутренней. Проколотая окрестность (dot{O}(x^0)) получается из (O(x^0)) удалением самой точки (x^0), то есть (dot{O}(x^0)=O(x^0)backslash{x^0}).
Будем рассматривать функции (f: Mrightarrow R), где (M) есть некоторое множество, принадлежащее метрическому пространству (X). Если (X=R^n), то функция (f: Mrightarrow R) называется функцией многих переменных и обозначается обычно следующим образом:
$$
f(x)=f(x_1,ldots,x_n),quad xin M.nonumber
$$
Например, функция (displaystyle sqrt{1-x_1^2-x_2^2}) определена в единичном круге пространства (R^2) с центром в точке ((0,0)), а функция (operatorname{ln}(x_1^2+x_2^2)) определена в любой проколотой окрестности точки ((0,0)).
Определение 1.
Пусть функция (f(x)) определена в проколотой окрестности (dot{O}(x^0)) точки (x^0) метрического пространства (X). Говорят, что число (A) есть предел функции (f(x)) при (xrightarrow x_0), если (forall varepsilon > 0 exists delta > 0) такое, что для (forall xindot{O}(x^0)), удовлетворяющего условию (rho(x,x^0) < delta), выполнено неравенство (|f(x)-A| < varepsilon).
Определение 2.
Говорят, что функция (f(x)), определенная в (dot{O}(x^0)), имеет при (xrightarrow x_0) предел (A), если для любой последовательности (x^{(k)}indot{O}(x^0)) такой, что (displaystylelim_{krightarrowinfty}x^{(k)}=x^0), выполнено равенство (displaystylelim_{krightarrowinfty}f(x^{(k)})=A).
Эквивалентность двух определений предела доказывается так же, как и для функций одной переменной.
Если число (A) есть предел функции (f(x)) при (xrightarrow x_0), то будем писать
$$
A=lim_{xrightarrow x^0}f(x).nonumber
$$
Если функция двух переменных (f(x,y)) определена в (dot{O}((a,b))), a число (A) есть ее предел при ((x,y)rightarrow(a,b)), то пишут
$$
A=lim_{xrightarrow a,yrightarrow b}f(x,y)nonumber
$$
и называют иногда число (A) двойным пределом.
Аналогично, для функции (n) переменных наряду с обозначением (A=displaystylelim_{xrightarrow x^0}f(x)) будем использовать обозначение
$$
A=lim_{xrightarrow x_1^0,ldots,x_nrightarrow x_n^0}f(x_1,ldots,x_n).nonumber
$$
Лемма 1.
Пусть функции (f(x)) и (varphi(x)) определены в (dot{O}(x^0)) и (|f(x)|leq varphi(x)) в (dot{O}(x^0)). Если (displaystylelim_{xrightarrow x^0}varphi(x)=0), то и (displaystylelim_{xrightarrow x^0}f(x)=0).
Доказательство.
(circ) Так как (displaystylelim_{xrightarrow x^0}varphi(x)=0), то для любого (varepsilon > 0) найдется шар (S_{delta}(x^0)) такой, что для всех (xin S_{delta}(x^0)) выполнено неравенство (|varphi(x)| < varepsilon). Тем более для всех (xin S_{delta}(x^0)) выполнено неравенство (|f(x)| < varepsilon), то есть (displaystylelim_{xrightarrow x^0}f(x)=0). (bullet)
Пример 1.
Доказать, что (displaystylelim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0), если (a > 0).
Решение.
(triangle) Возьмем любое (varepsilon > 0). Положим (delta=varepsilon^{1/(2a)}). Пусть ((x,y)in S_delta(0, 0)), тогда
$$
(x^2+y^2)^a < delta^{2a} < varepsilon,nonumber
$$
то есть
$$
lim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 2.
Показать, что (displaystyle lim_{xrightarrow 0,yrightarrow 0}frac{|x|^{alpha}|y|^{beta}}{(x^2+y^2)^{gamma}}=0), если (alpha+beta-2gamma > 0).
Решение.
(triangle) Так как
$$
|x| < sqrt{x^2+y^2},qquad |y| < sqrt{x^2+y^2},nonumber
$$
то при (x^2+y^2 > 0) имеем неравенства
$$
0leq f(x,y)=frac{vert xvert^alphavert yvert^beta}{(x^2+y^2)^gamma}leqfrac{(x^2+y^2)^{alpha/2}(x^2+y^2)^{beta/2}}{(x^2+y^2)^gamma}=\(x^2+y^2)^{(alpha+beta-2gamma)/2}=varphi(x,y).nonumber
$$
В силу примера выше (displaystylelim_{xrightarrow 0,yrightarrow 0}varphi(x,y)=0.), так как (alpha+beta-2gamma > 0). Применяя лемму 1, получаем, что
$$
lim_{xrightarrow 0,yrightarrow 0}f(x,y)=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 3.
Функция
$$
f(x,y)=frac{2xy}{x^2+y^2}label{ref1}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Рассмотрим последовательность точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)). Тогда (f(x_n,y_n)=1) и, следовательно, (displaystyle lim_{nrightarrowinfty}f(x_n,y_n)=1). Если же взять последовательность точек ((x_n’,y_n’)=displaystyleleft(frac{1}{n},-frac{1}{n}right)), то (displaystyle lim_{nrightarrowinfty}f(x_n’,y_n’)=-1).
Так как при любом (nin mathbb{N}) точки ((x_n,y_n)) и ((x_n’,y_n’)) не совпадают с точкой ((0,0)), а последовательности точек ((x_n,y_n)) и ((x_n’,y_n’)) сходятся к точке ((0,0)), то, используя определение 2 предела, получаем, что функция (f(x,y)) не имеет предела при ((x,y)rightarrow (0,0)). (blacktriangle)
Пример 4.
Функция
$$
f(x,y)=frac{2x^2y}{x^4+y^2}label{ref2}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Повторяя рассуждения примера 3, построим две последовательности точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)) и ((x_n’,y_n’)=displaystyleleft(frac{1}{n},frac{1}{n^2}right)). Так как ((x_n,y_n)rightarrow(0,0)) и ((x_n’,y_n’)rightarrow(0,0)), а (displaystylelim_{nrightarrowinfty}f(x_n,y_n)=0) и (displaystylelim_{nrightarrowinfty}f(x_n’,y_n’)=1), то двойной предел функции (f(x,y)) при ((x,y)rightarrow(0,0)) не существует. (blacktriangle)
Предел по множеству.
Предел (displaystylelim_{xrightarrow x^0}f(x)) был определен ранее для функции, заданной в (dot{O}(x^0)). Расширим определение предела, введя понятие предела по множеству.
Определение 3.
Пусть (M) есть подмножество области определения функции (f(x)), (x^0) — предельная точка множества (M). Будем говорить, что число (A) есть предел функции (f(x)) по множеству (M) при (xrightarrow x^0), если (forallvarepsilon > 0 exists delta > 0) такое, что (forall xin{dot S}_delta(x^0)cap M) выполнено неравенство (|f(x)-A| < varepsilon). В этом случае пишут
$$
A=lim_{xrightarrow x^0, xin M}f(x).nonumber
$$
Пусть функция двух переменных (f(x,y)) определена в проколотой окрестности (dot{O}(x_0,y_0)). Пределом функции (f(x,y)) в точке ((x_0,y_0)) по направлению (l=(cosalpha,sinalpha)) будем называть выражение
$$
lim_{trightarrow+0}f(x_0+tcosalpha, y_0+tsinleft(alpharight))=lim_{begin{array}{c}(x,y)rightarrow(x_0,y_0)\(x,y)indot O(x_0,y_0)cap L\end{array}}f(x,y),nonumber
$$
где (L) есть луч, выходящий из точки ((x_0,y_0)) в направлении (l).
Пример 5.
Показать, что предел функции (f(x,y)=displaystyle frac{2xy}{x^2+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен (sin 2alpha).
Решение.
(triangle) Так как при (t > 0) выполнено равенство
$$
f(tcosalpha, tsinalpha)=2sinalphacosalpha=sin 2alpha,nonumber
$$
то
$$
lim_{trightarrow 0}f(tcosalpha, tsinalpha)=sin 2alpha.quadblacktrianglenonumber
$$
Пример 6.
Показать, что предел функции (f(x,y)=displaystyle frac{2x^2y}{x^4+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен нулю.
Решение.
(triangle) При (t > 0) справедливо равенство
$$
f(tcosalpha, tsinalpha)=frac{2tcos^2alphasinalpha}{t^2cos^4alpha+sin^2alpha}.nonumber
$$
Если (sinalpha=0), то (f(tcosalpha, tsinalpha)=0) и, следовательно,
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.nonumber
$$
Если (sinalphaneq 0), то
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.quadblacktrianglenonumber
$$
Ясно, что из существования (displaystylelim_{xrightarrow x^0, xin M}f(x)) следует существование (displaystylelim_{xrightarrow x^0, xin M’}f(x)) для любого подмножества (M’subset M), для которого (x’) есть предельная точка. В частности, из существования двойного предела функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)) следует существование предела функции (f(x,y)) в точке ((x_0,y_0)) по любому направлению и равенство этих пределов двойному пределу функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)).
Из результатов примеров 4 и 6 следует, что из существования и равенства пределов по любому направлению в точке ((x_0,y_0)) не вытекает существование в этой точке предела функции.
Предел функции (f(x)) в точке (x^0in R^n) по направлению (l=(l_1,ldots,l_n)), где (l_1^2+ldots+l_n^2=1), определяется по аналогии со случаем функции двух переменных.
Повторные пределы. Бесконечные пределы.
Пусть функция двух переменных (f(x,y)) определена на множестве
$$
Pi={(x,y):quad 0 < |x-x_0| < a,quad 0 < |y-y_0| < b}.nonumber
$$
Пусть (forall xin (x_0-a, x_0+a), xneq x_0), существует (displaystylelim_{yrightarrow y_0}f(x,y)=g(x)), а функция (g(x)) определена в проколотой окрестности точки (x_0). Если существует (displaystylelim_{xrightarrow x_0}g(x)=lim_{xrightarrow x_0}lim_{yrightarrow y_0}f(x,y)), то этот предел называется повторным. Аналогично определяется другой повторный предел (displaystylelim_{yrightarrow y_0}lim_{xrightarrow x_0}f(x,y)).
Как показывают простые примеры, из существования двойного предела не следует существование повторных пределов, а из существования и равенства повторных пределов не следует существование двойного предела.
Так для функции (displaystyle f(x,y)=frac{2xy}{x^2+y^2}) примера 3 двойной предел при ((x,y)rightarrow (0,0)) не существует, но оба повторных предела равны нулю, так как
$$
lim_{xrightarrow0}f(x,y)=lim_{yrightarrow0}f(x,y)=0.nonumber
$$
Для функции
$$
f(x,y)=left{begin{array}{lc}xsinfrac1y,&yneq0,\0,&y=0,end{array}right.nonumber
$$
справедливо неравенство (|f(x,y)|leq|x|). В силу леммы 1 двойной предел этой функции при ((x,y)rightarrow (0,0)) равен нулю. Но при (xneq 0) не существует
$$
lim_{yrightarrow0}xsinfrac1y,nonumber
$$
а поэтому не существует и соответствующий повторный предел.
Бесконечные пределы для функций многих переменных определяются по той же схеме, что и для функций одной переменной. Например, (displaystylelim_{xrightarrow x^0}f(x)=+infty), если для любого числа (C > 0) число (delta > 0), что для всех (x) из проколотой окрестности (dot{O}(x^0)) точки (x^0) выполнено неравенство (f(x) > C).
Пример 7.
Показать, что
$$
lim_{xrightarrow +infty,yrightarrow +infty}(x^2+y^2)e^{-(x+y)}=0.nonumber
$$
Решение.
(triangle) Так как при (x > 0, y > 0) справедливо неравенство
$$
0leq (x^2+y^2)e^{-(x+y)}leq(x+y)^2e^{-(x+y)}nonumber
$$
и (displaystylelim_{trightarrow +infty}t^2e^{-t}=0), то (forall varepsilon > 0 existsdelta > 0) такое, что (forall t > delta) выполнено неравенство (t^2e^{-t} < varepsilon). Но тогда (forall x > displaystylefrac{delta}{2}) и (forall y > displaystylefrac{delta}{2}) справедливо неравенство
$$
0leq(x^2+y^2)e^{-(x+y)} < varepsilon.quadblacktrianglenonumber
$$
Макеты страниц
Для функции 
нескольких переменных можно определить понятие предела по одной из переменных 
при фиксированных значениях остальных переменных. В связи с этим возникает понятие повторного предела. Уясним это понятие на примере функции 
двух переменных 
Пусть функция 
задана в некоторой прямоугольной окрестности 
точки 
за исключением, быть может, самой точки 
Пусть для каждого фиксированного у, удовлетворяющего условию 
существует предел функции 
одной переменной х в точке 
и пусть, кроме того, существует предел b функции 
в точке
В этом случае говорят, что существует повторный предел Ь для функции 
в точке 
который обозначается следующим образом:
Аналогично определяется повторный предел
Установим достаточные условия равенства двух введенных повторных пределов.
Теорема 12.3. Пусть функция 
определена в некоторой прямоугольной окрестности 
точки 
и имеет в этой точке предел, равный 
Пусть, кроме того, для любого фиксированного 
существует предел 
и для любого фиксированного 
существует предел 
Тогда повторные предела 
существуют и оба равны 
Доказательство. Так как функция 
имеет в точке 
предел 
то для любого 
можно указать такое 
что при 
выполняется неравенство 
Таким образом, в прямоугольной окрестности 
точки 
значение функции 
отличается от b не больше чем на 
. Но тогда пределы 
указанные в формулировке теоремы при х и у,
удовлетворяющих неравенствам 
также отличаются от Ь не больше чем на 
. Следовательно, и пределы этих функций в точках 
соответственно существуют и равны 
Теорема доказана.
Можно определить понятие повторного предела для так называемых двойных последовательностей 
элементы 
которых определяются двумя индексами 
Именно символ 
означает, что сначала определяется последовательность 
а затем находится предел этой последовательности 
Рассмотрим, например, двойную последовательность 
где 
— фиксированное число. Докажем, что
В самом деле, если 
где 
— целые числа, второе из которых положительно, то при 
имеем 
и поэтому 
Иными словами, если х — рациональное число, то 
Если же х — иррациональное число, то при любом 
справедливо неравенство 
и поэтому
Замечание. Используя полученный результат, мы можем аналитическим способом задать функцию Дирихле (см. 
§ 4 гл. 3) как повторный предел 
Повторный предел
Материал из Большого Справочника
Для функции нескольких переменных 
можно определить понятие предела по одной из переменных при фиксированных значениях остальных переменных. В связи с этим возникает понятие повторного предела.
Определение
Рассмотрим функцию двух переменных , определенную в некоторой выколотой окрестности точки . Выберем и зафиксируем переменную . Получим функцию как бы одной переменной. Рассмотрим предел:
Будем считать, что существует. Теперь снимем фиксацию с переменной и рассмотрим следующий предел:
Если этот предел существует, то говорят, что есть повторный предел функции в точке .
Аналогично мы можем фиксировать сначала переменную . В этом случае мы также получим повторный предел, но, вообще говоря, другой:
Это определение можно распространить и на функции нескольких переменных .
Равенство повторных пределов
Пусть функция , определена в выколотой окрестности точки 
и имеет в этой точке предел (обычный). Тогда любой повторный предел в точке 
существует и равен обычному пределу этой функции в этой же точке.
В обратную сторону утверждение, вообще говоря, неверно.
См. также
- Предел функции
Литература
- Ильин, В. А., Позняк, Э. Г. Глава 14. Функции нескольких переменных // Основы математического анализа. — 4. — М.: ФИЗМАТЛИТ, 2002. — Т. 1. — 648 с. — (Курс высшей математики и математической физики). — 5000 экз. — ISBN 5-9221-0536-1.
