Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
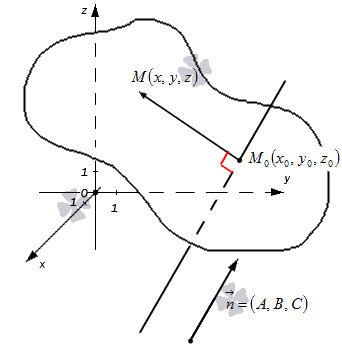
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )
Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
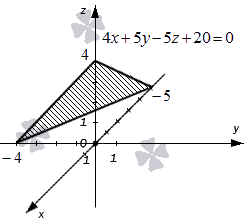
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0
Ответ: 3 x + 7 y — 5 z — 26 = 0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
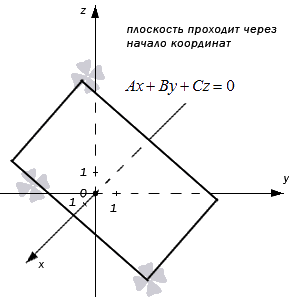
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0
Ответ: x — 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
Уравнение плоскости.
Общее уравнение плоскости
Любую плоскость можно задать уравнением плоскости первой степени вида
A x + B y + C z + D = 0
где A, B и C не могут быть одновременно равны нулю.
Уравнение плоскости в отрезках
Если плоскость пересекает оси OX, OY и OZ в точках с координатами ( a , 0, 0), (0, b , 0) и (0, 0, с ), то она может быть найдена, используя формулу уравнения плоскости в отрезках
| x | + | y | + | z | = 1 |
| a | b | c |
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x 0, y 0, z 0) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Уравнения плоскости: общее, через три точки, нормальное
Плоскость, общее уравнение плоскости
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.
Если известна какая-нибудь точка 

Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор 


Вектор 



Теперь, используя формулу скалярного произведения векторов 


Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, 
Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.
Пример 1. Составить уравнение плоскости, проходящей через точку 

Решение. Используем формулу (1), еще раз посмотрим на неё:

В этой формуле числа A , B и C координаты вектора 

Вычисления очень простые: подставляем эти числа в формулу и получаем

Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида

называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением 
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6) .
Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B(0; −3; 0) .
И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C(2; 0; 0) . По трём полученным в нашем решении точкам A(0; 0; 6) , B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение 
2. При A = 0 уравнение 



3. При A = D = 0 уравнение 


4. При A = B = 0 уравнение 


5. При A = B = D = 0 уравнение 
Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку 
Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид 

Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (
Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем
Подставив найденное значение A в уравнение 


Это и есть уравнение, требуемое в условии примера.
Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение
Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением 
Уравнение плоскости, проходящей через три точки
Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.
Пусть даны три различные точки 











Используя выражение смешанного произведения в координатах, получим уравнение плоскости

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.
Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:


и определить частный случай общего уравнения прямой, если такой имеет место.
Решение. По формуле (3) имеем:
Получили общее уравнение плоскости


Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.
Нормальное уравнение плоскости. Расстояние от точки до плоскости
Нормальным уравнением плоскости называется её уравнение, записанное в виде

где 

Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости — в трёх).
Пусть M — какая угодно точка пространства. Для нахождения отклонения 

Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.

так как расстояние не может быть отрицательным числом.
Общее уравнение плоскости
приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой

Знак нормирующего множителя берётся противоположным знаку свободного члена 
Пример 6. Привести уравнение плоскости 
Решение. Вычислим нормирующий множитель:

Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:

Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3) , а плоскость задана общим уравнением 
Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:

Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:

Вычислим отклонение точки от плоскости:
Найдём теперь расстояние от точки до плоскости как модуль отклонения:
источники:
http://ru.onlinemschool.com/math/library/analytic_geometry/plane/
http://function-x.ru/equations_of_plane.html
Задача 1.
Найти стационарную точку функции
Указание
В стационарной точке
Решение
Следовательно, координаты стационарной точки можно найти как решение системы
Ответ: (1,-2).
Задача 2.
Найти точку минимума функции
Указание
Пусть М0 – стационарная точка,
Тогда М0 является точкой минимума, если D > 0, A > 0.
Решение
Найдем стационарные точки функции:
Итак, стационарные точки функции –
Исследуем их на экстремум.
Нет экстремума.
Ответ:
Задача 3.
Найти экстремум функции
При условии 2Х + 5У + 3 = 0.
Указание
Найдите экстремум функции Лагранжа
Решение
Исследуем на экстремум функцию Лагранжа
Исследуем найденную точку на экстремум:
Следовательно, Точка условного максимума, и значение функции в этой точке равно
Ответ:
Задача 4.
На параболе
Найти точку, ближайшую к прямой Х – У = 2.
Указание
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Решение
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Составим функцию Лагранжа:
Не выполнено условие на знак подмодульного выражения.
Стационарная точка. При этом
Следовательно, найдена точка условного минимума.
Ответ:
Задача 5.
Найти множество значений функции
Указание
Найдите наибольшее и наименьшее значение функции в данной области,
Которые могут достигаться либо на границе, либо в стационарной точке внутри области.
Решение
Найдем стационарные точки функции:
Стационарная точка, Z(0,0) = 0.
Для определения наибольшего и наименьшего значения функции на границе области найдем условный экстремум функции Z = Xy при условии X2 + Y2 = 1.
Составим функцию Лагранжа:
Итак, найдены четыре стационарные точки:
При этом
Следовательно, наименьшее и наибольшее значения достигаются на границе области, а так как функция непрерывна, она принимает внутри области все промежуточные значения между наименьшим и наибольшим, то есть множество ее значений в данной области –
Ответ:
| < Предыдущая | Следующая > |
|---|
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Практические приложения подобия треугольников
- Измерительные работы на местности
Свойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности.
Определение высоты предмета
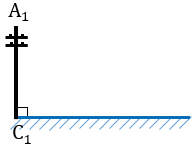
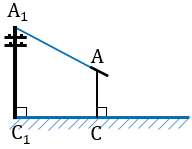
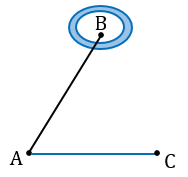
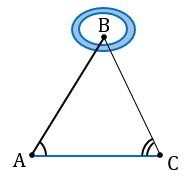
Пусть нам нужно определить высоту телеграфного столба А1С1.
Для этого на некотором расстоянии от столба ставим шест АС с вращающейся планкой и направляем планку на верхнюю точку столба А1.
Далее отмечаем на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли.
В 
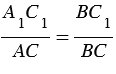
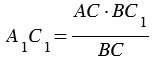
Измерив расстояния ВС1 и ВС, зная длину шеста АС, по полученной формуле вычисляем высоту А1С1 телеграфного столба. Пусть, например, ВС1 = 6,3 м, ВС = 2,1 м, АС = 1,7 м, тогда: 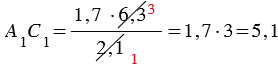
Определение расстояния до недоступной точки
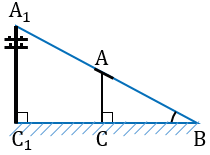
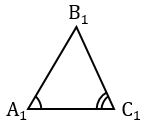
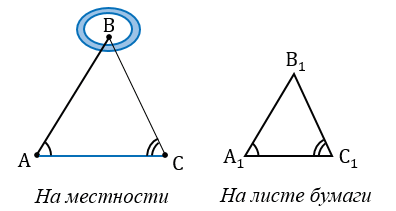
Пусть, нам нужно найти расстояние от пункта А до недоступного пункта В.
Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его.
Затем с помощью астролябии измеряем углы А и С.
На листе бумаги строим какой-нибудь треугольник А1В1С1, у которого 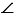
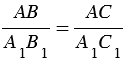
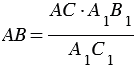
Измерив при помощи линейки длину отрезков А1В1 и А1С1, зная расстояние АС, по полученной формуле вычисляем расстояние АВ.
Чтобы сделать вычисления проще, 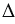
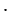
Пример:
Пусть АС = 130 м, 
Измеряем с помощью линейки отрезок А1В1. Он равен 153 мм, поэтому искомое расстояние АВ = 153 м.
Советуем посмотреть:
Задачи на построение
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 579,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 580,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 581,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 582,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 583,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Содержание
- Техническая механика
- Методы нахождения центра тяжести
- Метод симметрии
- Метод разбиения
- Метод отрицательных масс
- Практические методы определения центра тяжести тел
- Положение центра тяжести некоторых фигур
- Пример решения задачи на определение центра тяжести
- Лекция 8. Центр тяжести твердого тела
- 8.1. Понятие центра тяжести
- 8.2. Способы нахождения центра тяжести
- 8.3. Центры тяжести некоторых однородных тел
- 8.4. Пример расчета координат центра тяжести
- Вопросы для самоконтроля
- Задачи к лекции
Техническая механика
Методы нахождения центра тяжести
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1) .
В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a , тогда:
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G’ , G» , G»’ , абсциссы центров тяжести этих частей x’C, x»C, x»’C известны.
Формула для определения абсциссы центра тяжести всего тела:
Перепишем ее в следующем виде:
Последнее равенство запишем для каждой из трех частей тела отдельно:
Сложив левые и правые части этих трех равенств, получим:
Но правая часть последнего равенства представляет собой произведение GxC , так как
Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G , что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z :
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi , а силы тяжести конечных частей; под координатами xi , yi , zi понимают координаты центров тяжести частей, на которые разбито тело.
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания , который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания . Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а) .
Положение центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
Треугольник. Пусть дан треугольник АBD (см. рисунок 2) .
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD . Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски) , следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB , увидим, что искомый центр тяжести лежит и на медиане aD .
Проделав аналогичное действие с треугольником относительно стороны ВD , получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.
Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.
Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3) . Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC = 0 вследствие симметрии дуги относительно оси x . Определим координату центра тяжести xC .
Разобьем дугу АВ на элементарные части li , одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,
Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:
поскольку RΣΔyi = AB , а Σli = l – длина дуги АВ . Но АВ = 2R sinα , а l = 2Rα , следовательно,
При α = π/2 рад (полуокружность) , xC = 2R/π .
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а) . Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0 .
Определим xC , для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R . Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что
При α = π/2 рад (полукруг) : xC = 4R/(3π) .
Пример решения задачи на определение центра тяжести
Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4 .
Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y , то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0 .
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения: А1 = 15,2 см 2 ; y1 = 22/2 = 11 см.
Для швеллерного сечения: А2 = 12 см 2 ; y2 = 22 + d – z0 = 22 + 0,32 – 1,25 = 21,07 см ,
где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения координаты центра тяжести всего сечения:
Источник
Лекция 8. Центр тяжести твердого тела
8.1. Понятие центра тяжести
Частный случай распределенной нагрузки – сила притяжения, действующая на каждую точку тела со стороны Земли; говорят, что тело помещено в поле силы тяжести (или просто в поле тяжести).
Замечание. Силовым полем называют область пространства, в каждой точке которой на материальную частицу действует сила, зависящая от положения этой частицы. Например, поле, созданное с помощью магнита, действует на движущиеся заряженные частицы.
Если в поле тяжести помещена материальная точка, то действующая на нее сила тяжести численно равна mg и направлена вдоль прямой, соединяющей саму точку с центром Земли. Здесь m – масса точки, g – ускорение свободного падения.
Чтобы определить величину и направление силы тяжести, действующей на тело конечных размеров, разобьем его на мелкие части, каждую из которых можно считать материальной точкой. В принципе, силы, действующие на участки разбиения, образуют сходящуюся систему: они направлены к центру Земли (рис. 8.1 а). Но, как правило, радиус Земли во много раз больше размеров тела, а значит, эти силы можно считать сонаправленными (рис. 8.1 б).
Рис. 8.1. Распределенная нагрузка, действующая на тело со стороны Земли
Как известно, сила притяжения материальной точки к Земле зависит от расстояния до центра планеты и, как следствие, от высоты над ее поверхностью. Далее будем считать, что эта высота мала по сравнению с земным радиусом. Вместе с предположением о малых размерах самого тела это позволяет принять, что ускорение свободного падения для всех точек тела одинаково и равно ускорению на поверхности Земли.
Силовое поле называют однородным, если абсолютная величина и направление силы, действующей на помещенную в него материальную точку, не зависит от ее местоположения. Из вышесказанного следует, что если тело малых размеров находится вблизи поверхности Земли, то поле тяжести, в которое оно при этом попадает, можно считать однородным.
Замечание. Указанные предположения о малых размерах тела и малой высоте над поверхностью планеты – это не единственные сделанные нами упрощения. Строго говоря, Земля не имеет идеально шарообразной формы – она «сдавлена» у полюсов. Кроме того, на величину и направление силы тяжести влияет вращение Земли. В итоге ускорение свободного падения g зависит от географической широты: на полюсах оно максимально (9.832 м/с 2 ), на экваторе – минимально (9.780 м/с 2 ). В качестве стандартного (нормального) выбрано значение g на широте 45.5°, равное 9.80665 м/с 2 . Чаще всего в инженерных расчетах указанными поправками можно пренебречь и считать, что ускорение свободного падения равно 9.8 м/с 2 .
Пусть тело разбито на n участков, массы которых равны m1, m2. mn, соответственно. Складывая сонаправленные силы тяжести, приложенные к каждому из них, мы найдем суммарную силу тяжести, действующую на тело в целом: G = (m1 + m2 + . + mn)g. Учитывая, что m1 + m2 + . + mn = M – это масса всего тела, мы получим
Если тело однородно (имеет постоянную плотность), формула (8.1 а) принимает вид
где ρ – плотность тела, V – его объем (напомним, что плотностью тела называется масса, приходящаяся на единицу его объема).
Остается найти центр C параллельных сил, действующих на тело со стороны Земли. Он и называется центром тяжести тела. Для этого предположим, что силы тяжести, действующие на отдельные участки разбиения тела, приложены в точках с радиус-векторами (vec r_<1>,vec r_<2>,ldots,vec r_) относительно некоторого начала координат O (т.е. сами эти точки являются центрами тяжести участков разбиения). Тогда, подставив выражения для сил тяжести в (7.6) и сократив числитель и знаменатель на g, получим
| $$vec r_=fracvec r_<1>+m_<2>vec r_<2>+ldots+m_vec r_>.$$ | (8.2 а) |
Для однородных тел это соотношение после сокращения числителя и знаменателя на плотность ρ принимает вид
| $$vec r_=fracvec r_<1>+V_<2>vec r_<2>+ldots+V_vec r_>.$$ | (8.2 б) |
Здесь V1, V2. Vn – объемы отдельных участков, на которые разбито исходное тело, V1 + V2 + . + Vn = V. Если тело является плоским (например, представляет собой деталь, вырезанную из металлического листа малой толщины), объемы следует заменить на площади. Если тело составлено из отрезков линий (такой, к примеру, можно считать арматуру, поддерживающую железобетонные конструкции), вместо объемов в равенстве (8.2 б) должны фигурировать длины.
Соотношения (8.2 а) и (8.2 б) можно записать в координатной форме, аналогично (7.7):
| $$x_=fracx_<1>+V_<2>x_<2>+ldots+V_x_>,;y_=fracy_<1>+V_<2>y_<2>+ldots+V_y_>,; z_=fracz_<1>+V_<2>z_<2>+ldots+V_z_>.$$ | (8.3 а) |
Чтобы повысить точность вычислений, придется все более и более измельчать разбиение исходного тела. В конечном итоге это приведет к тому, что положение центра тяжести станет выражаться тройным интегралом по всему объему, занятому телом, подобно формуле (7.9). Например, для координаты x получится выражение
| $$x_=frac<1>iiint_xdV.$$ | (8.3 б) |
Замечание. Центр тяжести тела может и не принадлежать телу, если оно не является выпуклым. Напомним, что тело называют выпуклым, если отрезок, соединяющие две его любые точки, полностью принадлежит телу (рис. 8.2).
Рис. 8.2. а) – выпуклое тело; б), в) – невыпуклые тела
Например, с помощью метода разбиения легко показать, что центр тяжести фигуры, составленной из двух стержней одинаковй длины a и с равной погонной плотностью, расположенных под прямым углом, находится на растоянии a/4 от каждого из них и, тем самым, не принадлежит самой фигуре (рис. 8.3).
Помимо общих формул, существует несколько простых приемов, помогающих определить положение центра тяжести. Ниже будут изучены некоторые из них. При этом для простоты все изучаемые тела будут считаться однородными (хотя некоторые методы применимы и к неоднородным телам).
8.2. Способы нахождения центра тяжести
Метод симметрии. Этот способ основан на следующем факте: если однородное тело имеет некоторый элемент симметрии (зеркальную плоскость, ось или центр симметрии), то его центр тяжести должен лежать на этом элементе.
Действительно, пусть тело имеет плоскость симметрии π. Тогда на две его «половинки» действуют равные по модулю и сонаправленные силы тяжести (vec G_<1>) и (vec G_<2>), а точки C1 и C2 (центры тяжести «половинок») расположены симметрично относительно зеркальной плоскости (рис. 8.4).
Рис. 8.4. Положение центра тяжести зеркально-симметричного тела
Сила тяжести (vec G), действующая на тело в целом, является равнодействующей сил (vec G_<1>) и (vec G_<2>) и должна быть приложена вдоль линии, проходящей через середину отрезка C1C2 и принадлежащей плоскости π. Поэтому и центр тяжести тела, лежащий на линии действия (vec G), находится в этой же плоскости.
С помощью аналогичных рассуждений можно продемонстрировать, например, что центр тяжести осесимметричного тела лежит на этой оси.
Пример. Точка пересечения диагоналей паралеллограмма является его центром симметрии. Поэтому и центр тяжести однородного («сплошного») параллелограма находится в точке пересечения его диагоналей (рис. 8.5).
Рис. 8.5. Центр тяжести параллелограмма
Это утверждение в равной степени справедливо и для паралеллограмма, составленного из двух пар равных по длине стержней с одинаковой погонной плотностью.
Если однородное тело имеет несколько плоскостей или осей симметрии, то его центр тяжести находится на их пересечении. Это объясняется тем, что он должен принадлежать каждой из указанных плоскостей (осей).
Пример. Судно с нагруженным трюмом можно рассматривать как тело, разбитое на части: одной из них служит сам корпус судна, а другими – отдельные места груза. При дифферентовке (перемещении этих грузов) координаты их центров тяжести изменяются; согласно (8.3 а), меняться станет и положение центра тяжести всего нагруженного судна. Пользуясь этим, можно добиться максимальной остойчивости судна и предотвратить его переворот при сильной качке. Наоборот, неудачное закрепление грузов может привести к нежелательному смещению центра тяжести и перевороту судна.
Чтобы упростить вычисления, исследуемое тело стараются разбивать на небольшое количество участков возможно более простой формы.
Пример. Из квадрата KLMN со стороной 60 см вырезан квадрат MPQR со стороной 30 см (рис. 8.6 а). Найти центр тяжести полученного тела.
Разобьем исходное тело на два: прямоугольник KSPN и квадрат SLRQ. Пусть C1 и C2 – их центры тяжести. Введем систему координат с началом в точке K, ось x направим вдоль стороны KN, ось y – вдоль KL (рис. 8.6 б).
Исходя из сказанного выше, C1 есть точка пересечения диагоналей KSPN. В выбранной системе координат она имеет абсциссу x1 = 30 см и ординату y1 = 15 см. Аналогично, C2 (точка пересечения диагоналей квадрата SLRQ) находится на расстоянии SQ/2 = 15 см от оси y и на расстоянии KS + SL/2 = 45 см от оси x, а значит, имеет координаты x2 = 15 см, y2 = 45 см. Площади S1 и S2 участков KSPN и SLPQ равны, соответственно, 60·30 = 1800 см 2 и 30·30 = 900 см 2 . Пользуясь формулой (8.3 а), найдем координаты точки C – центра тяжести большого квадрата с вырезом:
xC = (1800·30 + 900·15)/(1800 + 900) = 25 см, yC = (1800·15 + 900·45)/(1800 + 900) = 25 см.
Таким образом, в данном случае абсцисса и ордината центра тяжести одинаковы. Этот результат легко объясним: полученное тело, несмотря на вырез, остается симметричным относительно диагонали KM, поэтому центр тяжести тела должен лежать на этой линии.
Рис. 8.7. Тело с вырезанной частью
Тогда центр тяжести C «тела с вырезом» имеет координаты
| $$x_=fracx_<1>-V_<2>x_<2>>-V_<2>>,;y_=fracy_<1>-V_<2>y_<2>>-V_<2>>,; z_=fracz_<1>-V_<2>z_<2>>-V_<2>>.$$ | (8.4) |
Это соотношение отличается от (8.3 а) лишь тем, что объем вырезаемого участка учитывается со знаком «–». Отсюда и присходит название метода (иногда вместо отрицательных объемов говорят о «методе отрицательных масс»).
Понятно, что центр тяжести объединенной системы, полученной из тела «с вырезом» и вырезанной части, должен находиться в исходной точке C1. Легко убедиться, что подстановка (8.4) в (8.3 а) дает правильный результат:
(остальные координаты вычисляются таким же образом). Изучаемый способ также называют способом дополнения, поскольку тело «с вырезом» дополняется до целого прибавлением объема V2.
Пример. Найти положение квадрата с вырезанной четвертью (см. предыдущий пример) методом отрицательных объемов.
Введем систему координат аналогично тому, как это было сделано ранее (рис. 8.8).
Центр тяжести C1 квадрата KLMN совпадает с точкой Q и имеет координаты x1 = 30 см, y1 = 30 см. Центр тяжести квадрата MPQR находится в точке C2(45; 45). Площади фигур равны 3600 см 2 и 900 см 2 , соответственно. Подставляя эти данные в формулу (8.4), найдем, что центр тяжести C фигуры KLRQPN имеет координаты
Как и следовало ожидать, результаты, найденные разными методами, совпадают.
Экспериментальный метод. Он основан на определении центра тяжести как центра параллельных сил: при одновременном их повороте (или, что то же самое, при повороте тела относительно линий действия этих сил) центр тяжести не меняет положения.
Представим, что тело подвешено за некоторую точку. Тогда на него действуют две силы: тяжести (vec G) и реакции в точке подвеса (рис. 8.9 а).
Рис. 8.9. Определение центра тяжести экспериментальным способом
Поскольку они уравновешены, линия действия силы (vec G), содержащая центр тяжести C, проходит через точку подвеса (см. первую аксиому статики). Поэтому можно отметить на теле линии действия силы тяжести при подвешивании его в нескольких разных точках (рис. 8.9 б), и искомый центр тяжести будет находиться на пересечении этих линий.
8.3. Центры тяжести некоторых однородных тел
Центр тяжести стержня располагается в его середине. Это следует из того, что стержень симметричен относительно указанной точки (рис. 8.10).
Рис. 8.10. Центр тяжести однородного стержня
Как уже было сказано ранее, центр тяжести параллелограмма располагается на пересечении его диагоналей. Аналогично, центр тяжести параллелепипеда (однородного либо «собранного» из плоских граней равной поверхностной плотности или ребер одинаковой погонной плотности) также располагается в точке пересечения его диагоналей (рис. 8.11).
Рис. 8.11. Центр тяжести однородного параллелепипеда
Центр тяжести площади треугольника располагается в точке пересечения его медиан (рис. 8.12).
Рис. 8.12. Центр тяжести однородного треугольника
Докажем это. Разрежем треугольник на полоски, паралелльные одной из его сторон. Сделаем полосы настолько тонкими, что каждую из них можно приближенно считать отрезком. В этом случае сила тяжести, действующая на треугольник в целом, станет эквивалентной системе сил, приложенных к серединам отрезков (рис. 8.13).
Эти середины заполняют собой медиану треугольника, проведенную к выбранной стороне. Следовательно, и искомый центр тяжести (точка приложения равнодействующей сил тяжести, действующих на все полоски) лежит на данной медиане.
Разрезая исходный треугольник на тонкие полоски, параллельные другой стороне, можно показать, что его центр тяжести принадлежит другой медиане. Но все медианы треугольника пересекаются в одной точке. Значит, именно в ней и находится искомый центр тяжести.
Далее найдем положение центра тяжести однородной дуги окружности с центральным углом 2α и радиусом R. Введем систему координат так, как показано на рис. 8.14.
Рис. 8.14. Определение центра тяжести однородной дуги окружности
Используя метод симметрии, легко получить, что искомая точка C лежит на оси Ox, т.е. yC = 0. Осталось найти координату xC. Для этого разобьем дугу на мелкие участки и соединим их концы с вершиной угла. Тогда он сам будет разбит на малые углы. Вследствие того, что длины участков разбиения дуги невелики, каждый из них можно считать прямолинейным отрезком длины dl = R dβ, где dβ – радианная мера соответствующего угла.
Пусть β – угол между осью Ox и отрезком, соединяющим точку O c серединой участка разбиения (см. рис. 8.14). Тогда абсцисса x центра тяжести этой дуги приближенно равна R cos β. Подставим это значение x в формулу (8.3 б). Вместо объема V в данном случае должна фигурировать длина дуги, равная R·2α, вместо множителя dV под интегралом – найденная ранее величина dl, причем угол β изменяется в пределах от –α до α:
Итак, центр тяжести однородной дуги лежит на ее оси симметрии на расстоянии (R sin α)/α от ее центра.
Замечание. Как видно, искомая точка не лежит на самой дуге. Это неудивительно, ибо дуга окружности не является выпуклой фигурой.
Выясним местоположение центра тяжести кругового сектора радиуса R и радианной меры 2α. Аналогично предыдущему случаю, можно утверждать, что искомая точка находится на оси симметрии фигуры.
Разобьем исходный центральный угол на меньшие углы Δα. Будем предполагать их настолько малыми, что соответствующие секторы можно приближенно считать равнобедренными треугольниками, боковые стороны которых равны R (рис. 8.15).
Рис. 8.15. Определение центра тяжести однородного кругового сектора
Центр тяжести каждого из таких треугольников лежит на его медиане, проведенной к основанию, и делит ее в отношении 2:1, считая от вершины (по свойству точки пересечения медиан). Поскольку в силу малости Δα длину каждой из таких медиан можно приближенно считать равной R, то центры тяжести треугольников, на которые разбит сектор, заполняют собой дугу окружности радиуса 2R/3 и той же радианной меры 2α, что и исходный сектор.
Таким образом, задача сводится к определению положения центра тяжести полученной дуги. Но из сказанного выше следует, что эта точка имеет абсциссу
Замечание 1. Правдоподобность полученных результатов можно проверить на простом частном случае. Если 2α = 2π, т.е. центральный угол является полным, то, как следует из полученных формул, центры тяжести дуги и сектора располагаются в точке с абсциссой xC = 0. Этот результат вполне предсказуем: при 2α = 2π дуга превращается в окружность, а сектор – в круг. Их центры тяжести должны лежать на элементе симметрии, т.е. в центре окружности или круга. Но у этой точки абсцисса xC заведомо равна нулю, что и требовалось.
Замечание 2. Легко видеть, что центр тяжести сектора располагается ближе к вершине центрального угла, чем центр тяжести дуги окружности того же радиуса и той же радианной меры. Этот факт нетрудно объяснить. Масса сектора распределена по его площади равномерно, а не сосредоточена вдоль криволинейной части его границы. Поэтому его центр тяжести и смещается в сторону от дуги, стягивающей центральный угол.
Центр тяжести объема конуса или пирамиды лежит на отрезке, соединяющем вершину с центром тяжести основания (рис. 8.16), и делит его в отношении 3:1, считая от этой вершины.
Рис. 8.16. Определение центра тяжести пирамиды или конуса
Тот факт, что искомый центр тяжести лежит на указанном отрезке, легко обосновать, рассуждая таким же образом, как и при поиске центра тяжести треугольника: достаточно разрезать конус на тонкие слои, параллельные основанию. Осталось найти отношение, в котором искомая точка делит отрезок OK = l (K – центр тяжести основания).
Каждая точка отрезка служит центром тяжести сечения конуса, проходящего через эту точку параллельно основанию. Значит, в произвольной точке L, лежащей на OK, сосредоточена сила, пропорциональная площади сечения, проходящего через L. Направим ось x вдоль OK; тогда K имеет абсциссу l. Рассечем изучаемое тело плоскостью OAK, проходящей через эту ось и одну из образующих конуса OA (см. рис. 8.16). Треугольники OBL и OAK подобны с коэффициентом k = x/l, где x – абсцисса L. Все сечения конуса, параллельные основанию, также подобны между собой, поэтому площадь сечения S, проходящего через L, равна k 2 S0, где S0 – площадь основания.
Для вычисления координаты центра тяжести воспользуемся формулой (7.9), в которой положим a = 0, b = l, p(x) = k 2 S0, k = x/l. После несложных вычислений получим, что xC = 3l/4. Тем самым, утверждение доказано.
Замечание. Можно воспользоваться и формулой (8.3 б), в которой тройной интеграл следует заменить интегралом по отрезку.
Как уже было сказано, рассуждения для конуса в пространстве аналогичны рассуждениям, проведенным для треугольника на плоскости. Различие состоит в отношении, в котором центр тяжести делит выбранный отрезок: на плоскости оно составляет 2:1, а в пространстве – 3:1.
Еще два результата приведем без доказательства. Пусть дан шаровой сектор радиуса R и высоты H и шаровой сегмент с теми же параметрами (рис. 8.17).
Рис. 8.17. Шаровые сектор и сегмент (сегмент выделен цветом)
Тогда центры тяжести объема сектора и площади сегмента расположены в точках с координатами
соответственно. Ось Ox является осью симметрии сектора (сегмента), начало отсчета располагается в центре шара.
Замечание. Объем шарового сектора и площадь сегмента (шарового свода) вычисляются по формулам V = 2/3 πR 2 H, S = 2πRH. При H = 2R эти равенства переходят в формулы для вычисления объема шара и площади сферы.
8.4. Пример расчета координат центра тяжести
Полусфера со срезанным верхом помещена на коробчатое основание в форме прямоугольного параллелепипеда, составленное из плоских граней. Срезанная часть заменена плоской «крышкой» в форме круга. Определить положение центра тяжести полученного тела, считая, что все его элементы однородны и имеют одинаковую поверхностную плотность. Размеры даны в см (рис. 8.18).
Изучаемое тело составлено из четырех других тел более простой формы: поверхностей параллелепипеда, круга и полусферы, от которой, в свою очередь, «отрезан» сегмент. Поскольку радиус полусферы R = 30 см, а высота полученной в итоге части равна 20 см, то высота срезанного сегмента составляет 10 см.
Введем систему координат с началом в центре полушара O, как показано на рис. 8.18. Ось Ox направим вдоль короткого горизонтального ребра параллелепипеда, ось Oy – вдоль длинного ребра, ось Oz – вертикально вверх. Поскольку тело симметрично относительно плоскости Oyz, то абсцисса центра тяжести C равна нулю. Требуется найти лишь ординату и аппликату этой точки. Используя методы разбиения и отрицательных объемов, получим, что эти координаты можно отыскать по формулам
| $$y_=fracy_<1>+S_<2>y_<2>+S_<3>y_<3>-S_<4>y_<4>>+S_<2>+S_<3>-S_<4>>,; z_=fracz_<1>+S_<2>z_<2>+S_<3>z_<3>-S_<4>z_<4>>+S_<2>+S_<3>-S_<4>>.$$ | (8.5) |
Индекс «1» относится к параллелепипеду, «2» – к полусфере, «3» – к кругу, а «4» – к срезанному сегменту (его площадь учитывается со знаком «–»). Поскольку конструкция составлена из поверхностных элементов, то в приведенных формулах фигурируют именно площади, а не объемы.
Поскольку второе по величине ребро параллелепипеда равно диаметру полушара, площадь его поверхности составляет S1 = 2·(100·60 + 100·10 + 60·10) = 15200 см 2 . Центр тяжести данной фигуры находится на расстоянии 100/2 = 50 см от ее левой грани и на расстоянии 20/2 = 10 см от ее верхней грани. Поскольку начало отсчета O лежит на верхней грани в 30 см от левого края параллелепипеда, координаты центра тяжести фигуры 1 таковы: y1 = 20 см, z1 = –5 см.
Фигура 2 представляет собой шаровой сегмент высоты H = R, с центром в точке O и осью симметрии Oz. Ее площадь S2 = 4π·30 2 /2 = 1800π см 2 , а координаты центра тяжести равны y2 = 0 см, z2 = 30 – 30/2 = 15 см.
Очевидно, что центр тяжести круга находится в точке (0; 0; 20). Радиус этого круга равен (sqrt<30^2-20^2>=sqrt<500>) см, поэтому его площадь S3 = 500π см 2 .
Площадь срезанного шарового свода равна S4 = 2π·30·10 = 600π см 2 . Ордината его центра тяжести y4 = 0 см, а аппликата z4 = 30 – 10/2 = 25 см.
Подставляя найденные параметры в (8.5), найдем, что yC ≈ 14.80 см, zC ≈ –0.34 см. Итак, C(0; 14.80; –0.34). Как и следовало ожидать, центр тяжести оказался смещен от начала координат вправо (за счет того, что фигура 1 несимметрична относительно Oz) и вниз (поскольку площадь поверхности, а значит, и вес параллелепипеда больше, чем у шарового сегмента).
Вопросы для самоконтроля
- Что такое центр тяжести? Является ли система сил тяжести, приложенных к телу, параллельной?
- В вершинах треугольника размещены материальные точки равной массы. Доказать, что центр тяжести этой системы находится в точке пересечения медиан треугольника.
- Как надо изменить расчетные формулы методов разбиения и отрицательных объемов, чтобы они оставались справедливыми и для неоднородных тел?
- На чем основан экспериментальный метод определения центра тяжести? Показать, что данный метод справедлив и для неоднородных тел.
- Как найти центр тяжести произвольного четырехугольника?
- Вывести формулу для определения координат центра тяжести однородного кругового сектора.
- Как определяется положение центра тяжести однородного конуса?
Задачи к лекции
- Вырезать из картона или плотной бумаги произвольный треугольник, определить положение его центра тяжести экспериментально. Провести в треугольнике медианы и сравнить положение их точки пересечения с положением центра тяжести.
От кругового сектора, радиус которого равен 10 см, а центральный угол – 60°, отделен сегмент (рис. 8.19). Найти положение его центра тяжести.
Найти координаты центра тяжести однородной плоской фигуры, изображенной на рис. 8.20.
Ответы. 2. Центр тяжести лежит на оси симметрии сегмента (сектора) на расстоянии около 9.2 см от вершины сектора. 3. Приближенное положение: C(4.50; 8.46).
Также рекомендуется решить задачи из §9 [2]; РГР С8 [3].
Источник
Задание 2.
На территории
района (рис.1) имеется 8 магазинов,
торгующих продовольственными товарами.
Определите узел транспортной сети
прямоугольной конфигурации, в которой
размещение распределительного склада
обеспечить минимум грузооборота
транспорта по доставке грузов в
обслуживаемую сеть.
Методические
указания
Задание выполняется
на чертеже, сделанном при выполнении
задания 1. Изучив следующие теоретические
пояснения к заданию 2, найдите и укажите
на чертеже рекомендуемую точку размещения
склада (точка М). Основой выполнения
задания 2 является изучение метода
определения оптимального места размещения
распределительного склада в случае
прямоугольной конфигурации сети
автомобильных дорог (метод пробной
точки).
Сначала на примере
отдельного участка транспортной сети
разберем суть метода. Пусть на участке
дороги, длиной 30 км (участок AD
на рис. 3), имеем четыре потребителя
материального потока: A,
B,
C
и D.
Месячный объем перевозок каждого из
них указан в скобках. Оптимальное место
расположения распределительного склада
легко определить методом, который можно
назвать как «метод пробной точки».
Рис. 3. Определение оптимального места
расположения распределительного склада
на участке обслуживания
Суть метода состоит
в последовательной проверке каждого
отрезка обслуживаемого участка. Введем
понятие пробной точки отрезка, а также
понятия левого и правого объема перевозок
пробной точки.
Пробной точкой
отрезка назовем любую точку, находящуюся
на этом отрезке и не принадлежащую его
концам (т.е. пробная точка не совпадает
с точками A,
B,
C
и D).
Левый объем
пробной точки
– объем перевозок потребителей,
расположенных на всем участке обслуживания
слева от пробной точки.
Правый объем
пробной точки
– объем перевозок потребителей,
расположенных справа.
Участок обслуживания
проверяют с крайнего левого конца.
Сначала анализируют первый отрезок
участка (в нашем случае – отрезок АВ).
На данном отрезке ставится пробная
точка и подсчитывается сумма грузооборотов
потребителей, находящихся слева и справа
от поставленной точки. Если грузооборот
потребителей, находящихся справа,
больше, то проверяется следующий отрезок.
Если меньше, то принимается решение о
размещении склада в начале анализируемого
отрезка.
Проверка пробных
точек продолжается до тех пор, пока не
появится точка, для которой сумма объемов
перевозок потребителей с левой стороны
не превысит сумму объемов перевозок
потребителей с правой стороны. Решение
принимается о размещении склада в начале
этого отрезка, т.е. слева от пробной
точки. В нашем примере – это точка С.
Рассмотрим вариант,
когда сумма объемов перевозок слева и
справа от пробной точки очередного
отрезка становится одинаковой. Начало
этого отрезка (точка М, рис. 4), является
первым, а конец (точка N)
последним из возможных мест расположения
распределительного склада на участке
обслуживания. Распределительный центр
может быть расположен в любой из точек
отрезка MN
участка обслуживания.
Рис. 4. Определение оптимального
расположения распределительного склада
при равенстве «левого» и «правого»
объемов перевозок пробной точки
Для определения
методом пробной точки оптимального
узла прямоугольной транспортной сети
(для размещения распределительного
склада) следует нанести на карту района
координатные оси, сориентированные
параллельно дорогам. Определив координаты
потребителей, необходимо на каждой
координатной оси найти методом пробной
точки оптимальное место расположения
координаты X
и координаты Y
искомого узла.
В качестве примера
рассмотрим обслуживаемую систему,
состоящую из 4 потребителей (рис. 5). Сеть
дорог прямоугольная. Присваивая ординатам
и абсциссам потребителей соответствующие
значения объемов перевозок, найдем
методом пробной точки ординату и абсциссу
оптимального узла транспортной сети.
Размещение распределительного склада
в найденном узле обеспечит минимальный
грузооборот по доставке товаров со
складов.
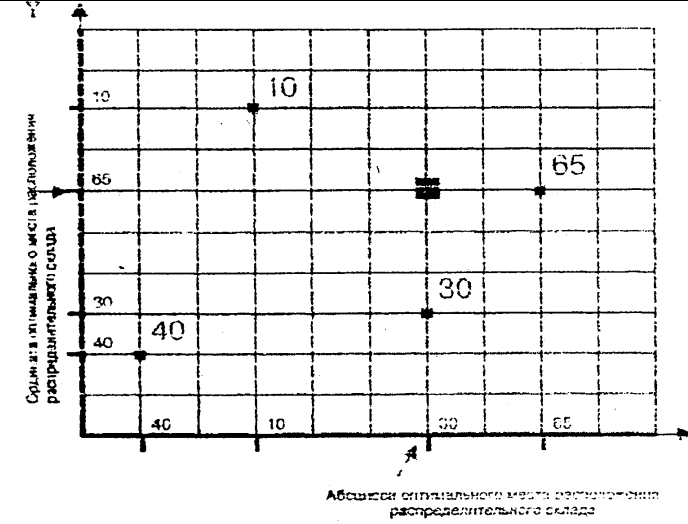
Рис. 5. Определение оптимального места
расположения распределительного склада
в условиях прямоугольной сети автомобильных
дорог:
Точками на схеме обозначены потребители
материального потока, числами – объем
перевозок потребителей, т/мес.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #