Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 марта 2022 года; проверки требуют 3 правки.
| Правильный двенадцатиугольник | |
|---|---|
|
|
| Углы | 12 |
| Символ Шлефли | {12} t{6} |
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, двенадцатиугольником называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае двенадцатиугольника углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
Правильный двенадцатиугольник[править | править код]
Площадь правильного двенадцатиугольника со стороной a находится по формуле:
Или, при радиусе описанной окружности R:
Или, при радиусе вписанной окружности r:
Монеты[править | править код]
Британская монета в три пенса в форме двенадцатиугольника
Схема построения правильного двенадцатиугольника с помощью циркуля и линейки[править | править код]
Правильный двенадцатиугольник, согласно теореме Гаусса — Ванцеля, относится к многоугольникам, которые можно построить с помощью циркуля и линейки.
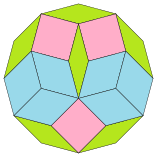
Разбиение правильного двенадцатиугольника[править | править код]
Гарольдом Коксетером было доказано, что правильный 
-угольник (в общем случае – -угольный зоногон) можно разбить на 
ромбов. Для двенадцатиугольника 
, так что он может быть разбит на 15 ромбов.
| Разбиение правильного двенадцатиугольника | |
|---|---|
|
|
|
См. также[править | править код]
- Последовательность двенадцатиугольника
Ссылки[править | править код]
- Двенадцатиугольник Архивная копия от 28 июля 2011 на Wayback Machine на MathWorld
- Dodecagon (12-gon) Архивная копия от 25 ноября 2010 на Wayback Machine
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Как найти внутренний и центральный угла правильного двенадцатиугольника?
На этой странице находится вопрос Как найти внутренний и центральный угла правильного двенадцатиугольника?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
Ученик
(21),
закрыт
9 лет назад
Ирина Бар
Гуру
(3674)
13 лет назад
Сумма углов n-угольника равна 180°(n-2).
В случае 12-угольника сумма равна 1800 градусов. Т. к. он правильный, то углы его равны 1800/12=150 градусов.
Удачи тебе!
лучший ответ, пожалуйста!
bob aibibekoff
Гуру
(3454)
13 лет назад
Ещё вариант. Порадуйте преподавателя двумя способами.
Сумма всех внешних углов любого выпуклого многоугольника равна 360 градусов. Значит нешний угол правильного 12-ти угольника – 360/12=30. Значит внутренний, смежный внешнему, 180-30=150 градусов.
Ответ: 150.
Опубликовано 3 года назад по предмету
Геометрия
от Moonstruckfox
Найдите углы правильного двенадцатиугольника.
-
Ответ
Ответ дан
PansСумма внутренних углов любого многоугольника равна 180(n-2), где n – число сторон. В случае двенадцатиугольника n=12. Все углы равны. Имеем:
180(12-2):12 = 180*10:12 = 150. Все углы по 150 градусов.
Самые новые вопросы
Математика – 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54
Информатика – 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
География – 3 года назад
Почему япония – лидер по выплавке стали?
Математика – 3 года назад
Чему равно: 1*(умножить)х? 0*х?
Русский язык – 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
