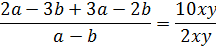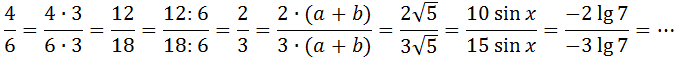Правило – преобразование
Cтраница 1
Правило преобразования легко выводится из примеров.
[1]
Правило преобразования еообще-ния из одной символической формы представления ( исходного алфавита) в другую ( объектный алфавит), обычно без каких-либо потерь информации. Процесс преобразования исходного алфавита б объектный называется кодированием, а обратный процесс – декодированием. Эти процессы реализуются соответственно кодером и декодером: поскольку процессы кодирования и декодирования являются в своей основе алгоритмическими, кодер я декодер могут реализовываться аппаратным или программным способом. Иногда термин coding используется как синоним термина code.
[2]
Правило преобразования математического ожидания при практическом применении затруднений не вызывает. Что касается двойного преобразования корреляционной функции, то оно в ряде случаев приводит к очень громоздким операциям, что затрудняет практическое использование рассмотренных методов.
[3]
Правило преобразования координат точки М0 при переходе от одной прямоугольной системы координат к другой можно сформулировать следующим образом.
[4]
Правило преобразования неоднородных статистических данных в эквивалентные им ( в указанном смысле) однородные данные зависит от планов испытания.
[5]
Правилом преобразования логических формул называется всякая пара ф ф, где р, ф – логические формулы.
[6]
Это правило преобразования показывает, что величины химического сродства преобразуются подобно соответствующим стехиометричес-ким уравнениям.
[7]
Выражение правила преобразования в виде уравнений ( 3) или ( 4) называется в соответствии с [17] дифференциальным видом этого правила.
[8]
Раздел Правила преобразования входных данных в выходные должен содержать описания технологии решения задачи, используемых алгоритмов и необходимых преобразований исходных данных.
[9]
Выведите правила преобразования блок-схемы устройства возведения в квадрат, полезный выходной сигнал которого определяется: а) составляющей удвоенной частоты, б) постоянной составляющей.
[10]
Согласно правилам преобразований по Лапласу-Карсону в дифференциальных уравнениях пространственные производные для такого изображения сохраняют то же выражение, как и для оригинала, а временная производная df / dt заменяется на величину p ( F – f0), где fo-f ( 0) – начальное значение оригинала. Аналогичным образом должны преобразовываться и граничные условия.
[11]
Согласно правилам преобразований по Лапласу – Карсону, в дифференциальных уравнениях пространственные производные для такого изображения сохраняют то же выражение, как и для оригинала, а временная производная df / dt заменяется на величину p ( F – fo), где fof ( 0) – начальное значение оригинала. Аналогичным образом должны преобразовываться и граничные условия.
[12]
Рассмотрим теперь правило преобразования А – A ( s) для дробных чисел.
[13]
Здесь применено правило преобразования проекций вектора на координатные оси при преобразовании координат.
[15]
Страницы:
1
2
3
4
Сегодня
на уроке мы познакомимся ещё с одним способом преобразования информации – по
заданным правилам. Часто этот способ преобразования информации встречается
при решении математических задач. Рассмотрим в качестве примера такую
математическую задачу. Ширина прямоугольного школьного коридора 5 метров, а
длина в 7 раз больше. Найдите площадь коридора, ответ запишите в квадратных
метрах.
Итак,
площадь школьного коридора получилась равной 175 метров квадратных. А нашли мы
её в результате преобразования исходных данных задачи по уже известным нам
правилам.
Рассмотрим
ещё одну задачу: Мистер Энтрик переписывался по электронной почте с мисс
Кнопкой и пригласил её на свидание. Их дома расположены на расстоянии 14 км
друг от друга. Они вышли навстречу друг другу и встретились только через 2
часа. Найдите скорость движения мисс Кнопки, если скорость движения Энтрика 3
километра в час.
Мы
нашли, что скорость мисс Кнопки равна 4 км в час. Зная правила нахождения пути
и скорости, решить эту задачу для нас не составило никакого труда.
Существуют
и правила для вычисления блок-схем. Вспомним, что блок-схема –
это графическое представление последовательности действий, алгоритма.
У
блок-схемы всегда есть начало и завершение. Слова «Начало» и «Конец»
записываются в скруглённых прямоугольниках. В параллелограммах записываются
входные и выходные данные. В прямоугольниках – операции, которые необходимо
выполнить. А в ромбе записывается условие, которое определяет дальнейший ход
вычисления. Давайте выполним этот алгоритм.
К 55
прибавляем 11 получаем 66. Затем к 66 прибавляем 167 равно 233. Рассмотрим
условие: число пятизначное? Нет, 233 это трёхзначное число. Значит дальше
двигаемся по стрелке с обозначением НЕТ и выполняем действия: к 233 прибавляем
1030, получаем 1263. Далее к 1263 прибавляем 5148, результат равен 6411.
Выполняем условие снова: число пятизначное? Нет, 6411 и 1030 получается 7441.
Затем сложим 7441 и 5148, получаем 12 589. Опять проверим условие. Число
пятизначное? Да. У нас получилось пятизначное число. Значит, двигаемся по
стрелке с надписью ДА. Выполняем действие: от 12 589 отнимаем 2589, в
результате получаем 10000. Выполнение алгоритма в виде блок-схемы успешно
завершено.
Эти
способы преобразования информации тесно связаны с математикой, и не всегда
возможно выполнять арифметические действия в уме, особенно если числа большие.
В таких случаях нам понадобится умение пользоваться калькулятором.
В
операционную систему компьютера тоже встроен калькулятор. Для его запуска надо
нажать: меню «Пуск», «Все программы», «Стандартные», «Калькулятор». На экране
появилось изображение калькулятора.
Изображение
можно легко перетянуть в любую область экрана. Для этого нужно навести
указатель мыши на верхнюю часть окна, зажать левую кнопку мыши и перетянуть
окно программы в нужное место. Работа с таким компьютерным калькулятором похожа
на работу с обычным, знакомым всем, карманным калькулятором. Но в отличие от
карманного, работать такой калькулятор может в нескольких режимах. Сейчас
калькулятор открыт в обычном режиме. Нажмём на кнопку «Вид» и посмотрим, какие
режимы работы ещё существуют. Например, режим «Инженерный» подойдёт для более
сложных вычислений, и пригодиться нам в старших классах.
Режим
«Программист» позволит без труда переводить числа из одной системы счисления в
другую.
Такой
режим как «Статистика», позволяет обрабатывать статистические данные.
Эти
режимы нам тоже пока не понадобятся. Вернёмся в обычный режим и познакомимся с
интерфейсом программы. Меню программы калькулятор включает в себя три вкладки:
«Вид», мы уже с ней познакомились, «Правка» даёт возможность копировать данные
в буфер обмена и наоборот, вставлять из буфера, и вкладка «Справка» позволяет
познакомиться с особенностями программы и найти интересующие нас сведения о
функциях программы.
Верхняя
белая строка называется индикатор, в ней отображаются вводимые с клавиатуры
цифры и результаты вычислений.
Рассмотрим
кнопки, располагающиеся ниже. Ряд кнопок с буквой «М» предназначен для работ с
памятью программы.
Кнопка
«МС» очищает память калькулятора, то есть нажатие на эту кнопку удаляет все
данные, которые были сохранены в его памяти.
«MR» – выводит информацию из памяти на экран
программы
«MS» – записывает значения в память калькулятора
«M+» – прибавляет число к
значению, которое находится в памяти.
«M-» – вычитает число из значения, которое находится
в памяти калькулятора.
Кнопка со стрелкой
(«Backspace») используется для удаления последней набранной цифры. Если неверно
набрано всё число, то его можно удалить целиком нажатием клавиши «CE» или
кнопкой сброса «C».
Рассмотрим кнопки для
совершения арифметических действий. Разделить (/), умножить (*), вычесть (-) и
сложить (+). Для получения результата нужно нажать на кнопку со знаком
равенства.
Ввод чисел осуществляется
при помощи кнопок с цифрами. Работать с программой можно непосредственно щелкая
указателем мыши по кнопкам. Но гораздо удобнее совершать вычисления при помощи
клавиатуры, вернее её дополнительного блока. Вспомним, чтобы включить
дополнительную клавиатуру нужно нажать на клавишу «Num
Lock», при этом загорится световой
индикатор «Num Lock».
Чтобы удалить последнюю
набранную цифру с помощью клавиатуры точно так же используется клавиша
«Backspace» на клавиатуре, удалить всё число можно клавишей «Delеte»
или клавишей сброса «Esc».
Для примера проделаем
простые вычисления:
·
20
+ 10 = 30;
·
7
* 8 = 56;
·
78
– 36 = 42.
Давайте решим такой
пример:
Найдём частное от суммы
чисел 10730 и 6438 и их разности. Итак, сначала найдём разность этих чисел:
10730 – 6438 = 4292 –
занесём это значение в память калькулятора, нажав кнопку «MS».
Затем вычислим сумму этих
же чисел. Отчистим окно индикатора нажатием кнопки «CE».
10730 + 6438 =
17 168.
Разделим получившееся
значение на то, которое находится в памяти калькулятора, то есть на разность
выражений. Нажимаем на кнопку деления, затем на кнопку «MR»,
которая позволяет выводить данные из памяти. В результате вычислений получили
4. Вы видите, как легко, без бумаги, ручки и утомительных вычислений в столбик
мы решили этот пример.
Сегодня на уроке мы
научились преобразовывать информацию по заданным правилам и производить
арифметические действия в программе калькулятор.
|
X = |
M |
Z + |
N |
F |
|||||||||
|
D |
|||||||||||||
|
D . |
|||||||||||||
|
В правую часть последнего равенства подставим выражение, найденное из |
|||||||||||||
|
уравнения (3.28): |
L |
||||||||||||
|
Z = |
G. |
||||||||||||
|
В результате получим: |
R |
||||||||||||
|
M |
L |
N |
|||||||||||
|
X = |
G + |
F. |
|||||||||||
|
D |
(3.30) |
||||||||||||
|
D R |
Приняв возмущающее воздействие равным нулю ( F = 0 ), найдем передаточную
функцию разомкнутой системы по управляющему воздействию
|
X = |
M |
L |
G |
|||||||||||||
|
, |
||||||||||||||||
|
откуда |
D R |
|||||||||||||||
|
X |
= |
ML |
= W |
|||||||||||||
|
DR |
||||||||||||||||
|
G |
. |
|||||||||||||||
|
Последнее выражение перепишем в развернутой форме следующим образом: |
||||||||||||||||
|
W (s) = |
X (s) |
= |
M (s)L(s) |
|||||||||||||
|
D(s)R(s) . |
||||||||||||||||
|
G(s) |
||||||||||||||||
|
Приняв во внимание (3.12) и (3.13), получим: |
||||||||||||||||
|
W (s) = Wp (s)Wo (s). |
(3.31) |
|||||||||||||||
|
В заключение найдем передаточную функцию разомкнутой системы по |
||||||||||||||||
|
возмущающему воздействию. |
||||||||||||||||
|
При отсутствии управляющего воздействия (Z = 0) из (3.29) имеем: |
||||||||||||||||
|
X = |
N |
F, |
||||||||||||||
|
D |
||||||||||||||||
|
откуда следует, что |
||||||||||||||||
|
X |
= |
N |
= W f |
|||||||||||||
|
, |
||||||||||||||||
|
F |
D |
|||||||||||||||
|
или окончательно |
X (s) |
N(s) |
||||||||||||||
|
Wf (s) = |
= |
. |
||||||||||||||
|
F(s) |
D(s) |
Структурные схемы САУ могут иметь различную сложность. С целью их упрощения и приведения к виду, более удобному для исследования, используют определенные правила. Эти правила базируются на принципе
суперпозиции и однонаправленности звеньев и легко доказываются сопоставлением между собой исходных и эквивалентных схем.
Правило преобразования цепочки последовательно соединенных звеньев. Дана цепочка звеньев с известными передаточными функциями Wi (s) , i =1, 2, …, n (рис.3.8).
91

|
Z(s) |
… |
X(s) |
|||||
|
W1(s) |
W2(s) |
Wn(s) |
|||||
Рис.3.8. Схема цепочки последовательно соединенных звеньев
Несложно показать, что данную цепочку звеньев можно представить одним звеном (рис.3.9)
|
Z(s) |
X(s) |
||||
|
W(s) |
|||||
Рис.3.9. Эквивалентное представление цепочки
последовательно соединенных звеньев
с эквивалентной передаточной функцией
|
n |
||
|
W (s) = ÕWi (s) |
. |
(3.32) |
|
i=1 |
Передаточная функция цепочки n последовательно соединенных звеньев равна произведению передаточных функций этих n звеньев. Кроме того, из уравнения (3.32) следует, что результат последовательного соединения звеньев не зависит от порядка соединения звеньев.
Правило преобразования цепочки параллельно соединенных звеньев. Дана
|
цепочка звеньев (рис.3.10). |
|||||
|
W1(s) |
|||||
|
Z(s) |
X(s) |
||||
W (s)
…2

|
Z(s) |
X(s) |
||||||
|
W(s) |
|||||||
Рис.3.10. Преобразование цепочки
параллельно соединенных звеньев
Звено, эквивалентное данной системе звеньев, имеет передаточную функцию
|
n |
|
|
W (s) = åWi (s). |
(3.33) |
|
i=1 |
Передаточная функция цепочки n параллельно соединенных звеньев равна сумме передаточных функций этих звеньев.
Правило определения передаточной функции замкнутой цепи с единичной отрицательной обратной связью. Если передаточная функция разомкнутой цепи равна
W (s) и используется единичная отрицательная обратная связь (рис.3.11),
92

|
Z(s) |
W (s) |
X(s) |
|
Z(s) |
Φ(s) |
X(s) |
|
Рис.3.11. Преобразование замкнутой цепи с
единичной отрицательной обратной связью
то передаточная функция замкнутой системы вычисляется по формуле
|
Ф(s) = |
X (s) |
= |
W (s) |
. |
||
|
G(s) |
1+W (s) |
|||||
|
(3.34) |
||||||
Правило определения передаточной функции замкнутой цепи с неединичной отрицательной обратной связью. Пусть известны передаточные функции
разомкнутой цепи W (s) и цепи обратной связи Wос (s) (рис.3.12),
Z(s) X(s)
W (s)
W oc(s)
|
Z(s) |
Φ(s) |
X(s) |
|
Рис.3.12. Преобразование замкнутой
цепи с неединичной отрицательной обратной связью
тогда передаточная функция замкнутой системы определяется соотношением
|
Ф(s) = |
X (s) |
= |
W (s) |
|||
|
G(s) |
1+ W (s) ×W (s) |
. (3.35) |
||||
|
ос |
Правило определения передаточной функции замкнутой цепи с неединичной положительной обратной связью. При использовании неединичной положительной обратной связи (в цепи обратной связи стоит звено с
передаточной функцией Wос (s) ) передаточная функция замкнутой системы (рис.3.13)
93

|
Z(s) |
W (s) |
X(s) |
|
W oc(s)
|
Z(s) |
Φ(s) |
X(s) |
|
Рис.3.13. Преобразование замкнутой
цепи с неединичной положительной обратной связью
рассчитывается следующим образом:
|
Ф(s) = |
W (s) |
|
|
1–W (s) ×W (s) |
. |
|
|
ос |
Правило определения передаточной функции замкнутой цепи с единичной положительной обратной связью. Если положительная обратная связь является
единичной (Wос (s) =1) (рис.3.14),
Z(s) X(s)
W (s)
|
Z(s) |
Φ(s) |
X(s) |
||
Рис.3.14. Преобразование замкнутой цепи с
единичной положительной обратной связью
то передаточная функция системы определяется по формуле
|
Ф(s) = |
W (s) |
. |
|||
|
1 |
–W (s) |
||||
Правило переноса узла. При преобразовании структурных схем часто возникает необходимость в переносе узла (точки разветвления сигнала) через звено, либо по направлению распространения сигнала, либо против направления передачи сигнала.
При переносе узла по направлению распространения сигнала через звено с передаточной функцией W (s) (рис.3.15)
94

|
Z (s) |
X(s) |
||||
|
W *(s) |
W (s) |
||||
|
Z (s) |
X(s) |
|||||
|
W *(s) |
W (s) |
|||||
|
1/W (s) |
||||||
Рис.3.15. Перенос узла по направлению
распространения сигнала
необходимо в новое ответвление включить элемент с передаточной функцией
1/W (s) .
При переносе узла против направления распространения сигнала через звено с передаточной функцией W (s) (рис.3.16) необходимо в новое ответвление включить звено с той же передаточной функцией W (s) .
|
Z (s) |
X(s) |
||||
|
W *(s) |
W (s) |
||||
|
Z (s) |
X(s) |
||||||
|
W *(s) |
W (s) |
||||||
W (s)
Рис.3.16. Перенос узла против направления
распространения сигнала
Правило переноса узла удовлетворяет условию: в исходной и преобразованной
эквивалентной схемах входной сигнал оказывает одинаковое влияние на формирование выходного сигнала.
Правило переноса сумматора. При переносе сумматора против направления
распространения сигнала через звено с передаточной функцией W (s) (рис.3.17)
необходимо в линию связи по второму входу сумматора включить элемент с передаточной функцией 1/W (s) .
95

|
Y (s) |
||||||||||||
|
Z (s) |
X(s) |
|||||||||||
|
W *(s) |
W (s) |
|||||||||||
|
Y (s) |
||||||||||||
|
1/W (s) |
||||||||||||
|
Z (s) |
X(s) |
|||||||||||
|
W *(s) |
W (s) |
|||||||||||
Рис.3.17. Перенос сумматора против направления
распространения сигнала
При переносе сумматора по направлению распространения сигнала через звено с передаточной функцией W (s) (рис.3.18) нужно в линию связи по второму входу сумматора включить элемент с передаточной функцией W (s) .
|
Y (s) |
||
|
Z (s) |
X(s) |
|
|
W *(s) |
W (s) |
|
|
Y (s) |
||
|
W (s) |
||
|
Z (s) |
X(s) |
|
|
W *(s) |
||
|
W (s) |
Рис.3.18. Перенос сумматора по направлению
распространения сигнала
Приведенные правила переноса сумматора не оказывают влияние на формирование выходного сигнала под действием входных сигналов, следовательно, схемы являются эквивалентными.
Правило перестановки сумматоров. Элементы сравнения (рис.3.19) и
сумматоры (рис.3.20), в которых осуществляется сложение либо вычитание сигналов можно менять местами.
Рис.3.19. Правило перестановки
элементов сравнения
96
Соседние файлы в папке Моделирова
- #
- #
- #
- #
- #
- #
Равносильные уравнения, правила преобразований
- Понятие равносильных уравнений
- Правила преобразования уравнений
- Примеры
п.1. Понятие равносильных уравнений
Равносильными называют уравнения, имеющие одни и те же корни.
Равносильными считаются также уравнения, каждое из которых не имеет корней.
Пара уравнений
Корни
Вывод
Каждое из уравнений имеет один и тот же корень x=1
$implies$ уравнения равносильны
(x – 3)(x + 2) = 0
2x + 4 = 0
$x_1 = 3 и x_2 = -2$
x = -2
Первое уравнение имеет два корня, а второе – только один корень
$implies$ уравнения неравносильны
$varnothing$
$varnothing$
Оба уравнения не имеют решений
$implies$ уравнения равносильны
п.2. Правила преобразования уравнений
При решении уравнения его стараются заменить более простым равносильным уравнением. При этом используют следующие правила.
Правила преобразования уравнений
- 1. В любой части уравнения можно раскрывать скобки и приводить подобные.
- 2. Любое слагаемое в уравнении можно перенести из одной части в другую, изменив его знак.
- 3. Обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.
В результате этих преобразований всегда получаем уравнение, равносильное данному.
п.3. Примеры
Пример 1. Решите уравнение $ frac {1}{5}x = 12 – 7x$
Решение:
$ frac {1}{5}x = 12 – 7x iff frac {1}{5}x + 7x = 12 iff 7 frac {1}{5}x = 12 iff x = 12:7 frac {1}{5} iff$
$ x = 12 cdot frac {5}{36} = frac {5}{3} =1 frac {2}{3} $
Ответ: x = 1 frac {2}{3}
Пример 2. Решите уравнение $ frac {3x}{7} – frac {x}{14} = 10$
Решение:
$ frac {3x}{7} – frac {x}{14} = 10 | times 14 iff 6x – x = 140 iff 5x = 140 iff x = 140 : 5 = 28$
Ответ: x = 28
Пример 3. Решите уравнение $7x – frac {2}{5} =frac 15 (3x+14)$
Решение:
$7x – frac 25 = frac 15 (3x + 14) | times 5 iff 35x – 2 = 3x + 14 iff 35x – 3x = 14 + 2 iff$
$ iff 32x = 16 iff x = frac {16}{32} = frac 12$
Ответ: x = frac 12
Пример 4. Решите уравнение $frac {5x-1}{2} – frac {3x+4}{8} = frac {x-3}{4}$
Решение:
$frac {5x-1}{2} – frac {3x+4}{8} = frac {x-3}{4} | times 8 iff 4(5x-1)-(3x+4)=2(x-3) iff $
$ iff 15x=2 iff x= frac {2}{15} $
Ответ: x = $frac {2}{15}$
Пример 5. При каких значениях a равносильны уравнения
3(x-1)=5-x и ax=x+a
Решение:
Найдём корень первого уравнения
$3(x-1)=5-x iff 3x-3=5-x iff 3x+x=5+3 iff 4x=8 iff x=2$
Подставим во второе
$a cdot 2=2+a iff 2a-a=2 iff a=2$
При a=2 оба уравнения имеют один корень x=2.
Ответ: a=2
Рейтинг пользователей
Итак, друзья, в прошлом уроке мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означают слова “выражение не имеет смысла”. А теперь пришла пора разобраться, что же такое преобразование выражений. И самое главное — зачем оно нужно.
Что такое преобразование выражения?
Ответ прост, до неприличия.) Это любое действие с выражением. И всё. Все эти преобразования вы делали с первого класса. Любое не буквально, конечно… Об этом чуть ниже будет.)
Например, возьмём какое-нибудь суперкрутое числовое выражение Скажем, 3+2. Как его можно преобразовать? Да очень просто! Хотя бы взять да посчитать:
3+2 = 5
Вот этот расчёт детского садика и будет преобразованием выражения. Можно записать то же самое выражение по-другому:
3+2 = 2+3
А тут мы вообще ничего не считали. Просто взяли и переписали наше выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать и по-другому. Например, вот так:
3+2 = 10-5
И эта запись — тоже преобразование выражения.
Или так:
3+2 = 10:2
Тоже преобразование выражения!
Если мы с вами постарше, с алгеброй дружим, то напишем:
Кто на “ты” с алгеброй, тот, даже особо не напрягаясь и ничего не считая, в уме сообразит, что слева и справа стоит обыкновенная пятёрка. Напрягитесь и попробуйте.)
А если мы совсем уж старшенькие, то можем записать и такие ужастики:
log28+log24 = log232
Или даже такие:
5sin2x+5cos2x=5tgx·ctgx
Внушает? И таких преобразований, очевидно, можно понаделать сколько хочешь! Насколько позволяет фантазия. И набор знаний математики.)
Уловили смысл?
Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто.
Простота, конечно, дело всегда хорошее и приятное, но за любую простоту где-то надо платить, да…. Есть здесь одно существенное “но”. Все эти загадочные превращения всегда подчиняются одному оч-чень важному правилу. Правило это настолько важное, что его смело можно назвать главным правилом всей математики. И нарушение этого простого правила неизбежно будет приводить к ошибкам. Вникаем?)
Предположим, мы преобразовали наше выражение как попало, от балды, как-нибудь вот так:
3+2 = 6+1
Преобразование? Конечно. Мы же записали выражение в другом виде! Но… что здесь не так?
Ответ: всё не так.) Дело всё в том, что преобразования “как попало и от балды” математику не интересуют вообще.) Почему? Потому, что вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Таково её жёсткое требование. И нарушение этого требования будет приводить к ошибкам. Три плюс два можно записать в каком угодно виде. В каком пример требует, в том виде и запишем. Но по своей сути это всегда должно быть пять. В каком бы виде мы эти самые 3+2 ни записали. А вот, если, вдруг, после записи выражения 3+2 в другом виде, у вас вместо пяти окажется двадцать пять, где-то вы ошиблись по дороге. Вернитесь да ляп-то и устраните.)
А теперь пришла пора мудрых зелёных мыслей.)
Запоминаем:
1. Любое действие над выражением, запись его в другом виде, называется преобразованием выражения.
2. Преобразования, не меняющие сути выражения, называются тождественными.
3. Вся математика построена на тождественных преобразованиях выражений.
Именно тождественные преобразования и позволяют нам, шаг за шагом, потихоньку-помаленьку, превращать сложный пример в простое, белое и пушистое выражение, сохраняя суть примера. Если, вдруг, в цепочке наших преобразований мы где-то ошибёмся, и на каком-то шаге сделаем НЕ ТОЖДЕСТВЕННОЕ преобразование, то дальше мы будем решать уже совсем другой пример. С другими ответами, да… Которые уже не будут иметь никакого отношения к правильным.) Нарушим тождественность и накосячим ещё где-то – приступим к решению уже третьего примера. И так далее, в зависимости от количества косяков, от задачки про поезд и автомобиль можно прийти к задачке про полтора землекопа.)
Ещё пример. Для школьников, уже вовсю изучающих алгебру. Допустим, нам надо найти значение выражения (40+7)2. Как можно выкрутиться, т.е. преобразовать наше злое выражение? Можно просто посчитать выражение в скобках (получим 47), перемножить столбиком само на себя и получить (если сосчитать) 2209. А можно воспользоваться формулой квадрата суммы
(a+b)2 = a2+2ab+b2.
Получим: (40+7)2 = 402+2∙40∙7+72 = 1600+560+49 = 2209.
Но! Есть соблазн (скажем, в силу незнания формулы) при возведении в квадрат записать просто:
(40+7)2 = 402+72.
К сожалению, на данном простом и, казалось бы, очевидном переходе, тождественность наших преобразований нарушается. Слева всё как надо, 2209, а вот справа — уже другое число. 1649. Посчитайте — и всё станет понятно. Вот вам типичный пример НЕ тождественного преобразования. И соответственно вылезшей ошибки.)
Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.
Пример с числовыми выражениями 3+2 и (40+7)2 я привёл чисто для наглядности.
А что же с алгебраическими выражениями? Всё то же самое! Только в алгебраических выражениях тождественные преобразования задаются формулами и правилами. Скажем, в алгебре есть формула:
a(b-c) = ab – ac
Значит, в любом примере мы имеем полное право вместо выражения a(b-c) смело написать альтернативное выражение ab – ac. И наоборот. Это тождественное преобразование. Математика предоставляет нам на выбор эти два выражения. А уж какое из них писать – от конкретного примера зависит.
Или популярное:
a2–b2 = (a–b)(a+b)
Опять же, два возможных варианта. Оба правильные.) Это тоже тождественное преобразование. Что выгоднее писать — разность квадратов или же произведение скобок — пример сам подскажет.)
Ещё пример. Одно из самых главных и нужных преобразований в математике – это основное свойство дроби. Подробнее можно (будет) по ссылочке почитать и посмотреть (когда урок сделаю), а здесь я просто напомню правило:
Если числитель и знаменатель дроби умножить (разделить) на одно и то же число, или неравное нулю выражение, дробь не изменится.
Вот вам пример тождественных преобразований по этому свойству:
Как вы, наверняка, догадались, эту славную цепочку можно продолжать до бесконечности…) Насколько хватит творческого порыва. Всякие там минусы, корни, синусы, логарифмы пусть вас не смущают. Это всё одна и та же дробь. По своей сути. Две трети. 2/3. Просто записанная в разном виде. 🙂 Очень важное свойство. Именно оно очень часто позволяет превращать всякие монстры-примеры в белые и пушистые.)
Конечно же, формул и правил, задающих тождественные преобразования, – много. Я бы даже сказал, очень много. Но самых главных, без которых в математике хотя бы троечного уровня обойтись нельзя, – вполне разумное количество.
Вот одни из базовых преобразований:
1. Работа с одночленами и многочленами. Приведение подобных слагаемых (или коротко — подобных);
2. Раскрытие скобок и заключение в скобки;
3. Разложение на множители;
4. Формулы сокращённого умножения и разложение квадратного трёхчлена.
5. Работа с дробями и дробными выражениями.
Эти пять базовых преобразований широко используются во всей математике. От элементарной до высшей. И, если вы не владеете хотя бы одной из этих пяти простых вещей, то вас неминуемо ждут большие проблемы как во всей математике средней школы, так и в старших классах, а уж в ВУЗе — тем более. Поэтому именно с них и начнём. В следующих уроках этого раздела.)
Есть и более крутые преобразования. Для продвинутых школьников и студентов.) Будь то:
6. Тригонометрия, логарифмы и всё что с ними связано;
7. Выделение полного квадрата из квадратного трёхчлена;
8. Деление многочленов уголком или по схеме Горнера;
9. Разложение рациональной дроби в сумму элементарных (простейших) дробей. Полезнейшая фишка для студентов при работе с серьёзными интегралами.
Итак, всё ясно насчёт тождественности преобразований и важности её соблюдения? Отлично! Тогда пора двигаться на следующий уровень и шагать из примитивной арифметики в более серьёзную алгебру окончательно. И с блеском в глазах.)