Как найти правостороннюю производную - Сайт, где вы сможете решить свои вопросы

Определение.
Правой (левой)
производной функции

в
точке

называется
правый (левый) предел отношения

при

(при условии,
что этот предел существует).

Обозначение:

Если функция

имеет в точке

производную, то она имеет в этой точке
правую и левую производные, которые
совпадают. Вместе с тем существуют
функции, имеющие в данной точке

правую и левую производные, но не имеющие
производной в этой точке. Это, например,
функция

,
которая имеет в точке

правую производную, равную

(при

),
и левую производную, равную

(при

),
но не имеет в этой точке производной,
так как

3.2. Дифференцируемость функции
1. Понятие дифференцируемости функции в данной точке.

Определение.
Функция

называется
дифференцируемой в точке

,
если ее приращение

в этой точке можно представить в виде

,

(3.1)

где
А


некоторое число,
не зависящее от

,
a

–

функция
аргумента
,
являющаяся
бесконечно малой при

,
т. е.

Установим связь
между дифференцируемостью функции в
точке и существованием производной в
той же точке.

Теорема
1. Для
того чтобы функция

была дифференцируема в точке

,
необходимо
и достаточно, чтобы она имела в
этой точке
конечную производную.

Таким образом, для
функций одной переменной дифференцируемость
и существование производной

понятия равносильные. Поэтому операцию
нахождения производной часто называют
дифференцированием.

2. Связь между понятиями дифференцируемости и непрерывности.

Теорема 2.
Если функция

дифференцируема в данной точке

,
то она и
непрерывна в этой точке.

З а м е ч а н и е.
Обратное утверждение неверно. Функция
может быть непрерывной в точке, но не
быть дифференцируемой, т.е. не иметь
производной в этой точке. Примером
такой функции служит функция

,
которая непрерывна в точке

,
но не имеет в этой точке производной,
т.е. не является дифференцируемой.

Если функция

имеет производную в каждой точке
некоторого промежутка (дифференцируема
в каждой точке этого промежутка), то
будем говорить, что функция

дифференцируема на указанном промежутке.

3.3. Дифференциал функции

1. Определение и
геометрический смысл дифференциала.
Пусть функция

дифференцируема в точке

,
т.е. ее приращение у
в этой
точке можно записать в виде суммы двух
слагаемых:

,
где

Слагаемое

является
при

бесконечно малой одного порядка с

(при А

0), оно линейно относительно

.
Слагаемое

при

–
бесконечно малая более высокого порядка,
чем

Таким образом,
первое слагаемое (при А

0) является главной частью приращения
функции

Определение.
Дифференциалом
функции

в точке

называется главная, линейная относительно

,
часть приращения функции в этой
точке:

.
(3.2)

Если

,
то

,
и поэтому слагаемое

уже не
является главной частью приращения
у,
так как слагаемое

,
вообще говоря, отлично от нуля. Однако
и в этом случае по определению полагаем
дифференциал функции в точке

равным

,
т.е.

.

Учитывая, что

,
формулу
(3.2) можно
записать в виде

.

(3.3)

Пусть

.
Тогда по формуле (3.3)

Поэтому дифференциалом
независимой переменной х
назовем приращение этой переменной

.
Соотношение
(3.3)
принимает теперь вид

.
(3.4)

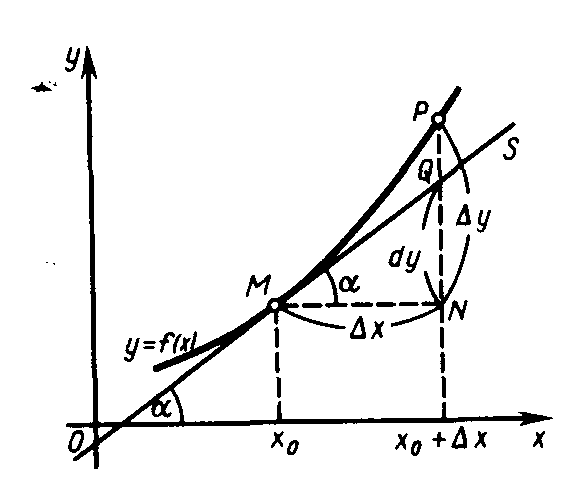
Рис.
51

аметим, что с помощью равенства
(3.4) производную

можно
вычислить как отношение дифференциала
функции

к дифференциалу

независимой переменной, т. е.

Рис. 11

Дифференциал
функции имеет следующий геометрический
смысл. Пусть точка М
на графике
функции

соответствует значению аргумента

,
точка Р 
значению аргумента

,
прямая MS

касательная
к графику

в точке М, 

угол между
касательной и осью Ох.
Пусть, далее MN
|| Ox,
PN
|| Оу ,
Q

точка
пересечения касательной MS
с прямой PN
(рис. 11). Тогда приращение функции

равно
величине отрезка NP.
В то же время из прямоугольного
треугольника MNQ
получаем:

,
т.е. дифференциал функции

равен
величине отрезка NQ.
Из геометрического рассмотрения видно,
что величины
отрезков
NP
и NQ
различны. Таким образом, дифференциал
функции

в точке

равен
приращению «ординаты касательной» к
графику этой функции в точке

,
а приращение функции y
есть приращение «ординаты самой функции»

в точке

,
соответствующее приращению аргумента,
равному

2. Приближенные
вычисления с помощью дифференциала.
Из определения
дифференциала следует, что он зависит
линейно от

и является
главной частью приращения функции y.
Само же y
зависит от

более сложно.
Во многих задачах приращение функции
в данной точке приближенно заменяют
дифференциалом функции в этой точке:

.

Пример.
Покажем, что
если 
мало, то можно использовать приближенную
формулу

Решение.
Рассмотрим функцию

При малых х
имеем

откуда, положив

,
х
= ,
получим

В частности,

при 
= 0.0003.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

У этого термина существуют и другие значения, см. Производная.

Производная — фундаментальное математическое понятие, используемое в различных вариациях (обобщениях) во многих разделах математики. Это базовая конструкция дифференциального исчисления, допускающая много вариантов обобщений, применяемых в математическом анализе, дифференциальной топологии и геометрии, алгебре.

Общее между различными вариациями и обобщениями заключается в том, что производная отображения характеризует степень изменения образа отображения при (бесконечно) малом изменении аргумента. В зависимости от рассматриваемых математических структур конкретизируется содержание данного понятия.

Только для случая топологических линейных пространств известно около 20 обобщений понятия производной.^[1]

Производная функции одной переменной[править | править код]

Базовое определение[править | править код]

Производная функции в точке $x_{0}$ определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:

$f'(x_{0})=lim _{{Delta xrightarrow 0}}{frac {Delta f}{Delta x}}$

, где ${displaystyle Delta x=x-x_{0}, Delta f=f(x)-f(x_{0})}$

Графически это тангенс угла наклона касательной в точке $x_{0}$ к кривой, изображающей функцию f(x) .

При достаточно малых изменениях аргумента выполнено равенство $df=f'(x_{0})dx$ . В общем случае именно такая форма определения принимается за основу для обобщения понятия производной.

Односторонние производные[править | править код]

Определяются также односторонние производные, где вместо соответствующего предела используется односторонний (левосторонний и правосторонний) предел. Правосторо́нняя произво́дная или произво́дная спра́ва обозначается символами $f^{+}(x_{0}), f'_{+}(x_{0}), {mathrm {D}}^{+}!f(x_{0})$ . Левосторо́нняя произво́дная или произво́дная сле́ва обозначается символами ${displaystyle f^{-}(x_{0}), f'_{-}(x_{0}), mathrm {D} ^{-}!f(x_{0})}$ . Обычная производная существует тогда и только тогда, когда существуют равные между собой односторонние производные (их величина и равна производной).

Производные высших порядков[править | править код]

Поскольку производная функции одной переменной также является некоторой функцией одной переменной, то можно рассматривать производную производной — вторую производную и вообще производную любого порядка (некоторое натуральное число).

Производные функций нескольких переменных[править | править код]

Частные производные[править | править код]

В случае функций нескольких переменных: ${displaystyle f:mathbb {R} ^{n}rightarrow mathbb {R} }$ , в первую очередь, определяются так называемые частные производные — производные по одной из переменных при условии фиксированных значений остальных переменных:

${displaystyle {frac {partial f(mathbf {x} )}{partial x^{i}}}=lim _{x^{i}rightarrow x_{0}^{i}}{frac {f(x^{1},...,x^{i},...,x^{n})-f(x_{0}^{1},...,x_{0}^{i},...,x_{0}^{n})}{x^{i}-x_{0}^{i}}}}$

Градиент[править | править код]

Собственно производной (учитывающей изменения вектора переменных в целом, то есть всех переменных) в случае функций нескольких переменных является так называемый градиент функции — вектор, компонентами которого являются частные производные:

${displaystyle f'(mathbf {x} )=mathbf {grad} f(mathbf {x} )=nabla f={frac {df(mathbf {x} )}{dmathbf {x} }}=left({frac {partial f}{partial x_{1}}},{frac {partial f}{partial x_{2}}},...,{frac {partial f}{partial x_{n}}}right)}$

По аналогии со случаем одной переменной, при малых изменениях ${displaystyle dmathbf {x} =(dx_{1},dx_{2},...,dx_{n})}$ вектора переменных выполнено равенство:

$df({mathbf {x}})=f'({mathbf {x_{0}}})d{mathbf {x}}=sum _{{i=1}}^{n}{frac {partial f}{partial x^{i}}}dx^{i}$

Производная по направлению[править | править код]

В случае функций нескольких переменных можно определить производную по направлению, то есть в предположении, что переменные изменяются в данном направлении. Производная функции по направлению вектора определяется следующим образом:

$f'_{{mathbf {e}}}({mathbf {x}}_{0})=lim _{{trightarrow 0}}{frac {f({mathbf {x}}_{0}+t{mathbf {e}})-f({mathbf {x}}_{0})}{t}}$

Если направление совпадает с направлением некоторой координатной оси, то производная по этому направлению фактически является соответствующей частной производной. Можно показать, что производная по направлению равна скалярному произведению вектора градиента на нормированный вектор направления (то есть вектор направления единичной длины, что можно получить из любого вектора направления делением на его длину):

$f'_{{mathbf {e}}}({mathbf {x}}_{0})=(f'({mathbf {x}}_{0}),{mathbf {e}})$

Производные высших порядков[править | править код]

По аналогии со случаем функций одной переменной можно рассматривать частные производные произвольного порядка. Причем в данном случае можно использовать как одну и ту же переменную несколько раз, так и одновременно несколько переменных:

${frac {partial ^{k}f}{partial x_{1}^{{k_{1}}}partial x_{2}^{{k_{2}}},...,partial x_{n}^{{k_{n}}}}}$ , где $sum k_{i}=k$

Аналогом второй производной в случае функции нескольких переменных является матрица вторых частных производных — матрица Гессе, которая является производной векторнозначной функции (см. ниже) — градиента скалярной функции. Элементами этой матрицы являются вторые производные ${frac {partial ^{2}f}{partial x^{i}partial x^{j}}}$ .

Полная производная[править | править код]

Во многих случаях возникает необходимость оценить зависимость функции от изменения данной переменной $x^{j}$ в ситуации, когда остальные переменные определенным образом изменяются в зависимости от $x^{j}$ , то есть на значение функции изменение данной переменной сказывается как непосредственно (что выражено частной производной), так и опосредованно через изменение других переменных. Полное влияние выражено в понятии полной производной:

${frac {df}{dx^{j}}}=sum _{{i=1}}^{n}{frac {partial f}{partial x^{i}}}{frac {partial x^{i}}{partial x^{j}}}$

В общем случае можно рассматривать траекторию изменения независимых переменных в параметрической форме $x^{i}(t)$ , где — некоторый параметр (в физике это чаще всего время). Тогда можно рассматривать полную производную по этому параметру:

${frac {df}{dt}}=sum _{{i=1}}^{n}{frac {partial f}{partial x^{i}}}{frac {dx^{i}}{dt}}$

При этом в параметр может выступать одной из переменных x^i .

Производная Лагранжа принимает во внимание изменения вследствие зависимости от времени и движения через пространство по векторному полю.

Набор функций нескольких переменных[править | править код]

Набор функций $f_{i}$ нескольких переменных можно интерпретировать как векторнозначную функцию: ${displaystyle mathbf {F} :mathbb {R} ^{n}rightarrow mathbb {R} ^{m}}$ . Производная такой функции представляет собой так называемую матрицу Якоби , строки которой — градиенты функций $f_{i}$ , составляющих набор , то есть элемент -ой строки и -го столбца равен частной производной функции $f_{i}$ по переменной $x^{j}$ :

$J_F=mathbf{F}'(mathbf{x}_0)=left[frac {partial f_i}{partial x^j}right]$

По аналогии со скалярными функциями при малых изменениях вектора аргументов справедливо равенство:

$d{mathbf {F}}={mathbf {F}}'({mathbf {x}}_{0})d{mathbf {x}}$

Частным случаем производной векторнозначной функции является производная от градиента некоторой скалярной функции , так как градиент фактически представляет собой вектор из нескольких функций — частных производных. Эта производная, как отмечалось выше, по сути является второй производной скалярной функции и представляет собой матрицу частных производных второго порядка этой функции — матрица Гессе ( $H_{f}$ ) или гессиан (гессианом обычно называют определитель матрицы Гессе).

Производные отображений произвольных линейных пространств[править | править код]

Предварительное обобщение[править | править код]

Скалярная функция нескольких переменных рассматривалась выше формально как функция от вектора, компонентами которого являлись независимые переменные. В общем случае следует рассмотреть скалярные (числовые) функции на произвольных векторных пространствах некоторой размерности. Тогда в каждом фиксированном базисе такое отображение можно рассмотреть как функцию нескольких переменных. Таким образом, все рассмотренные выше понятия можно интерпретировать как координатные определения производных при фиксированном базисе произвольного пространства (наделенного достаточной для этих целей топологической структурой).

Аналогично, значения набора функций также формально рассматривались компоненты некоторого вектора и этот набор функций трактовался (формально) как отображение одного вектора в другой. В общем случае следует рассмотреть отображение между произвольными векторными пространствами и различной размерности и природы (наделенных необходимой топологической структурой). Если зафиксировать базисы в обоих пространствах, то это отображение аналогично рассмотренному выше набору функций нескольких переменных. Таким образом, все соответствующие определения интерпретируются в общем случае как координатное определение производных при фиксированных базисах соответствующих пространств.

Данная интерпретация означает в то же время, что несмотря на то, что координатное представление производных зависит от базиса (меняются при переходе от одного базиса к другому), сами понятия производных от выбора базисов не должны зависеть. Поэтому вообще говоря требуются более общие определения производных напрямую не связанных с выбором базиса и их координатным представлением. Более того, указанные определения обобщаются на случай пространств бесконечной размерности, что используется, например, в функциональном анализе и вариационном исчислении.

Производная Гато[править | править код]

Достаточно общее понятие производной рассматривается в функциональном анализе, где концепция производной по направлению обобщается на произвольные локально выпуклые топологические векторные пространства. Соответствующая производная называется обычно производной Гато или слабой производной. Определение производной Гато по существу не отличается от производной по направлению для случая функции нескольких переменных:

$f'_{{e}}({x}_{0})=lim _{{trightarrow 0}}{frac {f({x}_{0}+t{e})-f({x}_{0})}{t}}$

Производная Фреше[править | править код]

В случае банаховых пространств определяется производная Фреше или сильная производная. Производной Фреше отображения называют такой линейный оператор , для которого выполнено равенство:

$lim _{{||h||_{X}rightarrow 0}}{frac {||F(x+h)-F(x)-F'(x)h||_{Y}}{||h||_{X}}}=0$ ,

Это означает, что при достаточно малых (по норме пространства ) изменениях аргумента изменение сходится (по норме пространства Y) к F'(x)dx , что формально можно записать в виде равенства:

Если эта производная существует, то она совпадает с производной Гато. Для конечномерных пространств в координатном представлении F'(x) является матрицей Якоби, а если Y=R , то — градиентом скалярной функции.

Вариационная производная[править | править код]

В вариационном исчислении, где рассматриваются интегральные функционалы на пространстве функций, в которых введено скалярное произведение (в форме интеграла от пары функций), вводится понятие вариационной производной, называемой также функциональной производной. Вариационная производная функционала F(f) — это функция (вообще говоря обобщенная функция) , для которой при малой вариации delta f функции выполнено равенство:

${displaystyle delta F=F(f+delta f)-F(f)=(delta F/delta f,delta f)=int {frac {delta F(f(x))}{delta f}}delta f(x)dx}$

Можно показать, что по сути вариационная производная есть производная Фреше.

Производная по мере[править | править код]

В теории меры производная Радона — Никодима обобщает якобиан, использовавшийся для изменяющихся переменных, на меры. Она выражает одну меру в терминах другой меры (при некоторых условиях).

Производная также допускает обобщение на пространстве обобщенных функций, используя интегрирование по частям в соответствующем хорошо устроенном подпространстве.

Дифференциальные операторы в конечномерных пространствах[править | править код]

1. Дивергенция (расходимость) векторнозначных функций (векторных полей) на конечномерном пространстве , даёт меру того, как силён «источник» или «сток» в этой точке. Она может быть использована для вычисления потока при помощи теоремы о дивергенции. В координатном представлении (в декартовых координатах) дивергенция равна

$operatorname {div}{mathbf {F}}=sum _{{i=1}}^{n}{frac {partial F_{{x^{i}}}}{partial x^{i}}}$

2. Ротор векторных полей в трехмерном пространстве $mathbb {R} ^{3}$ измеряет «вращение» векторного поля в этой точке. В координатном представлении (в декартовых координатах) равен:
${displaystyle operatorname {rot} mathbf {F} =operatorname {rot} ;(F_{x}mathbf {e} _{x}+F_{y},mathbf {e} _{y}+F_{z}mathbf {e} _{z})=left({frac {partial F_{z}}{partial y}}-{frac {partial F_{y}}{partial z}}right)mathbf {e} _{x}+left({frac {partial F_{x}}{partial z}}-{frac {partial F_{z}}{partial x}}right)mathbf {e} _{y}+left({frac {partial F_{y}}{partial x}}-{frac {partial F_{x}}{partial y}}right)mathbf {e} _{z}.}$

(F — векторное поле с декартовыми компонентами ${displaystyle (F_{x},F_{y},F_{z})}$ , а — орты декартовых координат)

3. Лапласиан — это дивергенция (расходимость) градиента скалярной функции (скалярного поля) на конечномерном пространстве. Часто обозначается как Delta или как $nabla ^{2}$ . В координатном представлении (в декартовых координатах) равен:

$operatorname {div}operatorname {grad}f=Delta f=nabla ^{2}f=sum _{{i=1}}^{n}{frac {partial ^{2}f}{partial x_{i}^{2}}}$

4. Д’Аламбертиан — определяется аналогично лапласиану, но используя метрику пространства Минковского, вместо метрики евклидова пространства. Рассматривается в физике для четырёхмерного пространства-времени. В координатном представлении (в декартовых координатах) равен:

$square f={frac {partial ^{2}f}{partial x^{2}}}+{frac {partial ^{2}f}{partial y^{2}}}+{frac {partial ^{2}f}{partial z^{2}}}-{frac {1}{c^{2}}}{frac {partial ^{2}f}{partial t^{2}}}.$

Производные в дифференциальной топологии, геометрии и тензорном анализе[править | править код]

Касательный вектор и касательное отображение[править | править код]

В дифференциальной топологии для гладких скалярных функций на гладком многообразии (далее – просто многообразие и просто функция) вводится понятие касательного вектора в точке pin M . Эти функции образуют алгебру по поточечным операциям сложения и умножения и умножения на число. Касательный вектор определяется как линейный функционал на алгебре таких функций, удовлетворяющий правилу Лейбница. Для многообразий, которые являются подмножествами $mathbb {R} ^{n}$ , этот касательный вектор будет аналогичен направленной производной в точке, определённой выше.

Линейный оператор на алгебре функций, удовлетворяющий правилу Лейбница, будет собственно дифференцированием на алгебре этих функций и фактически определяет производную скалярных функций. Такие линейные операторы на алгебре скалярных функций образуют векторное поле на многообразии. Это векторное поле также можно определить как отображение ставящее каждой точке многообразия касательный вектор к этой точке.

Множество всех касательных векторов к данной точке многообразия образуют касательное пространство к данной точке ${displaystyle T_{p}M}$ .

Для гладких отображений многообразий произвольных размерностей дифференциалом в точке pin M называется линейный оператор ${displaystyle d_{p}F:T_{p}Mrightarrow T_{F(p)}N}$ , который для любого касательного вектора ${displaystyle Xin T_{p}M}$ заключается в дифференцировании функции для произвольной числовой функции f на многообразии N .

В координатном представлении дифференциал представляет собой матрицу Якоби ${displaystyle left{{frac {partial F_{i}}{partial x_{j}}}right}}$ . Базисы в касательных пространствах определяются как частные производные числовых функций от координатного представления точки p.

Касательное отображение

Объединение всех касательных пространств (рассматриваемых как непересекающиеся множества) для всех точек многообразия называется касательным расслоением многообразия (имеет размерность 2n, поскольку касательное расслоение по существу это множество пар – точка и касательный вектор к нему). Точнее касательным расслоением является отображение пространства TM в многообразие M. Касательное отображение (англ. pushforward) является обобщением понятия якобиана и действует на касательных расслоениях многообразий: . Аргументами касательного отображения являются точка pin M и вектор . Для фиксированной точки pin M отображение ${displaystyle dF(x,cdot )colon ,T_{x}Mto T_{varphi (x)}N}$ является вышеуказанным дифференциалом в точке – линейным отображением касательного пространства $T_{p}$ в касательное пространство ${displaystyle T_{F(p)}N}$ .

Векторным полем на многообразии называется отображение многообразия M на TM, то есть ставящая в соответствие каждой точке многообразия касательный вектор к этой точке. Векторное поле можно рассматривать как сечение касательного расслоения – отображение М в TM. Векторные поля можно рассматривать также как дифференцирование алгебры функций, отображающее каждую функцию алгебры другую функцию этой же алгебры. Это линейное отображение удовлевояющее правилу Лейбница.

Для римановых многообразий градиент скалярной функции f определяется как вектор nabla f касательного пространства $T_{x}M$ , такой, что для любого касательного вектора Х дифференциал функции равен скалярному произведению ${displaystyle (d_{x}f)X=Xf=(nabla f,X)}$ . В координатном представлении это свертка метрики пространства частными производными функции: ${displaystyle nabla f=g^{ij}partial _{i}f}$

Производная Ли[править | править код]

Производная Ли — это скорость изменения тензорного поля (в частности скалярного или векторного поля) в направлении данного векторного поля. В случае скалярного поля производная Ли совпадает с производной по направлению. Для векторных полей производная Ли равна так называемой скобке Ли. Это пример применения скобки Ли (векторные поля образуют алгебру Ли на группе диффеоморфизмов многообразия). Это производная 0 порядка на алгебре.

Внешняя и внутренняя производная[править | править код]

На внешней алгебре дифференциальных форм над гладким многообразием, внешняя производная — это уникальное линейное отображение, которое удовлетворяет порядковой версии закона Лейбница и при возведении в квадрат равно нулю. Это производная 1 порядка на внешней алгебре.

Внутренняя производная — это производная «-1» порядка на внешней алгебре форм. Вместе, внешняя производная, производная Ли, и внутренняя производная образуют супералгебру Ли.

Ковариантная производная[править | править код]

В дифференциальной геометрии (и вытекающем из неё тензорном анализе), с помощью ковариантной производной берутся производные по направлениям векторных полей вдоль кривых или вообще в криволинейной системе координат. Это расширяет производную по направлению скалярных функций до сечений векторных расслоений или главных расслоений. В римановой геометрии существование метрики позволяет сделать канонический выбор свободной от кручения ковариантной производной, известной как связность Леви-Чивиты.

Для скалярных функций ковариантная производная $D_{v}f$ совпадает с производной по направлению векторного поля. Ковариантную производную векторного поля по векторному полю формально можно определить как отображение, F-линейное по (то есть по сумме и умножению на скалярную функцию), аддитивности по и стандартного правила Лейбница для произведения скалярного поля на векторное поле . В общем случае тензорных полей требуется выполнение правила Лейбница для их тензорного произведения.

В случае векторного поля ковариантную производную в координатном представлении можно записать как:

$D_{j}u^{i}=partial _{j}u^{i}+Gamma _{{kj}}^{i}u^{k}$

где $partial _{j}u^{i}$ — обычная частная производная по координате $x^{j}$ , а $Gamma _{{kj}}^{i}$ — символы Кристоффеля.

В случае декартовых координат символы Кристоффеля равны нулю, поэтому ковариантная производная равна обычной производной.

Внешняя ковариантная производная расширяет внешнюю производную на векторно-значимые формы.

Производная в других разделах математики[править | править код]

Производные в комплексном анализе[править | править код]

В комплексном анализе (анализе функций комплексных переменных), центральными объектами изучения являются голоморфные функции, которые являются комплекснозначными функциями на плоскости комплексных чисел и удовлетворяющие соответственно расширенному определению дифференцируемости.

Производная Шварца описывает, как комплексная функция аппроксимируется дробно-линейным отображением, аналогично тому, как обычная производная описывает, как функция аппроксимируется линейным отображением.

Производные в алгебре и алгебраической геометрии[править | править код]

Дифференцирование в общей алгебре — это линейное отображение на кольце или алгебре, которое удовлетворяет закону Лейбница (правилу произведения). Они изучаются в чистой алгебраической постановке в дифференциальной теории Галуа, но также появляются во многих других областях, где они часто употребляются с менее строгими алгебраическими определениями производных.

В алгебраической геометрии кэлеров дифференциал позволяет расширить определение внешней производной на произвольные алгебраические многообразия, вместо просто гладких многообразий.

Другие обобщения[править | править код]

Вполне можно скомбинировать два или больше различных понятий расширения или абстракции простой производной. Например, в геометрии Финслера изучаются пространства, которые локально выглядят как банаховы пространства. Таким образом можно создать производную с некоторыми особенностями функциональной производной и ковариантной производной.

В области квантовых групп -производная — это -деформация обычной производной функции.

Производные дробного порядка[править | править код]

Вдобавок к производным -го порядка для любого натурального числа , используя различные методы, возможно ввести производные в дробных степенях, получая при этом так называемые производные дробного порядка. Производные отрицательных порядков будут соответствовать интегрированию, откуда появляется термин дифферинтеграл. Изучение различных возможных определений и записей производных ненатуральных порядков известно под названием дробное исчисление.

Нуждающиеся в определении[править | править код]

Производная Дини
Матричное исчисление
Производная Пинкерле
Параметрическая производная
Полу-дифференцируемость

См. также[править | править код]

Производная функции
Контингенция и паратингенция
Теорема Лагерра
Теорема Шварца о второй производной

Примечания[править | править код]

↑ Фрёлихер, 1970, с. 131.

Литература[править | править код]

Фрёлихер, А., Бухер В. Дифференциальное исчисление в векторных пространствах без нормы. — М.: Мир, 1970.

Источник

Главная
Справочник
Односторонние производные

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Односторонние производные

Определение

Правой производной $y_{+}^{prime}$ функции
$y=f(x)$ в данной точке
$x_0$ называется величина:

$$y_{+}^{prime}=f^{prime}left(x_{0}+0right)=lim _{Delta x rightarrow 0_{+}} frac{Delta y}{Delta x}$$

а левой производной – величина:

$$y_{-}^{prime}=f^{prime}left(x_{0}-0right)=lim _{Delta x rightarrow 0_{-}} frac{Delta y}{Delta x}$$

если эти пределы существуют.

Теорема

Для того чтобы в точке $x$ существовала
производная $f^{prime}(x)$, необходимо и достаточно,
чтобы в точке $x$ функция
$y=f(x)$ имела правую и левую производные, и эти
производные были равны между собой: $y^{prime}(x)=y_{+}^{prime}(x)=y_{-}^{prime}(x)$ .

Читать дальше: дифференциал функции.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Все еще сложно?

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

80% ответов приходят в течение 10 минут

Источник

Левой производной функции f(x) в точке х называется левый предел отношения приращения функции $Delta $y к приращению аргумента $Delta $х, когда $Delta $х$to $0:

[f’_{-} (x)=mathop{lim }limits_{Delta xto 0-0} frac{Delta y}{Delta x} ]

Для того, чтобы функция f(x) имела производную в точке х, необходимо и достаточно, чтобы в этой точке функция была непрерывна, и существовали односторонние производные f`-(x) и f`+(x), равные между собой.

Если

[f’_{-} (x)ne f’_{+} (x)]

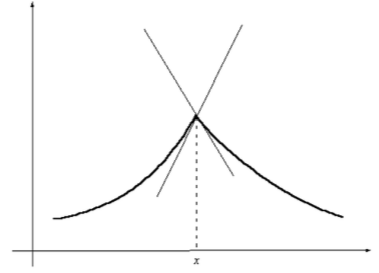
то в точке x производной не существует, и график функции имеет излом (рис. 1).

Рисунок 1. Излом функции

Пример 1

Найти левую и правую производные в точке $x_0 = 0$ функции:

y = $| Delta x|$

Решение.

[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{Delta y}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{f(0+Delta x)-f(0)}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{left|Delta xright|-0}{Delta x} =frac{left|Delta xright|}{Delta x} ]

Так как $Delta $х$to $0-, то $Delta $х является маленькой отрицательной величиной, а тогда по определению модуля $|Delta х|$ = -$Delta $х. Отсюда

[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|Delta xright|}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{-left|Delta xright|}{Delta x} =-1]

Аналогично найдем правую производную

[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{Delta y}{Delta x} =mathop{lim }limits_{Delta xto 0+} frac{f(0+Delta x)-f(0)}{Delta x} =mathop{lim }limits_{Delta xto 0+} frac{left|Delta xright|-0}{Delta x} =frac{left|Delta xright|}{Delta x} ]

[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{left|Delta xright|}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{+left|Delta xright|}{Delta x} =1]

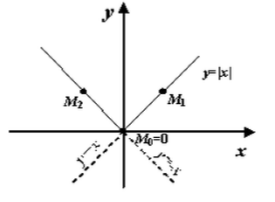
Графически это означает, что функция имеет излом в точке = 0

Рисунок 2. Излом функции

[y=left|xright|=left{begin{array}{c} {-x,begin{array}{cc} при & {x

Пример 2

Вычислить производные функции:

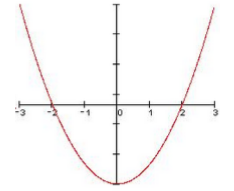
[y=left|x^{2} -1right|]

Рисунок 3. График функции

Решение.

Из графика функции видно, что производная не существует в точках -2 и 2. Найдем односторонние производные.

а) Левая производная

[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|(2+Delta x)^{2} -4right|-left|2^{2} -4right|}{Delta x} =-4]

[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|(-2+Delta x)^{2} -4right|-left|left(-2right)^{2} -4right|}{Delta x} =-4]

б) Правая производная

[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{left|(2+Delta x)^{2} -4right|-left|2^{2} -4right|}{Delta x} =4]

Вывод: Правая производная при 2 и -2 существует и равна 4. Левая производная при 2 и -2 существует и равна -4.

Найдем производные при х=1.

[mathop{lim }limits_{Delta xto 0} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]

[mathop{lim }limits_{Delta xto 0-} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]

[mathop{lim }limits_{Delta xto 0+} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]

Значит, производная в точке 1 существует и равна -2

Источник

3.2. Дифференцируемость функции

1. Понятие дифференцируемости функции в данной точке.

2. Связь между понятиями дифференцируемости и непрерывности.

3.3. Дифференциал функции

Производная функции одной переменной[править | править код]

Базовое определение[править | править код]

Односторонние производные[править | править код]

Производные высших порядков[править | править код]

Производные функций нескольких переменных[править | править код]

Частные производные[править | править код]

Градиент[править | править код]

Производная по направлению[править | править код]

Производные высших порядков[править | править код]

Полная производная[править | править код]

Набор функций нескольких переменных[править | править код]

Производные отображений произвольных линейных пространств[править | править код]

Предварительное обобщение[править | править код]

Производная Гато[править | править код]

Производная Фреше[править | править код]

Вариационная производная[править | править код]

Производная по мере[править | править код]

Дифференциальные операторы в конечномерных пространствах[править | править код]

Производные в дифференциальной топологии, геометрии и тензорном анализе[править | править код]

Касательный вектор и касательное отображение[править | править код]

Производная Ли[править | править код]

Внешняя и внутренняя производная[править | править код]

Ковариантная производная[править | править код]

Производная в других разделах математики[править | править код]

Производные в комплексном анализе[править | править код]

Производные в алгебре и алгебраической геометрии[править | править код]

Другие обобщения[править | править код]

Производные дробного порядка[править | править код]

Нуждающиеся в определении[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Односторонние производные

Все еще сложно?

Вам также может понравиться

Как найти проверенного работодателя

Как найти адрес родственников в москве

An error occurred trying to open that file как исправить

Добавить комментарий Отменить ответ