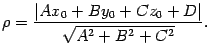Векторное произведение в трёхмерном евклидовом пространстве
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.
Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.
Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.
Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.
История[править | править код]
Векторное произведение было введено У. Гамильтоном в 1846 году[1] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[2].
Определение[править | править код]
Векторным произведением вектора 


Обозначения:
Замечания[править | править код]
В качестве определения можно использовать описанное далее выражение векторного произведения в координатах в правой (или левой) прямоугольной системе координат.
Также в качестве исходного определения может быть взят набор алгебраических свойств векторного произведения.
Правые и левые тройки векторов в трёхмерном евклидовом пространстве[править | править код]

Рассмотрим упорядоченную тройку некомпланарных (линейно независимых) векторов 
Геометрическое определение[править | править код]
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов 



Определение с помощью руки[править | править код]
Другое определение связано с правой рукой человека, откуда и берётся название. На рисунке тройка векторов 


Алгебраическое определение[править | править код]
Существует также аналитический способ определения правой и левой тройки векторов, который требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора 


- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Замечания[править | править код]
Определения «правой» и «левой» тройки векторов зависят от ориентации пространства, но не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого определение самого векторного произведения. При этом формулы выражения координат векторного произведения через координаты исходных векторов будут отличаться знаком в правой и левой прямоугольной системе координат.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
При заданной ориентации пространства система координат называется правой (левой), если тройка из векторов с координатами 


Геометрическое определение и определение с помощью руки сами задают ориентацию пространства. Алгебраическое определение задаёт способ разбить тройки некомпланарных векторов на два класса одинаково ориентированных векторов, но оно не задаёт ориентацию пространства, а использует уже заданную — ту, на основании которой данная система координат считается правой или левой. При этом, если ориентация системы координат неизвестна, можно сравнивать знак определителя со знаком определителя другой тройки некомпланарных векторов, ориентация которой известна — если знаки совпадают, то тройки одинаково ориентированы, если знаки противоположны — тройки ориентированы противоположно.
Свойства[править | править код]
Геометрические свойства векторного произведения[править | править код]

Рисунок 1: Площадь параллелограмма равна модулю векторного произведения

Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на
a × b и вектора
b × c на
a, первым шагом является нахождение векторного произведения (модуль которого равен площади одной из сторон), а вторым — нахождение скалярного произведения (которое равно объёму параллелепипеда)
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов так же, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения[править | править код]
Далее ![{displaystyle [{vec {a}},;{vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcceaa8d6f8c20cebf7ca9374dc08a23130ba6a)



| Представление | Описание |
|---|---|
![{displaystyle [{vec {a}},;{vec {b}}]=-[{vec {b}},{vec {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c267366cadb584259b3c50b0e4e36382c5f9e9bd)
|
Антикоммутативность. |
![{displaystyle [alpha cdot {vec {a}},;{vec {b}}]=[{vec {a}},;alpha cdot {vec {b}}]=alpha cdot [{vec {a}},;{vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b268a3e418241b2c2fc88d8472c2a2e1566f356)
|
Ассоциативность умножения на скаляр. |
![{displaystyle [{vec {a}}+{vec {b}},;{vec {c}}]=[{vec {a}},;{vec {c}}]+[{vec {b}},;{vec {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3161075b7aad486d9877967a12eb2d725bca5d3)
|
Дистрибутивность по сложению. |
![{displaystyle [[{vec {a}},;{vec {b}}],;{vec {c}}]+[[{vec {b}},;{vec {c}}],;{vec {a}}]+[[{vec {c}},{vec {a}}],;{vec {b}}]={vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00f9fa2cabab740204011537035a86bb96df0a3b)
|
Тождество Якоби. |
![{displaystyle [{vec {a}},;{vec {a}}]={vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b6acb122bbc38e8a68353a2a7230885ff4d8c5)
|
|
![{displaystyle [{vec {a}},;[{vec {b}},;{vec {c}}]]={vec {b}}cdot langle {vec {a}},;{vec {c}}rangle -{vec {c}}cdot langle {vec {a}},;{vec {b}}rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7b7dbf2d84c0db27feb86c85c41b7d122646f07)
|
Формула «БАЦ минус ЦАБ», тождество Лагранжа. |
![{displaystyle |[{vec {a}},,{vec {b}}]|^{2}+langle {vec {a}},,{vec {b}}rangle ^{2}=|{vec {a}}|^{2}cdot |{vec {b}}|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff5696724e36f03030ef3350e333494d1d774ec)
|
Частный случай мультипликативности нормы кватернионов. |
![{displaystyle langle [{vec {a}},,{vec {b}}],,{vec {c}}rangle =langle {vec {a}},,[{vec {b}},,{vec {c}}]rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b749162f3b3230fc7193d64f2f3910b791bcc9)
|
Значение этого выражения называют смешанным произведением векторов  , ,  , ,  . .
|
Выражение в координатах[править | править код]
В правом ортонормированном базисе[править | править код]
Если два вектора 

то их векторное произведение имеет координаты
Для запоминания этой формулы удобно использовать мнемонический определитель:
где 


где 
В левом ортонормированном базисе[править | править код]
Если базис левый ортонормированный, то векторное произведение в координатах имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы 


В произвольной аффинной системе координат[править | править код]
Векторное произведение в произвольной аффинной системе координат 
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}[{vec {e}}_{2},;{vec {e}}_{3}]&[{vec {e}}_{3},;{vec {e}}_{1}]&[{vec {e}}_{1},;{vec {e}}_{2}]\a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7e80caef757b2bce0dd092ebd459a32081f489)
Вариации и обобщения[править | править код]
Кватернионы[править | править код]
Координаты векторного произведения в правом ортонормированном базисе можно также записать в кватернионной форме, поэтому буквы 



Заметим, что соотношения через векторное произведение между 







Преобразование к матричной форме[править | править код]
Векторное произведение двух векторов в координатах в правом ортонормированном базисе можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть 
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь 

С такой формой записи также зачастую проще работать (например, в эпиполярной геометрии[en]).
Из общих свойств векторного произведения следует, что
и
а так как ![{displaystyle [{vec {a}}]_{times }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ce3ad0fa3e8a55fb73d95f8fda29459fdd7b2b2)
В такой форме записи легко доказывается тождество Лагранжа (правило «БАЦ минус ЦАБ»).
Распространение на матрицы[править | править код]
В трёхмерном случае можно определить в координатах в произвольном базисе векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу 
Умножение матрицы на вектор слева определяется аналогично, если представить 
Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (


После этого можно изменить форму записи для векторного произведения:


где ротор матрицы 

Размерности, не равные трём[править | править код]
Пусть 
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение 
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора 






Такое обобщение дает гиперплощадь размерности 
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при 
.
Эта конструкция называется внешним произведением.
Для двумерного случая операция
.
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению.)
Алгебра Ли векторов[править | править код]
Векторное произведение вводит на 



См. также[править | править код]
Произведения векторов
Другое
- Ротор
- Дивергенция
Примечания[править | править код]
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101.
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература[править | править код]
-
- Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. АН СССР: Изд-во «НАУКА», М. 1965.
Ссылки[править | править код]
- Многомерное векторное произведение Архивная копия от 5 сентября 2015 на Wayback Machine
- Векторное произведение и его свойства. Примеры решения задач Архивная копия от 23 февраля 2011 на Wayback Machine
- В. И. Гервидс. Правое и левое вращение. НИЯУ МИФИ (10 марта 2011). — Физические демонстрации. Дата обращения: 3 мая 2011. Архивировано 23 декабря 2015 года.
Три некомпланарных вектора $overline{a}$,
$overline{b}$ и $overline{c}$, приведенных к общему началу, образуют так
называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется левой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется правой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется против хода часовой стрелки (рис. 2).
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие тройки векторов
Из курса физики известно, что скалярные величины или скаляры – это величины, вполне определяемые одним численным значением (например, масса, температура, объём, расстояние и пр.). То есть любое вещественное число является скаляром.
Векторные величины или векторы – это величины, которые определяют и численным значением, и направлением. Например, скорость.
Линейно зависимыми называются такие векторы $a,b,c,…$, что если подобрать такие числа $x,y,z,…$, из которых по крайней мере одно не равно $0$, то будет иметь место тождество $xa+yb+zc+…=0$. Если три вектора $a,b,c$ не равны $0$ и линейно зависимы, то они компланарны.
Определение 1
Связка трёх векторов – это приведённая к общему началу тройка некомпланарных векторов $a,b,c$.
Определение правой и левой тройки векторов
Приведём чертёж правой связки.
Рисунок 1. Чертёж правой связки. Автор24 — интернет-биржа студенческих работ
Рассмотрим кратчайшее вращение $vec{OA}=a$ к $vec{OB}=b$ на плоскости $OAB$ со стороны направления $vec{OC}=c$. Мы увидим, что вращение идёт против часовой стрелки.
Если большой палец и указательный пальцы левой руки вытянуть, а средний согнуть под углом ладони, то три пальца в порядке большой-указательный-средний составят правую связку. Те же пальцы на левой руке составят левую связку.
На чертеже левой связки то же вращение идёт по часовой стрелке.
Рисунок 2. Чертеж левой связки. Автор24 — интернет-биржа студенческих работ
«Определение правой и левой тройки векторов» 👇
Способы преобразования правой связки в левую и обратно:
- перестановка местами двух любых векторов;
- изменение знака при одном из векторов;
- замена какого-нибудь вектора его зеркальным отображением относительно плоскости двух других векторов.
Правая и левая системы координат
Напомним, что координатная ось – это ось, на которой выбрано начало и единица масштаба.
Ортогональная или прямоугольная система координат в пространстве – это система из трёх взаимно перпендикулярных координатных осей $Ox, Oy$ и $Oz$ с общим началом $O$. Ортами в ортогональной системе координат называют единичные векторы (то есть векторы равные $1$).
Рассмотрим чертёж ортогональной системы координат в пространстве. Отметим на ней орты $i, j, k$.
Рисунок 3. Чертёж ортогональной системы координат в пространстве. Автор24 — интернет-биржа студенческих работ
$i, j, k$ образуют правую связку. Система координат в данном случае называется правой.
Система координат называется левой, когда орты образуют левую связку. То есть:
Рисунок 4. Левая система координат. Автор24 — интернет-биржа студенческих работ
Подведём итог. В статье мы дали определение связки тройки векторов, описали правую и левую тройку векторов, а также правую и левую систему координат, как вытекающую тему из определения правой и левой тройки векторов. Стоит сказать, что на практике определение правой и левой тройки векторов со временем происходит интуитивно или “на автомате”. Самое важное, это один раз понять, как это делается. Также стоит заметить, что чаще в задачах используется всё-таки правая тройка векторов и соответственно правая система координат.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Тройка
векторов
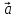 ,
,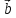 и
и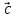 называется правой, если
называется правой, если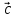 направлен так, что из его конца кратчайший
направлен так, что из его конца кратчайший
поворот от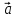 к
к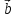 происходит против часовой стрелки.
происходит против часовой стрелки.
Векторным
произведением вектора
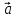 на вектор
на вектор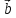 называется третий вектор
называется третий вектор который обладает следующими свойствами:
который обладает следующими свойствами:
-
Его
длина равна
![]()
-
Вектор
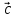 перпендикулярен к плоскости, в которой
перпендикулярен к плоскости, в которой
лежат вектора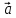 и
и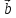
-
Вектор
 направлен так, что поворот от вектора
направлен так, что поворот от вектора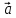 к вектору
к вектору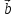 осуществляется против часовой стрелки,
осуществляется против часовой стрелки,
если смотреть из конца вектора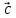 (тройка векторов
(тройка векторов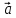 ,
,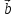 и
и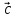 – правая).
– правая).
Основные
свойства векторного произведения:
1)
Векторное произведение
![]() равно
равно
нулю, если векторы![]() и
и![]() коллинеарны
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2)
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный
![]()
![]()
![]()
Геометрический
смысл векторного произведения: модуль
векторного произведения векторов
численно равен площади параллелограмма,
построенного на этих векторах как на
сторонах.
11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
Смешанным произведением векторов
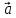 ,
,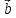 ,
,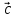 называется число, равное (
называется число, равное (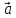 *
*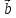 )*
)*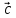 = (
= (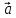 ,
,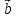 ,
,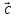 )
)
Модуль смешанного произведения векторов
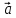 ,
,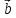 ,
,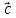 равен объёму параллелепипеда, построенного
равен объёму параллелепипеда, построенного
на векторах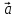 ,
,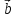 ,
,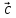 .
.
Свойства:
1)
(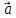 *
*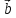 )*
)*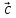 =
=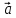 *(
*(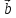 *
*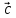 )
)
2)
(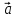 ,
,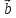 ,
,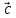 )
)
= (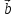 ,
,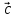 ,
,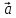 )
)
= (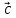 ,
,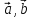 )
)
= – (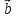 ,
,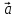 ,
,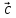 )
)
= … циклически меняем
3)
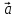 ,
,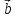 ,
,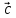 – компланарны (
– компланарны (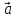 ,
,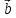 ,
,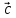 )
)
= 0
4)
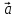 ,
,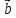 ,
,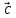 – правая (
– правая (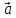 ,
,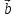 ,
, )
)
> 0
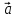 ,
,
 ,
,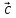 – левая (
– левая (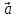 ,
,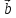 ,
,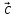 )
)
< 0
5)
(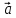 1+
1+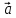 2,
2,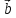 ,
,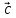 )
)
= (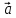 1,
1,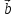 ,
,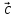 )
)
+ (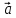 2,
2, ,
,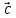 ) (α*
) (α*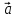 ,
,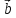 ,
,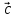 )
)
= α(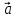 ,
,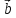 ,
,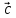 )
)
Вычисление
в координатах: 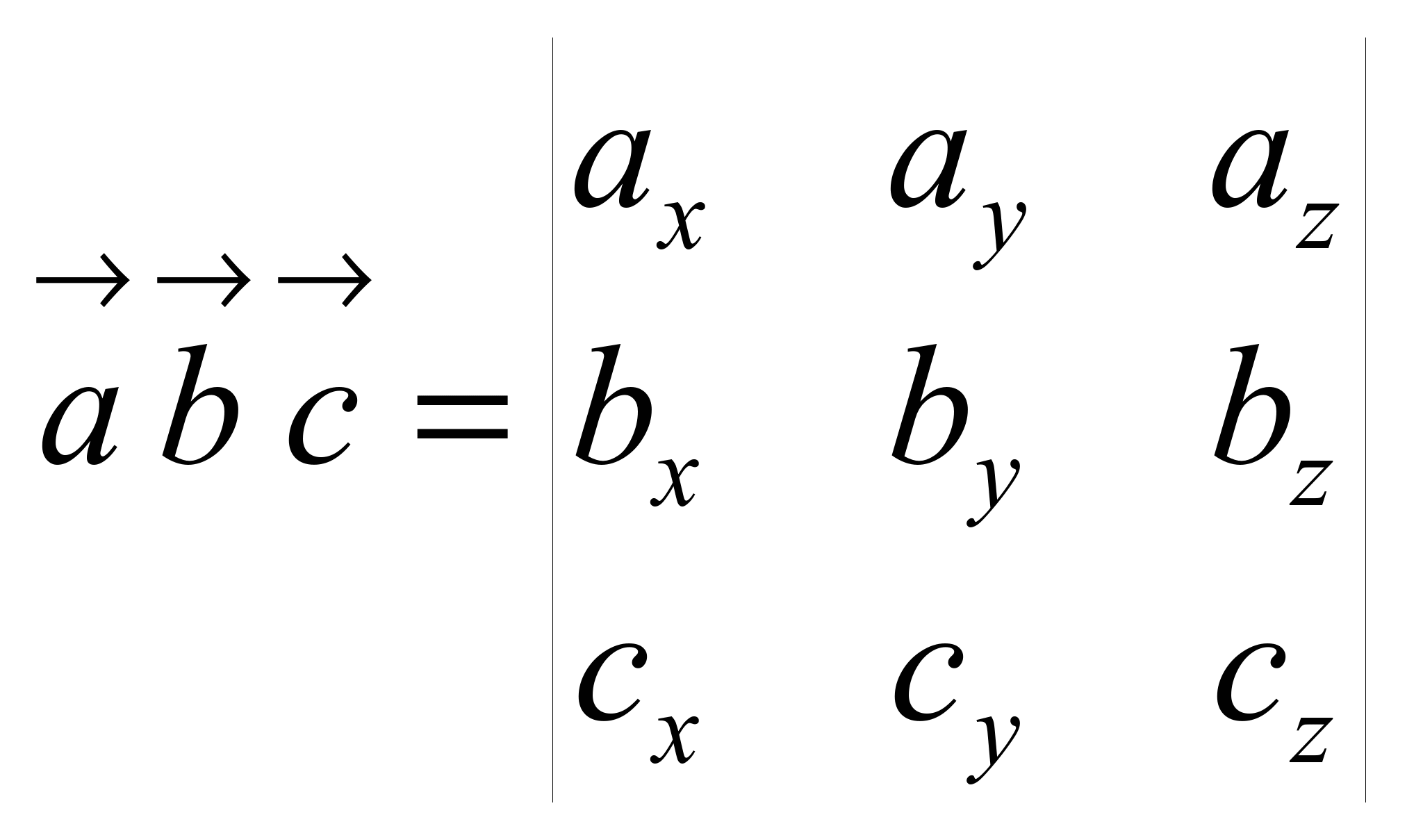
Необходимое
и достаточное условие компланарности
3-х векторов :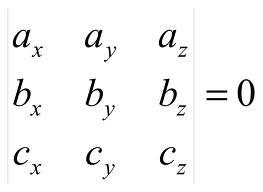
Аналитическая
геометрия
12.
Виды уравнений прямой на плоскости.
Расстояние от точки до прямой.

Виды:
1)
Общее
уравнение прямой: Ax
+ By
+ C
= 0
2)
Уравнение прямой в отрезках:
![]()
3)
Уравнение прямой с угловым коэффициентом:
y
= kx
+ b
4)
Каноническое уравнение прямой на
плоскости: ![]()
5)
Параметрические уравнения прямой на
плоскости:
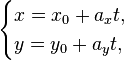
6)
Нормальное уравнение прямой:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
p– длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.
Расстояние
точки A(x1,
y1)
до прямой Ax
+ By
+ C
= 0 есть длина перпендикуляра, опущенного
из этой точки на прямую. Она определяется
по формуле:
![]()
![]()
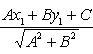
![]()
13.
Взаимное расположение двух прямых на
плоскости, угол между прямыми.
Если
прямые
![]() и
и![]() заданы
заданы
общими уравнениями![]() и
и![]() ,
,
тогда
угол между ними находится по формуле:
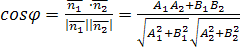
![]() –условие параллельности
–условие параллельности
прямых
![]() и
и![]() ;
;
![]() –условие перпендикулярности
–условие перпендикулярности
прямых
![]() и
и![]() .
.
 – прямые совпадают.
– прямые совпадают.
14.
Виды уравнений плоскости. Расстояние
от точки до плоскости.
Виды
уравнений плоскости:
1)
Общее:
Ax + By + Cz + D = 0
2)
В отрезках:
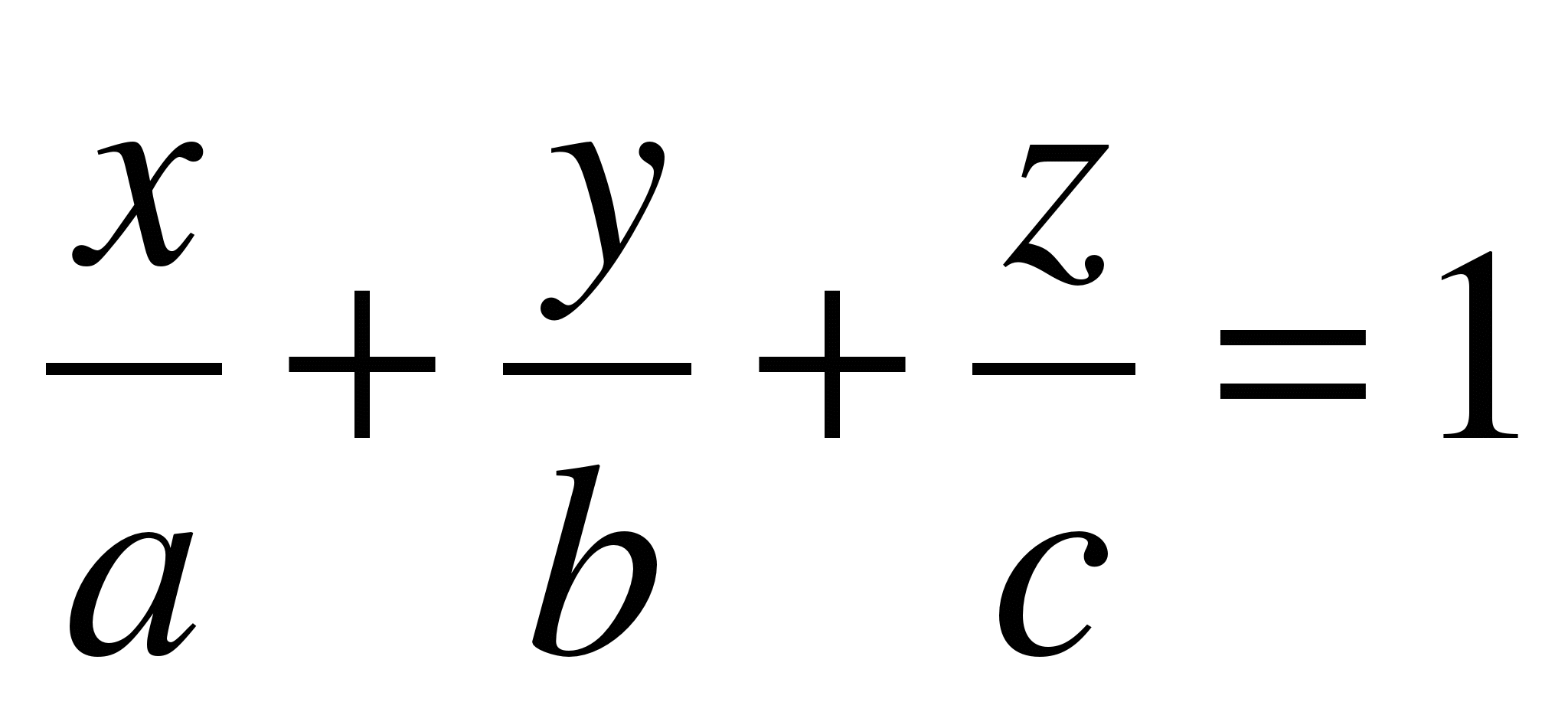
3)
Нормальное:
![]()
Пусть плоскость
![]() задана
задана
уравнениемAx
+ By
+ Cz
+ D
= 0 и дана
точка
![]() .
.
Тогда расстояниеp
от точки Mo
до плоскости
![]() определяется
определяется
по формуле
|
|
15.
Взаимное расположение двух плоскостей,
угол между плоскостями.
Взаимное расположение двух плоскостей
характеризуется двумя возможностями^
1) Две плоскости не имеют общих точек, и
, в таком случае, они называются
параллельными
2) Две плоскости имеют хотя бы одну общую
точку, и в таком случае они называются
пересекающимися.
Пусть
наши плоскости ![]() и
и![]() заданы
заданы
уравнениями:
![]() :
:
![]()
![]() :
:![]()
Косинус
угла ![]() между плоскостями находится по такой
между плоскостями находится по такой
формуле:
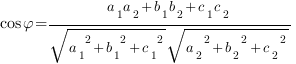
1)
Плоскости параллельны:
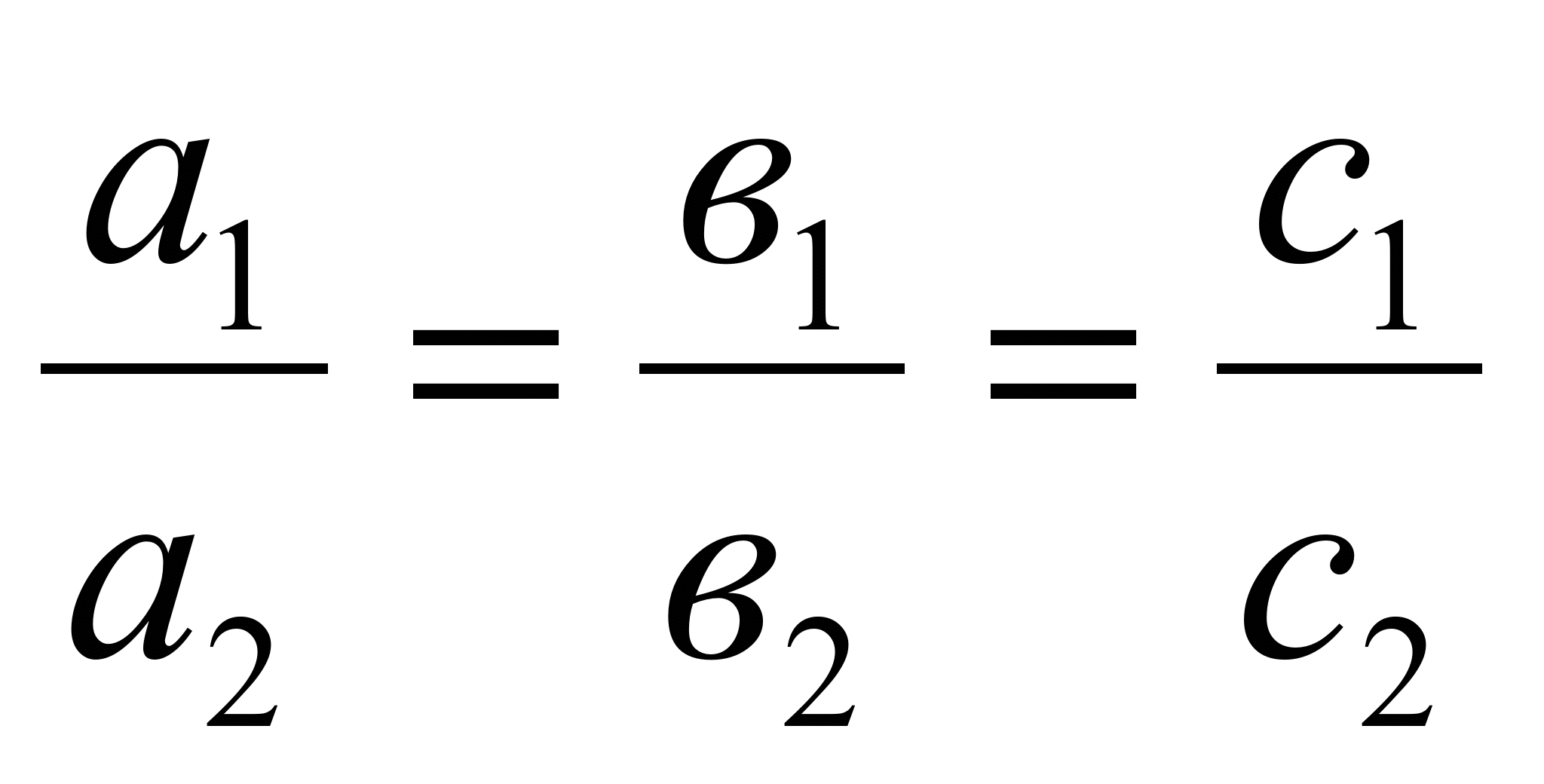
2)
Плоскости совпадают, если выполняются
следующие условия:
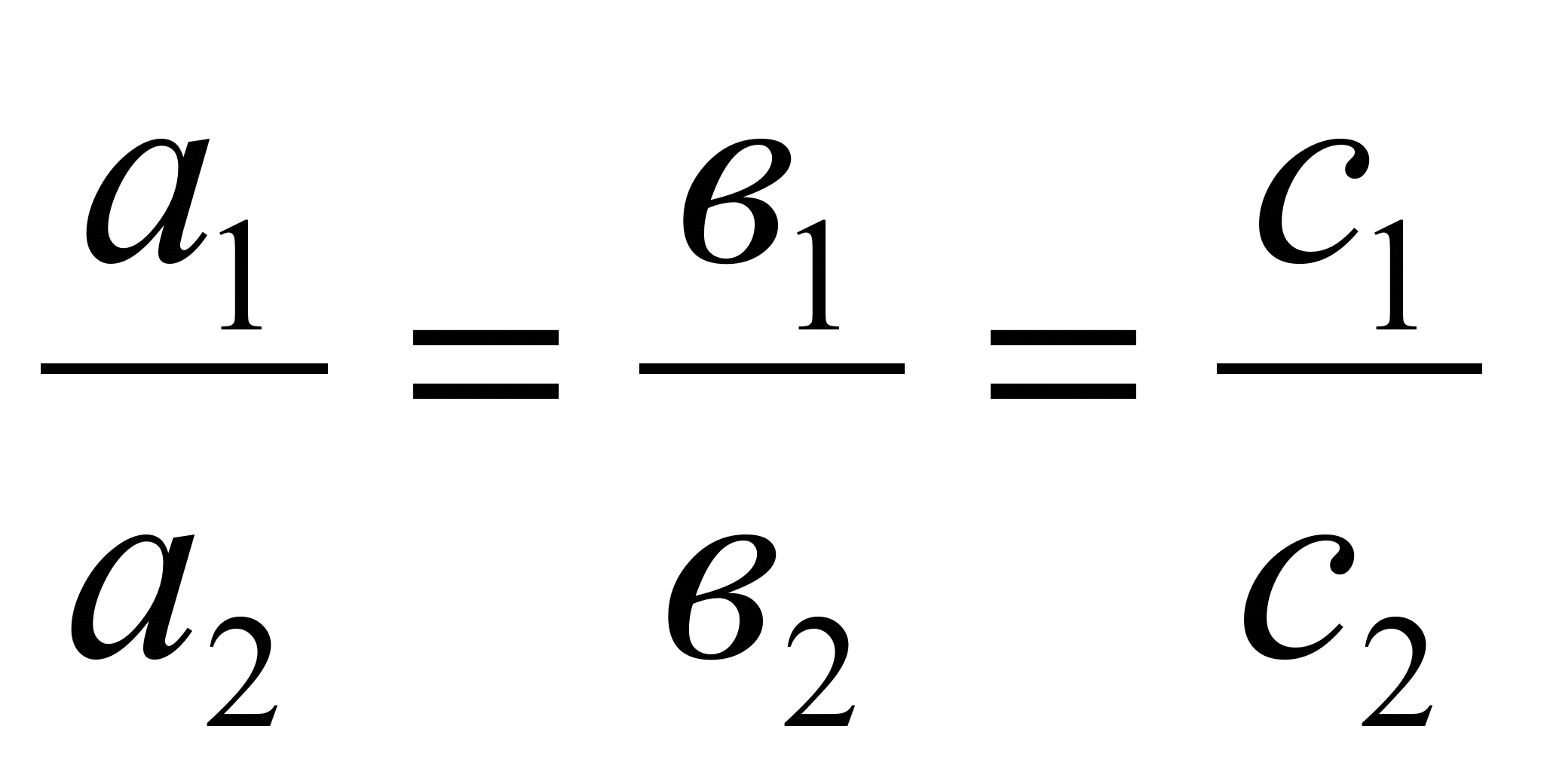
a2*x0
+ b2*y0
+ c2*z0
+ d2
= 0
существует
точка M0(x0,y0,z0),
принадлежащая плоскости П1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определить правая или левая тройка (векторы)?
В учебнике приводятся примеры параллелепипедов, построенных как написано на левой и правой тройке.
Но не могу понять почему тройки разные, если в обоих случаях направление против часовой стрелки.
Подскажите пожалуйста, почему на втором рисунке левая тройка?

-
Вопрос заданболее трёх лет назад
-
2530 просмотров
Пригласить эксперта
На левом рисунке a->b->c по часовой, на правом a->b->c – против часовой
Вопрос старый, но если у кого больше развито пространственно-образное мышление, то есть одна мнемоника. Нам в институте рассказывали, что можно определять по руке. Делаешь “базис” из пальцев: ладонь на себя, первый вектор – большой палец вверх, второй вектор – указательный палец в сторону, третий вектор – средний палец на себя. Дальше смотрим, какая рука больше подходит. Если получится “подставить” правую руку, не меняя продолжения пальцев (это важно), то тройка правая. Правило “против часовой” тоже подходит.
-
Показать ещё
Загружается…
24 мая 2023, в 22:26
9000 руб./за проект
24 мая 2023, в 22:20
1200 руб./за проект
24 мая 2023, в 21:54
100 руб./за проект
![{displaystyle {vec {c}}=[{vec {a}}{vec {b}}]=[{vec {a}},;{vec {b}}]={vec {a}}times {vec {b}}={vec {a}}wedge {vec {b}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5a3d46d305869c011f8a753ce0d97ef8e4a1d6b)
![{displaystyle [{vec {a}},;{vec {b}}]=Scdot {vec {e}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/659fe55fa7f1bfab81949bac7f9b6f460757c681)
![{displaystyle [{vec {a}},;{vec {c}}]=mathrm {Pr} _{vec {e}}{vec {a}}cdot |{vec {c}}|cdot {vec {g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26453e25f5aa1dc2dad2f1ed1f24b394eded9bb5)
![{displaystyle V=|langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972d8b2c2701aa4ae5182148ac7c6cb92a0d3413)
![{displaystyle V=langle [{vec {a}},;{vec {b}}],;{vec {c}}rangle =langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4ba1da1621205def6e3ddee53ed9da404935595)


![{displaystyle [{vec {a}},;{vec {b}}]=(a_{y}b_{z}-a_{z}b_{y},;a_{z}b_{x}-a_{x}b_{z},;a_{x}b_{y}-a_{y}b_{x}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8fa16c4870edfe489e439614c671ec685b64f9d)
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/818e785f93fc9cd53f4f882597537ad8476659bf)
![{displaystyle [{vec {a}},;{vec {b}}]_{i}=sum _{j,k=1}^{3}varepsilon _{ijk}a_{j}b_{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884a02d2b2631870d926e02e05aa096567f1e905)
![{displaystyle [{vec {a}},;{vec {b}}]=(a_{z}b_{y}-a_{y}b_{z},;a_{x}b_{z}-a_{z}b_{x},;a_{y}b_{x}-a_{x}b_{y}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4d1b7b0d23f2ccb4af924ee87204176da7fc0a8)
![{displaystyle [{vec {a}},;{vec {b}}]=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f56fb817c1e28c69a08c1a46c6f1be6437fdf1c)
![{displaystyle [{vec {a}},;{vec {b}}]_{i}=-sum _{j,k=1}^{3}varepsilon _{ijk}cdot a_{j}cdot b_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/705f278074d43d4cb83db2fd851bddd932582f0f)
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} '&mathbf {j} '&mathbf {k} '\a'_{x}&a'_{y}&a'_{z}\b'_{x}&b'_{y}&b'_{z}end{vmatrix}}={begin{vmatrix}mathbf {i} &mathbf {j} &-mathbf {k} \a_{x}&a_{y}&-a_{z}\b_{x}&b_{y}&-b_{z}end{vmatrix}}=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d05a08e910950583fa4c3f9e7b363fe82382c8a7)
![{displaystyle [{vec {a}},;{vec {b}}]=[{vec {a}}]_{times }{vec {b}}={begin{bmatrix},0&!-a_{3}&,,a_{2}\,,a_{3}&0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}}{begin{bmatrix}b_{1}\b_{2}\b_{3}end{bmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d1268e590490db993a3574e13841d9955073618)
![{displaystyle [{vec {b}},;{vec {a}}]={vec {b}}^{T}[{vec {a}}]_{times }={begin{bmatrix}b_{1}&b_{2}&b_{3}end{bmatrix}}{begin{bmatrix},0&!-a_{3}&,,,a_{2}\,,,a_{3}&,0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d163f8714882cb75d0fe91fd0fe0a93ac9c8195)
![{displaystyle [{vec {a}}]_{times }{stackrel {rm {def}}{=}}{begin{bmatrix},,0&!-a_{3}&,,,a_{2}\,,,a_{3}&0&!-a_{1}\!-a_{2}&,,a_{1}&,,0end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6701f98adf14d2921adea5a5d3cbbe6d9f9c2606)
![{displaystyle {vec {a}}=[{vec {c}},;{vec {d}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4bce0e24a417993522bf6133db91745b4ce931)
![{displaystyle [{vec {a}}]_{times }=({vec {c}}{vec {d}}^{T})^{T}-{vec {c}}{vec {d}}^{T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a53070c790d8540b97a2f17fa238bf7ff9cc6379)
![{displaystyle {vec {a}}^{T},[{vec {a}}]_{times }={vec {0}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6c6723cdec70d60f8c5831cdeeac63502f97898)
![{displaystyle {vec {b}}^{T},[{vec {a}}]_{times },{vec {b}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab0dc1827a8eeb2a15e00388fa40ca9e69786a8d)







![int limits _{{Sigma }}left[{mathbf {dSigma }};left[nabla ;{mathbf a}right]right]=int limits _{{partial Sigma }}{mathbf a}times d{mathbf {r}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ddc1050c16cf5e8d86331cd846329deba025ea5)