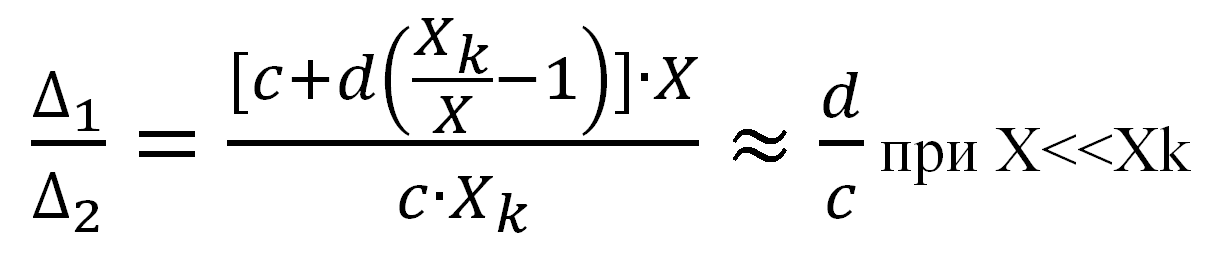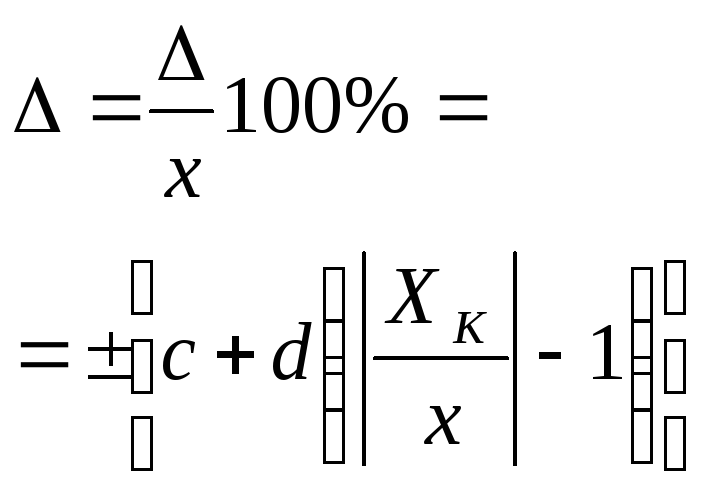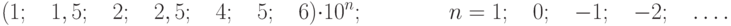Погрешность является одной из наиболее важных метрологических характеристик средства измерений (технического средства, предназначенного для измерений). Она соответствует разнице между показаниями средства измерений и истинным значением измеряемой величины. Чем меньше погрешность, тем более точным считается средство измерений, тем выше его качество. Наибольшее возможное значение погрешности для определенного типа средств измерений при определенных условиях (например, в заданном диапазоне значений измеряемой величины) называется пределом допускаемой погрешности. Обычно устанавливают пределы допускаемой погрешности, т.е. нижнюю и верхнюю границы интервала, за которые не должна выходить погрешность.
Как сами погрешности, так и их пределы, принято выражать в форме абсолютных, относительных или приведенных погрешностей. Конкретная форма выбирается в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений. Абсолютную погрешность указывают в единицах измеряемой величины, а относительную и приведённую – обычно в процентах. Относительная погрешность может характеризовать качество средства измерения гораздо более точно, чем приведённая, о чем будет рассказано далее более подробно.
Связь между абсолютной (Δ), относительной (δ) и приведённой (γ) погрешностями определяется по формулам:
δ=Δ/Х
(1)
γ=Δ/ХN
(2)
где X – значение измеряемой величины, XN – нормирующее значение, выраженное в тех же единицах, что и Δ. Критерии выбора нормирующего значения XN устанавливаются ГОСТ 8.401-80 в зависимости от свойств средства измерений, и обычно оно должно быть равно пределу измерений (XK), т.е.
γ=Δ/ХK
(3)
Пределы допускаемых погрешностей рекомендуется выражать в форме приведённых в случае, если границы погрешностей можно полагать практически неизменными в пределах диапазона измерений (например, для стрелочных аналоговых вольтметров, когда границы погрешности определяются в зависимости от цены деления шкалы, независимо от значения измеряемого напряжения). В противном случае рекомендуется выражать пределы допускаемых погрешностей в форме относительных согласно ГОСТ 8.401-80.
Однако на практике выражение пределов допускаемых погрешностей в форме приведённых погрешностей ошибочно используется в случаях, когда границы погрешностей никак нельзя полагать неизменными в пределах диапазона измерений. Это либо вводит пользователей в заблуждение (когда они не понимают, что заданная таким образом в процентах погрешность считается вовсе не от измеряемой величины), либо существенно ограничивает область применения средства измерений, т.к. формально в этом случае погрешность по отношению к измеряемой величине возрастает, например, в десять раз, если измеряемая величина составляет 0,1 от предела измерений.
Выражение пределов допускаемых погрешностей в форме относительных погрешностей позволяет достаточно точно учесть реальную зависимость границ погрешностей от значения измеряемой величины при использовании формулы вида
δ = ± [c+d(Xk/X-1)]
(4)
где с и d – коэффициенты, d<c.
При этом в точке X=Xk пределы допускаемой относительной погрешности, рассчитанные по формуле (4), будут совпадать с пределами допускаемой приведенной погрешности
γ = ±c
(5)
В точках X<Xk нельзя сравнивать непосредственно в процентах относительную и приведённую погрешности, потому что они считаются по отношению к разным значениям, но можно сравнить абсолютные значения погрешностей, выраженные в единицах измеряемой величины. Пределы допускаемой абсолютной погрешности (Δ1), рассчитанные по формуле (6), исходя из формул (1) и (4) для относительной погрешности, будут стремиться к значению, которое составляет (d/c)-ю часть от пределов допускаемой абсолютной погрешности (Δ2), рассчитанных по формуле (7), исходя из формул (3) и (5) для приведённой погрешности.
Δ1=δ·X=[c+d(Xk/X-1)]·X
(6)
Δ2=γ·ХK= c·Xk
(7)
(8)
Т.е. в большом диапазоне значений измеряемой величины может быть обеспечена гораздо более высокая точность измерений, если нормировать не пределы допускаемой приведённой погрешности по формуле (5), а пределы допускаемой относительной погрешности по формуле (4).
Это означает, например, что для измерительного преобразователя на основе АЦП с большой разрядностью и большим динамическим диапазоном сигнала выражение пределов погрешности в форме относительной адекватнее описывает реальные границы погрешности преобразователя, по сравнению с формой приведённой.
Использование терминологии
Данная терминология широко используется при описании метрологических характеристик различных Средств измерения, например, перечисленных ниже производства ООО “Л Кард”:
Измерительная система LTR
Модуль АЦП/ЦАП
16/32 каналов, 16 бит, 2 МГц, USB, Ethernet
E-502
Плата АЦП/ЦАП
16/32 каналов, 16 бит, 2 МГц, PCI Express
L-502
Модуль АЦП/ЦАП
16/32 каналов, 14 бит, 200 кГц, USB
E14-140M
Модуль АЦП/ЦАП
16/32 каналов, 14 бит, 400 кГц, USB
E14-440
Модуль АЦП/ЦАП
4 канала, 14 бит, 10 МГц, USB
E20-10
Прибор контроля качества электроэнергии
LPW-305
Прибор контроля качества электроэнергии
LPW-305-7
Пределы допускаемой основной погрешности средства измерений
Максимальная
основная погрешность измерительного
прибора, при которой он разрешён к
применению, называют пределом
допускаемой основной погрешности.
Пределы
допускаемой абсолютной основной
погрешности
устанавливают по одной из формул:
; (1)
,
(2)
где
х
– значение измеряемой величины;
a,
b
– положительные числа.
Формула
(1) описывает аддитивную составляющую
погрешности. Нормирование в соответствии
с (2) означает, что в составе погрешности
средства измерения присутствует сумма
аддитивной и мультипликативной
составляющих. В соотношениях (1) и (2)
значения
и х выражают
либо в единицах измеряемой величины,
либо в делениях шкалы прибора. Тогда
класс точности обозначают заглавными
латинскими буквами (L,
M,
C),
или римскими цифрами (I,
II,
III),
к буквам можно присоединить индексы в
виде арабской цифры.
Пределы
допускаемой приведённой основной
погрешности
определяют как:
. (3)
Здесь
XN
– нормирующее значение, выраженное в
единицах абсолютной погрешности ;
p
– отвлечённое положительное число,
выбираемое из ряда предпочтительных
чисел:
(4)
где
n=1,0,-1,-2
и т.д.
Для
приборов с равномерной шкалой XN
принимают равным большему из пределов
измерений или большему из модулей, если
нулевая метка находится на краю диапазона
измерений; сумме модулей пределов
измерений, если нулевое значение
находится внутри диапазона измерения.
Пределы
допускаемой относительной основной
погрешности:
, (5)
Если
погрешность задана формулой (1), т.е.
.
Здесьq-
отвлечённое положительное число,
выбираемое из ряда предпочтительных
чисел в (4).
Когда
допускаемая абсолютная основная
погрешность задана формулой (2), пределы
допускаемой относительной основной
погрешности
равны

где
с
– суммарная относительная погрешность
прибора;
d
– аддитивная
относительная погрешность прибора;
XK
– конечное
значение диапазона измерений;
c,
d
– отвлечённые
положительные числа, выбираемые из ряда
предпочтительных чисел в (4).
Числа
a,
b,
c,
d
в (2) и (6) связаны между собой как
, (7)
причём
всегда с>d.
Классы
точности приборов, пределы допускаемой
относительной основной погрешности
которых выражают в виде дольного значения
предела допускаемой основной погрешности,
т.е. по формуле (6), обозначают числами с
и
d,
разделяя их косой чертой.
Пределы допускаемой дополнительной погрешности
Предел
допускаемой абсолютной дополнительной
погрешности средства измерения может
указываться в виде:
-
постоянного
значения для всей рабочей области
влияющей величины; -
отношения
предела допускаемой дополнительной
погрешности, соответствующего
предписанному интервалу влияющей
величины, к этому интервалу; -
зависимости
предела допускаемой абсолютной
дополнительной погрешности от влияющей
величины.
Правила
и примеры обозначения классов точности
средств измерений даны в табл. 1.
Таблица
1
|
Формула основной |
Пределы |
Обозначение |
|
|
в |
на |
||
|
Абсолютная
|
|
L M |
L M |
|
Приведённая |
|
1,5 |
1,5 |
|
Относительная |
|
0,5 |
0,5 |
|
Относительная |
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Бывает три видов погрешности:
Абсолютная
Относительная
Приведенная
Погрешности средств измерения
Школьные средства измерения имеют вполне нормированные основные погрешности. Включенные в новый «Перечень оборудования», эти средства делятся на стрелочные приборы (амперметры, вольтметры, динамометры и др.), цифровые приборы (мультиметры демонстрационные и лабораторные, счетчик-секундомер и др.), многопредельные меры (линейка, мерная лента, мерный цилиндр), наборы мер (набор грузов по механике и набор гирь, набор резисторов).Несколько особняком в этой номенклатуре оказываются весы для фронтальных работ и практикума. Весы с точки зрения принципа действия можно отнести к нуль-индикаторам, в которых измерение сводится к прямому сравниванию массы взвешиваемого тела с массой гирь. Особенность погрешностей многопредельных мер состоит в том, что они линейно нарастают вдоль шкалы. Именно поэтому либо указано значение погрешностей номинальных значений (т.е. всей длины), либо значение на 100 мм шкалы. Обратим внимание на то, что погрешности деревянных инструментов меньше, чем пластмассовых. Все инструменты, маркированные знаком «ГОСТ», имеют погрешности меньшие, чем погрешности инструментов, не имеющих этих знаков.
В чем метрологический смысл погрешности меры? Она показывает интервал, внутри которого с вероятностью, близкой к 100% находится неизвестное истинное значение меры. Например, каждый груз из набора грузов имеет номинальное значение массы 100 г, погрешность меры ± 2 г. Следовательно, истинное значение груза находится в интервале (100 – 2) г < m < (100 + 2) г.
Если номинальное значение сопротивления резистора равно 4,0 Ом, а погрешность 0,12 Ом, следовательно, истинное значение сопротивления содержится в интервале (4,00 – 0,12) Ом Ј R Ј (4,00 + 0,12) Ом.
Погрешности стрелочных электроизмерительных приборов чаще всего задаются специальной величиной, которая называется классом точности и обозначается символом g. Класс точности g показывает значение допускаемой погрешности в процентах от предела измерения (или суммы пределов для приборов, нуль которых находится внутри шкалы). Например, если класс точности амперметра равен g = 2,5, то основная погрешность равна
Если миллиамперметр имеет ноль посередине шкалы, его основная погрешность равна
В чем смысл основной погрешности стрелочных приборов? Она показывает интервал, внутри которого с вероятностью равной 100% находится истинное значение измеряемой величины, если стрелка прибора совпадает со штрихом шкалы. Например, пусть стрелка амперметра совпадает со штрихом 1,6 А. Следовательно, истинное значение силы тока находится в интервале
(1,60 – 0,05) А Ј I Ј (1,60 + 0,05) А.
Основная погрешность весов складывается из погрешности гирь и чувствительности. Например, если на весах находится взвешиваемое тело и две гири номинальными значениями 100 г и 50 г, то погрешность весов складывается из погрешностей гирь (40 + 30) мг.
Погрешность мультиметра указана двумя числами. Например, для диапазона 700 В записано: «± 1,2% ± 3». Эта запись означает, что погрешность мультиметра в диапазоне от 200 В до 700 В равна сумме единицы младшего разряда считываемого показания U. Пусть считываемое показание равно U = 237 В. Следовательно, погрешность измерения равна
Истинное значение напряжения находится в интервале (237 – 6) В < U < (237 + 6) В.
Отметим, что погрешности измерений определяются, главным образом, погрешностями средств измерений, но они не тождественны им.
В общем случае погрешность средства измерений(меры измерительного преобразователя, измерительного прибора) – это отклонение его реальной функции преобразования от номинальной.
Отклонения реальной характеристики от номинальной, отсчитанные вдоль оси Х или оси У, т. е. разности вида y = Ур– Унилиx = Хр– Хн, естьабсолютные погрешности преобразования, выраженные в единицах величин Х или У (рис. 1).
Мерой точности абсолютная погрешность быть не может, т. к., например, Х = 0.5 мм при измерении высоты пенного слоя пульпы, равной Х = 200 мм, достаточно мала, а при измерении толщины листа стали, при Х = 1 мм, эта погрешность очень велика.
Абсолютная погрешность измерительного прибора XП– это разность между показанием прибора ХПи истинным (действительным) ХДзначением измеряемой величины:
XП= ХП– ХД.
Рис. 1. К пояснению понятия абсолютной погрешности
При этом за действительное значение физической величины при оценке погрешности рабочего средства измерений принимают показания образцового средства измерений, при оценке погрешности образцового средства – показания, полученные с помощью эталонного средства измерений.
Абсолютная погрешность измерительного преобразователя по входу– это разность между значением величины на входе преобразователя ХВи истинным (действительным) значением этой величины на входе ХВД. При этом значение величины на входе ХВопределяется по истинному (действительному) значению величины на выходе преобразователя с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
ХВ=Х*ВД – ХВД,
где ХВ– погрешность измерительного преобразователя по входу;
Х*ВД – истинное (действительное) значение величины на выходе, найденное по градировочной характеристике преобразователя;
ХВД– истинное (действительное) значение преобразуемой величины на входе.
Абсолютная погрешность измерительного преобразователя по выходу– это разность между истинным (действительным) значением величины преобразователя на выходеDХВЫХ.Д и значением величины на выходе Х*ВЫХ.Д, определяемым по истинному (действительному) значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
DХВЫХ.П = ХВЫХ.Д – Х*ВЫХ.Д ,
где DХВЫХ.П– погрешность измерительного преобразователя по выходу;
ХВЫХ.Д – действительное значение преобразуемой величины на выходе преобразователя;
Х*ВЫХ.Д – действительное значение преобразуемой величины на выходе, определяемое по действительному значению ее на входе с помощью градуировочной характеристики.
Абсолютная погрешность– это разность между номинальным значением меры ХН и истинным (действительным) ХД воспроизводимой ею величины, т. е.
ХМ= ХН– ХД,
где ХМ– абсолютная погрешность мepы;
ХН– номинальное значение мepы;
ХД– действительное значение воспроизводимой мерой величины.
Пример. Погрешность меры длины (линейки) с номинальным значением 100 мм и действительным значением 100,0006 мм равна 0,6 мкм; погрешность меры сопротивления с номинальным значением 1 Ом и действительным значением 1,0001 Ом равна 0,0001 Ом.
Относительная погрешность меры или измерительного прибора(П) – это отношение абсолютной погрешности меры или измерительного прибора к истинному (действительному) значению воспроизводимой или измеряемой величины.
Относительная погрешность меры или измерительного прибора, в процентах, может быть выражена как:
.
Относительная погрешность измерительного преобразователя по входу (выходу) – это отношение абсолютной погрешности измерительного преобразователя по входу (выходу) к истинному (действительному) значению величины на входе (выходе), определяемому по истинному значению величины на входе (выходе) с помощью номинальной характеристики, приписанной преобразователю.
Итак, относительная погрешность средства измерений, выражаемая в процентах или в относительных единицах, не остается постоянной вследствие изменения величин Х или Y по шкале измерительного устройства.
С учетом того, что относительная погрешность средства измерений не остается постоянной, то вводится понятие приведенной погрешности, в общем виде определяемой:
,
где - приведенная погрешность средства измерений;
XN- нормирующее значение измеряемой величины.
Приведенная погрешность измерительного прибора– это отношение абсолютной погрешности измерительного прибораХПк нормирующему значению.Нормирующее значение XN- это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений**, или длине шкалы***.
Приведенную погрешность обычно выражают в процентах:
.
Приведенная погрешность позволяет сравнивать по точности приборы, имеющие разные пределы точности.
Пример. Определить абсолютную, относительную и приведенную погрешности амперметра с диапазоном измерения 0 -15 А при показании его ХП= 12 А и действительном значении измеряемой силы тока ХД= 12,6 А. За нормирующее значение примем верхний предел измерения Xv = 15 А.
Абсолютная погрешность амперметра
ХП= ХП– ХД= 12 – 12,6 = -0,6 А.
Относительная погрешность амперметра
Приведенная погрешность
При характеристике погрешностей средств измерений часто пользуются понятием предела допускаемой погрешности измерений.
Предел допускаемой погрешности средства измерений– это наибольшая, без учета знака, погрешность средства измерений, при котором оно может быть признано и допущено к применению. Определение применимо к основной и дополнительной погрешности средств измерений.
Пример. Одинаков ли предел допускаемой относительной погрешности измерения во всех точках шкалы автоматического потенциометра?
Для всех точек шкалы одинаков предел допускаемой абсолютной погрешности, определяемой классом точности средства измерений и диапазоном измерений, а предел допускаемой относительной погрешности измерения зависит от конкретной отметки шкалы, т. е. чем меньше показания прибора по шкале, тем больше относительная погрешность. Вследствие этого верхний предел показаний прибора нужно выбирать таким образом, чтобы значение измеряемой величины находилось в конце шкалы.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности– это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений, К этим погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений
Методическая погрешность– это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Основная и дополнительная погрешности.Деление это чисто условно. Погрешность средств измерений, определяемую для работающих в нормальных условиях, называютосновной погрешностью. Нормальными условиями принято считать условия, когда температура окружающего воздуха t = (20 ± 5) 0C, относительная влажность W = 30 – 80 %, атмосферное давление Р = 630 – 795 мм рт. ст., напряжение питающей сети (U = (220 ± 4,4) В, частота питающей сети f = (50 ± 0,5) Гц. Такие условия выдерживаются в лабораторных условиях при градуировке средств измерений.
В реальных условиях производства эти параметры отличаются от лабораторных. Средства измерения помимо чувствительности к измеряемой величине обладают и некоторой чувствительностью к изменяющимся величинам окружающей среды, что приводит к искажению результатов измерения. Погрешность, появляющуюся у средств измерений, работающих в реальных производственных условиях, называют дополнительной погрешностью. Так же, как основная, дополнительная погрешность нормируется путем указания коэффициентов влияния изменения отдельных влияющих величин на изменение показаний в виде
α = , α =· Uпит.
Систематические и прогрессирующие погрешности средств измерений вызываются: первые – погрешностью градуировки шкалы или ее небольшим сдвигом, вторые – старением элементов средства измерения. Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Аддитивные и мультипликативные погрешности. Аддитивная погрешность не зависит от чувствительности прибора и является постоянной для всех значений входной (измеряемой) величины в пределах диапазона измерений (рис.2).
Если реальная характеристика 1 средства измерения смещена относительно номинальной 2 (см. рис. 2) так, что при всех значениях преобразуемой величины Х выходная величина У оказывается больше (или меньше) на одну и ту же величину Δ, то такая погрешность называется аддитивной погрешностью нуля.
Рис. 2. К пояснению понятия аддитивной погрешности средства измерения
К аддитивным погрешностям средств измерений можно отнести погрешности, вызванные трением в опорах электроизмерительных приборов, погрешность дискретности (квантования) в цифровых приборах. Аддитивная погрешность может носить систематический характер. В этом случае она может быть скорректирована смещением шкалы или нулевого положения указателя.
В случае же, если аддитивная погрешность является случайной, то она не может быть скорректирована, и реальная характеристика средства измерения, смещаясь произвольным образом, но, оставаясь параллельной самой себе, образует полосу погрешностей, ширина которой остается постоянной для любых значений измеряемой величины Х (см. рис. 4.2, б).
Мультипликативная погрешность– это погрешность чувствительности средства измерения. Она может иметь систематическую и случайную составляющие.
Сущность мультипликативной погрешности заключается в том, что если абсолютная погрешность возникает от некоторого независимого от Х изменения чувствительности преобразователя (изменение коэффициента деления делителя, добавочного сопротивления вольтметра и т. д.), то реальная характеристика 1 преобразователя отклоняется от номинальной 2 так, как это показано на рис. 4.3, а, или образует полосу погрешностей (рис. 4.3, б), если это отклонение является случайным.
Рис. 4.3. К пояснению понятия мультипликативной погрешности измерений
Список использованной литературы:
http://fiz.1september.ru/2001/16/no16_01.htm
https://studfiles.net/preview/6269920/page:2/
Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: 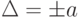
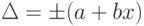
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, “Класс точности М”, а на приборе – буквой “М”. Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле 

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 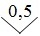
Рис.
3.1.
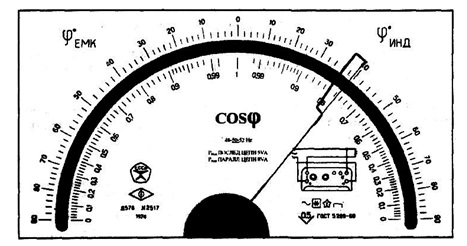
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
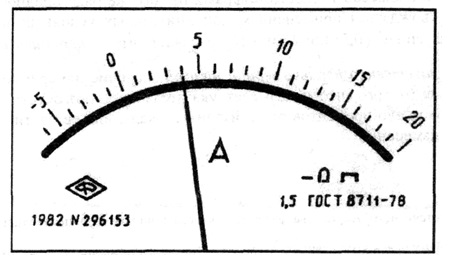
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
Рис.
3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой 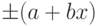
![delta=Delta/x=pm[c+d(|x_{k}/x|-1)]](https://intuit.ru/sites/default/files/tex_cache/3898a996678dab895193a1773d11ffc8.png) |
( 3.1) |
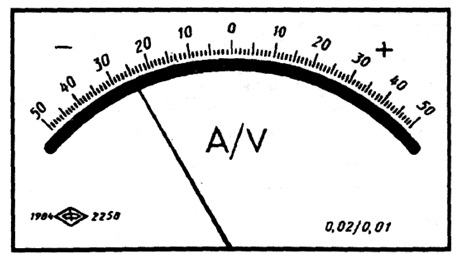
где с, d – отвлеченные положительные числа, выбираемые из ряда: 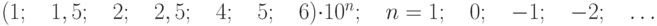
Рис.
3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле 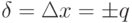
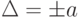
Рис.
3.4.
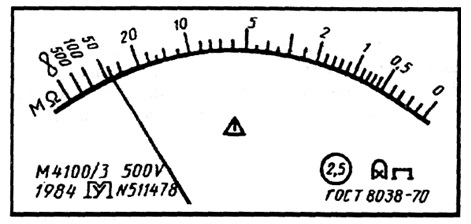
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?