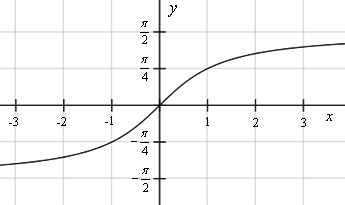Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.
Значение предела в точке непрерывности определено значением функции в этой точке.
При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.
Произвести вычисление предела функции limx→5arctg35·x
Решение
Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что
limx→5arctg35·x=arctg35·5=arctg3=π3
Ответ: π3.
Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса имеются такие значения x0=-1 или x0=1.
При x→+∞ или x→-∞ вычисляются пределы функции, заданные на бесконечностях.
Для упрощения выражений применяют свойства пределов:
- limx→x0(k·f(x))=k·limx→x0f(x), k является коэффициентом.
- limx→x0(f(x)·g(x))=limx→x0f(x)·limx→x0g(x), применяемое при получении неопределенности предела.
- limx→x0(f(g(x)))=flimx→x0gx,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.
Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.
Таблица пределов функции
Для упрощения и решения пределов используется данная таблица основных пределов.
|
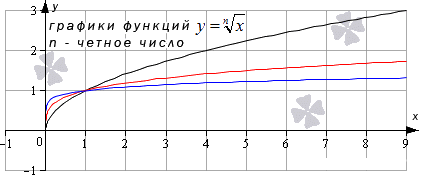
Функция корень n-ой степени y=xn, где n=2, 4, 6 … limx→∞xn=+∞n=+∞ Для любых x0 из опрелеления limx→x0xn=x0n |
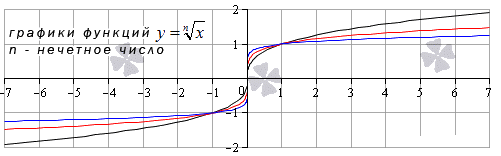
Функция корень n-ой степени y=xn, где n=3, 5, 7 … limx→∞xn=+∞n=+∞limx→∞xn=-∞n=-∞ limx→x0xn=x0n |
|
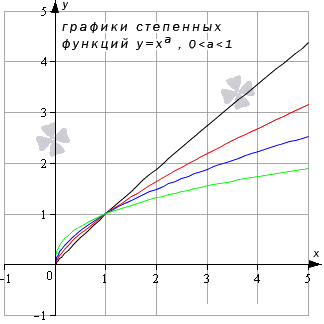
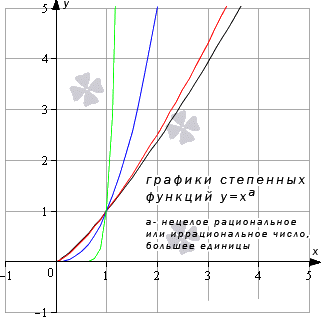
Степенная функция y=xa , a>0
|
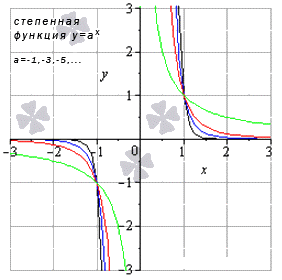
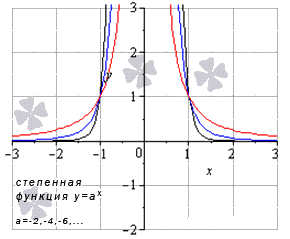
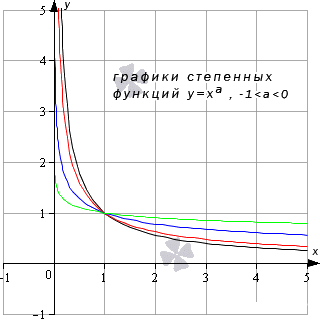
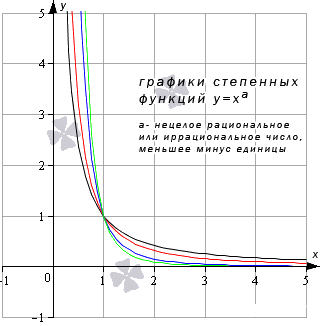
Степенная функция y=xa, a<0
|
|
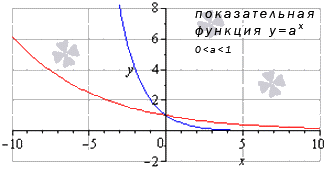
Показательная функия y=ax, 0<a<1 limx→∞ax=a-∞=+∞limx→∞ax=a+∞=+0 Для любых x0 из области опреления limx→x0ax=ax0 |
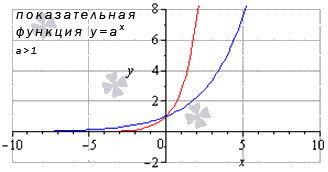
Показательная функия y=ax, a>1limx→∞ax=a-∞=+0limx→x0ax=a+∞=+∞ Для любых знвчений x0 из област опредения limx→x0ax=ax0 |
|
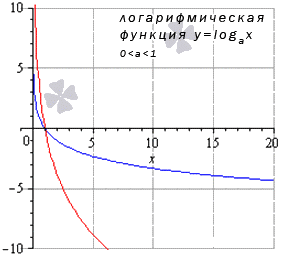
Логарифмическая функция y=loga(x), 0<a<1 limx→0+0logax=loga(0+0)=+∞limx→∞logax=loga(+∞)=-∞ Для любых x0 из области опрелеленияlimx→x0logax=logax0 |
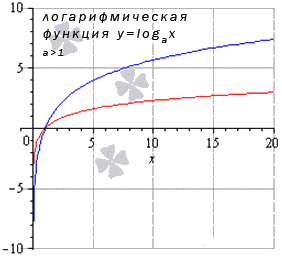
Логарифмическая функция y=loga(x), a>1 limx→0+0logax=loga(0+0)=-∞limx→∞logax=loga(+∞)=+∞ Для любых x0 из области опрелеления limx→x0logax=logax0 |
|
Тригонометрические функции
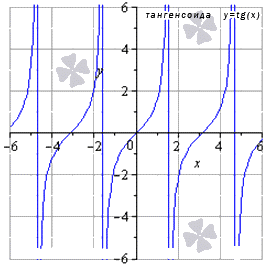
limx→∞tg x не существует Для любых x0 из области опрелеления limx→x0tg x=tg x0 |
Тригонометрические функции
limx→∞ctg x не существует Для любых x0 из области опрелеления |
|
Обратные тригонометрические функции
Для любых x0 из области опрелеления limx→x0arcsin x=arcsin x0
Для любых x0 из области опрелеления limx→x0arccis x=arccos x0 |
Обратные тригонометрические функции
Для любых x0 из области опрелеления limx→x0arctg x=arctg x0
Для любых x0 из области опрелеления limx→x0arcctg x=arcctg x0 |
Произвести вычисление предела limx→1×3+3x-1×5+3.
Решение
Для решения необходимо подставить значение х=1. Получаем, что
limx→1×3+3x-1×5+3=13+3·1-115+3=34=32
Ответ: limx→1×3+3x-1×5+3=32
Произвести вычисление предела функции limx→0(x2+2,5)1×2
Решение
Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку х=0. Подставляем числовое значение и получаем:
x2+2.5x=0=02+2.5=2.5
Предел записывается в виде limx→0(x2+2.5)1×2=limx→02.51×2. Далее необходимо заняться значением показателя. Он является степенной функцией 1×2=x-2. В таблице пределов, предоставленной выше, имеем, что limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞, значит, имеем право записать как limx→01×2=limx→0x-2=+∞
Теперь вычислим предел. Получит вид limx→0(x2+2.5)1×2=limx→02.51×2=2.5+∞
По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что
limx→0(x2+2.5)1×2=limx→02.51×22.5+∞=+∞
Ответ: limx→0(x2+2.5)1×2=+∞
Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.
Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.
Предел константы
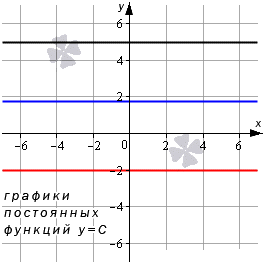
Из рисунка видно, что функция у=С имеет предел на бесконечности. Такой же предел при аргументе, который стремится к х0. Он равняется числу C.
Предел функции корень n-ой степени
Четные показатели корня применимы для limx→+∞xn=+∞n=+∞, а нечетные, равные больше, чем значение 1, – для limx→+∞xn=+∞n=+∞, limx→-∞xn=-∞n=-∞. Область определения может принимать абсолютно любое значение х предела заданной функции корня n-ой степени, равного значению функции в заданной точке.
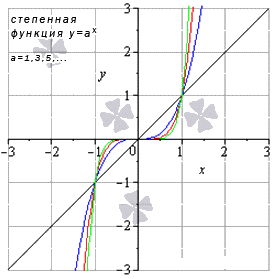
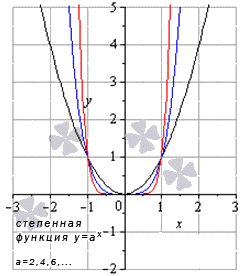
Предел степенной функции
Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.
- Когда a является положительным числом, тогда limx→+∞xa=+∞a=+∞ и limx→-∞xa=-∞a=-∞. Когда x принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как limx→∞xa=(∞)a=∞.
- Когда a является положительным четным числом, тогда получаем limx→+∞xa=(+∞)a=+∞ и limx→-∞xa=(-∞)a=+∞, причем x из данной области определения является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид limx→∞xa=∞a=+∞.
- Когда a имеет другие значения, тогда limx→+∞xa=(+∞)a=+∞, а область определения x способствует определению предела функции в заданной точке.
- Когда a имеет значение отрицательных чисел, тогда получаем limx→+∞xa=+∞a=+0, limx→-∞xa=(-∞)a=-0, limx→0-0xa=(0-0)a=-∞,limx→0+0xa=0+0a=+∞, а значения x может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что limx→∞xa=∞a=0 иlimx→0xa=0a=∞.
- Когда a является отрицательным четным числом, тогда получаем limx→+∞xa=(+∞)a=+0, limx→-∞xa=-∞a=+0, limx→0-0(0-0)a=+∞, limx→0+0xa=(0+0)a=+∞, а любое значение x на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как limx→∞xa=(∞)a=+0 и limx→0xa=(0)a=+∞.
- Когда значение a имеет другие действительные отрицательные числа, тогда получим limx→+∞xa=+∞a=+0 и limx→0+0xa=0+0a=+∞, когда x принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.
Предел показательной функции
Когда 0<a<1, имеем, что limx→-∞ax=a-∞=+∞, limx→+∞ax=(a)+∞=+∞, любое значение x из области определения дает пределу показательной функции значению функции в точке.
Когда a>1, тогда limx→-∞ax=(a)-∞=+0, limx→+∞ax=(a)+∞=+∞, а любое значение x из области определения дает предел функции равный значению этой функции в точке.
Предел логарифмической функции
Когда имеем 0<a<1, тогда limx→0+0logax=loga(0+0)=+∞, limx→+∞logax=loga(+∞)=-∞ , для всех остальных значений x из заданной области определения предел показательной функции равняется значению заданной функции в точках.
Когда a>1, получаем limx→0+0logax=loga(0+0)=-∞, limx→+∞logax=loga(+∞)=+∞,остальные значения x в заданной области определения дают решение предела показательной функции равному ее значению в точках.
Предел тригонометрических функций
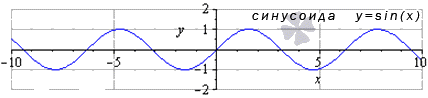
Предел бесконечности не существует для таких функций как y=sin x, y=cos x. Любое значение x, входящее в область определения, равняется значению функции в точке.
Функция тангенса имеет предел вида limx→π2-0+π·ktg(x)=+∞, limx→π2+π·ktg(x)=∞ или limx→π2+π·ktg(x)=∞, тогда остальные значения x, принадлежащие области определения тангенса, равняется значению функции в этих точках.
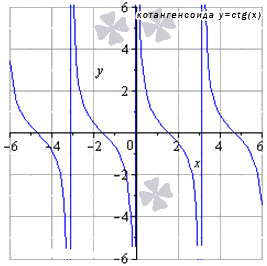
Для функции y=ctg x получаем limx→-0+π·kctg(x)=-∞, limx→+0+π·kctg(x)=+∞ или limx→π·kctg (x)=∞, тогда остальные значения x, принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.
Предел обратных тригонометрических функций
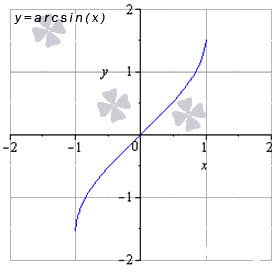
Функция арксинус имеет предел вида limx→-1+0arcsin(x)=-π2 и limx→1-0arcsin (x)=π2, остальные значения x из области определения равняются значению функции в заданной точке.
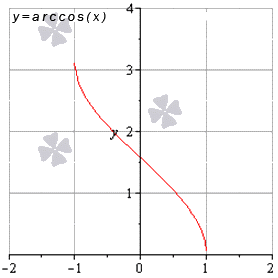
Функция арккосинус имеет предел вида limx→-1+0arccos(x)=π и limx→1-0arccos(x)=0, когда остальные значения x, принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.
Функция арктангенс имеет предел вида limx→-∞arctg(x)=-π2 и limx→+∞arctg(x)=π2, причем другие значения x, входящие в область определения, равняется значению функции в имеющихся точках.
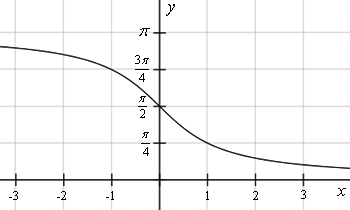
Функция котангенса имеет предел вида limx→-∞arcctg(x)=π и limx→+∞arctg(x)=0, где x принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.
Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.
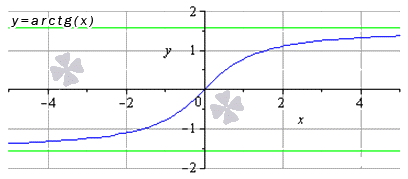
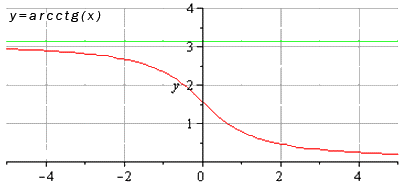
Чтобы найти предел арктангенса, (в частности, арктангенс на бесконечности, arctg 0) нужны свойства арктангенса и график функции y=arctg x.
Функция y=arctg x- обратная к функции y=tg x. Область определения функции y=arctg x — вся числовая прямая, область значений — проме
График функции y=arctg x наглядно иллюстрирует, как ведет себя арктангенс на бесконечности: если x стремится к бесконечности (точнее, к плюс бесконечности), арктангенс стремится к п/2, если икс стремиться к минус бесконечности, арктангенс стремится к -п/2. Отсюда предел арктангенса на бесконечности:
Поскольку на всей числовой прямой функция y=arctg x — непрерывна, предел арктангенса в любой точке равен значению арктангенса в этой точке: arctg 0 = 0 и т.д.
Для
расчета необходимо применить не только
основные функции арктангенса,
но и ее график.
Не следует забывать, что арктангенс
является обратной функцией тангенса
от минус
pi/2
до плюс
pi/2.
Графически определяется поведение
функции на бесконечности.
Если
икс
стремится
к отрицательному значению, значит,
арктангенс приближается к минус pi/2,
если стремится
к плюсу бесконечности,
то приближается к плюс pi/2.
Согласна,
именно к таким значениям стремится
арктангенс на плюс и минус бесконечности,
которые указаны в предыдущем ответе.
Точнее,
lim
(x->+00)
arctg
(x/2)
= pi/2.
Предел
арктангенса конечен. Никакой угол не
даст число больше чем число 2 pi.
По мере приближения значения к
бесконечности
равен pi
/2, а предел второй части функции равен
просто число pi.
Пример
предела в бесконечности. Не забываем,
что ∞ – не цифра. Как пример, попробуем
разделить число 1 на очень большое число.
Сейчас пробуйте делить 1 на парное
большее число. Вы получаете очень
маленькие цифры, правильно? Это означает,
что 1 делили на x подходы 0, когда x
приближается к бесконечности.
Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.
Первый замечательный предел
Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.
Формула
Формула первого замечательного предела имеет вид: $$ lim_{alphato 0} frac{sinalpha}{alpha} = 1 $$
Замечаем, что при $ alphato 0 $ получается $ sinalpha to 0 $, тем самым в числетеле и в знаменателе имеем нули. Таким образом формула первого замечательного предела нужна для раскрытия неопределенностей $ frac{0}{0} $.
Для применения формулы необходимо, чтобы были соблюдены два условия:
- Выражения, содержащиеся в синусе и знаменателе дроби совпадают
- Выражения, стоящие в синусе и знаменателе дроби стремятся к нулю
Внимание! $ lim_{xto 0} frac{sin(2x^2+1)}{2x^2+1} neq 1 $ Хотя выражения под синусом и в знаменателе одинаковые, однако $ 2x^2+1 = 1 $, при $ xto 0 $. Не выполнено второе условие, поэтому применять формулу НЕЛЬЗЯ!
Следствия
Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.
$$ lim_{alphato 0} frac{alpha}{sinalpha} = 1 $$
$$ lim_{alphato 0} frac{sin(aalpha)}{sin(balpha)} = frac{a}{b} $$
$$ lim_{alphato 0} frac{tgalpha}{alpha} = 1 $$
$$ lim_{alphato 0} frac{arcsinalpha}{alpha} = 1 $$
$$ lim_{alphato 0} frac{arctgalpha}{alpha} = 1 $$
Примеры решений
Рассмотрим первый замечательный предел, примеры решения которого на вычисление пределов содержащих тригонометрические функции и неопределенность $ bigg[frac{0}{0}bigg] $
| Пример 1 |
| Вычислить $ lim_{xto 0} frac{sin2x}{4x} $ |
| Решение |
|
Рассмотрим предел и заметим, что в нём присутствует синус. Далее подставим $ x = 0 $ в числитель и знаменатель и получим неопределенность нуль делить на нуль: $$ lim_{xto 0} frac{sin2x}{4x} = frac{0}{0} $$ Уже два признака того, что нужно применять замечательный предел, но есть небольшой нюанс: сразу применить формулу мы не сможем, так как выражение под знаком синуса отличается от выражения стоящего в знаменателе. А нам нужно, чтобы они были равны. Поэтому с помощью элементарных преобразований числителя мы превратим его в $ 2x $. Для этого мы вынесем двойку из знаменателя дроби отдельным множителем. Выглядит это так: $$ lim_{xto 0} frac{sin2x}{4x} = lim_{xto 0} frac{sin2x}{2cdot 2x} = $$ $$ = frac{1}{2} lim_{xto 0} frac{sin2x}{2x} = frac{1}{2}cdot 1 = frac{1}{2} $$ Обратите внимание, что в конце $ lim_{xto 0} frac{sin2x}{2x} = 1 $ получилось по формуле. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim_{xto 0} frac{sin2x}{4x} =frac{1}{2} $$ |
| Пример 2 |
| Найти $ lim_{xto 0} frac{sin(x^3+2x)}{2x-x^4} $ |
| Решение |
|
Как всегда сначала нужно узнать тип неопределенности. Если она нуль делить на нуль, то обращаем внимание на наличие синуса: $$ lim_{xto 0} frac{sin(x^3+2x)}{2x-x^4} = frac{0}{0} = $$ Данная неопределенность позволяет воспользоваться формулой первого замечательного предела, но выражение из знаменателя не равно аргументу синуса? Поэтом “в лоб” применить формулу нельзя. Необходимо умножить и разделить дробь на аргумент синуса: $$ = lim_{xto 0} frac{(x^3+2x)sin(x^3+2x)}{(2x-x^4)(x^3+2x)} = $$ Теперь по свойствам пределов расписываем: $$ = lim_{xto 0} frac{(x^3+2x)}{2x-x^4}cdot lim_{xto 0} frac{sin(x^3+2x)}{(x^3+2x)} = $$ Второй предел как раз подходит под формулу и равен единице: $$ = lim_{xto 0} frac{x^3+2x}{2x-x^4}cdot 1 = lim_{xto 0} frac{x^3+2x}{2x-x^4} = $$ Снова подставляем $ x = 0 $ в дробь и получаем неопределенность $ frac{0}{0} $. Для её устранения достоточно вынести за скобки $ x $ и сократить на него: $$ = lim_{xto 0} frac{x(x^2+2)}{x(2-x^3)} = lim_{xto 0} frac{x^2+2}{2-x^3} = $$ $$ = frac{0^2 + 2}{2 – 0^3} = frac{2}{2} = 1 $$ |
| Ответ |
| $$ lim_{xto 0} frac{sin(x^3+2x)}{2x-x^4} = 1 $$ |
| Пример 3 |
| Определить $ lim_{xto 3} frac{frac{sin(x^2-9)}{x+8}}{frac{x^2-9}{x+8}} $ |
| Решение |
|
Подставляя $ x = 3 $ в аргумент синуса обращаем внимание на то, что сам аргумент стремится к нулю, как и синус: $$ bigg(frac{x^2-9}{x+8}bigg) to 0, text{ при } xto 3 $$ $$ sinbigg(frac{x^2-9}{x+8}bigg) to 0, text{ при } frac{x^2-9}{x+8} to 0 $$ Выполняем решение, используя первый замечательный предел: $$ lim_{xto 3} frac{frac{sin(x^2-9)}{x+8}}{frac{x^2-9}{x+8}} = 1$$ |
| Ответ |
| $$ lim_{xto 3} frac{frac{sin(x^2-9)}{x+8}}{frac{x^2-9}{x+8}} = 1$$ |
| Пример 4 |
| Вычислить $ lim_{xto0} frac{sin2x}{tg3x} $ |
| Решение |
|
Вычисление начнём с подстановки $ x=0 $. В результате получаем неопределенность $ frac{0}{0} $. Предел содержит синус и тангенс, что намекает на возможное развитие ситуации с использованием формулы первого замечательного предела. Преобразуем числитель и знаменатель дроби под формулу и следствие: $$ lim_{xto0} frac{sin2x}{tg3x} = frac{0}{0} = lim_{xto0} frac{frac{sin2x}{2x}cdot 2x}{frac{tg3x}{3x}cdot 3x} = $$ Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей $$ = lim_{xto0} frac{1cdot 2x}{1cdot 3x} = frac{2}{3} $$ |
| Ответ |
| $$ lim_{xto0} frac{sin2x}{tg2x} = frac{2}{3} $$ |
В статье: “Первый замечательный предел, примеры решения” было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.
Арктангенс, арккотангенс – свойства, графики, формулы
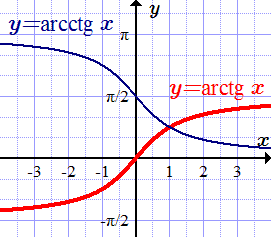
График функции y = arctg x .
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
Арккотангенс обозначается так:
.
График функции арккотангенс
График функции y = arcctg x .
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
Пределы с тригонометрическими функциями
Существует множество различных пределов тригонометрических функций. На помощь могут прийти основные методы вычисления:
- и его следствие с тангенсом $$limlimits_ frac= 1, qquad limlimits_ frac= 1$$
- Тригонометрические преобразования и формулы
Рассмотрим примеры подробного решения тригонометрических пределов для разбора каждого способа. Стоит отметить, что все методы можно комбинировать в одной задаче между собой для ускорения процесса вычисления.
Подставляя $x=0$ в предел получаем неопределенность $(frac)$. Сделаем преобразования в числителе и знаменателе таким образом, чтобы появился замечательный предел.
$$ tg 2x = fraccdot 2x $$ $$ sin 3x = frac cdot 3x $$
Подставляем получившиеся преобразования, чтобы применить формулу первого замечательного предела.
Теперь остается только сократить $x$ и записать ответ.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Обратим внимание на корень в числителе. От него нужно избавиться путём умножения и деления на сопряженное к нему число (отличающееся знаком между слагаемыми).
Теперь с помощью формулы разности квадратов $(a-b)(a+b)=a^2 — b^2$ упростим числитель.
В этой задаче не обойтись без тригонометрической формулы $1-cos x = 2sin^2 frac$. Выполним по ней преобразование выражение в знаменателе.
Видим, что в знаменателе появился синус, а это значит, что можно избавиться от него с помощью первого замечательного предела. Как в предыдущем примере одновременно умножаем и делим на аргумент синуса.
Подставляем преобразование синуса, чтобы применить замечательный предел.
Выносим константу перед пределом и сокращаем $x$ в числителе и знаменателе.
Подставляя $x=0$ получаем неопределенность (0^0). Под пределом показательно-степенная функция, поэтому нужно воспользоваться логарифмированием и свести к неопределенности $(frac)$, чтобы затем воспользоваться правилом Лопиталя.
Берем производные числителя и знаменателя дроби, стоящей в показателе экспоненты.
Подставляем полученное выражение под знак предела и применяем свойство предела для показательной функции.
Теперь, подставляя $x=0$ в предел, вычисляем окончательный ответ.
Итак, в пределе неопределенность ноль делить на ноль. Выполним замены на эквивалентные функции.
Первый замечательный предел
Первым замечательным пределом именуют следующее равенство:
Так как при $alphato$ имеем $sinalphato$, то говорят, что первый замечательный предел раскрывает неопределённость вида $frac$. Вообще говоря, в формуле (1) вместо переменной $alpha$ под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:
- Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида $frac$. Выражения под знаком синуса и в знаменателе совпадают.
Часто используются также следствия из первого замечательного предела:
На данной странице решены одиннадцать примеров. Пример №1 посвящен доказательству формул (2)-(4). Примеры №2, №3, №4 и №5 содержат решения с подробными комментариями. Примеры №6-10 содержат решения практически без комментариев, ибо подробные пояснения были даны в предыдущих примерах. При решении используются некоторые тригонометрические формулы, которые можно найти тут.
Замечу, что наличие тригонометрических функций вкупе с неопределённостью $frac $ ещё не означает обязательное применение первого замечательного предела. Иногда бывает достаточно простых тригонометрических преобразований, – например, см. пример №11.
Формула доказана. Более строгое доказательство (с обоснованием равенства $lim_>cosalpha=1$) можно посмотреть в решебнике Демидовича (№474.1).
б) Сделаем замену $alpha=sin$. Поскольку $sin=0$, то из условия $alphato$ имеем $yto$. Кроме того, существует окрестность нуля, в которой $arcsinalpha=arcsin(sin)=y$, поэтому:
в) Сделаем замену $alpha=tg$. Поскольку $tg=0$, то условия $alphato$ и $yto$ эквивалентны. Кроме того, существует окрестность нуля, в которой $arctgalpha=arctgtg)=y$, поэтому, опираясь на результаты пункта а), будем иметь:
Равенства а), б), в) часто используются наряду с первым замечательным пределом.
Так как $lim_>frac=frac=0$ и $lim_>sinleft(fracright)=sin=0$, т.е. и числитель и знаменатель дроби одновременно стремятся к нулю, то здесь мы имеем дело с неопределенностью вида $frac$, т.е. первое условие выполнено. Кроме того, видно, что выражения под знаком синуса и в знаменателе совпадают (т.е. выполнено и второе условие):
Итак, оба условия, перечисленные в начале страницы, выполнены. Из этого следует, что применима формула (1), т.е. $lim_> fracright)>>=1$.
Так как $lim_>sin=0$ и $lim_>x=0$, то мы имеем дело с неопределенностью вида $frac$, т.е. первое условие выполнено. Однако выражения под знаком синуса и в знаменателе не совпадают. Здесь требуется подогнать выражение в знаменателе под нужную форму. Нам необходимо, чтобы в знаменателе расположилось выражение $9x$, – тогда второе условие станет истинным. По сути, нам не хватает множителя $9$ в знаменателе, который не так уж сложно ввести, – просто домножить выражение в знаменателе на $9$. Естественно, что для компенсации домножения на $9$ придётся тут же на $9$ и разделить:
Теперь выражения в знаменателе и под знаком синуса совпали. Оба условия для предела $lim_>frac>$ выполнены. Следовательно, $lim_>frac>=1$. А это значит, что:
Так как $lim_>sin=0$ и $lim_>tg=0$, то здесь мы имеем дело с неопределенностью вида $frac$. Однако форма первого замечательного предела нарушена. Числитель, содержащий $sin$, требует наличия в знаменателе $5x$. В этой ситуации проще всего разделить числитель на $5x$, – и тут же на $5x$ домножить. Кроме того, проделаем аналогичную операцию и со знаменателем, домножив и разделив $tg$ на $8x$:
Сокращая на $x$ и вынося константу $frac$ за знак предела, получим:
Обратите внимание, что $lim_>frac>$ полностью удовлетворяет требованиям для первого замечательного предела. Для отыскания $lim_>frac>$ применима формула (2):
Так как $lim_>(cos-cos^3)=1-1=0$ (напомню, что $cos=1$) и $lim_>x^2=0$, то мы имеем дело с неопределённостью вида $frac$. Однако чтобы применить первый замечательный предел следует избавиться от косинуса в числителе, перейдя к синусам (дабы потом применить формулу (1)) или тангенсам (чтобы потом применить формулу (2)). Сделать это можно таким преобразованием:
Вернемся к пределу:
Дробь $frac>$ уже близка к той форме, что требуется для первого замечательного предела. Немного поработаем с дробью $frac>$, подгоняя её под первый замечательный предел (учтите, что выражения в числителе и под синусом должны совпасть):
Вернемся к рассматриваемому пределу:
Так как $lim_>(1-cos)=0$ и $lim_>(1-cos)=0$, то мы имеем дело с неопределенностью $frac$. Раскроем ее с помощью первого замечательного предела. Для этого перейдем от косинусов к синусам. Так как $1-cos=2sin^2$, то:
Переходя в заданном пределе к синусам, будем иметь:
Вычислить предел $lim_>frac)-cos(beta)>$ при условии $alphaneqbeta$.
Подробные пояснения были даны ранее, здесь же просто отметим, что вновь наличествует неопределенность $frac$. Перейдем от косинусов к синусам, используя формулу
Используя указанную формулу, получим:
Так как $lim_>(tg-sin)=0$ (напомню, что $sin=tg=0$) и $lim_>x^3=0$, то здесь мы имеем дело с неопределенностью вида $frac$. Раскроем её следующим образом:
Аналогичную задачу можно посмотреть в решебнике Демидовича (№475)
Так как $lim_>(1-cos(x-3))=0$ и $lim_>(x-3)tgfrac=0$, то наличествует неопределенность вида $frac$. Перед тем, как переходить к её раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alpha to 0$). Проще всего ввести переменную $t=x-3$. Однако ради удобства дальнейших преобразований (эту выгоду можно заметить по ходу приведённого ниже решения) стоит сделать такую замену: $t=frac$. Отмечу, что обе замены применимы в данном случае, просто вторая замена позволит поменьше работать с дробями. Так как $xto$, то $tto$.
Вновь мы имеем дело с неопределенностью $frac$. Перед тем, как переходить к ее раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alphato$). Проще всего ввести переменную $t=frac-x$. Так как $xtofrac$, то $tto$:
В данном случае нам не придётся использовать первый замечательный предел. Обратите внимание: как в первом, так и во втором пределах присутствуют только тригонометрические функции и числа. Зачастую в примерах такого рода удаётся упростить выражение, расположенное под знаком предела. При этом после упомянутого упрощения и сокращения некоторых сомножителей неопределённость исчезает. Я привёл данный пример лишь с одной целью: показать, что наличие тригонометрических функций под знаком предела вовсе не обязательно означает применение первого замечательного предела.
Так как $lim_>(1-sin)=0$ (напомню, что $sinfrac=1$) и $lim_>cos^2x=0$ (напомню, что $cosfrac=0$), то мы имеем дело с неопределенностью вида $frac$. Однако это вовсе не означает, что нам потребуется использовать первый замечательный предел. Для раскрытия неопределенности достаточно учесть, что $cos^2x=1-sin^2x$:
Аналогичный способ решения есть и в решебнике Демидовича (№475). Что же касается второго предела, то как и в предыдущих примерах этого раздела, мы имеем неопределённость вида $frac$. Отчего она возникает? Она возникает потому, что $tgfrac=-sqrt$ и $2cosfrac=-1$. Используем эти значения с целью преобразования выражений в числителе и в знаменателе. Цель наших действий: записать сумму в числителе и знаменателе в виде произведения. Кстати сказать, зачастую в пределах аналогичного вида удобна замена переменной, сделанная с таким расчётом, чтобы новая переменная устремилась к нулю (см., например, примеры №9 или №10 на этой странице). Однако в данном примере в замене смысла нет, хотя при желании замену переменной $t=x-frac$ несложно осуществить.
Как видите, нам не пришлось применять первый замечательный предел. Конечно, при желании это можно сделать (см. примечание ниже), но необходимости в этом нет.
Каким будет решение с использованием первого замечательного предела? показатьскрыть