Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:

Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:

Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Краткие теоретические сведения
1. Пределы и непрерывность функции
1.1. Предел числовой последовательности и функции в точке и на бесконечности. Односторонние пределы функции в точке.
Пусть
задано множество всех натуральных
чисел, расположенных в порядке их
возрастания:
![]() .
.
Если
каждому числу
![]() из множества натуральных чисел по
из множества натуральных чисел по
определённому закону ставится в
соответствие одно действительное число
![]() ,
,
то множество вещественных чисел
![]() называетсячисловой
называетсячисловой
последовательностью.
Кратко
числовая последовательность обозначается
![]() .
.
Чаще всего последовательность задается
формулой его общего члена![]() .
.
Например,
общий член
![]() определяет последовательность:
определяет последовательность:
![]() .
.
Число
![]() называется
называется
пределом
числовой последовательности
![]() ,
,
если для любого сколь угодно малого
наперед заданного числа![]() можно найти такой номер последовательности
можно найти такой номер последовательности![]() ,
,
что для всех членов последовательности
с номером![]() выполняется неравенство
выполняется неравенство![]() .
.
Графически это означает, что все члены
последовательности с номером![]() находятся в промежутке от
находятся в промежутке от![]() до
до![]() ( рис 1).
( рис 1).

Если
такой предел существует, то последовательность
называется сходящейся,
в противоположном случае – расходящейся.
Предел
последовательности обозначается:
![]()
Пусть
функция
![]() определена в некоторой окрестности
определена в некоторой окрестности
точки![]() .
.
В самой точке
![]()
функция
может быть и не определена.
Число
![]()
называется пределом
функции![]()
в точке
![]() (при
(при![]() ),
),
если для любой числовой последовательности![]() значений аргумента
значений аргумента![]() (
(![]() ),
),
соответствующая последовательность
значений функции![]() стремится к числуа.
стремится к числуа.
Данное
определение предела функции графически
показано на рис.2. При этом предполагается,
что последовательность
![]() принадлежит области определения функции.
принадлежит области определения функции.

Таким
образом, число
![]()
называется пределом
функции
![]() в
в
точке
![]() (при
(при![]() ),
),
если для любого сколь угодного малого
числа![]() найдётся такое число
найдётся такое число![]() ,
,
что для всех значений аргумента![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() ,
,
будет выполняться неравенство![]() .
.
Предел
функции
![]() в точке
в точке
![]() обозначается:
обозначается:
![]() .
.
Иногда
бывает так, что предел функции
![]() в точке
в точке
![]() имеет
имеет
разную величину, когда![]() слева, т.е.
слева, т.е.![]() меньше
меньше![]() ,
,
и когда![]() справа, т.е.
справа, т.е.![]() больше
больше![]() .
.
В таком случае говорят ободносторонних
пределах функции
в точке: левостороннем
и правостороннем
соответственно.
Левосторонний
предел функции
![]() в точке
в точке
![]() обозначается:
обозначается:
![]() .
.
Правосторонний
предел функции
![]() в точке
в точке
![]() обозначается:
обозначается:
![]() .
.
Число
![]() называетсяпределом
называетсяпределом
функции
![]()
на бесконечности
(при
![]() ),
),
если для любого сколь угодно малого
числа![]()
можно
указать такое число
![]() ,
,
что для всех значений аргумента
удовлетворяющих неравенству![]() ,
,
будет выполняться неравенство![]() .
.
Предел
функции
![]()
на бесконечности обозначается:
![]() .
.
Замечание:
Обозначение
![]() является обобщением для
является обобщением для![]() и
и![]() .
.
Если выбор знака является принципиальным,
то это должно отражаться в условии
задания.
1.2. Основные теоремы о пределах
Практическое
вычисление пределов основывается на
следующих теоремах.
Если
существует ![]()
и ![]() ,
,
то
-
Предел
суммы (разности) двух функций равен
сумме (разности) их пределов:
![]() .
.
-
Предел
произведения двух функций равен
произведению их пределов:
![]() .
.
-
Предел
частного равен пределу числителя,
деленного на предел знаменателя, при
условии, что предел знаменателя не
равен нулю:
 ,
,
если ![]() .
.
-
Постоянный
множитель можно выносить за знак
предела:
![]() ,
,
если
![]() .
.
-
Предел
степени с натуральным показателем
равен той же степени предела:
![]() .
.
Используются
также следующие замечательные
пределы:
І)
![]()
(первый
замечательный предел).
Следствия из
первого замечательного предела:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
а также:
![]() ;
;![]() ;
;![]() ;
;![]() ,
,
где
![]() – некоторая функция.
– некоторая функция.
ІІ)
![]() (второй
(второй
замечательный предел)
или
![]() .
.
Следствия из
второго замечательного предела:
![]() ;
;
![]() ,
,
где
![]() – некоторые функции.
– некоторые функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание “чайникам” 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними – это не так страшно как кажется 🙂 |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её 🙂 Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате – это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное – возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
У этого термина существуют и другие значения, см. Предел.

График функции, предел которой при аргументе, стремящемся к бесконечности, равен 
Преде́лом фу́нкции (предельным значением функции) в точке, предельной для области определения функции, называется такая величина, к которой значение рассматриваемой функции стремится при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.
Предел функции является обобщением понятия предела последовательности. Изначально под пределом функции 




Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в любой окрестности данной точки существуют точки области определения. Это позволяет говорить о стремлении аргумента функции к данной точке. При этом предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо конкретно указывать способ сходимости функции, для чего вводят так называемую базу подмножеств области определения функции, и тогда определение предела функции формулируют по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
Также благодаря рассмотрению расширенной вещественной прямой (на которой базу окрестностей можно построить и для бесконечно удалённой точки) можно определить такие понятия, как предел функции при стремлении аргумента к бесконечности, а также стремление самой функции к бесконечности. Предел последовательности (как предел функции натурального аргумента) как раз представляет собой пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции в точке означает, что для любого заданного значения области значений можно подобрать такую окрестность этого значения, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной в данной точке.
Определения[править | править код]
Рассмотрим функцию 


Предел функции по Гейне[править | править код]
Значение 








Предел функции по Коши[править | править код]
Значение 








где:
Окрестностное определение предела по Коши[править | править код]
Значение 








Предел по базе множеств[править | править код]
Наиболее общим определением является определение предела функции по базе (по базису фильтра, по фильтру).
Пусть 
Если 












При рассмотрении только числовых функций вещественного переменного также рассматриваются и базы односторонних окрестностей. Для этого рассматриваются два множества:
Соответственно этому вводятся две базы:
Эквивалентность определений[править | править код]
Все данные выше определения предела функции в точке эквивалентны[1]. Для доказательства этого необходимо и достаточно принять счётную аксиому выбора. Однако в иных формальных системах, например в конструктивной математике, эквивалентность опровергается на примерах.
Вариации и обобщения[править | править код]
Односторонний предел[править | править код]
Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция вещественной переменной имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.
Предел вдоль фильтра[править | править код]
Предел функции вдоль фильтра — это обобщение понятия предела на случай произвольной области определения функции. Задавая частные случаи области определения и базиса фильтра на ней, можно получить многие приведённые в этой статье определения пределов.
Пределы на бесконечности[править | править код]
Предел функции на бесконечности описывает поведение значений функции, когда по модулю её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.
Предел на бесконечности по Гейне[править | править код]
- Пусть числовая функция
задана на множестве
, в котором может находиться сколь угодно большой элемент, то есть для всякого положительного
найдётся элемент множества
лежащий за границами отрезка
. В этом случае число
называется пределом функции
на бесконечности, если для всякой последовательности точек
которая начиная с некоторого номера n будет по модулю неограниченно расти, соответствующая последовательность частных значений функции в этих точках
сходится к числу
- Пусть числовая функция
задана на множестве
, в котором для любого числа
найдётся элемент, лежащий правее него. В этом случае число
называется пределом функции
на плюс бесконечности, если для всякой последовательности точек
которая начиная с некоторого номера n будет неограниченно расти в положительную сторону, соответствующая последовательность частных значений функции в этих точках
сходится к числу
.
- где
— конъюнкция.
- Пусть числовая функция
задана на множестве
, в котором для любого числа
найдётся элемент, лежащий левее него. В этом случае число
называется пределом функции
на минус бесконечности только при условии, что для всякой бесконечно большой последовательности отрицательных точек
соответствующая последовательность частных значений функции в этих точках
сходится к числу
.
Предел на бесконечности по Коши[править | править код]
- Пусть числовая функция
задана на множестве
, в котором найдётся сколь угодно большой элемент, то есть для всякого положительного
в нём найдётся элемент, лежащий за границами отрезка
. В этом случае число
называется пределом функции
на бесконечности, если для произвольного положительного числа
отыщется отвечающее ему положительное число
такое, что для всех точек, превышающих
по абсолютному значению, справедливо неравенство
.
- Пусть числовая функция
задана на множестве
, в котором для любого числа
найдётся элемент, лежащий правее него. В этом случае число
называется пределом функции
на плюс бесконечности, если для произвольного положительного числа
найдётся отвечающее ему положительное число
такое, что для всех точек, лежащих правее
, справедливо неравенство
.
- Пусть числовая функция
задана на множестве
, в котором для любого числа
найдётся элемент, лежащий левее него. В этом случае число
называется пределом функции
на минус бесконечности, если для произвольного положительного числа
найдётся отвечающее ему положительное число
такое, что для всех точек, лежащих левее
, справедливо неравенство
.
Окрестностное определение по Коши[править | править код]
Пусть функция 




Частичный предел[править | править код]
Для функции, как и для последовательности, можно ввести понятие частичного предела. Число 













Обозначения[править | править код]
Если в точке 






- или
Если у функции 




- или
Если у функции 




- или
Если у функции 




- или
Свойства пределов числовых функций[править | править код]
Пусть даны числовые функции 

- Одна и та же функция в одной и той же точке может иметь только один предел.
- Сходящаяся функция сохраняет знак только локально и никак иначе. Более общо́:
- где
— проколотая окрестность точки
радиуса
- В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
- Сходящаяся функция локально ограничена в окрестности предельной точки:
- Отделимость от нуля функций, имеющих предел, отличный от нуля.
- Операция взятия предела сохраняет нестрогие неравенства.
- Теорема о двух милиционерах.
- тогда существует
.
- Предел суммы равен сумме пределов:
- Предел разности равен разности пределов:
- Предел произведения равен произведению пределов:
- Предел частного равен частному пределов:
- Предел композиции:
Примеры[править | править код]
См. также[править | править код]
- Правило Лопиталя
- Замечательные пределы
- Повторный предел
- Непрерывная функция
- Список пределов
Примечания[править | править код]
- ↑ 1 2 3 В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 105 — 121. — 672 с. — ISBN 5-482-00445-7.
- ↑ Демидович Б.П. Сборник задач и упражнений по математическому анализу. — 7-е изд. — М.: Наука, 1969. — С. 47.
Литература[править | править код]
- Математический энциклопедический словарь / Под ред. Ю. В. Прохорова. — М.: Советская энциклопедия, 1988. — С. 482—483. — 847 с.
- Зорич В. А. Математический анализ. — Москва: Издательство МЦНМО, 2012. — Т. В двух томах.
Ссылки[править | править код]
- Предел функции Архивная копия от 23 марта 2020 на Wayback Machine . Габович. И. Квант.1980 №10
- Предел функции в точке. Теоретическая справка Архивная копия от 7 мая 2009 на Wayback Machine
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
В математике принципиально важным является понятие бесконечности, обозначаемое символом ∞. Его следует понимать как бесконечно большое +∞ или бесконечно малое -∞ число. Когда мы говорим о бесконечности, часто мы имеем в виду сразу оба этих ее смысла, однако запись вида +∞ или -∞ не стоит заменять просто на ∞.
Запись предела функции имеет вид limx→x0f(x). В нижней части мы пишем основной аргумент x, а с помощью стрелочки указываем, к какому именно значению x0 он будет стремиться. Если значение x0 является конкретным действительным числом, то мы имеем дело с пределом функции в точке. Если же значение x0 стремится к бесконечности (не важно, ∞, +∞ или -∞), то следует говорить о пределе функции на бесконечности.
Предел бывает конечным и бесконечным. Если он равен конкретному действительному числу, т.е. limx→x0f(x)=A, то его называют конечным пределом, если же limx→x0f(x)=∞, limx→x0f(x)=+∞ или limx→x0f(x)=-∞, то бесконечным.
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
Число A является пределом функции f(x) при x→∞, если последовательность ее значений будет сходиться к A для любой бесконечно большой последовательности аргументов (отрицательной или положительной).
Запись предела функции выглядит так: limx→∞f(x)=A.
При x→∞ предел функции f(x) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Запись выглядит как limx→∞f(x)=∞.
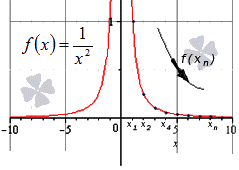
Докажите равенство limx→∞1×2=0 с помощью основного определения предела для x→∞.
Решение
Начнем с записи последовательности значений функции 1×2 для бесконечно большой положительной последовательности значений аргумента x=1, 2, 3,…, n,….
11>14>19>116>…>1n2>…
Мы видим, что значения будут постепенно уменьшаться, стремясь к 0. См. на картинке:
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
x=-1, -2, -3,…, -n,…
11>14>19>116>…>1-n2>…
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
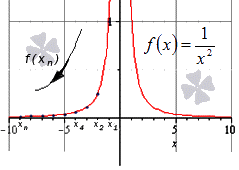
Ответ: Верность данного в условии равенства подтверждена.
Вычислите предел limx→∞e110x.
Решение
Начнем, как и раньше, с записи последовательностей значений f(x)=e110x для бесконечно большой положительной последовательности аргументов. Например, x=1, 4, 9, 16, 25,…, 102,…→+∞.
e110; e410; e910; e1610; e2510;…; e10010;…==1,10; 1,49; 2,45; 4,95; 12,18;…;22026,46;…
Мы видим, что данная последовательность бесконечно положительна, значит, f(x)=limx→+∞e110x=+∞
Переходим к записи значений бесконечно большой отрицательной последовательности, например, x=-1, -4, -9, -16,-25,…, -102,…→-∞.
e-110; e-410; e-910; e-1610; e-2510;…;e-10010;…==0,90; 0,67; 0,40; 0,20; 0,08;…;0,000045;…x=1, 4, 9, 16, 25,…,102 ,…→∞
Поскольку она тоже стремится к нулю, то f(x)=limx→∞1e10x=0.
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
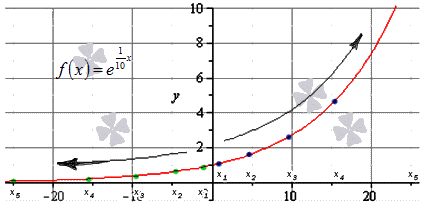
Ответ: limx→∞e110x=+∞, при x→+∞0, при x→-∞.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Число B является пределом функции f(x) слева при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются меньше a (xn<a).
Такой предел на письме обозначается как limx→a-0f(x)=B.
Теперь сформулируем, что такое предел функции справа.
Число B является пределом функции f(x) справа при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются больше a (xn>a).
Этот предел мы записываем как limx→a+0f(x)=B.
Мы можем найти предел функции f(x) в некоторой точке тогда, когда для нее существуют равные пределы с левой и правой стороны, т.е. limx→af(x)=limx→a-0f(x)=limx→a+0f(x)=B. В случае бесконечности обоих пределов предел функции в исходной точке также будет бесконечен.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Докажите, что существует конечный предел функции f(x)=16(x-8)2-8 в точке x0=2 и вычислите его значение.
Решение
Для того чтобы решить задачу, нам потребуется вспомнить определение предела функции в точке. Для начала докажем, что у исходной функции имеется предел слева. Запишем последовательность значений фукнции, которая будет сходиться к x0=2, если xn<2:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8,667; 2,667; 0,167; -0,958; -1,489; -1,747; -1,874;…; -1,998;…→-2
Поскольку приведенная последовательность сводится к -2, мы можем записать, что limx→2-016x-82-8=-2.
Далее докажем наличие предела справа: запишем аргументы в последовательности, которая будет сходиться к x0=2, если xn>2:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Значения функции в этой последовательности будут выглядеть так:
f(6); f(4); f(3); f212; f234; f278; f21516;…; f210231024;…==-7,333; -5,333; -3,833; -2,958; -2,489; -2,247;-2,124;…, -2,001,…→-2
Данная последовательность также сходится к -2, значит, limx→2+016(x-8)2-8=-2.
Мы получили, что пределы с правой и левой стороны у данной функции будут равными, значит, предел функции f(x)=16(x-8)2-8 в точке x0=2 существует, и limx→216(x-8)2-8=-2.
Вы можете увидеть ход решения на иллюстрации (зеленые точки– последовательность значений, сходящаяся к xn<2, синие – к xn>2).
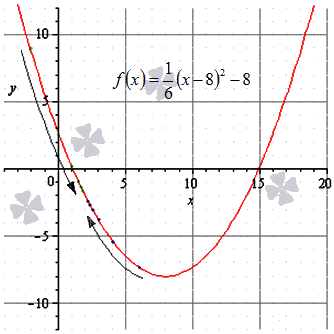
Ответ: Пределы с правой и левой стороны у данной функции будут равными, значит, предел функции существует, и limx→216(x-8)2-8=-2.
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
![{displaystyle lim _{xto x_{0}}f(x)=ALeftrightarrow {Big [}forall varepsilon >0~exists delta =delta {big (}varepsilon )>0~forall x~(0<|x-x_{0}|<delta {big )}Rightarrow {big (}|f(x)-A|<varepsilon {big )}{Big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e8fbe96a12925b0d6a32ba24377f25aba131bb9)
![{displaystyle lim _{xto x_{0}}f(x)=ALeftrightarrow {big [}forall O(A)~exists {dot {O}}(x_{0})~f{big (}{dot {O}}(x_{0}){big )}subseteq O(A){big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9fc422630cbb9c35a9407640e362075537be067)









![{displaystyle f(x)~{xrightarrow[{xto x_{0}}]{}}A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/412f2585dfca671af6fc7cf1200b70e5cae8234b)

![{displaystyle f(x)~{xrightarrow[{xto infty }]{}}A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98565584758ca050dbd6ca78908917e5268bddba)

![{displaystyle f(x)~{xrightarrow[{xto +infty }]{}}A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/913b0f98b4463237a4cbe2aea868c18b4bfbe163)

![{displaystyle f(x)~{xrightarrow[{xto -infty }]{}}A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19042dfa5e0cf65ac53494cb21a14b91b4812093)







![left( limlimits_{x to a} f(x) = A right) wedge left( limlimits_{x to a} g(x) = B right) Rightarrow left( limlimits_{x to a} bigl[f(x)+g(x)bigr] = A+B right);](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e30c8a5e021f2b16b0bdbd79aec853d42347605)
![left( limlimits_{x to a} f(x) = A right) wedge left( limlimits_{x to a} g(x) = B right) Rightarrow left( limlimits_{x to a} bigl[f(x)-g(x)bigr] = A-B right);](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c7b0d797c646127618a64f911db05b186460731)
![left( limlimits_{x to a} f(x) = A right) wedge left( limlimits_{x to a} g(x) = B right) Rightarrow left( limlimits_{x to a} bigl[f(x)cdot g(x)bigr] = Acdot B right);](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bfd85117c299fd0f913862d38ff58b2f7c8111)
![{displaystyle left(lim limits _{xto a}f(x)=Aright)wedge left(lim limits _{xto a}g(x)=Bneq 0right)Rightarrow left(lim limits _{xto a}left[{frac {f(x)}{g(x)}}right]={frac {A}{B}}right);}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b254bbd8f4c1825fbb15c1cd0b6002c232e358d)

