Пределы с логарифмами: примеры решений
Часто в контрольных работах нужно вычислить пределы с логарифмами. Такие задачи можно решить двумя способами:
- С помощью следствия второго замечательного предела: $$ lim limits_{x to 0} frac{ln(1+f(x))}{f(x)} = 1 text{, если } f(x) to 0 $$
- С помощью свойства бесконечно малой эквивалентной функции: $$ ln(1+f(x)) sim f(x) text{, если } f(x) to 0 $$
Оба метода решения допустимы к сдаче преподавателю на проверку. Выберите для себя самый удобный, который будете легко понимать
| Пример 1 |
| Вычислить предел с логарифмом: $ limlimits_{x to 0} frac{ln(1+8x)}{2x} $ |
| Решение |
|
Метод 1: Воспользуемся следствием замечательного предела и приведем предел к виду похожему на него: $$ limlimits_{x to 0} frac{ln(1+8x)}{2x} = limlimits_{x to 0} frac{frac{ln(1+8x)}{8x}cdot small 8x}{2x} = $$ Замечаем, что $ lim limits_{x to 0} frac{ln(1+8x)}{8x} = 1 text{, так как } 8x to 0 $ Продолжаем решение с учетом замечания: $$ = lim limits_{x to 0} frac{8x}{2x} = frac{8}{2} = 4 $$ Метод 2: Используем свойство б.м.э. функции для преобразования натурального логарифма: $$ ln(1+8x) sim 8x text{, при } 8x to 0 $$ Решаем с учетом вышеприведенной эквивалентности: $$ lim limits_{x to 0} frac{ln(1+8x)}{2x} = limlimits_{x to 0} frac{8x}{2x} =frac{8}{2} = 4 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{x to 0} frac{ln(1+8x)}{2x} = 4 $$ |
| Пример 2 |
| Найти предел $ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} $ |
| Решение |
|
Метод 1: Выполняем преобразование под следствие замечательного предела: $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = limlimits_{x to 2} frac{frac{ln(1 + x^2-7x+10)}{x^2-7x+10}cdot small (x^2-7x+10)}{x-2} = $$ Видно, что $ limlimits_{x to 2} frac{ln(1 + x^2-7x+10)}{x^2-7x+10} = 1 $ по след. замеч. предела. С учетом этого, продолжим вычислять интеграл: $$ = limlimits_{x to 2} frac{x^2-7x+10}{x-2} = $$ Логарифм пропал. Решим квадратное уравнение в числителе и распишем его на множители: $$ = limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = limlimits_{x to 2} (x-5) = 2-5=-3 $$ Метод 2: Решение начнем с преобразования предела: $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = limlimits_{x to 2} frac{ln(1 + (x^2-7x+10))}{x-2} = $$ Так как $ x^2-7x+10 = 0 text{при} x = 2 $ , то имеем: $$ ln(1 + (x^2-7x+10)) sim x^2-7x+10 $$ С учетом эквивалентности продолжаем решать: $$ = limlimits_{x to 2} frac{x^2-7x+10}{x-2} = $$ Выполним разложение многочлена второй степени на множители: $$ = limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = $$ Далее, выполняем сокращение на $ x-2 $: $$ limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = limlimits_{x to 2} (x-5) = 2-5 = -3 $$ |
| Ответ |
| $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = -3 $$ |
Приветствую вас, друзья. Сегодня будет очень краткая заметка по теме математического анализа. Допустим, вам нужно найти следующий предел:
Задача: Найти предел lim( ln(x² – x + 1) / ln(x¹⁰ + x + 1) ) при x → ∞
Решение:
Имеет место неопределённость вида [∞/∞].
Здесь возникает желание применить правило Лопиталя-Бернулли. Согласно этому правилу, предел отношения функций, стремящихся одновременно к бесконечности или к нулю (являющихся одновременно бесконечно большими или бесконечно малыми), равен пределу отношения их производных.
Да да, оно помогает справиться с самыми сложными и запутанными пределами, в которых есть неопределенности вида [0 / 0] или [∞/∞].
Но некоторые задачи подразумевают ограничение: не использовать правило Лопиталя. Как же тогда быть?
Без этого метода можно обойтись, вспомнив и применив свойства логарифмической функции. Вынесем за скобки старшие члены в аргументах логарифмов и воспользуемся свойством логарифма произведения и логарифма степени:
ln(x² + x + 1) = ln(x²·(1 – 1/x + 1/x²)) = ln(x²) + ln(1 – 1/x + 1/x²) =
= 2·ln x + ln(1 – 1/x + 1/x²)
ln(x¹⁰ + x + 1) = ln(x¹⁰·(1 + 1/x⁹ + 1/x¹⁰)) = ln(x¹⁰) + ln(1 + 1/x⁹ + 1/x¹⁰) =
= 10·ln x + ln(1 + 1/x⁹ + 1/x¹⁰)
Что получится в итоге:
Прошлая статья по теме пределов:
Математический анализ. Учимся решать пределы
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать в группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Содержание:
- Предел показательно-степенной функции
- Примеры с решением
Предел показательно-степенной функции
Показательно-степе иным и называют функции вида 

Функция 



Отсюда ясно, что показательно-степенная функция непрерывна при тех значениях х, при которых функции 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Если существуют пределы 





a) 


б) 
и потому 
Мы опускаем разбор остальных случаев и приводим следующую таблицу значений предела 
Возможно вам будут полезны данные страницы:
В случаях, соответствующих зачерненным клеткам, ответ неоднозначен и зависит от того, как именно стремятся
Примеры с решением
Пример 1.
Вычислим предел

Так как (см. п. 35)

Пример 2.
Вычислим предел:

а) Так как

б) Здесь 
Пример 3.
Вычислим предел:

а) Так как



66. Предел 



Последовательность с общим членом 











а из неравенств 
Итак, мы доказали, что
где, напомним, 

и 




Когда 


Если в этом равенстве положить 

Пример 4.
Вычислим
Решение:
Имеем:
Пример 5.
Вычислим
Решение:
Имеем:




и 

Если 




- Вычисление пределов, связанных с показательной и логарифмической функциями. Формулы (1) и (3) лежат в основе вычисления большинства пределов, связанных с показательной и логарифмической функциями.
Прологарифмировав обе части равенства (3) по основанию е, получаем 
Заметим теперь, что в силу непрерывности логарифмической функции для любого а > 0 имеем: 







Введем новую переменную z, положив 







Наконец докажем, что





Мы доказали в этом пункте следующие соотношения эквивалентности бесконечно малых (в дополнение к тем, что были получены выше в п. 53 и 58): если 
Пример 6.
Вычислим предел

Так как 




Пример 7.
Вычислим предел

Снова заменяем числитель и знаменатель эквива-лентными бесконечно малыми. Числитель запишем в виде 





а) 

б) 

в) 

Для вычисления таких пределов заменяют
, т. е. на e
и вычисляют предел
Тогда искомый предел равен 
Лекции:
- Исследовать сходимость ряда по признаку Даламбера
- Линейная комбинация векторов
- Площадь поверхности шара
- Производная сложной функции примеры решений
- Определение предела функции
- Криволинейный интеграл 2 рода
- Замечательные пределы, содержащие тригонометрические функции
- Уравнение в полных дифференциалах
- Действия со степенями
- Найти три первых отличных от нуля
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
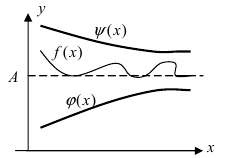
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции
значениями функций
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 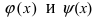
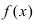
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 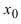
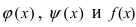
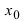
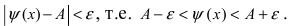
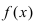
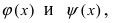
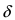
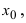
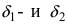
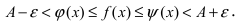
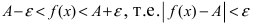
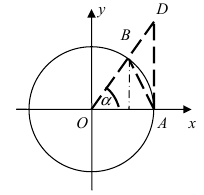
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 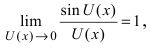
Пример:
Пределы являются первыми замечательными пределами 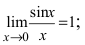
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 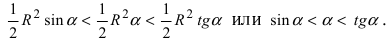
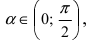
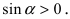
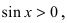
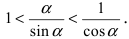
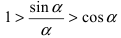
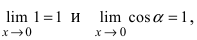
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 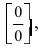
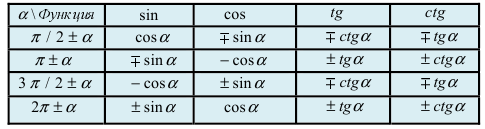
При вычислении первого замечательного предела используют следующие формулы:
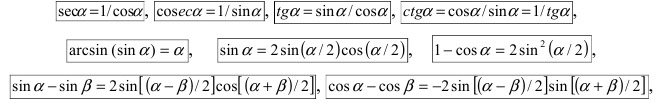
Табл. 1. Значения синуса и косинуса на интервале
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 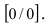
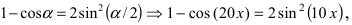
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 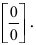
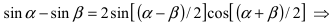
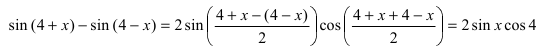
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 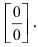
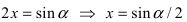
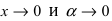
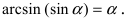
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 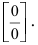
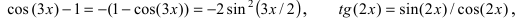
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 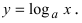
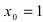
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 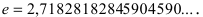
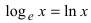
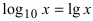
Определение: Вторым замечательным пределом называется предельное равенство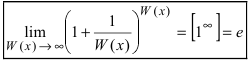
или
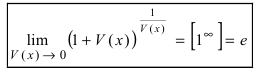
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 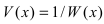
Замечание: Наличие неопределенности 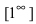
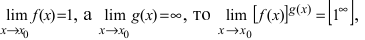
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
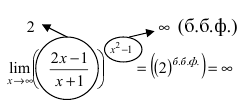
Пример:
Найти lim
Решение:
При подстановке предельного значения переменной х имеем неопределенность 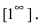
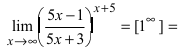
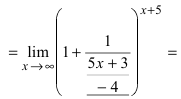
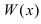
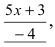
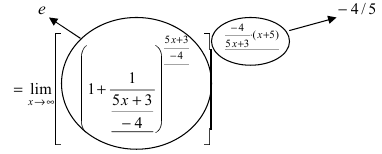
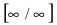
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 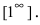
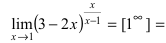
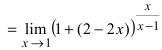
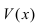
- Заказать решение задач по высшей математике
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 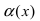
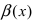
Определение: Если предел К не существует, то бесконечно малые функции 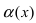
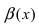
Пример:
Пусть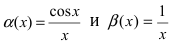
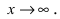
Решение:
Для доказательства вычислим предел 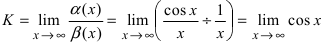
Определение: Если предел К равен нулю, то бесконечно малая функция 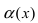
Пример:
Пусть 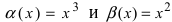
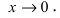
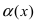
Решение:
Для доказательства вычислим предел 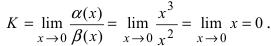
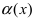
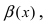
Определение: Если предел К равен 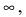
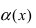
Пример:
Пусть 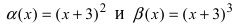
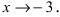
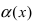
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 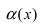
Определение: Если предел К равен конечному числу 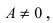
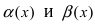
Пример:
Пусть 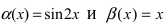
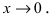
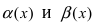
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 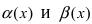
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 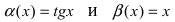
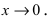
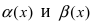
Решение:
Вычислим предел 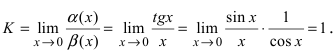

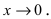
Теорема: Для того чтобы бесконечно малые функции 
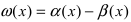

Доказательство:
1. Необходимость. Пусть бесконечно малая функция 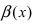
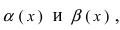
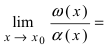
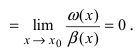
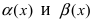
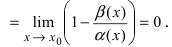
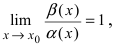
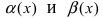
2. Достаточность. Пусть бесконечно малые функции 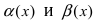
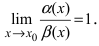
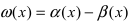
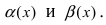
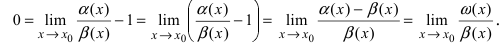
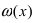
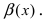
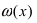
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 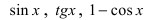
—вышмат
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
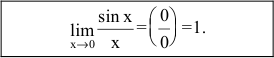
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
(Для запоминания: 2<е<3; 1828 – год рождения Л.Н. Толстого) Следовательно,
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил 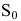
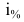
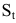
Решение:
Размер вклада будет увеличиваться ежегодно в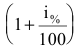
через t лет составит 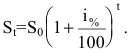
то будущая сумма составит 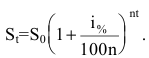
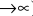
а за t лет:
Пример №26
Найти
Решение:
Т.к. 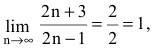
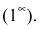
Пример №27
Найти
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
Рассмотрим пределы логарифмов, которые можно найти с помощью следствия из 2-го замечательного предела.
Следствие 2-го замечательного предела:
Это следствие распространяется и на пределы логарифмов, в которых на месте x стоит некоторая функция f(x), если f(x)→0 при x→0, то есть
Рассмотрим, как находят пределы на логарифмы на примерах.
Найти предел функции:
Приводим выражени под знаком предела к такому виду, чтобы можно было применить нашу формулу (*):
так как по следствию из 2-го замечательного предела
Преобразуем выражение -1+cos x:
Продолжим
Теперь приведем предел с логарифмом к виду (*)
С пределом логарифма разобрались:
осталось убрать неопределенность 0 на 0, возникшую с появлением синуса. По 1-му замечательному пределу
Преобразовываем выражение так, чтобы применить этот замечательный предел:
Сокращаем дробь на x², имеем:
По теореме о разложении квадратного трехчлена на множители: x²-7x+10=(x-2)(x-5).
Сокращаем дробь на (x-2):
Так как при x→2 x²-7x+10→0, то
Значит, окончательный ответ
Дальше мы увидим, что пределы на логарифмы удобно находить, используя эквивалентность бесконечно малых величин.






















 , т. е. на e
, т. е. на e и вычисляют предел
и вычисляют предел



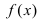
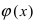
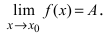
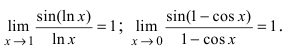
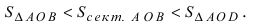
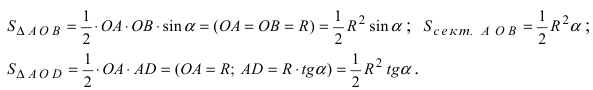
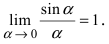
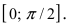

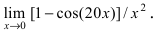
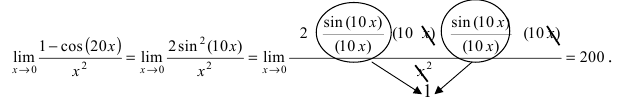
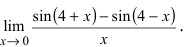
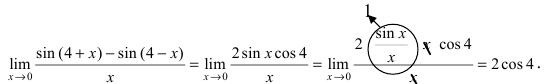
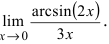
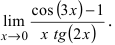
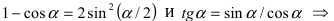
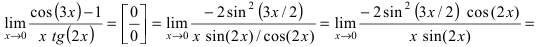
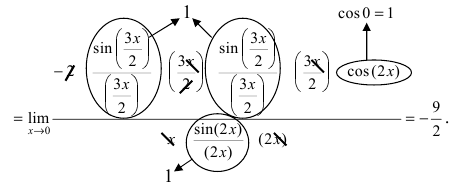
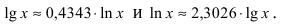
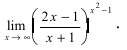
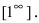
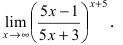
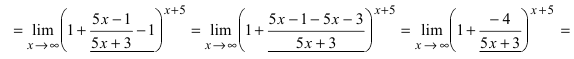
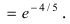
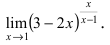
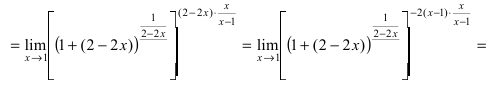
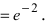
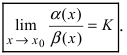
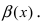
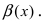
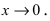
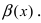
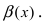
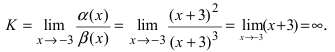
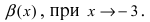
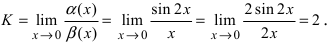
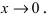
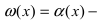
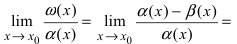
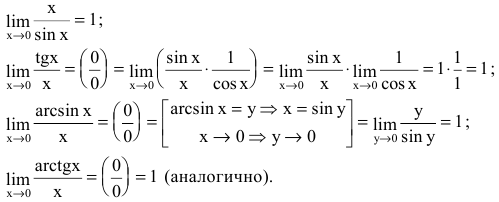
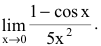
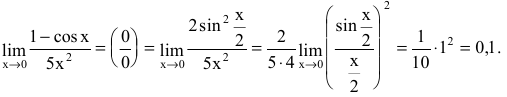
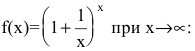
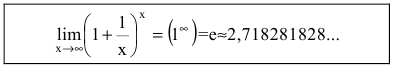
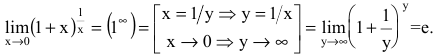
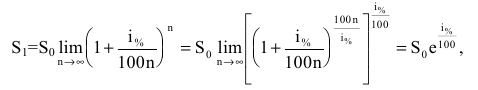
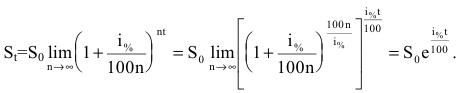
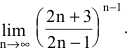
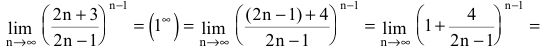
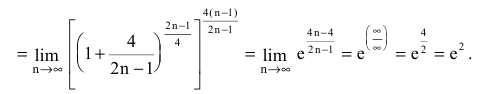
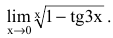
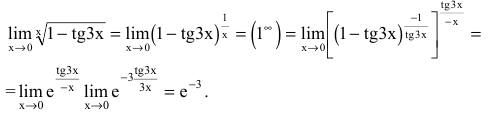
![Rendered by QuickLaTeX.com [ = mathop {lim }limits_{x to 0} frac{{frac{{ln (1 + ( - 2{{sin }^2}frac{x}{2}))}}{{ - 2{{sin }^2}frac{x}{2}}} cdot ( - 2{{sin }^2}frac{x}{2})}}{{{x^2}}} = ]](https://www.matematika.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ce0bdedd720fccbed194394237d1f6fa_l3.png)
![Rendered by QuickLaTeX.com [ = - 2mathop {lim }limits_{x to 0} frac{{frac{{ln (1 + ( - 2{{sin }^2}frac{x}{2}))}}{{ - 2{{sin }^2}frac{x}{2}}} cdot {{left[ {frac{{sin frac{x}{2}}}{{frac{x}{2}}}} right]}^2} cdot frac{{{x^2}}}{4}}}{{{x^2}}} = ]](https://www.matematika.uznateshe.ru/wp-content/ql-cache/quicklatex.com-64596bf5519eef8330fb147b785f05a3_l3.png)
