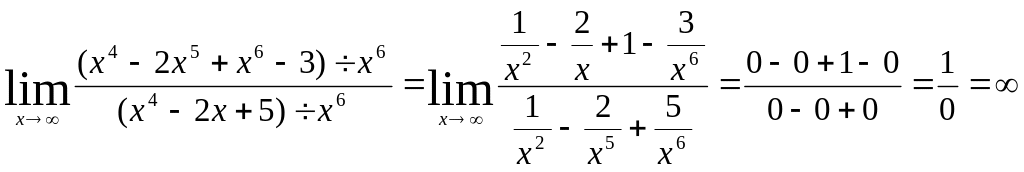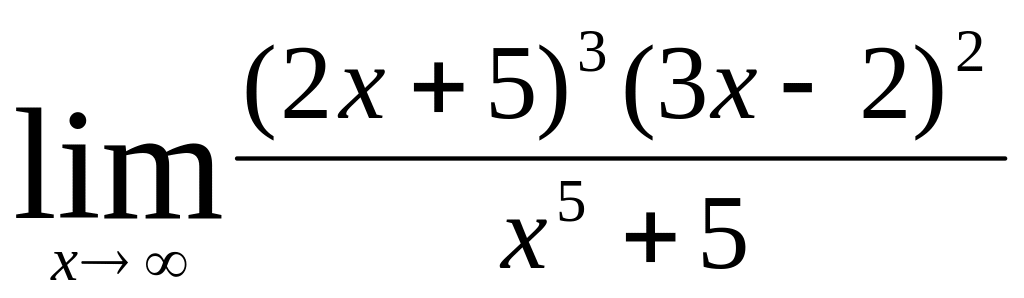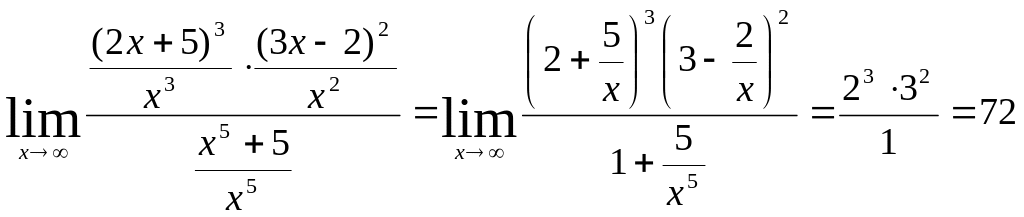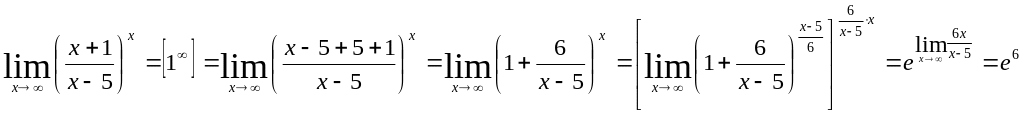Сообщения без ответов | Активные темы
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Предел со знаменателем 0
|
||||
|
При вычислении предела знаменатель превращается в 0, при этом числитель нет, как решать? Lim(((x^3)/(x-2))-(x+3)/(x^3-8)) x [math]to 2[/math]
|
|||
| Вернуться к началу |
|
|||
|
Nufus |
Заголовок сообщения: Re: Предел со знаменателем 0
|
|
Там решение получается – [math]varnothing[/math] + [math]varnothing[/math] Не понимаю, это нужно писать два решения при x 2 с минусом и x 2 с плюсом?
|
|
| Вернуться к началу |
|
|
Nufus |
Заголовок сообщения: Re: Предел со знаменателем 0
|
|
ой хотела написать – [math]infty[/math] и + [math]infty[/math]
|
|
| Вернуться к началу |
|
|
Nufus |
Заголовок сообщения: Re: Предел со знаменателем 0
|
|
привела получилась большая дробь в числителе самая большая степень = 5, в знаменателе 3, это нужно поделить на x в степени 5?
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Предел со знаменателем 0
|
|
Nufus писал(а): привела получилась большая дробь в числителе самая большая степень = 5, в знаменателе 3, это нужно поделить на x в степени 5? Нет. Получаем, что числитель стремится к числу, отличному от 0, а в знаменателе бесконечно малая функция. Дальше нужно рассматривать односторонние пределы при [math]xto 2+0[/math] и при [math]xto 2-0[/math].
|
|
| Вернуться к началу |
|
|
Nufus |
Заголовок сообщения: Re: Предел со знаменателем 0
|
|
Ясно спасибо, я так уже решила, но тогда ответ будет при 2+0 [math]infty[/math] , а при 2-0 – [math]infty[/math], правильно или числовые значения писать?
|
|
| Вернуться к началу |
|
|
Nufus |
Заголовок сообщения: Re: Предел со знаменателем 0
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Дробь со знаменателем 1
в форуме Размышления по поводу и без |
MrJoe |
23 |
714 |
24 ноя 2017, 13:08 |
|
Множество несократимых дробей с однозначным знаменателем
в форуме Алгебра |
Mikhail18 |
0 |
115 |
25 июл 2021, 21:10 |
|
Вычислить предел выражения, используя 1 замечательный предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
syncedzz |
7 |
149 |
13 окт 2022, 15:55 |
|
Решить предел. Второй замечательный предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
NuTysya |
1 |
65 |
21 фев 2023, 09:54 |
|
Решить предел. Второй замечательный предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
NuTysya |
10 |
174 |
21 фев 2023, 09:55 |
|
Предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
nata+++ |
3 |
323 |
09 май 2014, 08:26 |
|
Предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
jagdish |
4 |
283 |
05 фев 2016, 06:58 |
|
Предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
kss_13 |
4 |
533 |
01 ноя 2013, 15:56 |
|
Предел б. м. ф.
в форуме Пределы числовых последовательностей и функций, Исследования функций |
NoIdeaMan |
1 |
315 |
31 дек 2017, 06:16 |
|
Предел
в форуме Пределы числовых последовательностей и функций, Исследования функций |
nata+++ |
6 |
338 |
04 май 2014, 19:41 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью “Пределы. Понятие пределов. Вычисление пределов”.
Теперь перейдем к рассмотрению пределов с неопределенностью.
Существует группа пределов, когда x
, а функция представляет собой дробь, подставив в которую значение х =
получим неопределенность вида
.
Пример.
Необходимо вычислить предел
Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность
.
В числителе находим х в старшей степени, которая в нашем случае = 2:
То же самое проделаем со знаменателем:
Здесь также старшая степень = 2.
Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.
Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x2:
Ответ: 2/3.
Существуют также пределы с другой неопределенностью – вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к
, а к конечному числу.
Пример.
Необходимо вычислить предел .
Снова воспользуемся правилом №1 и подставим в место х число -1:
Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.
В нашем случае решаем уравнение:
Находим дискриминант:
.
Если корень не извлекается целый вероятней всего D вычислен неправильно.
Теперь находим корни уравнения:
Подставляем:
Числитель разложили.
В знаменателе у нас х + 1, что итак является простейшим множителем.
Тогда наш предел примет вид:
х + 1 красиво сокращается:
Теперь подставим вместо х значение -1 в функцию и получаем:
2*(-1) – 5 = -2 – 5 = -7
Ответ: -7.
Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:
- Предел суммы 2-х или более функций равен сумме пределов этих функций:
- Предел постоянной величины равен самой постоянной величине:
- За знак предела можно выносить постоянный коэффициент:
- Предел произведения 2-х и более функций равен произведению пределов этих функций ( последние должны существовать):
- Предел отношения 2-х функций равен отношению пределов этих функций (в том случае, если предел знаменателя
0:
- Степень функции, находящейся под знаком предела, применима к самому пределу этой функции (степень должна быть действительным числом):
На этом с вычислением пределов с неопределенностью всё. Еще в статье “Замечательные пределы: Первый и второй замечательный предел” мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.
Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Теоремы о пределах
Пусть
![]()
и
![]()
, тогда
1)
![]()
2)
![]()
3)
![]()
(при условии, что В ≠ 0)
Пусть х0
– предел переменной величины х,
то равенство
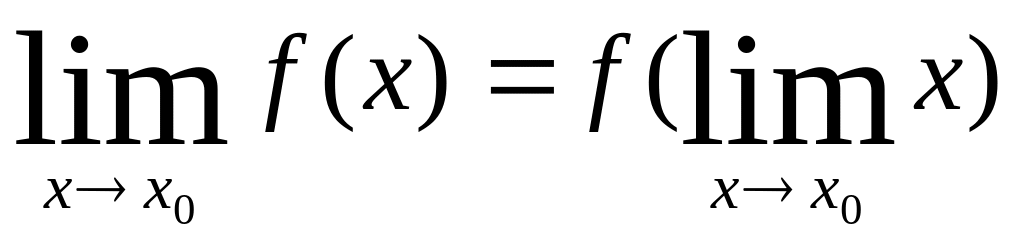
.
Эта формула выражает очень важное для
вычисления пределов правило: если
функция непрерывна, то при отыскании
ее предела можно вместо аргумента
подставить его предельное значение.
|
Пример 2. Вычислить
Решение:
|
Указанное правило
вычисления пределов нельзя применять
в следующих случаях:
-
Если
функция при х
= а не
определена; -
Если
знаменатель дроби при подстановке х
= а
оказывается равным нулю; -
Если
числитель и знаменатель дроби при
подстановке х
= а
одновременно оказываются равными нулю
или бесконечности.
В таких случаях
пределы функций находят с помощью
различных искусственных приемов.
Раскрытие
неопределенности вида
![]()
С отношением двух
бесконечно больших величин мы встречаемся
в выражениях типа
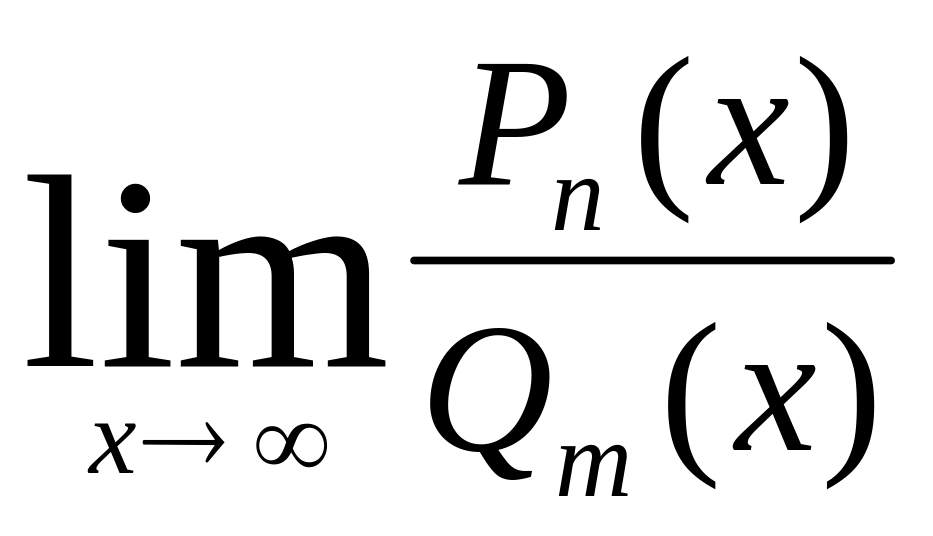
,
где Pn
(x) и Qm
(x) –
многочлены. При вычислении предела
необходимо избавиться в числителе либо
в знаменателе от бесконечно большой
величины. Для этого делим числитель и
знаменатель дроби на старшую степень
числителя (либо знаменателя).
|
Пример 3. Вычислить
Решение:
Пример 4. Вычислить
Решение:
|
Раскрытие
неопределенности
![]()
В
некоторых случаях при вычислении
пределов вида
![]()
после подстановки а
– предельного значения для х
получается неопределенность 0/ 0, т.е.
f(a)
= 0 и
q(a)
= 0.
Приемы
раскрытия неопределенности вида 0/0:
-
Пусть
f(х)
и q(х)
–
многочлены. Если f(a)
= 0 и q(a)
= 0, то
число а
является
корнем данных многочленов, т.е. в
разложении многочленов на множители
будет присутствовать сомножитель (х
– а). Сократив
дробь
на (х
– а), получаем новое выражение,
предел которого равен пределу исходного.
|
Пример 5. Вычислить Решение: |
-
Если
f(х)
и q(х) содержат иррациональность,
то избавившись от иррациональности,
нужно перейти к приему 1).
|
Пример 6. Вычислить Решение: |
-
В случае, если
неопределенность 0/0 содержит
тригонометрические функции, обычно
для ее раскрытия используется 1ый
замечательный предел.
|
|
|
Пример 7. Вычислить . Решение: |
Раскрытие
неопределенности вида
![]()
Для
ее раскрытия используется 2ой
замечательный предел.
|
|
|
Пример 8. Вычислить Решение: |
Контрольная работа
№1
Вычислите пределы:
Вариант 1
1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 2 1)
![]()
;
2)
![]()
;
3)
![]()
;4)
![]()
;
5)
![]()
.
Вариант 3 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 4 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 5 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
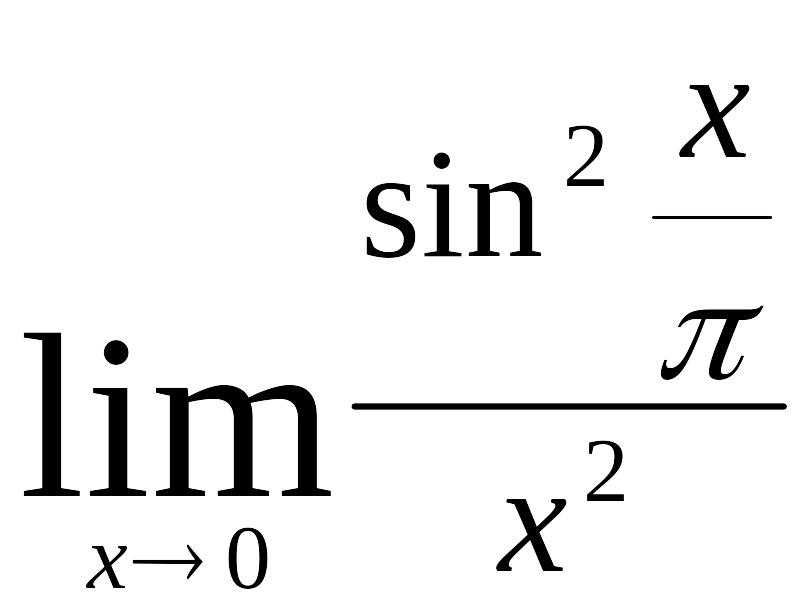
;
5)
![]()
.
Вариант 6 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)![]()
;
5)
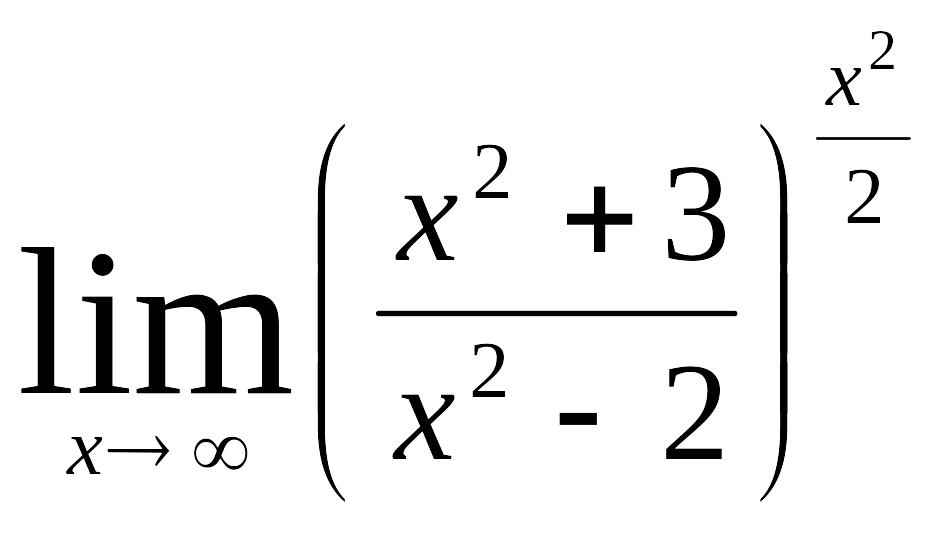
.
Вариант 7 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 8 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 9 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
![]()
;
5)
![]()
.
Вариант 10 1)
![]()
;
2)
![]()
;
3)
![]()
;
4)
;
5)

.
Вопросы для повторения:
-
Дайте определение
предела функции в точке. -
Перечислите свойства
пределов. -
Дайте определение
непрерывной функции. -
Какие пределы
называются односторонними? -
Каких видов бывают
точки разрыва функции? -
Сформулируйте и
запишите первый и второй замечательные
пределы. -
Объясните
основной метод раскрытия неопределенности( 0/0 ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
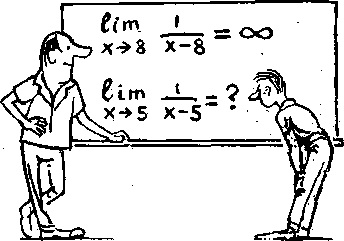
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание “чайникам” 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними – это не так страшно как кажется 🙂 |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её 🙂 Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате – это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное – возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
В предыдущей статье мы рассказывали, как правильно вычислять пределы элементарных функций. Если же мы возьмем более сложные функции, то у нас в расчетах появятся выражения с неопределенным значением. Они и называются неопределенностями.
Выделяют следующие основные виды неопределенностей:
- Деление 0 на 0 00;
- Деление одной бесконечности на другую ∞∞;
-
0, возведенный в нулевую степень 00;
- бесконечность, возведенная в нулевую степень ∞0.
Мы перечислили все основные неопределенности. Другие выражения в различных условиях могут принимать конечные или бесконечные значения, следовательно, они не могут считаться неопределенностями.
Раскрытие неопределенностей
Раскрыть неопределенность можно:
- С помощью упрощения вида функции (использование формул сокращенного умножения, тригонометрических формул, дополнительное умножение на сопряженные выражения и последующее сокращение и др. );
-
С помощью замечательных пределов;
-
С помощью правила Лопиталя;
-
Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
Всю информацию, представленную выше, можно наглядно представить в виде таблицы. С левой стороны в ней приводится вид неопределенности, с правой – подходящий метод ее раскрытия (нахождения предела). Этой таблицей очень удобно пользоваться при расчетах, связанных с нахождением пределов.
| Неопределенность | Метод раскрытия неопределенности |
| 1. Деление 0 на 0 | Преобразование и последующее упрощение выражения. Если выражение имеет вид sin(kx)kx или kxsin(kx) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений |
| 2. Деление бесконечности на бесконечность | Преобразование и упрощение выражения либо использование правила Лопиталя |
| 3. Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями | Преобразование в 00 или ∞∞ с последующим применением правила Лопиталя |
| 4. Единица в степени бесконечности | Использование второго замечательного предела |
| 5. Возведение нуля или бесконечности в нулевую степень | Логарифмирование выражения с применением равенства limx→x0ln(f(x))=lnlimx→x0f(x) |
Разберем пару задач. Эти примеры довольно простые: в них ответ получается сразу после подстановки значений и неопределенности при этом не возникает.
Вычислите предел limx→1×3+3x-1×5+3.
Решение
Выполняем подстановку значений и получаем ответ.
limx→1×3+3x-1×5+3=13+3·1-115+3=34=32
Ответ: limx→1×3+3x-1×5+3=32.
Вычислите предел limx→0(x2+2,5)1×2.
Решение
У нас есть показательно степенная функция, в основание которой нужно подставитьx=0.
(x2+2,5)x=0=02+2,5=2,5
Значит, мы можем преобразовать предел в следующее выражение:
limx→0(x2+2,5)1×2=limx→02,51×2
Теперь разберемся с показателем – степенной функцией 1×2=x-2. Заглянем в таблицу пределов для степенных функций с показателем меньше нуля и получим следующее: limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞
Таким образом, можно записать, что limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞.
Теперь берем таблицу пределов показательных функций с основаниями, большими 0, и получаем:
limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞=+∞
Ответ: limx→0(x2+2,5)1×2=+∞.
Далее мы приведем примеры решений задач на раскрытие неопределенностей с использованием метода преобразования. На практике выполнять это приходится довольно часто.
Вычислите предел limx→1×2-1x-1.
Решение
Выполняем подстановку значений.
limx→1×2-1x-1=12-11-1=00
В итоге у нас получилась неопределенность. Используем таблицу выше, чтобы выбрать метод решения. Там указано, что нужно выполнить упрощение выражения.
limx→1×2-1x-1=00=limx→1(x-1)·(x+1)x-1==limx→1(x-1)·(x+1)·(x+1)x-1=limx→1(x+1)·x-1==1+1·1-1=2·0=0
Как мы видим, упрощение привело к раскрытию неопределенности.
Ответ: limx→1×2-1x-1=0
Вычислите предел limx→3x-312-x-6+x.
Решение
Подставляем значение и получаем запись следующего вида.
limx→3x-312-x-6+x=3-312-3-6+3=09-9=00
Мы пришли к необходимости делить нуль на нуль, что является неопределенностью. Посмотрим нужный метод решения в таблице – это упрощение и преобразование выражения. Выполним дополнительное умножение числителя и знаменателя на сопряженное знаменателю выражение 12-x+6+x:
limx→3x-312-x-6+x=00=limx→3x-312-x+6+x12-x-6+x12-x+6+x
Домножение знаменателя выполняется для того, чтобы потом можно было воспользоваться формулой сокращенного умножения (разность квадратов) и выполнить сокращение.
limx→3x-312-x+6+x12-x-6+x12-x+6+x=limx→3x-312-x+6+x12-x2-6+x2=limx→3(x-3)12-x+6+x12-x-(6+x)==limx→3(x-3)12-x+6+x6-2x=limx→3(x-3)12-x+6+x-2(x-3)==limx→312-x+6+x-2=12-3+6+3-2=9+9-2=-9=-3
Как мы видим, в результате этих действий нам удалось избавиться от неопределенности.
Ответ: limx→3x-312-x-6+x=-3.
Важно отметить, что при решении подобных задач подход с использованием домножения используется очень часто, так что советуем запомнить, как именно это делается.
Вычислите предел limx→1×2+2x-33×2-5x+2.
Решение
Выполняем подстановку.
limx→1×2+2x-33×2-5x+2=12+2·1-33·12-5·1+2=00
В итоге у нас вышла неопределенность. Рекомендуемый способ решения задачи в таком случае – упрощение выражения. Поскольку при значении x, равном единице, числитель и знаменатель обращаются в 0, то мы можем разложить их на множители и потом сократить на х-1,и тогда неопределенность исчезнет.
Выполняем разложение числителя на множители:
x2+2x-3=0D=22-4·1·(-3)=16⇒x1=-2-162=-3×2=-2+162=1⇒x2+2x-3=x+3x-1
Теперь делаем то же самое со знаменателем:
3×2-5x+2=0D=-52-4·3·2=1⇒x1=5-12·3=23×2=5+12·3=1⇒3×2-5x+3=3x-23x-1
Мы получили предел следующего вида:
limx→1×2+2x-33×2-5x+2=00=limx→1x+3·x-13·x-23·x-1==limx→1x+33·x-23=1+33·1-23=4
Как мы видим, в ходе преобразования нам удалось избавиться от неопределенности.
Ответ: limx→1×2+2x-33×2-5x+2=4.
Далее нам нужно рассмотреть случаи пределов на бесконечности от степенных выражений. Если показатели этих выражений будут больше 0, то предел на бесконечности также окажется бесконечным. При этом основное значение имеет самая большая степень, а остальные можно не учитывать.
Например, limx→∞(x4+2×3-6)=limx→∞x4=∞ или limx→∞x4+4×3+21×2-115=limx→∞x45=∞.
Если под знаком предела у нас стоит дробь со степенными выражениями в числителе и знаменателе, то при x→∞ у нас возникает неопределенность вида ∞∞. Чтобы избавиться от этой неопределенности, нам нужно разделить числитель и знаменатель дроби на xmax(m,n). Приведем пример решения подобной задачи.
Вычислите предел limx→∞x7+2×5-43×7+12.
Решение
limx→∞x7+2×5-43×7+12=∞∞
Степени числителя и знаменателя равны 7. Делим их на x7 и получаем:
limx→∞x7+2×5-43×7+12=limx→∞x7+2×5-4x73x7+12×7==limx→∞1+2×2-4×73+12×7=1+2∞2-4∞73+12∞7=1+0-03+0=13
Ответ: limx→∞x7+2×5-43×7+12=13.
Вычислите предел limx→∞x8+113×2+x+1.
Решение
limx→∞x8+113×2+x+1=∞∞
Числитель имеет степень 83, а знаменатель 2. Выполним деление числителя и знаменателя на x83:
limx→∞x8+113×2+x+1=∞∞=limx→∞x8+113x83x2+x+1×83==limx→∞1+11x831x23+1×53+1×83=1+11∞31∞+1∞+1∞=1+030+0+0=10=∞
Ответ: limx→∞x8+113×2+x+1=∞.
Вычислите предел limx→∞x3+2×2-1×10+56×7+123.
Решение
limx→∞x3+2×2-1×10+56×7+123=∞∞
У нас есть числитель в степени 3 и знаменатель в степени 103. Значит, нам нужно разделить числитель и знаменатель на x103:
limx→∞x3+2×2-1×10+56×7+123=∞∞=limx→∞x3+2×2-1x103x10+56×7+123×103==limx→∞1×13+2×43-1×1031+56×3+12×103=1∞+2∞-1∞1+56∞+12∞3=0+0-01+0+03=0
Ответ: limx→∞x3+2×2-1×10+56×7+123=0.
Выводы
В случае с пределом отношений возможны три основных варианта:
-
Если степень числителя равна степени знаменателя, то предел будет равен отношению коэффициентов при старших степенях.
-
Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.
-
Если степень числителя меньше степени знаменателя, то предел будет равен нулю.
Другие методы раскрытия неопределенностей мы разберем в отдельных статьях.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта