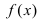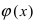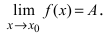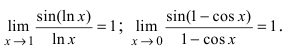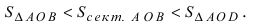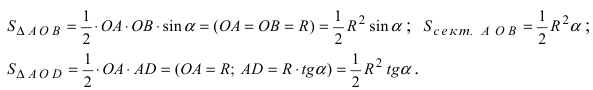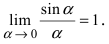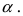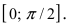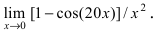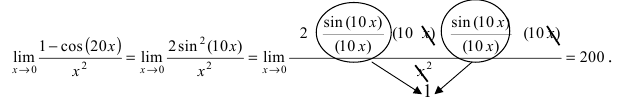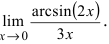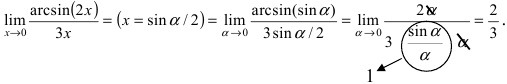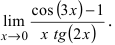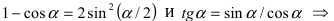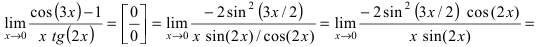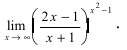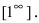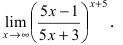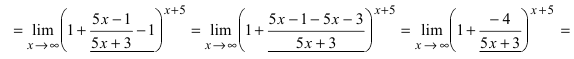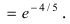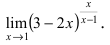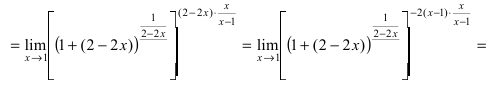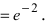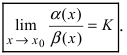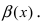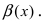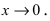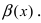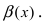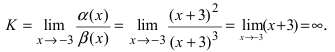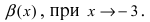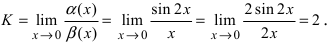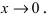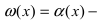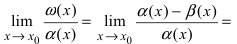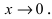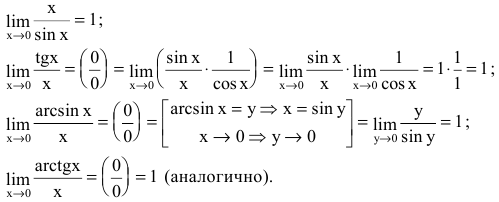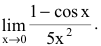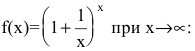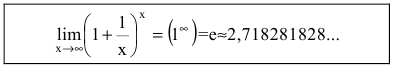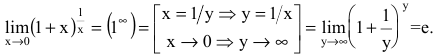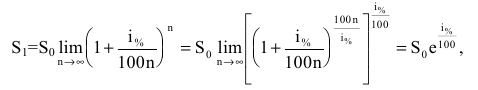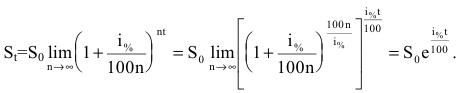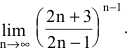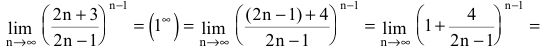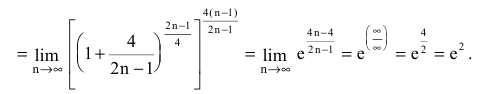Как найти предел функции используя замечательные пределы

Как найти предел функции используя замечательные пределы

Замечательные пределы

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 августа 2022 года; проверки требуют 4 правки.

Перейти к навигации
Перейти к поиску

Замеча́тельные преде́лы — термины, использующиеся в советских и российских учебниках по математическому анализу для обозначения двух широко известных математических тождеств со взятием предела:

Первый замечательный предел[править | править код]

lim _{{xto 0}}{frac {sin x}{x}}=1

Доказательство:

Sinx x limit proof.svg

Рассмотрим односторонние пределы {displaystyle lim _{xto +0}{frac {sin x}{x}}} и {displaystyle lim _{xto {displaystyle -}0}{frac {sin x}{x}}} и докажем, что они равны 1.

Рассмотрим случай {displaystyle xin left(0;{frac {pi }{2}}right)}. Отложим этот угол на единичной окружности так, чтобы его вершина совпадала с началом координат, а одна сторона совпадала с осью OX. Пусть K — точка пересечения второй стороны угла с единичной окружностью, а точка L — с касательной к этой окружности в точке {displaystyle A=left(1;0right)}. Точка H — проекция точки K на ось OX.

Очевидно, что:

{displaystyle S_{triangle OKA}<S_{sectKOA}<S_{triangle OAL}} (1)

(где {displaystyle S_{sectKOA}} — площадь сектора {displaystyle KOA})

Поскольку {displaystyle left|KHright|=sin x,,left|LAright|=operatorname {tg} x}:

{displaystyle S_{triangle OKA}={frac {1}{2}}cdot left|OAright|cdot left|KHright|={frac {1}{2}}cdot 1cdot sin x={frac {sin x}{2}}}
{displaystyle S_{sectKOA}={frac {1}{2}}cdot left|OAright|^{2}cdot x={frac {x}{2}}}
{displaystyle S_{triangle OAL}={frac {1}{2}}cdot left|OAright|cdot left|LAright|={frac {operatorname {tg} x}{2}}}

Подставляя в (1), получим:

{displaystyle {frac {sin x}{2}}<{frac {x}{2}}<{frac {operatorname {tg} x}{2}}}

Так как при {displaystyle xto +0:sin x>0,,x>0,,operatorname {tg} x>0}:

{displaystyle {frac {1}{operatorname {tg} x}}<{frac {1}{x}}<{frac {1}{sin x}}}

Умножаем на sin x:

cos x<{frac {sin x}{x}}<1

Перейдём к пределу:

{displaystyle lim _{xto +0}cos xleqslant lim _{xto +0}{frac {sin x}{x}}leqslant 1}
{displaystyle 1leqslant lim _{xto +0}{frac {sin x}{x}}leqslant 1}
{displaystyle lim _{xto +0}{frac {sin x}{x}}=1}

Найдём левый односторонний предел (так как функция четна, в этом нет необходимости, достаточно доказать это для правого предела):

{displaystyle lim _{xto -0}{frac {sin x}{x}}=left[{begin{matrix}u=-x\x=-u\uto +0\xto -0end{matrix}}right]=lim _{uto +0}{frac {sin(-u)}{-u}}=lim _{uto +0}{frac {-sin(u)}{-u}}=lim _{uto +0}{frac {sin(u)}{u}}=1}

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия:

  • {displaystyle lim _{xto 0}{frac {operatorname {tg} x}{x}}=1}
  • {displaystyle lim _{xto 0}{frac {operatorname {arcsin} x}{x}}=1}
  • {displaystyle lim _{xto 0}{frac {operatorname {arctg} x}{x}}=1}
  • lim _{{xto 0}}{frac {1-cos x}{{frac {x^{2}}{2}}}}=1

Второй замечательный предел[править | править код]

lim _{{xto infty }}left(1+{frac {1}{x}}right)^{x}=e или lim _{{xto 0}}left(1+xright)^{{1/x}}=e

Доказательство существования второго замечательного предела:

Доказательство для натуральных значений x

blacktriangleleft  Докажем вначале теорему для случая последовательности x_{{n}}=left(1+{frac {1}{n}}right)^{n}; nin {mathbb N}

По формуле бинома Ньютона: (a+b)^{n}=a^{n}~+~{frac {n}{1}}cdot a^{{n-1}}cdot b~+~{frac {n(n-1)}{1cdot 2}}cdot a^{{n-2}}cdot b^{2}~+~...~+~{frac {n(n-1)(n-2)...(n-(n-1))}{1cdot 2cdot 3cdot ...cdot n}}cdot b^{n}; nin {mathbb N}

Полагая a=1;~b={frac {1}{n}}, получим:

left(1+{frac {1}{n}}right)^{n}=1~+~{frac {n}{1}}cdot {frac {1}{n}}~+~{frac {n(n-1)}{1cdot 2}}cdot {frac {1}{n^{2}}}~+~{frac {n(n-1)(n-2)}{1cdot 2cdot 3}}cdot {frac {1}{n^{3}}}~+~...~+~{frac {n(n-1)(n-2)...(n-(n-1))}{1cdot 2cdot 3cdot ...cdot n}}cdot {frac {1}{n^{n}}}=
{displaystyle =1~+~1~+~{frac {1}{1cdot 2}}cdot left(1-{frac {1}{n}}right)~+~{frac {1}{1cdot 2cdot 3}}cdot left(1-{frac {1}{n}}right)cdot left(1-{frac {2}{n}}right)~+~...~+~{frac {1}{1cdot 2cdot 3cdot ...cdot n}}cdot left(1-{frac {1}{n}}right)cdot left(1-{frac {2}{n}}right)cdot ...cdot left(1-{frac {n-1}{n}}right)}       (1)

С увеличением n число положительных слагаемых в правой части равенства (1) увеличивается. Кроме того, при увеличении n число {frac {1}{n}} убывает, поэтому величины left(1-{frac {1}{n}}right),left(1-{frac {2}{n}}right),... возрастают. Поэтому последовательность {x_{{n}}}=left{left(1+{frac {1}{n}}right)^{n}right}; nin {mathbb N} — возрастающая, при этом

{displaystyle left(1+{frac {1}{n}}right)^{n}geq 2,nin mathbb {N} }      (2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

left(1+{frac {1}{n}}right)^{n}<1+1+{frac {1}{1cdot 2}}+{frac {1}{1cdot 2cdot 3}}~+~...~+~{frac {1}{1cdot 2cdot 3cdot ...cdot n}}

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

left(1+{frac {1}{n}}right)^{n}<1+left(1+{frac {1}{2}}+{frac {1}{2^{2}}}+...+{frac {1}{2^{{n-1}}}}right).

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

1+{frac {1}{2}}+{frac {1}{2^{2}}}+...+{frac {1}{2^{{n-1}}}}={frac {1cdot left(1-({frac {1}{2}})^{n}right)}{1-{frac {1}{2}}}}=2cdot left(1-{frac {1}{2^{n}}}right)<2.

Поэтому {displaystyle left(1+{frac {1}{n}}right)^{n}<1+2=3}      (3).

Итак, последовательность ограничена сверху, при этом forall nin {mathbb N} выполняются неравенства (2) и (3):   {displaystyle 2leq left(1+{frac {1}{n}}right)^{n}<3}.

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность x_{{n}}=left(1+{frac {1}{n}}right)^{n}, nin {mathbb N} монотонно возрастает и ограничена, значит имеет предел, обозначаемый буквой e. Т.е.
lim _{{nto infty }}left(1+{frac {1}{n}}right)^{n}=e blacktriangleright

blacktriangleleft   Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что
lim _{{xto infty }}left(1+{frac {1}{x}}right)^{x}=e; xin {mathbb R}. Рассмотрим два случая:

1. Пусть xrightarrow +infty . Каждое значение x заключено между двумя положительными целыми числами: nleqslant x<n+1, где {displaystyle n=[x]} — это целая часть x.

Отсюда следует: {frac {1}{n+1}}<{frac {1}{x}}leqslant {frac {1}{n}}~~Longleftrightarrow ~~1+{frac {1}{n+1}}<1+{frac {1}{x}}leqslant 1+{frac {1}{n}}, поэтому
{displaystyle left(1+{frac {1}{n+1}}right)^{n}<left(1+{frac {1}{x}}right)^{x}leqslant left(1+{frac {1}{n}}right)^{n+1}}.
Если xrightarrow +infty , то n rightarrow infty. Поэтому, согласно пределу lim _{{nto infty }}left(1+{frac {1}{n}}right)^{n}=e, имеем:
lim _{{nto infty }}left(1+{frac {1}{n+1}}right)^{n}={frac {lim limits _{{nto infty }}(1+{frac {1}{n+1}})^{{n+1}}}{lim limits _{{nto infty }}left(1+{frac {1}{n+1}}right)}}={frac {e}{1}}=e
lim _{{nto infty }}left(1+{frac {1}{n}}right)^{{n+1}}=lim _{{nto infty }}left(1+{frac {1}{n}}right)^{n}cdot lim _{{nto infty }}left(1+{frac {1}{n}}right)=ecdot 1=e.
По признаку (о пределе промежуточной функции) существования пределов lim _{{xto +infty }}left(1+{frac {1}{x}}right)^{x}=e.

2. Пусть xto -infty . Сделаем подстановку -x=t, тогда

lim _{{xto -infty }}left(1+{frac {1}{x}}right)^{x}=lim _{{tto +infty }}left(1-{frac {1}{t}}right)^{{-t}}=lim _{{tto +infty }}left({frac {t}{t-1}}right)^{t}=lim _{{tto +infty }}left(1+{frac {1}{t-1}}right)^{t}=
=lim _{{tto +infty }}left(1+{frac {1}{t-1}}right)^{{t-1}}cdot lim _{{tto +infty }}left(1+{frac {1}{t-1}}right)^{1}=ecdot 1=e.

Очевидно, из двух этих случаев вытекает, что lim _{{xto infty }}left(1+{frac {1}{x}}right)^{x}=e для вещественного x.   
blacktriangleright

Следствия

  1. lim _{{uto 0}}(1+u)^{{frac {1}{u}}}=e
  2. {displaystyle lim _{xto infty }left(1+{frac {k}{x}}right)^{x}=e^{k}}
  3. lim _{{xto 0}}{frac {ln(1+x)}{x}}=1
  4. lim _{{xto 0}}{frac {e^{x}-1}{x}}=1
  5. lim _{{xto 0}}{frac {a^{x}-1}{xln a}}=1 для a>0, {displaystyle aneq 1}
  6. lim _{{xto 0}}{frac {(1+x)^{alpha }-1}{alpha x}}=1
  7. {displaystyle lim _{xto infty }left(1-{frac {k}{x}}right)^{x}=e^{-k}}

Применение[править | править код]

Замечательные пределы и их следствия используются при раскрытии неопределённостей для нахождения других пределов.

См. также[править | править код]

  • Список пределов

Литература[править | править код]

  • Ильин В. А., Позняк Э. Г. Основы математического анализа (в двух частях). — М.: Физматлит, 2005. — С. 24-25. — ISBN 5-9221-0536-1.

Ссылки[править | править код]

  • Замечательные пределы на Wikia science Математика Архивная копия от 22 сентября 2018 на Wayback Machine
Источник

Содержание:

Замечательные пределы

Сравнение бесконечно малых функций

Признак существования предела (теорема о 2-х милиционерах)

Теорема: Если значения функции Замечательные пределы - определение и вычисление с примерами решения

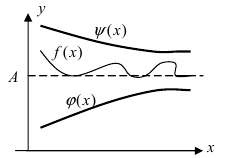
значениями функций Замечательные пределы - определение и вычисление с примерами решения

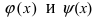
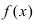
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции Замечательные пределы - определение и вычисление с примерами решения стягиваются к прямой у=А, то они “вынуждают” функцию Замечательные пределы - определение и вычисление с примерами решения также приближаться к той же самой прямой (“куда идут два милиционера, ведущие арестованного, туда идет и сам арестованный”). Замечательные пределы - определение и вычисление с примерами решения

Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.

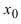
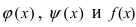
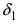
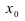
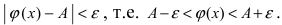
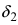
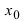
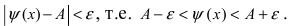
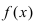
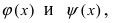
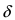
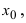
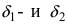
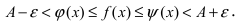
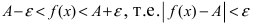
Доказательство: Пусть Замечательные пределы - определение и вычисление с примерами решения – точка сгущения для функций Замечательные пределы - определение и вычисление с примерами решения в общей области определения. Это означает, что в некоторой Замечательные пределы - определение и вычисление с примерами решения-окрестности точки Замечательные пределы - определение и вычисление с примерами решениявыполняется неравенство Замечательные пределы - определение и вычисление с примерами решения В Замечательные пределы - определение и вычисление с примерами решения-окрестности точки Замечательные пределы - определение и вычисление с примерами решения выполняется неравенство Замечательные пределы - определение и вычисление с примерами решения Так как значения функции Замечательные пределы - определение и вычисление с примерами решения заключены между значениями функций Замечательные пределы - определение и вычисление с примерами решения то в некоторой Замечательные пределы - определение и вычисление с примерами решения-окрестности точки Замечательные пределы - определение и вычисление с примерами решения меньшей из Замечательные пределы - определение и вычисление с примерами решения-окрестностей будет выполняться неравенство Замечательные пределы - определение и вычисление с примерами решения Отсюда следует, что выполняется неравенство Замечательные пределы - определение и вычисление с примерами решения или Замечательные пределы - определение и вычисление с примерами решения

Первый замечательный предел

Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 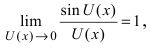Замечательные пределы - определение и вычисление с примерами решения и называется первым замечательным пределом.

Пример:

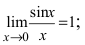
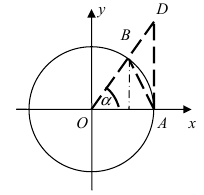
Пределы являются первыми замечательными пределами Замечательные пределы - определение и вычисление с примерами решения Замечательные пределы - определение и вычисление с примерами решения

Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 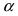Замечательные пределы - определение и вычисление с примерами решенияв первой координатной четверти и сравним площади трех фигур: треугольник АОВ, сектор АОВ и треугольник AOD (Рис. 63): Замечательные пределы - определение и вычисление с примерами решения

Рис. 63. Иллюстрация вывода формулы первого замечательного предела.

Из рисунка видно, что площади указанных фигу р связаны соотношением:

Замечательные пределы - определение и вычисление с примерами решения

Вычислим эти площади Замечательные пределы - определение и вычисление с примерами решения

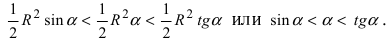
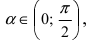
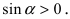
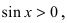
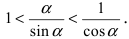
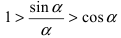
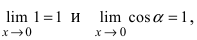
Следовательно, вышеприведенное неравенство приводится к виду Замечательные пределы - определение и вычисление с примерами решения В силу того, что Замечательные пределы - определение и вычисление с примерами решения получаем Замечательные пределы - определение и вычисление с примерами решения Разделим полученное неравенство на Замечательные пределы - определение и вычисление с примерами решения знак всех неравенств не изменится: Замечательные пределы - определение и вычисление с примерами решения Переходя к обратным неравенствам, Замечательные пределы - определение и вычисление с примерами решения или в силу того, что Замечательные пределы - определение и вычисление с примерами решения то по теореме о 2-х милиционерах Замечательные пределы - определение и вычисление с примерами решения

Аналогично проводится доказательство для любого значения угла Замечательные пределы - определение и вычисление с примерами решения

Таким образом, наличие в пределе, сводящемся к неопределенности 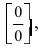Замечательные пределы - определение и вычисление с примерами решения тригонометрических функции может указывать на первый замечательный предел.

При вычислении первого замечательного предела используют следующие формулы:

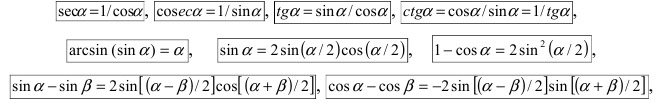
Замечательные пределы - определение и вычисление с примерами решения а также следующие таблицы:

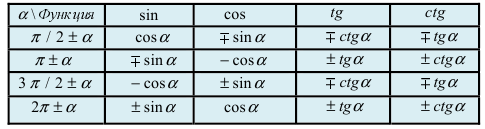
Табл. 1. Значения синуса и косинуса на интервале Замечательные пределы - определение и вычисление с примерами решенияЗамечательные пределы - определение и вычисление с примерами решения

Табл. 2. Формулы приведения.

Замечательные пределы - определение и вычисление с примерами решения

Пример:

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

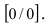
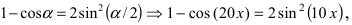
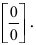
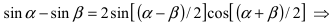
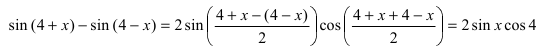
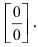
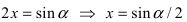
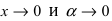
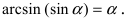
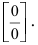
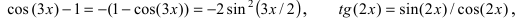
При подстановке предельной величины переменной х имеем неопределенность Замечательные пределы - определение и вычисление с примерами решения Воспользуемся формулой Замечательные пределы - определение и вычисление с примерами решения и преобразуем данный предел следующим образом: Замечательные пределы - определение и вычисление с примерами решения

Пример:

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

При подстановке предельного значения переменной х имеем неопределённость Замечательные пределы - определение и вычисление с примерами решения Воспользуемся формулой Замечательные пределы - определение и вычисление с примерами решения Замечательные пределы - определение и вычисление с примерами решения тогда данный предел равен:Замечательные пределы - определение и вычисление с примерами решения

Пример:

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

При подстановке предельного значения переменной х имеем неопределённость Замечательные пределы - определение и вычисление с примерами решения Введём замену Замечательные пределы - определение и вычисление с примерами решения (при Замечательные пределы - определение и вычисление с примерами решения) и воспользуемся следующей формулой Замечательные пределы - определение и вычисление с примерами решения Предел преобразуется к виду:

Замечательные пределы - определение и вычисление с примерами решения

Пример:

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

При подстановке предельного значения переменной х имеем неопределённость Замечательные пределы - определение и вычисление с примерами решения Воспользуемся формулами Замечательные пределы - определение и вычисление с примерами решенияЗамечательные пределы - определение и вычисление с примерами решения получим: Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения

Число e и натуральные логарифмы. Второй замечательный предел

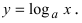
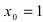
Рассмотрим логарифмическую функцию Замечательные пределы - определение и вычисление с примерами решения Выбирая различные значения основания, будем вычислять тангенсы угла наклона касательной к графику этой функции в точке Замечательные пределы - определение и вычисление с примерами решения(см. график логарифмической функции в Лекции № 22).

Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.

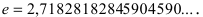
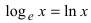
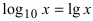
Основанием натурального логарифма является число Замечательные пределы - определение и вычисление с примерами решения Это число трансцедентное, т.е. не является решением ни одного алгебраического уравнения. Установим связь между натуральными Замечательные пределы - определение и вычисление с примерами решения и десятичными Замечательные пределы - определение и вычисление с примерами решения логарифмами: Замечательные пределы - определение и вычисление с примерами решения

Определение: Вторым замечательным пределом называется предельное равенство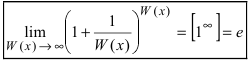Замечательные пределы - определение и вычисление с примерами решения (первая форма)

или

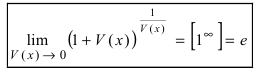
Замечательные пределы - определение и вычисление с примерами решения(вторая форма).

Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 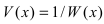Замечательные пределы - определение и вычисление с примерами решения с учетом теоремы о связи бесконечно большой функции с бесконечно малой функцией.

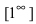
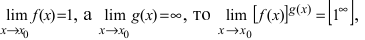
Замечание: Наличие неопределенности Замечательные пределы - определение и вычисление с примерами решения указывает на второй замечательный предел, т.е. если пределы функций Замечательные пределы - определение и вычисление с примерами решения что указывает на второй замечательный предел.

Пример:

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

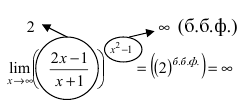
При подстановке предельного значения переменной х не имеем неопределенности Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения – не второй замечательный предел.

Пример:

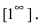
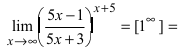
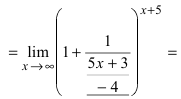
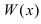
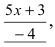
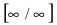
Найти lim Замечательные пределы - определение и вычисление с примерами решения

Решение:

При подстановке предельного значения переменной х имеем неопределенность Замечательные пределы - определение и вычисление с примерами решения Проведём преобразование подлимитной функции: Замечательные пределы - определение и вычисление с примерами решения( – первая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела) Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения (роль функции Замечательные пределы - определение и вычисление с примерами решения играет выражение Замечательные пределы - определение и вычисление с примерами решения возведем круглую скобку в эту степень, а за квадратной скобкой возведем в обратную степень для тождественности проводимых преобразований, получим) =

Замечательные пределы - определение и вычисление с примерами решения = (выражение в квадратных скобках стремится к числу е, а показатель степени – к числу -4/5 (см. раскрытие неопределённости Замечательные пределы - определение и вычисление с примерами решения для полиномов примере из пункта Вычисление пределов и раскрытие неопределенностей поэтому окончательный ответ имеет вид)= Замечательные пределы - определение и вычисление с примерами решения

Пример:

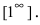
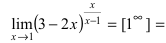
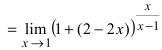
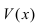
Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

При подстановке предельного значения переменной х имеем неопределенность Замечательные пределы - определение и вычисление с примерами решения Проведём преобразование подлимитной функции:

Замечательные пределы - определение и вычисление с примерами решения (вторая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела)= Замечательные пределы - определение и вычисление с примерами решения = (роль функции Замечательные пределы - определение и вычисление с примерами решения играет выражение (2-2х))= Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения=(выражение в квадратных скобках стремится к числу е, а показатель степени – к числу -2 (подставить в показатель степени вместо переменной х ее предельное значение 1), поэтому окончательный ответ имеет вид) Замечательные пределы - определение и вычисление с примерами решения

  • Заказать решение задач по высшей математике

Сравнение бесконечно малых функций

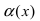
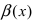
Сравнить две бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения и Замечательные пределы - определение и вычисление с примерами решения означает вычислить предел Замечательные пределы - определение и вычисление с примерами решения

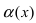
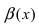
Определение: Если предел К не существует, то бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения и Замечательные пределы - определение и вычисление с примерами решенияназываются несравнимыми.

Пример:

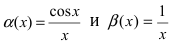
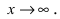
ПустьЗамечательные пределы - определение и вычисление с примерами решения – две бесконечно малые функции при Замечательные пределы - определение и вычисление с примерами решения Доказать, что эти бесконечно малые функции несравнимые.

Решение:

Для доказательства вычислим предел 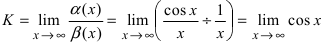Замечательные пределы - определение и вычисление с примерами решения -данный предел не существует, так как нельзя указать предельное значение для подлимитной функции cosx на бесконечности.

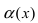
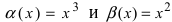
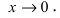
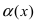
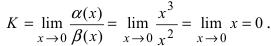
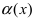
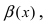
Определение: Если предел К равен нулю, то бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения называется бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения

Пример:

Пусть Замечательные пределы - определение и вычисление с примерами решения – две бесконечно малые функции при Замечательные пределы - определение и вычисление с примерами решения Доказать, что бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения

Решение:

Для доказательства вычислим предел Замечательные пределы - определение и вычисление с примерами решения Следовательно, бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решенияпри Замечательные пределы - определение и вычисление с примерами решения

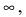
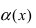
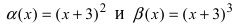
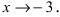
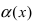
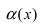
Определение: Если предел К равен Замечательные пределы - определение и вычисление с примерами решения то бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения называется бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения

Пример:

Пусть Замечательные пределы - определение и вычисление с примерами решения – две бесконечно малые функции при Замечательные пределы - определение и вычисление с примерами решения Доказать, что бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения

Решение:

Для доказательства вычислим предел Замечательные пределы - определение и вычисление с примерами решения

Следовательно, бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решения

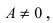
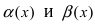
Определение: Если предел К равен конечному числу Замечательные пределы - определение и вычисление с примерами решения то бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения называются бесконечно малыми функциями одного порядка малости.

Пример:

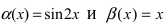
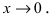
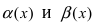
Пусть Замечательные пределы - определение и вычисление с примерами решения – две бесконечно малые функции при Замечательные пределы - определение и вычисление с примерами решения Доказать, что бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения являются бесконечно малыми функциями одного порядка малости.

Решение:

Для доказательства вычислим предел Замечательные пределы - определение и вычисление с примерами решения

Следовательно, бесконечно малые функции 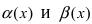Замечательные пределы - определение и вычисление с примерами решения являются бесконечно малыми функциями одного порядка малости при Замечательные пределы - определение и вычисление с примерами решения

Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.

Пример:

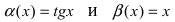
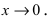
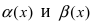
Пусть Замечательные пределы - определение и вычисление с примерами решения – две бесконечно малые функции при Замечательные пределы - определение и вычисление с примерами решения Доказать, что бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения являются эквивалентными.

Решение:

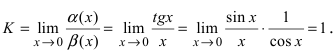
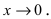
Вычислим предел Замечательные пределы - определение и вычисление с примерами решения Следовательно, бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения являются эквивалентными при Замечательные пределы - определение и вычисление с примерами решения Рассмотрим признак эквивалентности бесконечно малых функций.

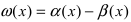
Теорема: Для того чтобы бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения были эквивалентными, необходимо и достаточно, чтобы разность бесконечно малых функций Замечательные пределы - определение и вычисление с примерами решения была бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения.

Доказательство:

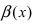
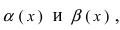
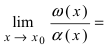
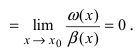
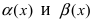
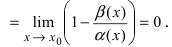
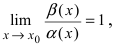
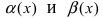
1. Необходимость. Пусть бесконечно малая функция Замечательные пределы - определение и вычисление с примерами решенияЗамечательные пределы - определение и вычисление с примерами решенияявляется бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения т.е. пределы Замечательные пределы - определение и вычисление с примерами решения Замечательные пределы - определение и вычисление с примерами решения Докажем, что бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения эквивалентны. Преобразуем первый из этих пределов: Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения Отсюда следует, что Замечательные пределы - определение и вычисление с примерами решения т.е. бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения эквивалентны. Аналогично преобразуется второй пре- дел.

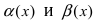
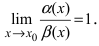
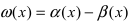
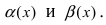
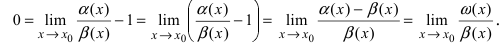
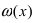
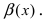
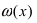
2. Достаточность. Пусть бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения являются эквивалентными, т.е. Замечательные пределы - определение и вычисление с примерами решения Докажем, что разность двух бесконечно малых функций Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения Преобразуем данный предел следующим образом: Замечательные пределы - определение и вычисление с примерами решения Отсюда следует, что функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения Аналогично доказывается, что функция Замечательные пределы - определение и вычисление с примерами решения является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции Замечательные пределы - определение и вычисление с примерами решения

Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 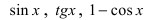Замечательные пределы - определение и вычисление с примерами решения эквивалентны функции х при Замечательные пределы - определение и вычисление с примерами решения

—вышмат

Замечательные пределы

Первый замечательный предел

Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:

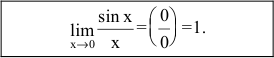
Замечательные пределы - определение и вычисление с примерами решения Следовательно,

Замечательные пределы - определение и вычисление с примерами решения

Пример №25

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

Применим первый замечательный предел:Замечательные пределы - определение и вычисление с примерами решения

Второй замечательный предел

Числом е называется предел функции

Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения

(Для запоминания: 2<е<3; 1828 – год рождения Л.Н. Толстого) Следовательно, Замечательные пределы - определение и вычисление с примерами решения

Задача о непрерывном начислении процентов

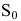
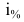
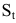
Первоначальный вклад в банк составил Замечательные пределы - определение и вычисление с примерами решения денежных единиц. Банк выплачивает ежегодно Замечательные пределы - определение и вычисление с примерами решения годовых. Необходимо найти размер вклада Замечательные пределы - определение и вычисление с примерами решения через t лет.

Решение:

Размер вклада будет увеличиваться ежегодно в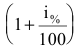Замечательные пределы - определение и вычисление с примерами решения раз и

через t лет составит 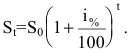Замечательные пределы - определение и вычисление с примерами решения Если же начислять проценты n раз в году,

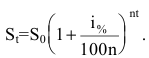
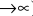
то будущая сумма составит Замечательные пределы - определение и вычисление с примерами решения Предположим, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365), каждый час (n=8760) и, наконец, непрерывно (nЗамечательные пределы - определение и вычисление с примерами решения). Тогда за год размер вклада составит:Замечательные пределы - определение и вычисление с примерами решения

а за t лет: Замечательные пределы - определение и вычисление с примерами решения

Пример №26

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

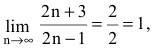
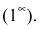
Т.к. Замечательные пределы - определение и вычисление с примерами решения имеем неопределенность вида Замечательные пределы - определение и вычисление с примерами решения Для ее раскрытия воспользуемся вторым замечательным пределом, выделив предварительно у дроби целую часть:

Замечательные пределы - определение и вычисление с примерами решения

Замечательные пределы - определение и вычисление с примерами решения

Пример №27

Найти Замечательные пределы - определение и вычисление с примерами решения

Решение:

Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:

Замечательные пределы - определение и вычисление с примерами решения

  • Непрерывность функций и точки разрыва
  • Точки разрыва и их классификация
  • Дифференциальное исчисление
  • Исследование функций с помощью производных
  • Скалярное произведение и его свойства
  • Векторное и смешанное произведения векторов
  • Преобразования декартовой системы координат
  • Бесконечно малые и бесконечно большие функции
Источник

Замечательные пределы

Термин “замечательный предел” широко используется в учебниках и методических пособиях для обозначения важных тождеств, которые помогают существенно упростить работу по нахождению пределов.

Но чтобы суметь привести свой предел к замечательному, нужно к нему хорошенько приглядеться, ведь они встречаются не в прямом виде, а часто в виде следствий, снабженные дополнительными слагаемыми и множителями. Впрочем, сначала теория, потом примеры, и все у вас получится!

Другие решенные примеры с пределами

Первый замечательный предел

Понравилось? Добавьте в закладки

Первый замечательный предел записывается так (неопределенность вида $0/0$):

$$
limlimits_{xto 0}frac{sin x}{x}=1.
$$

Следствия из первого замечательного предела

$$
limlimits_{xto 0}frac{x}{sin x}=1.
$$
$$
limlimits_{xto 0}frac{sin (ax)}{sin (bx)}=frac{a}{b}.
$$
$$
limlimits_{xto 0}frac{tan x}{x}=1.
$$
$$
limlimits_{xto 0}frac{arcsin x}{x}=1.
$$
$$
limlimits_{xto 0}frac{arctan x}{x}=1.
$$
$$
limlimits_{xto 0}frac{1-cos x}{x^2/2}=1.
$$

Примеры решений: 1 замечательный предел

Пример 1. Вычислить предел $$limlimits_{xto 0}frac{sin 3x}{8x}.$$

Решение. Первый шаг всегда одинаковый – подставляем предельное значение $x=0$ в функцию и получаем:

$$left[ frac{sin 0}{0} right] = left[frac{0}{0}right].$$

Получили неопределенность вида $left[frac{0}{0}right]$, которую следует раскрыть. Если посмотреть внимательно, исходный предел очень похож на первый замечательный, но не совпадает с ним. Наша задача – довести до похожести. Преобразуем так – смотрим на выражение под синусом, делаем такое же в знаменателе (условно говоря, умножили и поделили на $3x$), дальше сокращаем и упрощаем:

$$
limlimits_{xto 0}frac{sin 3x}{8x} =
limlimits_{xto 0}frac{sin 3x}{3x}frac{3x}{8x}=limlimits_{xto 0}frac{sin (3x)}{3x}frac{3}{8}=frac{3}{8}.
$$

Выше как раз и получился первый замечательный предел:
$$
limlimits_{xto 0}frac{sin (3x)}{3x} = limlimits_{yto 0}frac{sin (y)}{y}=1, text{ сделали условную замену } y=3x.
$$
Ответ: $3/8$.

Пример 2. Вычислить предел $$limlimits_{xto 0}frac{1-cos 3x}{tan 2xcdot sin 4x}.$$

Решение. Подставляем предельное значение $x=0$ в функцию и получаем:

$$left[ frac{1-cos 0}{tan 0cdot sin 0}right] =left[ frac{1-1}{ 0cdot 0}right] = left[frac{0}{0}right].$$

Получили неопределенность вида $left[frac{0}{0}right]$. Преобразуем предел, используя в упрощении первый замечательный предел (три раза!):

$$limlimits_{xto 0}frac{1-cos 3x}{tan 2xcdot sin 4x} = limlimits_{xto 0}frac{ 2 sin^2 (3x/2)}{sin 2xcdot sin 4x}cdot cos 2x =
$$
$$ = 2limlimits_{xto 0}frac{ sin^2 (3x/2)}{(3x/2)^2}
cdot frac{ 2x}{sin 2x} cdot frac{ 4x}{ sin 4x}cdot frac{ (3x/2)^2}{ 2x cdot 4x} cdot cos 2x =
$$
$$
=2limlimits_{xto 0} 1 cdot 1 cdot 1 cdot frac{ (9/4)x^2}{ 8x^2} cdot cos 2x= 2 cdot frac{ 9}{ 32} limlimits_{xto 0} cos 2x=frac{9}{16}.
$$

Ответ: $9/16$.

Пример 3. Найти предел $$limlimits_{xto 0}frac{sin (2x^3+3x)}{5x-x^5}.$$

Решение. А что если под тригонометрической функцией сложное выражение? Не беда, и тут действуем аналогично. Сначала проверим тип неопределенности, подставляем $x=0$ в функцию и получаем:

$$left[ frac{sin (0+0)}{0-0}right] = left[frac{0}{0}right].$$

Получили неопределенность вида $left[frac{0}{0}right]$. Умножим и поделим на $2x^3+3x$:

$$
limlimits_{xto 0}frac{sin (2x^3+3x)}{5x-x^5}=limlimits_{xto 0}frac{sin (2x^3+3x)}{(2x^3+3x)} cdot frac{2x^3+3x}{5x-x^5}=limlimits_{xto 0} 1 cdot frac{2x^3+3x}{5x-x^5}= left[frac{0}{0}right] =
$$

Снова получили неопределенность, но в этом случае это просто дробь. Сократим на $x$ числитель и знаменатель:

$$
=limlimits_{xto 0} frac{2x^2+3}{5-x^4}= left[frac{0+3}{5-0}right] =frac{3}{5}.
$$

Ответ: $3/5$.

Второй замечательный предел

Второй замечательный предел записывается так (неопределенность вида $1^infty$):

$$
limlimits_{xto infty} left( 1+frac{1}{x}right)^{x}=e, quad text{или} quad limlimits_{xto 0} left( 1+xright)^{1/x}=e.
$$

Следствия второго замечательного предела

$$
limlimits_{xto infty} left( 1+frac{a}{x}right)^{bx}=e^{ab}.
$$
$$
limlimits_{xto 0}frac{ln (1+x)}{x}=1.
$$
$$
limlimits_{xto 0}frac{e^x -1}{x}=1.
$$
$$
limlimits_{xto 0}frac{a^x-1}{x ln a}=1, a>0, a ne 1.
$$
$$
limlimits_{xto 0}frac{(1+x)^{a}-1}{ax}=1.
$$

Примеры решений: 2 замечательный предел

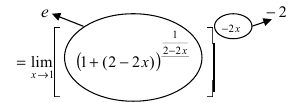
Пример 4. Найти предел $$limlimits_{xto infty}left( 1-frac{2}{3x}right)^{x+3}.$$

Решение. Проверим тип неопределенности, подставляем $x=infty$ в функцию и получаем:

$$left[ left( 1-frac{2}{infty}right)^{infty} right] = left[1^{infty}right].$$

Получили неопределенность вида $left[1^{infty}right]$. Предел можно свести к второму замечательному. Преобразуем:

$$
limlimits_{xto infty}left( 1-frac{2}{3x}right)^{x+3} = limlimits_{xto infty}left( 1+frac{1}{(-3x/2)}right)^{frac{-3x/2}{-3x/2}(x+3)}=
$$
$$
= limlimits_{xto infty}left(left( 1+frac{1}{(-3x/2)}right)^{(-3x/2)}right)^frac{x+3}{-3x/2}=
$$

Выражение в скобках фактически и есть второй замечательный предел $limlimits_{tto infty} left( 1+frac{1}{t}right)^{t}=e$, только $t=-3x/2$, поэтому

$$
= limlimits_{xto infty}left(eright)^frac{x+3}{-3x/2}= limlimits_{xto infty}e^frac{1+3/x}{-3/2}=e^{-2/3}.
$$

Ответ: $e^{-2/3}$.

Пример 5. Найти предел $$limlimits_{xto infty}left( frac{x^3+2x^2+1}{x^3+x-7}right)^{x}.$$

Решение. Подставляем $x=infty$ в функцию и получаем неопределенность вида $left[ frac{infty}{infty}right]$. А нам нужно $left[1^{infty}right]$. Поэтому начнем с преобразования выражения в скобках:

$$
limlimits_{xto infty}left( frac{x^3+2x^2+1}{x^3+x-7}right)^{x} = limlimits_{xto infty}left( frac{x^3+(x-7)-(x-7)+2x^2+1}{x^3+x-7}right)^{x} = limlimits_{xto infty}left(frac{(x^3+x-7)+(-x+7+2x^2+1)}{x^3+x-7}right)^{x} =
$$
$$
= limlimits_{xto infty}left(1+frac{2x^2-x+8}{x^3+x-7}right)^{x} = limlimits_{xto infty}left(left(1+frac{2x^2-x+8}{x^3+x-7}right)^{frac{x^3+x-7}{2x^2-x+8}}right)^{x frac{2x^2-x+8}{x^3+x-7}}=
$$

Выражение в скобках фактически и есть второй замечательный предел $limlimits_{tto infty} left( 1+frac{1}{t}right)^{t}=e$, только $t=frac{x^3+x-7}{2x^2-x+8} to infty$, поэтому

$$
= limlimits_{xto infty}left(eright)^{x frac{2x^2-x+8}{x^3+x-7}}= limlimits_{xto infty}e^{ frac{2x^2-x+8}{x^2+1-7/x}}= limlimits_{xto infty}e^{ frac{2-1/x+8/x^2}{1+1/x^2-7/x^3}}=e^{2}.
$$

Ответ: $e^{2}$.

Трудности с пределами? Поможем недорого и подробно

Дополнительная информация

  • Почему стоит заказать в МатБюро?
  • Другие примеры решений пределов
  • Контрольные по пределам на заказ
Источник

Первый замечательный предел

Первым замечательным пределом именуют следующее равенство:

$$
begin{equation}
lim_{alphato{0}}frac{sinalpha}{alpha}=1
end{equation}
$$

Так как при $alphato{0}$ имеем $sinalphato{0}$, то говорят, что первый замечательный предел раскрывает неопределённость вида $frac{0}{0}$. Вообще говоря, в формуле (1) вместо переменной $alpha$ под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:

  1. Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида $frac{0}{0}$.
  2. Выражения под знаком синуса и в знаменателе совпадают.

Часто используются также следствия из первого замечательного предела:

$$
begin{equation}
lim_{alphato{0}}frac{tgalpha}{alpha}=1
end{equation}
$$

$$
begin{equation}
lim_{alphato{0}}frac{arcsinalpha}{alpha}=1
end{equation}
$$

$$
begin{equation}
lim_{alphato{0}}frac{arctgalpha}{alpha}=1
end{equation}
$$

На данной странице решены одиннадцать примеров. Пример №1 посвящен доказательству формул (2)-(4). Примеры №2, №3, №4 и №5 содержат решения с подробными комментариями. Примеры №6-10 содержат решения практически без комментариев, ибо подробные пояснения были даны в предыдущих примерах. При решении используются некоторые тригонометрические формулы, которые можно найти тут.

Замечу, что наличие тригонометрических функций вкупе с неопределённостью $frac {0} {0}$ ещё не означает обязательное применение первого замечательного предела. Иногда бывает достаточно простых тригонометрических преобразований, – например, см. пример №11.

Пример №1

Доказать, что $lim_{alphato{0}}frac{tgalpha}{alpha}=1$,
$lim_{alphato{0}}frac{arcsinalpha}{alpha}=1$,
$lim_{alphato{0}}frac{arctgalpha}{alpha}=1$.

Решение

а) Так как $tgalpha=frac{sinalpha}{cosalpha}$, то:

$$
lim_{alphato{0}}frac{tg{alpha}}{alpha}=left|frac{0}{0}right|
=lim_{alphato{0}}frac{sin{alpha}}{alphacos{alpha}}
$$

Так как $lim_{alphato{0}}cos{0}=1$ и $lim_{alphato{0}}frac{sinalpha}{alpha}=1$, то:

$$
lim_{alphato{0}}frac{sin{alpha}}{alphacos{alpha}}
=frac{displaystylelim_{alphato{0}}frac{sin{alpha}}{alpha}}{displaystylelim_{alphato{0}}cos{alpha}}
=frac{1}{1}
=1.
$$

Формула доказана. Более строгое доказательство (с обоснованием равенства $lim_{alphato{0}}cosalpha=1$) можно посмотреть в решебнике Демидовича (№474.1).

б) Сделаем замену $alpha=sin{y}$. Поскольку $sin{0}=0$, то из условия $alphato{0}$ имеем $yto{0}$. Кроме того, существует окрестность нуля, в которой $arcsinalpha=arcsin(sin{y})=y$, поэтому:

$$
lim_{alphato{0}}frac{arcsinalpha}{alpha}=left|frac{0}{0}right|
=lim_{yto{0}}frac{y}{sin{y}}
=lim_{yto{0}}frac{1}{frac{sin{y}}{y}}
=frac{1}{displaystylelim_{yto{0}}frac{sin{y}}{y}}
=frac{1}{1}
=1.
$$

Равенство $lim_{alphato{0}}frac{arcsinalpha}{alpha}=1$ доказано.

в) Сделаем замену $alpha=tg{y}$. Поскольку $tg{0}=0$, то условия $alphato{0}$ и $yto{0}$ эквивалентны. Кроме того, существует окрестность нуля, в которой $arctgalpha=arctgtg{y})=y$, поэтому, опираясь на результаты пункта а), будем иметь:

$$
lim_{alphato{0}}frac{arctgalpha}{alpha}=left|frac{0}{0}right|
=lim_{yto{0}}frac{y}{tg{y}}
=lim_{yto{0}}frac{1}{frac{tg{y}}{y}}
=frac{1}{displaystylelim_{yto{0}}frac{tg{y}}{y}}
=frac{1}{1}
=1.
$$

Равенство $lim_{alphato{0}}frac{arctgalpha}{alpha}=1$ доказано.

Равенства а), б), в) часто используются наряду с первым замечательным пределом.

Пример №2

Вычислить предел $lim_{xto{2}}frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}$.

Решение

Так как $lim_{xto{2}}frac{x^2-4}{x+7}=frac{2^2-4}{2+7}=0$ и $lim_{xto{2}}sinleft(frac{x^2-4}{x+7}right)=sin{0}=0$, т.е. и числитель и знаменатель дроби одновременно стремятся к нулю, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$, т.е. первое условие выполнено. Кроме того, видно, что выражения под знаком синуса и в знаменателе совпадают (т.е. выполнено и второе условие):

Первый замечательный предел

Итак, оба условия, перечисленные в начале страницы, выполнены. Из этого следует, что применима формула (1), т.е. $lim_{xto{2}} frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}=1$.

Ответ: $lim_{xto{2}}frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}=1$.

Пример №3

Найти $lim_{xto{0}}frac{sin{9x}}{x}$.

Решение

Так как $lim_{xto{0}}sin{9x}=0$ и $lim_{xto{0}}x=0$, то мы имеем дело с неопределенностью вида $frac{0}{0}$, т.е. первое условие выполнено. Однако выражения под знаком синуса и в знаменателе не совпадают. Здесь требуется подогнать выражение в знаменателе под нужную форму. Нам необходимо, чтобы в знаменателе расположилось выражение $9x$, – тогда второе условие станет истинным. По сути, нам не хватает множителя $9$ в знаменателе, который не так уж сложно ввести, – просто домножить выражение в знаменателе на $9$. Естественно, что для компенсации домножения на $9$ придётся тут же на $9$ и разделить:

$$
lim_{xto{0}}frac{sin{9x}}{x}=left|frac{0}{0}right|
=lim_{xto{0}}frac{sin{9x}}{9xcdotfrac{1}{9}}
=9lim_{xto{0}}frac{sin{9x}}{9x}
$$

Теперь выражения в знаменателе и под знаком синуса совпали. Оба условия для предела $lim_{xto{0}}frac{sin{9x}}{9x}$ выполнены. Следовательно, $lim_{xto{0}}frac{sin{9x}}{9x}=1$. А это значит, что:

$$
9lim_{xto{0}}frac{sin{9x}}{9x}=9cdot{1}=9.
$$

Ответ: $lim_{xto{0}}frac{sin{9x}}{x}=9$.

Пример №4

Найти $lim_{xto{0}}frac{sin{5x}}{tg{8x}}$.

Решение

Так как $lim_{xto{0}}sin{5x}=0$ и $lim_{xto{0}}tg{8x}=0$, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$. Однако форма первого замечательного предела нарушена. Числитель, содержащий $sin{5x}$, требует наличия в знаменателе $5x$. В этой ситуации проще всего разделить числитель на $5x$, – и тут же на $5x$ домножить. Кроме того, проделаем аналогичную операцию и со знаменателем, домножив и разделив $tg{8x}$ на $8x$:

$$lim_{xto{0}}frac{sin{5x}}{tg{8x}}=left|frac{0}{0}right|
=lim_{xto{0}}frac{frac{sin{5x}}{5x}cdot{5x}}{frac{tg{8x}}{8x}cdot{8x}}$$

Сокращая на $x$ и вынося константу $frac{5}{8}$ за знак предела, получим:

$$
lim_{xto{0}}frac{frac{sin{5x}}{5x}cdot{5x}}{frac{tg{8x}}{8x}cdot{8x}}
=frac{5}{8}cdotlim_{xto{0}}frac{frac{sin{5x}}{5x}}{frac{tg{8x}}{8x}}
$$

Обратите внимание, что $lim_{xto{0}}frac{sin{5x}}{5x}$ полностью удовлетворяет требованиям для первого замечательного предела. Для отыскания $lim_{xto{0}}frac{tg{8x}}{8x}$ применима формула (2):

$$
frac{5}{8}cdotlim_{xto{0}}frac{frac{sin{5x}}{5x}}{frac{tg{8x}}{8x}}
=frac{5}{8}cdotfrac{displaystylelim_{xto{0}}frac{sin{5x}}{5x}}{displaystylelim_{xto{0}}frac{tg{8x}}{8x}}
=frac{5}{8}cdotfrac{1}{1}
=frac{5}{8}.
$$

Ответ: $lim_{xto{0}}frac{sin{5x}}{tg{8x}}=frac{5}{8}$.

Пример №5

Найти $lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}$.

Решение

Так как $lim_{xto{0}}(cos{5x}-cos^3{5x})=1-1=0$ (напомню, что $cos{0}=1$) и $lim_{xto{0}}x^2=0$, то мы имеем дело с неопределённостью вида $frac{0}{0}$. Однако чтобы применить первый замечательный предел следует избавиться от косинуса в числителе, перейдя к синусам (дабы потом применить формулу (1)) или тангенсам (чтобы потом применить формулу (2)). Сделать это можно таким преобразованием:

$$cos{5x}-cos^3{5x}=cos{5x}cdotleft(1-cos^2{5x}right)$$

Так как $sin^2{5x}=1-cos^2{5x}$ (см. тригонометрические формулы), то:

$$cos{5x}-cos^3{5x}=cos{5x}cdotleft(1-cos^2{5x}right)=cos{5x}cdotsin^2{5x}.$$

Вернемся к пределу:

$$
lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}=left|frac{0}{0}right|
=lim_{xto{0}}frac{cos{5x}cdotsin^2{5x}}{x^2}
=lim_{xto{0}}left(cos{5x}cdotfrac{sin^2{5x}}{x^2}right)
$$

Дробь $frac{sin^2{5x}}{x^2}$ уже близка к той форме, что требуется для первого замечательного предела. Немного поработаем с дробью $frac{sin^2{5x}}{x^2}$, подгоняя её под первый замечательный предел (учтите, что выражения в числителе и под синусом должны совпасть):

$$frac{sin^2{5x}}{x^2}=frac{sin^2{5x}}{25x^2cdotfrac{1}{25}}=25cdotfrac{sin^2{5x}}{25x^2}=25cdotleft(frac{sin{5x}}{5x}right)^2$$

Вернемся к рассматриваемому пределу:

$$
lim_{xto{0}}left(cos{5x}cdotfrac{sin^2{5x}}{x^2}right)
=lim_{xto{0}}left(25cos{5x}cdotleft(frac{sin{5x}}{5x}right)^2right)=\
=25cdotlim_{xto{0}}cos{5x}cdotlim_{xto{0}}left(frac{sin{5x}}{5x}right)^2
=25cdot{1}cdot{1^2}
=25.
$$

Ответ: $lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}=25$.

Пример №6

Найти предел $lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}$.

Решение

Так как $lim_{xto{0}}(1-cos{6x})=0$ и $lim_{xto{0}}(1-cos{2x})=0$, то мы имеем дело с неопределенностью $frac{0}{0}$. Раскроем ее с помощью первого замечательного предела. Для этого перейдем от косинусов к синусам. Так как $1-cos{2alpha}=2sin^2{alpha}$, то:

$$1-cos{6x}=2sin^2{3x};;1-cos{2x}=2sin^2{x}.$$

Переходя в заданном пределе к синусам, будем иметь:

$$
lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}=left|frac{0}{0}right|
=lim_{xto{0}}frac{2sin^2{3x}}{2sin^2{x}}
=lim_{xto{0}}frac{sin^2{3x}}{sin^2{x}}=\

=lim_{xto{0}}frac{frac{sin^2{3x}}{(3x)^2}cdot(3x)^2}{frac{sin^2{x}}{x^2}cdot{x^2}}
=lim_{xto{0}}frac{left(frac{sin{3x}}{3x}right)^2cdot{9x^2}}{left(frac{sin{x}}{x}right)^2cdot{x^2}}
=9cdotfrac{displaystylelim_{xto{0}}left(frac{sin{3x}}{3x}right)^2}{displaystylelim_{xto{0}}left(frac{sin{x}}{x}right)^2}
=9cdotfrac{1^2}{1^2}
=9.
$$

Ответ: $lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}=9$.

Пример №7

Вычислить предел $lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}$ при условии $alphaneqbeta$.

Решение

Подробные пояснения были даны ранее, здесь же просто отметим, что вновь наличествует неопределенность $frac{0}{0}$. Перейдем от косинусов к синусам, используя формулу

$$cosalpha-cosbeta=-2sinfrac{alpha+beta}{2}cdotsinfrac{alpha-beta}{2}.$$

Используя указанную формулу, получим:

$$
lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}=left|frac{0}{0}right|
=lim_{xto{0}}frac{-2sinfrac{alpha{x}+beta{x}}{2}cdotsinfrac{alpha{x}-beta{x}}{2}}{x^2}=\
=-2cdotlim_{xto{0}}frac{sinleft(xcdotfrac{alpha+beta}{2}right)cdotsinleft(xcdotfrac{alpha-beta}{2}right)}{x^2}

=-2cdotlim_{xto{0}}left(frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{x}cdotfrac{sinleft(xcdotfrac{alpha-beta}{2}right)}{x}right)=\
=-2cdotlim_{xto{0}}left(frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{xcdotfrac{alpha+beta}{2}}cdotfrac{alpha+beta}{2}cdotfrac{sinleft(xcdotfrac{alpha-beta}{2}right)}{xcdotfrac{alpha-beta}{2}}cdotfrac{alpha-beta}{2}right)=\

=-frac{(alpha+beta)cdot(alpha-beta)}{2}lim_{xto{0}}frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{xcdotfrac{alpha+beta}{2}}cdotlim_{xto{0}}frac{sinleft(xcdotfrac{alpha-beta}{2}right)}{xcdotfrac{alpha-beta}{2}}
=-frac{alpha^2-beta^2}{2}cdot{1}cdot{1}
=frac{beta^2-alpha^2}{2}.
$$

Ответ: $lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}=frac{beta^2-alpha^2}{2}$.

Пример №8

Найти предел $lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}$.

Решение

Так как $lim_{xto{0}}(tg{x}-sin{x})=0$ (напомню, что $sin{0}=tg{0}=0$) и $lim_{xto{0}}x^3=0$, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$. Раскроем её следующим образом:

$$
lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}=left|frac{0}{0}right|
=lim_{xto{0}}frac{frac{sin{x}}{cos{x}}-sin{x}}{x^3}
=lim_{xto{0}}frac{sin{x}cdotleft(frac{1}{cos{x}}-1right)}{x^3}
=lim_{xto{0}}frac{sin{x}cdotleft(1-cos{x}right)}{x^3cdotcos{x}}=\

=lim_{xto{0}}frac{sin{x}cdot{2}sin^2frac{x}{2}}{x^3cdotcos{x}}
=frac{1}{2}cdotlim_{xto{0}}left(frac{sin{x}}{x}cdotleft(frac{sinfrac{x}{2}}{frac{x}{2}}right)^2cdotfrac{1}{cos{x}}right)
=frac{1}{2}cdot{1}cdot{1^2}cdot{1}
=frac{1}{2}.
$$

Аналогичную задачу можно посмотреть в решебнике Демидовича (№475)

Ответ: $lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}=frac{1}{2}$.

Пример №9

Найти предел $lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}$.

Решение

Так как $lim_{xto{3}}(1-cos(x-3))=0$ и $lim_{xto{3}}(x-3)tgfrac{x-3}{2}=0$, то наличествует неопределенность вида $frac{0}{0}$. Перед тем, как переходить к её раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alpha to 0$). Проще всего ввести переменную $t=x-3$. Однако ради удобства дальнейших преобразований (эту выгоду можно заметить по ходу приведённого ниже решения) стоит сделать такую замену: $t=frac{x-3}{2}$. Отмечу, что обе замены применимы в данном случае, просто вторая замена позволит поменьше работать с дробями. Так как $xto{3}$, то $tto{0}$.

$$
lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}=left|frac{0}{0}right|
=left|begin{aligned}&t=frac{x-3}{2};\&tto{0}end{aligned}right|
=lim_{tto{0}}frac{1-cos{2t}}{2tcdottg{t}}
=lim_{tto{0}}frac{2sin^2t}{2tcdottg{t}}
=lim_{tto{0}}frac{sin^2t}{tcdottg{t}}=\
=lim_{tto{0}}frac{sin^2t}{tcdotfrac{sin{t}}{cos{t}}}
=lim_{tto{0}}frac{sin{t}cos{t}}{t}
=lim_{tto{0}}left(frac{sin{t}}{t}cdotcos{t}right)
=lim_{tto{0}}frac{sin{t}}{t}cdotlim_{tto{0}}cos{t}
=1cdot{1}
=1.
$$

Ответ: $lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}=1$.

Пример №10

Найти предел $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}$.

Решение

Вновь мы имеем дело с неопределенностью $frac{0}{0}$. Перед тем, как переходить к ее раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alphato{0}$). Проще всего ввести переменную $t=frac{pi}{2}-x$. Так как $xtofrac{pi}{2}$, то $tto{0}$:

$$
lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}
=left|frac{0}{0}right|
=left|begin{aligned}&t=frac{pi}{2}-x;\&tto{0}end{aligned}right|
=lim_{tto{0}}frac{1-sinleft(frac{pi}{2}-tright)}{t^2}
=lim_{tto{0}}frac{1-cos{t}}{t^2}=\
=lim_{tto{0}}frac{2sin^2frac{t}{2}}{t^2}

=2lim_{tto{0}}frac{sin^2frac{t}{2}}{t^2}
=2lim_{tto{0}}frac{sin^2frac{t}{2}}{frac{t^2}{4}cdot{4}}
=frac{1}{2}cdotlim_{tto{0}}left(frac{sinfrac{t}{2}}{frac{t}{2}}right)^2
=frac{1}{2}cdot{1^2}
=frac{1}{2}.
$$

Ответ: $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}=frac{1}{2}$.

Пример №11

Найти пределы $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}$, $lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}$.

Решение

В данном случае нам не придётся использовать первый замечательный предел. Обратите внимание: как в первом, так и во втором пределах присутствуют только тригонометрические функции и числа. Зачастую в примерах такого рода удаётся упростить выражение, расположенное под знаком предела. При этом после упомянутого упрощения и сокращения некоторых сомножителей неопределённость исчезает. Я привёл данный пример лишь с одной целью: показать, что наличие тригонометрических функций под знаком предела вовсе не обязательно означает применение первого замечательного предела.

Так как $lim_{xtofrac{pi}{2}}(1-sin{x})=0$ (напомню, что $sinfrac{pi}{2}=1$) и $lim_{xtofrac{pi}{2}}cos^2x=0$ (напомню, что $cosfrac{pi}{2}=0$), то мы имеем дело с неопределенностью вида $frac{0}{0}$. Однако это вовсе не означает, что нам потребуется использовать первый замечательный предел. Для раскрытия неопределенности достаточно учесть, что $cos^2x=1-sin^2x$:

$$
lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}
=left|frac{0}{0}right|
=lim_{xtofrac{pi}{2}}frac{1-sin{x}}{1-sin^2x}
=lim_{xtofrac{pi}{2}}frac{1-sin{x}}{(1-sin{x})(1+sin{x})}
=lim_{xtofrac{pi}{2}}frac{1}{1+sin{x}}
=frac{1}{1+1}
=frac{1}{2}.
$$

Аналогичный способ решения есть и в решебнике Демидовича (№475). Что же касается второго предела, то как и в предыдущих примерах этого раздела, мы имеем неопределённость вида $frac{0}{0}$. Отчего она возникает? Она возникает потому, что $tgfrac{2pi}{3}=-sqrt{3}$ и $2cosfrac{2pi}{3}=-1$. Используем эти значения с целью преобразования выражений в числителе и в знаменателе. Цель наших действий: записать сумму в числителе и знаменателе в виде произведения. Кстати сказать, зачастую в пределах аналогичного вида удобна замена переменной, сделанная с таким расчётом, чтобы новая переменная устремилась к нулю (см., например, примеры №9 или №10 на этой странице). Однако в данном примере в замене смысла нет, хотя при желании замену переменной $t=x-frac{2pi}{3}$ несложно осуществить.

$$
lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}
=lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cdotleft(cos{x}+frac{1}{2}right)}
=lim_{xtofrac{2pi}{3}}frac{tg{x}-tgfrac{2pi}{3}}{2cdotleft(cos{x}-cosfrac{2pi}{3}right)}=\

=lim_{xtofrac{2pi}{3}}frac{frac{sinleft(x-frac{2pi}{3}right)}{cos{x}cosfrac{2pi}{3}}}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}}
=lim_{xtofrac{2pi}{3}}frac{sinleft(x-frac{2pi}{3}right)}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}=\

=lim_{xtofrac{2pi}{3}}frac{2sinfrac{x-frac{2pi}{3}}{2}cosfrac{x-frac{2pi}{3}}{2}}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}
=lim_{xtofrac{2pi}{3}}frac{cosfrac{x-frac{2pi}{3}}{2}}{-2sinfrac{x+frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}=\

=frac{1}{-2cdotfrac{sqrt{3}}{2}cdotleft(-frac{1}{2}right)cdotleft(-frac{1}{2}right)}
=-frac{4}{sqrt{3}}.
$$

Как видите, нам не пришлось применять первый замечательный предел. Конечно, при желании это можно сделать (см. примечание ниже), но необходимости в этом нет.

Каким будет решение с использованием первого замечательного предела? показатьскрыть

Ответ: $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}=frac{1}{2}$, $lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}=-frac{4}{sqrt{3}}$.

Источник
  1. Первый замечательный предел
  2. Раскрытие неопределенностей (left[frac00right]) с тригонометрическими функциями
  3. Второй замечательный предел
  4. Раскрытие неопределенности (left[1^{infty}right])
  5. Примеры

п.1. Первый замечательный предел

Исследуем поведение функции (f(x)=frac{sinx}{x}) вблизи (x_0=0).
Построим график.
Первый замечательный предел
Заполним таблицу со значениями (f(x)) непосредственно вблизи (x_0=0).

x -0,01 -0,001 -0,0001 0 0,0001 0,001 0,01
sin(x)/x 0,999983 0,99999983 0,9999999983 [0/0] 0,9999999983 0,99999983 0,999983

В самой точке 0 возникает неопределенность (left[frac00right]), но при приближении к ней с обеих сторон значение функции стремится к 1. Можем записать: $$ lim_{xrightarrow 0}frac{sinx}{x}=1 $$ Это равенство называют первым замечательным пределом.

п.2. Раскрытие неопределенностей (left[frac00right]) с тригонометрическими функциями

Из первого замечательного предела с помощью тригонометрических преобразований можно получить другие пределы: begin{gather*} lim_{xrightarrow 0}frac{tgx}{x}=1, lim_{xrightarrow 0}frac{arctgx}{x}=1\ lim_{xrightarrow 0}frac{arcsinx}{x}=1, lim_{xrightarrow 0}frac{1-cosx}{frac{x^2}{2}}=1 end{gather*} Все полученные формулы используются для раскрытия неопределенностей [0/0] при поиске пределов функций с тригонометрическими компонентами.

Например:
Найдем предел (lim_{xrightarrow 0}frac{1-cos4x}{x^2}) begin{gather*} lim_{xrightarrow 0}frac{1-cos4x}{x^2} = lim_{xrightarrow 0}frac{2sin^2 2x}{x^2}= 2lim_{xrightarrow 0}left(left(frac{sin2x}{x}right)cdotleft(frac{sin2x}{x}right)right)=\ =2cdot 4lim_{xrightarrow 0}left(left(frac{sin2x}{2x}right)cdotleft(frac{sin2x}{2x}right)right)= 8cdotlim_{xrightarrow 0}frac{sin2x}{2x}cdot lim_{xrightarrow 0}frac{sin2x}{2x}=8cdot 1cdot 1=8 end{gather*} Ответ: 8

п.3. Второй замечательный предел

Исследуем поведение функции (f(x)=left(1+frac1xright)^x) при (xrightarrowpminfty)
Построим график.
Второй замечательный предел
Заполним таблицу со значениями (f(x)) для больших по модулю x.

(x) -1000 -100 -10 10 100 1000 10000
(left(1+frac1xright)^x) 2,7196 2,7320 2,8680 2,5937 2,7048 2,7169 2,7181

На бесконечностях функция стремится к одному и тому же значению begin{gather*} e=2,7182818284\ lim_{xrightarrowinfty}left(1+frac1xright)^x=e end{gather*} Это равенство называют вторым замечательным пределом.
Число e часто называют числом Эйлера.
Бесконечность пишется без знаков, т.к. равенство справедливо как при (xrightarrow -infty), так и при (xrightarrow +infty).

п.4. Раскрытие неопределенности (left[1^{infty}right])

Если учесть, что (lim_{xrightarrowinfty}frac1x=0), тогда второй замечательный предел $$ lim_{xrightarrowinfty}left(1+frac1xright)^x=left[1^{infty}right]=e $$ дает ответ, чему равна единица в степени (infty). Поэтому его можно использовать для раскрытия неопределенностей, сводящихся к (left[1^{infty}right]).

Из второго замечательного предела с помощью преобразований для показательных и логарифмических функций можно получить другие полезные пределы: begin{gather*} lim_{xrightarrow 0}(1+x)^{frac1x}=e, lim_{xrightarrow infty}left(1+frac kxright)^x=e^k\ lim_{xrightarrow 0}frac{ln(1+x)}{x}=1, lim_{xrightarrow 0}frac{e^x-1}{x}=1 end{gather*} Для тех, кто заинтересовался, строгое доказательство замечательных пределов и их следствий можно найти в университетских учебниках по математическому анализу. Ваших знаний уже достаточно, чтобы полностью разобраться с этими вопросами.

Например:
Найдем предел (lim_{xrightarrow infty}left(frac{x+6}{x-2}right)^{3x+2})
Т.к. (lim_{xrightarrow infty}frac{x+6}{x-2}) и (lim_{xrightarrow infty}(3x+2)=infty), получаем неопределенность (left[1^{infty}right]).
Выделим целую часть из основания степени: $$ frac{x+6}{x-2}=frac{(x-2)+8}{x-2}=frac{x-2}{x-2}+frac{8}{x-2}=1+frac{8}{x-2} $$ Получаем: $$ lim_{xrightarrow infty}left(frac{x+6}{x-2}right)^{3x+2} = lim_{xrightarrow infty}left(1+frac{8}{x-2}right)^{3x+2} =left[1^{infty}right] $$ Замена переменных: (frac1t=frac{8}{x-2}, trightarrowinfty). Тогда (x=8t+2). begin{gather*} lim_{trightarrow infty}left(1+frac1tright)^{3(8t+2)+2}= lim_{trightarrow infty}left(1+frac1tright)^{24t+8} = left(lim_{trightarrow infty}left(1+frac1tright)^tright)^{24}cdot lim_{trightarrow infty}left(1+frac1tright)^8=\ =e^{24}cdot 1^8=e^{24} end{gather*} Здесь мы использовали (1^{infty}=e) и (1^8=1).
Ответ: (e^{24})

п.5. Примеры

Пример 1. Найдите значения пределов, используя первый замечательный предел:
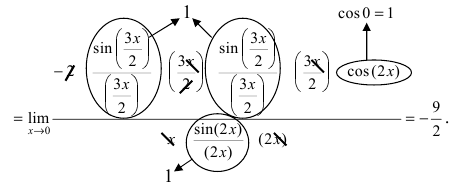
a) ( lim_{xrightarrow 0}frac{1-cosx}{xsinx} ) begin{gather*} lim_{xrightarrow 0}frac{1-cosx}{xsinx}=left[frac00right]=lim_{xrightarrow 0}frac{2sin^2frac x2}{x^2underbrace{frac{sinx}{x}}_{=1}}=2lim_{xrightarrow 0}frac{sin^2frac x2}{x^2}=2lim_{xrightarrow 0}left(frac{sinfrac x2}{2cdotfrac x2}cdotfrac{sinfrac x2}{2cdotfrac x2}right)=\ =frac24lim_{xrightarrow 0}frac{sinfrac x2}{frac x2}cdot lim_{xrightarrow 0}frac{sinfrac x2}{frac x2}=frac12cdot 1cdot 1=frac12 end{gather*}

б) ( lim_{xrightarrow 0}frac{sin8x}{sin2x} ) begin{gather*} lim_{xrightarrow 0}frac{sin8x}{sin2x}=left[frac00right]=lim_{xrightarrow 0}frac{8xcdotoverbrace{frac{sin8x}{8x}}^{=1}}{2xcdotunderbrace{frac{sin2x}{2x}}_{=1}}=frac82=4 end{gather*}

в) ( lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4} ) Заметим, что (lim_{xrightarrow 0}sin(x^2-4)=sin(-4)ne 0) и (lim_{xrightarrow 0}(x^2-4)=-4ne 0) $$ lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4}neleft[frac00right] $$ Т.е., неопределенности (left[frac00right]) в этом примере нет, и он решается обычной подстановкой значения предела (x_0=0) вместо x: begin{gather*} lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4}=frac{sin(-4)}{-4}=frac{-sin4}{-4}=frac{sin4}{4} end{gather*}

г) ( lim_{xrightarrow 2}frac{sin(x^2-4)}{x^2-4} ) А вот здесь при подстановке предела (x_0=2) получаем неопределенность (left[frac00right]). $$ lim_{xrightarrow 2}frac{sin(x^2-4)}{x^2-4}=left[frac00right] $$ Замена переменных: (t=x-2, trightarrow 0)
Тогда (x=t+2, x^2-4=(x-2)(x+2)=t(t+4)). Подставляем: begin{gather*} lim_{trightarrow 0}frac{sinleft(t(t+4)right)}{t(t+4)}=1 end{gather*} Последняя запись полностью соответствует определению первого замечательного предела с переменной (z=t(t+4), zrightarrow 0).

Внимание!

Следите, чтобы при подстановке значения предела в выражение действительно возникала неопределенность. И только тогда начинайте применять правила раскрытия неопределенностей и замечательные пределы.
Если неопределенности нет, то обычной подстановки достаточно, чтобы сразу получить ответ.
Что такое «неопределенность» – см. §37 данного справочника.

д) ( lim_{xrightarrow 0}frac{sqrt{x+3}-sqrt{3}}{sin5x} ) begin{gather*} lim_{xrightarrow 0}frac{sqrt{x+3}-sqrt{3}}{sin5x}=left[frac00right]=lim_{xrightarrow 0}frac{(sqrt{x+3}-sqrt{3})(sqrt{x+3}+sqrt{3})}{(sqrt{x+3}+sqrt{3})cdot sin5x}=\ =lim_{xrightarrow 0}frac{x+3-3}{(sqrt{x+3}+sqrt{3})cdot sin5x}= lim_{xrightarrow 0}frac{1}{(sqrt{x+3}+sqrt{3})cdotfrac{sin5x}{x}}=\ =lim_{xrightarrow 0}frac{1}{(sqrt{x+3}+sqrt{3})cdot 5cdot underbrace{frac{sin5x}{5x}}_{=1}}=frac15lim_{xrightarrow 0}frac{1}{sqrt{x+3}+sqrt{3}}=frac15cdotfrac{1}{2sqrt{3}}=frac{1}{10sqrt{3}}=frac{sqrt{3}}{30} end{gather*}
e*) ( lim_{xrightarrow 1}frac{sinpi x}{sin3pi x} ) При подстановке (x_0=1) получаем неопределенность (left[frac00right]).
Чтобы её раскрыть с помощью первого замечательного предела, нужно ввести новую переменную, которая стремится к 0.
Заметим, что: begin{gather*} sin(pi x-pi)=sinleft(pi(x-1)right)=-sinpi x\ sin(3pi x-3pi)=sinleft(3pi(x-1)right)=-sin3pi x end{gather*} Дробь можно заменить: $$ frac{sinpi x}{sin3pi x}=frac{-sinpi x}{-sin3pi x}=frac{sinleft(pi(x-1)right)}{sinleft(3pi(x-1)right)} $$ Замена переменной: (t=x-1, trightarrow 0). Получаем: begin{gather*} lim_{trightarrow 0}frac{sinpi t}{sin3pi t}=lim_{trightarrow 0}frac{pi tcdotoverbrace{frac{sinpi t}{pi t}}^{=1}}{3pi tcdotunderbrace{frac{sin3pi t}{3pi t}}_{=1}}=frac13 end{gather*} Ответ: а) (frac12); б) 4; в) (frac{sin4}{4}); г) 1; д) (frac{sqrt{3}}{30}); е) (frac 13)

Пример 2. Найдите значения пределов, используя второй замечательный предел:
a) ( lim_{xrightarrowinfty}left(1+frac{1}{3x}right)^{5x} ) $$ lim_{xrightarrowinfty}left(1+frac{1}{3x}right)^{5x}=left[1^{infty}right] $$ Замена переменной: (t=3x, trightarrowinfty). Тогда (x=frac t3). Подставляем: begin{gather*} lim_{xrightarrowinfty}left(1+frac 1tright)^{5cdotfrac t3}=left(underbrace{lim_{xrightarrowinfty}left(1+frac 1tright)^t}_{=e}right)^{frac53}=e^{frac53} end{gather*} б) ( lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x} ) Предел основания степени: $$ lim_{xrightarrowinfty}frac{x-1}{x+4}=left[frac{infty}{infty}right]=lim_{xrightarrowinfty}frac{xleft(1-frac1xright)}{xleft(1+frac4xright)}=lim_{xrightarrowinfty}frac{1-frac1x}{1+frac4x}= frac{1-0}{1+0}=1 $$ Диагностируем неопределенность: $$ lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x}=left[1^{infty}right] $$ Выделим целую часть из дроби: $$ frac{x-1}{x+4}=frac{(x+4)-5}{x+4}=1-frac{5}{x+4} $$ Замена: (t=-frac{(x+4)}{5}, trightarrowinfty) (знак бесконечности по условию не важен).
Тогда: (x=-5t-4). Подставляем: begin{gather*} lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x}=lim_{xrightarrowinfty}left(1-frac{5}{x+4}right)^{2x}= lim_{trightarrowinfty}left(1+frac1tright)^{2cdot(-5t-4)}=\ =lim_{trightarrowinfty}left(1+frac1tright)^{-10t-8}=left(lim_{trightarrowinfty}left(1+frac1tright)^tright)^{-10}cdotlim_{trightarrowinfty}left(1+frac1tright)^{-8}=\ =e^{-10}cdot 1^{-8}=e^{-10} end{gather*}

в) ( lim_{xrightarrow +infty}left(frac{2x-1}{x+4}right)^{2x} ) Предел основания степени: $$ lim_{xrightarrow +infty}frac{2x-1}{x+4}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{xleft(2-frac1xright)}{xleft(1+frac4xright)}=lim_{xrightarrow +infty}frac{2-frac1x}{1+frac4x}= frac{2-0}{1+0}=2 $$ Неопределенности здесь нет: $$ lim_{xrightarrow +infty}left(frac{2x-1}{x+4}right)^{2x}=2^{+infty}=+infty $$ Показательная функция с основанием >1 на плюс бесконечности стремится к плюс бесконечности.

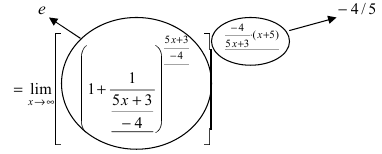
г) ( lim_{xrightarrow -infty}left(frac{5x+3}{4x-1}right)^{3x-2} )
Предел основания степени: $$ lim_{xrightarrow -infty}frac{5x+3}{4x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{xleft(5+frac3xright)}{xleft(4-frac1xright)}=lim_{xrightarrow -infty}frac{5+frac3x}{4-frac1x}= frac{5-0}{4+0}=frac54 $$ Неопределенности здесь нет: $$ lim_{xrightarrow -infty}left(frac{5x+3}{4x-1}right)^{3x-2}=left(frac54right)^{-infty}=left(frac45right)^{+infty}=0 $$ Показательная функция с основанием <1 на плюс бесконечности стремится к нулю.

д) ( lim_{xrightarrow 0}(1+tgx)^frac1x )
Подставляем (x_0=0) в функцию, и получаем неопределенность: $$ lim_{xrightarrow 0}(1+tgx)^frac1x=left[1^inftyright] $$ Используем следствие из второго замечательного предела: (lim_{xrightarrow 0}(1+x)^frac1x=e)
Преобразуем выражение: $$ lim_{xrightarrow 0}(1+tgx)^frac1x= lim_{xrightarrow 0}(1+tgx)^{frac{tgx}{xcdot tgx}}= lim_{xrightarrow 0}left((1+tgx)^{frac{1}{tgx}}right)^{frac{tgx}{x}} $$ Теперь используем следствие из первого замечательного предела: (lim_{xrightarrow 0}frac{tgx}{x}=1)
Тогда: $$ lim_{xrightarrow 0}(1+tgx)^{frac{1}{tgx}}= left[ begin{array}{l} t=tgx\ trightarrow 0 end{array} right] = lim_{trightarrow 0}(1+t)^frac1t=e $$ Здесь мы записали замену переменных «на ходу». Такая запись часто используется по необходимости, особенно при интегрировании.
Заметим, что если ввести понятие «эквивалентных бесконечно малых», то пример вообще решается в одну строку, т.к. (tgxsim x) при (xrightarrow 0).

e*) ( lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x} )
Подставляем (x_0=0) в функцию, и получаем неопределенность: $$ lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x}=left[1^inftyright] $$ Используем следствие из второго замечательного предела: (lim_{xrightarrow 0}(1+x)^frac1x=e)
Преобразуем выражение: begin{gather*} lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x}= lim_{xrightarrow 0}(1-2sin^2 x)^frac{1}{sin^2 3x}= lim_{xrightarrow 0}left(1+(-2sin^2 x)right)^{frac{-2sin^2 x}{-2sin^2 xcdot sin^2 3x}}=\ lim_{xrightarrow 0}left((1+(-2sin^2 x))^{frac{1}{-2sin^2 x}}right)^{frac{-2sin^2x}{sin^2 3x}} end{gather*} Найдем предел для внешней степени: $$ lim_{xrightarrow 0}frac{-2sin^2x}{sin^2 3x}=left[frac00right]=-2lim_{xrightarrow 0}frac{x^2cdotleft(frac{sinx}{x}right)^2}{(3x)^2cdotleft(frac{sin3x}{3x}right)^2}= -2cdotfrac{1cdot 1}{9cdot 1}=-frac29 $$ Получаем: $$ lim_{xrightarrow 0}left((1+(-2sin^2x))^{frac{1}{-2sin^2x}}right)^{-frac29}= left[ begin{array}{l} t=-2sin^2 x\ trightarrow 0 end{array} right] = left(lim_{trightarrow 0}(1+t)^frac1tright)^{-frac29}=e^{-frac29} $$ Ответ: a) (e^{frac53}); б) (e^{-10}); в) (+infty); г) 0; д) (e); e) (e^{-frac29})

Источник

Добавить комментарий