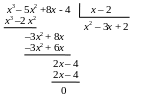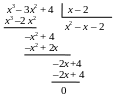Продолжаем наш цикл занятий связанный с пределами. На сегодня мы будем раскрывать новый вид неопределённости ноль делённый на ноль. В обычной алгебре с нулём как вы уже знаете работают очень аккуратно, стараются как можно реже иметь с ним дело, а про бесконечности там всякие я уже молчу. Но в теории пределов этих ребят совсем не боятся. Только если получается ноль на ноль, то всё, тут обычная арифметика уже бессильна, поэтому математики нашли различного рода обходные пути решения этой проблемы. С которыми мы сейчас познакомимся.
1. Пожалуй проще способа не найти, будет ясно даже чайнику, жаль что использовать его получится не везде. метод заключается в разложении числителя и/или знаменателя по формулам сокращённого умножения. Не будем копошиться в теории, сразу рассмотрим на примере, решение распишем сразу.
Хорошо, хорошо, уговорили, ещё один примерчик на закрепление.
С “мелюзгой” можно побаловаться, но нам не стоит стопориться на этом, едем дальше.
2. И пяти минут не прошло, а мы разбираемся со вторым методом. Он предназначен для пределов с иррациональностями, проще говоря, там, где присутствуют квадратные корни или кубические, вообще корни любой степени. Распознать примеры такого плана совсем не сложно. Видите иррациональность, считайте что всё, нашли. Устраняется она путём умножения числителя и знаменателя на сопряжённое выражение. Рассмотрим первый примерчик.
С первого примера уже что-то да стало понятно. Но чтобы наверняка, стоит и второй бахнуть.
Вот так-то лучше.
3. Последний рассмотренный на сегодня (есть ещё правило Лопиталя (ссылочка будет в конце статьи)) способ устранения неопределённости связан с табличкой эквивалентных величин.
Представим её здесь:
Использовать её очень просто, если видите функцию определённого вида как в табличке, то можете смело заменить эквивалентную ей. Работает это только при произведении и делении двух функций. При вычитании и сложении уже нельзя. Приведём пример:
Оказалось не так сложно, как предполагалось ранее. При таком раскладе, можно и второй пример рассмотреть.
На сегодня задачек достаточно, что-то мы сегодня “в ударе”. Подводя общие итоги занятия, имеет место сказать, что раскрывать неопределённость ноль на ноль гораздо интереснее. Ну и примерчики всевозможные могут попасться, объединяющие в себе сразу несколько методов решения. Оставляйте в комментариях какую тематику стоит добавить на канале, какие темы разобрать. Спасибо за внимание.
Другие темы:
Вычисление пределов функций y
= f(x),
значение которых в точке при х = х0
определено f(x)
= А не вызывает затруднений:
![]()
Затруднения возникают, когда в точке х
= х0 при вычислении значения
функции получаем неопределенности вида
![]()
В этом случае для вычисления пределов
нужно преобразовать исходную функцию,
чтобы неопределенность исчезла, либо
в результате преобразования привести
исходную функцию к первому или второму
замечательному пределу.
Пример 1.
Вычислить
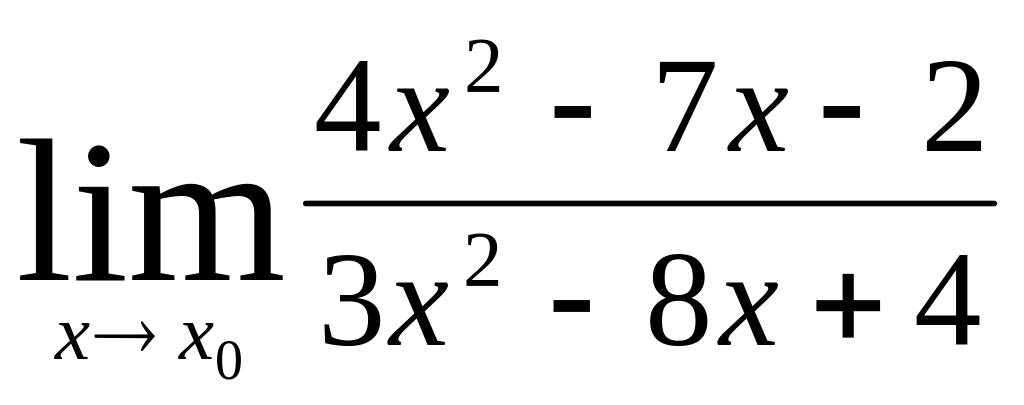
при
![]()
Решение. Так
как
![]()
определена
в точке
![]()
,
то предел функции в точке
равен значению функции в этой точке, т.
е.
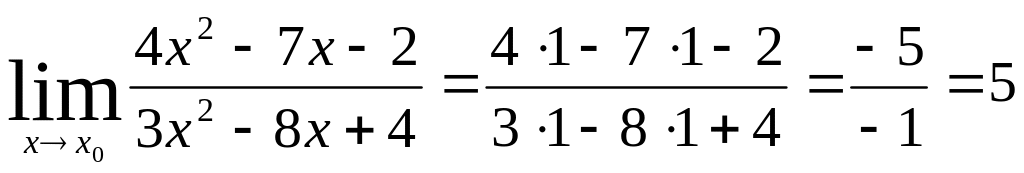
;
Пример 2.
Вычислить
при
![]()
Решение. В
точке
функция также определена. Тогда получим:
![]()
.
Пример 3.
Вычислить
при
![]()
.
Решение. При
получили неопределенность
![]()
.
Для решения разложим числитель и
знаменатель на множители, сократим
дробь:
![]()
![]()
;
![]()
;
![]()
;
![]()
.
![]()
;
![]()
;
;![]()
![]()
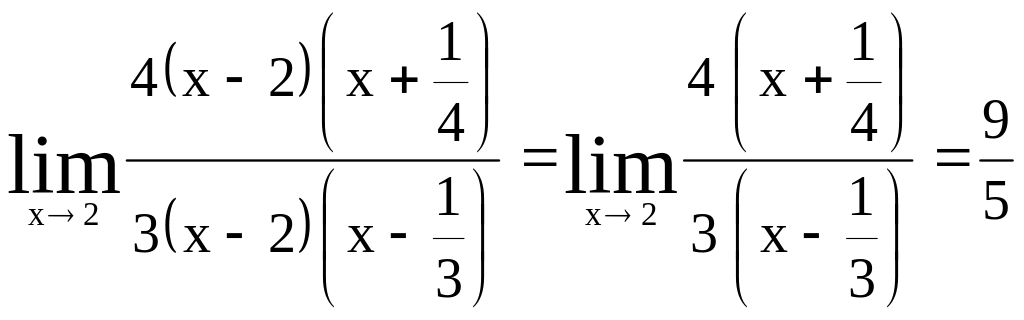
;
После сокращения дроби опять в предел
подставляем
и вычисляем предел.
Пример 4.
Найти предел:
![]()
Решение.
![]()
.
Избавимся от
иррациональности в знаменателе, умножив
и разделив дробь на выражение
![]()
,
сопряженное знаменателю, и применим
формулу
![]()
.
Выделим множитель
![]()
и сократим на него дробь.
![]()
![]()
Примечание.
Аналогично
избавляются от иррациональности в
числителе.
Пример 5.
Вычислить предел:
![]()
Решение. При непосредственной
подставке х = –1 получаем неопределенность
.
Для ее исключения проведем преобразование
функции:
![]()
При х = –1 знаменатель обращаться в
ноль за счет сомножителя х + 1. разделим
числитель на этот сомножитель:
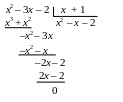
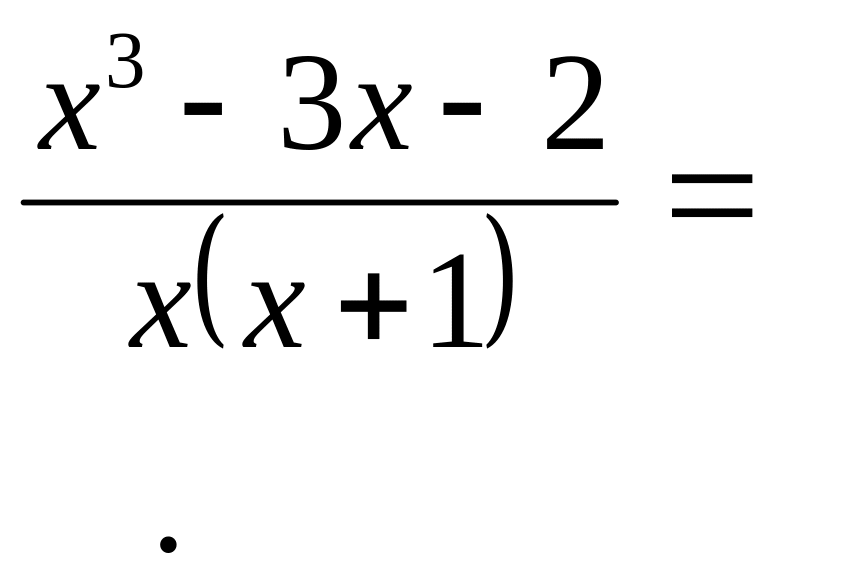
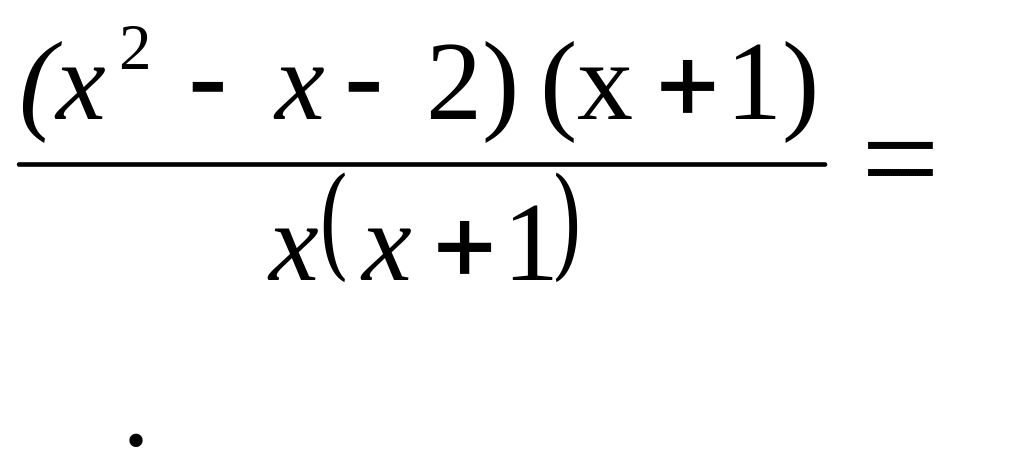
В результате предел преобразуется к
виду:
![]()
Пример 6.
Вычислить предел:
![]()
Решение. При непосредственной
подставке х = –2 получаем неопределенность
.
Для устранения неопределенности разложим
числитель и знаменатель на сомножители.
Так как и числитель, и знаменатель при
х = 2 обращаются в ноль, то они содержат
общий сомножитель х – 2. найдем
вторые сомножители числителя и
знаменателя:
|
|
|
В результате разложения на сомножители
числителя и знаменателя предел
преобразуется к виду:
![]()
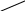
При подстановке х = 2 опять получаем
неопределенность
.
Еще раз разделим числитель и знаменатель
на х – 2 и в результате получим:
![]()
Пример 7.
Вычислить предел:
![]()
Решение. При непосредственной
подстановке х = 0 получаем
неопределенность
![]()
.
Для ее устранения умножим числитель и
знаменатель дроби на выражение,
сопряженное числителю, на
![]()
В результате мы избавимся от иррациональности
в числителе:
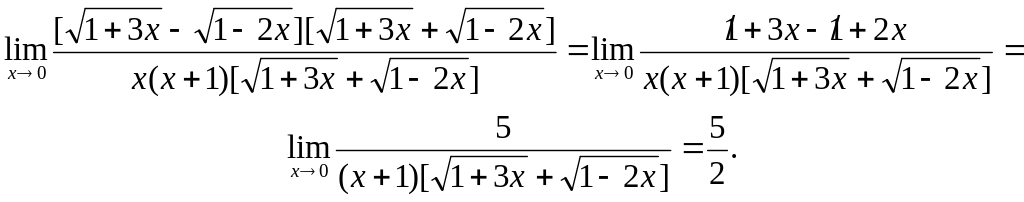
Соседние файлы в папке Предел и непрерывность
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущей статье мы рассказывали, как правильно вычислять пределы элементарных функций. Если же мы возьмем более сложные функции, то у нас в расчетах появятся выражения с неопределенным значением. Они и называются неопределенностями.
Выделяют следующие основные виды неопределенностей:
- Деление 0 на 0 00;
- Деление одной бесконечности на другую ∞∞;
-
0, возведенный в нулевую степень 00;
- бесконечность, возведенная в нулевую степень ∞0.
Мы перечислили все основные неопределенности. Другие выражения в различных условиях могут принимать конечные или бесконечные значения, следовательно, они не могут считаться неопределенностями.
Раскрытие неопределенностей
Раскрыть неопределенность можно:
- С помощью упрощения вида функции (использование формул сокращенного умножения, тригонометрических формул, дополнительное умножение на сопряженные выражения и последующее сокращение и др. );
-
С помощью замечательных пределов;
-
С помощью правила Лопиталя;
-
Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
Всю информацию, представленную выше, можно наглядно представить в виде таблицы. С левой стороны в ней приводится вид неопределенности, с правой – подходящий метод ее раскрытия (нахождения предела). Этой таблицей очень удобно пользоваться при расчетах, связанных с нахождением пределов.
| Неопределенность | Метод раскрытия неопределенности |
| 1. Деление 0 на 0 | Преобразование и последующее упрощение выражения. Если выражение имеет вид sin(kx)kx или kxsin(kx) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений |
| 2. Деление бесконечности на бесконечность | Преобразование и упрощение выражения либо использование правила Лопиталя |
| 3. Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями | Преобразование в 00 или ∞∞ с последующим применением правила Лопиталя |
| 4. Единица в степени бесконечности | Использование второго замечательного предела |
| 5. Возведение нуля или бесконечности в нулевую степень | Логарифмирование выражения с применением равенства limx→x0ln(f(x))=lnlimx→x0f(x) |
Разберем пару задач. Эти примеры довольно простые: в них ответ получается сразу после подстановки значений и неопределенности при этом не возникает.
Вычислите предел limx→1×3+3x-1×5+3.
Решение
Выполняем подстановку значений и получаем ответ.
limx→1×3+3x-1×5+3=13+3·1-115+3=34=32
Ответ: limx→1×3+3x-1×5+3=32.
Вычислите предел limx→0(x2+2,5)1×2.
Решение
У нас есть показательно степенная функция, в основание которой нужно подставитьx=0.
(x2+2,5)x=0=02+2,5=2,5
Значит, мы можем преобразовать предел в следующее выражение:
limx→0(x2+2,5)1×2=limx→02,51×2
Теперь разберемся с показателем – степенной функцией 1×2=x-2. Заглянем в таблицу пределов для степенных функций с показателем меньше нуля и получим следующее: limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞
Таким образом, можно записать, что limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞.
Теперь берем таблицу пределов показательных функций с основаниями, большими 0, и получаем:
limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞=+∞
Ответ: limx→0(x2+2,5)1×2=+∞.
Далее мы приведем примеры решений задач на раскрытие неопределенностей с использованием метода преобразования. На практике выполнять это приходится довольно часто.
Вычислите предел limx→1×2-1x-1.
Решение
Выполняем подстановку значений.
limx→1×2-1x-1=12-11-1=00
В итоге у нас получилась неопределенность. Используем таблицу выше, чтобы выбрать метод решения. Там указано, что нужно выполнить упрощение выражения.
limx→1×2-1x-1=00=limx→1(x-1)·(x+1)x-1==limx→1(x-1)·(x+1)·(x+1)x-1=limx→1(x+1)·x-1==1+1·1-1=2·0=0
Как мы видим, упрощение привело к раскрытию неопределенности.
Ответ: limx→1×2-1x-1=0
Вычислите предел limx→3x-312-x-6+x.
Решение
Подставляем значение и получаем запись следующего вида.
limx→3x-312-x-6+x=3-312-3-6+3=09-9=00
Мы пришли к необходимости делить нуль на нуль, что является неопределенностью. Посмотрим нужный метод решения в таблице – это упрощение и преобразование выражения. Выполним дополнительное умножение числителя и знаменателя на сопряженное знаменателю выражение 12-x+6+x:
limx→3x-312-x-6+x=00=limx→3x-312-x+6+x12-x-6+x12-x+6+x
Домножение знаменателя выполняется для того, чтобы потом можно было воспользоваться формулой сокращенного умножения (разность квадратов) и выполнить сокращение.
limx→3x-312-x+6+x12-x-6+x12-x+6+x=limx→3x-312-x+6+x12-x2-6+x2=limx→3(x-3)12-x+6+x12-x-(6+x)==limx→3(x-3)12-x+6+x6-2x=limx→3(x-3)12-x+6+x-2(x-3)==limx→312-x+6+x-2=12-3+6+3-2=9+9-2=-9=-3
Как мы видим, в результате этих действий нам удалось избавиться от неопределенности.
Ответ: limx→3x-312-x-6+x=-3.
Важно отметить, что при решении подобных задач подход с использованием домножения используется очень часто, так что советуем запомнить, как именно это делается.
Вычислите предел limx→1×2+2x-33×2-5x+2.
Решение
Выполняем подстановку.
limx→1×2+2x-33×2-5x+2=12+2·1-33·12-5·1+2=00
В итоге у нас вышла неопределенность. Рекомендуемый способ решения задачи в таком случае – упрощение выражения. Поскольку при значении x, равном единице, числитель и знаменатель обращаются в 0, то мы можем разложить их на множители и потом сократить на х-1,и тогда неопределенность исчезнет.
Выполняем разложение числителя на множители:
x2+2x-3=0D=22-4·1·(-3)=16⇒x1=-2-162=-3×2=-2+162=1⇒x2+2x-3=x+3x-1
Теперь делаем то же самое со знаменателем:
3×2-5x+2=0D=-52-4·3·2=1⇒x1=5-12·3=23×2=5+12·3=1⇒3×2-5x+3=3x-23x-1
Мы получили предел следующего вида:
limx→1×2+2x-33×2-5x+2=00=limx→1x+3·x-13·x-23·x-1==limx→1x+33·x-23=1+33·1-23=4
Как мы видим, в ходе преобразования нам удалось избавиться от неопределенности.
Ответ: limx→1×2+2x-33×2-5x+2=4.
Далее нам нужно рассмотреть случаи пределов на бесконечности от степенных выражений. Если показатели этих выражений будут больше 0, то предел на бесконечности также окажется бесконечным. При этом основное значение имеет самая большая степень, а остальные можно не учитывать.
Например, limx→∞(x4+2×3-6)=limx→∞x4=∞ или limx→∞x4+4×3+21×2-115=limx→∞x45=∞.
Если под знаком предела у нас стоит дробь со степенными выражениями в числителе и знаменателе, то при x→∞ у нас возникает неопределенность вида ∞∞. Чтобы избавиться от этой неопределенности, нам нужно разделить числитель и знаменатель дроби на xmax(m,n). Приведем пример решения подобной задачи.
Вычислите предел limx→∞x7+2×5-43×7+12.
Решение
limx→∞x7+2×5-43×7+12=∞∞
Степени числителя и знаменателя равны 7. Делим их на x7 и получаем:
limx→∞x7+2×5-43×7+12=limx→∞x7+2×5-4x73x7+12×7==limx→∞1+2×2-4×73+12×7=1+2∞2-4∞73+12∞7=1+0-03+0=13
Ответ: limx→∞x7+2×5-43×7+12=13.
Вычислите предел limx→∞x8+113×2+x+1.
Решение
limx→∞x8+113×2+x+1=∞∞
Числитель имеет степень 83, а знаменатель 2. Выполним деление числителя и знаменателя на x83:
limx→∞x8+113×2+x+1=∞∞=limx→∞x8+113x83x2+x+1×83==limx→∞1+11x831x23+1×53+1×83=1+11∞31∞+1∞+1∞=1+030+0+0=10=∞
Ответ: limx→∞x8+113×2+x+1=∞.
Вычислите предел limx→∞x3+2×2-1×10+56×7+123.
Решение
limx→∞x3+2×2-1×10+56×7+123=∞∞
У нас есть числитель в степени 3 и знаменатель в степени 103. Значит, нам нужно разделить числитель и знаменатель на x103:
limx→∞x3+2×2-1×10+56×7+123=∞∞=limx→∞x3+2×2-1x103x10+56×7+123×103==limx→∞1×13+2×43-1×1031+56×3+12×103=1∞+2∞-1∞1+56∞+12∞3=0+0-01+0+03=0
Ответ: limx→∞x3+2×2-1×10+56×7+123=0.
Выводы
В случае с пределом отношений возможны три основных варианта:
-
Если степень числителя равна степени знаменателя, то предел будет равен отношению коэффициентов при старших степенях.
-
Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.
-
Если степень числителя меньше степени знаменателя, то предел будет равен нулю.
Другие методы раскрытия неопределенностей мы разберем в отдельных статьях.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Рассмотрим примеры, в которых, чтобы найти пределы функций, надо раскрыть неопределенность вида 0 на 0.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Примеры для самопроверки:
![]()
![]()
![]()
Показать решение
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание “чайникам” 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними – это не так страшно как кажется 🙂 |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её 🙂 Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате – это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное – возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!